Interaction of the Cosmic Dark Fluid with Dynamic Aether: Parametric Mechanism of Axion Generation in the Early Universe
Abstract
:1. Introduction
1.1. Motivation of the Work
1.1.1. Inflation vs. Super-Inflation
1.1.2. Dynamic Aether as a Guiding Element of the Cosmic Evolution
1.1.3. Interaction of the Dynamic Aether with Dark Fluid
1.1.4. The Role of Axionic Dark Matter in Our Approach
1.2. The Structure of the Work
2. The Formalism
2.1. The Total Action Functional
2.2. Auxiliary Elements of Analysis
2.3. Master Equations of the Model
2.3.1. Master Equations for the Unit Vector Field
2.3.2. Master Equation for the Axion Field
2.3.3. Master Equations for the Gravitational Field
2.3.4. Bianchi Identity and Conservation Law
3. Application to the Spatially Isotropic Homogeneous Cosmological Model
3.1. The Spacetime Platform and Reduced Master Equations
3.1.1. Solution to the Equations of the Vector Field
3.1.2. Reduced Equation for the Axion Field
3.1.3. Key Equations for the Gravity Field
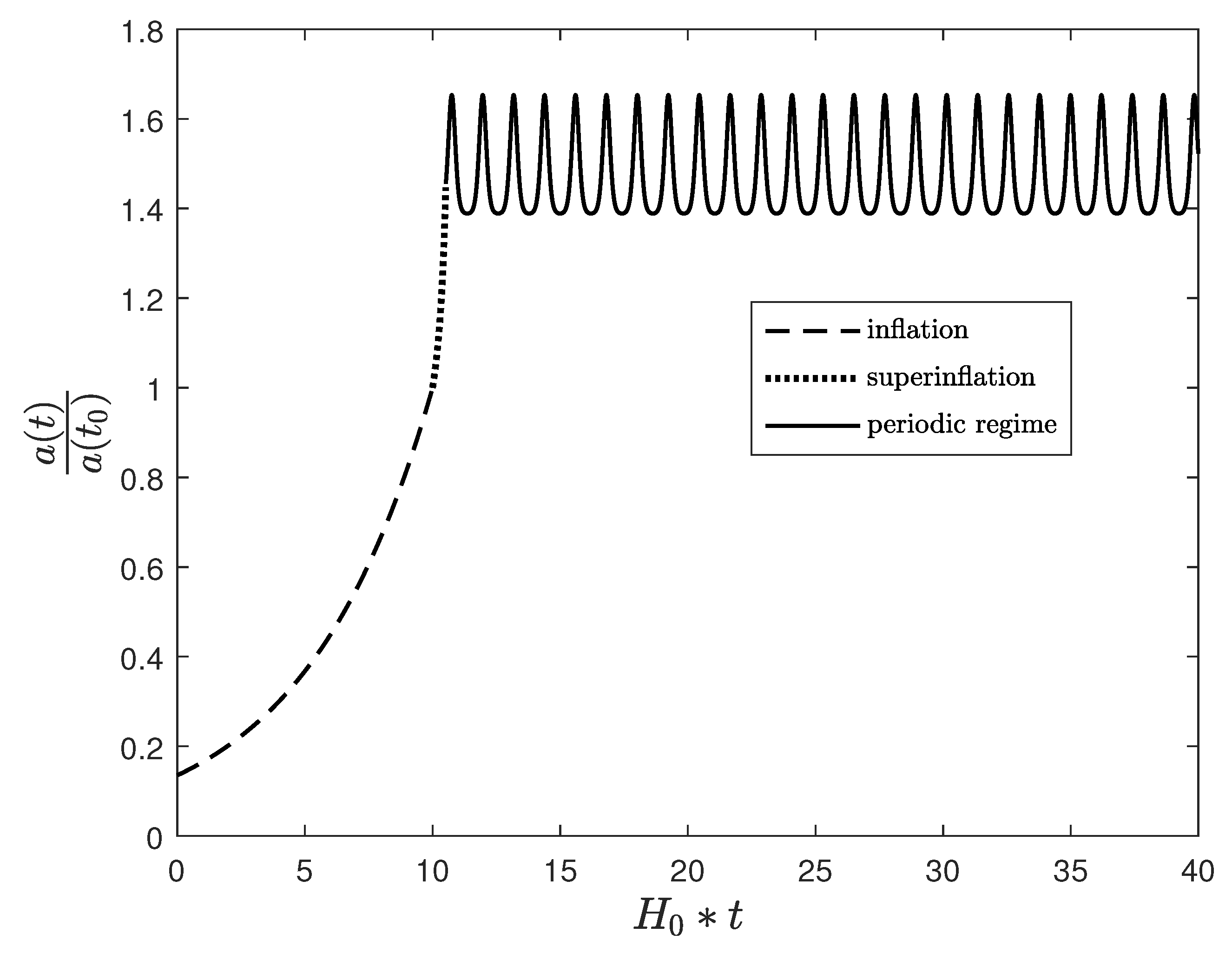
3.2. Super-Inflationary Scenario of Early Universe Evolution
3.2.1. Epoch of the Dark Fluid Domination
3.2.2. Exact Explicit Solutions in the Model of Super-Inflation
3.2.3. On the Stability of the Axion Field Configuration
3.3. Periodic Episode of the Early Universe Evolution
3.3.1. Modifications of the Model
3.3.2. Exact Solutions in the Periodic Model
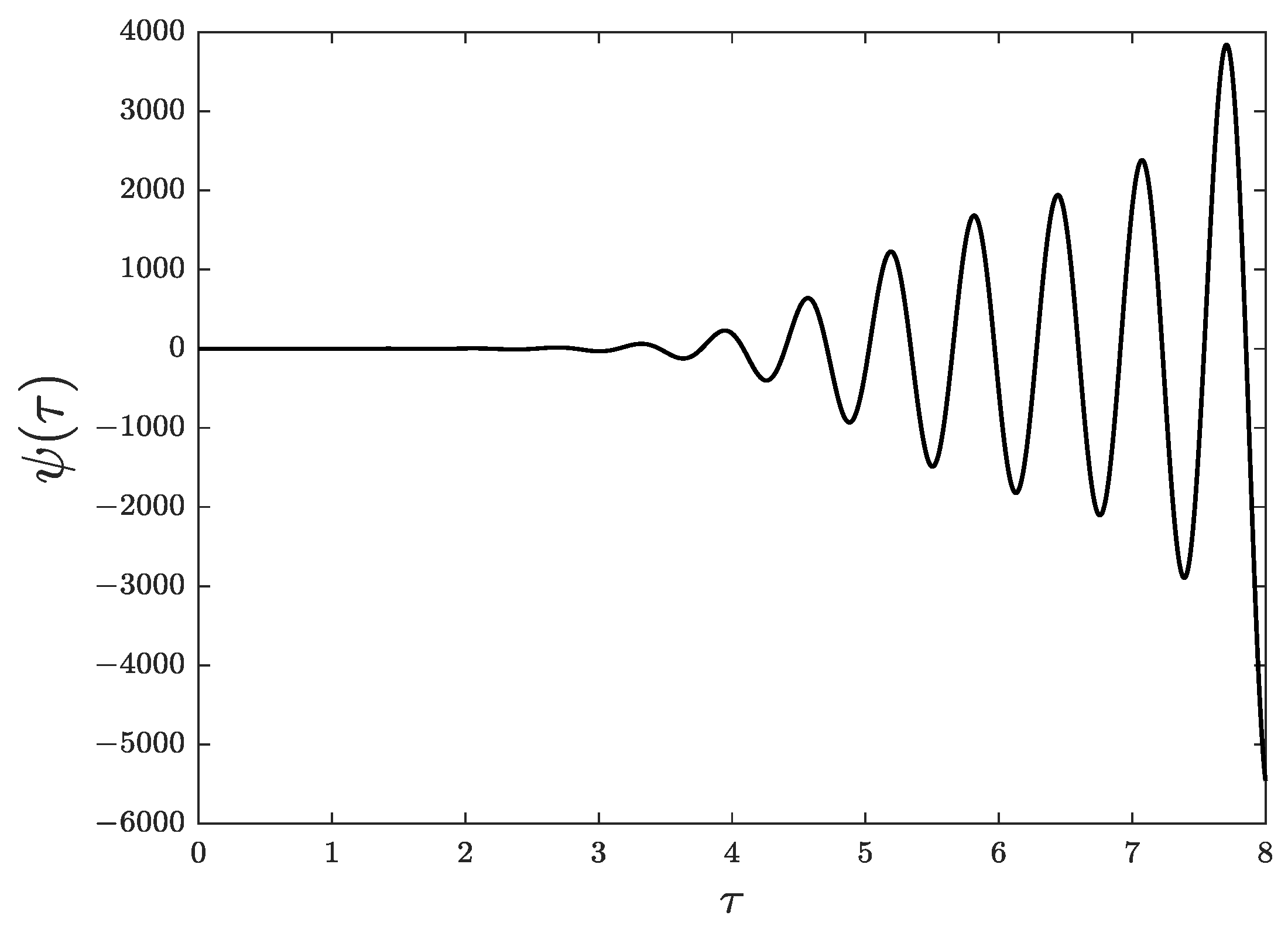
3.3.3. Parametric Generation of the Axion Field
3.4. Remark about the Post-Inflationary Stage of the Universe Evolution
3.4.1. Frozen Axion Field with Non-Vanishing Effective Cosmological Constant
3.4.2. Frozen Axion Field with Vanishing Effective Cosmological Constant
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weinberg, S. Gravitation and Cosmology; Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Diego, J.M.; Sun, B.; Yan, H.; Furtak, L.J.; Zackrisson, E.; Dai, L.; Kelly, P.; Nonino, M.; Adams, N.; Meena, A.K.; et al. JWST’s PEARLS: Mothra, a new kaiju star at z=2.091 extremely magnified by MACS0416, and implications for dark matter models. arXiv 2023, arXiv:2307.10363. [Google Scholar] [CrossRef]
- Spilker, J.S.; Phadke, K.A.; Aravena, M.; Archipley, M.; Bayliss, M.B.; Birkin, J.E.; Béthermin, M.; Burgoyne, J.; Cathey, J.; Chapman, S.C.; et al. Spatial variations in aromatic hydrocarbon emission in a dust-rich galaxy. Nature 2023, 618, 708–711. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, A.; Copeland, E.J.; Louko, J. Inflation in Loop Quantum Cosmology. Phys. Rev. D 2019, 99, 063520. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Causal limit of neutron star maximum mass in f(R) gravity in iew of GW190814. Phys. Lett. B 2021, 816, 136222. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V. Archimedean-type force in a cosmic dark fluid. I. Exact solutions for the late-time accelerated expansion. Phys. Rev. D 2011, 83, 024035. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V. Archimedean-type force in a cosmic dark fluid. III. Big Rip, Little Rip and Cyclic solutions. Phys. Rev. D 2013, 87, 024006. [Google Scholar] [CrossRef]
- Balakin, A.B.; Ilin, A.S. Dark Energy and Dark Matter Interaction: Kernels of Volterra Type and Coincidence Problem. Symmetry 2018, 10, 411. [Google Scholar] [CrossRef]
- Balakin, A.B.; Ilin, A.S. Self-interaction in a cosmic dark fluid: The four-kernel rheological extension of the equations of state. Phys. Rev. D 2022, 105, 103525. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle Dark Matter: Evidence, Candidates and Constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Gravity with a dynamical preferred frame. Phys. Rev. D 2001, 64, 024028. [Google Scholar] [CrossRef]
- Jacobson, T. Einstein-aether gravity: A status report. In Proceedings of the Workshop on from Quantum to Emergent Gravity: Theory and Phenomenology (QG-Ph), Trieste, Italy, 11–15 June 2007; p. 20. [Google Scholar]
- Jacobson, T.; Mattingly, D. Einstein-aether waves. Phys. Rev. D 2004, 70, 024003. [Google Scholar] [CrossRef]
- Heinicke, C.; Baekler, P.; Hehl, F.W. Einstein-aether theory, violation of Lorentz invariance, and metric-affine gravity. Phys. Rev. D 2005, 72, 025012. [Google Scholar] [CrossRef]
- Will, C.M.; Nordtvedt, K. Conservation laws and preferred frames in relativistic gravity. I. Preferred-frame theories and an extended PPN formalism. Astrophys. J. 1972, 177, 757. [Google Scholar] [CrossRef]
- Nordtvedt, K.; Will, C.M. Conservation laws and preferred frames in relativistic gravity. II. Experimental evidence to rule out preferred-frame theories of gravity. Astrophys. J. 1972, 177, 775–792. [Google Scholar] [CrossRef]
- Balakin, A.B.; Shakirzyanov, A.F. Axionic extension of the Einstein-aether theory: How does dynamic aether regulate the state of axionic dark matter? Phys. Dark Universe 2019, 24, 100283. [Google Scholar] [CrossRef]
- Balakin, A.B.; Shakirzyanov, A.F. Is the axionic Dark Matter an equilibrium System? Universe 2020, 6, 192. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP conservation in the presence of instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Weinberg, S. A new light boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Wei-Tou, N. Equivalence principles and electromagnetism. Phys. Rev. Lett. 1977, 38, 301–304. [Google Scholar]
- Sikivie, P. Experimental tests of the “invisible” axion. Phys. Rev. Lett. 1983, 51, 1415–1417. [Google Scholar] [CrossRef]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799–1802. [Google Scholar] [CrossRef] [PubMed]
- Duffy, L.D.; van Bibber, K. Axions as dark matter particles. New J. Phys. 2009, 11, 105008. [Google Scholar] [CrossRef]
- Khlopov, M. Fundamentals of Cosmic Particle Physics; Springer: Cambridge, UK, 2012. [Google Scholar]
- Del Popolo, A. Nonbaryonic dark matter in cosmology. Int. J. Mod. Phys. D 2014, 23, 1430005. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi Gamma-Ray Burst Monitor; INTEGRAL. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Zimdahl, W. Interacting dark energy and cosmological equations of state. Int. J. Mod. Phys. D 2005, 14, 2319–2326. [Google Scholar] [CrossRef]
- Del Campo, S.; Herrera, R.; Pavon, D. Interaction in the Dark Sector. Phys. Rev. D 2015, 91, 123539. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1995; 814p. [Google Scholar]
- Floquet, G. Sur les équations différentielles linéaires à coefficients périodiques. Ann. Sci. L’École Norm. Supér. 1883, 12, 47–88. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Far`ese, G. Tensor-scalar gravity and binary-pulsars experiments. Phys. Rev. D 1996, 54, 1474. [Google Scholar] [CrossRef] [PubMed]
- Oikonomou, V.K. Kinetic Axion F(R) Gravity Inflation. Phys. Rev. D 2022, 106, 044041. [Google Scholar] [CrossRef]
- Salgado, M.; Sudarsky, D.; Nucamendi, U. On spontaneous scalarization. Phys. Rev. D 1998, 58, 124003. [Google Scholar] [CrossRef]
- Ramazanoglu, F.M.; Pretorius, F. Spontaneous scalarization with massive fields. Phys. Rev. D 2016, 93, 064005. [Google Scholar] [CrossRef]
- Ramazanoglu, F.M. Spontaneous growth of vector fields in gravity. Phys. Rev. D 2017, 96, 064009. [Google Scholar] [CrossRef]
- Annulli, L.; Cardoso, V.; Gualtieri, L. Electromagnetism and hidden vector fields in modified gravity theories: Spontaneous and induced vectorization. Phys. Rev. D 2019, 99, 044038. [Google Scholar] [CrossRef]
- Ramazanoglu, F.M. Spontaneous tensorization from curvature coupling and beyond. Phys. Rev. D 2019, 99, 084015. [Google Scholar] [CrossRef]
- Ramazanoglu, F.M. Spontaneous growth of spinor fields in gravity. Phys. Rev. D 2018, 98, 044011. [Google Scholar] [CrossRef]
- Balakin, A.B.; Kiselev, G.B. Einstein-Yang-Mills-aether theory with nonlinear axion field: Decay of color aether and the axionic dark matter production. Symmetry 2022, 14, 1621. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying inflation with early and late-time dark energy in F(R) gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Unifying of inflation with early and late dark energy epochs in axion F(R) gravity. Phys. Rev. D 2021, 103, 044036. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of inflation with dark energy in f(R) Gravity and axion dark matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Aspects of axion F(R) gravity. Europhys. Lett. 2020, 129, 40001. [Google Scholar] [CrossRef]
- Koutvitsky, V.A.; Maslov, E.M. Analytical study of the parametric instability of an oscillating scalar field in an expanding universe. J. Math. Phys. 2018, 59, 113504. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balakin, A.; Ilin, A.; Shakirzyanov, A. Interaction of the Cosmic Dark Fluid with Dynamic Aether: Parametric Mechanism of Axion Generation in the Early Universe. Symmetry 2023, 15, 1824. https://doi.org/10.3390/sym15101824
Balakin A, Ilin A, Shakirzyanov A. Interaction of the Cosmic Dark Fluid with Dynamic Aether: Parametric Mechanism of Axion Generation in the Early Universe. Symmetry. 2023; 15(10):1824. https://doi.org/10.3390/sym15101824
Chicago/Turabian StyleBalakin, Alexander, Alexei Ilin, and Amir Shakirzyanov. 2023. "Interaction of the Cosmic Dark Fluid with Dynamic Aether: Parametric Mechanism of Axion Generation in the Early Universe" Symmetry 15, no. 10: 1824. https://doi.org/10.3390/sym15101824
APA StyleBalakin, A., Ilin, A., & Shakirzyanov, A. (2023). Interaction of the Cosmic Dark Fluid with Dynamic Aether: Parametric Mechanism of Axion Generation in the Early Universe. Symmetry, 15(10), 1824. https://doi.org/10.3390/sym15101824






