Phonon Blockade in Parametrically Pumped Acoustic Cavity at Finite Temperature
Abstract
1. Introduction
2. Model and Analysis
3. Quantum Statistics of Phonon Mode
3.1. Phonon Blockade Effect at Zero Temperature
3.2. Phonon Blockade Effect at Finite Temperature
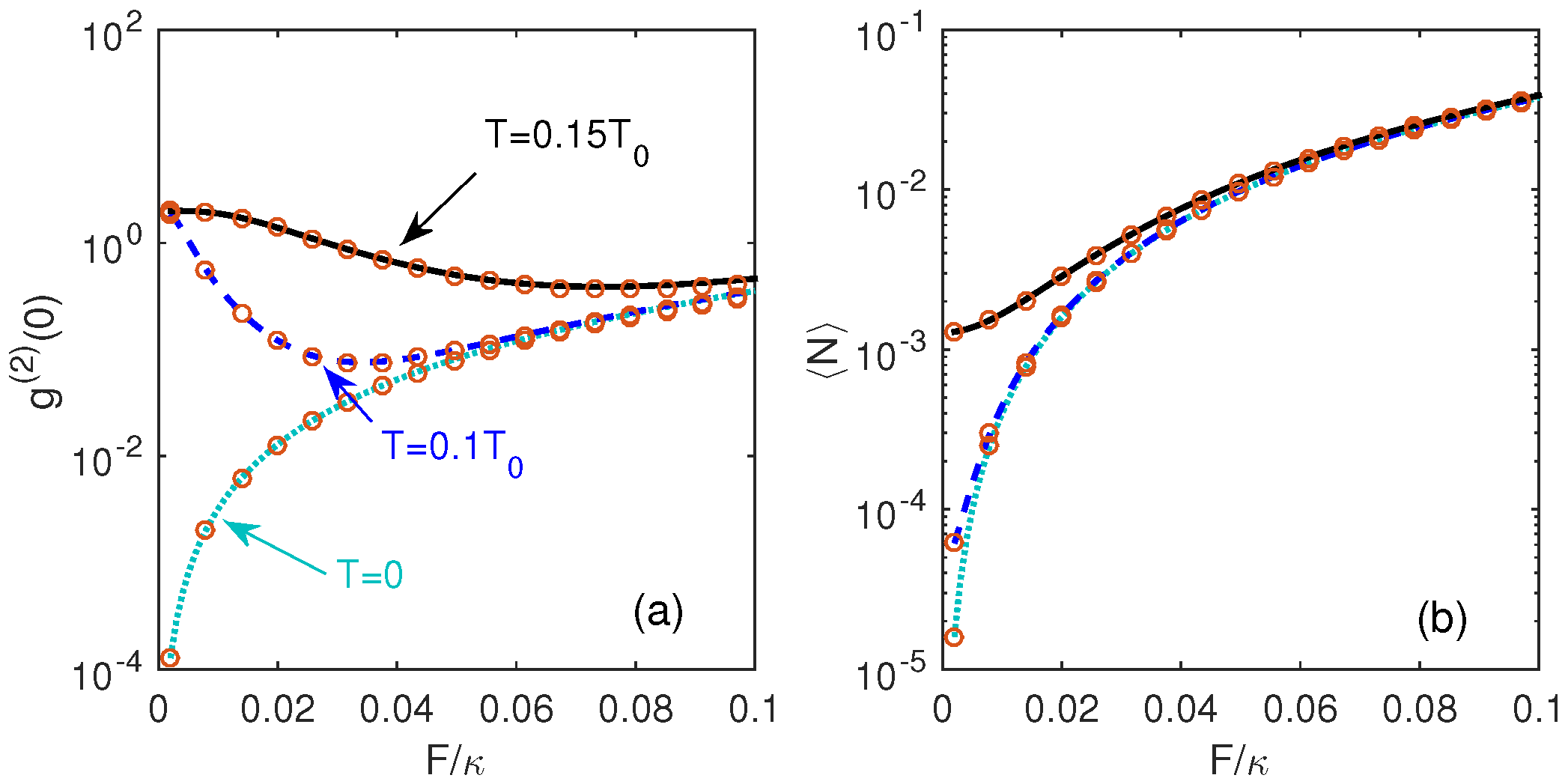
4. Quantum Statistics of Phonons with Monte Carlo Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Sklan, S.R. Splash, pop, sizzle: Information processing with phononic computing. AIP Adv. 2015, 5, 053302. [Google Scholar] [CrossRef]
- Meher, N. A proposal for the implementation of quantum gates in an optomechanical system via phonon blockade. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 205502. [Google Scholar] [CrossRef]
- Zhao, C.; Peng, R.; Yang, Z.; Chao, S.; Li, C.; Zhou, L. Atom Mediated Phonon Blockade and Controlled Z Gate in Superconducting Circuit System. Ann. Phys. 2021, 533, 2100039. [Google Scholar] [CrossRef]
- Cardenas-Lopez, F.; Romero, G.; Lamata, L.; Solano, E.; Retamal, J. Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics. Symmetry 2019, 11, 372. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, X.; Tang, S. Realization of Quantum Swap Gate and Generation of Entangled Coherent States. Symmetry 2022, 14, 1951. [Google Scholar] [CrossRef]
- Liu, Y.X.; Miranowicz, A.; Gao, Y.B.; Bajer, J.; Sun, C.P.; Nori, F. Qubit-induced phonon blockade as a signature of quantum behavior in nanomechanical resonators. Phys. Rev. A 2010, 82, 032101. [Google Scholar] [CrossRef]
- Cai, K.; Pan, Z.W.; Wang, R.X.; Ruan, D.; Yin, Z.Q.; Long, G.L. Single phonon source based on a giant polariton nonlinear effect. Opt. Lett. 2018, 43, 1163–1166. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Lambert, N.; Liu, Y.X.; Nori, F. Tunable multiphonon blockade in coupled nanomechanical resonators. Phys. Rev. A 2016, 93, 013808. [Google Scholar] [CrossRef]
- Xu, X.W.; Chen, A.X.; Liu, Y.X. Phonon blockade in a nanomechanical resonator resonantly coupled to a qubit. Phys. Rev. A 2016, 94, 063853. [Google Scholar] [CrossRef]
- Didier, N.; Pugnetti, S.; Blanter, Y.M.; Fazio, R. Detecting phonon blockade with photons. Phys. Rev. B 2011, 84, 054503. [Google Scholar] [CrossRef]
- Ramos, T.; Sudhir, V.; Stannigel, K.; Zoller, P.; Kippenberg, T.J. Nonlinear quantum optomechanics via individual intrinsic two-level defects. Phys. Rev. Lett. 2013, 110, 193602. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Miranowicz, A.; Li, H.R.; Nori, F. Method for observing robust and tunable phonon blockade in a nanomechanical resonator coupled to a charge qubit. Phys. Rev. A 2016, 93, 063861. [Google Scholar] [CrossRef]
- Guan, S.; Bowen, W.P.; Liu, C.; Duan, Z. Phonon antibunching effect in coupled nonlinear micro/nanomechanical resonator at finite temperature. EPL 2017, 119, 58001. [Google Scholar] [CrossRef]
- Sarma, B.; Sarma, A.K. Tunable phonon blockade in weakly nonlinear coupled mechanical resonators via Coulomb interaction. Sci. Rep. 2018, 8, 14583. [Google Scholar] [CrossRef]
- Shi, H.Q.; Zhou, X.T.; Xu, X.W.; Liu, N.H. Tunable phonon blockade in quadratically coupled optomechanical systems. Sci. Rep. 2018, 8, 2212. [Google Scholar] [CrossRef]
- Shi, H.Q.; Xie, Z.Q.; Xu, X.W.; Liu, N.H. Unconventional phonon blockade in multimode optomechanical system. Acta Phys. Sin. 2018, 67, 044203. [Google Scholar] [CrossRef]
- Yang, J.-Y.; Jin, Z.; Liu, J.-S.; Wang, H.-F.; Zhu, A.D. Unconventional Phonon Blockade in a Tavis–Cummings Coupled Optomechanical System. Ann. Phys. 2020, 532, 2000299. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Chao, S.; Peng, R.; Li, C.; Zhou, L. Simultaneous blockade of a photon, phonon, and magnon induced by a two-level atom. Phys. Rev. A 2020, 101, 063838. [Google Scholar] [CrossRef]
- Nema, J.K.; Gupta, S.; Thakkar, R.; Rajagopal, P. Novel hermetically sealed device to realize unconventional phonon blockade at near-micron dimensions and milliKelvin temperatures. AIP Adv. 2021, 11, 015112. [Google Scholar] [CrossRef]
- Wang, M.; Yin, T.-S.; Sun, Z.-Y.; Cheng, H.-G.; Zhan, B.-F.; Zheng, L.-L. Unconventional phonon blockade via atom-photon-phonon interaction in hybrid optomechanical systems. Opt. Express 2022, 30, 10251–10268. [Google Scholar] [CrossRef]
- Zeng, Y.X.; Gebremariam, T.; Shen, J.; Xiong, B.; Li, C. Application of machine learning for predicting strong phonon blockade. Appl. Phys. Lett. 2021, 118, 164003. [Google Scholar] [CrossRef]
- Restrepo, J.; Favero, I.; Ciuti, C. Fully coupled hybrid cavity optomechanics: Quantum interferences and correlations. Phys. Rev. A 2017, 95, 023832. [Google Scholar] [CrossRef]
- Xie, H.; Liao, C.-G.; Shang, X.; Ye, M.Y.; Lin, X.M. Phonon blockade in a quadratically coupled optomechanical system. Phys. Rev. A 2017, 96, 013861. [Google Scholar] [CrossRef]
- Xu, X.-W.; Shi, H.-Q.; Chen, A.-X.; Liu, Y.-X. Cross-correlation between photons and phonons in quadratically coupled optomechanical systems. Phys. Rev. A 2018, 98, 013821. [Google Scholar] [CrossRef]
- Yao, X.-Y.; Ali, H.; Li, F.-L.; Li, P.-B. Nonreciprocal Phonon Blockade in a Spinning Acoustic Ring Cavity Coupled to a Two-Level System. Phys. Rev. Appl. 2022, 17, 054004. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Jin, G.-R.; Yin, T.-S.; Chen, A.X. Two-phonon blockade in quadratically coupled optomechanical systems. Photonics 2022, 9, 70. [Google Scholar] [CrossRef]
- Kowalewska-Kudlaszyk, A.; Abo, S.I.; Chimczak, G.; Perina, J.; Nori, F.; Miranowicz, A. Two-photon blockade and photon-induced tunneling generated by squeezing. Phys. Rev. A 2019, 100, 053857. [Google Scholar] [CrossRef]
- LaHaye, M.D.; Buu, O.; Camarota, B.; Schwab, K.C. Approaching the quantum limit of a nanomechanical resonator. Science 2004, 304, 74–77. [Google Scholar] [CrossRef]
- Schwab, K.C.; Roukes, M.L. Putting mechanics into quantum mechanics. Phys. Today 2005, 58, 36–42. [Google Scholar] [CrossRef]
- Carmon, T.; Rokhsari, H.; Yang, L.; Kippenberg, T.J.; Vahala, K.J. Temporal behavior of radiation-pressure-induced vibrations of an optical microcavity phonon mode. Phys. Rev. Lett. 2005, 94, 223902. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.-Y.; Cheng, Y.-B.; Guan, S.-G.; Yu, D.-Y.; Duan, Z. Pulse-regulated single-photon generation via quantum interference in a χ(2) nonlinear nanocavity. Opt. Lett. 2018, 43, 5086–5089. [Google Scholar] [CrossRef] [PubMed]
- Lemonde, M.-A.; Didier, N.; Clerk, A.A. Enhanced nonlinear interactions in quantum optomechanics via mechanical amplification. Nat. Commun. 2016, 7, 11338. [Google Scholar] [CrossRef]
- Li, P.-B.; Zhou, Y.; Gao, W.-B.; Nori, F. Enhancing spin-phonon and spin-spin interactions using linear resources in a hybrid quantum system. Phys. Rev. Lett. 2020, 125, 153602. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.-L.; Han, J.-X.; Xia, Y.; Jiang, Y.-Y.; Song, J. Enhanced phonon blockade in a weakly coupled hybrid system via mechanical parametric amplification. Phys. Rev. Appl. 2022, 17, 024009. [Google Scholar] [CrossRef]
- Szorkovszky, A.; Brawley, G.A.; Doherty, A.C.; Bowen, W.P. Strong thermomechanical squeezing via weak measurement. Phys. Rev. Lett. 2013, 110, 184301. [Google Scholar] [CrossRef] [PubMed]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.-X.; Zagoskin, A.M.; Nori, F. State-dependent photon blockade via quantum-reservoir engineering. Phys. Rev. A 2014, 90, 033831. [Google Scholar] [CrossRef]
- Kimble, H.J.; Dagenais, M.; Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 1977, 39, 691. [Google Scholar] [CrossRef]
- Meiser, D.; Holland, M.J. Intensity fluctuations in steady-state superradiance. Phys. Rev. A 2010, 81, 063827. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P. Quantum Noise; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Z.; Shao, Y.; Ren, Y.; Huang, B. Phonon Blockade in Parametrically Pumped Acoustic Cavity at Finite Temperature. Symmetry 2023, 15, 245. https://doi.org/10.3390/sym15010245
Duan Z, Shao Y, Ren Y, Huang B. Phonon Blockade in Parametrically Pumped Acoustic Cavity at Finite Temperature. Symmetry. 2023; 15(1):245. https://doi.org/10.3390/sym15010245
Chicago/Turabian StyleDuan, Zhenglu, Yongkang Shao, Yi Ren, and Biao Huang. 2023. "Phonon Blockade in Parametrically Pumped Acoustic Cavity at Finite Temperature" Symmetry 15, no. 1: 245. https://doi.org/10.3390/sym15010245
APA StyleDuan, Z., Shao, Y., Ren, Y., & Huang, B. (2023). Phonon Blockade in Parametrically Pumped Acoustic Cavity at Finite Temperature. Symmetry, 15(1), 245. https://doi.org/10.3390/sym15010245





