Dynamical Stability in a Non-Hermitian Kicked Rotor Model
Abstract
1. Introduction
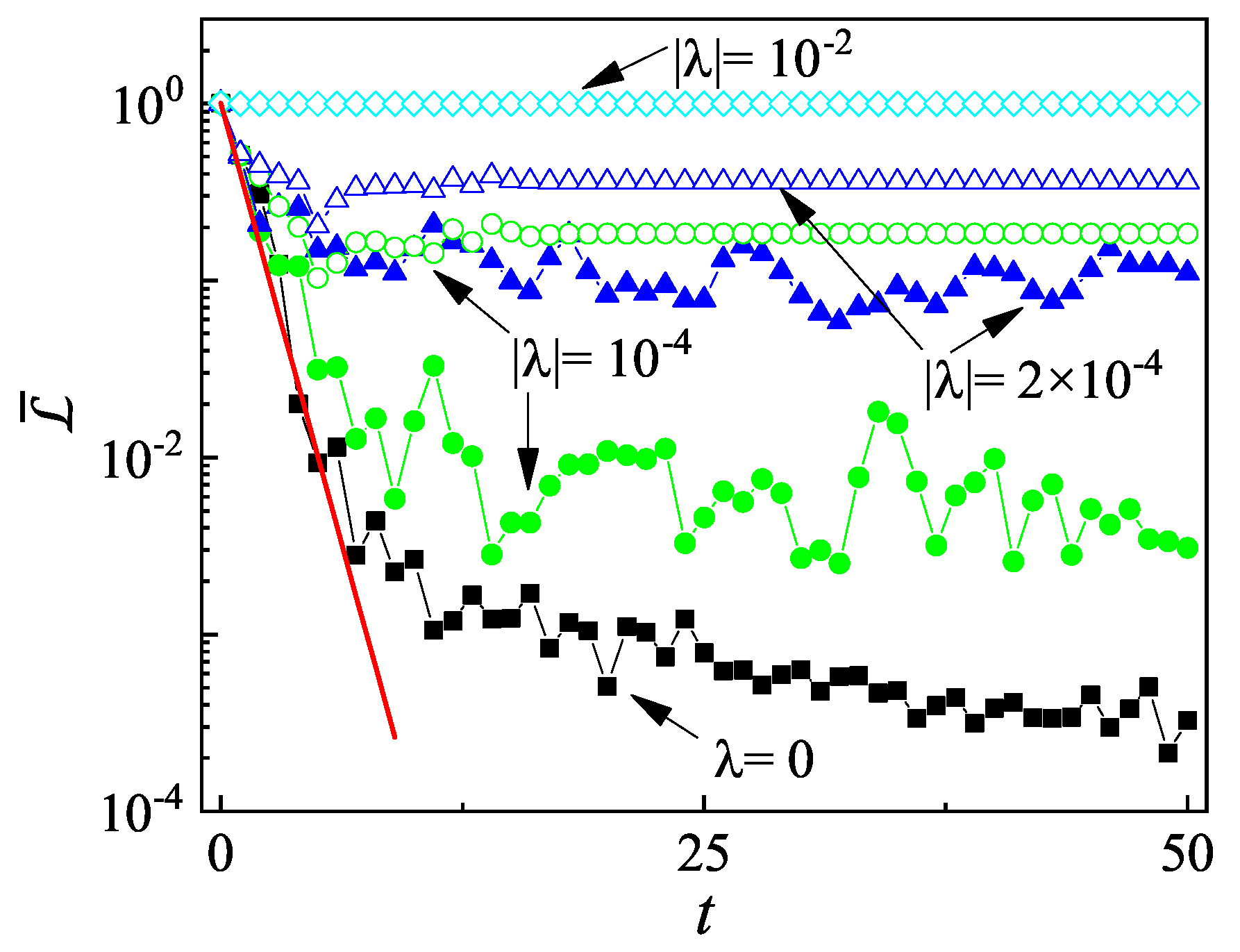
2. Dynamical Stability Induced by Non-Hermitian Driven Potential
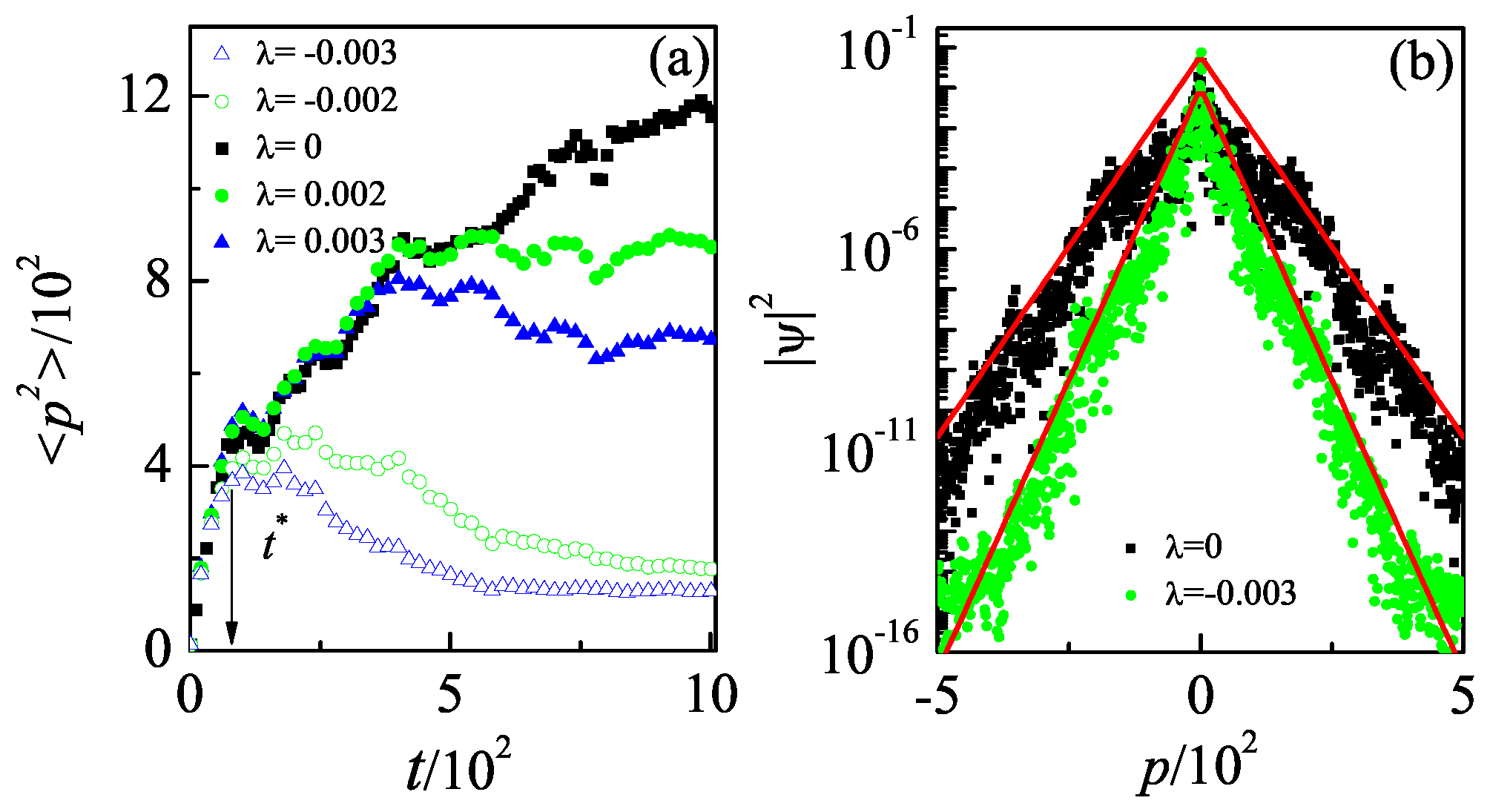
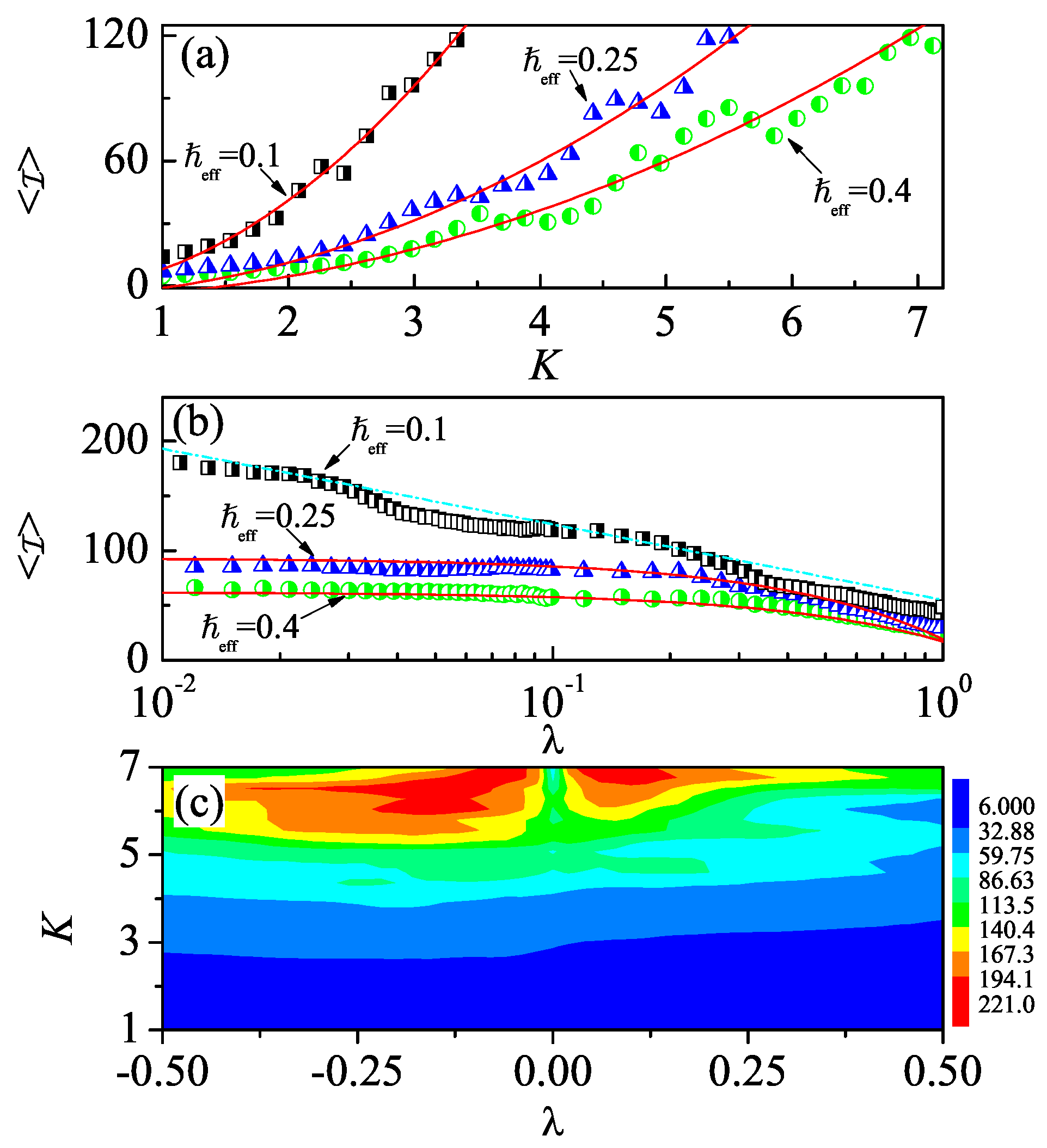
3. Enhancement of Dynamical Localization by Non-Hermitian Driven Potential
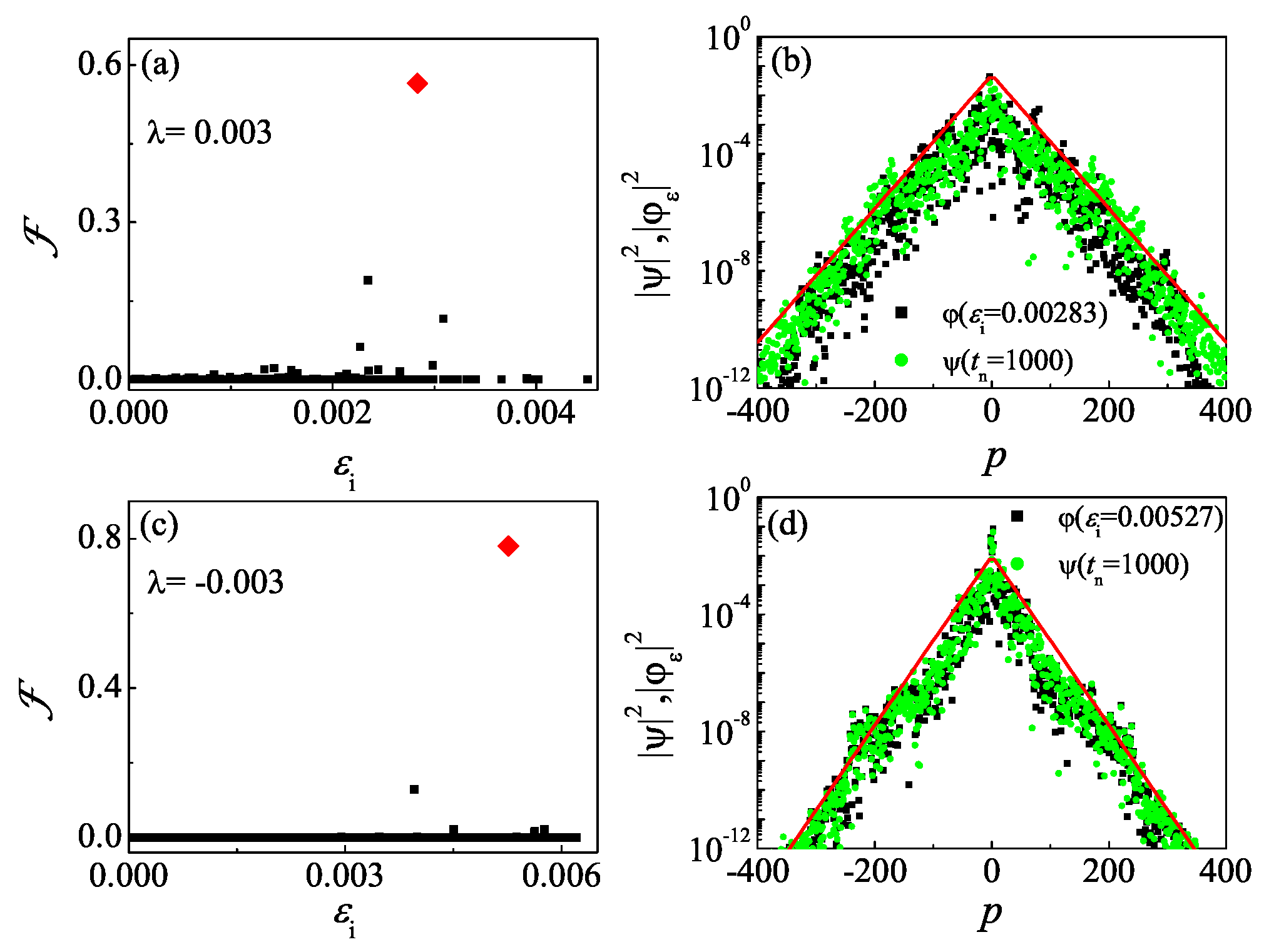
4. Mechanism of the Enhancement of Dynamical Localization by Non-Hermiticity
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haake, F. Quantum Signatures of Chaos, 3rd ed.; Springer Series in Synergetics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Wang, W.G.; He, L.W.; Gong, J. Preferred States of Decoherence under Intermediate System-Environment Coupling. Phys. Rev. Lett. 2012, 108, 070403. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.G.; Li, B.W. Uniform semiclassical approach to fidelity decay: From weak to strong perturbation. Phys. Rev. E 2005, 71, 066203. [Google Scholar] [CrossRef] [PubMed]
- Cao, A.; Sajjad, R.; Mas, H.; Simmons, E.Q.; Tanlimco, J.L.; Nolasco-Martinez, E.; Shimasaki, T.; Kondakci, H.E.; Galitski, V.; Weld, D.M. Interaction-driven breakdown of dynamical localization in a kicked quantum gas. Nat. Phys. 2022, 18, 1302. [Google Scholar] [CrossRef]
- Martinez, M.; Larré, P.; Delande, D.; Cherroret, N. Low-energy prethermal phase and crossover to thermalization in nonlinear kicked rotors. Phys. Rev. A 2022, 106, 043304. [Google Scholar] [CrossRef]
- Peres, A. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 1984, 30, 1610. [Google Scholar] [CrossRef]
- Casati, G.; Chirikov, B.V.; Izrailev, F.M.; Ford, J. Lecture Notes in Physics; Springer: Berlin, Germany, 1979; Volume 90, p. 334. [Google Scholar]
- Fishman, S.; Grempel, D.R.; Prange, R.E. Chaos, Quantum Recurrences, and Anderson Localization. Phys. Rev. Lett. 1982, 49, 509. [Google Scholar] [CrossRef]
- Santhanam, M.S.; Paul, S.; Kannan, J.B. Quantum kicked rotor and its variants: Chaos, localization and beyond. Phys. Rep. 2022, 956, 1. [Google Scholar] [CrossRef]
- Wang, W.G.; Casati, G.; Li, B.W. Stability of quantum motion: Beyond Fermi-golden-rule and Lyapunov decay. Phys. Rev. E 2004, 69, 025201(R). [Google Scholar] [CrossRef]
- Hainaut, C.; Fang, P.; Rançon, A.; Clément, J.F.; Szriftgiser, P.; Garreau, J.C.; Tian, C.; Chicireanu, R. Experimental Observation of a Time-Driven Phase Transition in Quantum Chaos. Phys. Rev. Lett. 2018, 121, 134101. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Gu, Y.; Gong, J. Dual topological characterization of non-Hermitian Floquet phases. Phys. Rev. B 2021, 103, L041404. [Google Scholar] [CrossRef]
- Gong, J.; Wang, Q. Time-dependent -symmetric quantum mechanics. J. Phys. A Math. Theor. 2013, 46, 485302. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Sheng, J.; Yang, L.; Miri, M.A.; Christodoulides, D.N.; He, B.; Zhang, Y.; Xiao, M. Observation of Parity-Time Symmetry in Optically Induced Atomic Lattices. Phys. Rev. Lett. 2016, 117, 123601. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Harter, A.K.; Liu, J.; Melo, L.; Joglekar, Y.N.; Luo, L. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun. 2019, 10, 855. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.M.; Guo, C.X.; Yang, M.L.; Liu, W.M.; Kou, S.P. Anomalous non-Abelian statistics for non-Hermitian generalization of Majorana zero modes. Phys. Rev. B 2021, 104, 214502. [Google Scholar] [CrossRef]
- Yu, Z.F.; Xue, J.K.; Zhuang, L.; Zhao, J.; Liu, W.M. Non-Hermitian spectrum and multistability in exciton-polariton condensates. Phys. Rev. B 2021, 104, 235408. [Google Scholar] [CrossRef]
- Zhao, X.M.; Guo, C.X.; Kou, S.P.; Zhuang, L.; Liu, W.M. Defective Majorana zero modes in a non-Hermitian Kitaev chain. Phys. Rev. B 2021, 104, 205131. [Google Scholar] [CrossRef]
- Hu, H.; Sun, S.; Chen, S. Knot topology of exceptional point and non-Hermitian no-go theorem. Phys. Rev. Res. 2022, 4, L022064. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Gullans, M.J. Entanglement and Purification Transitions in Non-Hermitian Quantum Mechanics. Phys. Rev. Lett. 2021, 126, 170503. [Google Scholar] [CrossRef]
- Pires, D.P.; Macrì, T. Probing phase transitions in non-Hermitian systems with multiple quantum coherences. Phys. Rev. B 2021, 104, 155141. [Google Scholar] [CrossRef]
- Bergholtz, E.J.; Budich, J.C.; Kunst, F.K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 2021, 93, 015005. [Google Scholar] [CrossRef]
- Zou, D.; Chen, T.; He, W.; Bao, J.; Lee, C.H.; Sun, H.; Zhang, X. Observation of hybrid higher-order skin-topological effect in non-Hermitian topolectrical circuits. Nat. Commun. 2021, 12, 7201. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Hang, C.; He, Y.; Bai, Z.; Jiao, Y.; Huang, G.; Zhao, J.; Jia, S. Experimental observation of partial parity-time symmetry and its phase transition with a laser-driven cesium atomic gas. Phys. Rev. A 2022, 105, 053516. [Google Scholar] [CrossRef]
- Budich, C.; Bergholtz, E.J. Non-Hermitian Topological Sensors. Phys. Rev. Lett. 2020, 125, 180403. [Google Scholar] [CrossRef] [PubMed]
- McDonald, A.; Clerk, A.A. Exponentially-enhanced quantum sensing with non-Hermitian lattice dynamics. Nat. Commun. 2020, 11, 5382. [Google Scholar] [CrossRef]
- Dai, C.; Shi, Z.; Yi, X. Floquet theorem with open systems and its applications. Phys. Rev. A 2016, 93, 032121. [Google Scholar] [CrossRef]
- Xiao, L.; Deng, T.; Wang, K.; Wang, K.; Zhu, G.; Wang, Z.; Yi, W.; Xue, P. Non-Hermitian bulk–boundary correspondence in quantum dynamics. Nat. Phys. 2020, 16, 761–766. [Google Scholar] [CrossRef]
- West, C.T.; Kottos, T.; Prosen, T. -Symmetric Wave Chaos. Phys. Rev. Lett. 2010, 104, 054102. [Google Scholar] [CrossRef]
- Zhao, W.L.; Wang, J.; Wang, X.; Tong, P. Directed momentum current induced by the -symmetric driving. Phys. Rev. E 2019, 99, 042201. [Google Scholar] [CrossRef]
- Zhao, W.L. Quantization of out-of-time-ordered correlators in non-Hermitian chaotic systems. Phys. Rev. Res. 2022, 4, 023004. [Google Scholar] [CrossRef]
- Zhao, W.L.; Zhou, L.W.; Liu, J.; Tong, P.; Huang, K.Q. Superexponential diffusion in nonlinear non-Hermitian systems. Phys. Rev. A 2020, 102, 062213. [Google Scholar] [CrossRef]
- Haug, F.; Bienert, M.; Schleich, W.P.; Seligman, T.H.; Raizen, M.G. Motional stability of the quantum kicked rotor: A fidelity approach. Phys. Rev. A 2015, 71, 043803. [Google Scholar] [CrossRef]
- Shrestha, R.K.; Wimberger, S.; Ni, J.; Lam, W.K.; Summy, G.S. Fidelity of the quantum δ-kicked accelerator. Phys. Rev. E 2013, 87, 020902. [Google Scholar] [CrossRef] [PubMed]
- Probst, B.; Dubertrand, R.; Wimberger, S. Fidelity of the near-resonant quantum kicked rotor. J. Phys. A Math. Theor. 2011, 44, 335101. [Google Scholar] [CrossRef]
- Chirikov, B.V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 1979, 52, 263. [Google Scholar] [CrossRef]
- Fishman, S.; Prange, R.E.; Griniasty, M. Scaling theory for the localization length of the kicked rotor. Phys. Rev. A 1989, 39, 1628. [Google Scholar] [CrossRef] [PubMed]
- Satpathi, U.; Sinha, S.; Sorkin, R.D. A quantum diffusion law. J. Stat. Mech. 2017, 2017, 123105. [Google Scholar] [CrossRef]
- Shepelyansky, D.L. Some statistical properties of simple classically stochastic quantum systems. Phys. D 1983, 8, 208. [Google Scholar] [CrossRef]
- Shirley, J.H. Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time. Phys. Rev. 1965, 138, B979. [Google Scholar] [CrossRef]
- Sambe, H. Steady States and Quasienergies of a Quantum-Mechanical System in an Oscillating Field. Phys. Rev. A 1973, 7, 2203. [Google Scholar] [CrossRef]
- Longhi, S. Localization, quantum resonances, and ratchet acceleration in a periodically kicked -symmetric quantum rotator. Phys. Rev. A 2017, 95, 012125. [Google Scholar] [CrossRef]
- Edwards, J.T.; Thouless, D.J. Numerical studies of localization in disordered systems. J. Phys. C Solid State Phys. 1972, 5, 807. [Google Scholar] [CrossRef]
- Izrailev, F. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299. [Google Scholar] [CrossRef]
- Keser, A.C.; Ganeshan, S.; Refael, G.; Galitski, V. Dynamical many-body localization in an integrable model. Phys. Rev. B 2016, 94, 085120. [Google Scholar] [CrossRef]
- Rozenbaum, E.B.; Galitski, V. Dynamical localization of coupled relativistic kicked rotors. Phys. Rev. B 2017, 95, 064303. [Google Scholar] [CrossRef]
- Čadež, T.; Mondaini, R.; Sacramento, P.D. Dynamical localization and the effects of aperiodicity in Floquet systems. Phys. Rev. B 2017, 96, 144301. [Google Scholar] [CrossRef]
- Harper, F.; Roy, R.; Rudner, M.S.; Sondhi, S.L. Topology and Broken Symmetry in Floquet Systems. Annu. Rev. Condens. Matter Phys. 2020, 11, 345–368. [Google Scholar] [CrossRef]
- Liang, H.; Li, L. Topological properties of non-Hermitian Creutz ladders. Chin. Phys. B 2022, 31, 010310. [Google Scholar] [CrossRef]
- Zhou, L.; Gu, Y. Topological delocalization transitions and mobility edges in the nonreciprocal Maryland model. J. Phys. Condens. Matter 2022, 34, 115402. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Bukov, M. Thermalization and prethermalization in periodically kicked quantum spin chains. Phys. Rev. B 2021, 103, 144307. [Google Scholar] [CrossRef]
- Xu, J.; Zhong, C.; Han, X.; Jin, D.; Jiang, L.; Zhang, X. Floquet Cavity Electromagnonics. Phys. Rev. Lett. 2020, 125, 237201. [Google Scholar] [CrossRef]
- Kumar, U.; Banerjee, S.; Lin, S. Floquet engineering of Kitaev quantum magnets. Commun. Phys. 2022, 5, 157. [Google Scholar] [CrossRef]
- Quito, V.L.; Flint, R. Floquet Engineering Correlated Materials with Unpolarized Light. Phys. Rev. Lett. 2021, 126, 177201. [Google Scholar] [CrossRef] [PubMed]
- Topp, G.E.; Jotzu, G.; McIver, J.W.; Xian, L.; Rubio, A.; Sentef, M.A. Topological Floquet engineering of twisted bilayer graphene. Phys. Rev. Res. 2019, 1, 023031. [Google Scholar] [CrossRef]
- Menu, R.; Roscilde, T. Anomalous Diffusion and Localization in a Positionally Disordered Quantum Spin Array. Phys. Rev. Lett. 2020, 124, 130604. [Google Scholar] [CrossRef] [PubMed]
- Bitter, M.; Milner, V. Control of quantum localization and classical diffusion in laser-kicked molecular rotors. Phys. Rev. A 2017, 95, 013401. [Google Scholar] [CrossRef]
- Paul, N.; Amir, A. Quantum diffusion in the strong tunneling regime. Phys. Rev. B 2019, 100, 024110. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Zhang, H. Dynamical Stability in a Non-Hermitian Kicked Rotor Model. Symmetry 2023, 15, 113. https://doi.org/10.3390/sym15010113
Zhao W, Zhang H. Dynamical Stability in a Non-Hermitian Kicked Rotor Model. Symmetry. 2023; 15(1):113. https://doi.org/10.3390/sym15010113
Chicago/Turabian StyleZhao, Wenlei, and Huiqian Zhang. 2023. "Dynamical Stability in a Non-Hermitian Kicked Rotor Model" Symmetry 15, no. 1: 113. https://doi.org/10.3390/sym15010113
APA StyleZhao, W., & Zhang, H. (2023). Dynamical Stability in a Non-Hermitian Kicked Rotor Model. Symmetry, 15(1), 113. https://doi.org/10.3390/sym15010113



