Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques
Abstract
1. Introduction
2. Preliminaries
2.1. Definition
2.2. Definition
2.3. Definition
2.4. Definition
3. General Implementation of the HPTM
4. General Implementation of the YTDM
5. Convergence Analysis
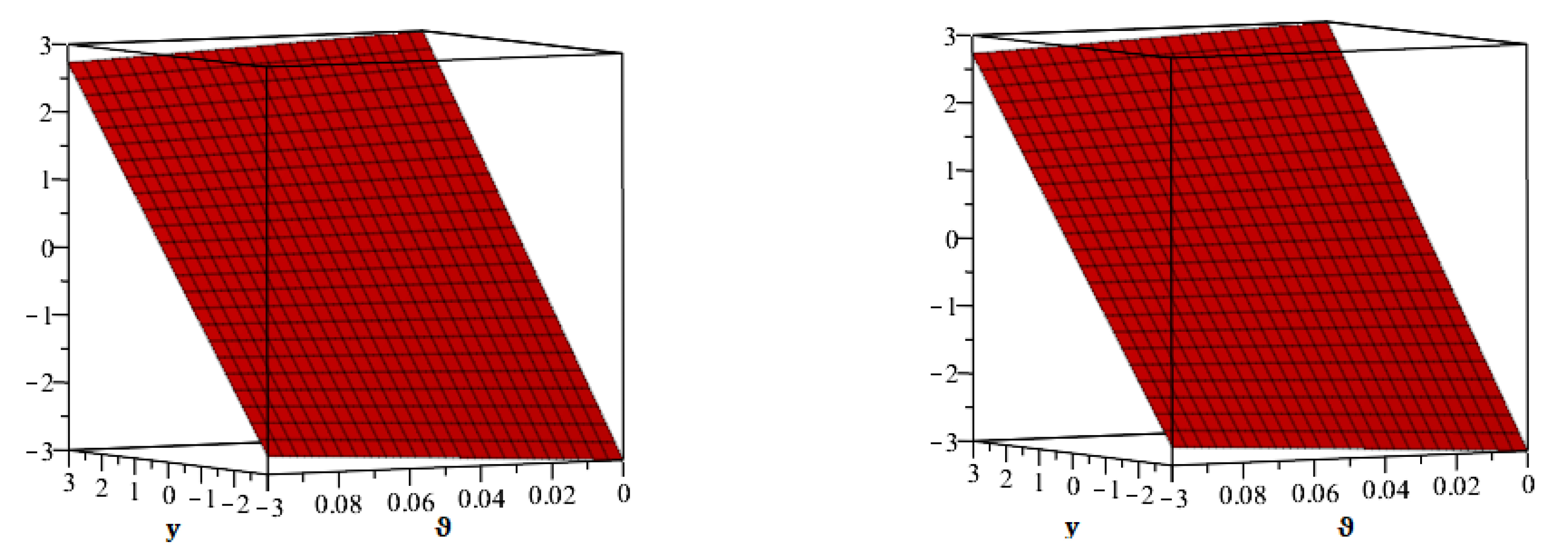
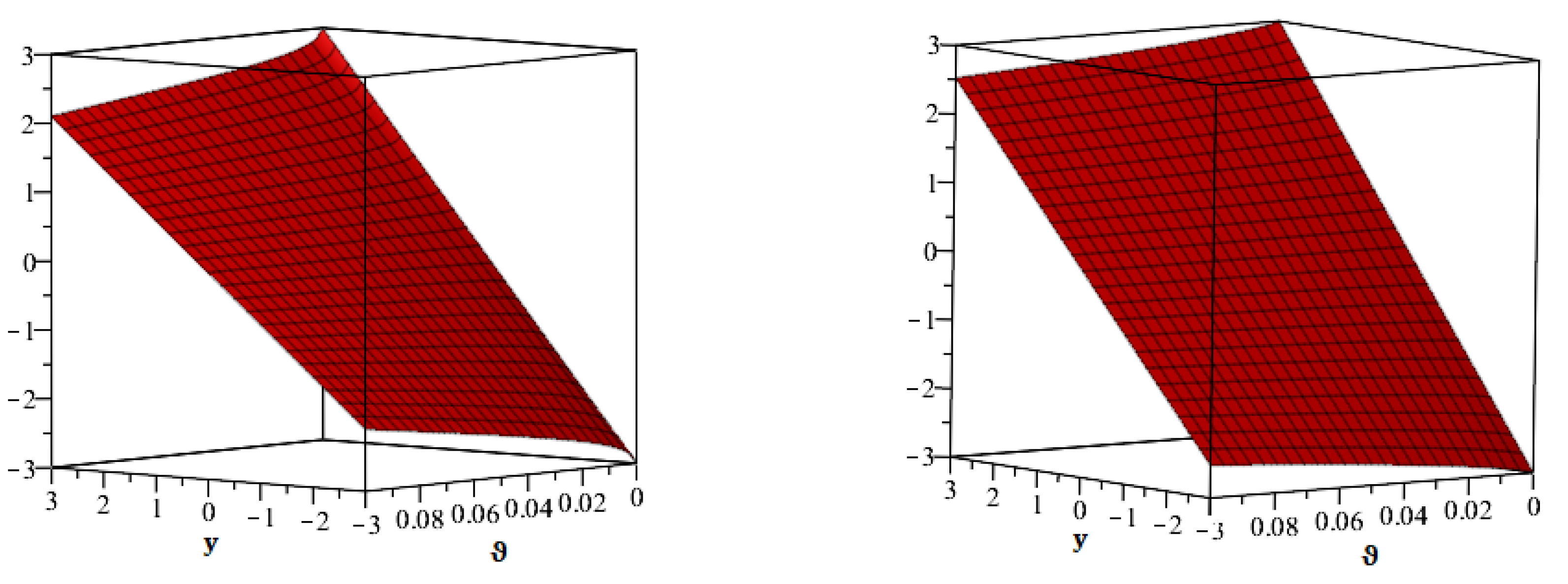
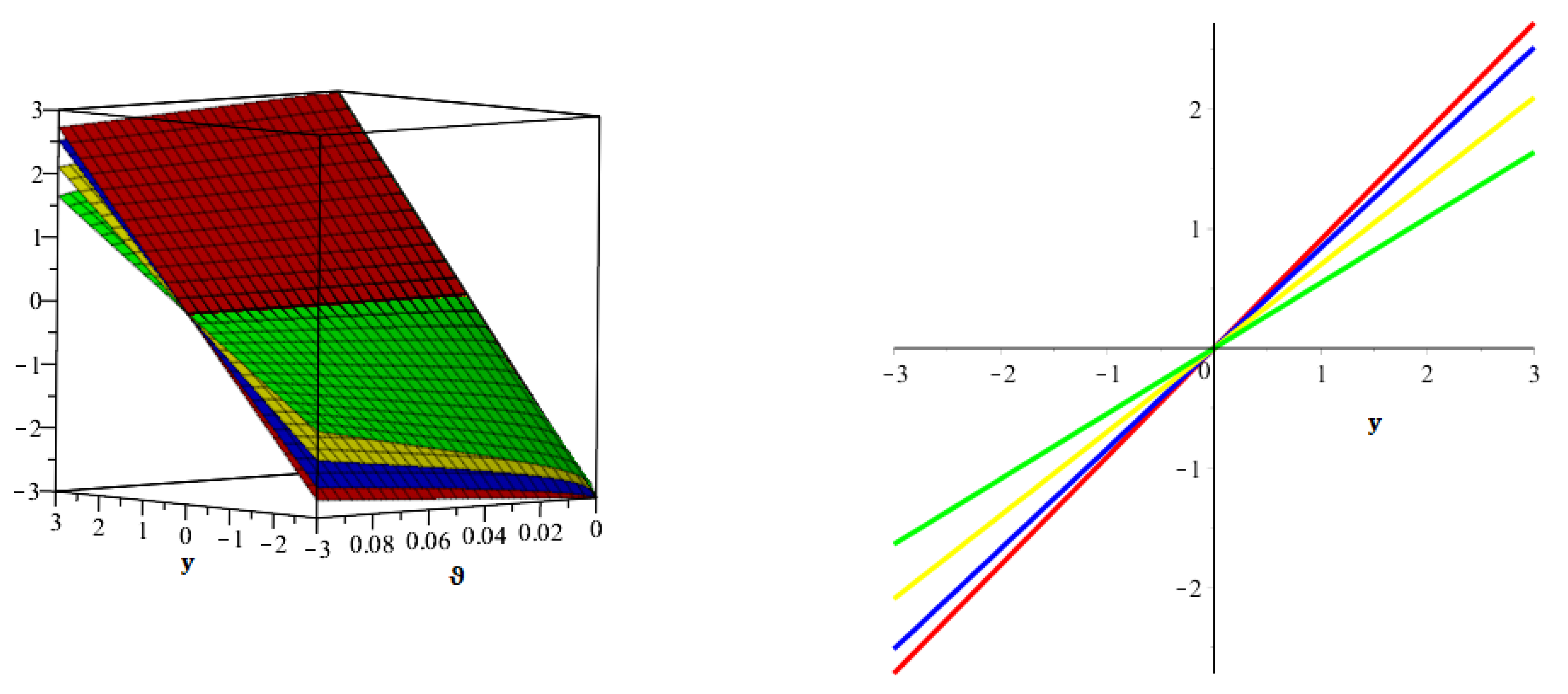
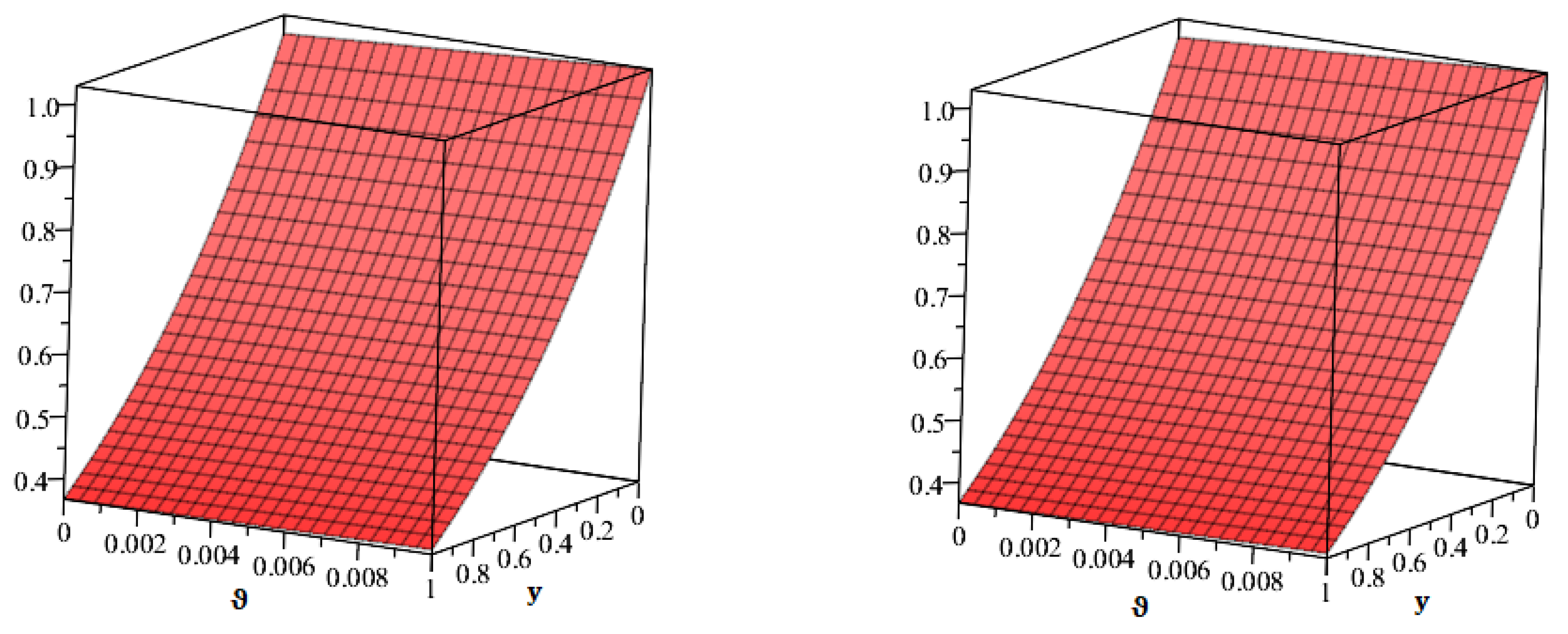
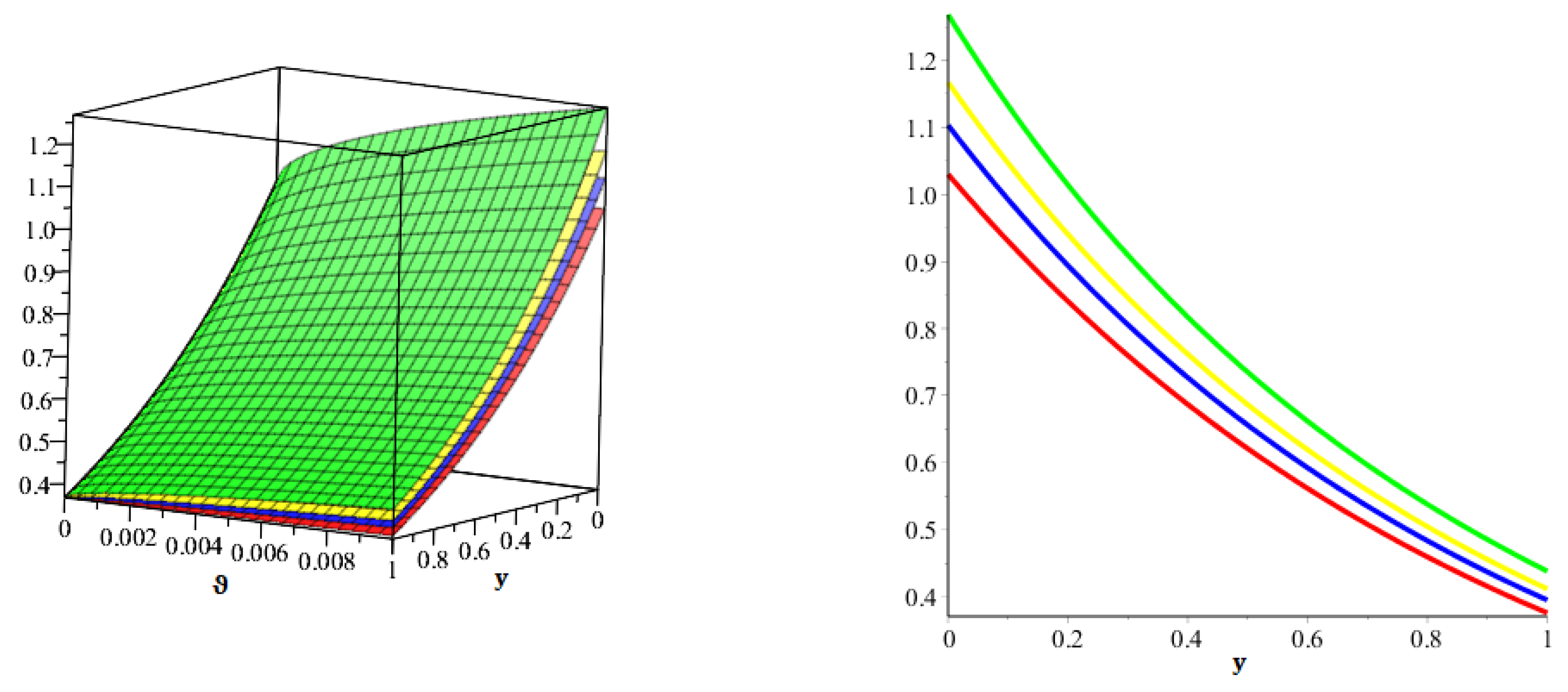
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhaosheng, Y.; Jianzhong, L. Numerical research on the coherent structure in the viscoelastic second-order mixing layers. Appl. Math. Mech. 1998, 19, 717–723. [Google Scholar] [CrossRef]
- Wu, J.; Nguang, S.K.; Shen, J.; Liu, G.; Li, Y.G. Robust H8 tracking control of boiler-turbine systems. ISA Trans. 2010, 49, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Oldham, K.B. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Hasançebi, O.G.; Carbas, S. Bat inspired algorithm for discrete size optimization of steel frames. Adv. Eng. Softw. 2014, 67, 173–185. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 378. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Köksal, M.E.; Yakar, A. Existence results for solutions of nonlinear fractional differential equations. Abstr. Appl. Anal. 2012, 2012, 267108. [Google Scholar]
- Vazquez, L. From Newton’s equation to fractional diffusion and wave equations. Adv. Differ. Equ. 2011, 2011, 1–13. [Google Scholar] [CrossRef]
- Bonforte, M.; Sire, Y.; Vázquez, J.L. Optimal existence and uniqueness theory for the fractional heat equation. Nonlinear Anal. Theory Methods Appl. 2017, 153, 142–168. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Ahmed, E.; Elgazzar, A.S. On fractional-order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Its Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, A.E.M.; El-Saka, H.A.A. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef]
- Aminikhah, H.; Refahi Sheikhani, A.; Rezazadeh, H. Stability analysis of linear distributed order system with multiple time delays. U.P.B. Sci. Bull. Ser. A 2015, 77, 207–218. [Google Scholar]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.E.; Tsitouras, C. New family for Runge-Kutta-Nystrom pairs of orders 6(4) with coefficients trained to address oscillatory problems. Math Meth Appl Sci. 2022, 1–13. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.E.; Tsitouras, C. Fitted modifications of Runge-Kutta-Nystrom pairs of orders7(5) for addressing oscillatory problems. Math. Meth. Appl. Sci. 2022, 1–10. [Google Scholar] [CrossRef]
- Sun, L.; Hou, J.; Xing, C.; Fang, Z. A Robust Hammerstein-Wiener Model Identification Method for Highly Nonlinear Systems. Processes 2022, 10, 2664. [Google Scholar] [CrossRef]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An Improved Algorithm of Drift Compensation for Olfactory Sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Dang, W.; Guo, J.; Liu, M.; Liu, S.; Yang, B.; Yin, L.; Zheng, W. A Semi-Supervised Extreme Learning Machine Algorithm Based on the New Weighted Kernel for Machine Smell. Appl. Sci. 2022, 12, 9213. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Zhang, L.; Zhang, S. Multi-AUV Dynamic Maneuver Countermeasure Algorithm Based on Interval Information Game and Fractional-Order DE. Fractal Fract. 2022, 6, 235. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Phys. A Stat. Mech. Its Appl. 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Liu, Y. Projective synchronization of chaotic fractional-order energy resources demand-supply systems via linear control. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 4479–4486. [Google Scholar] [CrossRef]
- Can, N.H.; Nikan, O.; Rasoulizadeh, M.N.; Jafari, H.; Gasimov, Y.S. Numerical computation of the time non-linear fractional generalized equal width model arising in shallow water channel. Therm. Sci. 2020, 24 (Suppl. S1), 49–58. [Google Scholar] [CrossRef]
- Li, S. Efficient algorithms for scheduling equal-length jobs with processing set restrictions on uniform parallel batch machines. Math. Biosci. Eng. 2022, 19, 10731–10740. [Google Scholar] [CrossRef]
- Shao, Z.; Zhai, Q.; Han, Z.; Guan, X. A linear AC unit commitment formulation: An application of data-driven linear power flow model. Int. J. Electr. Power Energy Syst. 2023, 145, 108673. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift–Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Kumam, P.; Baleanu, D.; Arif, M. An approximate analytical solution of the Navier–Stokes equations within Caputo operator and Elzaki transform decomposition method. Adv. Differ. Equ. 2020, 2020, 622. [Google Scholar]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long-wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Kbiri Alaoui, M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order Cahn–Hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes–Field model for time-fractional Belousov–Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shirzadi, A. The first integral method for modified Benjamin–Bona–Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1759–1764. [Google Scholar] [CrossRef]
- Feng, Z. The first-integral method to study the Burgers–Korteweg–de Vries equation. J. Phys. A Math. Gen. 2002, 35, 343. [Google Scholar] [CrossRef]
- Kurt, A.; Tasbozan, O.; Baleanu, D. New solutions for conformable fractional Nizhnik–Novikov–Veselov system via -expansion method and homotopy analysis methods. Opt. Quantum Electron. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S.; Abdou, M.A. New exact solutions for time-fractional Kaup–Kupershmidt equation using improved ()-expansion and extended ()-expansion methods. Alex. Eng. J. 2020, 59, 3105–3110. [Google Scholar] [CrossRef]
- Rasoulizadeh, M.N.; Avazzadeh, Z.; Nikan, O. Solitary Wave Propagation of the Generalized Kuramoto-Sivashinsky Equation in Fragmented Porous Media. Int. J. Appl. Comput. Math. 2022, 8, 1–20. [Google Scholar] [CrossRef]
- Rasoulizadeh, M.N.; Ebadi, M.J.; Avazzadeh, Z.; Nikan, O. An efficient local meshless method for the equal width equation in fluid mechanics. Eng. Anal. Bound. Elem. 2021, 131, 258–268. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Rasoulizadeh, M.N. Soliton solutions of the nonlinear sine-Gordon model with Neumann boundary conditions arising in crystal dislocation theory. Nonlinear Dyn. 2021, 106, 783–813. [Google Scholar] [CrossRef]
- Kumar, S.; Jiwari, R.; Mittal, R.C. Radial basis functions based meshfree schemes for the simulation of non-linear extended Fisher-Kolmogorov model. Wave Motion 2022, 109, 102863. [Google Scholar] [CrossRef]
- Mittal, R.C.; Pandit, S. A Numerical Algorithm to Capture Spin Patterns of Fractional Bloch Nuclear Magnetic Resonance Flow Models. J. Comput. Nonlinear Dyn. 2019, 14, 081001. [Google Scholar] [CrossRef]
- Mittal, R.C.; Pandit, S. Quasilinearized Scale-3 Haar wavelets-based algorithm for numerical simulation of fractional dynamical systems. Eng. Comput. 2018, 35, 1907–1931. [Google Scholar] [CrossRef]
- Saad Alshehry, A.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long-waves in nonlinear dispersive systems. Philos. Trans. R. Soc. A 1972, 272, 47–78. [Google Scholar]
- Rasoulizadeh, M.N.; Nikan, O.; Avazzadeh, Z. The impact of LRBF-FD on the solutions of the nonlinear regularized long-wave equation. Math. Sci. 2021, 15, 365–376. [Google Scholar] [CrossRef]
- Bellman, R.E.; Adomian, G. Partial Differential Equations: New Methods for Their Treatment and Solution; D. Reidel: Dordrecht, The Netherlands, 1985. [Google Scholar]
- He, J.-H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D.; Gupta, S. An efficient analytical technique for fractional partial differential equations occurring in ion acoustic waves in plasma. J. Ocean. Eng. Sci. 2019, 4, 85–99. [Google Scholar] [CrossRef]
- Yavuz, M.; Abdeljawad, T. Nonlinear regularized long-wave models with a new integral transformation applied to the fractional derivative with power and Mittag-Leffler kernel. Adv. Differ. Equ. 2020, 2020, 367. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Phys. A 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Yavuz, M.; Sulaiman, T.A.; Usta, F.; Bulut, H. Analysis and numerical computations of the fractional regularized long-wave equation with damping term. Math. Methods Appl. Sci. 2020, 44, 7538–7555. [Google Scholar] [CrossRef]
- Stoker, J.J.; Waves, W. The Mathematical Theory with Applications; Interscience: New York, NY, USA, 1966. [Google Scholar]
- Kumar, S.; Jiwari, R.; Mittal, R.C.; Awrejcewicz, J. Dark and bright soliton solutions and computational modeling of nonlinear regularized long-wave model. Nonlinear Dyn. 2021, 104, 661–682. [Google Scholar] [CrossRef]
- Pandit, S. Local radial basis functions and scale-3 Haar wavelets operational matrices based numerical algorithms for generalized regularized long-wave model. Wave Motion 2022, 109, 102846. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractionalorder Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Dattu, M.K.U. New integral transform: Fundamental properties, investigations and applications. IAETSD J. Adv. Res. Appl. Sci. 2018, 5, 534–539. [Google Scholar]
- Singh, P.; Sharma, D. Convergence and error analysis of series solution of nonlinear partial differential equation. Nonlinear Eng. 2018, 7, 303–308. [Google Scholar] [CrossRef]
- Kumar, M. Numerical solution of singular boundary value problems using advanced Adomian decomposition method. Eng. Comput. 2021, 37, 2853–2863. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Nonlaopon, K. Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry 2023, 15, 220. https://doi.org/10.3390/sym15010220
Naeem M, Yasmin H, Shah R, Shah NA, Nonlaopon K. Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry. 2023; 15(1):220. https://doi.org/10.3390/sym15010220
Chicago/Turabian StyleNaeem, Muhammad, Humaira Yasmin, Rasool Shah, Nehad Ali Shah, and Kamsing Nonlaopon. 2023. "Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques" Symmetry 15, no. 1: 220. https://doi.org/10.3390/sym15010220
APA StyleNaeem, M., Yasmin, H., Shah, R., Shah, N. A., & Nonlaopon, K. (2023). Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry, 15(1), 220. https://doi.org/10.3390/sym15010220









