Abstract
The paper considers the problem of a small-spacecraft elastic elements’ temperature shock that occurs when the spacecraft immerses into the Earth’s shadow or comes out of it. A small spacecraft with two elastic elements is simulated. In the first approximation, such a problem is considered to be a symmetric problem. Estimations of disturbing factors from the temperature shock in a symmetric formulation are obtained. The differences from the results for a small spacecraft with a single elastic element are analyzed. The results of the work can be used for promising small technological spacecraft development, as well as for solving problems of space debris removal and remote sensing of the Earth.
1. Introduction
A temperature shock occurs when a spacecraft enters into the Earth’s shadow or comes out of it [1,2,3]. The problem of the small-spacecraft large elastic elements’ temperature shock during its orbit movement is extremely relevant when solving certain tasks. Thus, for space debris transportation from near-Earth orbits, a number of methods for space debris removal have been developed [4,5,6]. Space debris is quite diverse in its structure: from small particles formed as a result of accidents and collisions to entire spacecraft for which the active service life has already expired. These particles pose a threat to space equipment [7,8,9]. Different methods of space debris removal are being developed depending on the size of the debris. Thus, for spent small spacecraft with elastic elements, an algorithm for de-orbiting using a tug spacecraft on a cable has been developed [10,11,12]. There may be a loss of contact between the tug and the garbage due to the temperature shock [13]; therefore, the movement of the tug–garbage bundle should be considered with the temperature shock.
Experiments with promising new solar panels (Roll-Out Solar Array, Figure 1) on board the International Space Station have shown a whole range of problems associated with temperature shock [14,15].

Figure 1.
ROSA solar panel in the deployed state as a part of the International Space Station.
Significant natural oscillations of the panels were excited after the temperature shock. These oscillations did not allow the panels to roll up at the end of the experiment. Therefore, they had to be shot off in an expanded state [16]. Despite all these difficulties, Roll-Out Solar Array contributes to a significant (up to 20%) reduction in the mass of solar panels while maintaining their energy efficiency [17]. Therefore, such panels are very promising for use on spacecraft, especially on small ones, in which the problem of rational mass use is particularly acute [18]. However, when using them, it is necessary to study and take into account the influence of temperature shock because it will affect the controllability of the small spacecraft [19].
Another target task in which it is necessary to take into account temperature shock is remote sensing of the Earth [20,21,22]. In order to successfully solve the problems of remote sensing of the Earth, it is necessary to meet the requirements of the small-spacecraft orientation relative to the survey object. Thus, as a result of flight tests, the currently operating small “Aist-2D” spacecraft for remote sensing of the Earth confirmed the implementation of a uniaxial solar orientation with an error of 0.5 ° in angular position and 0.01 °/s in angular velocity, as well as a triaxial orientation in the orbital coordinate system with an error of 2 ° in angular position and 0.0005 °/s in angular velocity [23]. At the same time, the design and layout scheme of the small “Aist-2D” spacecraft contains two solar panels (Figure 2, [23]). Temperature shock and the small-spacecraft motion caused by it can disrupt the exact orientation and reduce the effectiveness of solving the target task. This conclusion is confirmed by the studies conducted in [13]. Therefore, taking into account temperature shock is crucial when conducting remote sensing of the Earth by small spacecraft.

Figure 2.
Appearance of the small «Aist-2D» spacecraft for remote sensing of the Earth.
Small technological spacecraft are even more sensitive to disturbances arising from temperature shock. Gravity-sensitive technological processes [24,25,26,27] impose significant restrictions on the micro-acceleration field of the small-spacecraft internal environment [28,29,30]. The most significant disturbing factor generating micro-accelerations is usually the work of the motion-control system executive bodies [31,32,33]. However, the temperature shock can also cause oscillations in the elastic elements of the small spacecraft that violate the requirements for micro-accelerations [2,3,15,34]. Experiments on directed crystallization have shown that the intensity of convective-type movements in melts is related to the magnitude of micro-accelerations [35,36]. These movements determine the impurity capture during crystallization and, as a consequence, the size of the cultivated monocrystals [37]. Non-compliance with micro-acceleration requirements may jeopardize the successful completion of a space mission from a technological point of view. Therefore, when designing a small technological spacecraft, it is important to investigate and take into account disturbances from the temperature shock.
2. One-Dimensional Model of Thermal Conductivity in a Symmetric Formulation
The problem of temperature shock for a spacecraft scheme with one elastic element was considered in [3,38] for a one-dimensional model of thermal conductivity and in [15,39] for a two-dimensional model of thermal conductivity. In [3,38], the most dangerous case of temperature shock is considered: when its effect on the spacecraft motion is maximal. The heat flux falls normally to the plane of the elastic element, which appears to be a homogeneous plate. At the same time, it is noted in [38] that the most significant disturbing factor is the internal longitudinal force affecting the translational motion of the small spacecraft. Numerical modeling carried out in [38] shows that the micro-accelerations caused by this force exceeds the maximum permissible by more than an order of magnitude. Therefore, when implementing gravity-sensitive processes, it is highly relevant to take into account the temperature shock for spacecraft with one elastic element (Starlink [13,40], Spot-4, etc.). In [3], an algorithm for controlling the executive bodies of the motion-control system has been developed, which makes it possible to significantly reduce micro-accelerations from the temperature shock for the small spacecraft with one elastic element.
In the real case, taking into account the preliminary bending of the elastic element at the moment of the temperature shock makes it necessary to solve the two-dimensional problem of thermal conductivity [15,39]. In this formulation, the heating of the plate surface layer is not maximal. It is also necessary to take into account not only the heat fluxes that penetrate deep into the plate but also the fluxes which are parallel to its plane. This determines the two-dimensionality of the initial boundary value problem. It is shown in [39] that the temperature shock effect in such a formulation is somewhat lower than in the one-dimensional problem. At the same time, the paper [41] revealed the effect of stability loss, which can occur in the presence of initial stresses caused by preliminary bending of the elastic element. According to studies [41], micro-accelerations resulting from stability loss may exceed the values obtained by the one-dimensional model.
However, high energy requirements for technological spacecraft determine the presence of two or more solar panels in the design and layout scheme. Thus, for the promising «Vozvrat-MKA» spacecraft (Figure 3), four solar panels are provided.

Figure 3.
Appearance of the «Vozvrat-MKA» spacecraft.
This makes it necessary to formulate the problem of temperature shock for small spacecraft with more than one elastic element. Of course, this is a more difficult task. Moreover, this complexity is not limited only to the complication of the small spacecraft model. It is about the differences between a real spacecraft and its model. Thus, in [42], the influence of three types of solar panel asymmetry (mass asymmetry, length asymmetry and asymmetry of the panel attachment points to the spacecraft body) on the micro-accelerations generated from the natural oscillations of the panel is considered. It is shown that the values of micro-accelerations are less in the case of the symmetric scheme than in the case of asymmetries [42]. Therefore, the symmetric formulation will not estimate the maximum micro-accelerations, as in the case of the single elastic element, even in the case when the solar flux falls normally. On the other hand, differences between the real spacecraft and the model can significantly affect the magnitude of the created micro-accelerations. This gives the problem a substantially stochastic character. The symmetric formulation cannot give a comprehensive answer to the question of the temperature-shock influence significance. It can only serve as a basic assessment which should be clarified if necessary. One-dimensionality, as is evident from the scheme with one elastic element, should slightly overestimate the evaluation of the resulting disturbances. However, as it was already noted, it should not be expected that this evaluation will be maximal when taking into account possible asymmetries.
3. Simplifying Assumptions
Let us consider the scheme of a small symmetrical spacecraft with two elastic elements in the form of solar panels (Figure 4).
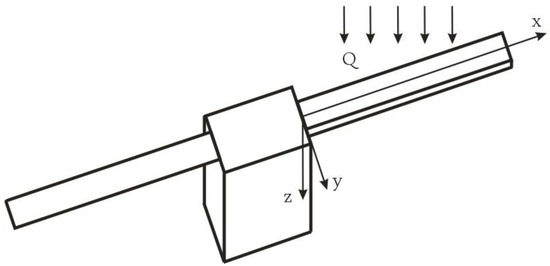
Figure 4.
The scheme of a spacecraft for the symmetric formulation of the temperature shock influence problem.
Let us introduce the following simplifying assumptions to solve the one-dimensional thermoelasticity problem in the symmetric formulation:
1. The small spacecraft is an axisymmetric body both in terms of shape and inertial mass characteristics, with two elastic elements symmetrically attached to it.
In reality, this is quite difficult to achieve. The layout scheme of the small spacecraft does not allow its inertial mass characteristics to be considered symmetrical, even in an axisymmetric shape or a shape slightly different from an axisymmetric one [43]. Deviations from the symmetric model lead to the asymmetry of the model and the stochastic solution of the problem and should be investigated in each case separately. This is especially true if the asymmetry is dynamic [44] because in the case of a significant asymmetry, the corresponding perturbations from various elastic elements will no longer compensate each other. Then the perturbations estimation in the symmetric formulation may be incorrect for the simulated case.
2. The fastening of elastic elements to the body of the small spacecraft is a rigid seal on one edge; the other three edges are free.
In practice, it is quite difficult to provide a rigid fastening. However, it is necessary for effective spacecraft rotational-motion control. Thus, for the “NIKA-T” technological spacecraft project, the minimum allowable value of the cosine of the angle between the normal to the plane of the solar panel and the direction to the Sun was 0.9. Such requirements can be met only if the panel is firmly attached. On the other hand, in the implementation of the project of the “Spot-4” spacecraft, in order to neutralize the influence of the solar panel vibrations on the rotational motion, its fastening was elastic. At the same time, the average value of the cosine of the angle between the normal to the plane of the solar panel and the direction to the Sun was no more than 0.36. In modern application programs, it is possible to implement fastening of various degrees of rigidity. Thus, in [41], it is shown that with absolutely rigid fastening, in the case of a preliminary bending of the elastic element at the moment of the temperature shock, a stability loss is possible. With a more elastic fastening, there was no stability loss. In this model, rigid sealing is used because in this case, the maximum effect of the dynamic bending on the rotational motion of the small spacecraft is observed, and it also has simple boundary conditions. All possible disturbing effects are transmitted to the spacecraft body through the sealing. Therefore, this assumption should not be abandoned when constructing more complex models than the symmetric formulation. However, in the case in which there is a stability loss [41], the fastening of the elastic element should be more elastic because it is highly undesirable to allow stability loss [41].
3. Each elastic element is a homogeneous plate with unchanged thermophysical properties.
This assumption significantly simplifies the problem being solved. Firstly, significant differences in the heterogeneity of elastic elements in combination with differences in thermophysical properties can affect the stress–strain state of elastic elements as a result of the temperature shock. Secondly, modeling of thermophysical properties depending on temperature is a rather difficult task [45]. In order to solve practical problems, in some cases for individual materials, the thermophysical properties of which significantly depend on temperature, it is necessary to abandon the constancy of these properties. On the other hand, there are modern composite materials, the thermophysical properties of which are constant over a large temperature range [46]. Therefore, in some cases, a symmetrical statement will be quite justified.
4. Elastic elements are absolutely identical to each other.
The influence of various types of elastic elements asymmetry in the study of perturbations from their natural oscillations is considered in [42]. It is shown that the perturbations in the symmetric formulation are minimal. This is explained by the compensation of a number of perturbations from one elastic element by corresponding perturbations from another element. In the symmetric formulation, it is assumed that some perturbations completely compensate each other. The appearance of asymmetry causes an imbalance between perturbations, so they cannot be fully compensated [42]. For our problem, the rejection of this assumption creates another source of stochasticity, the significance of which can be determined in each specific case separately. However, it can be assumed that elastic elements differ significantly from each other only when they are different structural elements. For example, a solar panel, radiator, antenna, etc. Therefore, in most cases, this assumption will not worsen the quality of the temperature shock disturbances assessment.
5. Temperature shock occurs absolutely simultaneously for both elastic elements.
In the most critical case, the difference between the onset of the temperature shock of two elastic elements will be less than 2 × 10−8 s for a small spacecraft with 2.5 m long elastic elements. Therefore, this assumption does not reduce the estimation accuracy. Another factor is if we take into account the transition from the shadow area of the orbit to the illuminated one through the penumbral area. In this case, the structure of the temperature shock somewhat changes compared to the instantaneous exit from the shadow to the illuminated area of the orbit. Studies [47] show that due to this, temperature shock is somewhat stretched over time. In [47] it was noted that the consideration of the penumbral area gives more adequate results. However, it can be argued that the symmetric formulation contains more significant simplifications than not taking into account the penumbral area. On the other hand, if we take into account the penumbral area, it will reduce the assessment of the temperature shock effect on the small-spacecraft rotational-motion dynamics [47]. Therefore, in the context of the symmetric formulation, this assumption is quite justified.
6. At the moment of the temperature shock, both elastic elements had a flat shape and were in the same plane.
This assumption describes the most dangerous case when the greatest disturbances from temperature shock occur. In this case, the heating intensity of the elastic element is maximal. When solving the problem of cooling an elastic element for any of its initial position, the cooling intensity will be the same. However, if the shadow area is preceded by an illuminated area in which this simplifying assumption is fulfilled, then the maximum temperature value in the temperature field of the elastic element will be higher. Therefore, on the one hand, this assumption allows us to estimate the maximum effect of the temperature shock from all the initial positions of elastic elements. On the other hand, it is sufficient to solve the one-dimensional problem of thermal conductivity to obtain this estimation. The identity of the elastic elements’ initial positions is characteristic only for the one-dimensional model of thermal conductivity. If we use a two-dimensional formulation and take into account the preliminary bending of elastic elements [15,39], then the identity of the initial positions is practically not feasible. The loss of this identity will become a source of stochasticity because the corresponding perturbations from various elastic elements will not compensate each other. Therefore, when we were talking about the maximum value of perturbations, we meant the value within the framework of the symmetric formulation. When considering different initial positions of elastic elements, larger values of perturbations from the temperature shock can be obtained.
7. The incident flux of solar radiation is strictly perpendicular to the plane of both elastic elements during the entire time of the temperature shock.
This assumption reinforces the previous assumption, creating a condition for the maximum possible disturbance from the temperature shock. With temperature deformations of the elastic element, as well as the rotation of the small spacecraft, the condition of perpendicularity will be violated. This will lead to a certain decrease in the intensity of heating of the elastic element surface layer when the small spacecraft comes out of the Earth’s shadow. When the spacecraft is immersed in the shadow, as already noted above, the cooling intensity will not depend on the deformed shape of the elastic element. Studies [15,39] show that it is relevant to take into account the decrease in the heating intensity of the elastic element surface layer for a two-dimensional formulation, for which preliminary bending is taken into account. One paper [15] presents a criterion for taking into account two-dimensionality depending on the initial bending. In the symmetric formulation, temperature deformations are not able to significantly affect the heating of the surface layer. As for the rotation of the small spacecraft, the restrictions imposed on the rotational motion parameters when performing the target tasks [13,23] suggest that it also will not significantly affect the temperature field of elastic elements.
8. The solar radiation flux is uniform and stationary:
The symmetric formulation of the problem does not involve more complex heat flux models due to the number of other simplifying assumptions. It can also be argued that the study of the real unevenness and unsteadiness of the heat flux is unlikely to be correct in the symmetric formulation.
9. The natural oscillations of elastic elements are negligible for the entire time of the temperature shock.
Taking into account the longitudinal and transverse vibrations of elastic elements in the general case would lead to the need to formulate and solve a three-dimensional problem of thermal conductivity. At the same time, the symmetric formulation is not practically feasible because it is difficult to imagine absolutely synchronous oscillations of elastic elements, even while maintaining other assumptions. On the other hand, studies show that natural oscillations themselves are a source of significant disturbances [26,29,31,33]. Therefore, temperature shock should be isolated, with oscillations excluded, to study its effect. If natural oscillations are considered, then it will significantly change the very formulation of the problem. It will be necessary to consider the effect of temperature shock on natural oscillations and then to investigate how this will affect the rotational motion of the small spacecraft. In this case, the problem becomes essentially stochastic. This is even expressed in the fact that it is possible to use one-dimensional, two-dimensional or three-dimensional models of thermal conductivity with different parameters of natural oscillations.
10. Fourier’s law is valid for describing a one-dimensional model of thermal conductivity.
The proportionality of the internal heat flux to the temperature gradient of a homogeneous stationary environment will not be disturbed by the orbital motion of the small spacecraft in orbits, the height of which is sufficient for negligible aerodynamic drag. Adjustments should be made in cases in which a small spacecraft is operated in low orbits. Such a situation is possible for Earth remote-sensing spacecraft [22]. However, technological spacecraft are operated in higher orbits. Thus, the expediency of this simplifying assumption is determined by the objectives of the small spacecraft.
11. The initial temperature distribution field is the same in both elastic elements and is also homogeneous.
This simplifying assumption fully corresponds to the symmetric formulation and allows us to consider the dynamics of the stress–strain state of only one elastic element, because in the symmetric formulation, the second elastic element will deform in the same way. In a real situation, the rejection of this assumption will create another source of stochasticity. Moreover, a significant difference in the initial temperature distribution will make the use of assumption 6 incorrect, because the shapes of elastic elements will have to differ from each other. The rejection of the assumption of homogeneity may be caused by a small shadow area of the orbit. During the movement along it, thermal equilibrium may not occur. If the shadow area is sufficiently long, then the homogeneity of the initial temperature field is quite feasible.
12. The thickness of elastic elements is negligible compared to their length and width.
This assumption is quite justified for real solar panels and allows us to use the theory of thin plates to solve the problem of thermoelasticity.
In fact, the one-dimensional thermoelasticity problem in the symmetric formulation for the small spacecraft scheme with two elastic elements is reduced to a similar problem with one elastic element and will not differ from it in terms of the thermal conductivity problem solved in [15,39]. However, the mutual influence of two elastic elements’ deformations will give a completely different result when studying the disturbing effect of elastic elements’ temperature deformations on the dynamics of the small spacecraft than in a scheme with one elastic element. This work is devoted to the study of this influence in the symmetric formulation 1–12.
4. Model Equations
Let us consider the third initial boundary value problem [3], supplementing it with the Sophie Germain equation [48], in accordance with the simplifying assumption 12, to solve the one-dimensional thermoelasticity problem:
Designation in the system (2):
a—the coefficient of thermal conductivity; h—the thickness of the elastic element; —bending of the elastic element points in the direction of the z axis; ρ—the density of the elastic element; D—the cylindrical stiffness of the elastic element to the bending; L—the length of the elastic element; λ—the coefficient of thermal conductivity; ε—the degree of blackness of the elastic element; and σ—the Stefan–Boltzmann constant.
The first equation of the system (2) is a one-dimensional model of thermal conductivity with constant thermophysical characteristics. The application of Fourier’s law in the classical form, without taking into account the inertial term, means that the heat flux instantly turns when the direction of the temperature gradient changes. We can tolerate this for smoothly flowing processes. Because temperature shock is a fast, dynamic phenomenon, it is necessary to take into account the inertial term. However, the one-dimensional model of thermal conductivity assumes that the temperature gradient is not always directed along the z axis and does not change its direction. Therefore, even with temperature shock, it is not necessary to take into account the inertial term in the thermal conductivity equation.
The second equation of the system (2) is the Sophie Germain equation for thin plates, which takes into account the inertial term . Here, in contrast to the thermal conductivity equation, it is necessary to consider the inertial term due to significant changes in the bending over time. Physically, the inertial term represents the forces of inertia during the accelerated movement of the elastic element points during its deformation.
The following three equations of the system (2) complement the boundary and initial conditions of the thermal conductivity equation to the third initial boundary value problem. The upper part of the elastic element, according to the first of these three equations, is illuminated by the incident solar flux in accordance with the simplifying assumption 8.
The following two equations of the system (2) express the geometric boundary conditions of rigid fixation of an elastic element in the body of the small spacecraft.
Thus, the symmetric formulation of the thermoelasticity problem is mathematically formalized by system (2), which is identical for both elastic elements of the small spacecraft.
5. Numerical Simulation for the «Aist-2D» Spacecraft
Let us consider a spacecraft, the scheme of which corresponds to Figure 4, and the characteristics of which correspond to the small remote-sensing «Aist-2D» spacecraft (Figure 2) (Table 1 [13,23]) for numerical analysis.

Table 1.
The values of the parameters used in the numerical experiment in the thermoelasticity problem.
To solve the problem of numerical modeling, ANSYS software package was used (v. 18.2, developed by ANSYS Inc.). The solution of the one-dimensional problem of thermal conductivity in this formulation was considered in [39]. A basic model was chosen there (Figure 5), which fully corresponds to simplifying assumptions 1–12 of this paper.
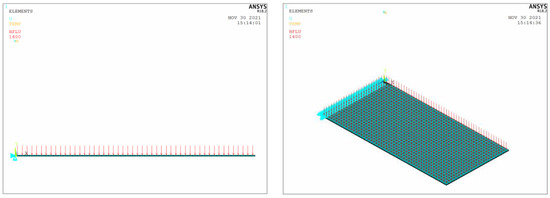
Figure 5.
The elastic element at the moment of the temperature shock [39].
According to the model shown in Figure 5, the dynamics of the elastic element temperature field were obtained within the framework of the third initial boundary value problem (1). This dynamic is shown in Figure 6.
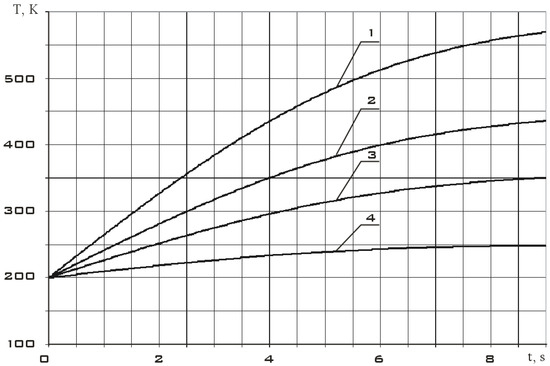
Figure 6.
The dynamics of the elastic element temperature field: 1—top layer; 2, 3—middle layer; 4—bottom layer.
Such a temperature distribution within the framework of the third initial boundary value problem (1) corresponds to the picture of the stress–strain state shown in Figure 7, in which the bending can be represented as a three-dimensional surface.
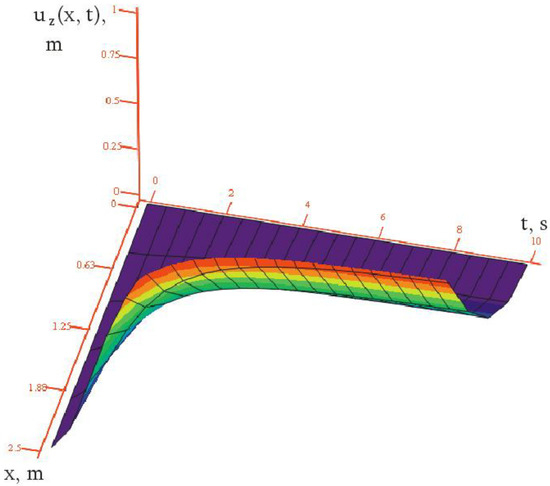
Figure 7.
The dynamics of the bending as a result of the temperature shock for the elastic element (Figure 5) in the framework of the symmetric formulation (2).
The symmetric formulation of problem (1) leads to the fact that the temperature and bending fields for both elastic elements (Figure 4) will be exactly the same and synchronous.
6. Analysis of the Disturbing Factors Significance
Let us consider the disturbing factors arising as a result of temperature shock within the framework of the symmetric formulation (2). In [38,39], it is noted that the main disturbing factor is the internal longitudinal force arising from the rigid sealing of one of the elastic element edges [38]:
where is an infinitesimal element of the elastic element cross-section; —the element of the strain tensor; —the coefficient of thermal expansion; and —the initial temperature field.
However, in the considered symmetric formulation, the internal longitudinal forces of the two elastic elements defined by expression (3) will be equal in magnitude and opposite in direction. Therefore, they will compensate each other and will not create disturbances.
The inertia force arising in the x-axis direction (Figure 4) due to the expansion of the elastic element under the temperature shock is uncompensated for one elastic element [38]. However, in the considered symmetric formulation, as well as the internal longitudinal force, this inertia force from one elastic element will be compensated by a similar inertia force of another elastic element.
For each elastic element, the force of inertia arising in the direction of the y axis (Figure 4) due to the expansion of the elastic element during the temperature shock will still (as in [38]) be zero, because points with positive y coordinates will have positive acceleration components , and points with negative y coordinates will have negative ones. Simplifying assumptions 1–12 determine the free edges of the elastic element parallel to the x-axis. Thus, deformation in this direction passes freely and is symmetrical with respect to the x axis.
During deformations of elastic elements (Figure 7), a moment arises from inertia forces [38]. However, in the symmetric formulation, this disturbing factor will be mutually compensated, given the total effect of two elastic elements.
The only disturbing factor arising from the temperature shock in the symmetric formulation will be the force of inertia in the direction of the z axis (Figure 4). It has the same direction for both elastic elements and doubles when added in the symmetric formulation, rather than being compensated. It was noted in [38] that this perturbation is less significant than the internal longitudinal force and the force of inertia in the direction of the x axis. Therefore, it was not studied in [38]. Its total value, given the doubling for two elastic elements, can be represented as follows:
where m1 is the mass of the elastic element.
The sign of approximate equality means that the coordinates of the elastic elements’ points change slightly. Therefore, the second derivative of these coordinates in time can be neglected. This makes it possible to move from the full time derivative, which in expression (4) is indicated by a dot above, to the partial derivative.
Based on the dynamics of bending (Figure 7), it is possible to construct a function (Figure 8) which is included in the expression for the inertia force (4) and to estimate the dynamics of changes in the inertia force over time (Figure 9).
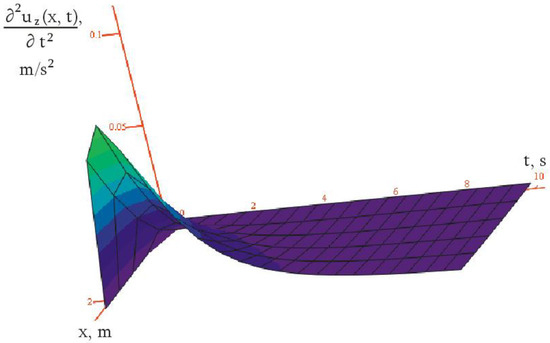
Figure 8.
The dynamics of the elastic element points’ accelerations (Figure 5) in the framework of the symmetric formulation (2).
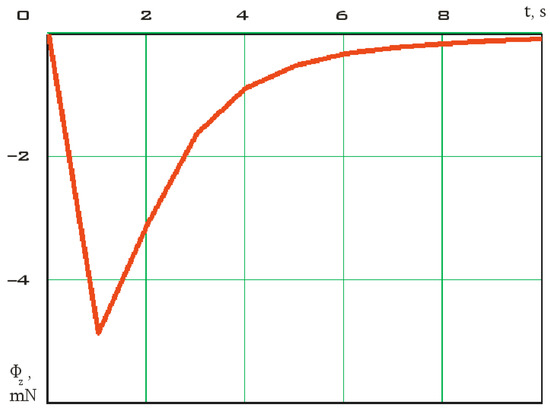
Figure 9.
The dynamics of the total inertia force changes (4) in the direction of the z axis from the movement of the elastic elements’ points during their deformation.
Figure 9 shows that the maximum value of the inertia force is approximately 5 mN. Let us evaluate the corresponding micro-accelerations:
In [38], the maximum values of micro-accelerations from this inertia force were estimated at 1.2 µm/s2. Thus, the influence of the inertia force in the direction of the z axis increased with the symmetric formulation of the problem with two elastic elements. It can also be stated that the temperature shock is still a significant disturbance in the implementation of gravity-sensitive processes. This is because the limits on micro-accelerations are up to 1 µm/s2 [29].
7. Conclusions
Thus, a symmetric formulation of the third initial boundary value problem of thermoelasticity is presented. The problem is solved numerically in the ANSYS software package (v. 18.2, developed by ANSYS Inc., Canonsburg, PA, USA) for the scheme of the “Aist-2D” spacecraft. Given the fact that the symmetric formulation does not reveal the maximum effect of the temperature shock on the movement of the small spacecraft, the relevance of taking into account the temperature shock when implementing gravity-sensitive processes on board a small spacecraft was shown.
Despite the similarity of the problem with one elastic element, the significance of disturbing factors in the symmetric formulation of the third initial boundary value problem of thermoelasticity has changed significantly. If the most significant factors were the internal longitudinal force and the force of inertia in the direction of the x axis [38], then in the symmetric formulation, the most significant factor is the force of inertia in the direction of the z axis.
The results of the work can be used to estimate perturbations from the temperature shock in a more complex formulation in the presence of various asymmetries leading to a stochastic problem. The obtained assessment shows how feasible specific requirements (for example, micro-accelerations) are for the successful completion of the small-spacecraft target tasks.
Author Contributions
Conceptualization, A.S.; methodology, A.S.; software, D.O. and A.N.; validation, A.S., V.S. and A.N.; formal analysis, A.S. and D.O.; investigation, A.S. and V.S.; resources, A.S. and D.O.; data curation, A.S. and A.N.; writing—original draft preparation, A.S., D.O. and V.S.; writing—review and editing, A.S., D.O., V.S. and A.N.; visualization, V.S. and A.N.; supervision, A.S. and D.O.; project administration, A.S.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation grant number Project No. 22-19-00160.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shen, Z.; Hu, G. Thermally Induced Dynamics of a Spinning Spacecraft with an Axial Flexible Boom. J. Spacecr. Rockets 2015, 52, 1503–1508. [Google Scholar] [CrossRef]
- Shen, Z.; Tian, Q.; Liu, X.; Hu, G. Thermally induced vibrations of flexible beams using Absolute Nodal Coordinate Formulation. Aerosp. Sci. Technol. 2013, 29, 386–393. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Orlov, D.I. Development of control algorithms for the orbital motion of a small technological spacecraft with a shadow portion of the orbit. Microgravity Sci. Technol. 2020, 32, 941–951. [Google Scholar] [CrossRef]
- Priyant, C.M.; Surekha, K. Review of Active Space Debris Removal Methods. Space Policy 2019, 47, 194–206. [Google Scholar]
- Ledkov, A.; Aslanov, V. Review of contact and contactless active space debris removal approaches. Prog. Aerosp. Sci. 2022, 134, 100858. [Google Scholar] [CrossRef]
- Hidri, L.; Mrad, M.; Alkahtani, M. Suitable Mass Density Function for an Artificial Satellite to Prevent Chaotic Motion after Collision with Space Debris. Symmetry 2022, 14, 818. [Google Scholar] [CrossRef]
- Fowler, K.; Teixeira-Dias, F. Hybrid Shielding for Hypervelocity Impact of Orbital Debris on Unmanned Spacecraft. Appl. Sci. 2022, 12, 7071. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Ledkov, A.S. Detumbling of axisymmetric space debris during transportation by ion beam shepherd in 3D case. Adv. Space Res. 2022, 69, 570–580. [Google Scholar] [CrossRef]
- Puente, C.; Sáenz-Nuño, M.A.; Villa-Monte, A.; Olivas, J.A. Satellite Orbit Prediction Using Big Data and Soft Computing Techniques to Avoid Space Collisions. Mathematics 2021, 9, 2040. [Google Scholar] [CrossRef]
- Sizov, D.A.; Aslanov, V.S. Optimal thrust control during tether deployment after harpoon capture of space debris. AIP Conf. Proc. 2021, 2318, 050005. [Google Scholar]
- Trushlyakov, V.I.; Yudintsev, V.V. Rotary space tether system for active debris removal. J. Guid. Control Dyn. 2020, 43, 354–364. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Contact Dynamics Modeling and Simulation of Tether-Nets for Space Debris Capture. J. Guid. Control Dyn. 2017, 40, 110–123. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, D.; Rui, X. Dynamic Simulation of Space Debris Cloud Capture Using the Tethered Net. Space Sci. Technol. 2021, 2021, 9810375. [Google Scholar] [CrossRef]
- Spence, B.R.; White, S.; La Pointe, M.; Kiefer, S.; La Corte, P.; Banik, J.; Chapman, D.; Merrill, J. International Space Station (ISS) Roll-Out Solar Array (ROSA) Spaceflight Experiment Mission and Results. In Proceedings of the IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Serdakova, V.V.; Khnyreva, E.S. Construction of the criterion for using a two-dimensional thermal conductivity model to describe the stress-strain state of a thin plate under the thermal shock. Microgravity Sci. Technol. 2021, 33, 65. [Google Scholar] [CrossRef]
- Chamberlain, M.K.; Kiefer, S.H.; Banik, J.A. On-Orbit Structural Dynamics Performance of the Roll-Out Solar Array. In Proceedings of the AIAA Spacecraft Structures Conference, Kissimmee, FL, USA, 8–12 January 2018; Available online: https://arc.aiaa.org/doi/abs/10.2514/6.2018-1942 (accessed on 12 November 2022).
- Jiang, G.; Dong, T.; Guo, Z. Nonlinear Dynamics of an Unsymmetric Cross-Ply Square Composite Laminated Plate for Vibration Energy Harvesting. Symmetry 2021, 13, 1261. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Salmin, V.V. Modeling the disturbing effect on the aist small spacecraft based on the measurements data. Sci. Rep. 2022, 12, 1300. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.F.S.; Elipe, A.; De Moraes, R.V.; Prado, A.F.B.A.; Winter, O.C.; Gomes, V.M. Low Thrust Propelled Close Approach Maneuvers. Symmetry 2022, 14, 1786. [Google Scholar] [CrossRef]
- Ye, Z.; Cai, W.; Liu, S.; Liu, K.; Wang, M.; Zhou, W. A Band Selection Approach for Hyperspectral Image Based on a Modified Hybrid Rice Optimization Algorithm. Symmetry 2022, 14, 1293. [Google Scholar] [CrossRef]
- Platonov, V.N. About accuracy of an Earth remote sensing spacecraft Attitude-keeping without using data from inertial sensors. Space Eng. Technol. 2014, 3, 33–38. [Google Scholar]
- Krestina, A.S.; Tkachenko, I.S. Efficiency Assessment of the Deorbiting Systems for Small Satellite. J. Aeronaut. Astronaut. Aviat. 2022, 54, 227–239. [Google Scholar]
- Kirilin, A.N.; Akhmetov, R.N.; Shakhmatov, E.V. Experimental Technological Small Spacecraft “Aist–2D”; Publishing House of the Samara Scientific Center of the Russian Academy of Sciences: Samara, Russia, 2017; p. 324. [Google Scholar]
- Perminov, A.V.; Nikulina, S.A.; Lyubimova, T.P. Analysis of Thermovibrational Convection Modes in Square Cavity under Microgravity Conditions. Microgravity Sci. Technol. 2022, 34, 34. [Google Scholar] [CrossRef]
- Shevchenko, V.; Mialdun, A.; Yasnou, V.; Lyulin, Y.V.; Ouerdane, H.; Shevtsova, V. Investigation of diffusive and optical properties of vapour-air mixtures: The benefits of interferometry. Chem. Eng. Sci. 2021, 233, 116433. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarkar, B.; Yahya, B.N. Imperfect Multi-Stage Lean Manufacturing System with Rework under Fuzzy Demand. Mathematics 2019, 7, 13. [Google Scholar] [CrossRef]
- Baranov, M.; Velichko, E.; Greshnevikov, K. Analysis of Fractal Structures in Dehydrated Films of Protein Solutions. Symmetry 2021, 13, 123. [Google Scholar] [CrossRef]
- Porter, J.; Salgado Sánchez, P.; Shevtsova, V.; Yasnou, V. A review of fluid instabilities and control strategies with applications in microgravity. Math. Model. Nat. Phenom. 2021, 16, 24. [Google Scholar] [CrossRef]
- Belousov, A.I.; Sedelnikov, A.V. Probabilistic estimation of fulfilling favorable conditions to realize the gravity-sensitive processes aboard a space laboratory. Russ. Aeronaut. 2013, 56, 60–63. [Google Scholar] [CrossRef]
- Hu, W.R.; Zhao, J.F.; Long, M. Space Program SJ–10 of Microgravity Research. Microgravity Sci. Technol. 2014, 26, 159–169. [Google Scholar] [CrossRef]
- Abrashkin, V.I.; Puzin, Y.Y.; Voronov, K.E.; Piyakov, I.V.; Semkin, N.D.; Sazonov, V.V.; Chebukov, S.Y. Determining the rotational motion of the BION M-1 satellite with the GRAVITON instrument. Cosm. Res. 2015, 53, 286–299. [Google Scholar] [CrossRef]
- Taneeva, A.S.; Lukyanchik, V.V.; Khnyryova, E.S. Modeling the Dependence of the Specific Impulse on the Temperature of the Heater of an Electrothermal Micro-Motor Based on the Results of Its Tests. J. Phys. Conf. Ser. 2021, 20212096, 012059. [Google Scholar] [CrossRef]
- Sedelnikov, A.V. Modeling of microaccelerations caused by running of attitude-control engines of spacecraft with elastic structural elements. Microgravity Sci. Technol. 2016, 28, 491–498. [Google Scholar] [CrossRef]
- Liu, W.; Gao, Y.; Dong, W.; Li, Z. Flight Test Results of the Microgravity Active Vibration Isolation System in China’s Tianzhou-1 Mission. Microgravity Sci. Technol. 2018, 30, 995–1009. [Google Scholar] [CrossRef]
- Zemskov, V.S.; Raukhman, M.R.; Shalimov, V.P. Influence of an arrangement of growth installations on board the spacecraft on microgravitational conditions of carrying out experiments (on the example of bestigelny zonal melting InSb:Te on FOTON-3 artificial satellite). Cosm. Res. 2004, 42, 144–154. [Google Scholar] [CrossRef]
- Boguslavsky, A.A.; Sazonov, V.V.; Sokolov, S.M.; Zemskov, V.S.; Raukhman, M.R.; Shalimov, V.P. About influence of microaccelerations on distribution of impurity in crystals of InSb:Te which are grown up in orbital flight by method of bestigelny zonal melting. Cosm. Res. 2004, 42, 155–161. [Google Scholar]
- Bratsun, D.A.; Krasnyakov, I.V.; Zyuzgin, A.V. Active Control of Thermal Convection in a Rectangular Loop by Changing its Spatial Orientation. Microgravity Sci. Technol. 2018, 30, 43–52. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Orlov, D.I. Analysis of the significance of the influence of various components of the disturbance from a temperature shock on the level of microaccelerations in the internal environment of a small spacecraft. Microgravity Sci. Technol. 2021, 33, 22. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Serdakova, V.V.; Glushkov, S.V.; Nikolaeva, A.S.; Evtushenko, M.A. Consideration of the Initial Deformation from Natural Oscillations of Large Elastic Elements of the Spacecraft When Assessing Microaccelerations from Thermal Shock Using a Two-dimensional Model of Thermal Conductivity. Microgravity Sci. Technol. 2022, 34, 22. [Google Scholar]
- McDowell, J.C. The Low Earth Orbit Satellite Population and Impacts of the SpaceX Starlink Constellation. Astrophys. J. Lett. 2020, 892, L36. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Serdakova, V.V.; Orlov, D.I.; Nikolaeva, A.S.; Evtushenko, M.A. Modeling the Effect of a Temperature Shock on the Rotational Motion of a Small Spacecraft. Considering the Possible Loss of Large Elastic Elements Stability. Microgravity Sci. Technol. 2022, 34, 78. [Google Scholar] [CrossRef]
- Sedelnikov, A.V.; Molyavko, D.P.; Potienko, K.I. Study of over-assessment of microaccelerations when using a beam-model of elastic elements. Int. Rev. Aerosp. Eng. 2016, 9, 9–12. [Google Scholar] [CrossRef]
- Lyubimov, V.V. Method of an Asymptotic Analysis of the Nonlinear Monotonic Stability of the Oscillation at the Problem of Damping of the Angle of Attack of a Symmetric Spacecraft. Symmetry 2022, 14, 2135. [Google Scholar] [CrossRef]
- Doroshin, A.V.; Eremenko, A.V. Synthesis of dynamics of nanosatellites with variable inertial-mass parameters. J. Phys. Conf. Ser. 2022, 2182, 012049. [Google Scholar] [CrossRef]
- Kartashov, E.M.; Stomakhin, I.V. Thermal reaction of viscoelastic bodies to thermal impact on the basis of a new equation of dynamic thermoviscoelasticity. J. Eng. Phys. 1991, 59, 1116–1125. [Google Scholar] [CrossRef]
- Skvortsov, Y.V.; Evtushenko, M.A.; Khnyryova, E.S. Investigation of the edge effect in laminated composites using the ANSYS software. J. Aeronaut. Astronaut. Aviat. 2022, 54, 421–431. [Google Scholar]
- Sedelnikov, A.V.; Orlov, D.I.; Leskova, Y.D. Investigation of the dynamics of a small spacecraft elastic element temperature change under a temperature shock considering a penumbral section. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1061, 012028. [Google Scholar] [CrossRef]
- Kawano, A. A uniqueness theorem for the determination of sources in the Germain–Lagrange plate equation. J. Math. Anal. Appl. 2013, 402, 191–200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).