Abstract
This communication predominately discusses the rheological attributes of the Darcy–Forchheimer flow of a nanoliquid over a stretchy sheet with a magnetic impact. The present model considers the two diverse nanoparticles, such as and , and water as a base liquid. The heat equation accounts for the consequences of thermal radiation and a nonlinear heat sink/source when evaluating heat transmission phenomena. The current mechanical system is represented by higher-order PDEs, which are then remodeled into nonlinear higher-order ODEs that employ appropriate symmetry variables. The current mathematical systems are numerically computed by implementing the bvp4c technique. The characteristic attitudes of the related pertinent factors on the non-dimensional profiles are sketched via the figures, tables, and charts. The analysis predicts that the speed of the nanoliquid particles becomes slower when there is more presence of a magnetic field and injection/suction parameters. The growing amount of radiation is also pointed out, and the Eckert number corresponds to enriching the thermal profile.
1. Introduction
The liquid thermic conductivity acts as a key part in many mechanical and industrial procedures, such as cooling microelectronic devices, heat exchangers, solar collectors, mining processes, etc. The common base liquids such as and transmit a lower quantity of heat due to their poor thermic conductivity. Many researchers are working on perfecting the process through which base fluids transfer more heat. To improve the thermic conductivity of a base liquid, one of the most straightforward approaches is to suspend the nano-scale materials (, , , , , , and ) inserted in the base liquid. Choi and Eastman [1] were the first to initiate the nanoliquid idea. The MHD flow of water-based nanoliquid past an SS with entropy generation was analyzed by Govindaraju et al. [2]. They proved that the larger EG number was observed in nanoparticles and a lesser EG number was observed in nanoparticles. Malvandi et al. [3] probed the nanoliquid flow on an SS. They identified that the HBL (hydrodynamic boundary layer) becomes thinner when the nanoparticles are present. The effect of water-based CNTs on a superlinear stretching/shrinking sheet was reviewed by Mahabaleshwar et al. [4]. Sandeep and Sulochana [5] explored the flow of a nanoliquid with injection/suction. They revealed that the temperature profile upsurges when increasing the Brownian motion parameter. The influence of the Lorentz force in a nanoliquid flow was interpreted by Iqbal et al. [6]. Waini et al. [7] examined the uniform shearing flow on hybrid nanoliquids past a shrinking/stretching sheet. They observed that the HTG increases when the NPVF increases. Some pertinent research on this subject is emphasized in Refs. ([8,9,10,11,12,13,14,15,16,17]).
Many researchers have recently become interested in liquid flowing past a permeable space and the particles of various shapes enclosed in a porous medium. Darcy’s law is commonly used to understand the flow of porous gaps. However, this law is applicable only for poor porosity and low-velocity cases. Nowadays, the non-uniform porosity distribution and the greater flow transport occur in many problems. In this situation, Forchheimer [18] overcame this limitation by incorporating a square speed factor into the Darcian model. The numerical solution of the DF flow of a nanoliquid by a rotating disc was presented by Ullah et al. [19]. They identified that the liquid temperature enriches for a greater quantity of the Forchheimer number. Sarkar and Kundu [20] examined the -water-based nanoliquid past a vertical sheet. They found that increasing the amount of the porosity parameter caused the heat transmission rate to progress. The entropy generation of the DF flow of a nanoliquid with radiation was probed by Khan et al. [21]. They noted the liquid velocity decrepitude by raising the porosity parameter and Forchheimer number. Sureshkumar Raju et al. [22] examined the DF flow of a moving needle. They observed that the TBL thickness slumps when elevating the Forchheimer number. Hayat et al. [23] discussed the nonlinear mixed convective DF flow of viscous liquid past a nonlinear SS. They noted that the nanoliquid velocity dwindles by improving the porosity parameter. Khan et al. [24] scrutinized the DF flow of viscous liquid past an SS with homogeneous–heterogeneous reactions. The liquid velocity decrepitude was observed when upturning the quantity of the reverse Darcy number. Some essential studies on these concepts are collected in Refs. ([25,26,27,28]).
The study of viscous dissipation on heat transfer is essential, notably for high viscous flows with mild velocities. In a viscous dissipation procedure, the adhesiveness of the liquid and energy transforms from an initial to a final form. Viscous dissipation in the porous medium can be classified into two terms: the first type, the Darcy term, arises from internal heating, and the second type, the Brinkman term, arises due to frictional heating. The MHD nanoliquid flow upon a nonlinear stretched flat plate with viscous-Ohmic dissipation was studied by Pal and Mandal [29]. They noted that the Eckert number plays an opposite behavior in stretching and shrinking sheets. Das et al. [30] examined the MHD flow over a porous surface subject to viscous dissipation. They found that the surface shear stress enhances when improving the Eckert number. Bhukta et al. [31] examined how thermal dissipation affects the MHD flow through a porous medium. The Carreau liquid flow with viscous dissipation was studied by Salahuddin et al. [32]. They proved that the liquid temperature upsurges for higher values of the Eckert number. The influence of a viscously dissipated energy flow of an MHD nanoliquid past an SS was numerically investigated by Gopal et al. [33]. They noticed that the velocity profile improved when the viscous dissipation quantity was enhanced. Hussain et al. [34] discovered the effect of viscous dissipation on an MHD hyperbolic liquid over a convective boundary condition. They noted that the temperature of the liquid upsurges when raising the Eckert number. The viscous dissipative flow of an MHD nanoliquid with dual stratification was illustrated by Daniel et al. [35]. They concluded that the liquid thermal profile enhances when raising the Eckert number.
The heat source can supply an enormous amount of energy without a change in its temperature, and the heat sink can receive a tremendous amount of energy without a change in its temperature. Therefore, the heat sink/source effect is also an essential aspect of heat transmissions in many real-world problems. A few applications are the power cycle, refrigeration, and heat pump cycle. Hakeem et al. [36] explained a non-uniform heat sink/source with heat radiation in Walter’s B liquid. They proved that the liquid temperature enhanced when improving the non-uniform heat sink parameter. The reactions of a heat sink/source of an Oldroyd-B nanoliquid past an SS were presented by Sandeep and Sulochana [37]. They noticed that the LNN slumps when upturning the non-uniform heat sink parameter. The flow of an MHD Eyring–Powell liquid over an SS with a non-uniform heat sink/source was delved into by Manvi et al. [38]. They noted that the heat sink parameter causes the liquid temperature to diminish. Pal and Chatterjee [39] analyzed the convective flow of micropolar liquid past an SS with a non-uniform heat sink/source. The radiative flow of an MHD micropolar liquid on an SS with a non-uniform heat sink/source was addressed by Mabood et al. [40]. Ramandevi et al. [41] inspected an MHD flow with a CCHF with a combination of viscous dissipation and a non-uniform heat sink/source. They discovered that the irregular heat parameters had an inversely proportional relationship to the heat transmission gradient. The time-dependent flow of the MHD Williamson nanoliquid past a stretched cylinder with a non-uniform heat source/sink phenomenon was deliberated by Song et al. [42]. They proved that the space-dependent heat source parameter enriches the liquid thermal profile. Mumraiz et al. [43] numerically presented the MHD flow of a hybrid nanoliquid past a vertical annulus. They saw that the temperature-reliant heat sink/source parameter upsurges the liquid thermal profile.
The primary purpose of this research communication is to examine the MHD DF flow of the nanoliquid in water past a heated stretchy sheet. We derive the energy equations by reimplementing the Cattaneo–Christov theory, a nonlinear heat sink/source, and viscous dissipation. The flow-through stretchy sheet is significant in many disciplines, including crystal growing, paper production, glass fiber, wire drawing, etc. Our computational outcomes are unique and novel, and it is applied in the manufacturing industry to build new thermal equipment. Our conclusions are compared to those of previously published publications for confirmation intent. The MATLAB bvp4c methodology is used to make all of the representative estimations.
2. Mathematical Formulation
Consider the 2D flow of water-based nanoliquid on a heated stretchy sheet. Let direction be taken along the sheet and direction be perpendicular to the sheet. Then, the equation is used to explain the sheet’s wall’s expansion in a symmetric plane about the origin. The magnetic field is applied in direction and the induced magnetic field is not considered because of the small Reynolds number. The sheet is kept at a uniform temperature which is higher than the free stream temperature . The heat sink/source, radiation, and Cattaneo–Christov theory are added to energy transfer equations. The down part of the sheet is heated by hot liquid with temperature , which creates a heat transfer coefficient . The physical scaling of the flow model is depicted in Figure 1. The governing equations are defined with the help of the above assumptions and presented as follows, see Hamad [44], Kameswaran et al. [45], and Shankar and Gorfie [46]:
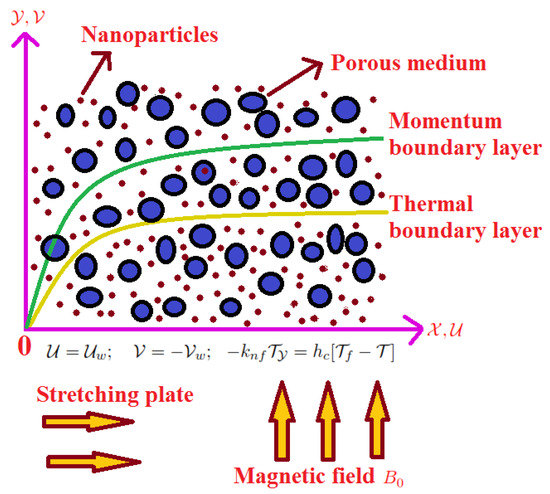
Figure 1.
Sketch of the flow model.
The corresponding boundary conditions are
The flow variable details are all in the nomenclature section.
Define the variables
The reduced boundary conditions are
Here,
The skin friction coefficient and local Nusselt number are expressed as
3. Numerical Solution
The reformatting ODE Equations (6) and (7) and corresponding boundary conditions (8) are numerically solved using the MATLAB bvp4c technique (see Eswaramoorthi et al. [47,48]). In this case, higher-order ODEs are converted into 1st ODEs.
Let .
The system of equations are
The reformatting boundary constraints are
The aforementioned problems are solved numerically by incorporating the MATLAB bvp4c function with an error of and a step size of .
4. Results and Discussion
The main goal of this segment is to examine the nanoliquid velocity, temperature, SFC, and LNN for various flow parameters. The physical properties of the nanoparticles and water are portrayed in Table 1. Table 2 presents our results which are compared with Hamad et al. [44], and it is noticed that our results perfectly coincided with Hamad et al. [44]. The contrast of the SFC and LNN for various values of , and is portrayed in Table 3 and Table 4 for the and nanoparticles. It is detected from these tables that the SFC and LNN decrease when improving the values of for both cases. The greater presence of the values improves the LNN and suppresses the SFC. Table 5 shows the upshot of the , and Bi on the LNN. It is realized that the greater amount of leads to enriching the HTG and the reverse behavior attains larger quantities of , and .

Table 1.
Physical characteristics, see Rahim et al. [49].

Table 2.
Comparison of for disparate values of with to Hamad et al. [44].

Table 3.
The contrast of SFC and LNN for different values of , Fr, M, and fw.

Table 4.
The contrast of SFC and LNN for different values of and .

Table 5.
LNN variation for various combinations of and .
Figure 2a–d draw the consequences of , and on the nanoliquid velocity profile for both nanoparticles. It is detected that the nanoliquid velocity declines as the quantity of , and heightens for both nanoparticles. It is also noted that the larger MBL occurs in the nanoparticles than the nanoparticles because the nanoparticles have a lower density than the nanoparticles. Physically, the larger porosity parameter enhances the nanoliquid resistance and this causes the nanoliquid motion to slow down. Moreover, the larger magnetic field parameters create a drag force called the Lorentz force, which slows down the liquid motion. The effectuates of the , , Ec, and M on the nanoliquid temperature for both nanoparticles are illustrated in Figure 3a–d. It is seen that the nanoliquid temperature enhances when it exalts the values of the , , Ec, and M. Physically, the higher quantity of the radiation parameter improves the energy transport rate of the liquid. Thus, the liquid temperature improves. Figure 4a–d give the effect of the , and on the nanoliquid temperature for both nanoparticles. It is observed that the liquid temperature suppresses when enhancing the and values, and the opposite trend is observed when changing the and values. Physically, the greater presence of a Biot number leads to strengthening the liquid thermal state which escalates the liquid temperature. The contrast between the SFC for distinct combinations of , and is plotted in Figure 5a–d. It is discovered that the surface shear stress declines when heightening the , values. In addition, the larger SFC occurs in the nanoparticles than in the nanoparticles. This is because the nanoparticles have a larger density than the nanoparticles. Figure 6a–d show the contrast between the LNN for various combinations of for both nanoparticles. The graph shows that the LNN grows as the values of the increase, but it slumps when enhancing the values of the for both nanoparticles.
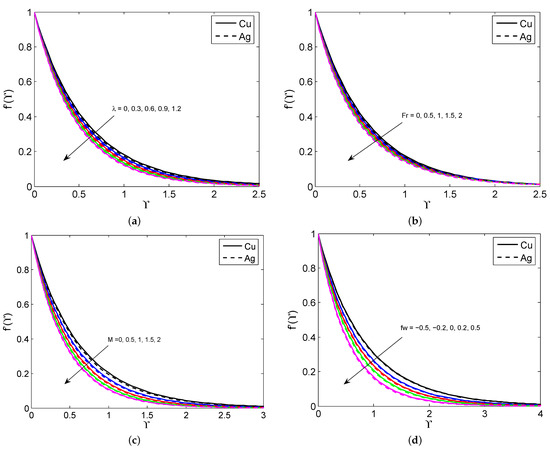
Figure 2.
The variation in against (a), Fr (b), M (c), and fw (d).
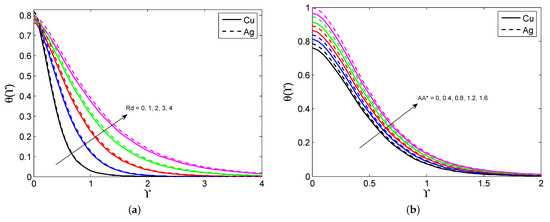
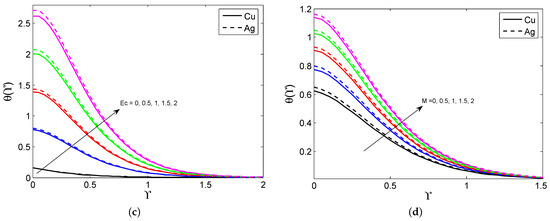
Figure 3.
The variation in against Rd (a), (b), Ec (c), and M (d).
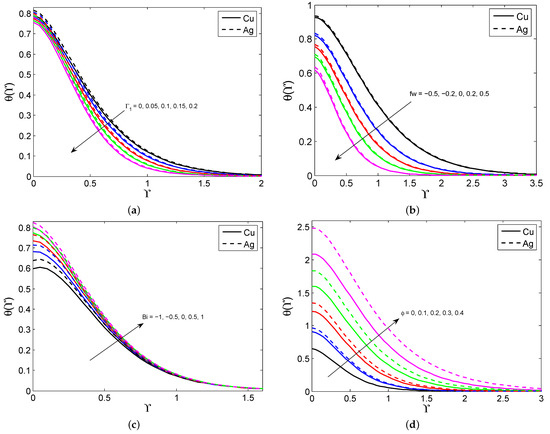
Figure 4.
The variation in against (a), fw (b), Bi (c), and (d).
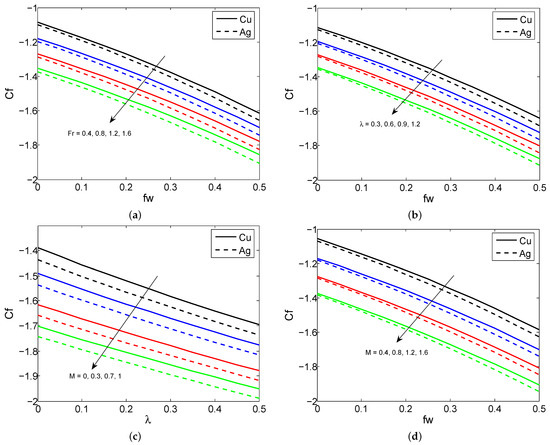
Figure 5.
The variation in SFC for diverged values of (a) , , (b) , , (c) M, , and (d) M, .
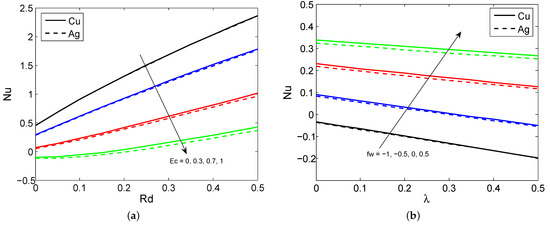
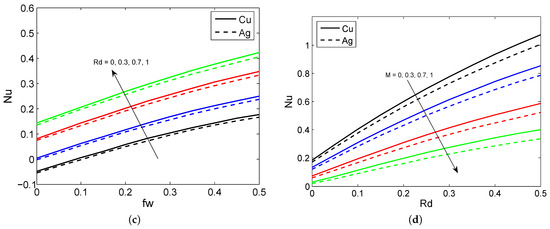
Figure 6.
The LNN variation for diverged values of (a) , , (b) , , (c) , , and (d) M, .
Figure 7a–d show the conversions of the SFC for a different combination of values of , , M, and . In the case of the porosity parameter, the highest decimating percentage (6.78%) was exhibited in the viscous nanoliquid when modifying from 0 to 0.3, and the lowest decimating percentage (3.97%) occurred in the based nanoliquid when changing from 0.9 to 1.2. In the case of the Forchheimer number, the highest decimating percentage (7.29%) was exhibited in the based nanoliquid when modifying from 0 to 0.5, and the lowest decimating percentage (4.93%) occurred in the viscous nanoliquid when modifying from 1.5 to 2. In the magnetic field parameter case, the highest decimating percentage (7.99%) was exhibited in the viscous nanoliquid when changing M from 0 to 0.3, and the lowest decimating percentage (4.42%) occurred in the based nanoliquid when modifying M from 0.9 to 1.2. In the case of the injection/suction parameter, the highest decimating percentage (12.74%) was exhibited in the based nanoliquid when modifying from 0 to 0.3, and the lowest decimating percentage (10.76%) occurred in the viscous nanoliquid when was changed from −0.6 to −0.3. The ameliorating percentage of the LNN on , , , and for all the cases are deliberated in Figure 8a–d. In the case of the Rd, the highest ameliorating percentage (74.70%) was exhibited in the based nanoliquid when changing from 0 to 0.5, and the lowest ameliorating percentage (19.99%) occurred in the viscous nanoliquid when modifying from 1.5 to 2. In the case of the heat relaxation time parameter, the highest ameliorating percentage (4.52%) was exhibited in the based nanoliquid when modifying from 0.15 to 0.2, and the lowest ameliorating percentage (2.40%) occurred in the viscous nanoliquid when modifying from 0 to 0.05. In the case of the parameter, the highest ameliorating percentage (19.78%) was exhibited in the based nanoliquid when modifying from 0.6 to 0.8, and the lowest ameliorating percentage (5.21%) occurred in the viscous nanoliquid when modifying from 0 to 0.2. In the case of the parameter, the highest ameliorating percentage (18.11%) was exhibited in the based nanoliquid when modifying from 0.6 to 0.8, and the lowest ameliorating percentage (2.89%) occurred in the viscous nanoliquid when modifying from 0 to 0.2.
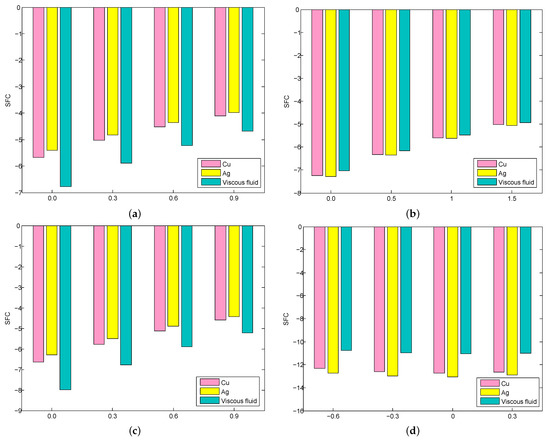
Figure 7.
The declining percentage of SFC on (a), (b), M (c), and (d).
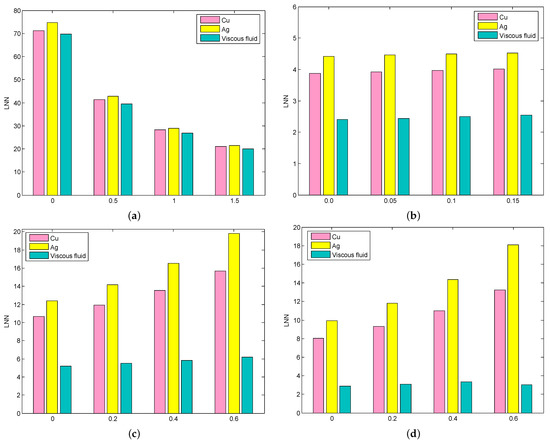
Figure 8.
The ameliorating percentage of LNN on (a), (b), (c), and (d).
5. Conclusions
The current exploration scrutinizes the consequences of a magnetic field with a Darcy–Forchheimer flow of a -based nanoliquid over a heated stretchy sheet with the CCHF theory, radiation, and viscous dissipation. Consider water as a base liquid and as a nanoliquid. First, the energy equation is framed by the heat sink/source and Cattaneo–Christov’s theory. Next, suitable symmetry variables reform the governing PDE expressions into ODE expressions. Finally, the obtained ODEs are resolved by using the BVP4c scheme. Our study’s key findings are as follows:
- The nanoliquid speed reduces when strengthening the porosity parameter, Forchheimer number, magnetic parameter, and injection/suction parameter.
- The nanoliquid warmth rises when enhancing the radiation, heat sink/source, viscous dissipation, and magnetic field parameter.
- The nanoliquid temperature declines when raising the heat relaxation time and injection/suction parameter, and it exalts when strengthening the Biot number and nanoparticle volume fraction.
- The skin friction depresses for the higher quantity of the Forchheimer number, porosity, and magnetic field parameter.
- The Nusselt number slumps when mounting the values of the Eckert number and magnetic field parameter. It strengthens the radiation and injection/suction parameters.
- In the future, we will expand this flow model to include the Riga plate and the convective heating scenario.
Author Contributions
Conceptualization, S.E. and K.L.; methodology, S.E.; software, K.L.; validation, S.E., N.A. and K.L.; formal analysis, S.D.; investigation, N.A.; resources, K.L.; data curation, N.A.; writing—original draft preparation, S.D.; writing—review and editing, K.L. and S.E.; visualization, S.E.; supervision, K.L.; project administration, N.A.; funding acquisition, N.A. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R59), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R59), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | Description |
| axes coordinates | |
| ambient temperature | |
| Biot number | |
| density | |
| dynamic viscosity | |
| dimensionless variable | |
| dimensionless temperature | |
| factors of velocity | |
| heat transfer coefficient | |
| kinematic viscosity | |
| liquid temperature | |
| nanoparticle volume fraction | |
| Nusselt number | |
| permeability of the porous medium | |
| surface stretching velocities | |
| specific heat capacity | |
| subscript represents nanoliquid and base liquid | |
| space-dependent coefficient | |
| skin friction coefficient | |
| suction/injection parameter | |
| Stefen–Boltzmann constant | |
| temperature of the hot liquid | |
| thermal conductivity | |
| temperature-dependent coefficient | |
| Eckert number | |
| Forchheimer number | |
| heat relaxation time parameter | |
| local porosity parameter | |
| magnetic field parameter | |
| Prandtl number | |
| radiation parameter | |
| Abbreviations | Expansions |
| BLT | boundary layer thickness |
| CCHF | Cattaneo–Christov heat flux |
| DF | Darcy–Forchheimer |
| EG | entropy generation |
| HTG | heat transfer gradient |
| LNN | local Nusselt number |
| MBL | momentum boundary layer |
| MHD | magnetohydrodynamics |
| NPVF | nanoparticle volume fraction |
| ODE | ordinary differential equations |
| PDE | partial differential equations |
| SS | stretching sheet/surface |
| SFC | skin friction coefficient |
| TBL | thermal boundary layer |
| WB | water based |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticle, Developments and Applications of Non-Newtonian Flows. In Proceedings of the ASME International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Volume 231, pp. 99–105. [Google Scholar]
- Govindaraju, M.; Ganesh, N.V.; Ganga, B.; Hakeem, A.A. Entropy generation analysis of magneto hydrodynamic flow of a nanofluid over a stretching sheet. J. Egypt. Math. Soc. 2015, 23, 429–434. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Ganji, D.D. Nanofluid flow on the stagnation point of a permeable non-linearly stretching/shrinking sheet. Alex. Eng. J. 2018, 57, 2199–2208. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Sneha, K.N.; Huang, H.N. An effect of MHD and radiation on CNTs-Water based nanofluids due to a stretching sheet in a Newtonian fluid. Case Stud. Therm. Eng. 2021, 28, 101462. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection. Alex. Eng. J. 2016, 55, 819–827. [Google Scholar]
- Iqbal, Z.; Mehmood, R.; Ahmad, B.; Maraj, E.N. Combined impact of viscosity variation and Lorentz force on slip flow of radiative nanofluid towards a vertical stretching surface with convective heat and mass transfer. Alex. Eng. J. 2018, 57, 3189–3197. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alex. Eng. J. 2020, 59, 91–99. [Google Scholar] [CrossRef]
- Waqas, H.; Bukhari, F.F.; Farooq, U.; Alqarni, M.S.; Muhammad, T. Numerical computation of melting heat transfer in nonlinear radiative flow of hybrid nanofluids due to permeable stretching curved surface. Case Stud. Therm. Eng. 2021, 27, 101348. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Kakar, N.; Khalid, A.; Al-Johani, A.S.; Alshammari, N.; Khan, I. Melting heat transfer of a magnetized water-based hybrid nanofluid flow past over a stretching/shrinking wedge. Case Stud. Therm. Eng. 2022, 30, 101674. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Divya, S.; Faisal, M.; Namgyel, N. Entropy and heat transfer analysis for MHD flow of-water-based nanofluid on a heated 3D plate with nonlinear radiation. Math. Probl. Eng. 2022, 2022, 7319988. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Afsharpanah, F.; Zamani, S.; Gholinia, M.; Ganji, D.D. A numerical investigation on ethylene glycol-titanium dioxide nanofluid convective flow over a stretching sheet in presence of heat generation/absorption. Case Stud. Therm. Eng. 2018, 12, 228–236. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alex. Eng. J. 2021, 60, 915–926. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. MHD flow of dusty nanofluid over a stretching surface with volume fraction of dust particles. Ain Shams Eng. J. 2016, 7, 709–716. [Google Scholar]
- Das, K.; Sarkar, A.; Kundu, P.K. Cu-water nanofluid flow induced by a vertical stretching sheet in presence of a magnetic field with convective heat transfer. Propuls. Power Res. 2017, 6, 206–213. [Google Scholar] [CrossRef]
- Ali, F.; Loganathan, K.; Eswaramoorthi, S.; Prabu, K.; Zaib, A.; Chaudhary, D.K. Heat Transfer Analysis on Carboxymethyl Cellulose Water-Based Cross Hybrid Nanofluid Flow with Entropy Generation. J. Nanomater. 2022, 2022, 5252918. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Mahdy, A.E.N.; Rashad, A.M.; Saad, W.; Seddek, L.F. Unsteady MHD mixed convection flow of Non-Newtonian Casson hybrid nanofluid in the stagnation zone of sphere spinning impulsively. Fluids 2021, 6, 197. [Google Scholar] [CrossRef]
- Forchheimer, P.Z. Wasserbewegungdurch Boden. Z. VDI 1901, 45, 1781–1788. [Google Scholar]
- Ullah, M.Z.; Serra-Capizzano, S.; Baleanu, D. A numerical simulation for Darcy-Forchheimer flow of nanofluid by a rotating disk with partial slip effects. Front. Phys. 2020, 7, 219. [Google Scholar] [CrossRef]
- Sarkar, A.; Kundu, P.K. Darcy-Forchheimer flow of Cu-water nanofluid over a vertical sheet owing to solar radiation. J. Phys. 2021, 95, 1–7. [Google Scholar] [CrossRef]
- Khan, S.A.; Hayat, T.; Alsaedi, A.; Alhodaly, M.S. Thermal analysis for radiative flow of Darcy-Forchheimer nanomaterials subject to entropy generation. J. Comput. Des. Eng. 2022, 9, 1756–1764. [Google Scholar] [CrossRef]
- Sureshkumar Raju, S.; Ganesh Kumar, K.; Rahimi-Gorji, M.; Khan, I. Darcy-Forchheimer flow and heat transfer augmentation of a viscoelastic fluid over an incessant moving needle in the presence of viscous dissipation. Microsyst. Technol. 2019, 25, 3399–3405. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Alsaedi, A. Darcy-Forchheimer flow with nonlinear mixed convection. J. Appl. Math. Mech. 2020, 41, 1685–1696. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Alsaedi, A. Numerical analysis for Darcy-Forchheimer flow in presence of homogeneous-heterogeneous reactions. Results Phys. 2017, 7, 2644–2650. [Google Scholar] [CrossRef]
- Nayak, M.K.; Shaw, S.; Khan, M.I.; Pandey, V.S.; Nazeer, M. Flow and thermal analysis on Darcy-Forchheimer flow of copper-water nanofluid due to a rotating disk: A static and dynamic approach. J. Mater. Res. Technol. 2020, 9, 7387–7408. [Google Scholar] [CrossRef]
- Mahdy, A.; El-Zahar, E.R.; Rashad, A.M.; Saad, W.; Al-Juaydi, H.S. The magneto-natural convection flow of a micropolar hybrid nanofluid over a vertical plate saturated in a porous medium. Fluids 2021, 6, 202. [Google Scholar] [CrossRef]
- Jakeer, S.; Reddy, P.B.; Rashad, A.M.; Nabwey, H.A. Impact of heated obstacle position on magneto-hybrid nanofluid flow in a lid-driven porous cavity with Cattaneo-Christov heat flux pattern. Alex. Eng. J. 2021, 60, 821–835. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Rashad, A.M.; Al-Juaydi, H.S. Studying massive suction impact on magneto-flow of a hybridized Casson nanofluid on a porous continuous moving or fixed surface. Symmetry 2022, 14, 627. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Double diffusive magnetohydrodynamic heat and mass transfer of nanofluids over a nonlinear stretching/shrinking sheet with viscous-Ohmic dissipation and thermal radiation. Propuls. Power Res. 2017, 6, 58–69. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N.; Makinde, O.D. Magnetohydrodynamic mixed convective slip flow over an inclined porous plate with viscous dissipation and Joule heating. Alex. Eng. J. 2015, 54, 251–261. [Google Scholar] [CrossRef]
- Bhukta, D.; Dash, G.C.; Mishra, S.R.; Baag, S. Dissipation effect on MHD mixed convection flow over a stretching sheet through porous medium with non-uniform heat source/sink. Ain Shams Eng. J. 2017, 8, 353–361. [Google Scholar] [CrossRef]
- Salahuddin, T.; Awais, M.; Salleh, Z. A flow study of Carreau fluid near the boundary layer region of paraboloid surface with viscous dissipation and variable fluid properties. J. Mater. Res. Technol. 2021, 14, 901–909. [Google Scholar] [CrossRef]
- Gopal, D.; Saleem, S.; Jagadha, S.; Ahmad, F.; Othman Almatroud, A.; Kishan, N. Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alex. Eng. J. 2021, 60, 1861–1871. [Google Scholar] [CrossRef]
- Hussain, A.; Malik, M.Y.; Salahuddin, T.; Rubab, A.; Khan, M. Effects of viscous dissipation on MHD tangent hyperbolic fluid over a nonlinear stretching sheet with convective boundary conditions. Results Phys. 2017, 7, 3502–3509. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J. Appl. Res. Technol. 2017, 15, 464–476. [Google Scholar] [CrossRef]
- Hakeem, A.A.; Ganesh, N.V.; Ganga, B. Effect of heat radiation in a Walter’s liquid B fluid over a stretching sheet with non-uniform heat source/sink and elastic deformation. J. King Saud Univ. Eng. Sci. 2014, 26, 168–175. [Google Scholar]
- Sandeep, N.; Sulochana, C. Momentum and heat transfer behaviour of Jeffrey, Maxwell and Oldroyd-B nanofluids past a stretching surface with non-uniform heat source/sink. Ain Shams Eng. J. 2018, 9, 517–524. [Google Scholar] [CrossRef]
- Manvi, B.; Tawade, J.; Biradar, M.; Noeiaghdam, S.; Fernandez-Gamiz, U.; Govindan, V. The effects of MHD radiating and non-uniform heat source/sink with heating on the momentum and heat transfer of Eyring-Powell fluid over a stretching. Results Eng. 2022, 14, 100435. [Google Scholar] [CrossRef]
- Pal, D.; Chatterjee, S. Effects of radiation on Darcy-Forchheimer convective flow over a stretching sheet in a micropolar fluid with non-uniform heat source/sink. J. Appl. Fluid Mech. 2015, 8, 207–212. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Rashidi, M.M.; Shadloo, M.S.; Lorenzini, G. Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int. J. Heat Mass Transf. 2016, 93, 674–682. [Google Scholar] [CrossRef]
- Ramandevi, B.; Ramana Reddy, J.V.; Sugunamma, V.; Sandeep, N. Combined influence of viscous dissipation and non-uniform heat source/sink on MHD non-Newtonian fluid flow with Cattaneo-Christov heat flux. Alex. Eng. J. 2018, 57, 1009–1018. [Google Scholar] [CrossRef]
- Song, Y.Q.; Hamid, A.; Sun, T.C.; Khan, M.I.; Qayyum, S.; Kumar, R.N.; Prasannakumara, B.C.; Khan, S.U.; Chinram, R. Unsteady mixed convection flow of magneto-Williamson nanofluid due to stretched cylinder with significant non-uniform heat source/sink features. Alex. Eng. J. 2022, 61, 195–206. [Google Scholar] [CrossRef]
- Mumraiz, S.; Ali, A.; Awais, M.; Shutaywi, M.; Shah, Z. Entropy generation in electrical magnetohydrodynamic flow of Al2O3-Cu/H2O hybrid nanofluid with non-uniform heat flux. J. Therm. Anal. Calorim. 2021, 143, 2135–2148. [Google Scholar] [CrossRef]
- Hamad, M.A.A. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2011, 38, 487–492. [Google Scholar] [CrossRef]
- Kameswaran, P.K.; Narayana, M.; Sibanda, P.; Murthy, P.V.S.N. Hydromagnetic nanofluid flow due to a stretching or shrinking sheet with viscous dissipation and chemical reaction effects. Int. J. Heat Mass Transf. 2012, 55, 7587–7595. [Google Scholar] [CrossRef]
- Shankar, B.; Gorfie, E.H. Magnetohydrodynamic nanofluid flow over a stretching sheet with thermal radiation, viscous dissipation, chemical reaction and ohmic effects. J. Nanofluids 2014, 3, 227–237. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Loganathan, K.; Faisal, M.; Botmart, T.; Shah, N.A. Analytical and numerical investigation of Darcy-Forchheimer flow of a nonlinear-radiative non-Newtonian fluid over a Riga plate with entropy optimization. Ain Shams Eng. J. 2022, 101887. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Alessa, N.; Sangeethavaanee, M.; Kayikci, S.; Namgyel, N. Mixed Convection and Thermally Radiative Flow of MHD Williamson Nanofluid with Arrhenius Activation Energy and Cattaneo–Christov Heat-Mass Flux. J. Math. 2021, 2021, 2490524. [Google Scholar] [CrossRef]
- Rahim, T.; Hasnain, J.; Abid, N.; Abbas, Z. Entropy generation for mixed convection flow in vertical annulus with two regions hydromagnetic viscous and Cu-Ag water hybrid nanofluid through porous zone: A comparative numerical study. Propuls. Power Res. 2022, 11, 401–415. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).