A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform
Abstract
:1. Introduction
2. Preliminaries
3. Construction of HPTM
4. Construction of YTDM
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roberts, M. Signals and Systems: Analysis Using Transform Methods and Matlab, 2nd ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Ortigueira, M.D.; Valério, D. Fractional Signals and Systems; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2020. [Google Scholar]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Status Solidi B 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Coussot, C.; Kalyanam, S.; Yapp, R.; Insana, M.F. Fractional derivative models for ultrasonic characterization of polymer and breast tissue viscoelasticity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 715–726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noeiaghdam, S.; Sidorov, D. Caputo-Fabrizio fractional derivative to solve the fractional model of energy supply-demand system. Math. Model. Eng. Probl. 2020, 7, 359–367. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Wakif, A.; Shah, N.A.; Singh, J. A study on cylindrical moving boundary problem with variable thermal conductivity and convection under the most realistic boundary conditions. Int. Commun. Heat Mass Transf. 2022, 138, 106312. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Rai, K.N.; Singh, J. Legendre wavelet residual approach for moving boundary problem with variable thermal physical properties. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 957–970. [Google Scholar]
- Kiliç, S.Ş.Ş.; Çelik, E. Complex solutions to the higher-order nonlinear boussinesq type wave equation transform. Ric. Mat. 2022, 1–8. [Google Scholar] [CrossRef]
- Xie, Z.; Feng, X.; Chen, X. Partial least trimmed squares regression. Chemom. Intell. Lab. Syst. 2022, 221, 104486. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.E.; Tsitouras, C. New family for Runge-Kutta-Nystrom pairs of orders 6(4)with coefficients trained to address oscillatory problems. Math. Meth. Appl. Sci. 2022, 45, 7715–7727. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Chukalin, A.V.; Simos, T.E.; Tsitouras, C. Eighth Order Two-Step Methods Trained to Perform Better onKeplerian-Type Orbits. Mathematics 2021, 9, 3071. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, H.; Kuo, L.-H. A comparison study of the lmaps method and the ldq method for time-dependent problems. Eng. Anal. Bound. Elem. 2013, 37, 1408–1415. [Google Scholar] [CrossRef]
- Harris, P.J. The mathematical modelling of the motion of biological cells in response to chemical signals. In Computational and Analytic Methods in Science and Engineering; Springer: Berlin, Germany, 2020; pp. 151–171. [Google Scholar]
- Yazgan, T.; Ilhan, E.; Çelik, E.; Bulut, H. On the new hyperbolic wave solutions to Wu-Zhang system models. Opt. Quantum Electron. 2022, 54, 1–19. [Google Scholar] [CrossRef]
- Tazgan, T.; Celik, E.; Gülnur, Y.E.L.; Bulut, H. On Survey of the Some Wave Solutions of the Non-Linear Schrödinger Equation (NLSE) in Infinite Water Depth. Gazi Univ. J. Sci. 2022, 1. [Google Scholar] [CrossRef]
- Wang, H.; Yamamoto, N. Using a partial differential equation with google mobility data to predict COVID-19 in Arizona. Math. Biosci. Eng. 2020, 17, 4891–4904. [Google Scholar] [CrossRef]
- Viguerie, A.; Lorenzo, G.; Auricchio, F. Simulating the spread of COVID-19 via a spatially-resolved susceptible-exposed-infected-recovered-deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2021, 111, 106617. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, J.J. Designing the shape of corona virus using the PDE method. Gen. Lett. Math. 2020, 8, 75–82. [Google Scholar] [CrossRef]
- Wang, L.; Liu, G.; Xue, J.; Wong, K. Channel Prediction Using Ordinary Differential Equations for MIMO systems. IEEE Trans. Veh. Technol. 2022, 1–9. [Google Scholar] [CrossRef]
- Ban, Y.; Liu, M.; Wu, P.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Depth Estimation Method for Monocular Camera Defocus Images in Microscopic Scenes. Electronics 2022, 11, 2012. [Google Scholar] [CrossRef]
- Xu, L.; Liu, X.; Tong, D.; Liu, Z.; Yin, L.; Zheng, W. Forecasting Urban Land Use Change Based on Cellular Automata and the PLUS Model. Land 2022, 11, 652. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. Aims Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Dang, W.; Guo, J.; Liu, M.; Liu, S.; Yang, B.; Yin, L.; Zheng, W. A Semi-Supervised Extreme Learning Machine Algorithm Based on the New Weighted Kernel for Machine Smell. Appl. Sci. 2022, 12, 9213. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Kbiri, M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order cahn-hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Arafa, A.A.; Hagag, A.M.S. Q-homotopy analysis transform method applied to fractional Kundu-Eckhaus equation and fractional massive Thirring model arising in quantum field theory. Asian-Eur. J. Math. 2019, 12, 1950045. [Google Scholar] [CrossRef]
- Alquran, M. Analytical solutions of fractional foam drainage equation by residual power series method. Math. Sci. 2014, 8, 153–160. [Google Scholar] [CrossRef]
- Abu Arqub, O. Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space. Fundam. Inform. 2019, 166, 87–110. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Feng, Z. The first-integral method to study the Burgers-Korteweg-de Vries equation. J. Phys. A Math. Gen. 2002, 35, 343. [Google Scholar] [CrossRef]
- Sarwar, S.; Alkhalaf, S.; Iqbal, S.; Zahid, M.A. A note on optimal homotopy asymptotic method for the solutions of fractional order heat-and wave-like partial differential equations. Comput. Math. Appl. 2015, 70, 942–953. [Google Scholar] [CrossRef]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An Improved Algorithm of Drift Compensation for Olfactory Sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear Stochastic Systems and Applications to Physics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- He, J.H. Homotopy perturbation technique, Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Ziane, D.; Cherif, M.H.; Cattani, C.; Belghaba, K. Yang-Laplace decomposition method for nonlinear system of local fractional partial differential equations. Appl. Math. Nonlinear Sci. 2019, 4, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022. [Google Scholar] [CrossRef]
- Yasmin, H.; Iqbal, N. A comparative study of the fractional-order nonlinear system of physical models via analytical methods. Math. Probl. Eng. 2022, 2022. [Google Scholar] [CrossRef]
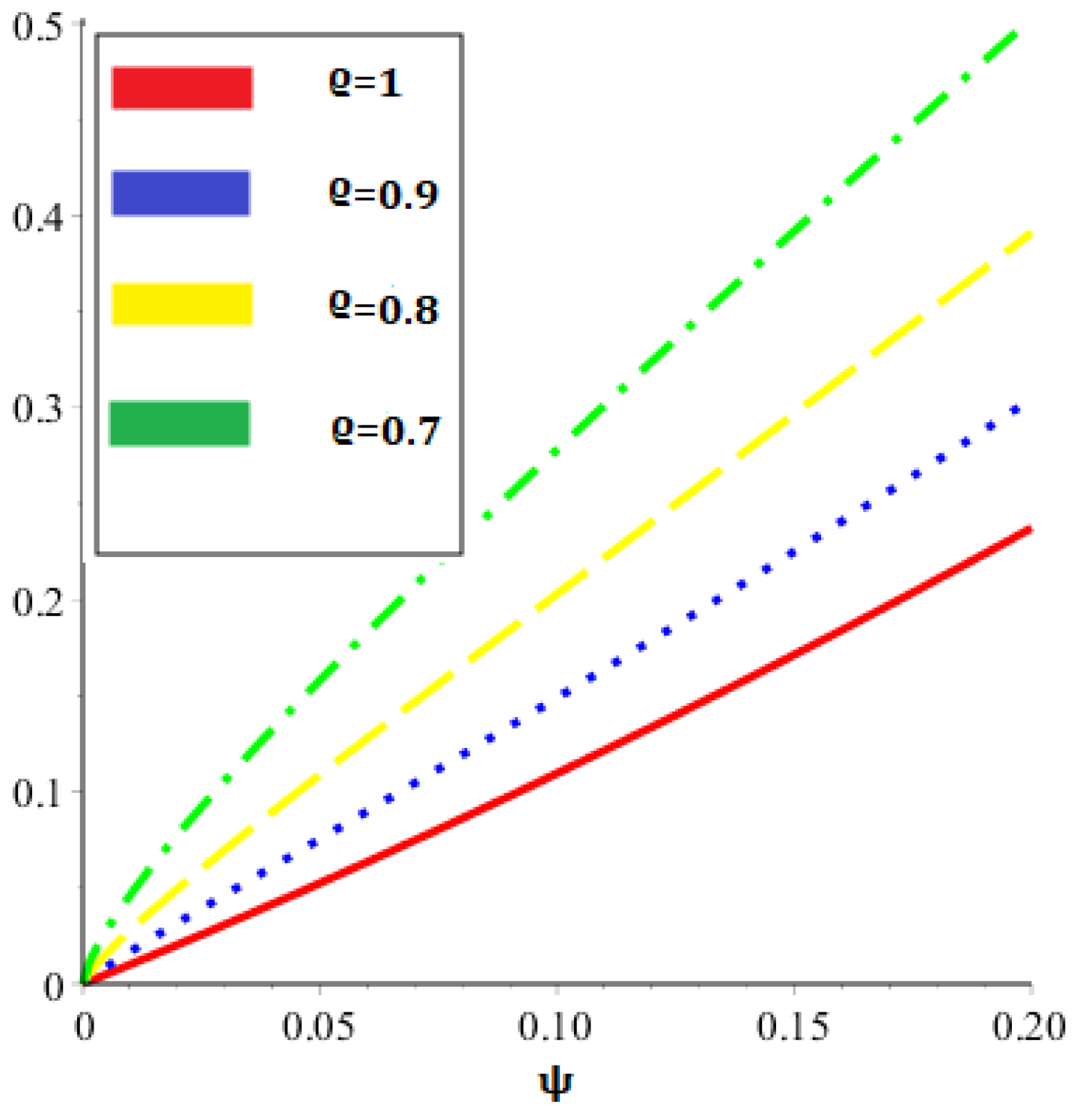
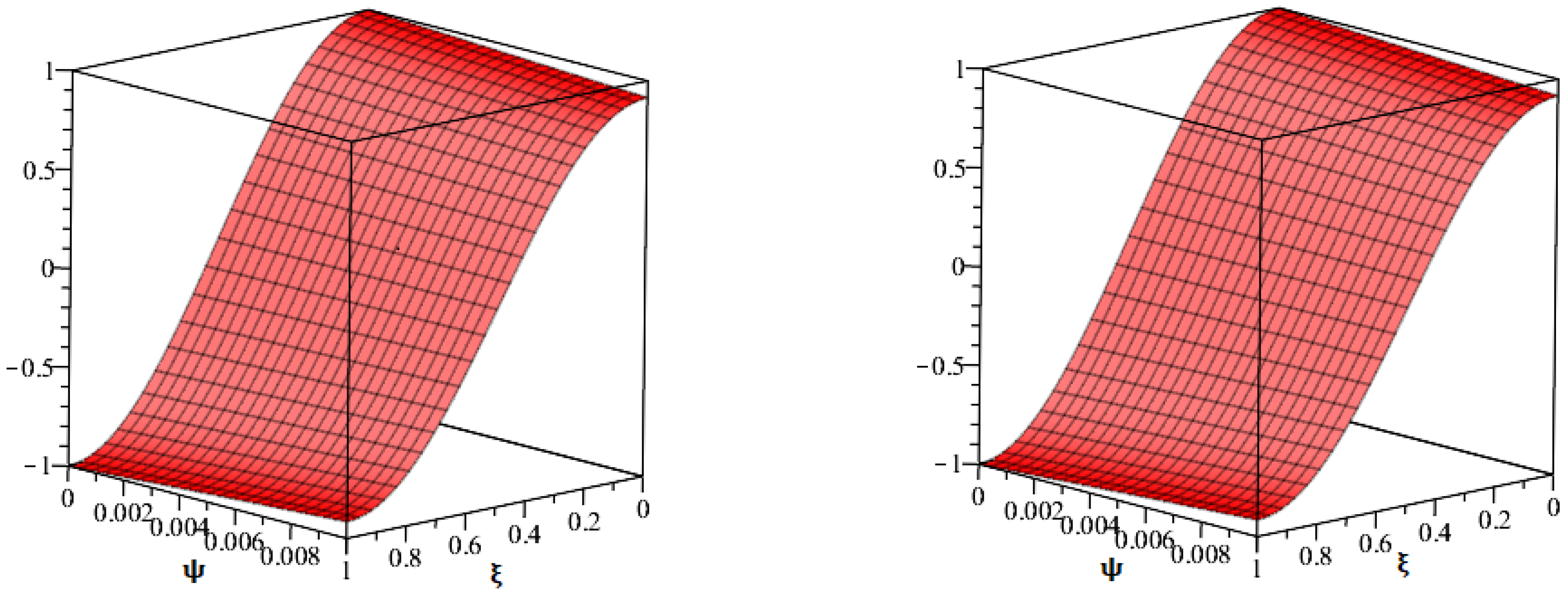
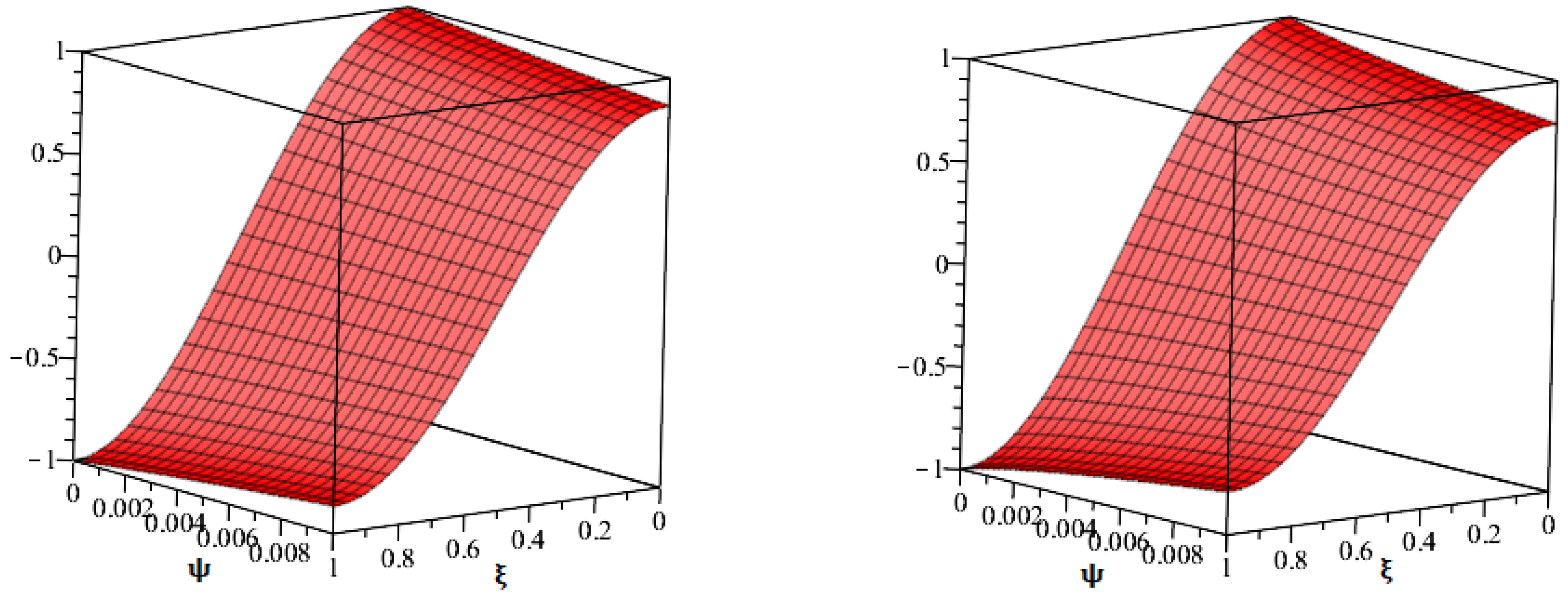

| 0.01 | 0.01176337 | 0.01118070 | 0.01062659 | 0.01010032 | 0.01010032 |
| 0.02 | 0.02330104 | 0.02229010 | 0.021322844 | 0.02040261 | 0.02040261 |
| 0.03 | 0.03490317 | 0.03351089 | 0.03217427 | 0.03090871 | 0.03090871 |
| 0.04 | 0.04662356 | 0.04487682 | 0.04319605 | 0.04162043 | 0.04162043 |
| 0.05 | 0.05848489 | 0.05640176 | 0.05439387 | 0.05253943 | 0.05253943 |
| 0.06 | 0.07049871 | 0.06809248 | 0.06576994 | 0.06366731 | 0.06366731 |
| 0.07 | 0.08267136 | 0.07995237 | 0.07732490 | 0.07500552 | 0.07500552 |
| 0.08 | 0.09500633 | 0.09198297 | 0.08905846 | 0.08655544 | 0.08655544 |
| 0.09 | 0.10750540 | 0.10418476 | 0.10096983 | 0.09831830 | 0.09831830 |
| 0.10 | 0.12016928 | 0.11655748 | 0.11305785 | 0.11029519 | 0.11029519 |
| 0.2 | 0.800752 | 0.801332 | 0.801820 | 0.801873 | 0.801873 | |
| 0.4 | 0.305860 | 0.306081 | 0.306268 | 0.306288 | 0.306288 | |
| 0.01 | 0.6 | −0.305860 | −0.306081 | −0.306268 | −0.306288 | −0.306288 |
| 0.8 | −0.800752 | −0.801332 | −0.801820 | −0.801873 | −0.801873 | |
| 1 | −0.989784 | −0.990501 | −0.991104 | −0.991169 | −0.991169 | |
| 0.2 | 0.792798 | 0.793827 | 0.794698 | 0.794792 | 0.794792 | |
| 0.4 | 0.302822 | 0.303214 | 0.303547 | 0.303583 | 0.303583 | |
| 0.02 | 0.6 | −0.302822 | −0.303214 | −0.303547 | −0.303583 | −0.303583 |
| 0.8 | −0.792798 | −0.793827 | −0.794698 | −0.794792 | −0.794792 | |
| 1 | −0.979952 | −0.981224 | −0.982301 | −0.982417 | −0.982417 | |
| 0.2 | 0.785006 | 0.786431 | 0.787643 | 0.787773 | 0.787773 | |
| 0.4 | 0.299845 | 0.300389 | 0.300852 | 0.300902 | 0.300902 | |
| 0.03 | 0.6 | −0.299845 | −0.300389 | −0.300852 | −0.300902 | −0.300902 |
| 0.8 | −0.785006 | −0.786431 | −0.787643 | −0.787773 | −0.787773 | |
| 1 | −0.970321 | −0.972082 | −0.973580 | −0.973742 | −0.973742 | |
| 0.2 | 0.777344 | 0.779129 | 0.780652 | 0.780817 | 0.780817 | |
| 0.4 | 0.296919 | 0.297600 | 0.298182 | 0.298245 | 0.298245 | |
| 0.04 | 0.6 | −0.296919 | −0.297600 | −0.298182 | −0.298245 | −0.298245 |
| 0.8 | −0.777344 | −0.779129 | −0.780652 | −0.780817 | −0.780817 | |
| 1 | −0.960850 | −0.963056 | −0.964940 | −0.965143 | −0.965143 | |
| 0.2 | 0.769797 | 0.771914 | 0.773726 | 0.773922 | 0.773922 | |
| 0.4 | 0.294036 | 0.294844 | 0.295537 | 0.295612 | 0.295612 | |
| 0.05 | 0.6 | −0.294036 | −0.294844 | −0.295537 | −0.295612 | −0.295612 |
| 0.8 | −0.769797 | −0.771914 | −0.773726 | −0.773922 | −0.773922 | |
| 1 | −0.951521 | −0.954138 | −0.956378 | −0.956620 | −0.956620 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Chung, J.D. A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform. Symmetry 2023, 15, 146. https://doi.org/10.3390/sym15010146
Naeem M, Yasmin H, Shah R, Shah NA, Chung JD. A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform. Symmetry. 2023; 15(1):146. https://doi.org/10.3390/sym15010146
Chicago/Turabian StyleNaeem, Muhammad, Humaira Yasmin, Rasool Shah, Nehad Ali Shah, and Jae Dong Chung. 2023. "A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform" Symmetry 15, no. 1: 146. https://doi.org/10.3390/sym15010146
APA StyleNaeem, M., Yasmin, H., Shah, R., Shah, N. A., & Chung, J. D. (2023). A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform. Symmetry, 15(1), 146. https://doi.org/10.3390/sym15010146









