An Efficient Approach for Solving Differential Equations in the Frame of a New Fractional Derivative Operator
Abstract
:1. Introduction
2. Mathematical Concepts
2.1. The New Fractional Derivative Operator
- 1.
- The proportional-Caputo (PC, for short) hybrid operator of order for ℏ is given by
- 2.
- The constant proportional-Caputo (CPC, for short) hybrid operator of order for ℏ is given by
- 1.
- For any we take
- 2.
- For any we take
2.2. The Reproducing Kernel Theory
- 1.
- 2.
- , and
3. The RKHS Approach
- represents the RKF associated with
- is the formal adjoint of
- is a dense countable set in
- 1.
- converges uniformly to
- 2.
- converges uniformly to
4. Numerical Experiments
- 1.
- First situation (FS, for short):
- 2.
- Second situation (SS, for short):
- 1.
- First situation (FS, for short):
- 2.
- Second situation (SS, for short):
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kapoor, M.; Shah, N.A.; Weera, W. Analytical solution of time-fractional Schrödinger equations via Shehu Adomian Decomposition Method. AIMS Math. 2022, 7, 19562–19596. [Google Scholar] [CrossRef]
- Ozkan, E.M. New exact solutions of some important nonlinear fractional partial differential Equations with beta derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, M. A local projection stabilization virtual element method for the time-fractional Burgers equation with high Reynolds numbers. Appl. Math. Comput. 2023, 436, 127509. [Google Scholar] [CrossRef]
- Iqbal, J.; Shabbir, K.; Guran, L. Stability analysis and computational interpretation of an effective semi analytical scheme for fractional order non-linear partial differential equations. Fractal Fract. 2022, 6, 393. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional view analysis of Kuramoto-Sivashinsky equations with non-singular kernel operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Cao, Q.-H.; Dai, C.-Q. Symmetric and anti-symmetric solitons of the fractional second- and third-order nonlinear Schrödinger equation. Chin. Phys. Lett. 2021, 38, 090501. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, Y.-L.; Wang, X.-T. Lie symmetry analysis of the time fractional generalized KdV equations with variable coefficients. Symmetry 2019, 11, 1281. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: San Diego, CA, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simulat 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 2004, 154, 621–640. [Google Scholar] [CrossRef]
- Akgül, A. A novel method for a fractional derivative with non-local and non-singular kernel. Chaos Solitons Fractals 2018, 144, 478–482. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D.; Fokas, A.S. Solving PDEs of fractional order using the unified transform method. Appl. Math. Comput. 2018, 339, 738–749. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Fernandez, A.; Akgül, A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef] [Green Version]
- Zaremba, S. Sur le calcul numérique des fonctions demandées dans le problème de Dirichlet et le problème hydrodynamique. Bull. Int. de l’Académie Sci. Crac. 1908, 68, 125–195. [Google Scholar]
- Geng, F.; Cui, M. New method based on the HPM and RKHSM for solving forced Duffing equations with integral boundary conditions. J. Comput. Appl. Math. 2009, 233, 165–172. [Google Scholar] [CrossRef] [Green Version]
- Geng, F.; Cui, M. A reproducing kernel method for solving nonlocal fractional boundary value problems. Appl. Math. Lett. 2012, 25, 818–823. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Tian, T. Numerical solution of nonlinear Volterra integro-differential equations of fractional order by the reproducing kernel method. Appl. Math. Model. 2015, 39, 4871–4876. [Google Scholar] [CrossRef]
- Babolian, E.; Javadi, S.; Moradi, E. RKM for solving Bratu-type differential equations of fractional order. Math Methods Appl. Sci. 2016, 39, 1548–1557. [Google Scholar] [CrossRef]
- Sakar, M.G. Iterative reproducing kernel Hilbert spaces method for Riccati differential equation. J. Comput. Appl. Math. 2017, 309, 163–174. [Google Scholar] [CrossRef]
- Sakar, M.G.; Saldir, O.; Akgül, A. A novel technique for fractional Bagley-Torvik equation. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2018, 59, 539–545. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific Publishing: Singapore, 2012. [Google Scholar]
- Anderson, D.R.; Ulness, D.J. Newly Defined Conformable Derivatives. Adv. Dyn. Syst. Appl. 2015, 10, 109–137. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Jarad, F.; Alqudah, M.A.; Abdeljawad, T. On more general forms of proportional fractional operators. Open Math. 2020, 18, 167–176. [Google Scholar] [CrossRef]
- Cui, M.; Lin, Y. Nonlinear Numerical Analysis in the Reproducing Kernel Space; Nova Science Publishers, Inc.: New York, NY, USA, 2009. [Google Scholar]

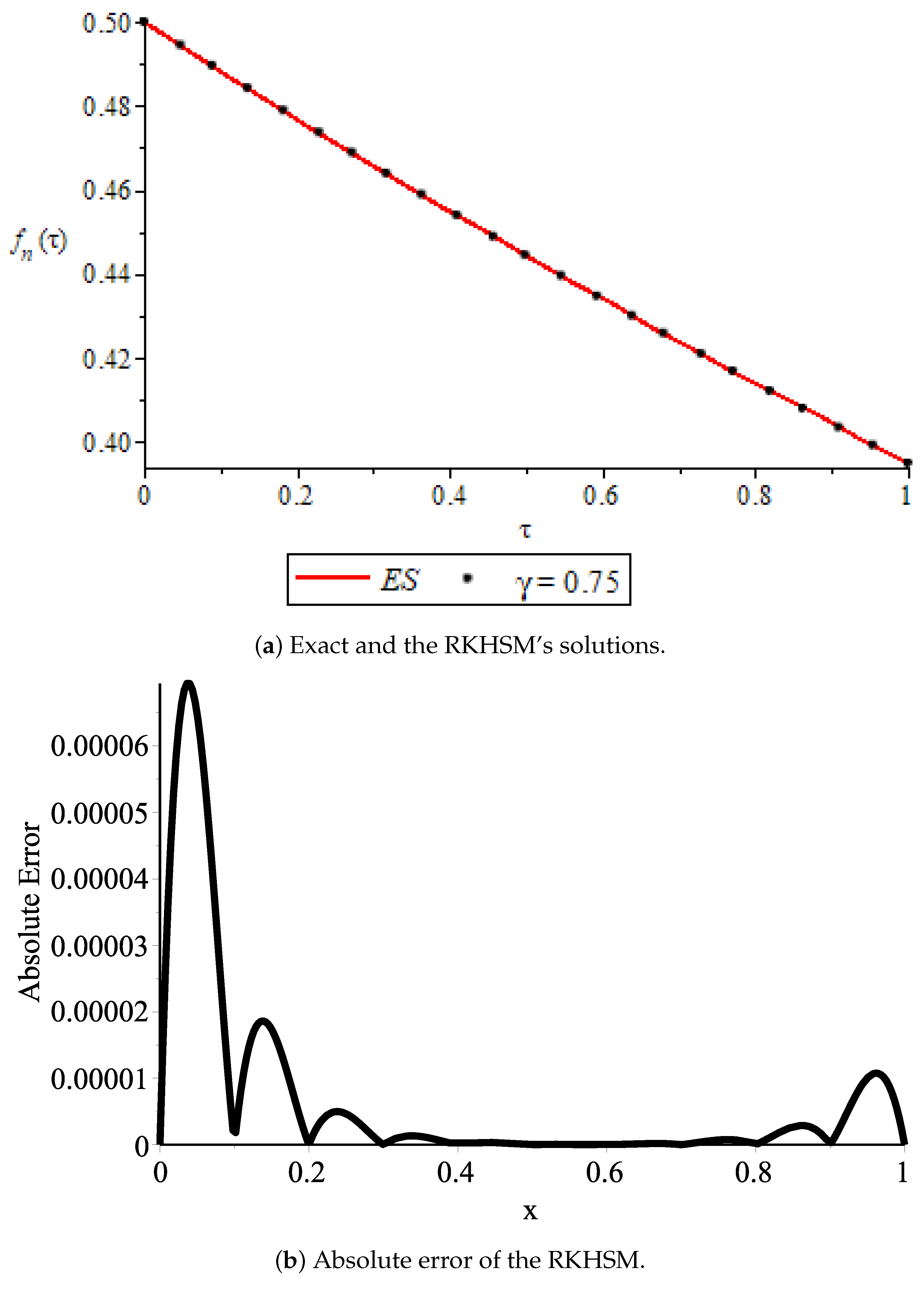


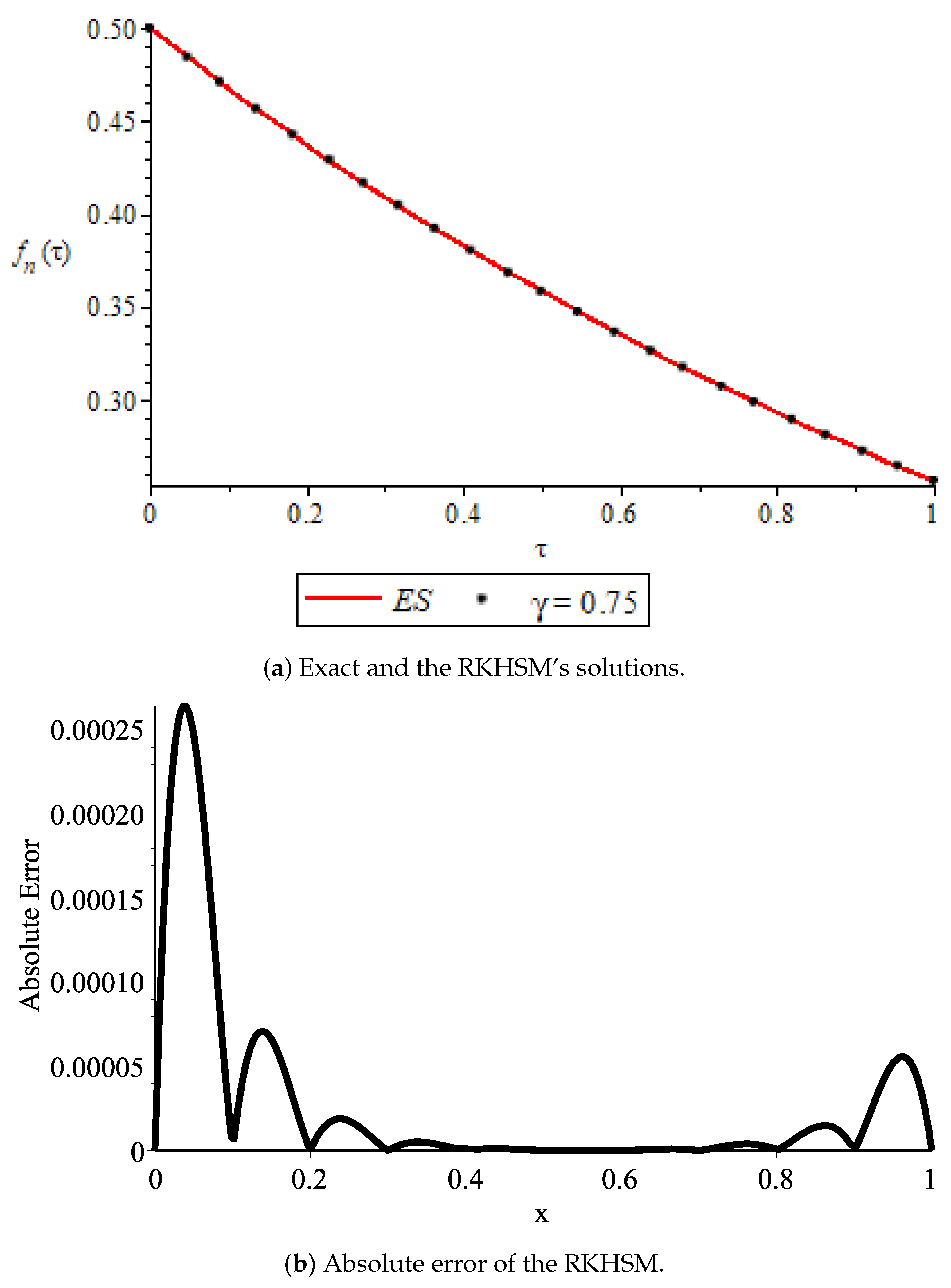

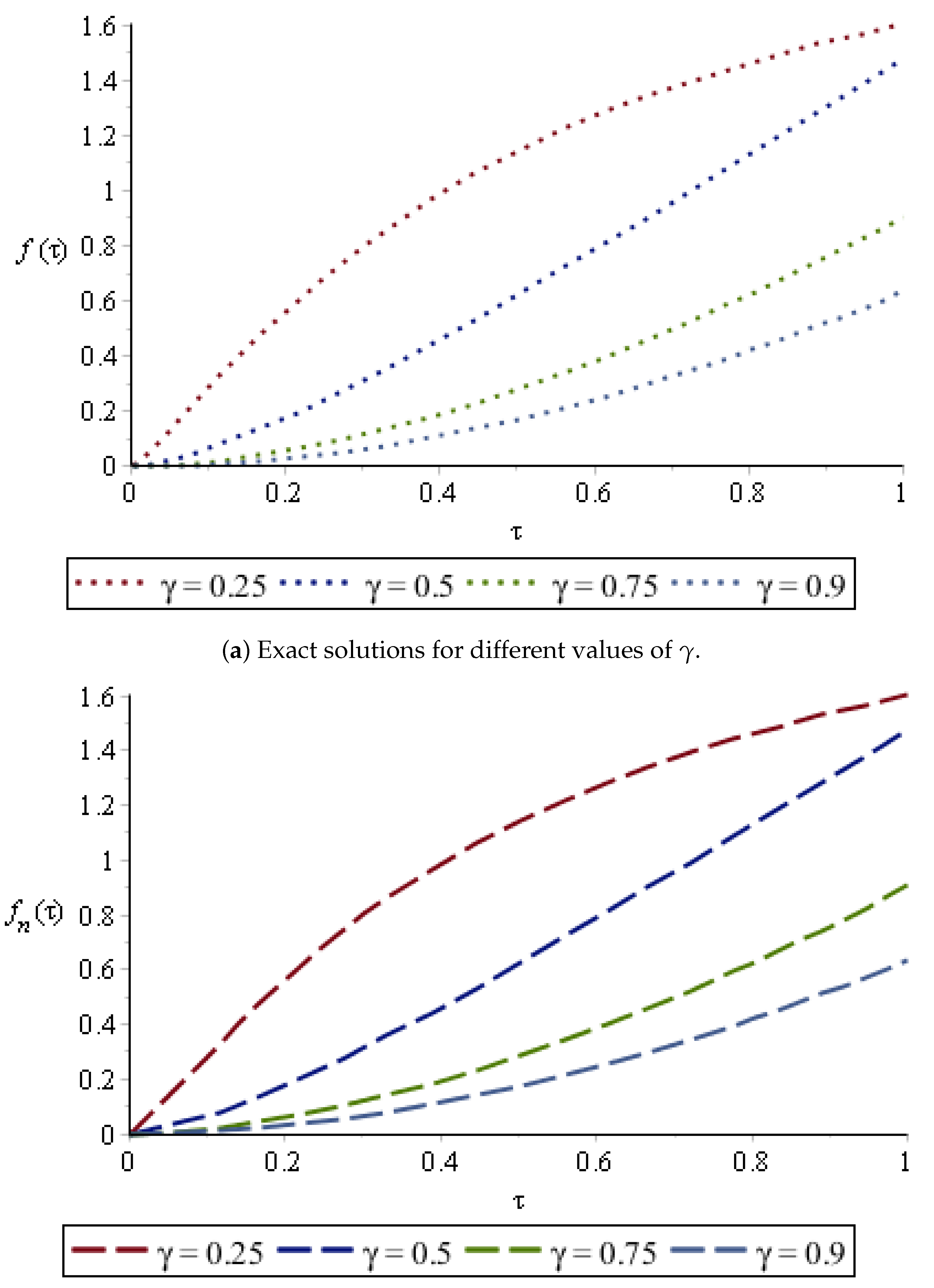
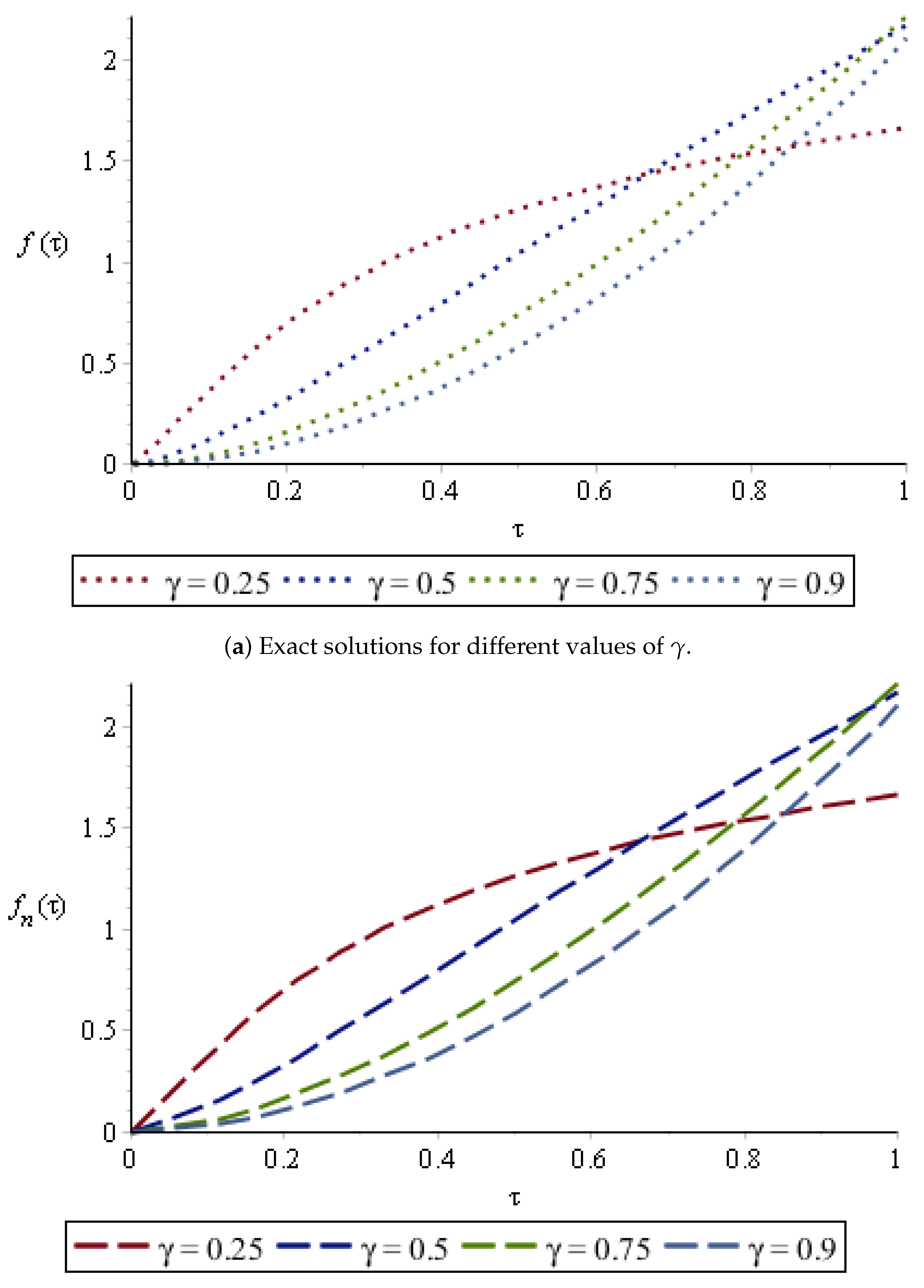
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 0 | 0 | 0 | 0 | 0 | |||||
| 1 | |||||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | ||||||||
| 1 | |||||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 0 | 0 | 0 | 0 | 0 | |||||
| 1 | |||||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 1 | 0 | 0 | |||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 1 | |||||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 1 | 0 | 0 | |||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 1 | |||||||||
| First Situation | Second Situation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| t | ES | AS | AE | RE | ES | AS | AE | RE | |
| 1 | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attia, N.; Akgül, A.; Seba, D.; Nour, A.; la Sen, M.D.; Bayram, M. An Efficient Approach for Solving Differential Equations in the Frame of a New Fractional Derivative Operator. Symmetry 2023, 15, 144. https://doi.org/10.3390/sym15010144
Attia N, Akgül A, Seba D, Nour A, la Sen MD, Bayram M. An Efficient Approach for Solving Differential Equations in the Frame of a New Fractional Derivative Operator. Symmetry. 2023; 15(1):144. https://doi.org/10.3390/sym15010144
Chicago/Turabian StyleAttia, Nourhane, Ali Akgül, Djamila Seba, Abdelkader Nour, Manuel De la Sen, and Mustafa Bayram. 2023. "An Efficient Approach for Solving Differential Equations in the Frame of a New Fractional Derivative Operator" Symmetry 15, no. 1: 144. https://doi.org/10.3390/sym15010144
APA StyleAttia, N., Akgül, A., Seba, D., Nour, A., la Sen, M. D., & Bayram, M. (2023). An Efficient Approach for Solving Differential Equations in the Frame of a New Fractional Derivative Operator. Symmetry, 15(1), 144. https://doi.org/10.3390/sym15010144









