Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices
Abstract
:1. Introduction
Entropy Related to Valency-Based Indices
- Entropy related to the 1st -Banhatti index
- Entropy related to the 2nd -Banhatti index
- Entropy related to the 1st hyper Banhatti index
- Entropy related to the 2nd hyper Banhatti index
- The first redefined Zagreb entropy
- The second redefined Zagreb entropy
- The third redefined Zagreb entropy
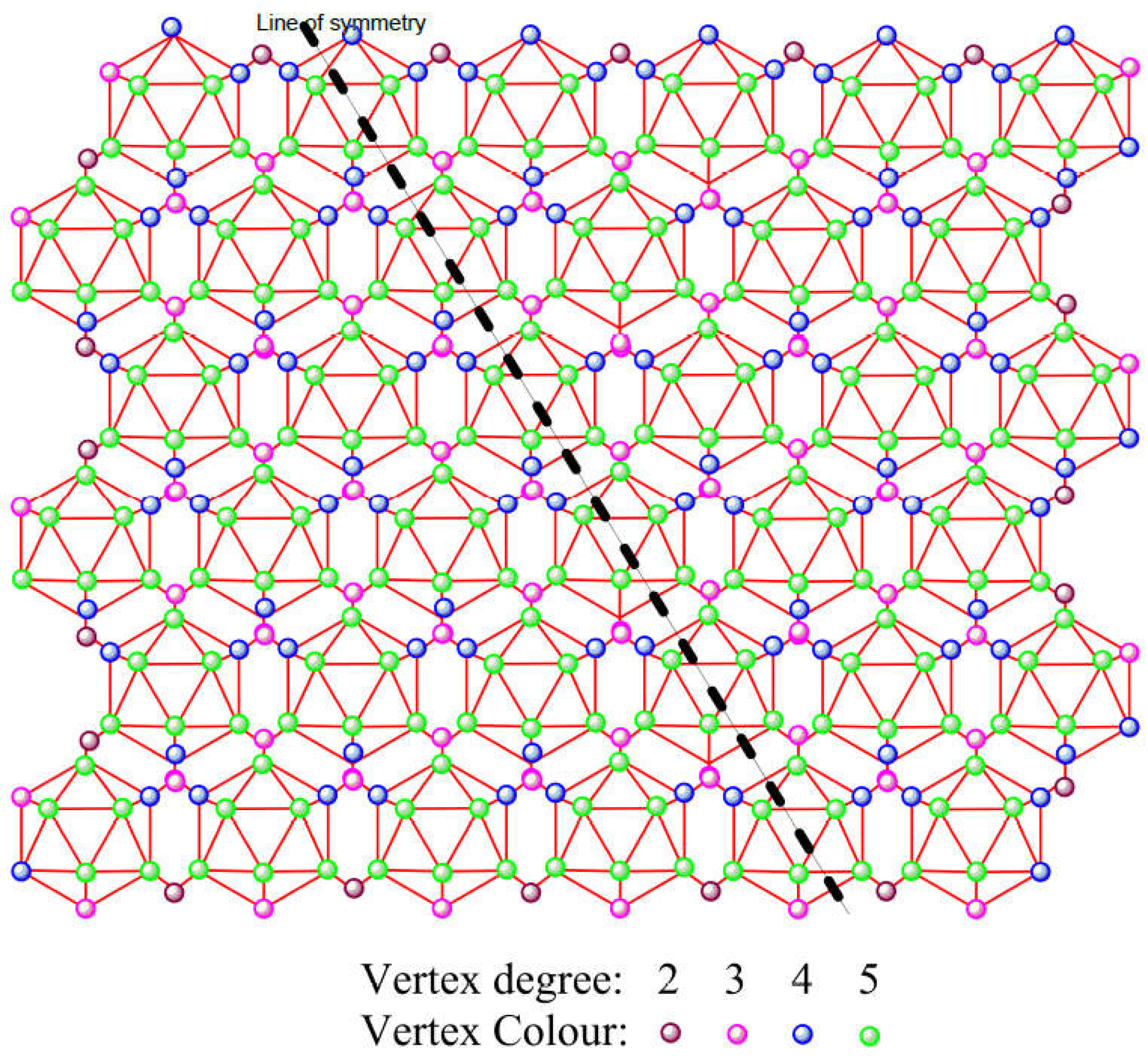
2. The Boron Network
2.1. Results and Discussion
- The 1st -Banhatti entropy of
- The second -Banhatti entropy of
- The 1st hyper -Banhatti entropy of
- The 2nd hyper -Banhatti entropy of
- The 1st redefined Zagreb entropy of
- The 2nd redefined Zagreb entropy of
- The 3rd redefined Zagreb entropy of
2.2. Comparison of K-Banhatti and Redefined Zagreb Indices of
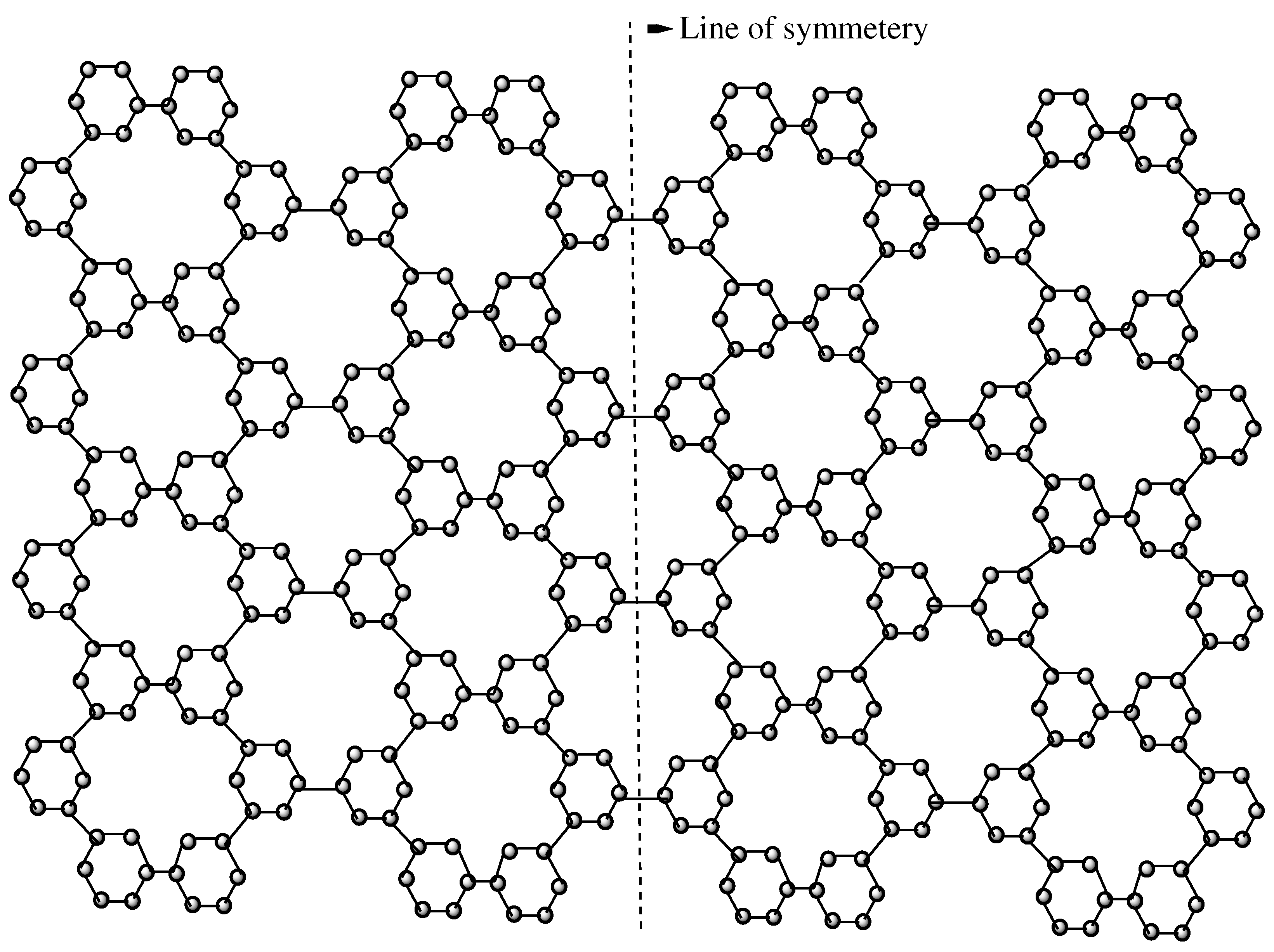
3. The Polyphenylenes Network
- Entropy related to the 1st -Banhatti index of
- Entropy related to 2nd -Banhatti index of
- Entropy related to the 1st hyper Banhatti index of
- Entropy related to the 2nd hyper Banhatti index of
- Entropy related to the 1st redefined Zagreb index of
- Entropy related to the 2nd redefined Zagreb in the index of
- Entropy related to the 3rd redefined Zagreb index of
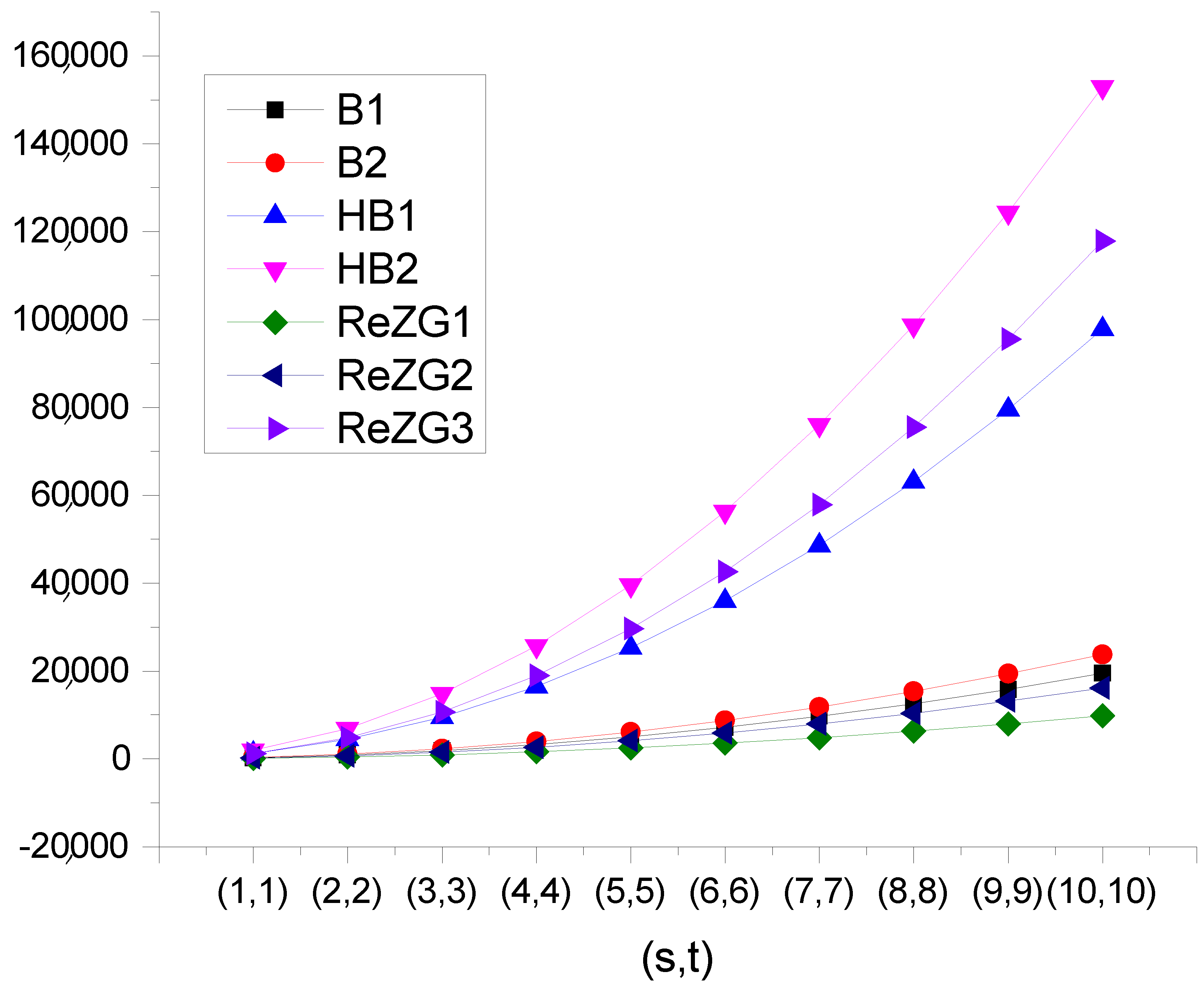
Comparison of K-Banhatti and Redefined Zagreb Indices of
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tag El Din, E.S.M.; Sultan, F.; Ghani, M.U.; Liu, J.-B.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Alhushaybari, A. Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO 4 Embedded in a Chain of Silicates. Molecules 2022, 28, 201. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, A.R.; Ghani, M.U.; Ghaffar, A.; Inc, M. Computation of Zagreb Polynomials and Zagreb Indices for Benzenoid Triangular & Hourglass System. Polycycl. Aromat. Compd. 2022. [Google Scholar] [CrossRef]
- Kulli, V.R. HDR Zagreb Indices of Remdesivir, Chloroquine, Hydroxychloroquine: Research for the Treatment of COVID-19. SSRG Int. J. Appl. Chem. 2022, 9, 1–9. [Google Scholar]
- Ghani, M.U.; Sultan, F.; El Sayed, M.; Cancan, M.; Ali, S. SiO4 Characterization in a Chain and C6H6 Embedded in a Non-Kekulean Structure for Kulli Temperature Indices. Preprints 2022. under review. [Google Scholar] [CrossRef]
- Ali, A.; Furtula, B.; Redžepović, I.; Gutman, I. Atom-bond sum-connectivity index. J. Math. Chem. 2022, 60, 2081–2093. [Google Scholar] [CrossRef]
- Chartrand, G.; Eroh, L.; Johnson, M.A.; Oellermann, O.R. Resolvability in graphs and the metric dimension of a graph. Discret. Appl. Math. 2000, 105, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Alam, A.; Ghani, M.U.; Kamran, M.; Shazib Hameed, M.; Hussain Khan, R.; Baig, A.Q. Degree-Based Entropy for a Non-Kekulean Benzenoid Graph. J. Math. 2022, 2022, 2288207. [Google Scholar]
- Zhang, Y.F.; Ghani, M.U.; Sultan, F.; Inc, M.; Cancan, M. Connecting SiO4 in Silicate and Silicate Chain Networks to Compute Kulli Temperature Indices. Molecules 2022, 27, 7533. [Google Scholar] [CrossRef]
- Kulli, V.R. On K Banhatti indices of graphs. J. Comput. Math. Sci. 2016, 7, 213–218. [Google Scholar]
- Kulli, V.R.; On, K. On K hyper-Banhatti indices and coindices of graphs. Int. Res. J. Pure Algebra 2016, 6, 300–304. [Google Scholar]
- Kulli, V.R. On multiplicative K Banhatti and multiplicative K hyper-Banhatti indices of V-Phenylenic nanotubes and nanotorus. Ann. Pure Appl. Math. 2016, 11, 145–150. [Google Scholar]
- Ranjini, P.S.; Lokesha, V.; Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 2013, 1, 116–121. [Google Scholar]
- Ali, S.; Falcón, R.M.; Mahmood, M.K. Local fractional metric dimension of rotationally symmetric planar graphs arisen from planar chorded cycles. arXiv 2021, arXiv:2105.07808. [Google Scholar]
- Ali, S.; Mahmmod, M.K.; Falcón Ganfornina, R.M. A paradigmatic approach to investigate restricted hyper totient graphs. AIMS Math. 2021, 6, 3761–3771. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Hayat, S. Computing distance-based topological descriptors of complex chemical networks: New theoretical techniques. Chem. Phys. Lett. 2017, 688, 51–58. [Google Scholar] [CrossRef]
- Hu, M.; Ali, H.; Binyamin, M.A.; Ali, B.; Liu, J.B.; Fan, C. On distance-based topological descriptors of chemical interconnection networks. J. Math. 2021, 2021, 5520619. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Kavitha, S.; Balasubramanian, K. Vertex cut method for degree and distance-based topological indices and its applications to silicate networks. J. Math. Chem. 2016, 54, 1728–1747. [Google Scholar] [CrossRef]
- Rashid, T.; Faizi, S.; Zafar, S. Distance based entropy measure of interval-valued intuitionistic fuzzy sets and its application in multicriteria decision-making. Adv. Fuzzy Syst. 2018, 2018, 3637897. [Google Scholar] [CrossRef]
- Anjum, M.S.; Safdar, M.U. K Banhatti and K hyper-Banhatti indices of nanotubes. Eng. Appl. Sci. Lett. 2019, 2, 19–37. [Google Scholar] [CrossRef]
- Asghar, A.; Rafaqat, M.; Nazeer, W.; Gao, W. K Banhatti and K hyper Banhatti indices of circulant graphs. Int. J. Adv. Appl. Sci. 2018, 5, 107–109. [Google Scholar] [CrossRef]
- Kulli, V.R.; Chaluvaraju, B.; Boregowda, H.S. Connectivity Banhatti indices for certain families of benzenoid systems. J. Ultra Chem. 2017, 13, 81–87. [Google Scholar] [CrossRef]
- Manzoor, S.; Siddiqui, M.K.; Ahmad, S. On entropy measures of molecular graphs using topological indices. Arab. J. Chem. 2020, 13, 6285–6298. [Google Scholar] [CrossRef]
- Ghani, M.U.; Sultan, F.; Tag El Din, E.S.M.; Khan, A.R.; Liu, J.B.; Cancan, M. A Paradigmatic Approach to Find the Valency-Based K-Banhatti and Redefined Zagreb Entropy for Niobium Oxide and a Metal–Organic Framework. Molecules 2022, 27, 6975. [Google Scholar] [CrossRef]
- Imran, M.; Ali, M.A.; Ahmad, S.; Siddiqui, M.K.; Baig, A.Q. Topological Characterization of the Symmetrical Structure of Bismuth Tri-Iodide. Symmetry 2018, 10, 201. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Rodriguez, N.; Miramontes, O. Shannon Entropy: An Econophysical Approach to Cryptocurrency Portfolios. Entropy 2022, 24, 1583. [Google Scholar] [CrossRef] [PubMed]
- Furlong, R.; Hilal, M.; O’Brien, V.; Humeau-Heurtier, A. Parameter Analysis of Multiscale Two-Dimensional Fuzzy and Dispersion Entropy Measures Using Machine Learning Classification. Entropy 2021, 23, 1303. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Dehmer, M.; Shi, Y. A Note on Distance-based Graph Entropies. Entropy 2014, 16, 5416–5427. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B.D. Estimating Mixture Entropy with Pairwise Distances. Entropy 2017, 19, 361. [Google Scholar] [CrossRef] [Green Version]
- Cui, W.-H.; Ye, J. Generalized Distance-Based Entropy and Dimension Root Entropy for Simplified Neutrosophic Sets. Entropy 2018, 20, 844. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Gao, J.; Wei, D. A New Belief Entropy Based on Deng Entropy. Entropy 2019, 21, 987. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Mowshowitz, A.; Emmert-Streib, F. On Properties of Distance-Based Entropies on Fullerene Graphs. Entropy 2019, 21, 482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misagh, F.; Yari, G. Interval Entropy and Informative Distance. Entropy 2012, 14, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Yang, N.; Ding, X.; Ma, L. An unsupervised feature selection algorithm: Laplacian score combined with distance-based entropy measure. In Proceedings of the 2009 Third International Symposium on Intelligent Information Technology Application, Nanchang, China, 21–22 November 2009; Volume 3. [Google Scholar]
- Ghani, M.U.; Kashif Maqbool, M.; George, R.; Ofem, A.E.; Cancan, M. Entropies Via Various Molecular Descriptors of Layer Structure of H3BO3. Mathematics 2022, 10, 4831. [Google Scholar] [CrossRef]
- Saeed, N.; Long, K.; Mufti, Z.S.; Sajid, H.; Rehman, A. Degree-based topological indices of boron B12. J. Chem. 2021, 2021, 5563218. [Google Scholar] [CrossRef]
- Oganov, A.R.; Chen, J.; Gatti, C.; Ma, Y.; Ma, Y.; Glass, C.W.; Liu, Z.; Yu, T.; Kurakevych, O.O.; Solozhenko, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boustani, I. Systematic ab initio investigation of bare boron clusters: mDetermination of the geometryand electronic structures of B n (n = 2–14). Phys. Rev. B 1997, 55, 16426. [Google Scholar] [CrossRef]
- Li, H.; Shao, N.; Shang, B.; Yuan, L.F.; Yang, J.; Zeng, X.C. Icosahedral B12-containing core–shell structures of B 80. Chem. Commun. 2010, 46, 3878–3880. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.; Numan, M.; Butt, S.I.; Siddiqui, M.K.; Ullah, R.; Ali, U. Computing Topological Indices for Molecules Structure of Polyphenylene via M-Polynomials. Polycycl. Aromat. Compd. 2022, 42, 1103–1112. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Shen, P.; Chen, Z. Two-dimensional polyphenylene: Experimentally available porous graphene as a hydrogen purification membrane. Chem. Commun. 2010, 46, 3672–3674. [Google Scholar] [CrossRef]
- Deng, H.; Yang, J.; Xia, F. A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Comput. Math. Appl. 2011, 61, 3017–3023. [Google Scholar] [CrossRef]
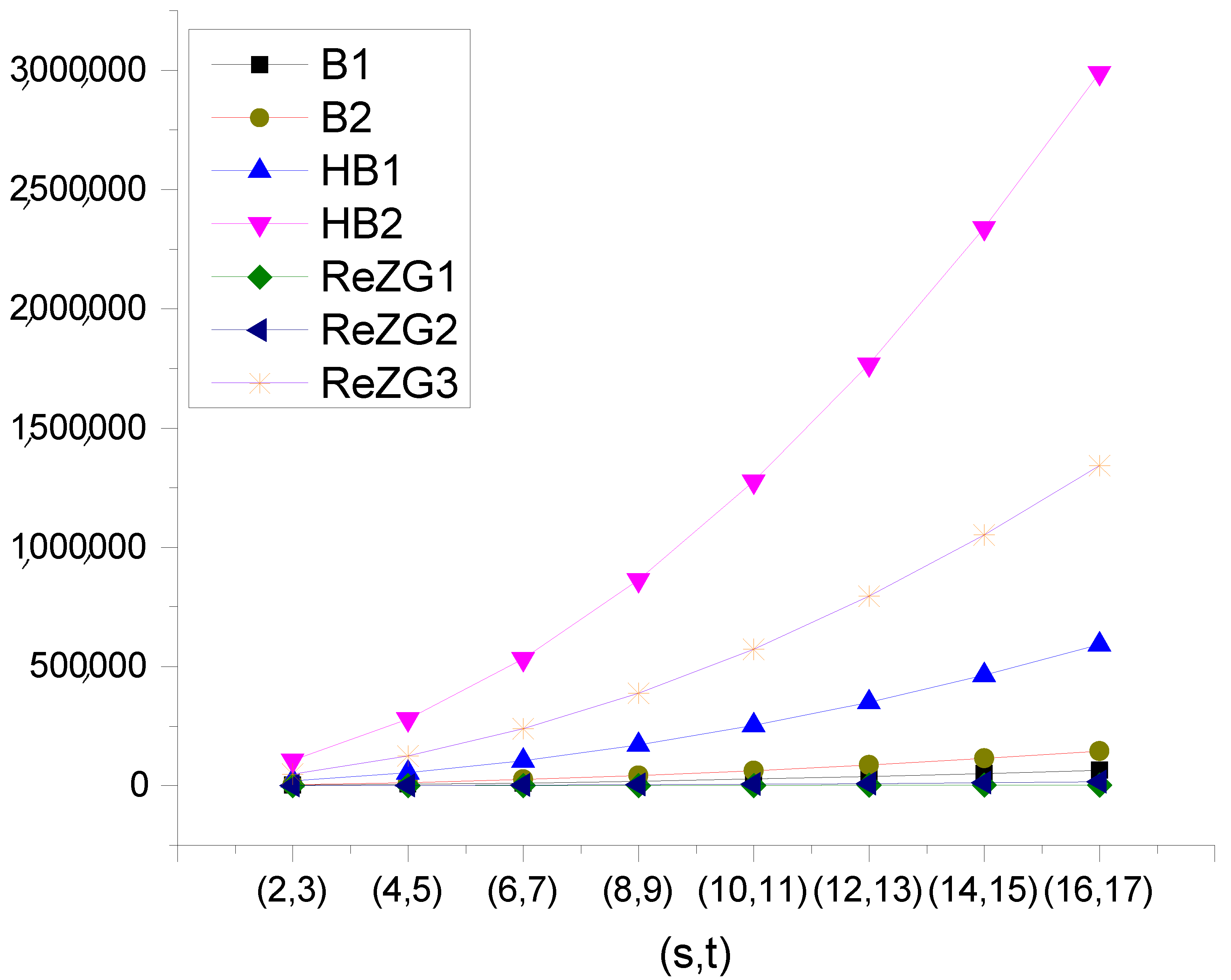
| (2, 3) | 2393 | 5269 | 21,462 | 106,319 | 130 | 586.35 | 48,012 |
| (4, 5) | 6177 | 13,707 | 55,722 | 278,973 | 328 | 1516.20 | 125,520 |
| (6, 7) | 11,689 | 26,033 | 105,726 | 531,403 | 614 | 2872.20 | 238,884 |
| (8, 9) | 18,929 | 42,247 | 171,474 | 863,609 | 988 | 4654.36 | 388,104 |
| (10, 11) | 27,897 | 62,349 | 252,966 | 1,275,591 | 1450 | 6862.68 | 573,180 |
| (12, 13) | 38,593 | 86,339 | 350,202 | 1,767,349 | 2000 | 9497.16 | 794,112 |
| (14, 15) | 51,017 | 114,217 | 463,182 | 2,338,883 | 2638 | 12,557.80 | 1,050,900 |
| (16, 17) | 65,169 | 145,983 | 591,906 | 2,990,193 | 3364 | 16,044.60 | 1,343,544 |
| Edge-Partition | |||
|---|---|---|---|
| Number of bonds |
| (1, 1) | 256 | 312 | 1280 | 1992 | 120 | 198 | 1236 |
| (2, 2) | 888 | 1084 | 4448 | 6940 | 432 | 712 | 4816 |
| (3, 3) | 1896 | 2316 | 9504 | 14,844 | 936 | 1542 | 10,740 |
| (4, 4) | 3280 | 4008 | 16,448 | 25,704 | 1632 | 2688 | 19,008 |
| (5, 5) | 5040 | 6160 | 25,280 | 39,520 | 2520 | 4150 | 29,620 |
| (6, 6) | 7176 | 8772 | 36,000 | 56,292 | 3600 | 5928 | 42,576 |
| (7, 7) | 9688 | 11,844 | 48,608 | 76,020 | 4872 | 8022 | 57,876 |
| (8, 8) | 12,576 | 15,376 | 63,104 | 98,704 | 6336 | 10,432 | 75,520 |
| (9, 9) | 15,840 | 19,368 | 79,488 | 124,344 | 7992 | 13,158 | 95,508 |
| (10, 10) | 19,480 | 23,820 | 97,760 | 152,940 | 9840 | 16,200 | 117,840 |
| (11, 11) | 23,496 | 28,732 | 117,920 | 184,492 | 11,880 | 19,558 | 142,516 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghani, M.U.; Campena, F.J.H.; Ali, S.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Galal, A.M. Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices. Symmetry 2023, 15, 143. https://doi.org/10.3390/sym15010143
Ghani MU, Campena FJH, Ali S, Dehraj S, Cancan M, Alharbi FM, Galal AM. Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices. Symmetry. 2023; 15(1):143. https://doi.org/10.3390/sym15010143
Chicago/Turabian StyleGhani, Muhammad Usman, Francis Joseph H. Campena, Shahbaz Ali, Sanaullah Dehraj, Murat Cancan, Fahad M. Alharbi, and Ahmed M. Galal. 2023. "Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices" Symmetry 15, no. 1: 143. https://doi.org/10.3390/sym15010143
APA StyleGhani, M. U., Campena, F. J. H., Ali, S., Dehraj, S., Cancan, M., Alharbi, F. M., & Galal, A. M. (2023). Characterizations of Chemical Networks Entropies by K-Banhatii Topological Indices. Symmetry, 15(1), 143. https://doi.org/10.3390/sym15010143










