Conductive Heat Transfer in Materials under Intense Heat Flows
Abstract
:1. Introduction
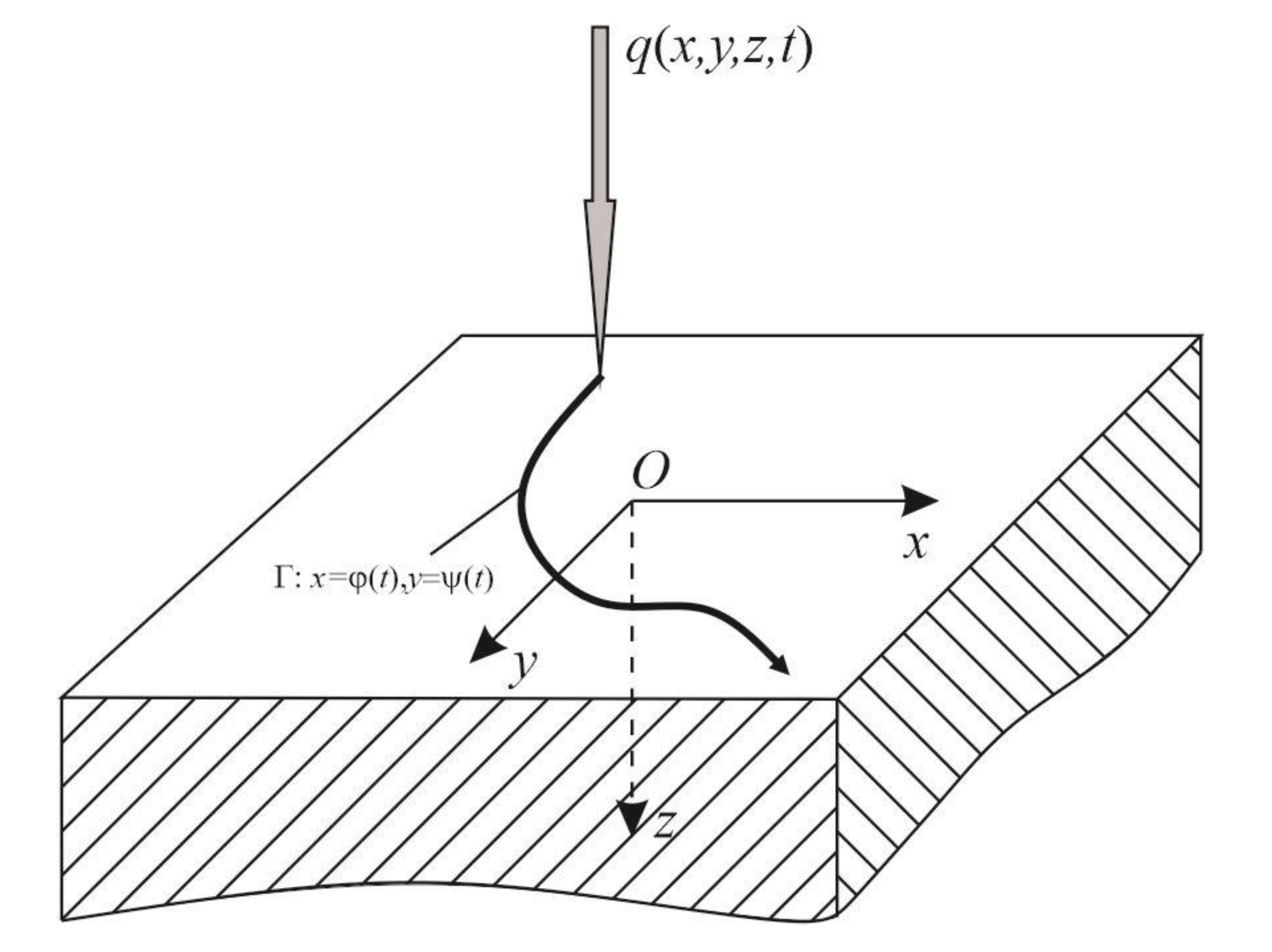
2. Formulation of the Problem
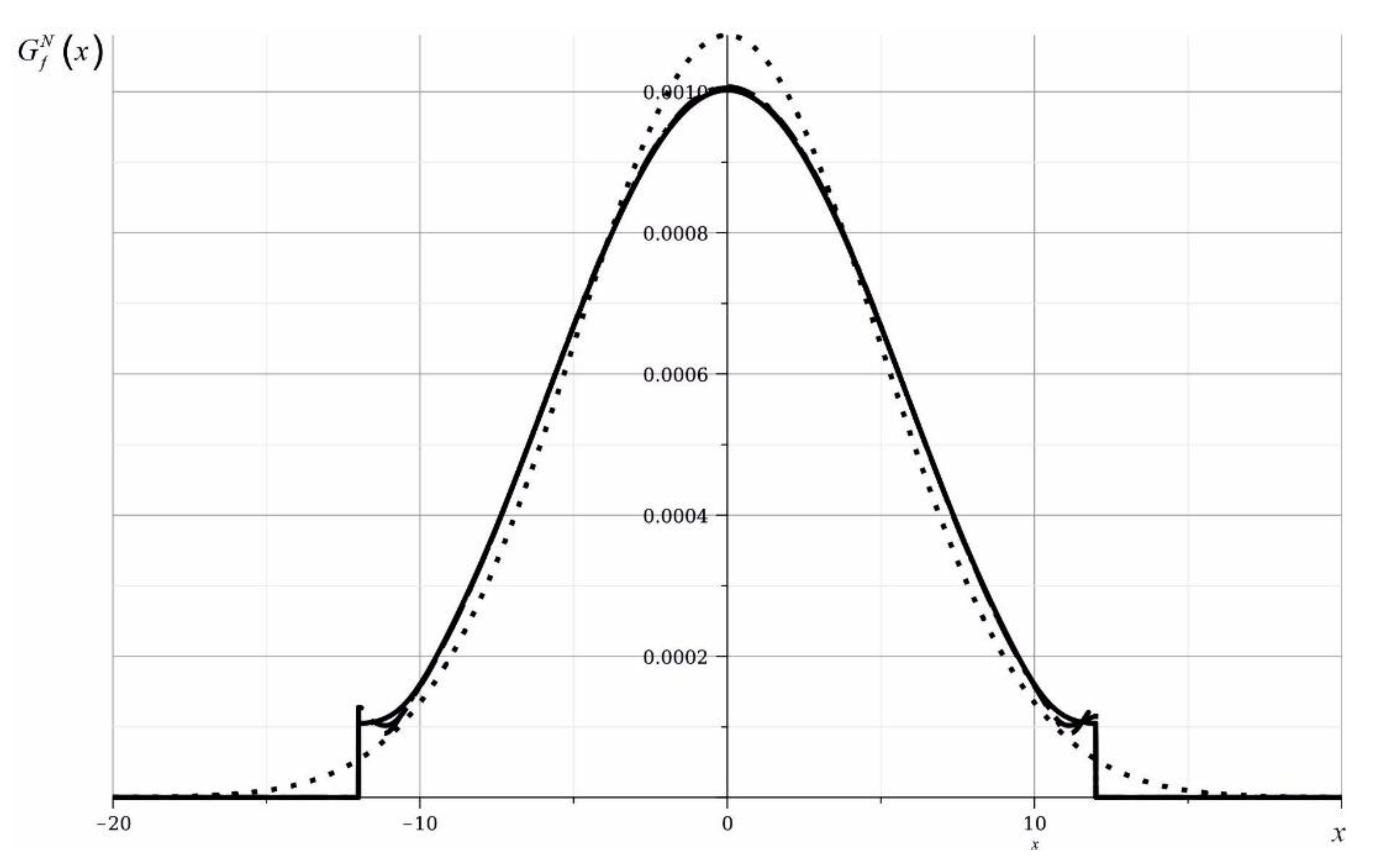
3. The Surface Spatial Transient Function
4. Symmetric Model of a Laser Pulse Source
5. Integral Representation of the Solution
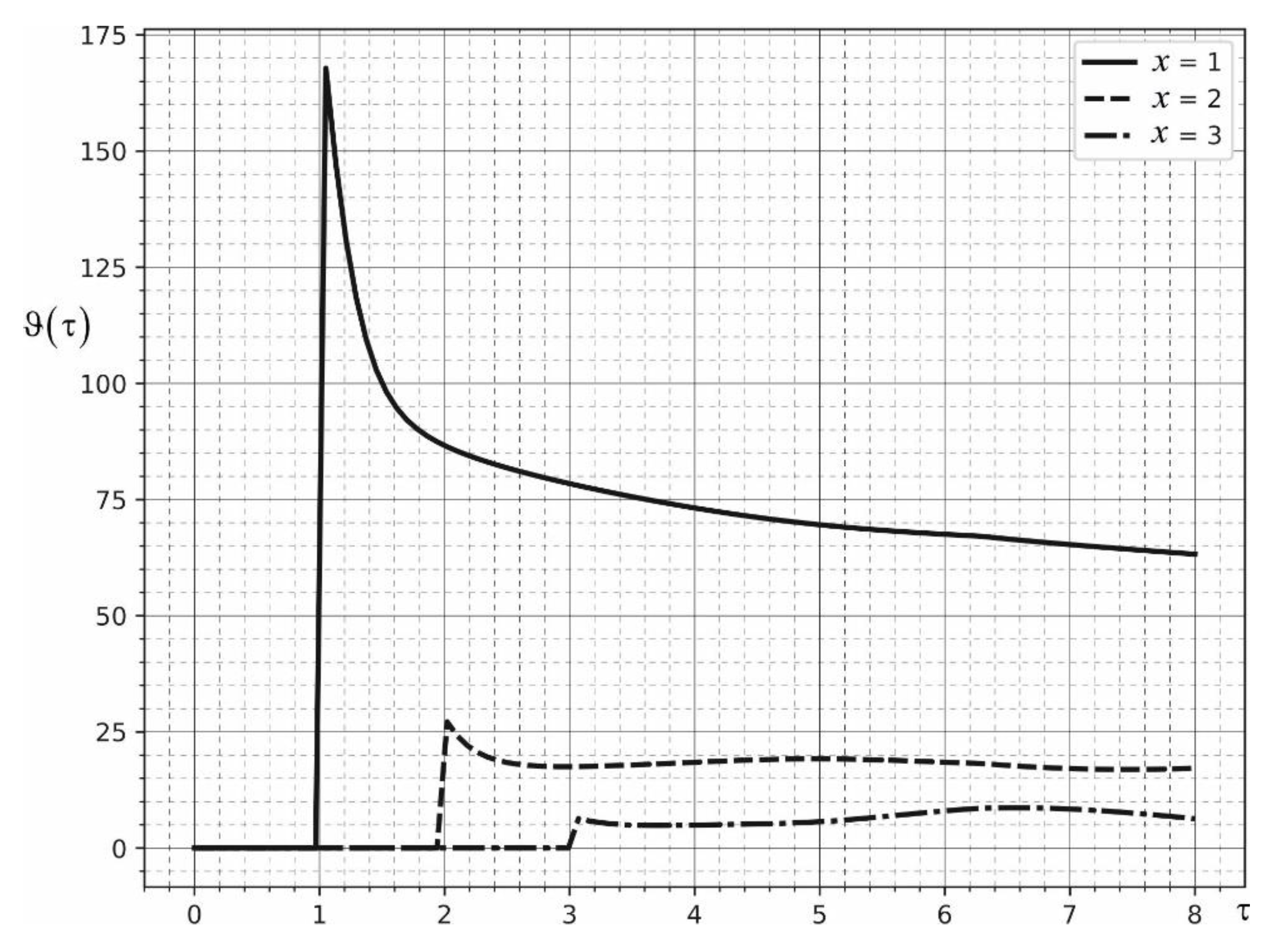
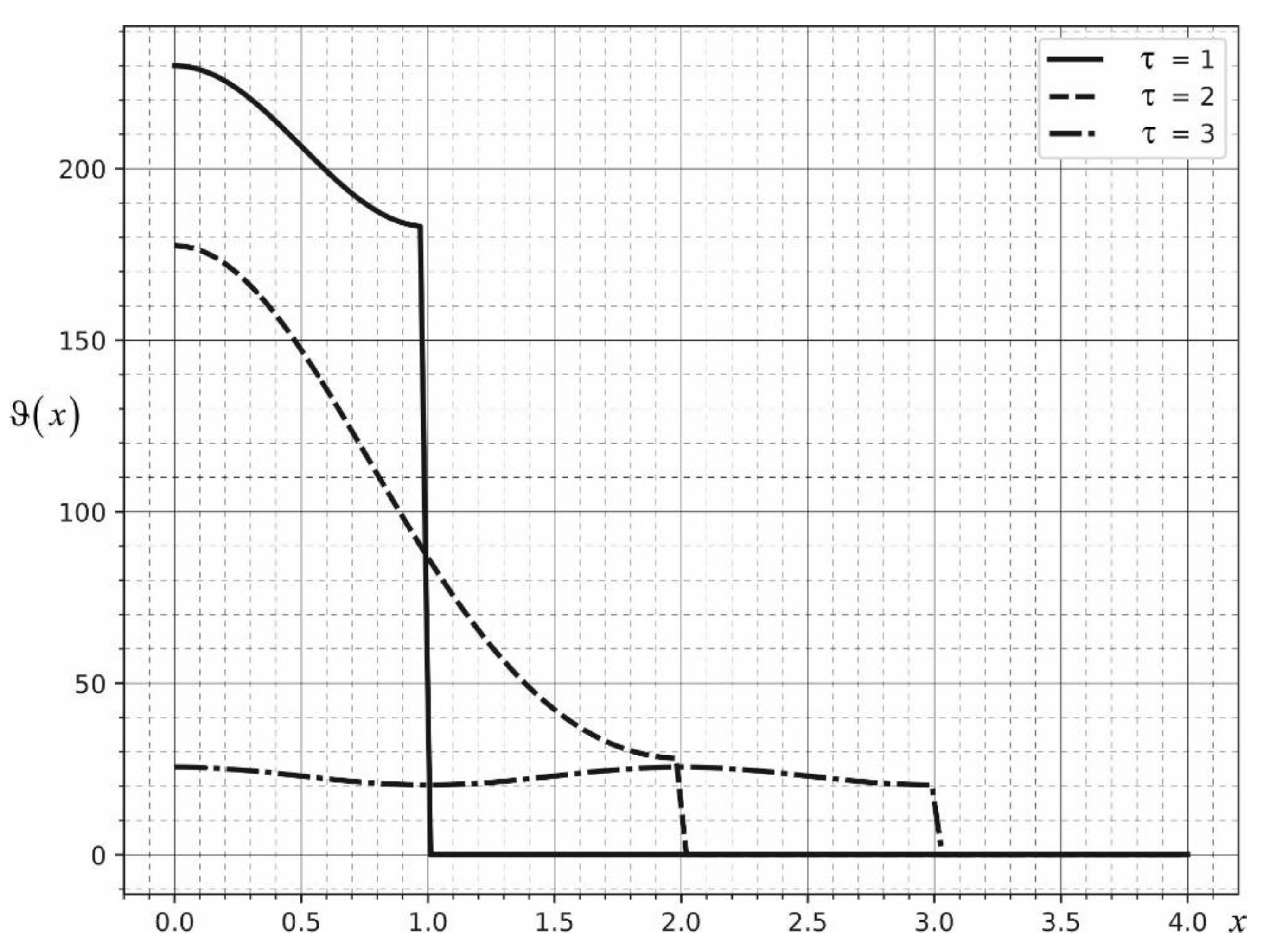
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biot, M. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A Generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Green, A.; Naghdi, P. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. A 1991, 432, 171–194. [Google Scholar]
- Green, A.; Naghdi, P. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Quintanilla, R. Moore-Gibson-Thompson Thermoelasticity. Math. Mech. Solids 2019, 24, 4020–4031. [Google Scholar] [CrossRef]
- Quintanilla, R. Moore-Gibson-Thompson Thermoelasticity with two temperatures. Appl. Eng. Sci. 2020, 1, 100006. [Google Scholar] [CrossRef]
- Thompson, P. Compressible-Fluid Dynamics; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Starovoitov, E.I.; Leonenko, D.V.; Orekhov, A.A. Bending of an elastoplastic circular sandwich plate on an elastic foundation in a temperature field. INCAS Bull. 2021, 13, 233–244. [Google Scholar] [CrossRef]
- Starovoitov, E.I.; Leonenko, D.V.; Orekhov, A.A. Dynamic behavior of thin-walled elements of aircraft made of composite materials, excited by heat shock. J. Appl. Eng. Sci. 2020, 18, 724–731. [Google Scholar] [CrossRef]
- Tushavina, O.V. Coupled heat transfer between a viscous shock gasdynamic layer and a transversely streamlined anisotropic half-space. INCAS Bull. 2020, 12, 211–220. [Google Scholar] [CrossRef]
- Tushavina, O.V.; Kriven, G.I.; Hein, T.Z. Study of thermophysical properties of polymer materials enhanced by nanosized particles. Int. J. Circuits Syst. Signal Processing 2021, 15, 1436–1442. [Google Scholar] [CrossRef]
- Abouelregal, A.; Alesemi, M.; Alfadil, H. Thermoelastic reactions in a long and thin flexible viscoelastic cylinder due to non-uniform heat flow under the non-Fourier model with fractional derivative of two different orders. AIMS Math. 2022, 7, 8510–8533. [Google Scholar] [CrossRef]
- Abouelregal, A.E. Response of thermoelastic cylindrical cavity in a non-local infinite medium due to a varying heat source. Waves Random Complex Media 2020, 32, 1725–1742. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Khalil, K.M.; Mohammed, W.W.; Atta, D. Thermal vibration in rotating nanobeams with temperature-dependent due to exposure to laser irradiation. AIMS Math. 2022, 7, 6128–6152. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Shirazi, A.H.; Malikan, M.; Eremeyev, V.A. Computational analysis of an infinite magneto-thermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach. Contin. Mech. Thermodyn. 2021, 34, 1067–1085. [Google Scholar] [CrossRef]
- Biswas, S. Fundamental solution of steady oscillations equations in nonlocal thermoelastic medium with voids. J. Therm. Stresses 2020, 43, 284–304. [Google Scholar] [CrossRef]
- Biswas, S. Three-dimensional nonlocal thermoelasticity in orthotropic medium based on Eringen’s nonlocal elasticity. Waves Random Complex Media 2022, 32, 1128–1149. [Google Scholar] [CrossRef]
- Das, N.; De, S.; Sarkar, N. Reflection of plane waves in generalized thermoelasticity of type III with nonlocal effect. Math. Methods Appl. Sci. 2020, 43, 1313–1336. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S.; Othman, M.I.A. Effect of the laser pulse on transient waves in a non-local thermoelastic medium under Green-Naghdi theory. Struct. Eng. Mech. 2020, 74, 471–479. [Google Scholar] [CrossRef]
- Zhao, X.; Zhu, W.D.; Li, Y.H. Analytical solutions of nonlocal coupled thermoelastic forced vibrations of micro-/nano-beams by means of Green’s functions. J. Sound Vib. 2020, 481, 115407. [Google Scholar] [CrossRef]
- Sarkar, N.; Bachher, M.; Das, N.; De, S.; Sarkar, N. Waves in nonlocal thermoelastic solids of type III. ZAMM Z. Fur Angew. Math. Und Mech. 2020, 100, e201900074. [Google Scholar] [CrossRef]
- Deng, W.; Li, L.; Hu, Y.; Wang, X.; Li, X. Thermoelastic damping of graphene nanobeams by considering the size effects of nanostructure and heat conduction. J. Therm. Stresses 2018, 41, 1182–1200. [Google Scholar] [CrossRef]
- Huang, M.; Wei, P.; Zhao, L.; Li, Y. Multiple fields coupled elastic flexural waves in the thermoelastic semiconductor microbeam with consideration of small scale effects. Compos. Struct. 2021, 270, 114104. [Google Scholar] [CrossRef]
- Huang, Y.; Wei, P. Modelling the flexural waves in a nanoplate based on the fractional order nonlocal strain gradient elasticity and thermoelasticity. Compos. Struct. 2021, 266, 113793. [Google Scholar] [CrossRef]
- Po, G.; Admal, N.C.; Svendsen, B. Non-local Thermoelasticity Based on Equilibrium Statistical Thermodynamics. J. Elast. 2020, 139, 37–59. [Google Scholar] [CrossRef]
- Ge, X.; Li, P.; Fang, Y.; Yang, L. Thermoelastic damping in rectangular microplate/nanoplate resonators based on modified nonlocal strain gradient theory and nonlocal heat conductive law. J. Therm. Stresses 2021, 44, 690–714. [Google Scholar] [CrossRef]
- Kumar, H.; Mukhopadhyay, S. Surface energy effects on thermoelastic vibration of nanomechanical systems under Moore–Gibson–Thompson thermoelasticity and Eringen’s nonlocal elasticity theories. Eur. J. Mech. A/Solids 2022, 93, 104530. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Abouelregal, A.E.; Atta, D.; Khelifi, F. Thermoelastic responses in a nonlocal infinite solid with a circular cylindrical cavity due to a moving heat supply under the MGT model of thermal conductivity. Phys. Scr. 2022, 97, 035705. [Google Scholar] [CrossRef]
- Belov, P.A.; Lurie, S.A.; Dobryanskiy, V.N. Variational Formulation of Linear Equations of Coupled Thermohydrodynamics and Heat Conductivity. Lobachevskii J. Math. 2020, 41, 1949–1963. [Google Scholar] [CrossRef]
- Lomakin, E.V.; Lurie, S.A.; Belov, P.A.; Rabinskiy, L.N. On the Generalized Heat Conduction Laws in the Reversible Thermodynamics of a Continuous Medium. Dokl. Phys. 2018, 63, 503–507. [Google Scholar] [CrossRef]
- Lurie, S.A.; Belov, P.A. On the nature of the relaxation time, the Maxwell–Cattaneo and Fourier law in the thermodynamics of a continuous medium, and the scale effects in thermal conductivity . Contin. Mech. Thermodyn. 2020, 32, 503–507. [Google Scholar] [CrossRef]
- Lurie, S.A.; Belov, P.A.; Volkov-Bogorodskii, D.B. Variational models of coupled gradient thermoelasticity and thermal conductivity. Mater. Phys. Mech. 2019, 42, 564–581. [Google Scholar] [CrossRef]
- Zhang, K.Z.; AliShah, N.; Vieru, D.; El-Zahar, E.R. Memory effects on conjugate buoyant convective transport of nanofluids in annular geometry: A generalized Cattaneo law of thermal flux. Int. Commun. Heat and Mass Transf. 2022, 135, 106138. [Google Scholar] [CrossRef]
- Bég, O.A.; Venkatadri, K.; Prasad, V.; Bég, T.; Leonard, H.J.; Gorla, R.; Rajarajeswari, P. Numerical study of magnetohydrodynamic natural convection in a non-Darcian porous enclosure filled with electrically conducting helium gas. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2203–2223. [Google Scholar] [CrossRef]
- Cataneo, C.A. Form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compte. Rendus. 1958, 247, 431–4433. [Google Scholar]
- Vernotte, P. Les paradoxes de la theorie continue de lequation de la chaleur. CR Acad. Sci. 1958, 246, 3154–31555. [Google Scholar]
- Lykov, A. Teoriya Teploprovodnosti; Vysshaya Shkola: Moscow, Russia, 1967. [Google Scholar]
- Ditkin, V.; Prudnikov, A. Handbook on Operational Calculation; Vysshaya Shkola: Moscow, Russia, 1965. [Google Scholar]
- Okonechnikov, A.; Tarlakovsky, D.; Fedotenkov, G. Spatial Non-Stationary Contact Problem for a Cylindrical Shell And Absolutely Rigid Body. Mech. Solids 2020, 55, 366–376. [Google Scholar] [CrossRef]
- Serdyuk, A.; Serdyuk, D.; Fedotenkov, G. Stress-strain state of a composite plate under the action of a transient movable load. Mech. Compos. Mater. 2021, 57, 493–502. [Google Scholar] [CrossRef]
- Fedotenkov, G.; Gritskov, A.; Levitskiy, D.; Vahterova, Y.; Sun, Y. Timoshenko beam and plate non-stationary vibrations. INCAS Bull. 2021, 13, 41–56. [Google Scholar] [CrossRef]
- Serdyuk, A.; Serdyuk, D.; Fedotenkov, G. Unsteady bending function for an unlimited anisotropic plate. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2021, 25, 111–126. [Google Scholar] [CrossRef]
- Orekhov, A.; Rabinskiy, L.; Fedotenkov, G. Analytical Model of Heating an Isotropic Half-Space by a Moving Laser Source with a Gaussian Distribution. Symmetry 2022, 14, 650. [Google Scholar] [CrossRef]
- Orekhov, A.; Rabinskiy, L.; Fedotenkov, G.; Hein, T. Heating of a half-space by a moving thermal laser pulse source. Lobachevskii J. Math. 2021, 42, 1912–1919. [Google Scholar] [CrossRef]
- Fedotenkov, G.V.; Tarlakovskii, D.V.; Mitin, A.Y. Transient spatial motion of cylindrical shell under influence of non–stationary pressure. In Proceedings of the Second International Conference on Theoretical, Applied and Experimental Mechanics, Structural Integrity. Corfu, Greece, 23–26 June 2019; Springer: Cham, Switzerland, 2019; pp. 264–269. [Google Scholar]
- Title of Site. Available online: https://github.com/sigma-py/quadpy (accessed on 3 August 2022).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedotenkov, G.; Rabinskiy, L.; Lurie, S. Conductive Heat Transfer in Materials under Intense Heat Flows. Symmetry 2022, 14, 1950. https://doi.org/10.3390/sym14091950
Fedotenkov G, Rabinskiy L, Lurie S. Conductive Heat Transfer in Materials under Intense Heat Flows. Symmetry. 2022; 14(9):1950. https://doi.org/10.3390/sym14091950
Chicago/Turabian StyleFedotenkov, Gregory, Lev Rabinskiy, and Sergey Lurie. 2022. "Conductive Heat Transfer in Materials under Intense Heat Flows" Symmetry 14, no. 9: 1950. https://doi.org/10.3390/sym14091950
APA StyleFedotenkov, G., Rabinskiy, L., & Lurie, S. (2022). Conductive Heat Transfer in Materials under Intense Heat Flows. Symmetry, 14(9), 1950. https://doi.org/10.3390/sym14091950





