Quasi-Linearization Analysis for Entropy Generation in MHD Mixed-Convection Flow of Casson Nanofluid over Nonlinear Stretching Sheet with Arrhenius Activation Energy
Abstract
:1. Introduction
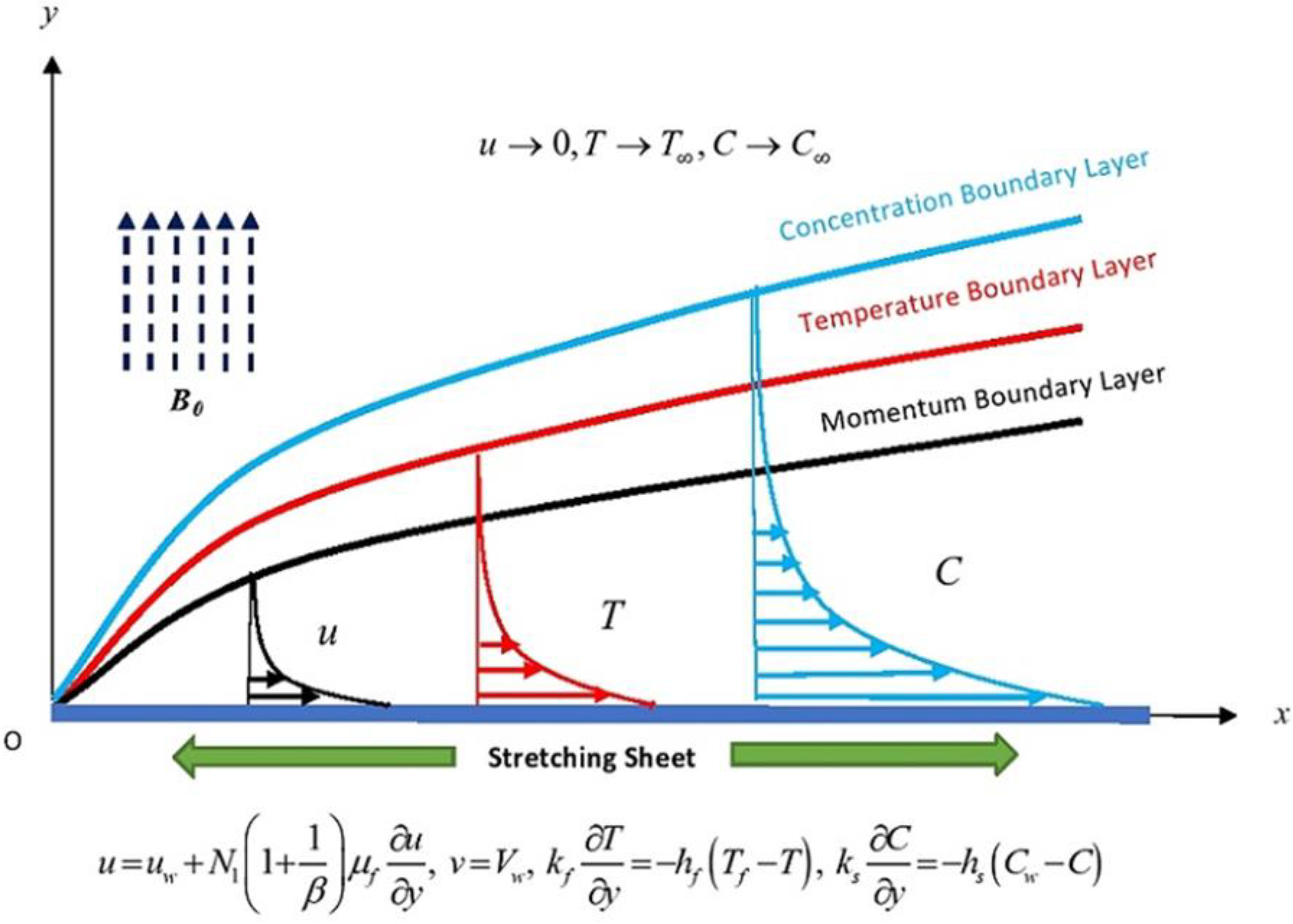
2. Formulation of Flow Model
3. Entropy Generation Analysis
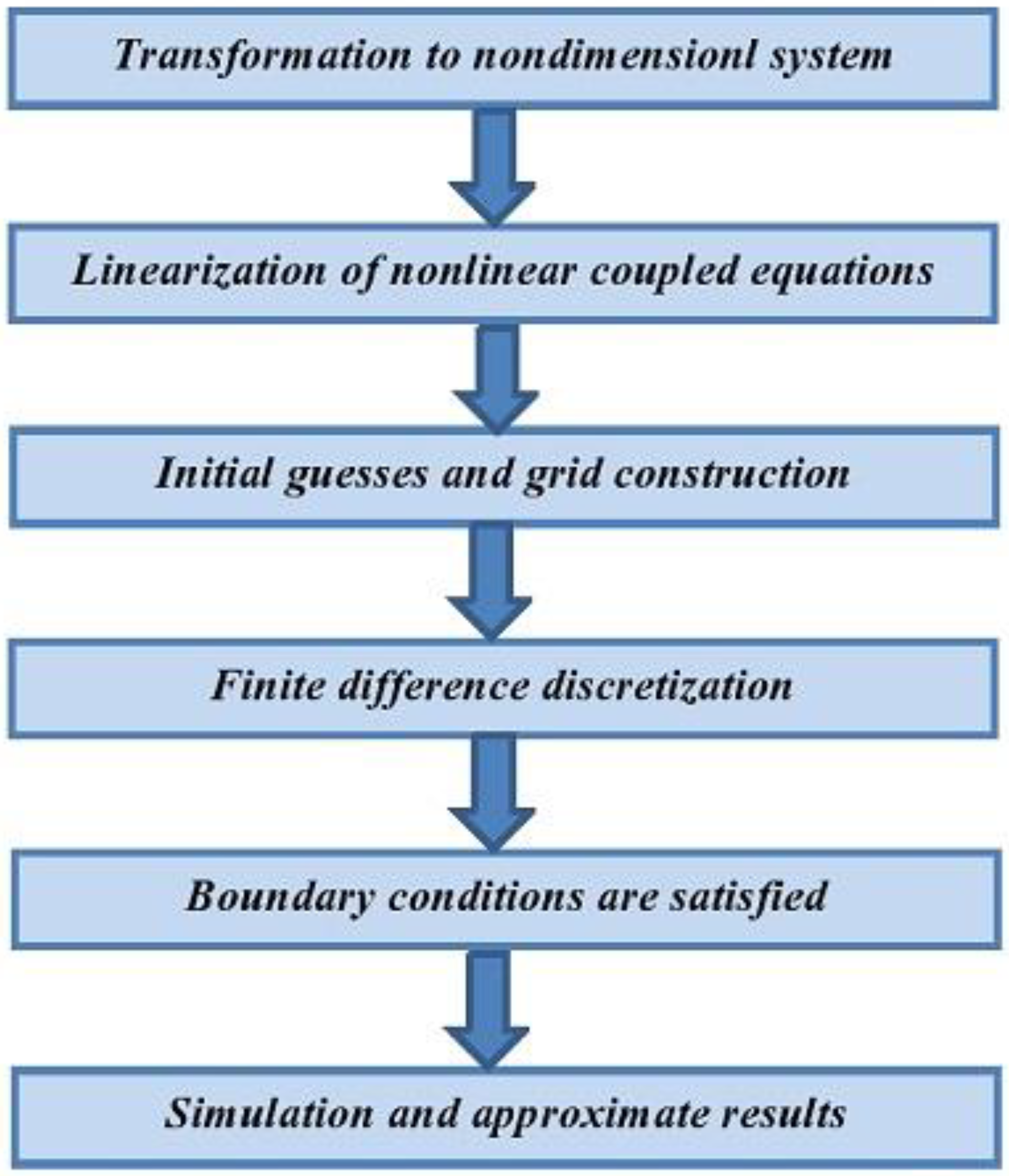
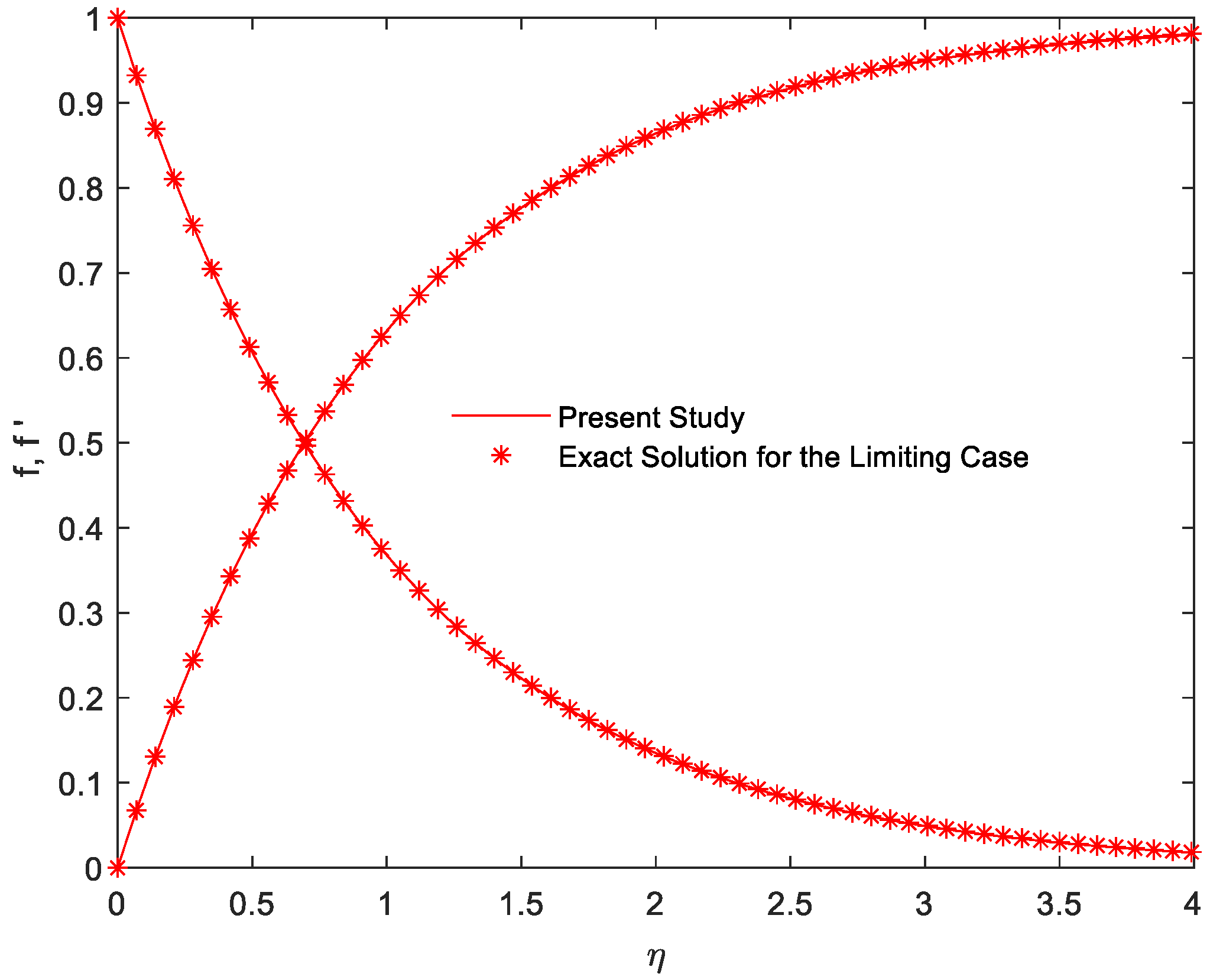
4. Solution Procedure
5. Results and Discussion
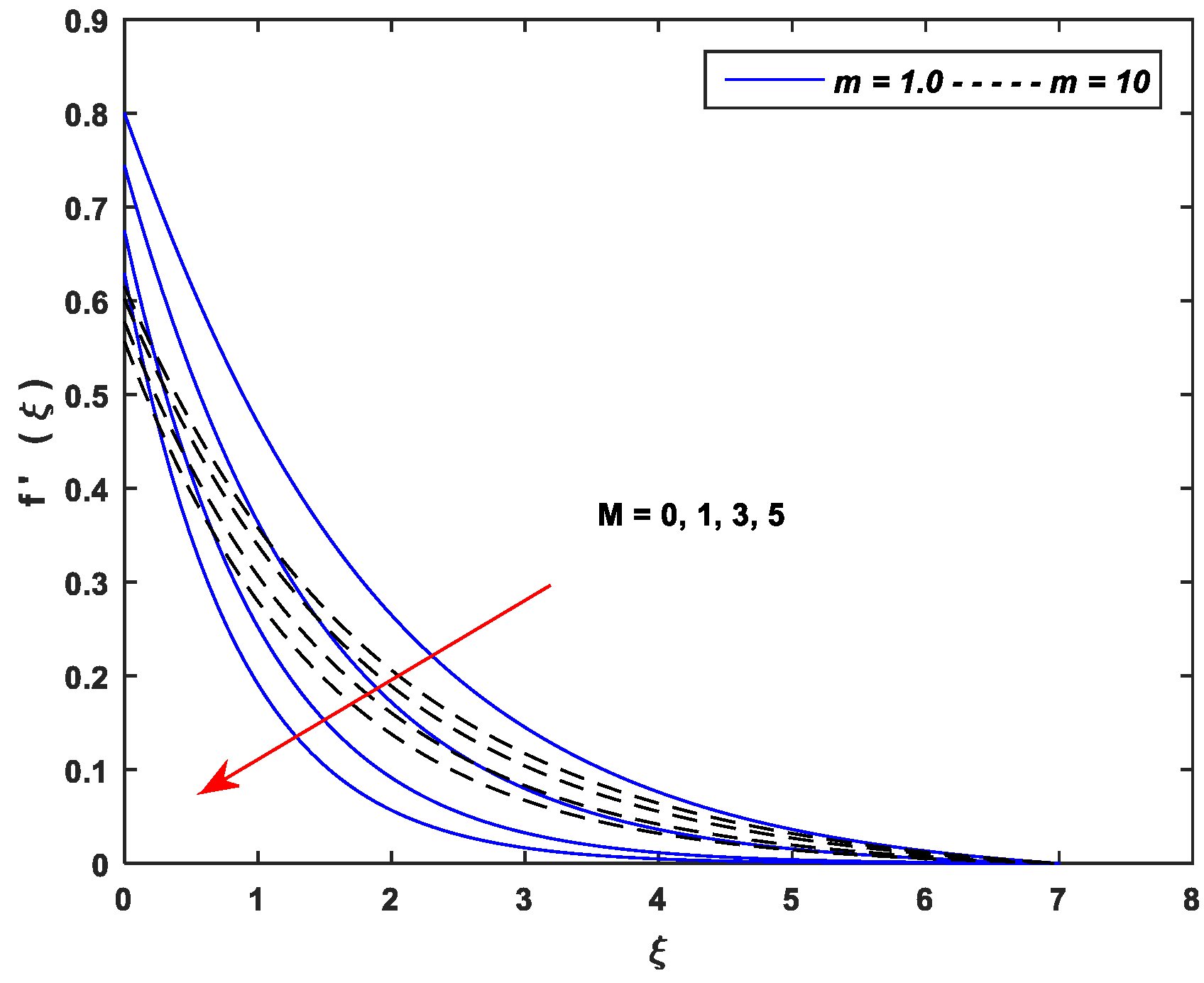
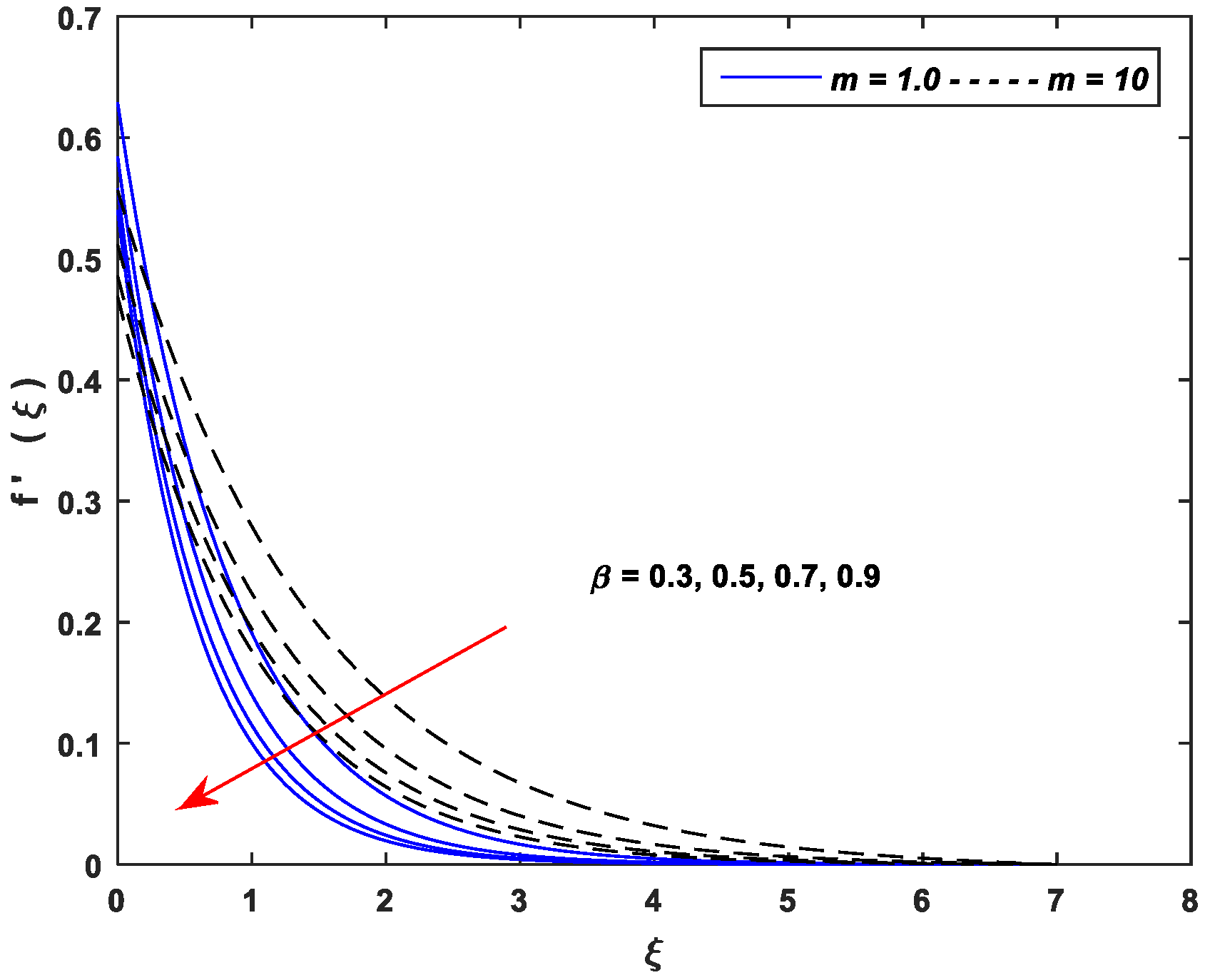
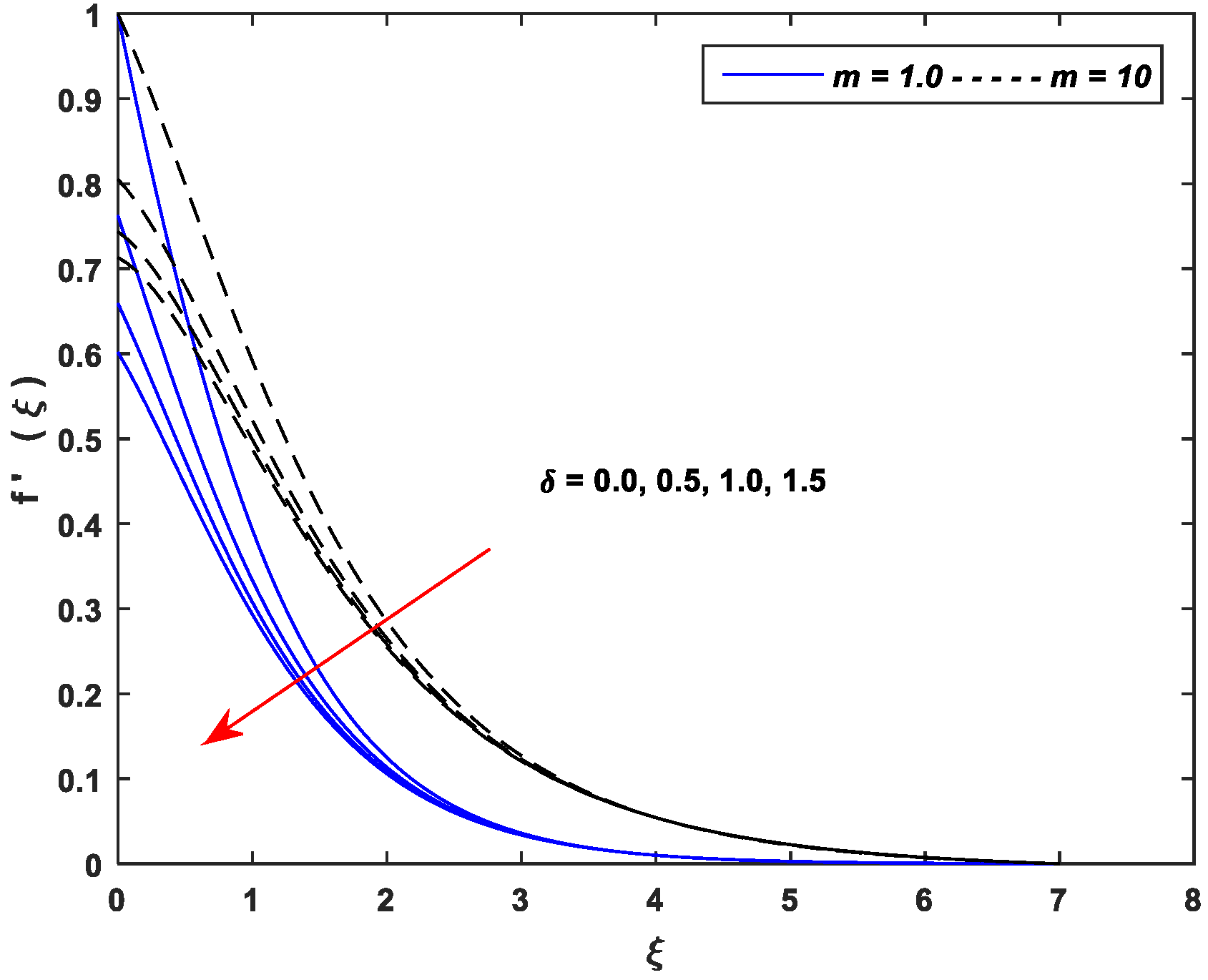
5.1. Velocity Profiles
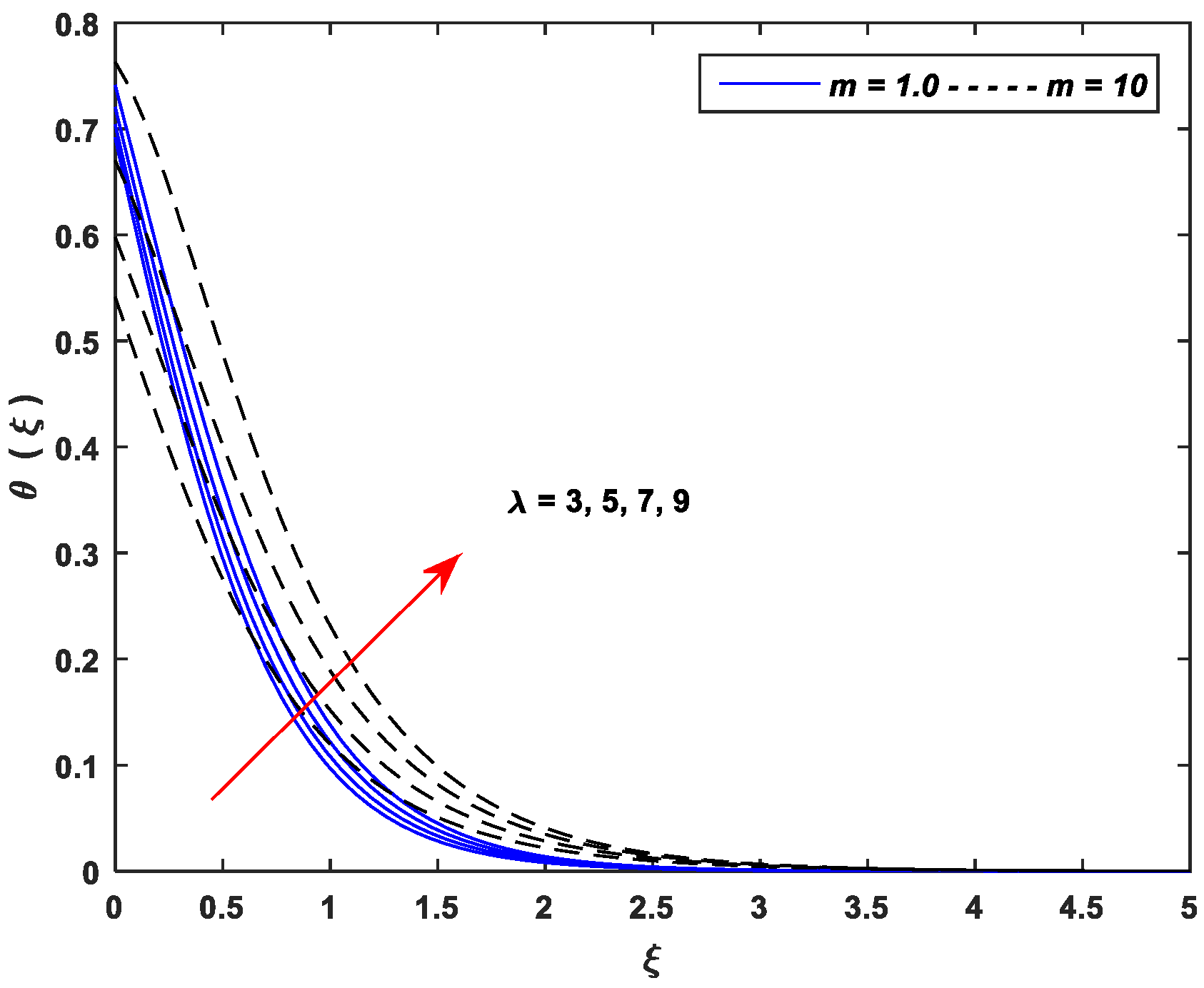
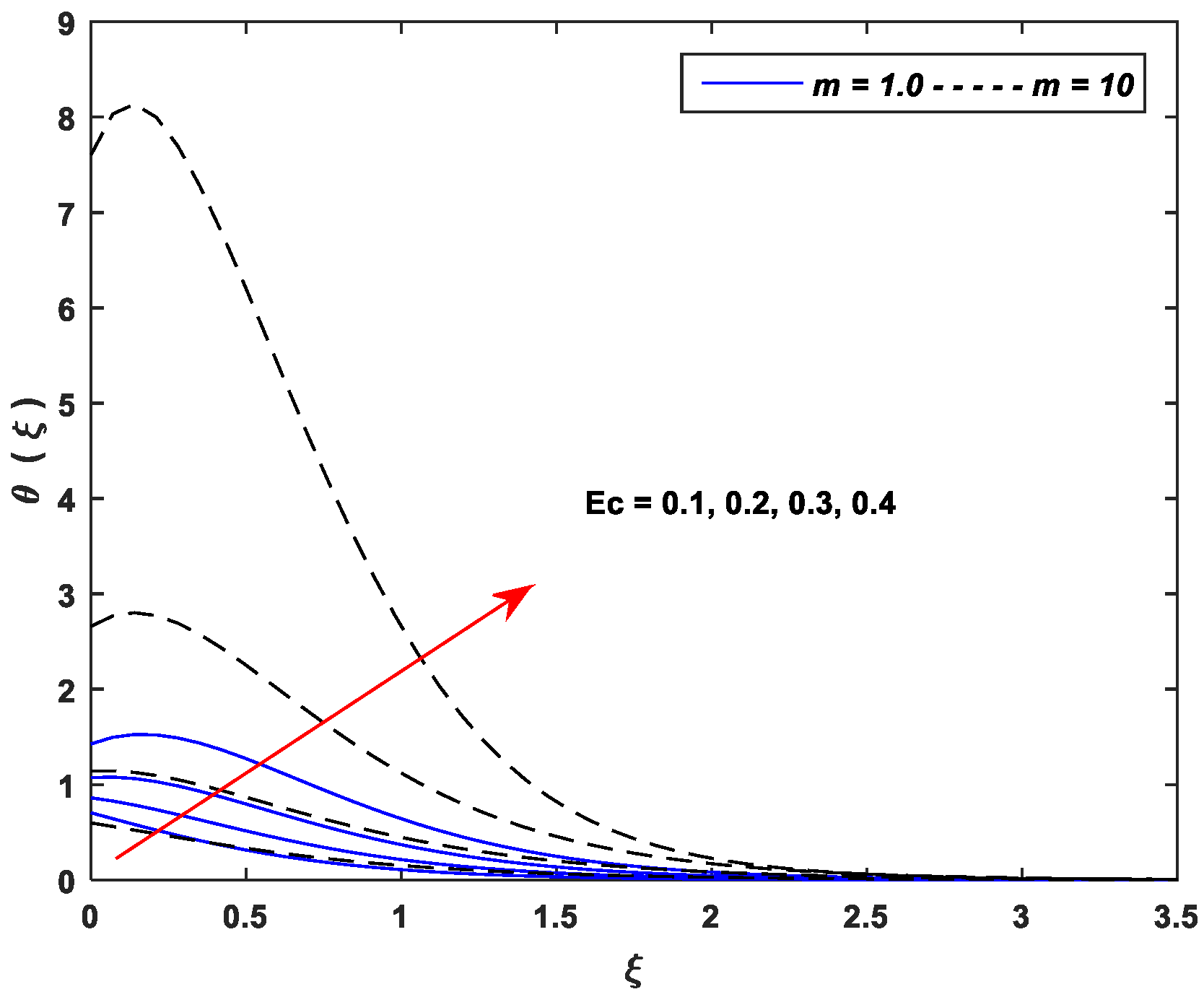
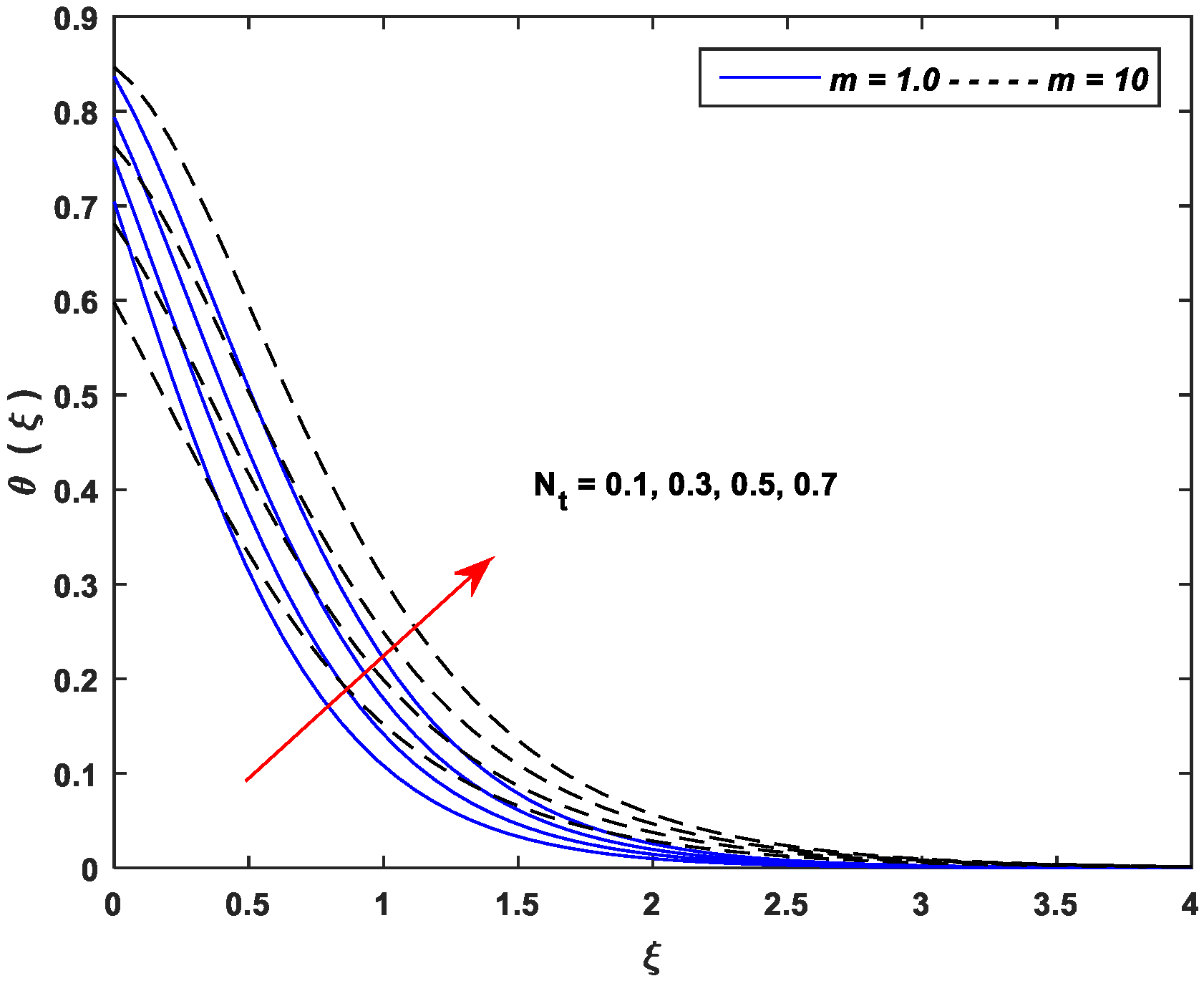
5.2. Thermal Profiles
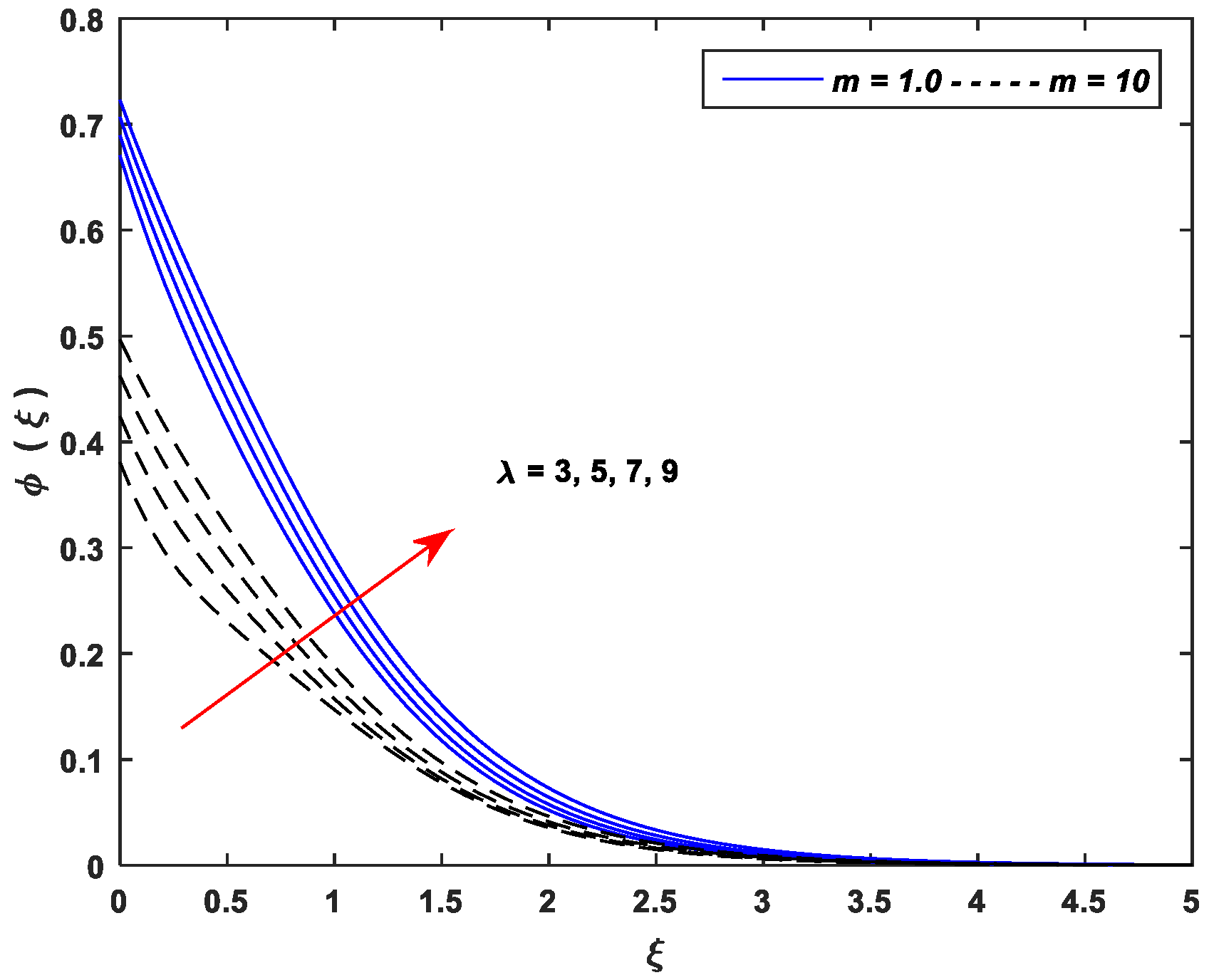
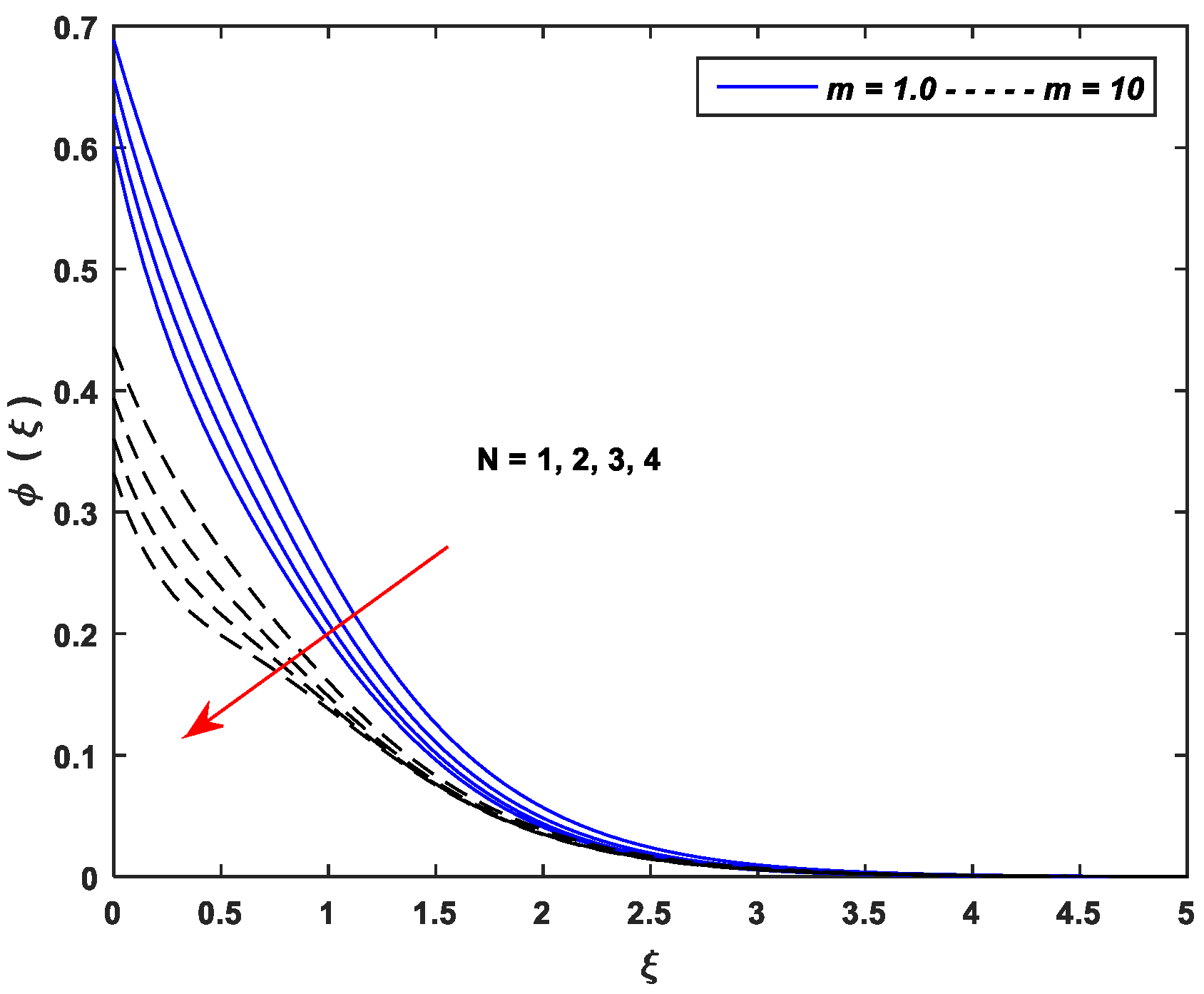
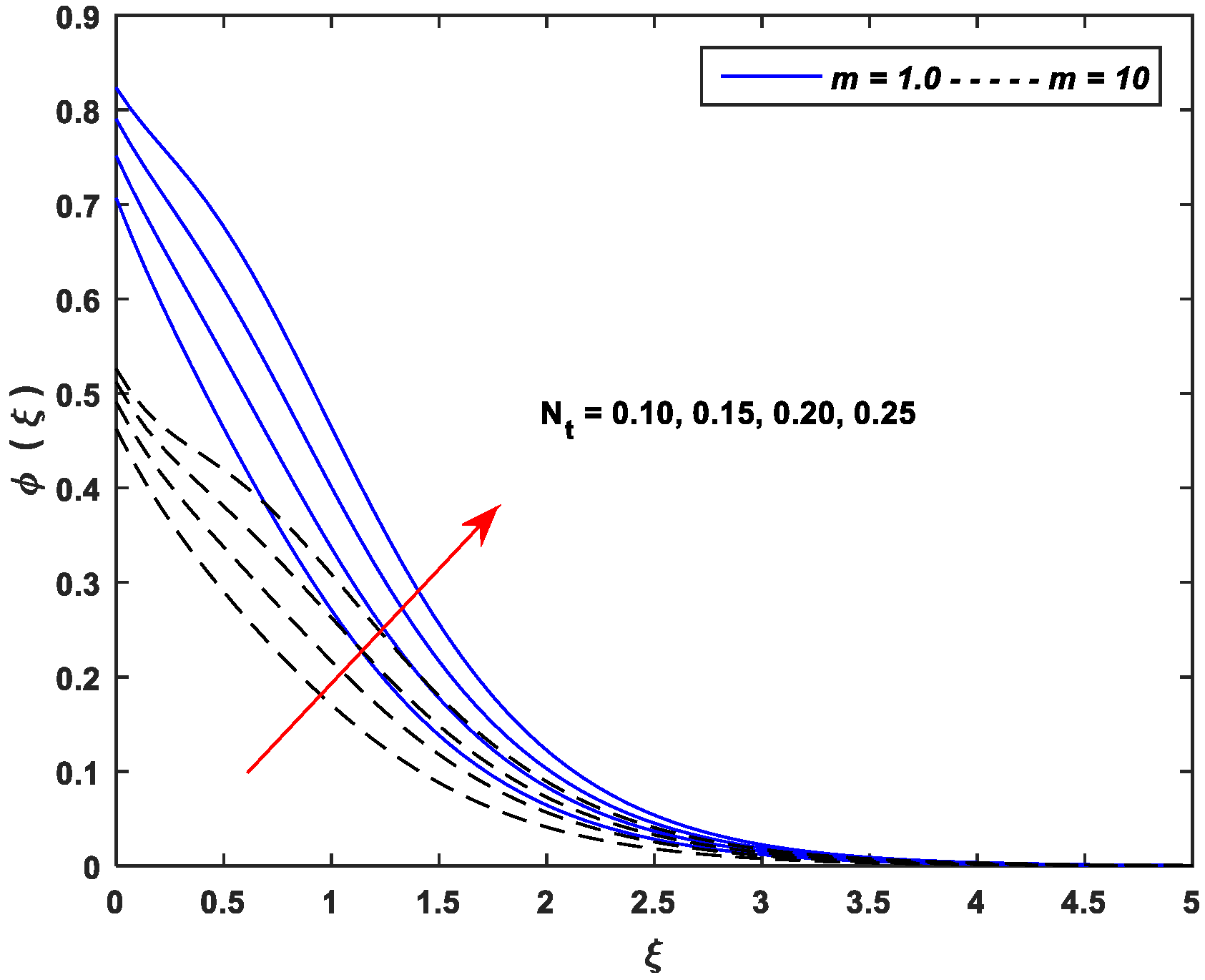
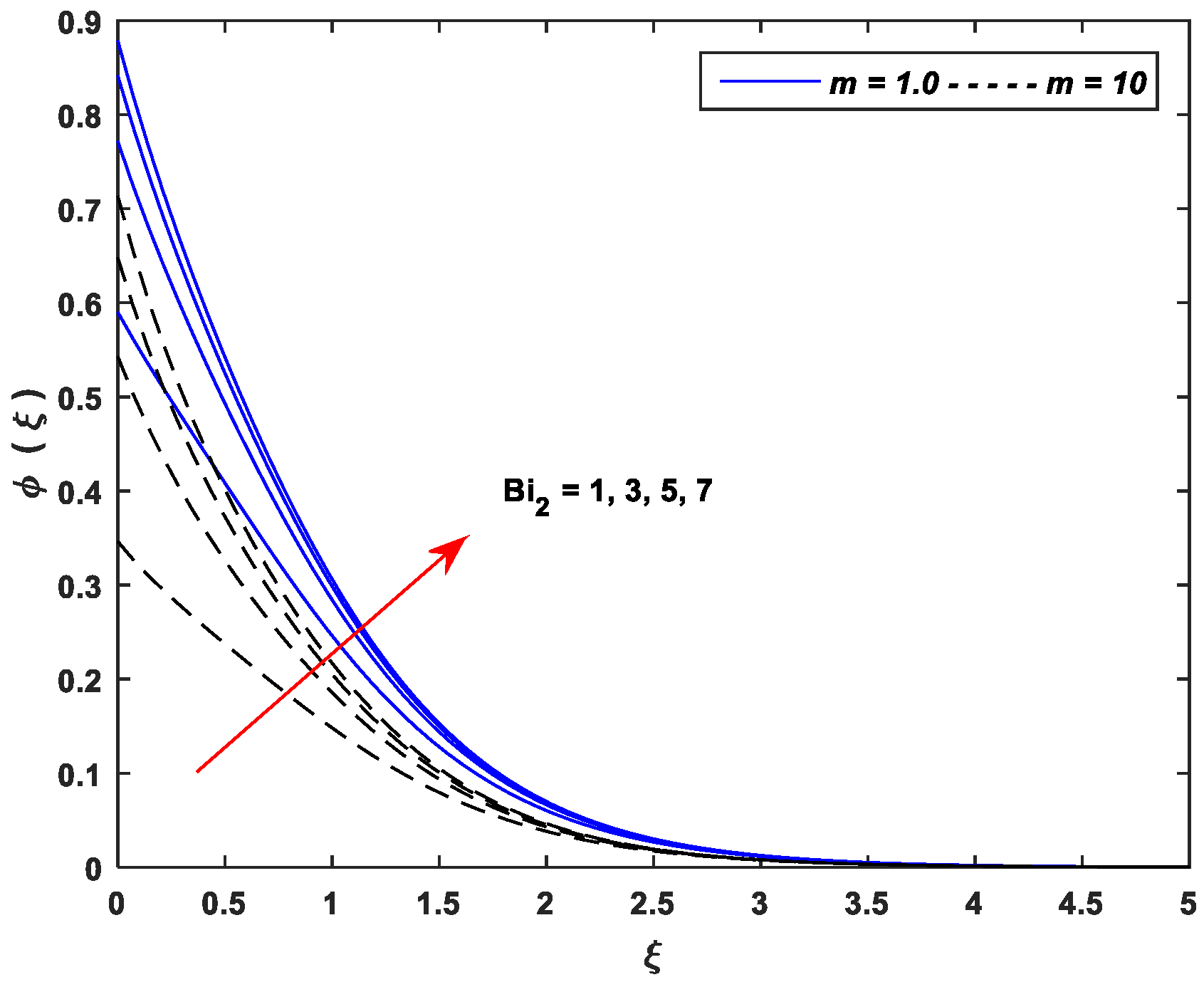
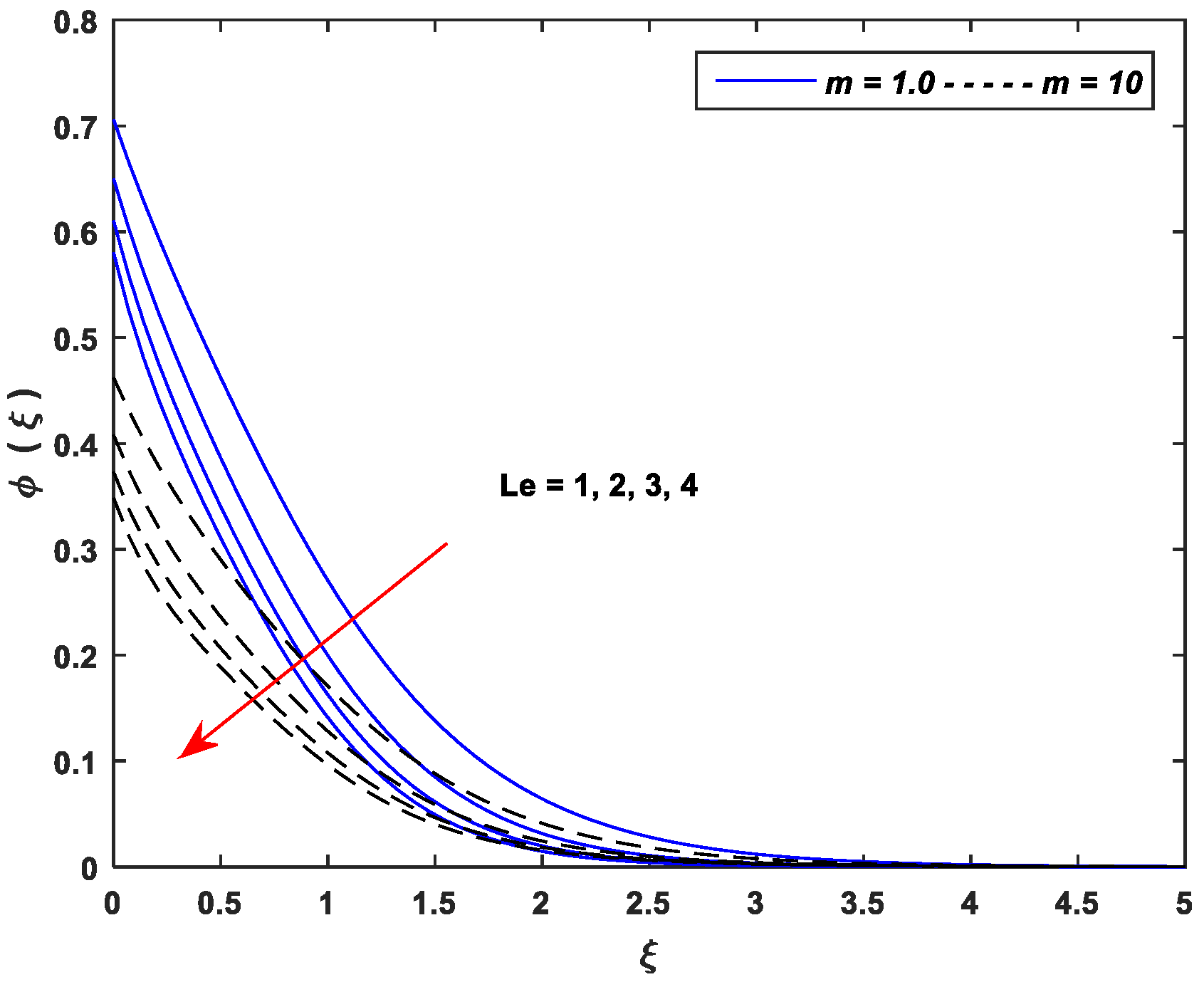
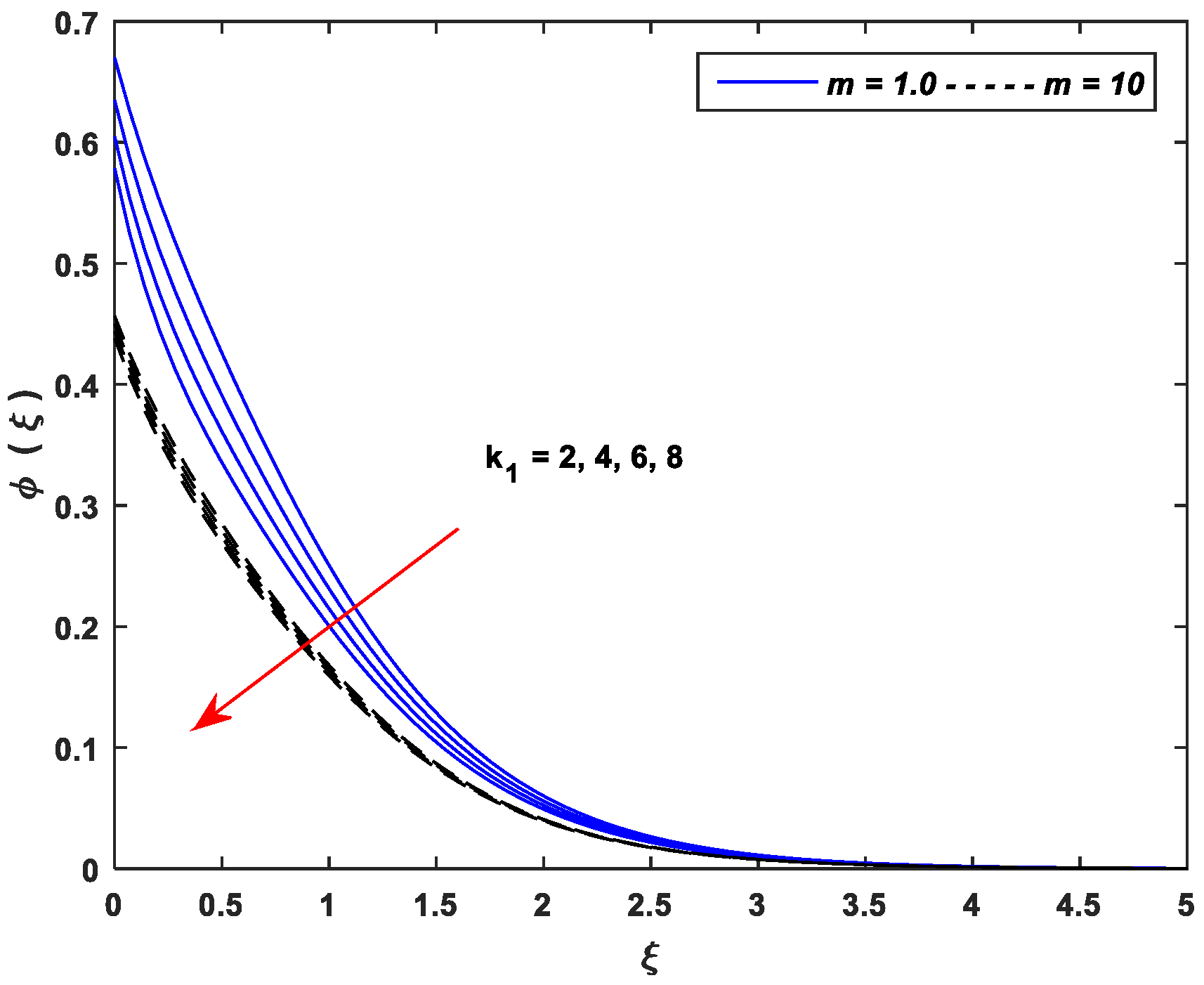
5.3. Concentration Profiles
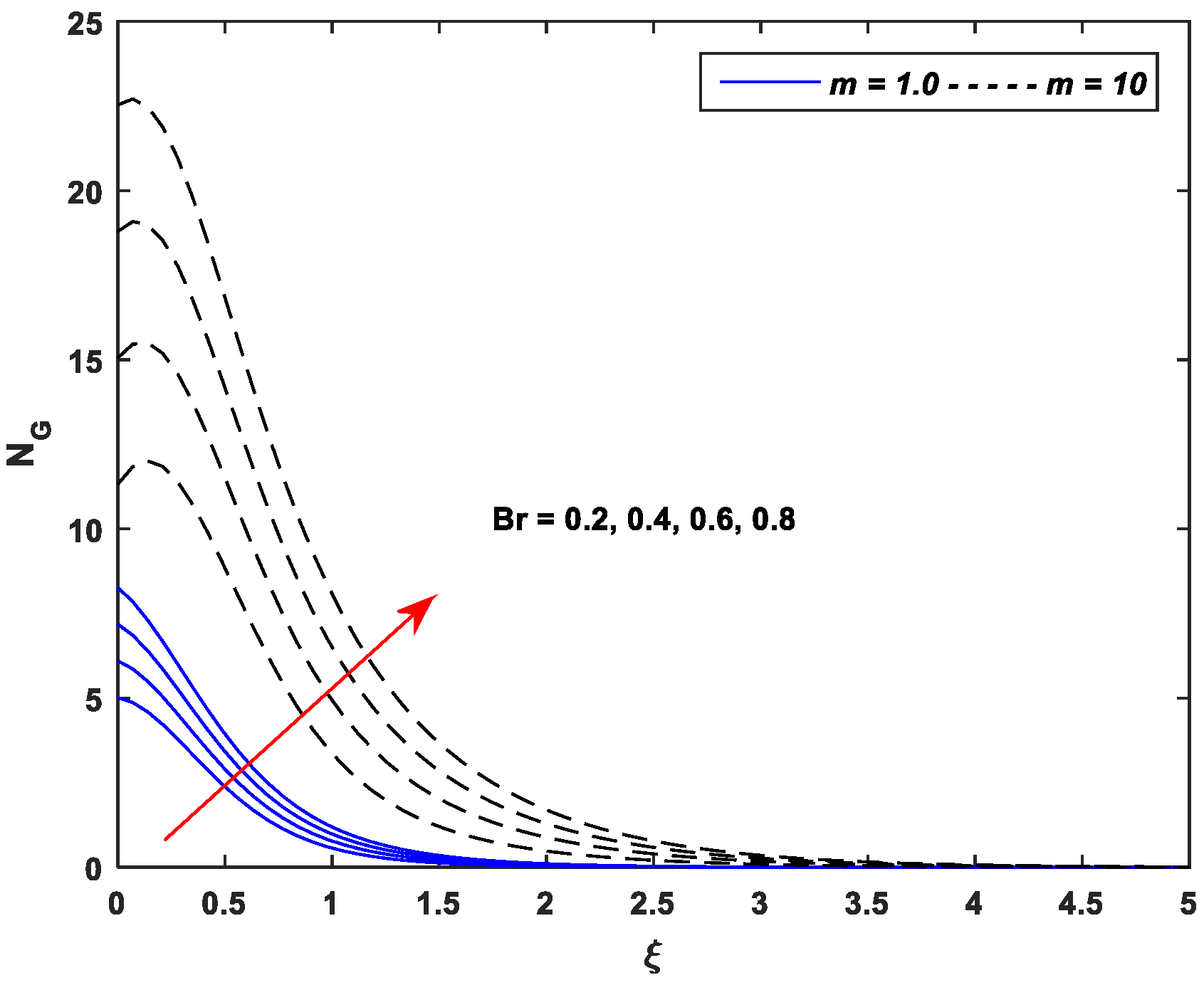
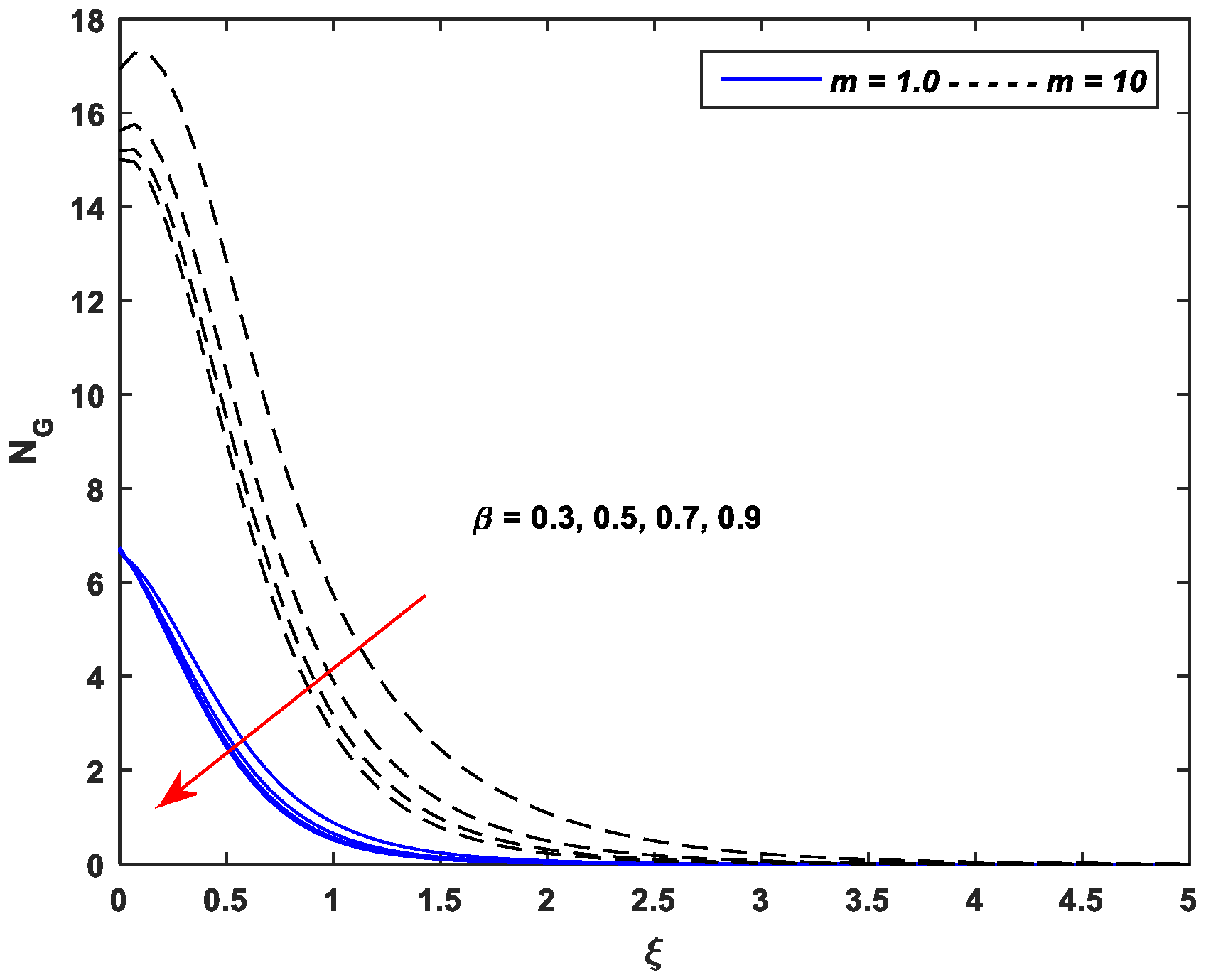
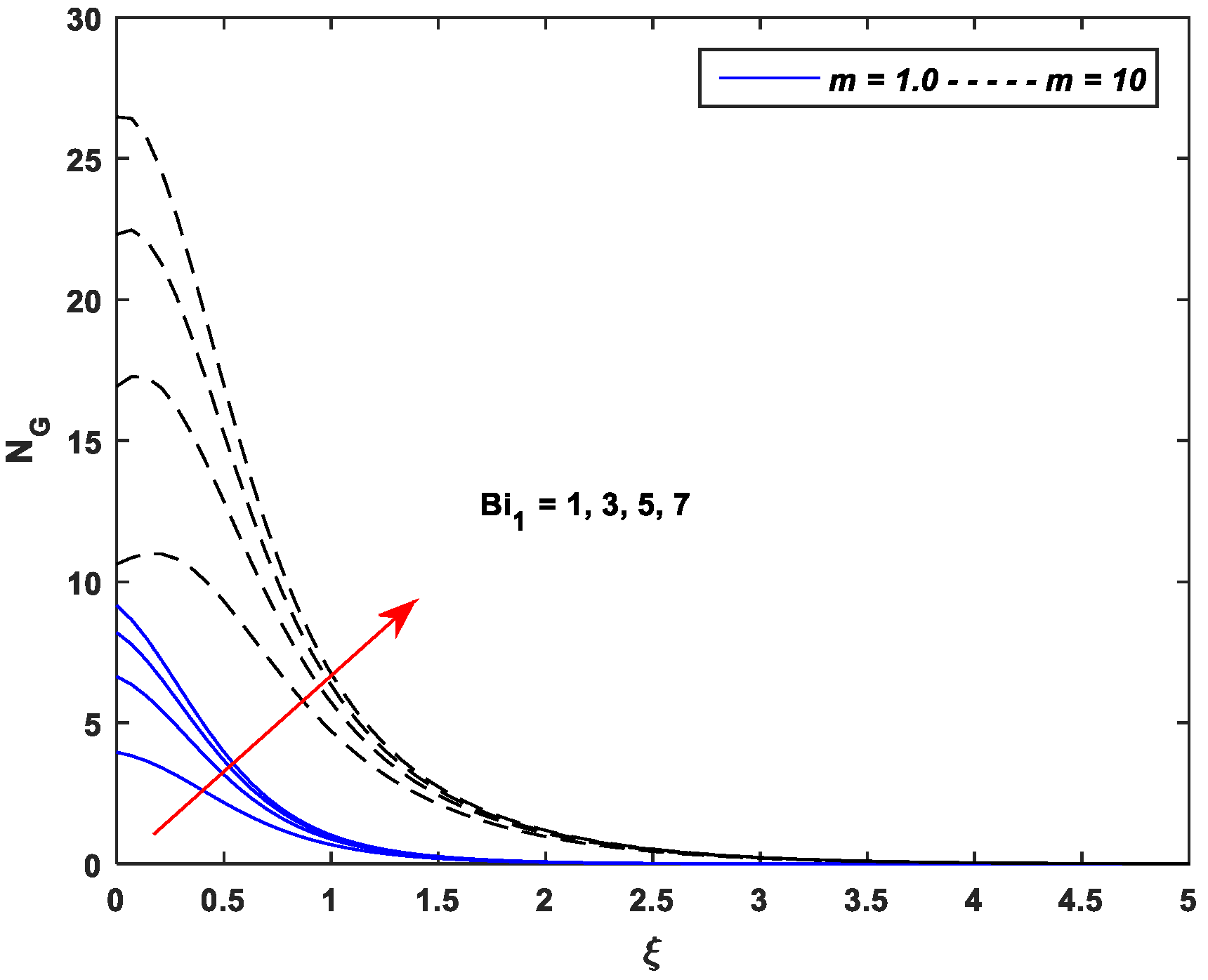
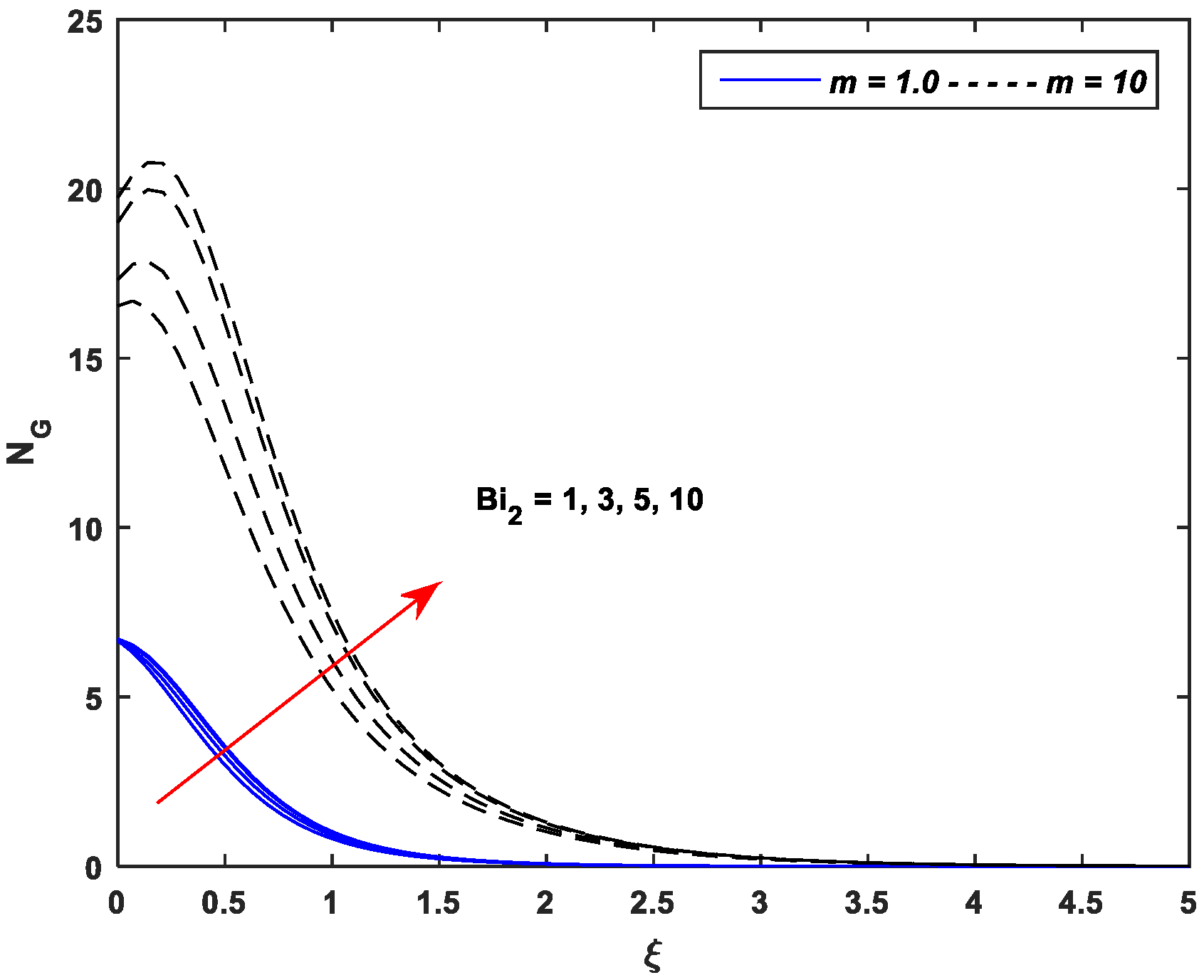
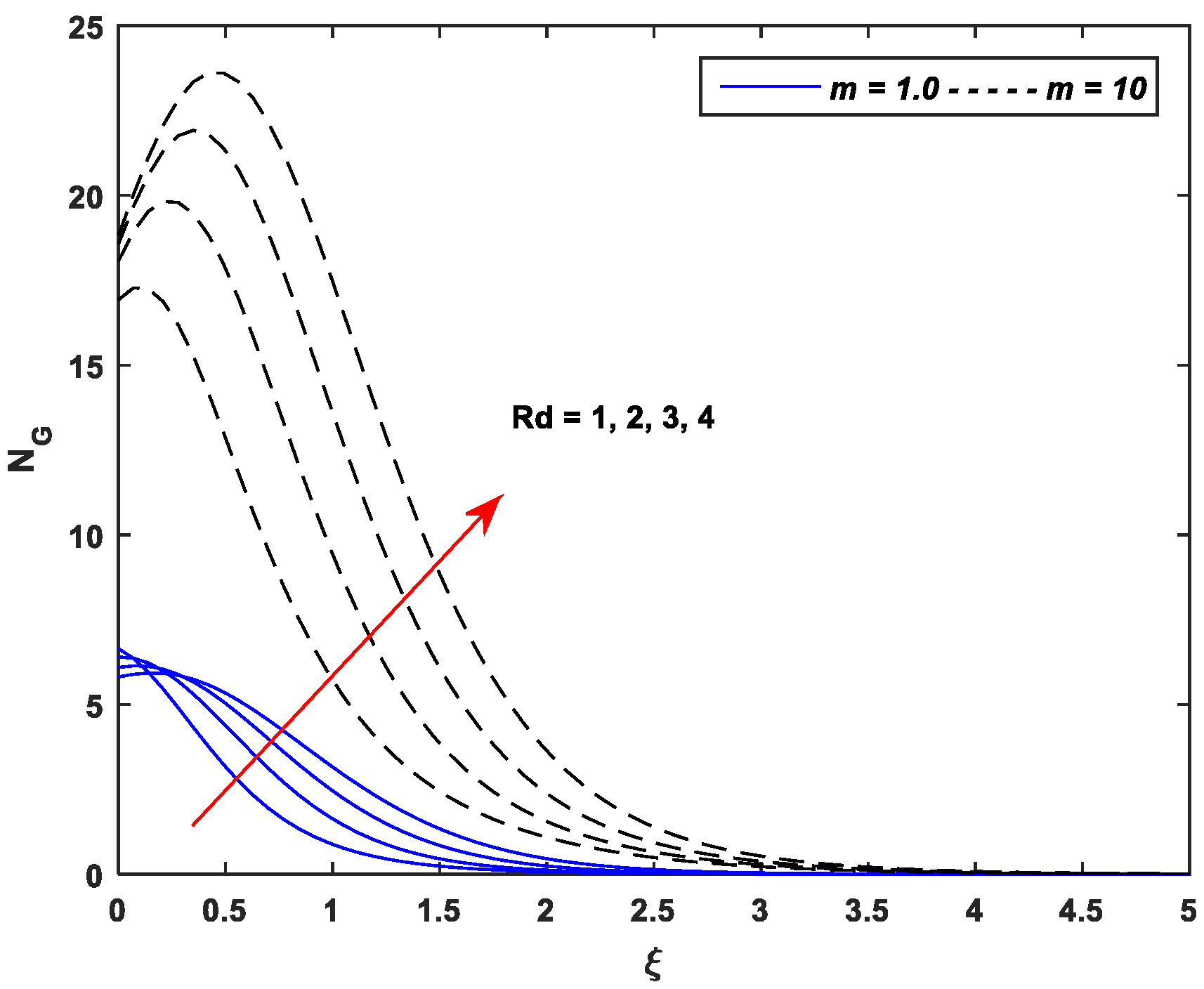
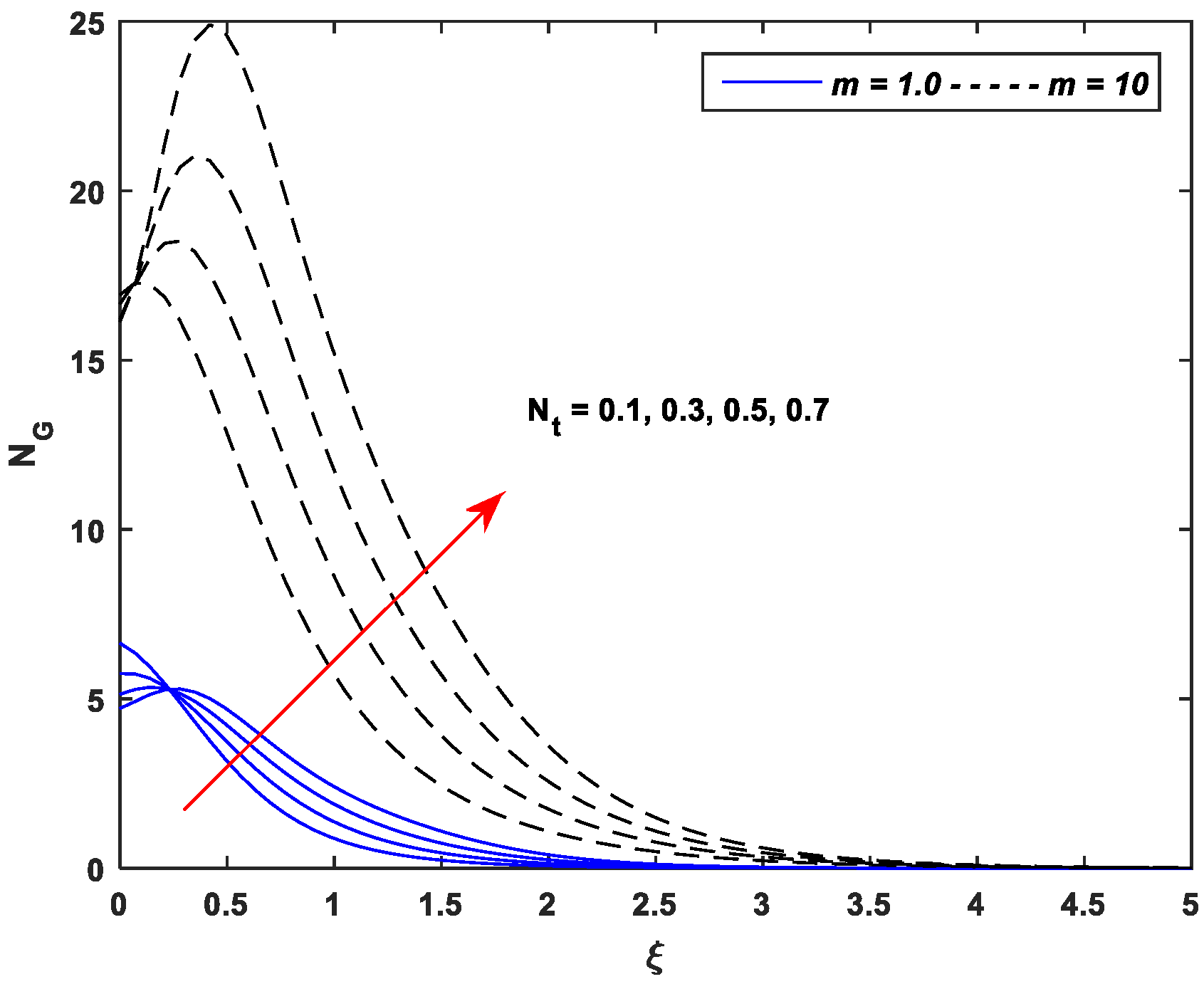
5.4. Entropy Generation Profiles
6. Physical Quantities of Engineering Interest
7. Conclusions
- Growing values of , and cause a significant decline in the velocity while exhibits an opposite trend.
- Thermal profiles fall off with enhancing values of and , whereas increasing values of , , , , and improve thermal profiles significantly.
- Improving the values of , , and upsurge the concentration profiles; however, the parameters , , and cause a remarkable reduction in the concentration distributions.
- The linear stretching dominates the nonlinear stretching for all controlling parameters of the concentration profiles.
- Entropy generation is an incremental function of the parameters , , , , and while a declining function of parameters and .
- Implications of Brownian motion and thermophoresis are to minimize the entropy generation near the surface of the stretching sheet while maximizing the sheet.
- Entropy generation against nonlinear stretching leads as compared to the linear stretching for all pertinent parameters of the MHD flow of Casson nanofluid.
- Nusselt number and Sherwood number decrease significantly with growing values of activation energy in the case of nonlinear stretching.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| acceleration due to gravity () | Reynolds number | ||
| temperature of fluid () | Lewis number | ||
| specific heat at constant pressure () | Prandtl number | ||
| magnetic field strength () | Eckert number | ||
| thermal conductivity () | Grashof number | ||
| molecular diffusivity () | Brinkman number | ||
| fluid concentration () | |||
| thermal Biot number | Greek Symbols | ||
| solutalBiot number | fluid viscosity () | ||
| radiative heat flux () | fluid density () | ||
| magnetic parameter | Casson parameter | ||
| heat generation coefficient () | electrical conductivity () | ||
| activation energy factor () | stream function () | ||
| thermophoresis parameter | dimensionless temperature | ||
| Brownian motion parameter | mixed convection parameter | ||
| rate of reaction () | dimensionless concentration | ||
| index parameter | similarity variable | ||
| components of velocity () | dimensionless reaction rate | ||
| Cartesian coordinates along the stretching sheet, respectively () | heat generation parameter | ||
| slip parameter | |||
References
- Cui, X.; Wang, J.; Xia, G. Enhanced thermal conductivity of nanofluids by introducing Janus particles. Nanoscale 2022, 14, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Argonne, IL, USA, 1995. [Google Scholar]
- Choi, S.U. Nanofluid Technology: Current Status and Future Research; Illinois, University of North Texas Libraries, UNT Digital Library. 1998. Available online: https://digital.library.unt.edu (accessed on 12 September 2022).
- Ahmad, S.; Akhter, S.; Shahid, M.I.; Ali, K.; Akhtar, M.; Ashraf, M. Novel thermal aspects of hybrid nanofluid flow comprising of manganese zinc ferrite MnZnFe2O4, nickel zinc ferrite NiZnFe2O4 and motile microorganisms. Ain Shams Eng. J. 2022, 13, 101668. [Google Scholar] [CrossRef]
- Ali, K.; Faridi, A.A.; Ahmad, S.; Jamshed, W.; Khan, N.; Alam, M.M. Quasi-linearization analysis for heat and mass transfer of magnetically driven 3rd-grade (Cu-TiO2/engine oil) nanofluid via a convectively heated surface. Int. Commun. Heat Mass Transf. 2022, 135, 106060. [Google Scholar] [CrossRef]
- Ayub, R.; Ahmad, S.; Ahmad, S.; Akhtar, Y.; Alam, M.M.; Mahmoud, O. Numerical Assessment of Dipole Interaction with the Single-Phase Nanofluid Flow in an Enclosure: A Pseudo-Transient Approach. Materials 2022, 15, 2761. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, X.; Xu, B.; Yuan, M. Nanofluid research and applications: A review. Int. Commun. Heat Mass Transf. 2021, 127, 105543. [Google Scholar] [CrossRef]
- Asim, M.; Siddiqui, F.R. Hybrid Nanofluids Next Generation Fluids for Spray Cooling Based Thermal Management of High Heat Flux Devices. Nanomaterials 2022, 12, 507. [Google Scholar] [CrossRef]
- Doan, D.Q. Interfacial characteristics and their impact on the indentation behavior of CuTa/CuTa amorphous/amorphous nanolaminates. Int. J. Mech. Sci. 2022, 223, 107297. [Google Scholar] [CrossRef]
- Ekiciler, R.; Çetinkaya, M.S.A.; Arslan, K. Heat transfer enhancement in an equilateral triangular duct by using an Al2O3/water nanofluid: Effect of nanoparticle shape and volume fraction. Heat Transf. Res. 2020, 51, 741–757. [Google Scholar] [CrossRef]
- Yadav, P.; Gupta, S.M.; Sharma, S.K. A review on stabilization of carbon nanotube nanofluid. J. Therm. Anal. Calorim. 2022, 147, 6537–6561. [Google Scholar] [CrossRef]
- Arslan, K.; Ekiciler, R. Effects of SiO2/Water Nanofluid Flow in a Square Cross-Sectioned Curved Duct. Eur. J. Eng. Sci. Tech. 2019, 3, 101–109. [Google Scholar]
- Ahmad, S.; Ashraf, M.; Ali, K. Nanofluid flow comprising gyrotactic microorganisms through a porous medium. J. Appl. Fluid Mech. 2020, 13, 1539–1549. [Google Scholar]
- Ahmad, S.; Ali, K.; Ashraf, M. MHD flow of Cu-Al2O3/water hybrid nanofluid through a porous media. J. Porous Media 2021, 24, 61–73. [Google Scholar] [CrossRef]
- Casson, N. A flow equation for pigment-oil suspensions of the printing ink type. In Rheology of Disperse Systems; Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Shahzad, F.; Jamshed, W.; Sathyanarayanan, S.U.D.; Aissa, A.; Madheshwaran, P.; Mourad, A. Thermal analysis on Darcy-Forchheimer swirling Casson hybrid nanofluid flow inside parallel plates in parabolic trough solar collector: An application to solar aircraft. Int. J. Energy Res. 2021, 45, 20812–20834. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahammad, N.A.; Chamkha, A.J. Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng. 2021, 27, 101229. [Google Scholar] [CrossRef]
- Venkatesan, J.; Sankar, D.S.; Hemalatha, K.; Yatim, Y. Mathematical analysis of Casson fluid model for blood rheology in stenosed narrow arteries. J. Appl. Math. 2013, 2013, 583809. [Google Scholar] [CrossRef]
- Obalalu, A.M. Chemical entropy generation and second-order slip condition on hydrodynamic Casson nanofluid flow embedded in a porous medium: A fast convergent method. J. Egypt. Math. Soc. 2020, 30, 6. [Google Scholar] [CrossRef]
- Salahuddin, T.; Arshad, M.; Siddique, N.; Alqahtani, A.S.; Malik, M.Y. Thermophyical properties and internal energy change in Casson fluid flow along with activation energy. Ain Shams Eng. J. 2020, 11, 1355–1365. [Google Scholar] [CrossRef]
- Hirpho, M. Mixed convection of Casson fluid in a differentially heated bottom wavy wall. Heliyon 2021, 7, e07361. [Google Scholar] [CrossRef]
- Ennaouri, M.; Hachem, E.K. Modeling and study of the arterial blood flow loaded with nanoparticles under squeezing action in presence of a magnetic field. In Proceedings of the E3S Web of Conferences, Bandung, Indonesia, 11–12 October 2022; EDP Sciences: Ulis, France, 2022; Voulme 336, p. 00033. [Google Scholar] [CrossRef]
- Jamil, D.F.; Uddin, S.; Kamardan, M.G.; Roslan, R. The effects of magnetic Casson blood flow in an inclined multi-stenosed artery by using Caputo-Fabrizio fractional derivatives. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 82, 28–38. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jamshed, W.; Kumar, V.; Kumar, V.; Nisar, K.S.; Eid, M.R.; Yahia, I.S. Computational analysis of thermal energy distribution of electromagnetic Casson nanofluid across stretched sheet: Shape factor effectiveness of solid-particles. Energy Rep. 2021, 7, 7460–7477. [Google Scholar] [CrossRef]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K.L. Numerical treatment of MHD flow of Casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Contin. 2020, 66, 229–245. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Alotaibi, H.; Aljohani, H.M.; Wakif, A.; Khan, I.; Akram, S. Thermally enhanced Darcy-Forchheimer Casson-water/glycerine rotating nanofluid flow with uniform magnetic field. Micromachines 2021, 12, 605. [Google Scholar] [CrossRef] [PubMed]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy–Forchheimer nanofluid flow over a nonlinear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef]
- Matthew, O.L.; Kazeem, B.K.; Hammed, A.O.; Michael, O.O.; Yusuf, O.T.; Yussuff, T.L. On the mathematical model of Eyring–Powell nanofluid flow with non-linear radiation, variable thermal conductivity and viscosity. Dyn. Partial. Differ. Equ. 2022, 5, 100318. [Google Scholar]
- Vishalakshi, A.B.; Mahabaleshwar, U.S.; Sarris, I.E. An MHD Fluid Flow over a Porous Stretching/Shrinking Sheet with Slips and Mass Transpiration. Micromachines 2022, 13, 116. [Google Scholar] [CrossRef] [PubMed]
- Seid, E.; Haile, E.; Walelign, T. Multiple slip, Soret and Dufour effects in fluid flow near a vertical stretching sheet in the presence of magnetic nanoparticles. Int. J. Therm. Fluids 2022, 13, 100136. [Google Scholar] [CrossRef]
- Alali, E.; Megahed, A.M. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev. 2022, 11, 463–472. [Google Scholar] [CrossRef]
- Sadiq, K.; Siddique, I.; Ali, R.; Jarad, F. Impact of Ramped Concentration and Temperature on MHD Casson Nanofluid Flow through a Vertical Channel. J. Nanomater. 2021, 2021, 3743876. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Gul, T.; Bariq, A. MHD Darcy-Forchheimer flow of Casson nanofluid due to a rotating disk with thermal radiation and Arrhenius activation energy. J. Phys. Commun. 2021, 5, 025008. [Google Scholar] [CrossRef]
- Yu, J.; Hu, F.; Zhu, Q.; Li, X.; Ren, H.; Fan, S.; Yang, D. PD-L1 monoclonal antibody-decorated nanoliposomes loaded with paclitaxel and P-gp transport inhibitor for the synergistic chemotherapy against multidrug resistant gastric cancers. Nanoscale Res. Lett. 2020, 15, 59. [Google Scholar] [CrossRef] [PubMed]
- Al-Kouz, W.; Owhaib, W. Numerical analysis of Casson nanofluid three-dimensional flow over a rotating frame exposed to a prescribed heat flux with viscous heating. Sci. Rep. 2022, 12, 4256. [Google Scholar] [CrossRef] [PubMed]
- Bejawada, S.G.; Reddy, Y.D.; Jamshed, W.; Nisar, K.S.; Alharbi, A.N.; Chouikh, R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex. Eng. J. 2022, 61, 8207–8220. [Google Scholar] [CrossRef]
- Bala Anki Reddy, P.; Jakeer, S.; Thameem Basha, H.; Reddisekhar Reddy, S.R.; Mahesh Kumar, T. Multi-layer artificial neural network modeling of entropy generation on MHD stagnation point flow of Cross-nanofluid. Waves Random Complex Media 2022, 2067375. [Google Scholar] [CrossRef]
- Kanti, P.; Sharma, K.V.; Minea, A.A.; Kesti, V. Experimental and computational determination of heat transfer, entropy generation and pressure drop under turbulent flow in a tube with fly ash-Cu hybrid nanofluid. Int. J. Therm. Sci. 2021, 167, 107016. [Google Scholar] [CrossRef]
- Kanti, P.; Sharma, K.V.; Said, Z.; Kesti, V. Entropy generation and friction factor analysis of fly ash nanofluids flowing in a horizontal tube: Experimental and numerical study. Int. J. Therm. Sci. 2021, 166, 106972. [Google Scholar] [CrossRef]
- Kanti, P.K.; Sharma, K.V.; Said, Z.; Gupta, M. Experimental investigation on thermo-hydraulic performance of water-based fly ash–Cu hybrid nanofluid flow in a pipe at various inlet fluid temperatures. Int. Commun. Heat Mass Transf. 2022, 124, 105238. [Google Scholar] [CrossRef]
- Kanti, P.; Sharma, K.V.; Said, Z. Numerical study on the thermo-hydraulic performance analysis of fly ash nanofluid. J. Therm. Anal. Calorim. 2022, 147, 2101–2113. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Kumar, M.D.; Raju, C.S.K.; Sajjan, K.; El-Zahar, E.R.; Shah, N.A. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int. Commun. Heat Mass Transf. 2022, 134, 105995. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khan, I.; Baleanu, D.; Sooppy Nisar, K.; Shahzadi, G. Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface. Symmetry 2020, 12, 652. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Alqarni, M.S.; Wakif, A.; Khan, I.; Bhutta, M.S. Numerical Scrutinization of Darcy-Forchheimer Relation in Convective Magnetohydrodynamic Nanofluid Flow Bounded by Nonlinear Stretching Surface in the Perspective of Heat and Mass Transfer. Micromachines 2021, 12, 374. [Google Scholar] [CrossRef] [PubMed]
- Rasool, G.; Saeed, A.M.; Lare, A.I.; Abderrahmane, A.; Guedri, K.; Vaidya, H. Darcy-Forchheimer Flow of Water Conveying Multi-Walled Carbon Nanoparticles through a Vertical Cleveland Z-Staggered Cavity Subject to Entropy Generation. Micromachines 2022, 13, 744. [Google Scholar] [CrossRef] [PubMed]
- Shafiq, A.; Mebarek-Oudina, F.; Sindhu, T.N.; Rasool, G. Sensitivity analysis for Walters-B nanoliquid flow over a radiative Riga surface by RSM. Sci. Iran. 2022, 29, 1236–1249. [Google Scholar]
- Batool, S.; Rasool, G.; Alshammari, N.; Khan, I.; Kaneez, H.; Hamadneh, N. Numerical analysis of heat and mass transfer in micropolar nanofluids flow through lid driven cavity: Finite volume approach. Case Stud. Thermal Eng. 2022, 37, 102233. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Hussain, S.; Zaydan, M.; Wakif, A.; Chamkha, A.J.; Bhutta, M.S. Significance of Rosseland’s Radiative Process on Reactive Maxwell Nanofluid Flows over an Isothermally Heated Stretching Sheet in the Presence of Darcy-Forchheimer and Lorentz Forces: Towards a New Perspective on Buongiorno’s Model. Micromachines 2022, 13, 368. [Google Scholar] [CrossRef]
- Zari, I.; Shafiq, A.; Rasool, G.; Sindhu, T.N.; Khan, T.S. Double-stratified Marangoni boundary layer flow of Casson nanoliquid: Probable error application. J. Thermal Anal. Calorim. 2022, 147, 6913–6929. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation and dissipative heat transfer analysis of mixed convective hydromagnetic flow of a Casson nanofluid with thermal radiation and Hall current. Sci. Rep. 2021, 11, 3926. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation in convective radiative flow of a Casson nanofluid in non-Darcy porous medium with Hall current and activation energy. The multiple regression model. Appl. Math. Comput. 2021, 402, 125923. [Google Scholar] [CrossRef]
- Ali, K.; Ahmad, S.; Nisar, K.S.; Faridi, A.A.; Ashraf, M. Simulation analysis of MHD hybrid CuAl2O3/H2O nanofluid flow with heat generation through a porous media. Int. J. Energy Res. 2021, 45, 19165–19179. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Nisar, K.S.; Faridi, A.A.; Khan, N.; Jamshed, W.; Khan, T.M.Y.; Saleel, A. Features of Cu and TiO2 in the flow of engine oil subject to thermal jump conditions. Sci. Rep. 2021, 11, 19592. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Faridi, A.A.; Ashraf, M. Novel thermal aspects of hybrid nanoparticles Cu-TiO2 in the flow of ethylene glycol. Int. Commun. Heat Mass Transf. 2021, 129, 105708. [Google Scholar] [CrossRef]
- Nisar, K.S.; Faridi, A.A.; Ahmad, S.; Khan, N.; Ali, K.; Jamshed, W.; Abdel-Aty, A.-H.; Yahia, I.S. Cumulative Impact of Micropolar Fluid and Porosity on MHD Channel Flow: A Numerical Study. Coatings 2022, 12, 93. [Google Scholar] [CrossRef]
- Vajravelu, K. Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 2001, 124, 281–288. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Entropy Analysis of TiO2-Cu/EG Casson Hybrid Nanofluid via Cattaneo-Christov Heat Flux Model. Appl. Nanosci. 2018, 8, 1–14. [Google Scholar]
- Jamshed, W. Numerical Investigation of MHD Impact on Maxwell Nanofluid. Int. Commun. Heat Mass Transf. 2021, 120, 104973. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S. Computational single phase comparative study of Williamson nanofluid in parabolic trough solar collector via Keller box method. Int. J. Energy Res. 2021, 45, 10696–10718. [Google Scholar] [CrossRef]



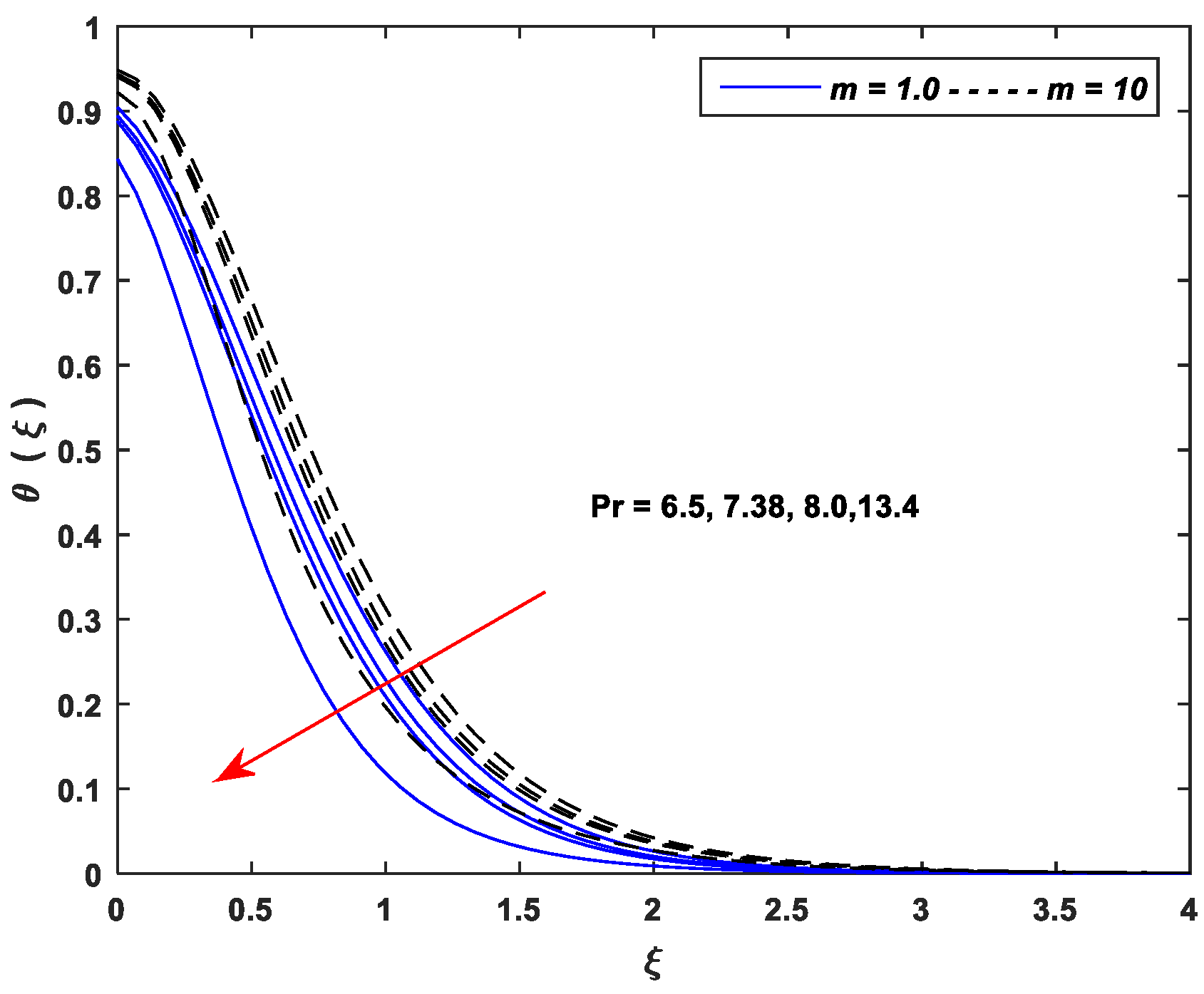
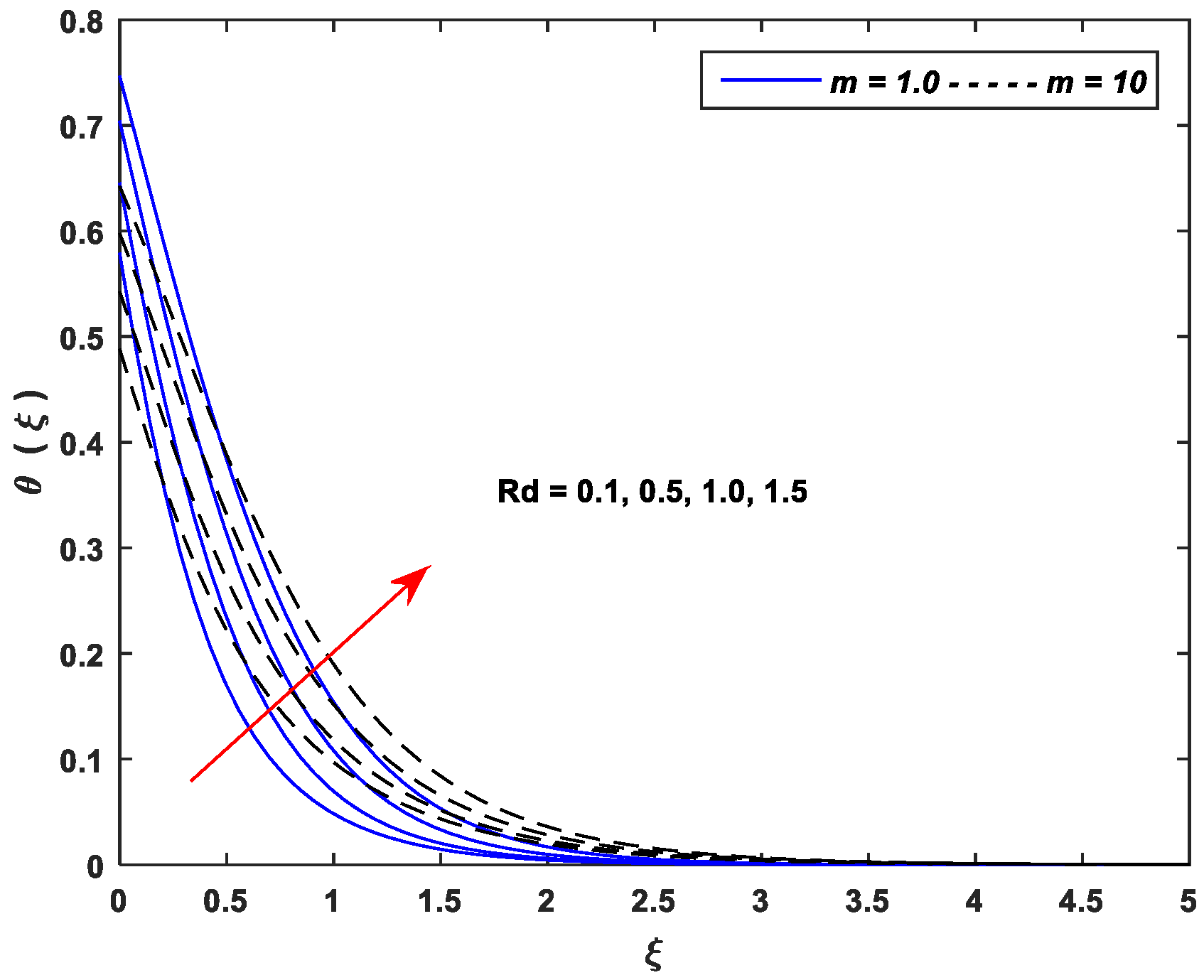
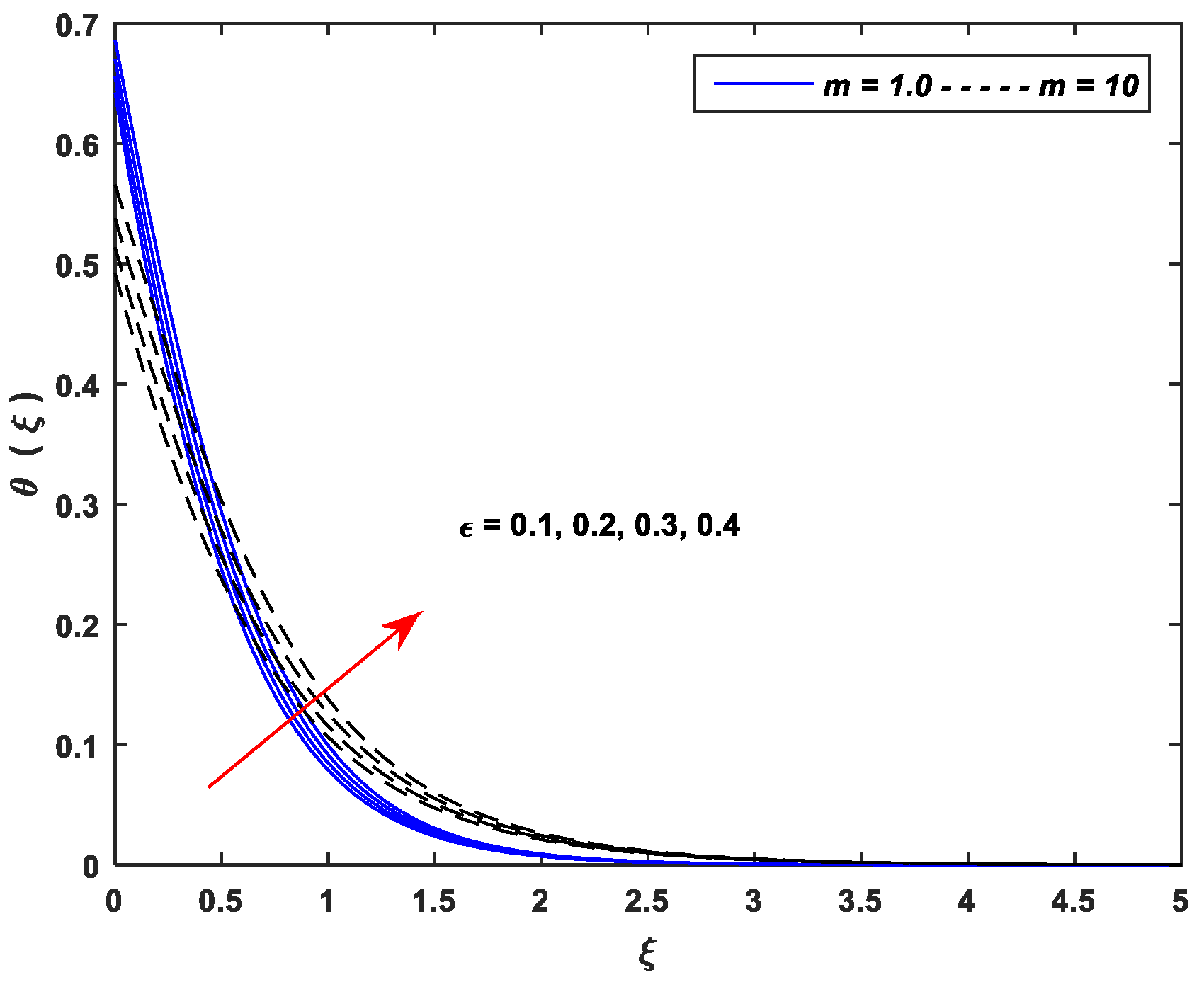
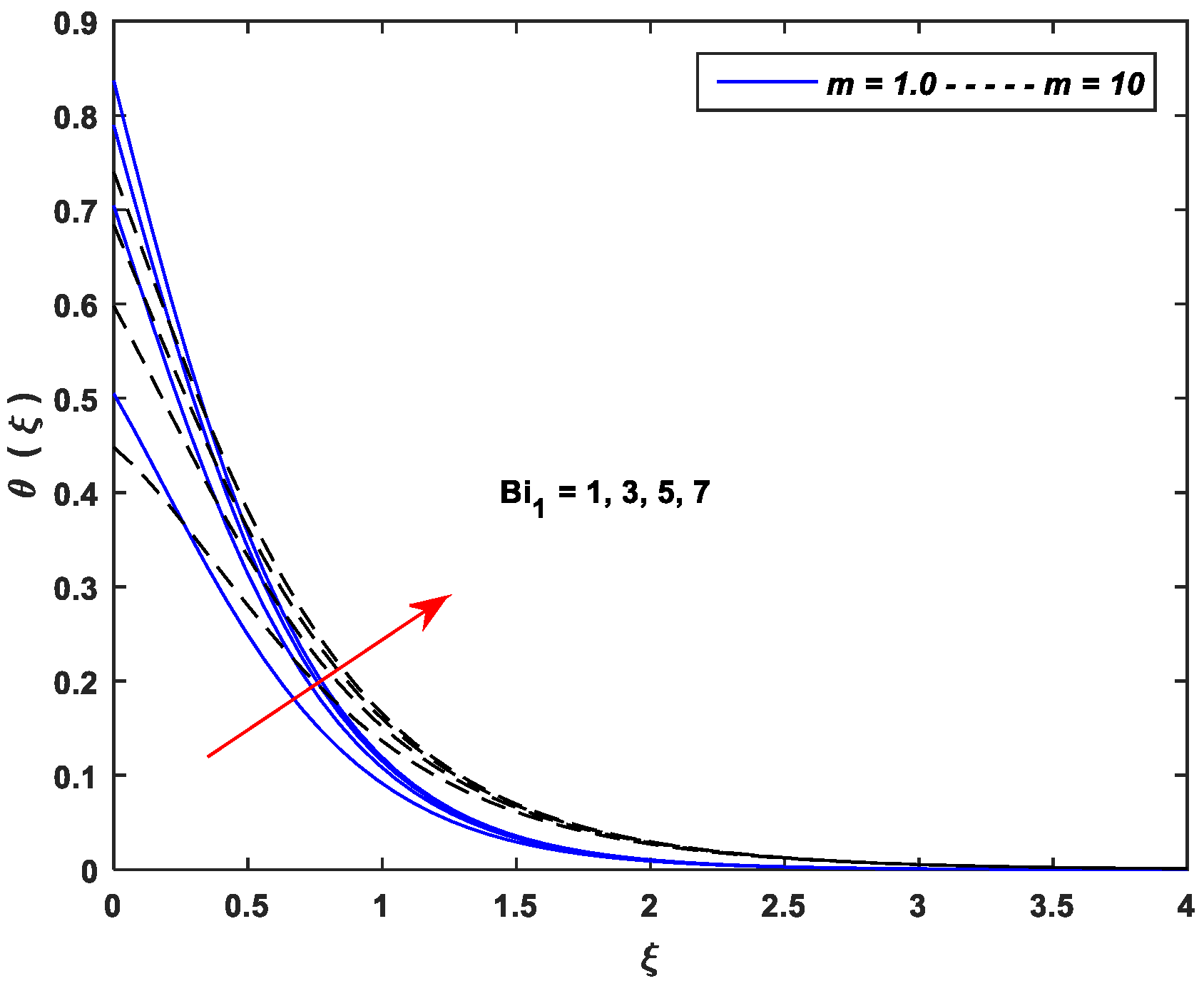





| Linear Stretching (m = 1.0) | Nonlinear Stretching (m = 10) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.38 | 5 | 1 | 0.3 | 0.1 | 0.5 | 3 | 2 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 |
| 6.50 | −2.0127 | 2.0215 | 0.6359 | −3.4058 | 6.3840 | 2.6385 | |||||||
| 7.38 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 8.00 | −2.2307 | 2.6936 | 0.3959 | −4.6823 | 7.9332 | 2.3796 | |||||||
| 2 | −1.2522 | 2.3938 | 0.5796 | −4.1249 | 8.6631 | 2.3350 | |||||||
| 3 | −1.5627 | 2.2560 | 0.5846 | −4.0620 | 7.9686 | 2.3984 | |||||||
| 5 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 1 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 2 | −1.8494 | 2.4286 | 0.6672 | −3.0301 | 8.2835 | 2.6653 | |||||||
| 3 | −1.6812 | 2.6148 | 0.7170 | −2.2438 | 9.3106 | 2.7633 | |||||||
| 0.3 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 0.4 | −1.7368 | 2.1591 | 0.5699 | −3.3178 | 6.9686 | 2.4786 | |||||||
| 0.5 | −1.5323 | 2.2149 | 0.5582 | −2.9036 | 7.2003 | 2.4498 | |||||||
| 0.1 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 0.2 | −1.9087 | 1.5545 | 0.6638 | −2.1724 | 3.1598 | 2.8806 | |||||||
| 0.3 | −1.7386 | 0.9730 | 0.7487 | 0.4449 | −2.3094 | 3.4186 | |||||||
| 1 | −1.4760 | 2.2093 | 0.5532 | −2.6048 | 6.9133 | 2.4712 | |||||||
| 2 | −0.9426 | 2.3126 | 0.5238 | −1.5491 | 7.1415 | 2.4314 | |||||||
| 3 | −0.6922 | 2.3526 | 0.5110 | −1.1027 | 7.2341 | 2.4147 | |||||||
| 2 | −2.1431 | 1.7297 | 0.6219 | −4.3114 | 5.0947 | 2.6169 | |||||||
| 4 | −1.9997 | 2.2955 | 0.5658 | −3.6926 | 7.7490 | 2.4516 | |||||||
| 6 | −1.9288 | 2.5737 | 0.5388 | −3.3207 | 9.3719 | 2.3522 | |||||||
| 1 | −2.1399 | 2.1294 | 0.4108 | −4.3904 | 6.8786 | 1.5333 | |||||||
| 3 | −2.0109 | 2.0375 | 0.6871 | −3.6629 | 6.4114 | 3.2167 | |||||||
| 5 | −1.9613 | 2.0017 | 0.7946 | −3.2843 | 6.1605 | 4.1298 | |||||||
| Linear Stretching (m = 1.0) | Nonlinear Stretching (m = 10) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 0.5 | 0.1 | 0.2 | 0.5 | 0.5 | 5 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 |
| 3 | −2.2710 | 2.1076 | 0.8862 | −4.9178 | 7.1047 | 3.1427 | |||||||
| 5 | −2.3261 | 2.1325 | 1.0030 | −5.1124 | 7.2187 | 3.3437 | |||||||
| 3 | −2.5725 | 2.1562 | 0.5556 | −6.3210 | 7.5287 | 2.3616 | |||||||
| 5 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 7 | −1.5259 | 1.9566 | 0.6226 | −1.2865 | 5.4147 | 2.7014 | |||||||
| 0.1 | −2.1670 | 2.5039 | 0.5244 | −4.7874 | 8.3329 | 2.3381 | |||||||
| 0.3 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 0.7 | −1.8019 | 1.1148 | 0.7273 | −1.9781 | 2.2189 | 2.9742 | |||||||
| 0.1 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
| 0.2 | −1.8532 | 1.9129 | 0.4212 | −3.0659 | 5.9165 | 2.2900 | |||||||
| 0.3 | −1.6681 | 1.7556 | 0.3002 | −2.2718 | 5.2373 | 2.1905 | |||||||
| 0.2 | −1.9023 | 2.1395 | 0.3580 | −3.2647 | 6.4004 | 2.1942 | |||||||
| 0.4 | −2.0569 | 2.0705 | 0.5880 | −3.9580 | 6.5409 | 2.5225 | |||||||
| 0.6 | −2.0902 | 1.9707 | 0.6694 | −4.1510 | 6.6033 | 2.6524 | |||||||
| 1 | −1.5483 | 1.9574 | 0.6233 | −2.1734 | 5.7906 | 2.6467 | |||||||
| 2 | −0.6506 | 1.6999 | 0.6878 | 0.6823 | 4.3577 | 2.8435 | |||||||
| 3 | 0.1247 | 1.4286 | 0.7456 | 2.9520 | 3.1026 | 3.0005 | |||||||
| 2 | −2.0762 | 2.0765 | 0.6203 | −3.9735 | 6.6115 | 2.5343 | |||||||
| 4 | −2.1000 | 2.0837 | 0.6601 | −3.9938 | 6.6327 | 2.5498 | |||||||
| 6 | −2.1217 | 2.0902 | 0.6966 | −4.0136 | 6.6425 | 2.5650 | |||||||
| 1 | −2.1188 | 2.0818 | 0.6730 | −4.0139 | 6.6320 | 2.5568 | |||||||
| 3 | −2.0714 | 2.0739 | 0.6094 | −3.9700 | 6.6096 | 2.5306 | |||||||
| 5 | −2.0569 | 2.0693 | 0.5880 | −3.9580 | 6.6033 | 2.5225 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, K.; Faridi, A.A.; Ahmad, S.; Jamshed, W.; Hussain, S.M.; Tag-Eldin, E.S.M. Quasi-Linearization Analysis for Entropy Generation in MHD Mixed-Convection Flow of Casson Nanofluid over Nonlinear Stretching Sheet with Arrhenius Activation Energy. Symmetry 2022, 14, 1940. https://doi.org/10.3390/sym14091940
Ali K, Faridi AA, Ahmad S, Jamshed W, Hussain SM, Tag-Eldin ESM. Quasi-Linearization Analysis for Entropy Generation in MHD Mixed-Convection Flow of Casson Nanofluid over Nonlinear Stretching Sheet with Arrhenius Activation Energy. Symmetry. 2022; 14(9):1940. https://doi.org/10.3390/sym14091940
Chicago/Turabian StyleAli, Kashif, Aftab Ahmed Faridi, Sohail Ahmad, Wasim Jamshed, Syed M. Hussain, and El Sayed M. Tag-Eldin. 2022. "Quasi-Linearization Analysis for Entropy Generation in MHD Mixed-Convection Flow of Casson Nanofluid over Nonlinear Stretching Sheet with Arrhenius Activation Energy" Symmetry 14, no. 9: 1940. https://doi.org/10.3390/sym14091940
APA StyleAli, K., Faridi, A. A., Ahmad, S., Jamshed, W., Hussain, S. M., & Tag-Eldin, E. S. M. (2022). Quasi-Linearization Analysis for Entropy Generation in MHD Mixed-Convection Flow of Casson Nanofluid over Nonlinear Stretching Sheet with Arrhenius Activation Energy. Symmetry, 14(9), 1940. https://doi.org/10.3390/sym14091940








