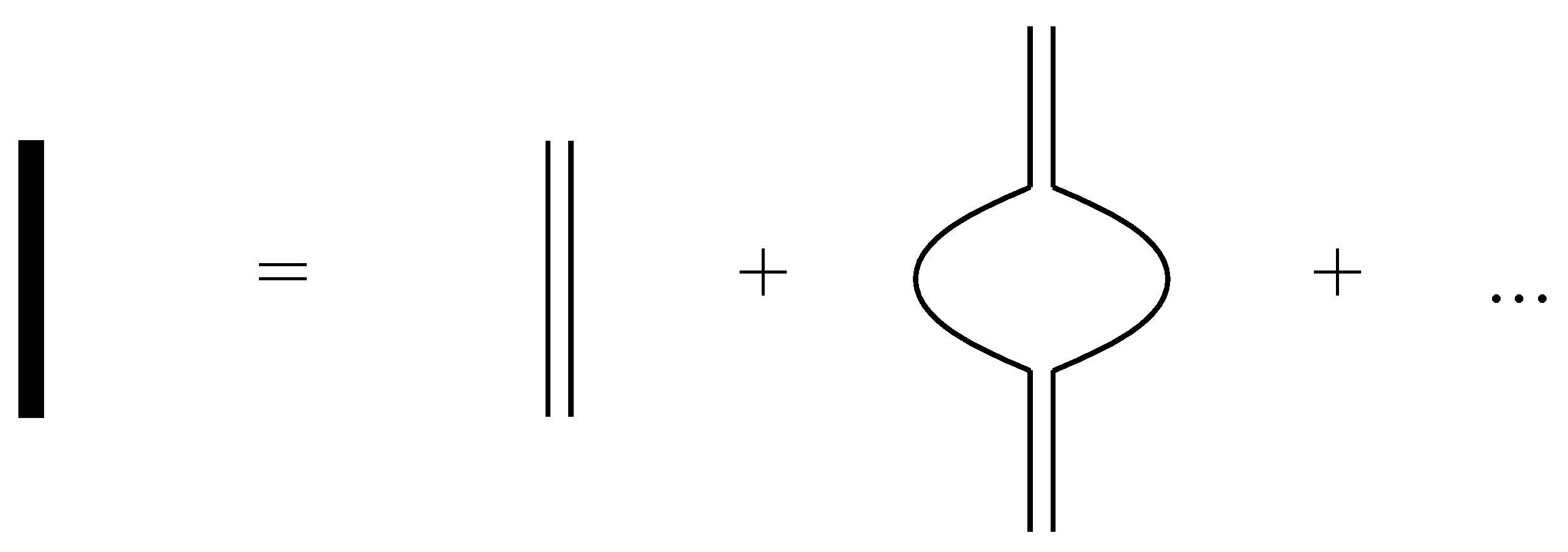Weinberg’s Compositeness ^†

Abstract

Nearly 60 years ago, Weinberg suggested a criterion for particle “compositeness”, which has acquired a new life with the discovery of new, exotic hadrons. His idea resonates with model-based intuition. I discuss the role it plays in the context of another of Weinberg’s creations, the model-independent framework of effective field theories.

1. Introduction

Steven Weinberg was one of those physicists who turned everything they touched into gold—except, of course, for their less well-known work. Steve once or twice told me that few things gave him as much pleasure as some recognition, such as a citation, of one of his more obscure papers that he nevertheless was proud of. The context was his paper on the algebraic realization of chiral symmetry [1], a beautiful and underappreciated idea related to some work we were performing in the early 1990s [2,3,4].

Steve was not a conceited man, and he realized some of his work was not golden—even though by other people’s standards, it could very well seem so. He has also told me—and is even on record in some YouTube video I can no longer find—that some of his papers in the 1960s were better forgotten. I do not know that this is for sure the case, but he might have been referring to his paper on the evidence that the deuteron is not an “elementary” particle [5], which followed a series of papers on “quasiparticles” [6,7,8]. By 2007, this paper had been cited in only about 20 publications, according to inSpire. The only citation by Steve himself I could locate is [9], where the “compositeness” condition $Z=0$ is not considered particularly “useful” in quantum field theories, except that “it fixes the coupling of the deuteron to the neutron and proton”. When we were looking into the deuteron also in the 1990s [10,11,12], not once did Steve recommend [5] to me. Yet, it has now 300+ citations (again, in inSpire) due to the explosion of interest in the new exotic hadronic states found since the $X\left(3872\right)$ in 2003 [13]. (For a recent review, see [14].) In this context, Steve’s result has been invoked as a criterion to decide which of the new states should be viewed as hadronic molecules.

I believe Steve’s loss of interest in that paper [5] is due to his later, much grander, idea of effective field theory (EFT) [15], where, from the very beginning, experimental limitations on accessible energies are explicitly incorporated into theory construction. The notion of compositeness is tied to resolution: one effective field theorist’s “elementary” particle is most likely another’s “composite” particle. In the nuclear EFTs formulated since the 1990s [16], Steve’s criterion of compositeness is automatically satisfied. The naive interpretation that an “elementary” particle is one associated with an explicit degree of freedom is muddled by the fact that one can always introduce an auxiliary field for the deuteron and/or another for the virtual spin-singlet S-wave state. If anything, it is for the latter [17,18] that the auxiliary field [19] has been more useful despite its intuitively higher “compositeness” coming from its extreme proximity to the scattering threshold. More generally, because an EFT includes all interactions allowed by symmetries, the choice of fields is to some extent arbitrary as far as observables, such as the location of S-matrix poles, go.

Nevertheless, identifying the relevant degrees of freedom is one of the cornerstones of EFT. I have long had the feeling that Steve’s criterion should have an EFT interpretation. I discovered the paper [5] on my own as a graduate student and have reread it every 5–10 years since, hoping to understand its EFT ramifications. Only recently did I succeed, thanks to a formulation of EFT for short-range forces [20] that is different from the one [21,22,23,24] that best applies to the two-nucleon problem. Since EFT is the current paradigm for theory construction [25], it seems worthwhile to relate Weinberg’s compositeness to the choice of the degrees of freedom and the organization of interactions (“power counting”).

This paper is not intended as a comprehensive review of the literature on Weinberg’s compositeness, but instead, should be viewed as a reconstruction of some known results from the point of view of a single-minded effective field theorist. In Section 2, the short-range EFT relevant for a discussion of Weinberg’s compositeness criterion is presented and contrasted with the short-range EFT normally considered in the two-nucleon system. The relevant EFT contains two S-wave poles, in terms of which Weinberg’s relations are rewritten in Section 3. In Section 4, the EFT is recast in terms of a “diparticle” field, and Weinberg’s Z is shown to track the relative importance of the diparticle kinetic term. In both of these sections, the “elementary” limit is seen to be special, with some of the results from [26] for narrow resonances extended to a bound/virtual state pair. The generalization of Weinberg’s criterion to resonances is discussed in Section 5 based on the similarities between the symmetric bound/virtual state and narrow resonances. Section 6 concludes with some additional thoughts.

2. EFT of Short-Range Forces

I will limit myself to the situation considered by Weinberg [5], namely a two-body process at characteristic momentum Q much smaller than the mass m of the particles, $Q\ll m$, and the inverse of the force range R, $Q\ll R^{-1}$. In this situation, particles are nonrelativistic and share a trivial factor $exp(-imt)$ in their temporal evolution. We introduce a field $\psi$ that involves only particle annihilation, from which the trivial evolution factor is removed. That is, we measure energies in the two-body system with respect to $2m$. Lorentz symmetry is implemented through “reparametrization invariance” [27] and gives rise to an expansion of observables in powers of $Q/m$. Particles cannot resolve the details of the underlying interaction, which can be treated via a multipole expansion as in electrodynamics: operators in the Lagrangian involve multiple powers of $\psi$ and ${\psi }^{†}$ and their derivatives at the same point and generate an expansion of observables in powers of $QR$. The coefficients of these operators—“Wilson” or “low-energy coefficients” (LECs)—account for the details of the underlying interaction and the effects of particle–antiparticle loops. Moreover, I assume for simplicity the conservation of particle number (i.e., the particle is stable), which means all operators involve the same number of $\psi$s and ${\psi }^{†}$s. The theory is separated into sectors of a given particle number, and here, we can limit ourselves to operators with at most two $\psi$s. In addition, to focus on the essential points, I impose parity and time-reversal invariance and neglect spin and internal quantum numbers such as isospin.

Under these conditions, the most general Lagrangian can be written as [20,24]

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\psi }^{†}\left(i\frac{\partial }{\partial t}+\frac{{\overrightarrow{\nabla }}^2}{2m}+\dots \right)\psi -\frac{4\pi }{m}\{C_0{\left(\psi \psi \right)}^{†}\left(\psi \psi \right)-\frac{C_2}{8}\left[{\left(\psi \psi \right)}^{†}\left(\psi {\overleftrightarrow{\nabla }}^2\psi \right)+\mathrm{H}.\mathrm{c}.\right]\hfill \\ & & +\frac{C_4}{64}\left[{\left(\psi \psi \right)}^{†}\left(\psi {\overleftrightarrow{\nabla }}^4\psi \right)+\mathrm{H}.\mathrm{c}.+2{\left(\psi {\overleftrightarrow{\nabla }}^2\psi \right)}^{†}\left(\psi {\overleftrightarrow{\nabla }}^2\psi \right)\right]+\dots \},\hfill \end{array}$$

(1)

where $\overleftrightarrow{\nabla }\equiv \overrightarrow{\nabla }-\overleftarrow{\nabla }$ and $C_{2n}$ are real LECs. The “…” represent operators that only contribute at higher orders and/or higher waves.

Using the rules of quantum field theory, we can calculate the T matrix for two-body scattering. At sufficiently low energy $E\equiv k^2/m$ in the center-of-mass (CM) frame, we expect S waves to dominate. The corresponding S matrix can be written as

$$S_0\left(k\right)=exp\left(2i{\delta }_0\left(k\right)\right)=1-\frac{imk}{2\pi }{T}_0\left(k\right)$$

(2)

in terms of the S-wave phase shift ${\delta }_0\left(k\right)$ and on-shell T matrix $T_0\left(k\right)$. Because we are considering only short-range interactions, the EFT T matrix is related to the effective range expansion (ERE) [28],

$$T_0\left(k\right)=-\frac{4\pi }{m}{\left(kcot{\delta }_0\left(k\right)-ik\right)}^{-1}=-\frac{4\pi }{m}{\left[-\frac{1}{a_0}+\frac{r_0}{2}{k}^2-P_0{\left(\frac{r_0}{2}\right)}^3{k}^4+\dots -ik\right]}^{-1},$$

(3)

where $a_0$, $r_0$, $P_0$, etc., are, respectively, the scattering length, effective range, shape parameter, etc. (Note that I use the original convention for the sign of the scattering length.) While at the two-body level short-range EFT can only amount to a reorganization of the ERE, it does allow for a consistent description of three and more particles [16].

What reorganization of the ERE is needed depends on the magnitudes of the ERE parameters in Equation (3) or, equivalently, of the LECs in Equation (1) connected to them by renormalization. Contact interactions are singular and require regularization, as in any other EFT. Since we are in general interested in a nonperturbative problem, a momentum regulator is more useful than dimensional regularization. I denote the regulator cutoff parameter by $\mathsf{\Lambda }$ and the regulator function by $F(q^2/{\mathsf{\Lambda }}^2)$, with $F\left(0\right)=1$ and $F(x^2\gg 1)\ll 1$. Regulator dependence enters through odd powers, ${\mathsf{\Lambda }}^{2n+1}$, each accompanied by a regulator-dependent number

$${\theta }_{2n+1}\equiv \frac{2}{\pi }{\int }_0^{\infty }dx{x}^{2n}F\left(x^2\right).$$

(4)

For example, ${\theta }_{2n+1}=2/(2n+1)\pi$ for a sharp-cutoff regulator, $F(q^2/{\mathsf{\Lambda }}^2)=\theta (1-q/\mathsf{\Lambda })$. Renormalization ensures that, at any order, regulator artifacts appear in observables only through terms with positive powers of $Q/\mathsf{\Lambda }$. After renormalization, residual regulator effects are no larger than the relative error $\mathcal{O}\left(QR\right)$ arising from the truncation of the Lagrangian once the cutoff parameter is sufficiently large, $\mathsf{\Lambda }\gtrsim R^{-1}$.

Order-by-order renormalization requires that the bare parameters in the Lagrangian (1) be specific functions of the cutoff, which cancel the cutoff dependence coming from the loops. The critical issue for an EFT is the magnitude of the surviving parts, which do contribute to observables. They can be estimated with the principle of naturalness [29,30]: the sensitivity to high-momentum physics reflected in the cutoff dependence of the bare LECs is captured in the surviving parts by the replacement $\mathsf{\Lambda }\to R^{-1}$.

In particle physics, naturalness is usually employed in a perturbative context. Here, adding to an existing diagram a (nonrelativistic) loop with an extra $C_{2n}$ interaction brings in a factor of $l^3/4\pi$ from the integration measure, $m/l^2$ from the two-particle propagator, and $4\pi C_{2n}{l}^{2n}/m$ from the vertex, where l is the loop momentum. These factors combine for a net $C_{2n}{l}^{2n+1}$, which increases the cutoff dependence by $C_{2n}{\mathsf{\Lambda }}^{2n+1}$. Naturalness then suggests $C_{2n}=\mathcal{O}\left(R^{2n+1}\right)$. This, in turn, implies that, after renormalization, the series is a perturbative expansion in $QR$ [24], justifying looking at the addition of a single loop in the first place. In first nontrivial order, we have the tree graph with $C_0$, at next order the one-loop graph with two $C_0$ vertices, and so on, corresponding to an expansion of Equation (3), where $a_0^{-1}$ is the largest term, $ik$ the second largest, $r_0{k}^2/2$ the next largest, and so on. Higher waves start at third nontrivial order. This notion of naturalness incorporates the simpler idea that, in the absence of a specific arrangement of parameters in an underlying potential, all ERE parameters are given by R according to their dimensions, for example $|a_0|\sim |r_0|/2\sim R$ and $|P_0|\sim 1$. An example is provided by the spherical well [24]. Note the difference from naturalness applied to relativistic loops, where we normally estimate the measure as $l^4/{\left(4\pi \right)}^2$ and the two-particle propagator as $l^{-2}$, leading to the so-called naive dimensional analysis [31,32].

Unfortunately, in the natural case, there are no S-matrix poles within the range of validity of the EFT. To produce shallow poles, at least one $C_{2n}$ must have an unnaturally large part and demand a nonperturbative treatment at LO. In the two-nucleon system, each S wave, ${}^3{S}_1$ and ${}^1{S}_0$, contains a single shallow pole, respectively, a bound state (the deuteron) and a virtual state. In an S-wave channel with a single shallow pole, there is a low-energy scale $\aleph \ll R^{-1}$ corresponding to the magnitude of the binding momentum. This situation can be described in the EFT if $C_0=\mathcal{O}\left({\aleph }^{-1}\right)$ and, thus, $|a_0|\sim {\aleph }^{-1}$, while the remaining S-wave LECs scale as $C_{2n>0}=\mathcal{O}\left({\aleph }^{-2}{R}^{2n-1}\right)$ [24]. In this case, an additional insertion of $C_0$ incurs in a penalty of $Q/\aleph$, which demands resummation with a pole at $Q\sim \aleph$ within the EFT range of validity. The leading order (LO) consists of the exact solution of the Lippmann–Schwinger (or Schrödinger) equation for the momentum space potential

$$V_0^{\left(0\right)}\left(\mathsf{\Lambda }\right)=\frac{4\pi }{m}{C}_0^{\left(0\right)}\left(\mathsf{\Lambda }\right),$$

(5)

which can be renormalized as long as the LO piece of $C_0$ is

$$C_0^{\left(0\right)}\left(\mathsf{\Lambda }\right)=-\frac{1}{{\theta }_1\mathsf{\Lambda }}\left[1+\delta +\mathcal{O}\left({\delta }^2\right)\right],$$

(6)

where

$$\delta \equiv \frac{1}{{\theta }_1{a}_0\mathsf{\Lambda }}$$

(7)

because I chose to reproduce $a_0$ exactly at LO. Meanwhile, corrections from $C_{2n>0}$ remain perturbative in $QR$, with higher ERE parameters still taking natural values, for example $|r_0|\sim R$ and $|P_0|\sim 1$. At next-to-leading order (NLO), we have one insertion of $C_2$, at next-to-next-to-leading order (N${}^2$LO) two insertions of $C_2$, and so on, with higher waves unchanged and, thus, starting with P at N${}^3$LO. This unnatural case requires a fine-tuning in the underlying potential, for example a precise adjustment of the depth of a spherical well to produce a shallow S-wave pole [24]. For a discussion of naturalness in a nonperturbative context, see [33].

The case relevant for a discussion of Weinberg’s compositeness requires both $C_0=\mathcal{O}\left({\aleph }^{-1}\right)$ and $C_2=\mathcal{O}\left({\aleph }^{-3}\right)$ to be enhanced. Both interactions need to be iterated at LO, which is equivalent to an exact solution of

$$V_0^{\left(0\right)}(\overrightarrow{p}{}^{\prime },\overrightarrow{p};\mathsf{\Lambda })=\frac{4\pi }{m}\left[C_0^{\left(0\right)}\left(\mathsf{\Lambda }\right)+C_2^{\left(0\right)}\left(\mathsf{\Lambda }\right)\frac{\overrightarrow{p}{}^2+\overrightarrow{p}{}^{\prime }{}^2}{2}\right],$$

(8)

written in terms of the incoming and outgoing relative momenta $\overrightarrow{p}$ and $\overrightarrow{p}{}^{\prime }$, respectively. It is not obvious that the increased singularity of the two-derivative contact interaction allows for renormalization, and yet, it does if the LO bare LECs are [20,34,35]

$$\begin{array}{ccc}\hfill C_0^{\left(0\right)}\left(\mathsf{\Lambda }\right)& =& \frac{{\theta }_5}{{\theta }_3^2\mathsf{\Lambda }}\left[1\mp 2\epsilon +\left(1-\frac{{\theta }_3^2}{{\theta }_5{\theta }_1}\right){\epsilon }^2\pm \left(1-\frac{{\theta }_3{\theta }_{-1}}{{\theta }_1^2}-\frac{{\theta }_3{r}_0}{{\theta }_1^3{a}_0}\right){\epsilon }^3+\mathcal{O}\left({\epsilon }^4,\frac{r_0}{a_0}{\epsilon }^4\right)\right],\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill C_2^{\left(0\right)}\left(\mathsf{\Lambda }\right)& =& -\frac{2}{{\theta }_3{\mathsf{\Lambda }}^3}\left[1\mp \epsilon \pm \left(1-\frac{{\theta }_3{\theta }_{-1}}{{\theta }_1^2}-\frac{{\theta }_3{r}_0}{{\theta }_1^3{a}_0}\right)\frac{{\epsilon }^3}{2}+\mathcal{O}\left({\epsilon }^5,\frac{r_0}{a_0}{\epsilon }^5\right)\right],\hfill \end{array}$$

(10)

where

$$\epsilon \equiv {\left(-\frac{2{\theta }_1^2}{{\theta }_3{r}_0\mathsf{\Lambda }}\right)}^{1/2}.$$

(11)

While $C_0^0\left(\mathsf{\Lambda }\right)$ is $\propto {\mathsf{\Lambda }}^{-1}$, as in Equation (6), now there are two solutions indicated by the ± signs accompanying the unusual inverse powers of ${(-r_0\mathsf{\Lambda })}^{1/2}$. This square root means that we must have $r_0<0$ for real $C_{0,2}^{\left(0\right)}$. This result is consistent with the Wigner bound [36], which puts a condition on the rate of change of the phase shift with respect to the energy for a finite-range, energy-independent potential and implies [37,38]

$$r_0\le 2R\left(1-\frac{R}{a_0}+\frac{R^2}{3a_0^2}\right).$$

(12)

For a zero-range potential, there is no positive effective range consistent with Equation (12) [35]. The requirement of renormalizability for our LO interactions automatically yields the same constraint and leads to the situation considered by Weinberg.

With this power counting, the EFT results not only in $|a_0|\sim {\aleph }^{-1}$, but also in $|r_0|\sim {\aleph }^{-1}$. There are now two poles within the EFT domain. They can be:

• For $a_0<0$, either two resonance poles in the lower half of the complex k plane, which are symmetric with respect to the imaginary axis (when $|a_0|<2|r_0|$), or two (separate or coincident) poles on the negative imaginary axis (when $|a_0|\ge 2|r_0|$).
• For $a_0>0$, one pole on the negative and the other on the positive imaginary axis.

At NLO, $C_4=\mathcal{O}\left({\aleph }^{-4}R\right)$ enters, causing a small shift in pole positions if $a_0$ and $r_0$ are kept fixed and generating a shape parameter $|P_0|\sim \aleph R$. Naturalness applied to the error at NLO implies [20] that $C_6=\mathcal{O}\left({\aleph }^{-5}{R}^2\right)$ appears at N${}^2$LO, and it was speculated that $C_{2n>0}=\mathcal{O}\left({\aleph }^{-2n}{R}^{n-1}\right)$. This situation requires a potential with two fine-tuned parameters, an example being a repulsive delta shell added at the rim of a spherical well [20,39].

The three cases—natural S waves, one fine-tuning, and two fine-tunings—are contrasted in

Table 1. Schematic representation of interaction orderings in short-range EFT with different numbers of shallow S-wave poles. At each of the three lowest orders—leading (LO), next-to-leading (NLO), and next-to-next-to-leading (N${}^2$LO)—the relevant low-energy constants (LECs) $C_{2n}$ are indicated. For an LO LEC, all powers are understood.

# S-Wave Poles	0	1	2
LO	0	$C_0$	$C_{0,2}$
NLO	$C_0$	$C_2$	$C_4$
N${}^2$LO	$C_0^2$	$C_2^2$	$C_4^2$, $C_6$

. As elaborated below, the case of interest for Weinberg’s argument involves two poles. The emphasis in [20] was on resonances—in fact, resonances in the sense of Weinberg [7], meaning poles of the S matrix regardless of the existence of a sharp peak in the cross section. Resonances were revisited with an auxiliary resonance field in [26], elaborating on earlier work [39,40,41]. I will consider in more detail here the case where one of the two poles is a bound state.

3. Poles

The distinctive feature of the short-range EFT with two fine-tunings is the existence of two poles $k_{\pm }$ for the S-wave S matrix,

$$S_0\left(k\right)=e^{2i\varphi \left(k\right)}\frac{(k+k_{-})(k+k_{+})}{(k-k_{-})(k-k_{+})},$$

(13)

where $\varphi \left(k\right)$ is the nonresonant or “background” contribution to the phase shift. For $a_0>0$, the two poles are on opposite sides of the imaginary axis [20], and at LO,

$$k_{\pm }^{\left(0\right)}=\mp i{\kappa }_{\pm },$$

(14)

where

$${\kappa }_{\pm }=\frac{1}{|r_0|}\left(\sqrt{1+\frac{2|r_0|}{a_0}}\pm 1\right),{\kappa }_{+}>{\kappa }_{-}>0.$$

(15)

The residues of $i{S}_0^{\left(0\right)}$ at both poles obey [20,42]

$$1-Z\equiv \frac{1}{2{\kappa }_{\pm }}{\left.\mathrm{Res}\left(i{S}_0^{\left(0\right)}\right)\right|}_{\mp i{\kappa }_{\pm }}=\frac{{\kappa }_{+}-{\kappa }_{-}}{{\kappa }_{+}+{\kappa }_{-}}={\left(1+2\frac{|r_0|}{a_0}\right)}^{-1/2},1>Z>0.$$

(16)

The positive value indicates that the pole $k_{-}$ on the positive imaginary axis is a bound state [43]. The constraint $r_0<0$ from renormalization thus excludes [20] the possibility of a “redundant” pole [44,45,46] on the positive imaginary axis with a negative residue.

Weinberg’s Z parameter, as defined for this type of EFT, is thus an observable, essentially the inverse relative splitting of the two states [47]. It allows us to rewrite other quantities in terms of Z and the binding momentum ${\kappa }_{-}$:

$${\kappa }_{+}={\kappa }_{-}\frac{2-Z}{Z}$$

(17)

and

$$\begin{array}{ccc}\hfill a_0& =& \frac{1-Z}{1-Z/2}{\kappa }_{-}^{-1},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill r_0& =& -\frac{Z}{1-Z}{\kappa }_{-}^{-1},\hfill \end{array}$$

(19)

which are the Weinberg relations, valid up to corrections of $\mathcal{O}(\aleph R)$ [5]. At LO, ${\varphi }^{\left(0\right)}\left(k\right)=0$ and

$$kcot{\delta }^{\left(0\right)}\left(k\right)=-{\kappa }_{-}\left[1+\frac{Z}{2(1-Z)}\left(1+\frac{k^2}{{\kappa }_{-}^2}\right)\right].$$

(20)

The appearance of a new parameter at NLO obviously implies modifications of these relations, as there are then three independent parameters instead of two. For the effects of an additional parameter, see [48].

When the bound state is within the regime of the EFT, ${\kappa }_{-}\sim \aleph \ll R^{-1}$, both the scattering length and effective range are large compared to R, unless $Z\to 0$ or $Z\to 1$. These limits deserve special consideration, as additional small parameters lead to a reorganization of the hierarchy of interactions. When Z is within the expansion parameter ${\kappa }_{-}R$ of 0 or 1, some contributions we have considered LO so far are demoted to higher orders.

The case $Z\lesssim {\kappa }_{-}R$ corresponds to a natural effective range, $|r_0|\lesssim R$, and an unnaturally large scattering length, $a_0\sim {\kappa }_{-}^{-1}$. We recover the situation dealt with for general short-range potentials in [24], where the virtual state is outside the EFT regime. Range effects, contained in the second term in Equation (20), are included in perturbation theory. How well the EFT works for the deuteron can be seen in [49]. It has had much use in nuclear [16] and cold atomic systems [50]. This is the case Weinberg [5] deemed “composite”, with $1-Z$ being then the “compositeness” of the bound state.

Since multiple shallow poles are associated with $|r_0|\gg R$, Morgan [51] suggested that their existence is likely an indication of “elementarity”. As [51] admits, however, there are potentials with two poles. A local class of such potentials, with a perhaps unphysical exponential fall-off at large distances, was given long ago [52]. For more abrupt fall-off, it does seem that an increasing number of shallow poles requires additional fine-tuning. In contrast, it might be reasonable to expect that the strong dynamics of two particles coupled to an elementary “diparticle” with the two-particle quantum numbers could give rise to multiple poles. Even in this case, however, the close proximity of the diparticle mass to $2m$ would still presumably require explanation—if there is no symmetry, then it is likely that we would be back to fine-tuning. Without further information, the mere existence of two shallow poles is far from the certain fulfillment of an intuitive notion of “elementariness”.

However, the case $1-Z\lesssim {\kappa }_{-}R$ does seem special. Up to $\mathcal{O}\left({\kappa }_{-}R\right)$ corrections, it corresponds to two poles ${\kappa }_{+}={\kappa }_{-}$ close to the origin and a large effective range [5] $|r_0|\gtrsim 1/\left({\kappa }_{-}^{2}R\right)$, while the scattering length is limited, $a_0\lesssim 2R$. For real $k^2$ not too close to the origin, scattering is dominated by the second term in Equation (20). In fact, for $k\sim {\kappa }_{-}$, it is $\mathcal{O}\left({\left({\kappa }_{-}R\right)}^{-1}\right)$ and larger than the unitarity term $-ik$ in $T_0\left(k\right)$. As for narrow resonances [20], this poses a problem for power counting: a subleading unitarity term means perturbation theory, but at the tree level, the sum of the two interactions with LECs $C_0$ and $C_2$ supports no pole.

The way to obtain two poles very close to the real axis is to assume that there is a correlation between an infinite number of interactions in Equation (1) such that, at leading nontrivial order, they add to a nonlocal potential, such as

$$V_0^{\left(1\right)}(\overrightarrow{p}{}^{\prime },\overrightarrow{p})=\frac{4\pi }{m}{C}_0^{\left(1\right)}\frac{1}{\sqrt{1-C_2^{\left(1\right)}\overrightarrow{p}{}^{\prime }{}^2/C_0^{\left(1\right)}}}\frac{1}{\sqrt{1-C_2^{\left(1\right)}\overrightarrow{p}{}^2/C_0^{\left(1\right)}}},$$

(21)

instead of Equation (8). For very different reasons, this type of potential has recently been considered as an alternative LO for the two-nucleon system at physical [53] (also with explicit pions [54]) and unphysical [55] quark masses. Here, it is easy to see that it yields Equation (20) if

$$\begin{array}{ccc}\hfill C_0^{\left(1\right)}& =& a_0,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill C_2^{\left(1\right)}& =& a_0{\kappa }_{-}^{-2}.\hfill \end{array}$$

(23)

Since $C_0^{\left(1\right)}=\mathcal{O}\left(R\right)$ and $C_2^{\left(1\right)}=\mathcal{O}\left(R{\aleph }^{-2}\right)$, the potential is $\mathcal{O}\left(R\right)$ and perturbative for generic momenta $\mathcal{O}(\aleph )$, but it produces the correct poles. They are poles of the potential itself, not of the iteration of the potential to all orders, as one would expect from a “composite” state. This is the simplest rationale for the interpretation of $Z\to 1$ as the “elementary” particle limit.

The price we pay in the EFT without a field for the diparticle is a loss of locality. Locality is usually taken as one of the principles in EFT construction. By locality, I mean not that interactions are momentum independent—they cannot be forbidden by symmetries—but that at any order, only a finite number of these interactions is present. As we will see next, this intrinsic nonlocality can be traded for energy dependence.

4. Diparticle

In an EFT, the choice of fields is arbitrary. We may, in particular, introduce an auxiliary “diparticle” (“dibaryon” or “dimer” in nuclear or atomic physics) field d [6,19] with the quantum numbers of the bound state. Consistent with our choice of $\psi$, d is a heavy field from which the trivial evolution $exp(-2imt)$ has been removed, leaving behind a residual mass $\Delta$. The most general Lagrangian can be written as [19,26]

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\psi }^{†}\left(i\frac{\partial }{\partial t}+\frac{{\overrightarrow{\nabla }}^2}{2m}\right)\psi +d^{†}\left(i\frac{\partial }{\partial t}+\frac{{\overrightarrow{\nabla }}^2}{4m}-\Delta \right)d\hfill \\ & & +\sqrt{\frac{4\pi }{m}}\frac{g_0}{4}\left(d^{†}\psi \psi +{\psi }^{†}{\psi }^{†}d\right)-\frac{4\pi }{m}{\tilde{C}}_0{\left(\psi \psi \right)}^{†}\left(\psi \psi \right)+\dots ,\hfill \end{array}$$

(24)

where ${\tilde{C}}_0$ and $g_0$ are real LECs and “…” indicates terms with additional derivatives (and fields, were we considering more-body systems). There is a certain redundancy in the Lagrangian (24), since, when one integrates out d, one obtains a string of four-$\psi$ interactions of the form already present in $\mathcal{L}$ [56]. However, these terms are all correlated in a way that is explicit only once the dimer field is kept. LECs such as ${\tilde{C}}_0$ can be thought of as the uncorrelated part of these interactions.

Two particles can now interact, through the coupling $g_0$, by the exchange of the diparticle in the s channel. The bare diparticle propagator in its CM frame is

$$D_0^{\left(0\right)}(k,\mathsf{\Lambda })={\left[k^2/m-{\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)+iϵ\right]}^{-1}$$

(25)

in terms of the LO residual mass ${\Delta }^{\left(0\right)}$. This propagator has two poles on the imaginary k axis for ${\Delta }^{\left(0\right)}<0$, but they are equidistant from the origin. For them to be shallow, ${\Delta }^{\left(0\right)}=\mathcal{O}({\aleph }^2/m)$. The splitting between ${\kappa }_{+}$ and ${\kappa }_{-}$, and thus $1-Z$, comes from the dressing of the propagator with loops. The first quantum effect in the bare diparticle propagator (25) is the one-loop diparticle self-energy

$${\mathsf{\Pi }}^{\left(0\right)}(k,\mathsf{\Lambda })=g_0^{\left(0\right)2}{I}_0(k,\mathsf{\Lambda }),$$

(26)

where $g_0^{\left(0\right)}$ is the LO diparticle-particle coupling and

$$I_0(k,\mathsf{\Lambda })=4\pi \int \frac{d^{3}l}{{\left(2\pi \right)}^3}\frac{1}{l^2-k^2-iϵ}={\theta }_1\mathsf{\Lambda }+ik+{\theta }_{-1}{k}^2/\mathsf{\Lambda }+\dots$$

(27)

is the two-particle bubble. If $g_0^{\left(0\right)}=\mathcal{O}\left(\sqrt{\aleph /m}\right)$ [26], at LO we need to resum the diparticle self-energy as in Figure 1, resulting in the dressed dimer propagator

$$D^{\left(0\right)}\left(k\right)={\left[D_0^{\left(0\right)-1}(k,\mathsf{\Lambda })+{\mathsf{\Pi }}^{\left(0\right)}(k,\mathsf{\Lambda })\right]}^{-1}$$

(28)

and the LO amplitude

$$T_0^{\left(0\right)}\left(k\right)=\frac{4\pi }{m}{g}_0^{\left(0\right)2}{D}^{\left(0\right)}\left(k\right)=-\frac{4\pi g_0^{\left(0\right)2}}{m}{\left[{\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)-k^2/m-{\mathsf{\Pi }}^{\left(0\right)}(k,\mathsf{\Lambda })\right]}^{-1}.$$

(29)

The poles $\pm i{\kappa }_{\mp }$ of $T_0^{\left(0\right)}\left(k\right)$ obviously satisfy

$${\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)+{\kappa }_{\mp }^2/m-{\mathsf{\Pi }}^{\left(0\right)}(\pm i{\kappa }_{\mp },\mathsf{\Lambda })=0.$$

(30)

Since $B_{-}={\kappa }_{-}^2/m$ is the binding energy of the bound state, ${\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)$ can be viewed as the bare or “unrenormalized” energy of the state. As pointed out by Weinberg [6], this relation does not allow us to calculate $B_{-}$; it only relates bare and renormalized energies. The essential cutoff dependence of the self-energy can be removed through the renormalization conditions:

$$\begin{array}{ccc}\hfill {\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)& =& -\frac{2}{m{r}_0}\left({\theta }_1\mathsf{\Lambda }-\frac{1}{a_0}\right)=\frac{2{\kappa }_{-}}{m}\frac{1}{Z}\left[(1-Z){\theta }_1\mathsf{\Lambda }-(1-Z/2){\kappa }_{-}\right],\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill g_0^{\left(0\right)}& =& {\left(-\frac{2}{m{r}_0}\right)}^{1/2}={\left(\frac{1-Z}{Z}\frac{2{\kappa }_{-}}{m}\right)}^{1/2},\hfill \end{array}$$

(32)

which lead again to Equations (15) and (20). The scalings ${\Delta }^{\left(0\right)}=\mathcal{O}({\aleph }^2/m)$ and $g_0^{\left(0\right)}=\mathcal{O}\left(\sqrt{\aleph /m}\right)$ when Z is not particularly close to 0 or 1 are evident from the finite pieces, respectively $\propto B_{-}$ and $\propto {\left(B_{-}\right)}^{1/4}$ [6]. The negative finite part of ${\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)$ ensures the two poles have imaginary momentum.

The residual cutoff dependence $\propto {\mathsf{\Lambda }}^{-1}$ of the LO amplitude (29) implies that there are corrections at NLO. In addition to shifts ${\Delta }^{\left(1\right)}\left(\mathsf{\Lambda }\right)$ and $g_0^{\left(1\right)}\left(\mathsf{\Lambda }\right)$ in parameters that appear already at LO, renormalization requires the inclusion of ${\tilde{C}}_0^{\left(1\right)}=\mathcal{O}\left(R\right)$, which is determined by the shape parameter $P_0$, $|P_0|\sim \aleph R$ [26]. This is the EFT sense in which a nonperturbative interaction ($C_0=\mathcal{O}\left({\aleph }^{-1}\right)$ in the previous section) becomes weak enough (${\tilde{C}}_0=\mathcal{O}\left(R\right)$) for perturbation theory to apply, thanks to the introduction of a field with the quantum numbers of a bound state [6,7]. This EFT has been applied to the deuteron in [57], and some of its atomic ramifications were discussed in [50].

The historical interpretation of the limit $Z\to 0$ as compositeness seems to be more closely related to this formulation of the EFT. It is tempting to assign compositeness to this limit on the basis of the $Z^{-1}$ behavior of ${\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)$. After all, one might expect compositeness to correspond to a large diparticle energy [6] and dispense with the need for a field to represent the bound state. However, $\Delta \left(\mathsf{\Lambda }\right)$ is not an observable, and the use of the dimer field is not tied to $Z\lesssim {\kappa }_{-}R$. In contrast, $g_0^{\left(0\right)}$ does not run with $\mathsf{\Lambda }$ and is also large for $Z\lesssim {\kappa }_{-}R$ because $|r_0|$ is small: from Equation (32), we see that

$$g_0^{\left(0\right)2}\le \frac{2{\kappa }_{-}}{mZ},$$

(33)

thus diverging as $Z\to 0$. This relation supports the intuitive interpretation of compositeness as resulting from a strong interaction of the two-particle state with the diparticle [6]. However, again, $g_0\left(\mathsf{\Lambda }\right)$ is not an observable.

Bruns [58,59] provided insight into the discussion of Weinberg’s compositeness by looking at wavefunctions for specific models. It is seen that $1-Z$ is approximately the probability to find the two particles beyond the range of the potential. Illuminating as it is, this sort of approach shares the limitation of others, which focus on non-observable quantities. Only the long-range properties of the wavefunction are related to observables; the short-range behavior, which affects the probability of finding particles widely separated via the normalization of the wavefunction, is intrinsically tied to two-body currents. This is reflected in the wavefunctions obtained in EFT. It is not difficult to see that the LO wavefunction for the bound state is

$${\psi }^{\left(0\right)}(\overrightarrow{r})=\sqrt{\frac{{\kappa }_{-}}{2\pi }}\frac{e^{-{\kappa }_{-}r}}{r}$$

(34)

in coordinate space. Not surprisingly, this is the asymptotic behavior of the wavefunctions considered by Bruns [58,59]. However, since the wavefunction (34) extends to the origin, the probability of finding the particles outside the potential is 1. This was to be expected, since at LO in the EFT the interaction has zero range.

These historical observations do, however, reflect a change in the power counting when $Z\to 0,1$. For $Z\lesssim {\kappa }_{-}R$, ${\Delta }^{\left(0\right)}=\mathcal{O}(\aleph /mR)$ and $g_0^{\left(0\right)}=\mathcal{O}(1/\sqrt{mR})$. The $k^2/m$ in Equation (29) is subleading by a power of $\aleph R$ compared to the other terms. This means the diparticle’s kinetic energy enters only at NLO [24] to account for energy dependence, while the scattering length is produced by the diparticle’s residual mass. The consequence of Weinberg’s condition for Z not particularly close to 0 is thus not the need for a diparticle field per se, but for its kinetic term to enter at LO.

More dramatic changes take place for $1-Z\lesssim {\kappa }_{-}R$, when the coupling is reduced to $g_0^{\left(1\right)}=\mathcal{O}\left(\sqrt{{\aleph }^{2}R/m}\right)$ and the whole diparticle self-energy is an NLO effect. We are in a perturbative regime where ${\Delta }^{\left(0\right)}\left(\mathsf{\Lambda }\right)={\Delta }^{\left(0\right)}<0$ gives rise at LO to two nearby, shallow poles ${\kappa }_{+}={\kappa }_{-}\equiv \kappa =\sqrt{m|{\Delta }^{\left(0\right)}|}$ from the bare particle propagator (25). Because, in this limit, the diparticle behaves like a weakly interacting particle of mass $\simeq 2m+{\Delta }^{\left(0\right)}$ just below the two-particle threshold, it is indeed natural to interpret it as an “elementary” particle. This relates to the usual interpretation of Z as the overlap between “dressed” and “bare” diparticle states [6]. Again, one might expect some fine-tuning to produce $|{\Delta }^{\left(0\right)}|\ll 2m$, but in this situation a single fine-tuning would be needed.

This interpretation is supported by the diparticleless formulation. When multiplied by $4\pi g_0^2/m$, the diparticle propagator (25) can be seen as an energy-dependent potential, which replaces the diparticleless nonlocal potential (21). The s-channel exchange of the diparticle automatically accounts for the correlations needed in the diparticleless formulation, and the EFT remains local. However, as pointed out in [39] in the closely related case of narrow resonances, $g_0^{\left(1\right)2}{D}_0^{\left(0\right)}=\mathcal{O}\left(R\right)$ should now be comparable to the “uncorrelated” part of the short-range interaction, ${\tilde{C}}_0^{\left(1\right)}=\mathcal{O}\left(R\right)$, on the basis of naturalness. In the $Z\to 1$ limit, we thus expect the potential to be not just the diparticle propagator, but

$$V_0^{\left(1\right)}\left(k\right)=\frac{4\pi }{m}\left[{\tilde{C}}_0^{\left(1\right)}+\frac{m{g}_0^{\left(1\right)2}}{k^2-m{\Delta }^{\left(0\right)}}\right].$$

(35)

This potential was discussed for the two-nucleon ${}^1{S}_0$ channel in [18] and for narrow resonances in [26], elaborating on the earlier work of [39,40,41]. An analogous argument justifies the addition of a constant to the nonlocal potential (21) in the diparticleless formulation.

Many of the resonance results can immediately be translated to the case of a symmetric bound/virtual state pair. In particular, the LO amplitude (29) becomes

$$T_0^{\left(1\right)}\left(k\right)=V_0^{\left(1\right)}\left(k\right)=\frac{4\pi }{m}{a}_0\frac{1-k^2/k_0^2}{1+k^2/{\kappa }^2},$$

(36)

with

$$\begin{array}{ccc}\hfill {\Delta }^{\left(0\right)}& =& -\frac{{\kappa }^2}{m},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill g_0^{\left(1\right)}& =& {\left[a_0\left(1+\frac{{\kappa }^2}{k_0^2}\right)\frac{{\kappa }^2}{m}\right]}^{1/2},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\tilde{C}}_0^{\left(1\right)}& =& -a_0\frac{{\kappa }^2}{k_0^2}.\hfill \end{array}$$

(39)

In addition to the poles at $\pm i\kappa$, $\kappa =\mathcal{O}(\aleph )>0$, the amplitude has zeros at $\pm k_0$, $|k_0|=\mathcal{O}(\aleph )$. The latter occurs on the real axis, $k_0>0$, for $0>{\tilde{C}}_0^{\left(1\right)}>-g_0^{\left(1\right)2}/\left|{\Delta }^{\left(0\right)}\right|$—this is the Ramsauer–Townsend effect [60,61]. Otherwise, the zeros are on the imaginary axis. An example is the neutron–deuteron system in the spin-doublet channel [62], although the bound state (the triton) and the virtual state are not symmetric with respect to the origin. The sign of the scattering length $a_0=\mathcal{O}\left(R\right)$ is constrained by the reality of $g_0^{\left(1\right)}$ (38),

$$a_0\left(1+\frac{{\kappa }^2}{k_0^2}\right)>0.$$

(40)

Although the amplitude (36) has a pole on the positive imaginary axis with a positive residue, $\mathrm{Res}(i{S}_0^{(1)}(k)){|}_{k=i\kappa }=\kappa a_0(1+{\kappa }^2/k_0^2)>0$, this is a pole of the potential itself. Just as in the diparticleless formulation, the interpretation of this pole as an “elementary” particle (in the EFT) seems justified.

5. Resonances

Much work in the recent literature has been dedicated to generalizing Weinberg’s criterion to resonances. A resonance is associated with two poles:

$$k_{\pm }=\pm k_R-i{k}_I,$$

(41)

where, when they are shallow,

$$\begin{array}{ccc}\hfill k_I& =& \frac{1}{|r_0|}>0,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill k_R& =& k_I\sqrt{\frac{2r_0}{a_0}-1}>0.\hfill \end{array}$$

(43)

Here, $2r_0<a_0<0$. For $2r_0<a_0<r_0$, the poles are closer to the imaginary axis than to the real axis, $k_R<k_I$. This is sometimes referred to as a subthreshold resonance since the real part of its energy is negative. Its effect on scattering is limited, and the background phase shift is not negligible. For $r_0<a_0<0$, in contrast, $k_R>k_I$: the proximity of the resonance poles to the real axis makes the phase shift cross $\pi /2$ at the real (positive) part of the resonance energy.

From the EFT perspective, what stands out is that the “elementary” bound-state limit $Z\to 1$ shares the same power counting issues as narrow resonances [20], for which $k_I\ll k_R$ as a consequence of $|r_0|\gg |a_0|$. This should not be surprising. Typically, a resonance emerges from a combination of attraction and repulsion, and as attraction increases, the two resonant poles collide on the negative imaginary axis at $-i/|r_0|$. Narrow resonances will collide close to the origin, and as attraction increases further, the bound state will emerge almost symmetrically with respect to the virtual state. In other words, for large $|r_0|$, the relative splitting between the poles (15) is small, reflecting the continuity with narrow resonances.

Except in a very small window around it, a narrow resonance can be described perturbatively with a diparticle field [26] just as a symmetric bound/virtual pair in the previous section. Their shared property is a relatively large effective range $|r_0|\gg |a_0|$. This suggests a simple generalization of Weinberg’s parameter Z (16),

$$1-\mathcal{Z}\equiv {\left(1+2\frac{|r_0|}{|a_0|}\right)}^{-1/2},1>\mathcal{Z}>0.$$

(44)

This quantity has in fact been proposed recently [63] as an extension to resonances that preserves the bounds on Z. An alternative quantity that has a simpler expression in terms of pole positions is

$$1-\tilde{\mathcal{Z}}\equiv \left|\mp \frac{i}{2k_{\pm }}{\left.\mathrm{Res}\left(i{S}_0^{\left(0\right)}\right)\right|}_{k_{\pm }}\right|=\left|\frac{k_{+}+k_{-}}{k_{+}-k_{-}}\right|=\left\{\begin{array}{c}1-Z(\mathrm{bound}/\mathrm{virtual}\mathrm{pair}),\hfill \\ k_I/k_R\left(\mathrm{resonance}\right),\hfill \end{array}\right.$$

(45)

which falls in the ranges

$$\left\{\begin{array}{c}0<1-\tilde{\mathcal{Z}}<1(\mathrm{bound}/\mathrm{virtual}\mathrm{pair}\mathrm{or}\mathrm{narrow}\mathrm{resonance}),\hfill \\ 1<1-\tilde{\mathcal{Z}}<\infty \left(\mathrm{subthreshold}\mathrm{resonance}\right).\hfill \end{array}\right.$$

(46)

This in turn corresponds to the proposal in [42].

Both of these quantities account for the view of the diparticle as elementary—in the sense of weakly coupling and responsible for the poles—as $\mathcal{Z}\to 1$ or $\tilde{\mathcal{Z}}\to 1$ for either a narrow resonance or a bound/virtual pair. In this limit, the two symmetric real poles collide at the origin to produce two symmetric imaginary poles. For $|r_0|\gg |a_0|$, the two quantities agree, $1-\mathcal{Z}\simeq \sqrt{|a_0|/2|r_0|}\simeq 1-\tilde{\mathcal{Z}}$. Within $1-\mathcal{Z}=\mathcal{O}(\aleph R)$ of this limit, the simplest formulation of the EFT consists of a bare diparticle propagator and a non-derivative contact interaction at LO, with subleading orders including loops and derivative interactions.

For $|a_0|\gg |r_0|$, both quantities are small, $\mathcal{Z}\simeq |r_0|/|a_0|$ and $\tilde{\mathcal{Z}}\simeq \left|r_0\right|/a_0$. Within the region $\mathcal{Z}=|\tilde{\mathcal{Z}}|=\mathcal{O}(\aleph R)$, the low-energy dynamics is dominated by a single bound-state or virtual-state pole. However, $\mathcal{Z}$ and $\tilde{\mathcal{Z}}$ differ for $a_0\sim r_0<0$ [63]. The difference is particularly large for a subthreshold resonance, but this type of resonance has limited impact on observables despite being shallow. From the EFT perspective, the main drawback of $\tilde{\mathcal{Z}}$ is that it vanishes when $k_I=k_R$ without having an obvious association with a change in power counting. In contrast, on that line of the complex momentum plane, $\mathcal{Z}=1-1/\sqrt{2}$. Thus, only $\mathcal{Z}$ tracks the changes in power counting needed in the two special limits $\mathcal{Z}\to 0,1$.

6. Conclusions

I looked at Weinberg’s ancient compositeness criterion through the glasses of Weinberg’s modern framework of effective field theories. I employed two versions of an EFT for short-range interactions, which incorporates the situation he originally considered of two low-energy two-body S-wave poles: a bound state and a virtual state. In the first version, only contact interactions are present. In the second, an auxiliary diparticle field is included to represent correlations among contact interactions.

In this EFT, Weinberg’s parameter Z (16) is an observable related to the relative pole distance in the relative momentum plane. Its value can thus be used as a criterion for something, but it is not immediately clear at the level of poles why it is for compositeness. Most of the literature focuses on quantities that are scheme and/or model dependent. In contrast, EFT provides a model-independent framework to describe observables. At least at the two-body level discussed here, the two poles can, in most arrangements, be equivalently described by either version of the EFT. This includes the limit $Z\to 0$, where the virtual pole is outside the regime of validity of the EFT. The equivalence between the two versions of the EFT in that case is well known (see, e.g., [24]). Neither the existence of two poles nor the convenience of a diparticle field provide a compelling justification for Weinberg’s criterion from the EFT perspective.

It is only the $Z\to 1$ limit that leads to significant challenges to the diparticleless formulation. It requires a perturbative nonlocal interaction that seems at odds with the usual requirement of an expansion in derivatives at the Lagrangian level. In the diparticle formulation, in the same limit, the dominant interaction is still perturbative, but energy dependent, being produced by the s-channel exchange of the diparticle. The bound state arises from the diparticle propagator, as one would expect when two particles couple weakly to an “elementary” particle that shares the two-particle quantum numbers. The unusual correlation among momentum-dependent interactions in the diparticleless formulation can be justified a posteriori by the integrating-out of the “elementary” diparticle. It is an example of Weinberg’s dictum: “You may use any degrees of freedom you like to describe a physical system, but if you use the wrong ones, you’ll be sorry” [64]. This seems to me the strongest rationale for the notion of “elementarity”.

There is a similarity between this limit and the extreme case of a zero-width resonance, both stemming from a relatively large effective range, $|r_0|\gg |a_0|$. This similarity suggests the generalization $\mathcal{Z}$ (44) of Weinberg’s Z, which was proposed recently in [63] on the basis of a different, but related argument. The limit $\mathcal{Z}\to 1$ can be considered that of an “elementary” diparticle, in the sense described above. If the diparticle mass is above the two-particle threshold, it generates two narrow resonance poles and, if below, a bound/virtual pair. Why the diparticle mass is close enough to the two-particle threshold for the two poles to be shallow is not a question one can in general address without more information about the underlying theory.

Although this criterion provides a reasonable interpretation of “elementarity”, in the end, it is just a classification of different power countings for the EFT with underlying physics at distance $\mathcal{O}\left(R\right)$ and two shallow poles at momenta $\mathcal{O}(\aleph )$:

• For $\mathcal{Z}=\mathcal{O}(\aleph R)$, physics is dominated by a single pole, which represents a bound or virtual state. The kinetic term of the diparticle field is an NLO effect. If the diparticle is integrated out, the only LO interaction is a non-derivative contact interaction.
• For $\mathcal{Z}\sim 1/2$, the two poles are important. The kinetic term of the diparticle field is LO. If the diparticle is integrated out, the LO interactions consist of non-derivative and two-derivative contact interactions.
• For $1-\mathcal{Z}=\mathcal{O}(\aleph R)$, the two poles are nearly symmetrical with respect to the origin of the complex momentum plane, either on the imaginary axis or very close to the real axis. The poles arise from a weakly coupled diparticle or, if it is integrated out, from an infinite number of correlated contact interactions.

Different power countings are, ultimately, a reflection of the size of observable quantities such as $a_0$ and $r_0$. The impact of these different power countings on more-body systems should be studied [65].

Useful as it is for an EFT of short-range forces, which is implicit in Weinberg’s original paper [5], $\mathcal{Z}$ is in principle limited to this EFT. In applications to exotic hadrons, where experimental information is limited, the first issue to sort out is what EFT to use. For example, for the $X\left(3872\right)$, an EFT with (perturbative) pions [66,67] could replace a short-range EFT [68] if the pole momenta are not small compared to the inverse force range $R^{-1}\sim \sqrt{{\Delta }^2-m_{\pi }^2}$, where $m_{\pi }$ is the neutral-pion mass and $\Delta$ is the mass splitting between the charmed mesons $D^{*0}$ and $D^0$. What role $\mathcal{Z}$ can play in the presence of such long-range forces and/or additional thresholds is a matter for further investigation. One can mine for gold even in Steve’s less well-known work!