The QCD Adler Function and the Muon g − 2 Anomaly from Renormalons
Abstract
1. Introduction
2. The Adler Function
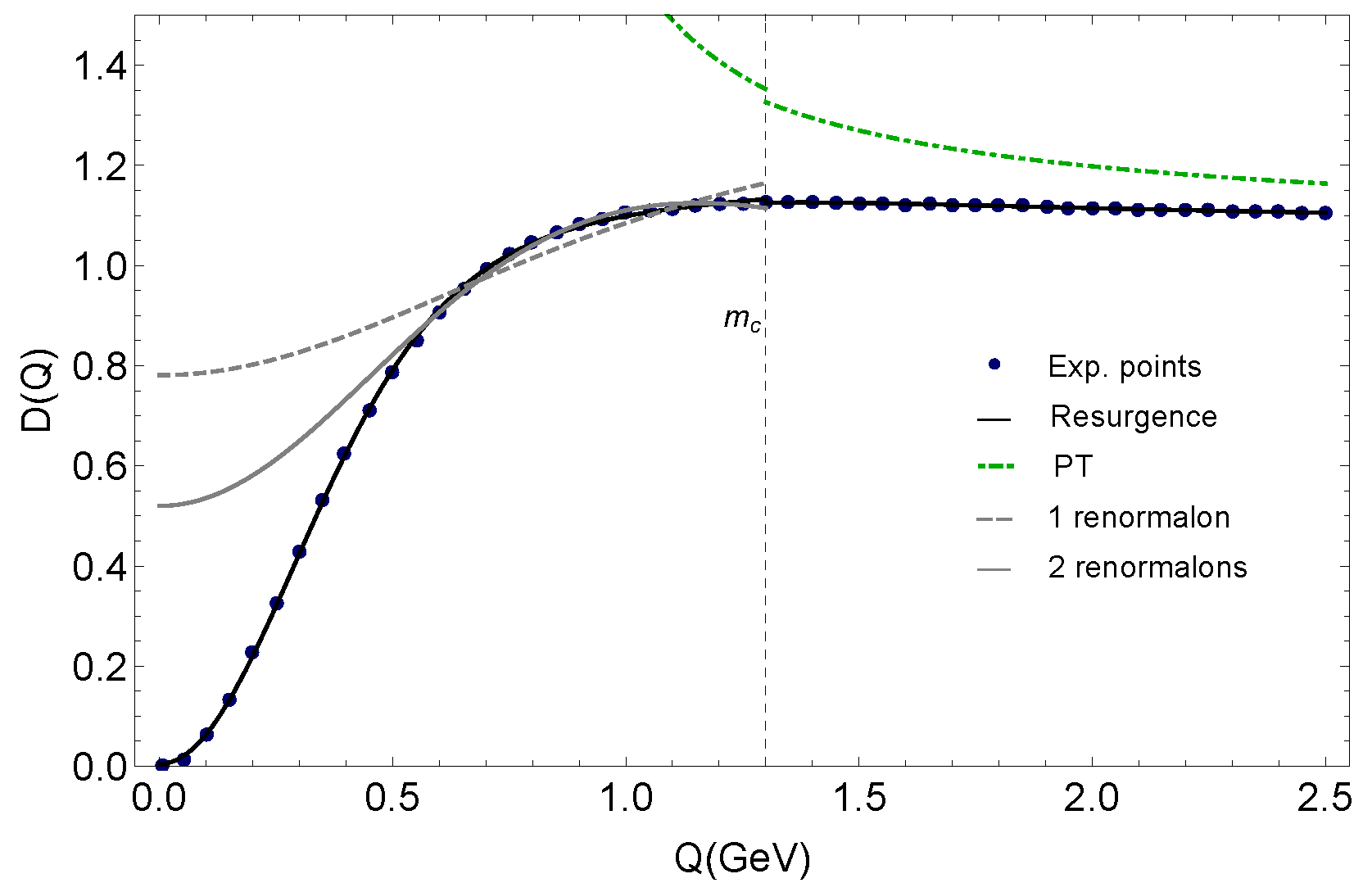
3. Resurgent Adler Function
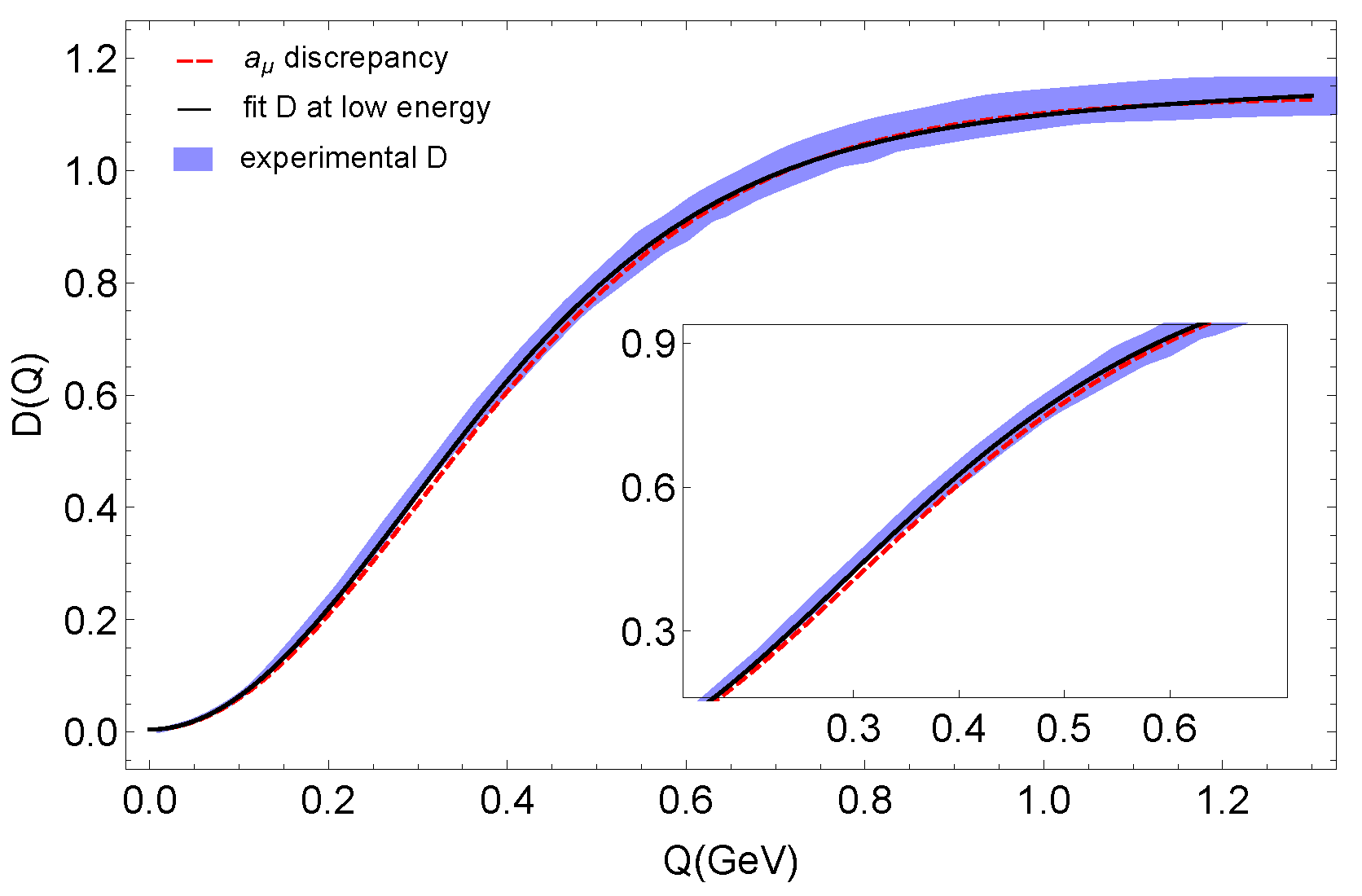
4. Effective Running and the QCD Adler Function at Low Energies
5. Saturating the Experimental Discrepancy of the Muon Anomalous Magnetic Moment of the Muon
6. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Borel-Ecalle Resummation Based on the Non-Linear Ordinary Differential Equations
Appendix B. Highlights on ODE-Based Resurgence
Appendix C. Resurgence and the Adler Function
Quadratic Poles
References
- Adler, S.L. Some simple vacuum-polarization phenomenology: e+e−→hadrons; the muonic-atom X-ray discrepancy and gμ−2. Phys. Rev. D 1974, 10, 3714–3728. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kuhn, J.H. Order alpha**4(s) QCD Corrections to Z and tau Decays. Phys. Rev. Lett. 2008, 101, 012002. [Google Scholar] [CrossRef] [PubMed]
- Francis, A.; Jäger, B.; Meyer, H.B.; Wittig, H. New representation of the Adler function for lattice QCD. Phys. Rev. D 2013, 88, 054502. [Google Scholar] [CrossRef]
- Gross, D.J.; Neveu, A. Dynamical symmetry breaking in asymptotically free field theories. Phys. Rev. D 1974, 10, 3235–3253. [Google Scholar] [CrossRef]
- Lautrup, B. On high order estimates in QED. Phys. Lett. B 1977, 69, 109–111. [Google Scholar] [CrossRef]
- ’t Hooft, G. Can We Make Sense Out of Quantum Chromodynamics? Subnucl. Ser. 1979, 15, 943. [Google Scholar]
- Parisi, G. The Borel Transform and the Renormalization Group. Phys. Rept. 1979, 49, 215–219. [Google Scholar] [CrossRef]
- Wilson, K.G.; Zimmermann, W. Operator product expansions and composite field operators in the general framework of quantum field theory. Comm. Math. Phys. 1972, 24, 87–106. [Google Scholar] [CrossRef]
- Shifman, M. Yang-Mills at Strong vs. Weak Coupling: Renormalons, OPE And All That. Eur. Phys. J. Spec. Top. 2021, 230, 2699–2709. [Google Scholar] [CrossRef]
- Beneke, M. Renormalons. Phys. Rept. 1999, 317, 1–142. [Google Scholar] [CrossRef]
- Shifman, M. New and Old about Renormalons: In Memoriam Kolya Uraltsev. Int. J. Mod. Phys. A 2015, 30, 1543001. [Google Scholar] [CrossRef]
- Cvetič, G. Renormalon-motivated evaluation of QCD observables. Phys. Rev. D 2019, 99, 014028. [Google Scholar] [CrossRef]
- Caprini, I. Conformal mapping of the Borel plane: Going beyond perturbative QCD. Phys. Rev. D 2020, 102, 054017. [Google Scholar] [CrossRef]
- Shirkov, D.V.; Solovtsov, I.L. Analytic model for the QCD running coupling with universal alpha-s (0) value. Phys. Rev. Lett. 1997, 79, 1209–1212. [Google Scholar] [CrossRef]
- Nesterenko, A.V. Adler function in the analytic approach to QCD. eConf 2007, C0706044, 25. [Google Scholar]
- Cvetic, G.; Valenzuela, C. Analytic QCD: A Short review. Braz. J. Phys. 2008, 38, 371–380. [Google Scholar]
- Peris, S.; Perrottet, M.; de Rafael, E. Matching long and short distances in large N(c) QCD. JHEP 1998, 5, 11. [Google Scholar] [CrossRef]
- Maiezza, A.; Vasquez, J.C. Resurgence of the QCD Adler function. Phys. Lett. B 2021, 817, 136338. [Google Scholar] [CrossRef]
- Écalle, J. Six Lectures on Transseries, Analysable Functions and the Constructive Proof of Dulac’s Conjecture; Springer: Berlin/Heidelberg, Germany, 1993; pp. 75–184. [Google Scholar] [CrossRef]
- Argyres, P.C.; Unsal, M. The semi-classical expansion and resurgence in gauge theories: New perturbative, instanton, bion, and renormalon effects. JHEP 2012, 8, 63. [Google Scholar] [CrossRef]
- Dunne, G.V.; Unsal, M. Resurgence and Trans-series in Quantum Field Theory: The CP(N-1) Model. JHEP 2012, 11, 170. [Google Scholar] [CrossRef]
- Dorigoni, D. An Introduction to Resurgence, Trans-Series and Alien Calculus. Ann. Phys. 2019, 409, 167914. [Google Scholar] [CrossRef]
- Aniceto, I.; Basar, G.; Schiappa, R. A Primer on Resurgent Transseries and Their Asymptotics. Phys. Rept. 2019, 809, 1–135. [Google Scholar] [CrossRef]
- Clavier, P.J. Borel-Ecalle resummation of a two-point function. Ann. Henri Poincaré 2019, 22, 2103–2136. [Google Scholar] [CrossRef]
- Borinsky, M.; Dunne, G.V. Non-Perturbative Completion of Hopf-Algebraic Dyson-Schwinger Equations. Nucl. Phys. B 2020, 957, 115096. [Google Scholar] [CrossRef]
- Fujimori, T.; Honda, M.; Kamata, S.; Misumi, T.; Sakai, N.; Yoda, T. Quantum phase transition and Resurgence: Lessons from 3d = 4 SQED. Prog. Theor. Exp. Phys. 2021, 2021, 103B04. [Google Scholar] [CrossRef]
- Costin, O.; Dunne, G.V. Resurgent extrapolation: Rebuilding a function from asymptotic data. Painlevé I. J. Phys. A 2019, 52, 445205. [Google Scholar] [CrossRef]
- Costin, O.; Dunne, G.V. Physical Resurgent Extrapolation. Phys. Lett. B 2020, 808, 135627. [Google Scholar] [CrossRef]
- Borinsky, M.; Broadhurst, D. Resonant resurgent asymptotics from quantum field theory. Nucl. Phys. 2022, 981, 115861. [Google Scholar] [CrossRef]
- Costin, O. Exponential asymptotics, transseries, and generalized Borel summation for analytic, nonlinear, rank-one systems of ordinary differential equations. Int. Math. Res. Not. 1995, 1995, 377. [Google Scholar] [CrossRef]
- Costin, O. Asymptotics and Borel Summability. Monographs and Surveys in Pure and Applied Mathematics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Maiezza, A.; Vasquez, J.C. Non-local Lagrangians from Renormalons and Analyzable Functions. Ann. Phys. 2019, 407, 78–91. [Google Scholar] [CrossRef]
- Bersini, J.; Maiezza, A.; Vasquez, J.C. Resurgence of the Renormalization Group Equation. Ann. Phys. 2020, 415, 168126. [Google Scholar] [CrossRef]
- Landau, L.D. Niels Bohr and the Development of Physics; Pergamon Press: London, UK, 1955. [Google Scholar]
- Cornwall, J.M. Dynamical Mass Generation in Continuum QCD. Phys. Rev. D 1982, 26, 1453. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Cornwall, J.M. Coupled fermion gap and vertex equations for chiral-symmetry breakdown in QCD. Phys. Rev. D 1991, 44, 1285–1297. [Google Scholar] [CrossRef] [PubMed]
- Deur, A.; Brodsky, S.J.; de Teramond, G.F. The QCD Running Coupling. Nucl. Phys. 2016, 90, 1. [Google Scholar] [CrossRef]
- Miller, J.P.; de Rafael, E.; Roberts, B.L. Muon (g − 2): Experiment and theory. Rept. Prog. Phys. 2007, 70, 795. [Google Scholar] [CrossRef]
- Miller, J.P.; de Rafael, E.; Roberts, B.L.; Stöckinger, D. Muon (g − 2): Experiment and Theory. Ann. Rev. Nucl. Part. Sci. 2012, 62, 237–264. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Marciano, W.J.; Passera, M.; Sirlin, A. Muon g − 2 and Δα connection. Phys. Rev. D 2020, 102, 033002. [Google Scholar] [CrossRef]
- Abi, B.; Albahri, T.; Al-Kilani, S.; Allspach, D.; Alonzi, L.P.; Anastasi, A.; Anisenkov, A.; Azfar, F.; Badgley, K.; Baeßler, S.; et al. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Guenther, J.N.; Hoelbling, C.; Katz, S.D.; Lellouch, L.; Lippert, T.; Miura, K.; Parato, L.; Szabo, K.K.; et al. Leading hadronic contribution to the muon magnetic moment from lattice QCD. Nature 2021, 593, 51–55. [Google Scholar] [CrossRef]
- Gorishnii, S.G.; Kataev, A.L.; Larin, S.A. The -corrections to σtot(e+e−→hadrons) and Γ(τ−→ντ+hadrons) in QCD. Phys. Lett. B 1991, 259, 144–150. [Google Scholar] [CrossRef]
- Surguladze, L.R.; Samuel, M.A. Total hadronic cross-section in e+e− annihilation at the four loop level of perturbative QCD. Phys. Rev. Lett. 1991, 66, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Kataev, A.L.; Starshenko, V.V. Estimates of the higher order QCD corrections to R(s), R(tau) and deep inelastic scattering sum rules. Mod. Phys. Lett. A 1995, 10, 235–250. [Google Scholar] [CrossRef]
- Beneke, M.; Braun, V.M. Naive nonAbelianization and resummation of fermion bubble chains. Phys. Lett. B 1995, 348, 513–520. [Google Scholar] [CrossRef]
- Lipatov, L.N. Multi-Regge Processes and the Pomeranchuk Singularity in Nonabelian Gauge Theories. In Proceedings of the Proceedings, XVIII International Conference on High-Energy Physics Volume 1, Tbilisi, USSR, Tbilisi, Georgia, 15–21 July 1976; pp. A5.26–A5.28. [Google Scholar]
- Maiezza, A.; Vasquez, J.C. On Haag’s Theorem and Renormalization Ambiguities. Found. Phys. 2021, 51, 80. [Google Scholar] [CrossRef]
- Neubert, M. Scale setting in QCD and the momentum flow in Feynman diagrams. Phys. Rev. D 1995, 51, 5924–5941. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L.; Marchesini, G.; Webber, B.R. Dispersive approach to power behaved contributions in QCD hard processes. Nucl. Phys. B 1996, 469, 93–142. [Google Scholar] [CrossRef]
- Parisi, G. Singularities of the Borel Transform in Renormalizable Theories. Phys. Lett. B 1978, 76, 65–66. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L.; Uraltsev, N.G. Are IR renormalons a good probe for the strong interaction domain? Phys. Lett. B 1996, 380, 141–150. [Google Scholar] [CrossRef][Green Version]
- Peris, S.; de Rafael, E. On renormalons and Landau poles in gauge field theories. Phys. Lett. B 1996, 387, 603–608. [Google Scholar] [CrossRef]
- Maiezza, A.; Vasquez, J.C. Non-Wilsonian ultraviolet completion via transseries. Int. J. Mod. Phys. A 2021, 36, 2150016. [Google Scholar] [CrossRef]
- Klaczynski, L.; Kreimer, D. Avoidance of a Landau Pole by Flat Contributions in QED. Ann. Phys. 2014, 344, 213–231. [Google Scholar] [CrossRef]
- Cvetic, G.; Valenzuela, C. An Approach for evaluation of observables in analytic versions of QCD. J. Phys. G 2006, 32, L27. [Google Scholar] [CrossRef]
- Cvetic, G.; Valenzuela, C. Various versions of analytic QCD and skeleton-motivated evaluation of observables. Phys. Rev. D 2006, 74, 114030. [Google Scholar] [CrossRef]
- Cvetic, G. Techniques of evaluation of QCD low-energy physical quantities with running coupling with infrared fixed point. Phys. Rev. D 2014, 89, 036003. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J. The Muon anomalous magnetic moment: Standard model theory and beyond. In Proceedings of the 5th International Symposium on Radiative Corrections: Applications of Quantum Field Theory to Phenomenology, Carmel, CA, USA, 11–15 September 2000. [Google Scholar]
- Czarnecki, A.; Marciano, W.J. The Muon anomalous magnetic moment: A Harbinger for ‘new physics’. Phys. Rev. D 2001, 64, 013014. [Google Scholar] [CrossRef]
- Knecht, M. The Anomalous magnetic moment of the muon: A Theoretical introduction. Lect. Notes Phys. 2004, 629, 37–84. [Google Scholar] [CrossRef]
- Davier, M.; Marciano, W.J. The theoretical prediction for the muon anomalous magnetic moment. Ann. Rev. Nucl. Part. Sci. 2004, 54, 115–140. [Google Scholar] [CrossRef]
- Jegerlehner, F.; Nyffeler, A. The Muon g − 2. Phys. Rept. 2009, 477, 1–110. [Google Scholar] [CrossRef]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Carloni Calame, C.M.; Cè, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rept. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Cvetič, G.; Kögerler, R. Lattice-motivated QCD coupling and hadronic contribution to muon g − 2. J. Phys. G 2021, 48, 055008. [Google Scholar] [CrossRef]
- Davier, M.; Hoecker, A.; Malaescu, B.; Zhang, Z. Reevaluation of the Hadronic Contributions to the Muon g − 2 and to alpha(MZ). Eur. Phys. J. C 2011, 71, 1515. [Google Scholar] [CrossRef]
- Davier, M.; Hoecker, A.; Malaescu, B.; Zhang, Z. Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon g − 2 and using newest hadronic cross-section data. Eur. Phys. J. C 2017, 77, 827. [Google Scholar] [CrossRef]
- Davier, M.; Hoecker, A.; Malaescu, B.; Zhang, Z. A new evaluation of the hadronic vacuum polarisation contributions to the muon anomalous magnetic moment and to . Eur. Phys. J. C 2020, 80, 241. [Google Scholar] [CrossRef]
- Lautrup, B.E.; Peterman, A.; de Rafael, E. Recent developments in the comparison between theory and experiments in quantum electrodynamics. Phys. Rept. 1972, 3, 193–259. [Google Scholar] [CrossRef]
- Crivellin, A.; Hoferichter, M.; Manzari, C.A.; Montull, M. Hadronic Vacuum Polarization: (g − 2)μ versus Global Electroweak Fits. Phys. Rev. Lett. 2020, 125, 091801. [Google Scholar] [CrossRef]
- Malaescu, B.; Schott, M. Impact of correlations between aμ and αQED on the EW fit. Eur. Phys. J. C 2021, 81, 46. [Google Scholar] [CrossRef]
- Colangelo, G.; Hoferichter, M.; Stoffer, P. Constraints on the two-pion contribution to hadronic vacuum polarization. Phys. Lett. B 2021, 814, 136073. [Google Scholar] [CrossRef]
- Banerjee, P.; Calame, C.; Chiesa, M.; Di Vita, S.; Engel, T.; Fael, M.; Laporta, S.; Mastrolia, P.; Montagna, G.; Nicrosini, O.; et al. Theory for muon-electron scattering @ 10 ppm: A report of the MUonE theory initiative. Eur. Phys. J. C 2020, 80, 591. [Google Scholar] [CrossRef]
- Davier, M.; Hocker, A.; Zhang, Z. The Physics of Hadronic Tau Decays. Rev. Mod. Phys. 2006, 78, 1043–1109. [Google Scholar] [CrossRef]
- Webber, B.R. Estimation of power corrections to hadronic event shapes. Phys. Lett. B 1994, 339, 148–150. [Google Scholar] [CrossRef]
- Manohar, A.V.; Wise, M.B. Power suppressed corrections to hadronic event shapes. Phys. Lett. B 1995, 344, 407–412. [Google Scholar] [CrossRef][Green Version]
- Korchemsky, G.P.; Sterman, G.F. Nonperturbative corrections in resummed cross-sections. Nucl. Phys. B 1995, 437, 415–432. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L.; Webber, B.R. Calculation of power corrections to hadronic event shapes. Phys. Lett. B 1995, 352, 451–455. [Google Scholar] [CrossRef]
- Akhoury, R.; Zakharov, V.I. On the universality of the leading, 1/Q power corrections in QCD. Phys. Lett. B 1995, 357, 646–652. [Google Scholar] [CrossRef]
- Nason, P.; Seymour, M.H. Infrared renormalons and power suppressed effects in e+e− jet events. Nucl. Phys. B 1995, 454, 291–312. [Google Scholar] [CrossRef]
- Beneke, M.; Braun, V.M. Heavy quark effective theory beyond perturbation theory: Renormalons, the pole mass and the residual mass term. Nucl. Phys. B 1994, 426, 301–343. [Google Scholar] [CrossRef]
- Bigi, I.I.Y.; Shifman, M.A.; Uraltsev, N.G.; Vainshtein, A.I. The Pole mass of the heavy quark. Perturbation theory and beyond. Phys. Rev. D 1994, 50, 2234–2246. [Google Scholar] [CrossRef]
- Aglietti, U.; Ligeti, Z. Renormalons and confinement. Phys. Lett. B 1995, 364, 75. [Google Scholar] [CrossRef]
- Costin, O. On Borel summation and Stokes phenomena for rank- 1 nonlinear systems of ordinary differential equations. Duke Math. J. 1998, 93, 289–344. [Google Scholar] [CrossRef]
- Broadhurst, D.J. Large N expansion of QED: Asymptotic photon propagator and contributions to the muon anomaly, for any number of loops. Z. Phys. C 1993, 58, 339–346. [Google Scholar] [CrossRef]
| Parameter | Low Energy Fit (4-Loop) | Low Energy Fit (5-Loop) |
|---|---|---|
| K | 1.422 | 0.805 |
| C | 0.629 | 0.240 |
| 0.0326 | −0.358 | |
| 731 MeV | 697 MeV |
| Parameter | Discrepancy |
|---|---|
| K | 0.865 |
| C | 0.764 |
| −0.184 | |
| 677 MeV |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiezza, A.; Vasquez, J.C. The QCD Adler Function and the Muon g − 2 Anomaly from Renormalons. Symmetry 2022, 14, 1878. https://doi.org/10.3390/sym14091878
Maiezza A, Vasquez JC. The QCD Adler Function and the Muon g − 2 Anomaly from Renormalons. Symmetry. 2022; 14(9):1878. https://doi.org/10.3390/sym14091878
Chicago/Turabian StyleMaiezza, Alessio, and Juan Carlos Vasquez. 2022. "The QCD Adler Function and the Muon g − 2 Anomaly from Renormalons" Symmetry 14, no. 9: 1878. https://doi.org/10.3390/sym14091878
APA StyleMaiezza, A., & Vasquez, J. C. (2022). The QCD Adler Function and the Muon g − 2 Anomaly from Renormalons. Symmetry, 14(9), 1878. https://doi.org/10.3390/sym14091878






