The Characterizations of Parallel q-Equidistant Ruled Surfaces

Abstract

In this paper, parallel q-equidistant ruled surfaces are defined such that the binormal vectors of given two differentiable curves are parallel along the striction curves of their corresponding binormal ruled surfaces, and the distance between the asymptotic planes is constant at proper points, which is related to symmetry. The characterizations and some other useful relations are drawn for these surfaces as well. If the surfaces are considered to be closed, then the integral invariants such as the pitch, the angle of the pitch, and the drall of them are given. Finally, some examples are presented to indicate that the distance between the proper points on the corresponding asymptotic planes is always constant.

1. Introduction and Preliminaries

In 3-dimensional Euclidean space, the surfaces generated by the motion of lines along a given curve are called as ruled surfaces [1,2,3]. As these surfaces are easy to handle by means of their mathematical formulation, they are used in many fields, such as architectural design, computer aided geometric design and kinematics. The basic theory behind the ruled surfaces and their associations on the relative fields can be found in many textbooks [1,2,3,4,5,6]. In 1986, Valeontis defined parallel p-equidistant ruled surfaces such that the generator vectors of two ruled surfaces are parallel along their striction curves, and the distance between the polar planes is constant [7]. After this conceptualization, researchers studied such ruled surfaces by means of their generalizations and geometric properties, such as integral invariants, shape operators, spherical indicatrix and the corresponding relations among them [8,9,10,11,12,13]. There are other studies that coined this practice by using other frames in different spaces [14,15,16,17]. Furthermore, the dual expression of parallel p-equidistant ruled surfaces was introduced in [18]. In addition to these, the notion of parallel z-equidistant ruled surfaces was given by As and Şenyurt, by which, this time, the principal normal vectors are considered to be parallel along the striction curves and the distance between the corresponding two central planes is constant at proper points, and these are all related to symmetry [18,19].

Motivated by these studies, in this paper, we address and introduce parallel q-equidistant ruled surfaces such that the binomial vectors of the base curve are parallel along their striction curves of two ruled surfaces and the distance between asymptotic planes is constant. We then provide some characteristics of these new q-equidistant ruled surfaces. For the case in which the ruled surfaces are closed, we compute the corresponding integral invariants and the relations among them.

Let $r=r\left(t\right)$ be a regular unit speed curve in $E^3$. By regular, we mean the curve is at least $C^2$. A ruled surface is then defined as the motion of the line $X=X\left(t\right)$ along the curve $r\left(t\right)$. Thus, we parameterize it as follows:

$${\phi }_X\left(t,v\right)=r\left(t\right)+vX\left(t\right).$$

(1)

When we denote $\{T,N,B,\kappa ,\tau \}$ as the Frenet apparatus of the curve $r\left(t\right)$, then the corresponding Darboux vector is given by $W=\tau T+\kappa B$. If $\theta$ is taken to be the angle between the binormal vector and Darboux vector, then we form the unit Darboux vector as follows:

$$C=sin\theta T+cos\theta B,cos\theta =\frac{\kappa }{\sqrt{{\kappa }^2+{\tau }^2}},sin\theta =\frac{\tau }{\sqrt{{\kappa }^2+{\tau }^2}}$$

(2)

Let $r=r\left(t\right)$ be a closed curve in $E^3$; then the Steiner rotation and Steiner translation vectors are

$$D=T\underset{\left(r\right)}{\oint }\tau dt+B\underset{\left(r\right)}{\oint }\kappa dt,V\left(t\right)=T\underset{\left(r\right)}{\oint }dt,$$

(3)

respectively. Moreover, if ${\phi }_X\left(t,v\right)$ is a closed ruled surface and $X\left(t\right)$ is a unit vector, then the striction curve, drall, pitch and the angle of the pitch are given as

$$\gamma =r-\frac{〈r^{\prime },X^{\prime }〉}{{∥X^{\prime }∥}^2}X\left(t\right),P_X=\frac{det\left(r^{\prime },X,X^{\prime }\right)}{{∥X^{\prime }∥}^2},{\lambda }_X=〈D,X〉,L_X=〈V,X〉,$$

(4)

respectively. If, instead of $X\left(t\right)$, one of the vectors of Frenet frame is considered to be as the generator line for a closed ruled surface, then the pitch, the angle of pitch and the distribution parameter for each case are shown as in the following:

$$\begin{array}{cc}\hfill {\lambda }_T& =\underset{\left(r\right)}{\oint }\tau dt,{\lambda }_N=0,{\lambda }_B=\underset{\left(r\right)}{\oint }\kappa dt,\hfill \\ \hfill L_T& =\underset{\left(r\right)}{\oint }dt,L_N=L_B=0,\hfill \\ \hfill P_T& =0,P_N=\frac{\tau }{{\left(\kappa \right)}^2+{\left(\tau \right)}^2},P_B=\frac{1}{\tau }.\hfill \end{array}$$

(5)

The planes with subspaces $Sp\left\{T,N\right\},Sp\left\{N,B\right\}$ and $Sp\left\{T,B\right\}$ along the striction curves of a ruled surface are called the asymptotic plane, polar plane and central plane, respectively [20].

2. Characteristics of $\mathit{q}$-Equidistant Ruled Surfaces

In this section, we first define q-equidistant ruled surfaces by following Valeontis’s introduction [7]. We then provide some relations between their Frenet elements and compute distance function. Finally, we present a couple of examples to denote that the corresponding distances are constant for various cases.

Definition 1.

Let $r\left(t\right)$ and $r^{*}\left(t\right)$ be any two curves in $E^3$ and denote their corresponding unit binormal vectors as B and $B^{*}$, respectively. If the two ruled surfaces defined as ${\phi }_B\left(t,v\right)=r\left(t\right)+vB\left(t\right)$ and ${\phi }_{B^{*}}\left(t,v\right)=r^{*}\left(t\right)+v{B}^{*}\left(t\right)$ satisfy the following two conditions:

• the binormal vectors are parallel along the striction curves;
• the distance between two proper points on asymptotic planes is constant,

then the pair of these ruled surfaces $\left({\phi }_B,{\phi }_{B^{*}}\right)$ are called q-equidistant ruled surfaces:

Theorem 1.

The relations among the Frenet vectors of the base curve of q-equidistant ruled surfaces ${\phi }_B\left(t,v\right)$ and ${\phi }_{B^{*}}\left(t,v\right)$ are given

$$T^{*}=cos\varphi T-sin\varphi N,N^{*}=sin\varphi T+cos\varphi N,B^{*}=B$$

(6)

where $\angle \left(T,T^{*}\right)=\varphi$.

Proof. 

Rewrite $T^{*}$ as $T^{*}=a_{1}T+b_{1}N+c_{1}B$. Since $B\Vert B^{*}$, we have $a_1=cos\varphi$, $b_1=-sin\varphi$ and $c_1=0$. Upon substitution, $T^{*}=cos\varphi T-sin\varphi N$, and similarly $N^{*}=sin\varphi T+cos\varphi N$. □

Theorem 2.

The relations between the two curvatures of the base curves of q-equidistant ruled surfaces are

$${\kappa }^{*}=\left(\kappa -1\right)\frac{dt}{d{t}^{*}},{\tau }^{*}=\tau cos\varphi \frac{dt}{d{t}^{*}}.$$

(7)

Proof. 

By taking the derivative of $T^{*}$ and $N^{*}$, we have

$$\begin{array}{cc}\hfill {T^{*}}^{\prime }& =\left(-sin\varphi +\kappa sin\varphi \right)\frac{dt}{d{t}^{*}}T+\left(-cos\varphi +\kappa cos\varphi \right)\frac{dt}{d{t}^{*}}N+\tau sin\varphi \frac{dt}{d{t}^{*}}B,\hfill \\ \hfill {N^{*}}^{\prime }& =\left(cos\varphi -\kappa sin\varphi \right)\frac{dt}{d{t}^{*}}T+\left(\kappa sin\varphi -sin\varphi \right)\frac{dt}{d{t}^{*}}N+\tau cos\varphi \frac{dt}{d{t}^{*}}B.\hfill \end{array}$$

Using the advantage of the definitions of curvatures ${\kappa }^{*}=〈T^{{*}^{\prime }},N^{*}〉$ and ${\tau }^{*}=〈N^{{*}^{\prime }},B^{*}〉$ completes the proof. □

Theorem 3.

The relations between the striction curves of the q-equidistant ruled surfaces are

$${\gamma }^{*}=\gamma +pT+zN+\left(\frac{z^{\prime }+p\kappa }{\tau }\right)B.$$

(8)

Proof. 

From the given relation (4), the striction curves are found to be the same as the base curves of two ruled surfaces; that is, $\gamma \left(t\right)=r\left(t\right)$ and ${\gamma }^{*}\left(t\right)=r^{*}\left(t\right)$. Note that, as a consequence of this, we may re-express the ruled surfaces as in the following way:

$${\phi }_B\left(t,v\right)=\gamma \left(t\right)+vB\left(t\right)\mathrm{and}{\phi }_{B^{*}}\left(t,v\right)={\gamma }^{*}\left(t\right)+v{B}^{*}\left(t\right)$$

Now, if we denote $\left|p\right|$, $\left|z\right|$ and $\left|q\right|$ as the distances between polar, central and asymptotic planes in respective order, then the striction curve ${\gamma }^{*}$ can be rewritten as

$${\gamma }^{*}=\gamma +pT+zN+qB.$$

Conversely, if we consider $\gamma$ and ${\gamma }^{*}$ as the base curve, then we may write this time $r^{*}=r+pT+zN+qB$. By taking the derivative of the this and applying the inner product for both sides by ${B^{*}}^{\prime }$, we have

$$〈{\left(r^{*}\right)}^{\prime },B^{\prime }〉=-\kappa \tau p-\tau {\tau }^{\prime }+{\tau }^{2q}.$$

By referring the relation (4) and considering that $\gamma \left(t\right)=r\left(t\right)$, the proof is complete. □

Corollary 1.

The distance between the asymptotic planes of q-equidistant ruled surfaces is given by the following relation:

$$q=\frac{z^{\prime }+\kappa p}{\tau }.$$

(9)

Example 1.

Let us consider the two following helical curves parameterized as

$$r\left(t\right)=\left(\frac{1}{\sqrt{2}}sint,\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right)\mathrm{and}{r}^{*}\left(t\right)=\left(4\sqrt{2}+\frac{1}{\sqrt{2}}sint,4\sqrt{2}+\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right).$$

The binormal vector fields of these and the corresponding ruled surfaces are given as

$$\begin{array}{cc}\hfill B\left(t\right)=& B^{*}\left(t\right)=\left(\frac{1}{\sqrt{2}}cost,-\frac{1}{\sqrt{2}}sint,-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill {\phi }_B\left(t,v\right)& =\left(\frac{1}{\sqrt{2}}sint,\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right)+v\left(\frac{1}{\sqrt{2}}cost,-\frac{1}{\sqrt{2}}sint,-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill {\phi }_{B^{*}}\left(t,v\right)& =\left(4\sqrt{2}+\frac{1}{\sqrt{2}}sint,4\sqrt{2}+\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right)+v\left(\frac{1}{\sqrt{2}}cost,-\frac{1}{\sqrt{2}}sint,-\frac{1}{\sqrt{2}}\right).\hfill \end{array}$$

The striction curves of the ruled surfaces ${\phi }_B\left(t,v\right)$ and ${\phi }_{B^{*}}\left(t,v\right)$ are

$$\gamma \left(t\right)=\left(\frac{1}{\sqrt{2}}sint,\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right)\mathrm{and}{\gamma }^{*}\left(t\right)=\left(4\sqrt{2}+\frac{1}{\sqrt{2}}sint,4\sqrt{2}+\frac{1}{\sqrt{2}}cost,\frac{t}{\sqrt{2}}\right).$$

Since $\overrightarrow{\gamma {\gamma }^{*}}={\gamma }^{*}-\gamma$, we have $\overrightarrow{\gamma {\gamma }^{*}}=\left(4\sqrt{2},4\sqrt{2},0\right)$. In this case, the distances between polar and central planes denoted by p and z can be calculated by $p=4cost-4sint\mathrm{and}z=-4\sqrt{2}sint-4\sqrt{2}cost$, respectively. When the derivative of z is substituted in (9), we have the final parametric form for the distance q as below:

$$q=4cost-4sint.$$

By referring the classical definition of planes, we define two of asymptotic planes as in the following way:

$$\begin{array}{cc}\hfill H\dots & 〈\overrightarrow{\gamma X},B〉=0\Rightarrow xcost-ysint-z+\frac{\sqrt{2}}{2}t=0,\hfill \\ \hfill H^{*}\dots & 〈\overrightarrow{{\gamma }^{*}{X}^{*}},B^{*}〉=0\Rightarrow xcost-ysint-z+4\sqrt{2}\left(sint-cost\right)+\frac{\sqrt{2}}{2}t=0\hfill \end{array}$$

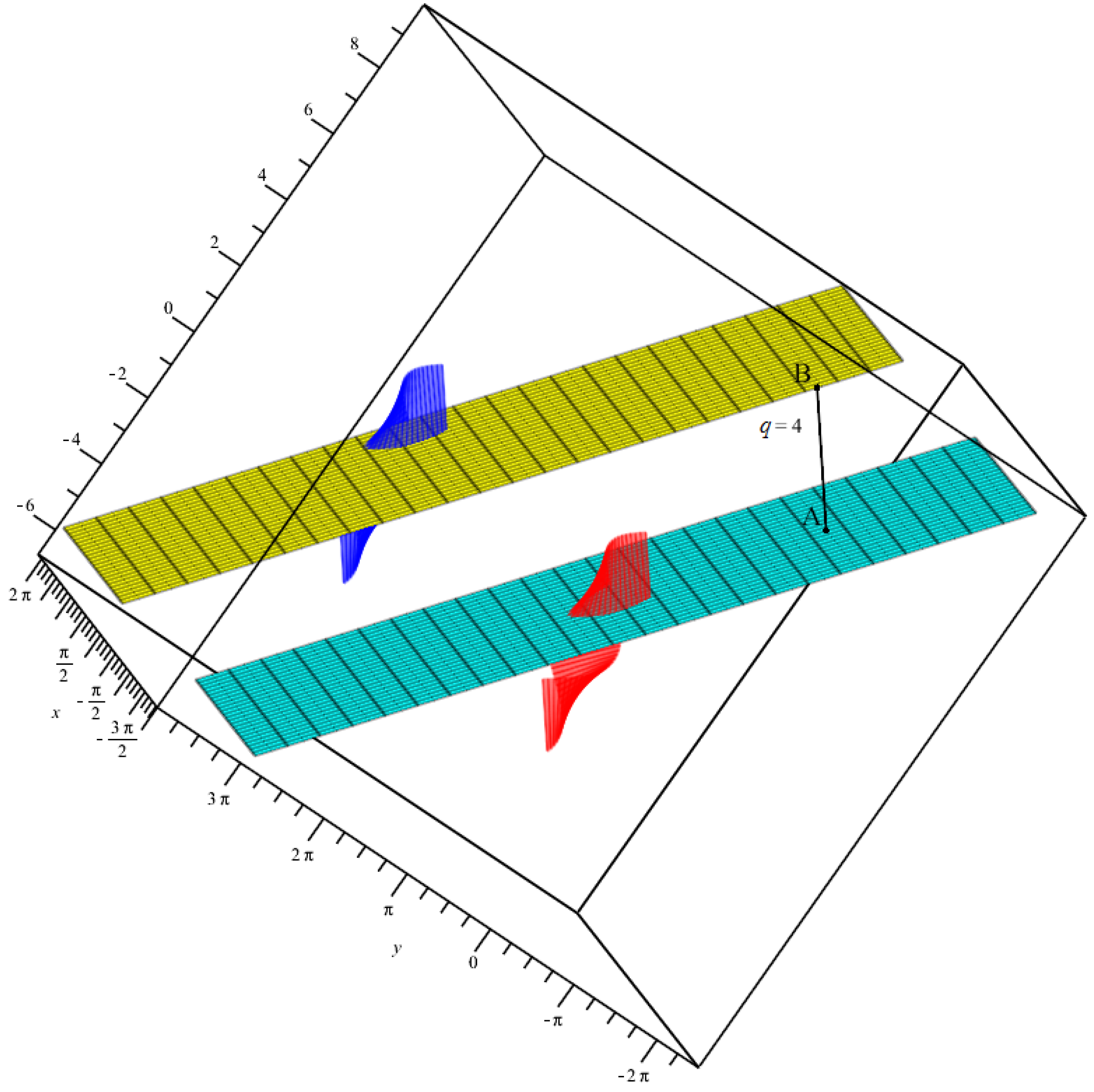
• For $t=0$, the striction points, the binormal vectors, the asymptotic planes and the q distance are computed as

  $$\begin{array}{cc}\hfill \gamma \left(0\right)& =\left(0,\frac{1}{\sqrt{2}},0\right),{\gamma }^{*}\left(0\right)=\left(4\sqrt{2},\frac{9}{\sqrt{2}},0\right),\hfill \\ \hfill B\left(0\right)& =\left(\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}}\right),B^{*}\left(0\right)=\left(\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill H\dots & x-z=0,H^{*}\dots x-z-4\sqrt{2}=0,q=4.\hfill \end{array}$$
  Now, let us take two proper points from two asymptotic planes as $A\left(a,0,a\right)\in H$ and $B\left(b,0,b-4\sqrt{2}\right)\in H^{*}.$ Since the distance $q=4$, we can establish a relation for a and b as $b-a=2\sqrt{2}$. For $a=\sqrt{2}$ and $b=3\sqrt{2}$, we have $A\left(\sqrt{2},0,\sqrt{2}\right)\mathrm{and}B\left(3\sqrt{2},0,-\sqrt{2}\right).$ (See Figure 1).
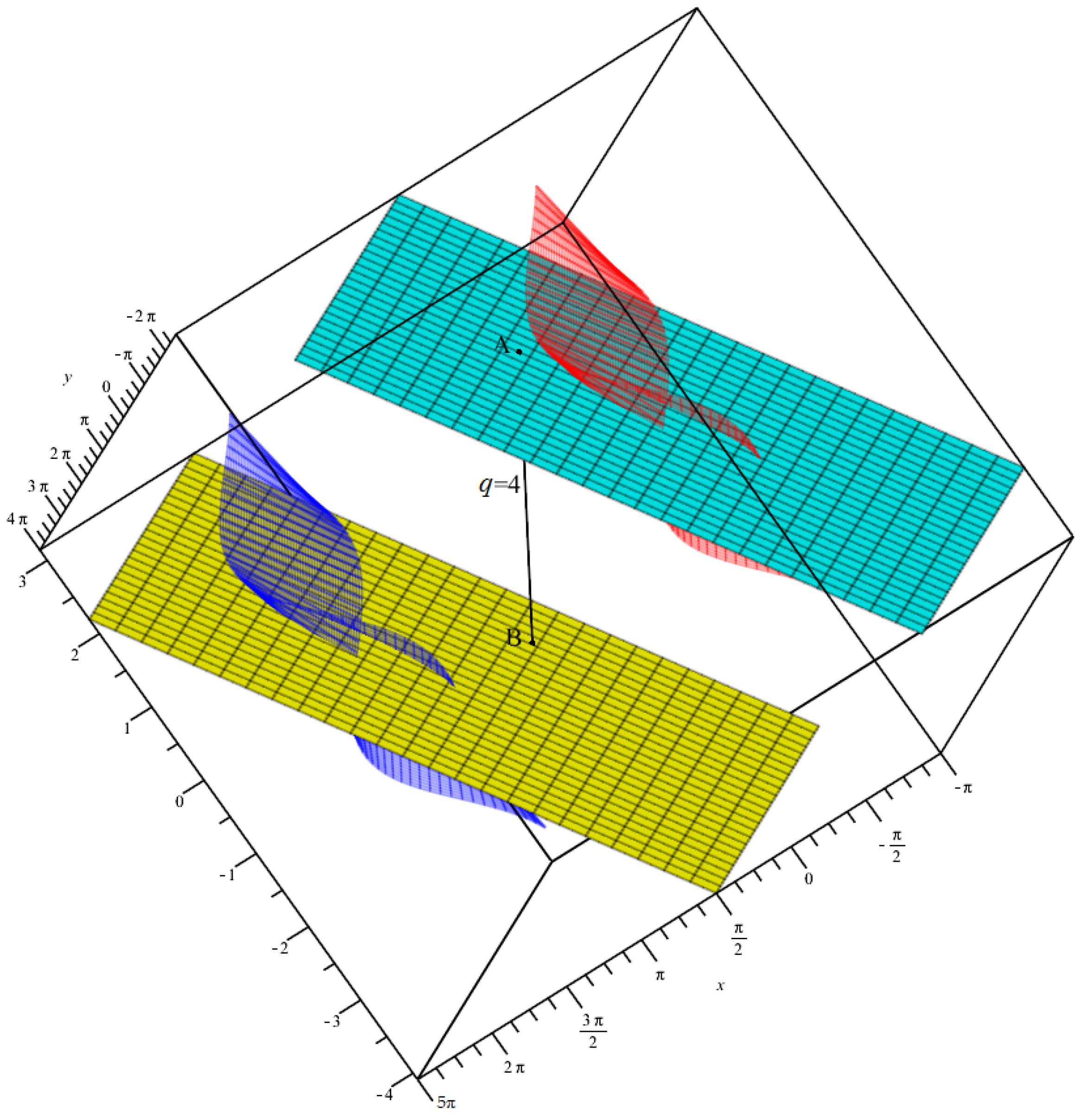
• For ${\displaystyle t=\frac{\pi }{6},}$ the striction points, the binormal vectors, the asymptotic planes and the q distance are computed as

  $$\begin{array}{cc}\hfill \gamma \left(\frac{\pi }{6}\right)& =\left(\frac{1}{2\sqrt{2}},\frac{\sqrt{3}}{2\sqrt{2}},\frac{\pi }{6\sqrt{2}}\right),{\gamma }^{*}\left(\frac{\pi }{6}\right)=\left(\frac{17}{2\sqrt{2}},\frac{16+\sqrt{3}}{2\sqrt{2}},\frac{\pi }{6\sqrt{2}}\right),\hfill \\ \hfill B\left(\frac{\pi }{6}\right)& =\left(\frac{\sqrt{3}}{2\sqrt{2}},-\frac{1}{2\sqrt{2}},-\frac{1}{\sqrt{2}}\right),B^{*}\left(\frac{\pi }{6}\right)=\left(\frac{\sqrt{3}}{2\sqrt{2}},-\frac{1}{2\sqrt{2}},-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill H\dots & 6\sqrt{3}x-6y-12z+\sqrt{2}\pi =0,\hfill \\ \hfill H^{*}\dots & 6\sqrt{3}x-6y-12z+12\sqrt{2}-12\sqrt{6}+\sqrt{2}\pi =0,\hfill \\ \hfill q& =2\sqrt{3}-2.\hfill \end{array}$$
  Similarly, when taken proper points from both asymptotic planes such as
  ${\displaystyle A\left(a_1,a_2,\frac{\sqrt{3}}{2}{a}_1-\frac{1}{2}{a}_2+\frac{\sqrt{2}\pi }{12}\right)\in H}$ and
  ${\displaystyle B\left(b_1,b_2,\frac{\sqrt{3}}{2}{b}_1-\frac{1}{2}{b}_2+2\sqrt{2}-2\sqrt{6}+\frac{\sqrt{2}\pi }{12}\right)\in H^{*},}$ we may write

  $${\left(b_1-a_1\right)}^2+{\left(b_2-a_2\right)}^2+{\left(\frac{\sqrt{3}}{2}\left(b_1-a_1\right)-\frac{1}{2}\left(b_2-a_2\right)+2\sqrt{2}-2\sqrt{6}\right)}^2={\left(2\sqrt{3}-2\right)}^2.$$
  If ${\lambda }_1=b_1-a_1$ and ${\lambda }_2=b_2-a_2$, then we can rewrite the last relation as

  $$7{\lambda }_1^2+5{\lambda }_2^2-2\sqrt{3}{\lambda }_1{\lambda }_2+\left(8\sqrt{6}-24\sqrt{2}\right){\lambda }_1+\left(8\sqrt{6}-8\sqrt{2}\right){\lambda }_2+64-32\sqrt{3}=0.$$
  If this relation is arranged for ${\lambda }_1$, then the roots can be computed as ${\displaystyle {\mu }_1=\frac{3\sqrt{2}-\sqrt{6}}{2}}$ and ${\displaystyle {\mu }_2=\frac{\sqrt{2}-\sqrt{6}}{2}}$; that is, ${\displaystyle b_1-a_1=\frac{3\sqrt{2}-\sqrt{6}}{2}}$ and ${\displaystyle b_2-a_2=\frac{\sqrt{2}-\sqrt{6}}{2}.}$
  Particularly for ${\displaystyle b_1=2\sqrt{2}-\sqrt{6},b_2=\sqrt{2},a_1=\frac{\sqrt{2}-\sqrt{6}}{2},a_2=\frac{\sqrt{2}+\sqrt{6}}{2},}$ we have the corresponding points as

  $$A\left(\frac{\sqrt{2}-\sqrt{6}}{2},\frac{\sqrt{2}+\sqrt{6}}{2},\frac{\sqrt{2}\pi -12\sqrt{2}}{12}\right)\mathrm{and}B\left(2\sqrt{2}-\sqrt{6},\sqrt{2},\frac{\sqrt{2}\pi -12\sqrt{6}}{12}\right).$$
  See Figure 2.
  Note that similar steps can be followed by considering ${\lambda }_2$ to find different roots and distinct proper points.
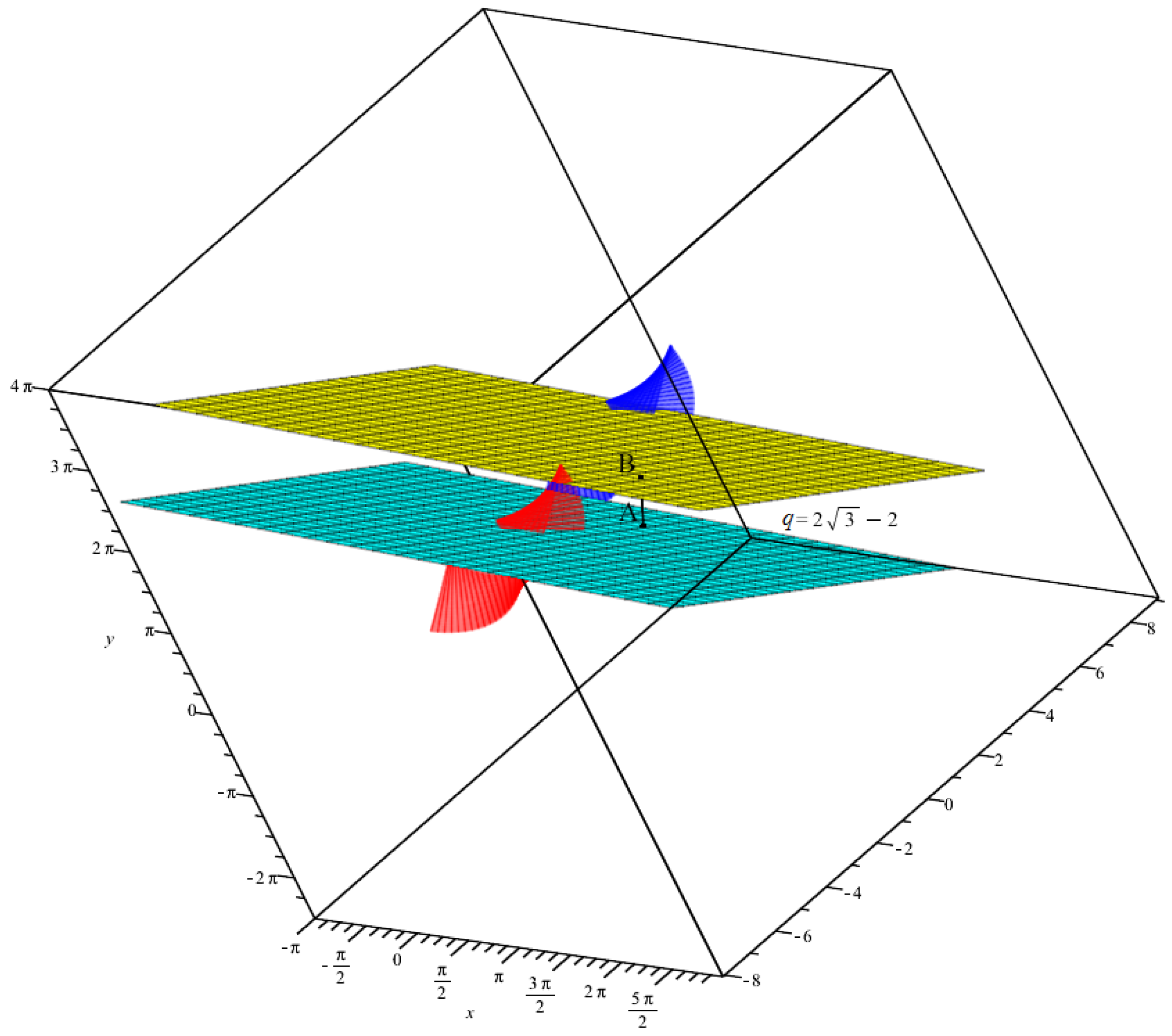
• For ${\displaystyle t=\frac{\pi }{4},}$ the striction points, the binormal vectors, the asymptotic planes and the q distance are computed as

  $$\begin{array}{cc}\hfill \gamma \left(\frac{\pi }{4}\right)=& \left(\frac{1}{2},\frac{1}{2},\frac{\pi }{4\sqrt{2}}\right),{\gamma }^{*}\left(\frac{\pi }{4}\right)=\left(4\sqrt{2}+\frac{1}{2},4\sqrt{2}+\frac{1}{2},\frac{\pi }{4\sqrt{2}}\right),\hfill \\ \hfill B\left(\frac{\pi }{4}\right)=& \left(\frac{1}{2},-\frac{1}{2},-\frac{1}{\sqrt{2}}\right)B^{*}\left(\frac{\pi }{4}\right)=\left(\frac{1}{2},-\frac{1}{2},-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill H\dots & 4\sqrt{2}x-4\sqrt{2}y-8z+\sqrt{2}\pi =0,\hfill \\ \hfill H^{*}\dots & 4\sqrt{2}x-4\sqrt{2}y-8z+\sqrt{2}\pi =0,q=0.\hfill \end{array}$$
  For any two points from these asymptotic planes

  $$A\left(a_1,a_2,\frac{\sqrt{2}}{2}{a}_1-\frac{\sqrt{2}}{2}{a}_2+\frac{\sqrt{2}\pi }{8}\right)\in H\mathrm{and}B\left(b_1,b_2,\frac{\sqrt{2}}{2}{b}_1-\frac{\sqrt{2}}{2}{b}_2+\frac{\sqrt{2}\pi }{8}\right)\in H^{*},$$
  we have $d(A,B)=q=0.$ Thus,

  $${\left(b_1-a_1\right)}^2+{\left(b_2-a_2\right)}^2+{\left(\frac{\sqrt{2}}{2}\left(b_1-a_1\right)+\frac{\sqrt{2}}{2}\left(b_2-a_2\right)\right)}^2=0.$$
  If again ${\lambda }_1=b_1-a_1$ and ${\lambda }_2=b_2-a_2$, then we re-express the last relation as $3{\lambda }_1^2+3{\lambda }_2^2+2{\lambda }_1{\lambda }_2=0.$ By rearranging the last relation according to ${\lambda }_1$, the corresponding roots are found as ${\mu }_1={\mu }_2=0$; that is, $b_1-a_1=b_2-a_2=0$. Note that, in this situation, the asymptotic planes are coincided. See Figure 3.
• For ${\displaystyle t=\frac{\pi }{3},}$ the striction points, the binormal vectors, the asymptotic planes and the q distance are computed as

  $$\begin{array}{cc}\hfill \gamma \left(\frac{\pi }{3}\right)=& \left(\frac{\sqrt{3}}{2\sqrt{2}},\frac{1}{2\sqrt{2}},\frac{\pi }{3\sqrt{2}}\right),{\gamma }^{*}\left(\frac{\pi }{3}\right)=\left(\frac{16+\sqrt{3}}{2\sqrt{2}},\frac{17}{2\sqrt{2}},\frac{\pi }{3\sqrt{2}}\right),\hfill \\ \hfill B\left(\frac{\pi }{3}\right)=& \left(\frac{1}{2\sqrt{2}},-\frac{\sqrt{3}}{2\sqrt{2}},-\frac{1}{\sqrt{2}}\right),B^{*}\left(\frac{\pi }{3}\right)=\left(\frac{1}{2\sqrt{2}},-\frac{\sqrt{3}}{2\sqrt{2}},-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill H\dots & 3x-3\sqrt{3}y-6z+\sqrt{2}\pi =0,\hfill \\ \hfill H^{*}\dots & 3x-3\sqrt{3}y-6z+12\sqrt{2}\left(\sqrt{3}-1\right)+\sqrt{2}\pi =0,q=2\sqrt{3}-2.\hfill \end{array}$$
  For such two points on asymptotic planes as ${\displaystyle A\left(a_1,a_2,\frac{1}{2}{a}_1-\frac{\sqrt{3}}{2}{a}_2+\frac{\sqrt{2}\pi }{6}\right)\in H\mathrm{and}}$ ${\displaystyle B\left(b_1,b_2,\frac{1}{2}{b}_1-\frac{\sqrt{3}}{2}{b}_2+2\sqrt{6}-2\sqrt{2}+\frac{\sqrt{2}\pi }{6}\right)\in H^{*},}$ the distance $d(A,B)=2\sqrt{3}-2.$ Hence,

  $${\left(b_1-a_1\right)}^2+{\left(b_2-a_2\right)}^2+{\left(\frac{1}{2}\left(b_1-a_1\right)-\frac{\sqrt{3}}{2}\left(b_2-a_2\right)+2\sqrt{6}-2\sqrt{2}\right)}^2={\left(2\sqrt{3}-2\right)}^2.$$
  Following the same manner as before, if ${\lambda }_1=b_1-a_1$ and ${\lambda }_2=b_2-a_2$, then the above relation takes the form

  $$5{\lambda }_1^2+7{\lambda }_2^2-2\sqrt{3}{\lambda }_1{\lambda }_2+\left(8\sqrt{6}-8\sqrt{2}\right){\lambda }_1+\left(8\sqrt{6}-24\sqrt{2}\right){\lambda }_2+64-32\sqrt{3}=0.$$
  By arranging this for ${\lambda }_1$, the roots are found as ${\displaystyle {\mu }_1=\frac{\sqrt{2}-\sqrt{6}}{2}}$ and ${\displaystyle {\mu }_2=\frac{3\sqrt{2}-\sqrt{6}}{2};}$ that is, ${\displaystyle b_1-a_1=\frac{\sqrt{2}-\sqrt{6}}{2}}$ and ${\displaystyle b_2-a_2=\frac{3\sqrt{2}-\sqrt{6}}{2}.}$
  For ${\displaystyle b_1=\sqrt{2},b_2=2\sqrt{2}-\sqrt{6},a_1=\frac{\sqrt{2}+\sqrt{6}}{2},a_2=\frac{\sqrt{2}-\sqrt{6}}{2},}$ we have the following coordinates for the points A and B as

  $$A\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{6}}{2},\frac{\sqrt{2}}{2}-\frac{\sqrt{6}}{2},\sqrt{2}+\frac{\sqrt{2}\pi }{6}\right)\mathrm{and}B\left(\sqrt{2},2\sqrt{2}-\sqrt{6},\sqrt{6}+\frac{\sqrt{2}\pi }{6}\right).$$
  See Figure 4 If the arrangements are to be done for ${\lambda }_2$, another different point pairs can be obtained.
• Lastly, for ${\displaystyle t=\frac{\pi }{2},}$ the striction points, the binormal vectors, the asymptotic planes and the q distance are computed as

  $$\begin{array}{cc}\hfill \gamma \left(\frac{\pi }{2}\right)=& \left(\frac{1}{\sqrt{2}},0,\frac{\pi }{2\sqrt{2}}\right),{\gamma }^{*}\left(\frac{\pi }{2}\right)=\left(\frac{9}{\sqrt{2}},4\sqrt{2},\frac{\pi }{2\sqrt{2}}\right),\hfill \\ \hfill B\left(\frac{\pi }{2}\right)=& \left(0,-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right),B^{*}\left(\frac{\pi }{2}\right)=\left(0,-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right),\hfill \\ \hfill H\cdots & 4y+4z-\sqrt{2}\pi =0,\hfill \\ \hfill H^{*}\cdots & 4y+4z-16\sqrt{2}-\sqrt{2}\pi =0,q=4.\hfill \end{array}$$
  For two points from the asymptotic planes
  ${\displaystyle A\left(0,-a,a+\frac{\sqrt{2}\pi }{4}\right)\in H\mathrm{and}B\left(0,-b,b+4\sqrt{2}+\frac{\sqrt{2}\pi }{4}\right)\in H^{*}}$, $d(A,B)=4.$
  Therefore, ${\left(b-a\right)}^2+{\left(b-a-4\sqrt{2}\right)}^2=16.$ If $\lambda =b-a,$ then we have ${\lambda }^2+4\sqrt{2}\lambda +16=0.$ The root to this relation is $\lambda =-2\sqrt{2}$ which corresponds to $a-b=2\sqrt{2}.$
  For $a=3\sqrt{2}$ and $b=\sqrt{2}$, we have ${\displaystyle A\left(0,-3\sqrt{2},3\sqrt{2}+\frac{\sqrt{2}\pi }{4}\right)}$ and
  ${\displaystyle B\left(0,-\sqrt{2},5\sqrt{2}+\frac{\sqrt{2}\pi }{4}\right).}$ See Figure 5.

One may question the amount of the examples given; however, the concretion of the conceptualization for the equidistant ruled surface is something that literature is lacking. Therefore, the given examples are worth sharing for various cases to gain insight into main theme.

Now, let us denote the tangent vectors of the striction curves of q-equidistant ruled surfaces by $T_s$ and ${T_s}^{*}$, respectively. Then, the following relations hold:

$$T_s=cos\sigma T+sin\sigma B,{T_s}^{*}=cos{\sigma }^{*}{T}^{*}+sin{\sigma }^{*}{B}^{*}$$

(10)

where $\angle \left(T_s,T\right)=\sigma$ and $\angle \left({T_s}^{*},T^{*}\right)={\sigma }^{*}$, respectively.

Theorem 4.

The parameters t of ${\phi }_B\left(t,v\right)$ and $t^{*}$ of ${\phi }_{B^{*}}\left(t,v\right)$ have the following relation

$${\left(\frac{d{t}^{*}}{dt}\right)}^2={\left(cos\sigma +p^{\prime }-z\kappa \right)}^2+{\left(sin\sigma +z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)}^2$$

(11)

Proof. 

If the derivative is taken from the relation (8), we have

$${T_s}^{*}\frac{d{t}^{*}}{dt}=T_s+\left(p^{\prime }-z\kappa \right)T+\left(z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)B.$$

Next, substituting (10) into this completes the proof. □

Corollary 2.

The expression for the vector ${T_s}^{*}$ in terms of Frenet vectors of the base curve $r\left(t\right)$ is given as follows:

$${T_s}^{*}=\frac{\left(cos\sigma +p^{\prime }-z\kappa \right)T+\left(sin\sigma +z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)B}{{\left({\left(cos\sigma +p^{\prime }-z\kappa \right)}^2+sin\sigma +z\tau +{\left({\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)}^2\right)}^{\frac{1}{2}}}$$

(12)

Theorem 5.

If σ and ${\sigma }^{*}$ are taken to be the strictions of q-equidistant ruled surface, then there exist the following relations:

$$\begin{array}{cc}\hfill cos{\sigma }^{*}=& \frac{sec\varphi \left(cos\sigma +p^{\prime }-z\kappa \right)}{\sqrt{{\left(cos\sigma +p^{\prime }-z\kappa \right)}^2+{\left(sin\sigma +z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)}^2}},\hfill \\ \hfill cos{\sigma }^{*}sin\varphi =& 0,\hfill \\ \hfill sin{\sigma }^{*}=& \frac{sin\sigma +z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }}{\sqrt{{\left(cos\sigma +p^{\prime }-z\kappa \right)}^2+{\left(sin\sigma +z\tau +{\left(\frac{z^{\prime }+\kappa p}{\tau }\right)}^{\prime }\right)}^2}}\hfill \end{array}$$

(13)

Proof. 

Consider the relation (6) to rewrite ${T_s}^{*}=cos{\sigma }^{*}{T}^{*}+sin{\sigma }^{*}{B}^{*}$ as

$${T_s}^{*}=cos{\sigma }^{*}cos\varphi T-cos{\sigma }^{*}sin\varphi N+sin{\sigma }^{*}B.$$

Next, by referring to (12) we have the proof. □

Corollary 3.

The tangent vectors of the base curves of q-equidistant ruled surfaces are parallel.

Proof. 

From (13), we recall $cos{\sigma }^{*}sin\varphi =0$. If $cos{\sigma }^{*}=0$—that is, ${\sigma }^{*}=\frac{\pi }{2}+k\pi ,k\in \mathcal{N}$—then $〈{T_s}^{*},T^{*}〉=0$. In this case, the vector has to be on the polar plane. However, this contradicts the relation (10). Thus, $sin\varphi =0$—that is, $\varphi =k\pi$—which clearly means that the vectors T and $T^{*}$ are parallel or equivalently $cos\varphi =1$ and $sin\varphi =0$. □

Corollary 4.

The relations between the Frenet vectors of the base curve for q-equidistant ruled surfaces are given by the following.

$$T^{*}=\mp T,N^{*}=\mp N,B^{*}=B.$$

Corollary 5.

The relations between the natural curvatures of the base curve for q-equidistant ruled surfaces are given by the following.

$${\kappa }^{*}=\left(\kappa -1\right)\frac{dt}{d{t}^{*}},{\tau }^{*}=\mp \tau \frac{dt}{d{t}^{*}}$$

(14)

Corollary 6.

If ${\phi }_{B^{*}}\left(t,v\right)$ is a closed ruled surface, then the pitch, the angle of pitch and the distribution parameter (drall) for each ruled surface drawn by Frenet vectors are given as

$$\begin{array}{cc}\hfill {\lambda }_{T^{*}}=& \underset{\left(r^{*}\right)}{\oint }{\tau }^{*}d{t}^{*},{\lambda }_{N^{*}}=0,{\lambda }_{B^{*}}=\underset{\left(r^{*}\right)}{\oint }{\kappa }^{*}d{t}^{*},\hfill \\ \hfill L_{T^{*}}=& \underset{\left(r^{*}\right)}{\oint }d{t}^{*},L_{N^{*}}=L_{B^{*}}=0,\hfill \\ \hfill P_{T^{*}}=& 0,P_{N^{*}}=\frac{{\tau }^{*}}{{\left({\kappa }^{*}\right)}^2+{\left({\tau }^{*}\right)}^2},P_{B^{*}}=\frac{1}{{\tau }^{*}},\hfill \end{array}$$

(15)

respectively.

Theorem 6.

For q-equidistant closed ruled surfaces, the following relations hold among the angles of the pitches of the closed ruled surfaces drawn by Frenet vectors of base curve as

$$\begin{array}{cc}\hfill {\lambda }_{T^{*}}=& cos\varphi {\lambda }_T+\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,\hfill \\ \hfill {\lambda }_{N^{*}}=& {\lambda }_N=0,\hfill \\ \hfill {\lambda }_{B^{*}}=& {\lambda }_B-L_T+\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt.\hfill \end{array}$$

(16)

Proof. 

If we substitute ${\tau }^{*}$ of (7) into (15), then we have ${\lambda }_{T^{*}}=\underset{\left(r^{*}\right)}{\oint }\tau cos\varphi dt$. By recalling the relation $r^{*}=r+pT+zN+qB$ to substitute into the last equation, we have

$${\lambda }_{T^{*}}=\underset{\left(r\right)}{\oint }\tau cos\varphi dt+\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt=cos\varphi {\lambda }_T+\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt.$$

When a similar procedure is followed in ${\lambda }_{B^{*}}=\underset{\left(r^{*}\right)}{\oint }{\kappa }^{*}d{t}^{*}$ we have the expression

$${\lambda }_{B^{*}}={\lambda }_B-L_T+\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt,$$

which completes the proof. □

Corollary 7.

Other useful relations among the angles of pitch can be drawn as

$$\begin{array}{cc}\hfill {\lambda }_{T^{*}}=& \mp {\lambda }_T\mp \underset{\left(pT+zN+qB\right)}{\oint }\tau dt,\hfill \\ \hfill {\lambda }_{N^{*}}=& {\lambda }_N=0,\hfill \\ \hfill {\lambda }_{B^{*}}=& {\lambda }_B-L_T+\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt.\hfill \end{array}$$

(17)

Theorem 7.

If the base curves of closed q-equidistant ruled surfaces are considered to be as curvature lines, then the relations between the angles of pitch are given as

$$L_{T^{*}}{\tau }^{*}=cos\varphi \tau L_T+\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,L_{N^{*}}=L_{B^{*}}=L_N=L_B=0$$

(18)

Proof. 

Since ${\displaystyle d{t}^{*}=\frac{\tau }{{\tau }^{*}}cos\varphi dt,L_{T^{*}}=\underset{\left(r^{*}\right)}{\oint }d{t}^{*}}$ and the base curves are assigned to be curvature line, we write ${\displaystyle L_{T^{*}}=\frac{\tau }{{\tau }^{*}}cos\varphi \underset{\left(r^{*}\right)}{\oint }dt}$. By recalling $r^{*}=r+pT+zN+qB$, we complete the proof. □

Corollary 8.

If the base curves are curvature lines for the q-equidistant closed ruled surfaces, then the following relations hold among the pitches of ruled surfaces drawn by Frenet vectors.

$$L_{T^{*}}{\tau }^{*}=\mp \tau L_T\mp \underset{\left(pT+zN+qB\right)}{\oint }\tau dt,L_{N^{*}}=L_{B^{*}}=L_N=L_B=0.$$

(19)

Theorem 8.

The relations between the distribution parameters of q-equidistant ruled surfaces are

$$P_{T^{*}}=P_T=0,P_{N^{*}}=\left(\frac{P_{B}cos\varphi }{{\left(\kappa -1\right)}^2{P}_B^2+{cos}^2\varphi }\right)\frac{d{t}^{*}}{dt},P_{B^{*}}=P_{B}sec\varphi \frac{d{t}^{*}}{dt}.$$

(20)

Proof. 

It is clear that $P_{T^{*}}=P_T=0.$ From (15), we write the reciprocal of ${\displaystyle P_{N^{*}}}$ as ${\displaystyle \frac{1}{P_{N^{*}}}=\frac{{\left({\kappa }^{*}\right)}^2+{\left({\tau }^{*}\right)}^2}{{\tau }^{*}}}$. By doing some arrangements and using (7) we have

${\displaystyle P_{N^{*}}=\left(\frac{P_{B}cos\varphi }{{\left(\kappa -1\right)}^2{P}_B^2+{cos}^2\varphi }\right)\frac{d{t}^{*}}{dt}.}$ By following similar steps, we find ${\displaystyle P_{B^{*}}=P_{B}sec\varphi \frac{d{t}^{*}}{dt},}$ and this completes the proof. □

Corollary 9.

For q-equidistant ruled surfaces, the following relations exist among the dralls of ruled surface drawn by Frenet vectors:

$$P_{T^{*}}=P_T=0,P_{N^{*}}=\mp \left(\frac{P_B}{{\left(\kappa -1\right)}^2{P}_B^2+1}\right)\frac{d{t}^{*}}{dt},P_{B^{*}}=\mp P_B\frac{d{t}^{*}}{dt}$$

(21)

Corollary 10.

If q-equidistant ruled surfaces have the same distribution parameter, then the angle between the tangents is ${\displaystyle \varphi =arccos\left(\frac{d{t}^{*}}{dt}\right).}$ If both the ruled surfaces ${\phi }_C\left(t,v\right)$ and ${\phi }_{C^{*}}\left(t,v\right)$ whose generator lines are Darboux vectors are closed, then the pitch, the angle of pitch and the distribution parameter (drall) are given as the following:

$$\begin{array}{cc}\hfill {\lambda }_C=& {\lambda }_{T}sin\theta +{\lambda }_{B}cos\theta ,{\lambda }_{C^{*}}={\lambda }_{T^{*}}sin{\theta }^{*}+{\lambda }_{B^{*}}cos{\theta }^{*}\hfill \\ \hfill L_C=& L_{T}sin\theta ,L_{C^{*}}=L_{T^{*}}sin{\theta }^{*}\hfill \\ \hfill P_C=& P_{C^{*}}=0.\hfill \end{array}$$

(22)

Theorem 9.

For q-equidistant ruled surfaces, if ${\theta }^{*}$ is the angle between the unit Darboux vector $C^{*}$ and the binormal vector $B^{*}$, then the following relations exist:

$$cos{\theta }^{*}=\frac{\kappa -1}{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}},sin{\theta }^{*}=\frac{\tau cos\varphi }{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}$$

(23)

Proof. 

If ${\kappa }^{*}$ and ${\tau }^{*}$ from relation (7) are substituted into the relation (2), and by applying some arrangements, the proof is clear. □

Theorem 10.

For q-equidistant ruled surfaces, the following relation exists for the unit Darboux vector of $r^{*}=r^{*}\left(t\right).$

$$C^{*}=\frac{\tau {cos}^2\varphi }{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}T-\frac{\tau cos\varphi sin\varphi }{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}N+\frac{\kappa -1}{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}B$$

(24)

Proof. 

By considering the relations (2), (6) and (9), the proof is straightforward. □

Theorem 11.

For q-equidistant ruled surfaces the pitch, the angle of pitch and the distribution parameter of the closed ruled surface whose generator is unit Darboux vector are as follows:

$$\begin{array}{cc}\hfill {\lambda }_{C^{*}}=& \frac{\tau cos\varphi }{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}\left(cos\varphi {\lambda }_T+a_1\right)+\frac{\kappa -1}{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}}\left({\lambda }_B-L_T+a_3\right),\hfill \\ \hfill L_{C^{*}}{\tau }^{*}=& \frac{{\tau }^2{cos}^2\varphi L_T+a_1\tau cos\varphi }{\sqrt{{\tau }^2{cos}^2\varphi +{\left(\kappa -1\right)}^2}},\hfill \\ \hfill P_{C^{*}}=& P_C=0\hfill \end{array}$$

(25)

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,a_3=\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt.$

Proof. 

Using the relations (9) and (16) together with (22) completes the proof. □

Theorem 12.

For the two vectors defined by the Frenet vectors’ motion, which are as $X=x_{1}T+x_{2}N+x_{3}B$ and $X=x_1^{*}{T}^{*}+x_2^{*}{N}^{*}+x_3^{*}{B}^{*}$, there exists the following relation.

$$\begin{array}{cc}\hfill X^{*}=& \left(\left(x_1-p\right)cos\varphi -\left(x_2-z\right)sin\varphi \right)T^{*}\hfill \\ \hfill & +\left(\left(x_1-p\right)sin\varphi +\left(x_2-z\right)cos\varphi \right)N^{*}+\left(x_3-q\right)B^{*}\hfill \end{array}$$

(26)

Proof. 

We can express the vector $X^{*}$ as

$$\begin{array}{cc}\hfill X^{*}& =X-\gamma {\gamma }^{*}\hfill \\ & =x_{1}T+x_{2}N+x_{3}B-pT-zN-qB\hfill \\ & =\left(x_1-p\right)T+\left(x_2-z\right)N+\left(x_3-q\right)B\hfill \end{array}$$

Next, applying (6) to the above completes the proof. □

Theorem 13.

The pitch, the angle of pitch and the distribution parameter of the closed ruled surface whose generator is the vector X are

$${\lambda }_X=x_1{\lambda }_T+x_3{\lambda }_B,L_X=x_1{L}_T,P_X=\frac{\tau \left(x_2^2+x_3^2\right)-x_1{x}_3\kappa }{{\kappa }^2\left(x_1^2+x_2^2\right)+{\tau }^2\left(x_2^2+x_3^2\right)-2x_1{x}_3\kappa \tau }$$

(27)

Proof. 

We first find ${\lambda }_X$ and $L_X$ by using both the relations, (4) and (5). Next the derivative of the vector X and its corresponding norm are calculated as $X^{\prime }=-x_2\kappa T+\left(x_1\kappa -x_3\tau \right)N+x_2\tau B,$ and ${∥X^{\prime }∥}^2={\kappa }^2\left(x_2^2+x_1^2\right)+{\tau }^2\left(x_2^2+x_3^2\right)-2x_1{x}_3\kappa \tau .$ Upon substitution of these into the $P_X$ of (4), we complete the proof. □

Theorem 14.

The angle of the pitch of the closed ruled surface whose generator vector is $X^{*}$ is as follows:

$$\begin{array}{cc}\hfill {\lambda }_{X^{*}}=& {\lambda }_T\left({cos}^2\varphi \left(x_1-p\right)-sin\varphi cos\varphi \left(x_2-z\right)\right)+\left({\lambda }_B-L_T\right)\left(x_3-q\right)\hfill \\ \hfill & +a_1\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right)+a_3\left(x_3-q\right),\hfill \end{array}$$

(28)

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,a_3=\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt.$

Proof. 

By the definition of the angle of pitch, we have

$$\begin{array}{cc}\hfill {\lambda }_{X^{*}}=& 〈D^{*},X^{*}〉,\hfill \\ \hfill =& {\lambda }_{T^{*}}\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right)+{\lambda }_{B^{*}}\left(x_3-q\right)\hfill \\ \hfill =& \left(cos\varphi {\lambda }_T+a_1\right)\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right)+\left({\lambda }_B-L_T+a_3\right)\left(x_3-q\right),\hfill \\ \hfill =& \left(cos\varphi {\lambda }_T+a_1\right)cos\varphi \left(x_1-p\right)-\left(cos\varphi {\lambda }_T+a_1\right)sin\varphi \left(x_2-z\right)\hfill \\ & +\left({\lambda }_B-L_T+a_3\right)\left(x_3-q\right),\hfill \\ \hfill =& {\lambda }_T\left({cos}^2\varphi \left(x_1-p\right)-sin\varphi cos\varphi \left(x_2-z\right)\right)+\left({\lambda }_B-L_T\right)\left(x_3-q\right)\hfill \\ & +a_1\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right)+a_3\left(x_3-q\right),\hfill \end{array}$$

which completes the proof. □

Theorem 15.

The angle of the pitch of the closed ruled surface whose generator vector is $X^{*}$ is given by

$$L_{X^{*}}{\tau }^{*}=L_T\tau \left({cos}^2\varphi \left(x_1-p\right)-cos\varphi sin\varphi \left(x_2-z\right)\right)+a_1\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right)$$

(29)

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt.$

Proof. 

If we substitute (3) and (26) into (4), then $L_{X^{*}}=L_{T^{*}}\left(cos\varphi \left(x_1-p\right)-sin\varphi \left(x_2-z\right)\right).$ Next, by considering this time (18), we simply complete the proof. □

Theorem 16.

The distribution parameter of the closed ruled surface whose generator vector $X^{*}$ is

$$P_{X^{*}}=\frac{\left(\left(x_1-p\right)sin\varphi +\left(x_2-z\right)cos\varphi \right)C_q-\left(x_3-q\right)B_q}{A_q^2+B_q^2+C_q^2}$$

(30)

where

$$\begin{array}{cc}\hfill A_q=& sin\varphi \left(z^{\prime }-x_1+p-\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ & +cos\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right),\hfill \\ \hfill B_q=& sin\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ & +cos\varphi \left(-z^{\prime }+x_1-p+\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)-cos\varphi \tau \left(x_3-q\right)\frac{dt}{d{t}^{*}},\hfill \\ \hfill C_q=& sin\varphi cos\varphi \tau \left(x_1-p\right)\frac{dt}{d{t}^{*}}+{cos}^2\varphi \tau \left(x_2-z\right)\frac{dt}{d{t}^{*}}-q^{\prime }.\hfill \end{array}$$

Proof. 

By differentiating the relation (26), we first have

$$\begin{array}{cc}\hfill {\left(X^{*}\right)}^{\prime }=& \left(\begin{array}{c}\left(z^{\prime }-x_1+p-{\kappa }^{*}{x}_1+{\kappa }^{*}p\right)sin\varphi \hfill \\ +\left(z-p^{\prime }-x_2-{\kappa }^{*}-{\kappa }^{*}{x}_2+{\kappa }^{*}z\right)cos\varphi \hfill \end{array}\right)T^{*}\hfill \\ & +\left(\begin{array}{c}\left(z-p^{\prime }-x_2-{\kappa }^{*}{x}_2+{\kappa }^{*}z\right)sin\varphi \hfill \\ +\left({\kappa }^{*}{x}_1-z^{\prime }+x_1-p-{\kappa }^{*}p-{\tau }^{*}{x}_3+{\tau }^{*}q\right)cos\varphi \hfill \end{array}\right)N^{*}\hfill \\ & +\left(\left({\tau }^{*}{x}_1-{\tau }^{*}p\right)sin\varphi +\left({\tau }^{*}{x}_2-{\tau }^{*}z\right)cos\varphi -q^{\prime }\right)B^{*}.\hfill \end{array}$$

If ${\kappa }^{*}$ and ${\tau }^{*}$ of (7) are applied to the above, we then obtain

$$\begin{array}{cc}\hfill {\left(X^{*}\right)}^{\prime }=& \left(\begin{array}{c}sin\varphi \left(z^{\prime }-x_1+p-\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ +cos\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right)\hfill \end{array}\right)T^{*}\hfill \\ & +\left(\begin{array}{c}sin\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ +cos\varphi \left(-z^{\prime }+x_1-p+\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)-cos\varphi \tau \left(x_3-q\right)\frac{dt}{d{t}^{*}}\hfill \end{array}\right)N^{*}\hfill \\ & +\left(sin\varphi cos\varphi \tau \left(x_1-p\right)\frac{dt}{d{t}^{*}}+{cos}^2\varphi \tau \left(x_2-z\right)\frac{dt}{d{t}^{*}}-q^{\prime }\right)B^{*}\hfill \end{array}$$

By using (4), the drall $P_{X^{*}}$ can be easily computed to complete the proof. □

Proposition 1.

When the vector X lies on osculating plane, the pitch, the angle of pitch and the distribution parameter of the two closed ruled surfaces whose generators are the vectors X and $X^{*}$ are given as the following

$$\begin{array}{cc}\hfill X=& x_{1}T+x_{2}N,{\lambda }_X=x_1{\lambda }_T,L_X=x_1{L}_T,P_X=\frac{\tau x_2^2}{{\kappa }^2\left(x_1^2+x_2^2\right)+{\tau }^2{x}_2^2},\hfill \\ \hfill X^{*}=& \left(\left(x_1-p\right)cos\varphi -\left(x_2-z\right)sin\varphi \right)T^{*}\hfill \\ & +\left(\left(x_1-p\right)sin\varphi +\left(x_2-z\right)cos\varphi \right)N^{*}-q{B}^{*},\hfill \\ \hfill {\lambda }_{X^{*}}=& {\lambda }_T\left(\left(x_1-p\right){cos}^2\varphi -\left(x_2-z\right)sin\varphi cos\varphi \right)\hfill \\ & -{\lambda }_{B}q+L_{T}q+a_1\left(x_1-p\right)cos\varphi -a_1\left(x_2-z\right)sin\varphi -a_{3}q,\hfill \\ \hfill L_{X^{*}}{\tau }^{*}=& L_T\tau \left(\left(x_1-p\right){cos}^2\varphi -\left(x_2-z\right)cos\varphi sin\varphi \right)\hfill \\ & +a_1\left(x_1-p\right)cos\varphi -a_1\left(x_2-z\right)sin\varphi ,\hfill \\ \hfill P_{X^{*}}=& \frac{C_q\left(sin\varphi \left(x_1-p\right)+cos\varphi \left(x_2-z\right)\right)+B_{q}q}{A_q^2+B_q^2+C_q^2}.\hfill \end{array}$$

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,a_3=\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt.$

Proof. 

Since X is on the osculating plane, from (26)–(30), we complete the proof. □

Proposition 2.

When the vector X lies on the normal plane, the pitch, the angle of pitch and the distribution parameter of the two closed ruled surfaces, whose generators are the vectors X and $X^{*}$, are given as the following:

$$\begin{array}{cc}\hfill X=& x_{2}N+x_{3}B,{\lambda }_X=x_3{\lambda }_B,L_X=0,P_X=\frac{\tau \left(x_2^2+x_3^2\right)}{{\kappa }^2{x}_2^2+{\tau }^2\left(x_2^2+x_3^2\right)},\hfill \\ \hfill X^{*}=& \left(-pcos\varphi -sin\varphi \left(x_2-z\right)\right)T^{*}\hfill \\ & +\left(-psin\varphi +cos\varphi \left(x_2-z\right)\right)N^{*}+\left(x_3-q\right)B^{*},\hfill \\ \hfill {\lambda }_{X^{*}}=& {\lambda }_T\left(-p{cos}^2\varphi -sin\varphi cos\varphi \left(x_2-z\right)\right)+{\lambda }_B\left(x_3-q\right)-L_T\left(x_3-q\right)\hfill \\ & +a_1\left(-pcos\varphi -sin\varphi \left(x_2-z\right)\right)+a_3\left(x_3-q\right),\hfill \\ \hfill L_{X^{*}}{\tau }^{*}=& L_T\tau \left(-p{cos}^2\varphi -cos\varphi sin\varphi \left(x_2-z\right)\right)\hfill \\ & +a_1\left(-pcos\varphi -sin\varphi \left(x_2-z\right)\right),\hfill \end{array}$$

$$P_{X^{*}}=\frac{C_q\left(-psin\varphi +cos\varphi \left(x_2-z\right)\right)-B_q\left(x_3-q\right)}{A_q^2+B_q^2+C_q^2}$$

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,a_3=\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt,$

$$\begin{array}{cc}\hfill A_q=& sin\varphi \left(z^{\prime }+p+p\left(\kappa -1\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ & +cos\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right),\hfill \\ \hfill B_q=& sin\varphi \left(-p^{\prime }-x_2+z-\left(\kappa -1\right)\left(x_2-z\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ & +cos\varphi \left(-z^{\prime }+x_1-p+p\left(\kappa -1\right)\frac{dt}{d{t}^{*}}\right)-cos\varphi \tau \left(x_3-q\right)\frac{dt}{d{t}^{*}},\hfill \\ \hfill C_q=& -p\tau sin\varphi cos\varphi \frac{dt}{d{t}^{*}}+{cos}^2\varphi \tau \left(x_2-z\right)\frac{dt}{d{t}^{*}}-q^{\prime }.\hfill \end{array}$$

Proof. 

Similarly, since X is on the normal plane, we complete the proof by referring to the relations (26)–(30). □

Proposition 3.

While the vector X is on the rectifying plane, the pitch, the angle of pitch and the distribution parameter of the two closed ruled surfaces whose generators are the vectors X and $X^{*}$ are given as the following.

$$\begin{array}{cc}\hfill X=& x_{1}T+x_{3}B,{\lambda }_X=x_1{\lambda }_T+x_3{\lambda }_B,L_X=x_1{L}_T,P_X=\frac{\tau x_3^2-x_1{x}_3\kappa }{{\left(\kappa x_1-\tau x_3\right)}^2},\hfill \\ \hfill X^{*}=& \left(cos\varphi \left(x_1-p\right)+zsin\varphi \right)T^{*}\hfill \\ & +\left(sin\varphi \left(x_1-p\right)-zcos\varphi \right)N^{*}+\left(x_3-q\right)B^{*},\hfill \\ \hfill {\lambda }_{X^{*}}=& {\lambda }_T\left({cos}^2\varphi \left(x_1-p\right)+zsin\varphi cos\varphi \right)+{\lambda }_B\left(x_3-q\right)-L_T\left(x_3-q\right)\hfill \\ & +a_1\left(cos\varphi \left(x_1-p\right)+zsin\varphi \right)+a_3\left(x_3-q\right),\hfill \\ \hfill L_{X^{*}}{\tau }^{*}=& L_T\tau \left({cos}^2\varphi \left(x_1-p\right)+zcos\varphi sin\varphi \right)+a_1\left(cos\varphi \left(x_1-p\right)+zsin\varphi \right),\hfill \\ \hfill P_{X^{*}}=& \frac{C_q\left(sin\varphi \left(x_1-p\right)-zcos\varphi \right)-B_q\left(x_3-q\right)}{A_q^2+B_q^2+C_q^2}\hfill \end{array}$$

where $a_1=\underset{\left(pT+zN+qB\right)}{\oint }\tau cos\varphi dt,a_3=\underset{\left(pT+zN+qB\right)}{\oint }\left(\kappa -1\right)dt,$

$$\begin{array}{cc}\hfill A_q=& sin\varphi \left(z^{\prime }-x_1+p-\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)\hfill \\ & +cos\varphi \left(-p^{\prime }+z\left(1+\left(\kappa -1\right)\frac{dt}{d{t}^{*}}\right)\right),\hfill \\ \hfill B_q=& sin\varphi \left(-p^{\prime }+z\left(1+\left(\kappa -1\right)\frac{dt}{d{t}^{*}}\right)\right)\hfill \\ & +cos\varphi \left(-z^{\prime }+x_1-p+\left(\kappa -1\right)\left(x_1-p\right)\frac{dt}{d{t}^{*}}\right)-cos\varphi \tau \left(x_3-q\right)\frac{dt}{d{t}^{*}},\hfill \\ \hfill C_q=& sin\varphi cos\varphi \tau \left(x_1-p\right)\frac{dt}{d{t}^{*}}-z\tau {cos}^2\varphi \frac{dt}{d{t}^{*}}-q^{\prime }.\hfill \end{array}$$

Proof. 

Similarly again, since X is on the rectifying plane, by using (26)–(30), we complete the proof. □

3. Conclusions and Discussion

Overall, in this study, parallel q-equidistant ruled surfaces were introduced such that the binormal vectors are parallel along the striction curves of their corresponding binormal ruled surfaces and the distance between the asymptotic planes is constant at proper points. The geometric properties of these ruled surfaces were examined, and some useful relations were given to be used for future research. In our next work, we are going to proceed to study geometric properties and symmetric properties of these ruled surfaces combined with the techniques and results in [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] to find more new results.