Abstract
Blockchains (BCs) are distributed database systems, popular for their innovative, unsupervised maintenance process. They use a so-called consensus protocol to prevent inference by any third party of absolute trust. Security, privacy, consistency, and energy consumption have been identified as the main issues involved in BC maintenance. According to the recent literature, some of these issues can be formulated as combinatorial optimization (CO) problems, and this fact motivated us to consider incorporating CO approaches into a BC. In this paper, we propose the new combinatorial optimization consensus protocol (COCP) based on the proof-of-useful-work (PoUW) concept that assumes solving instances of real-life CO problems. Due to the complexity of the underlying CO problems, we have developed various types of heuristic methods, which are utilized in the COCP. Most of these methods are problem-dependent stochastic heuristic or metaheuristic methods. As is the case with the majority of consensus protocols, PoUW exhibits the property of asymmetry. It is difficult to find a solution for the considered CO problem; however, once a solution is found, its verification is straightforward. We present here a BC framework combining the two above-mentioned fields of research: BC and CO. This framework consists of improvements aiming towards developing the COCP of the PoUW type. The main advantage of this consensus protocol is the efficient utilization of computing resources (by exploring them for finding solutions of real-life CO problem instances), and the provision of a broad range of incentives for the various BC participants. We enumerate the potential benefits of the COCP with respect to its practical impacts and savings in power consumption, describing in detail an illustrative example based on part of the real-life BC network. In addition, we identify several challenges that should be resolved in order to implement a useful, secure, and efficient PoUW consensus protocol.
1. Introduction
We investigated the application of combinatorial optimization (CO) methods in the maintenance of blockchain (BC) systems. BCs can be seen as public or private autonomous (unsupervised) distributed data storage systems with the property of immutability. Autonomy means that a BC should be maintained without any third party of absolute trust; instead, all participants may be responsible for BC maintenance. It is generally assumed that reliability, security, and consistency are in the interest of all participants; however, this may not always be the case. Therefore, BC communication protocols should be designed in such a way as to prevent malicious actions and data corruption. Digital signatures, time-stamping, and hashing (encoding) provide data security and consistency. Distribution in BC systems refers to the fact that each participant has a copy of the whole database in order to prevent data loss and misuse. Due to the delays in peer-to-peer (P2P) communication, it is very important to pay close attention to synchronization and data consistency when making decisions about BC maintenance. Immutability means that data stored in BCs cannot be changed anymore. This property is explored by checking the security and consistency of the whole BC system.
The first BC implementation was related to the financial domain—performing transactions with Bitcoin cryptocurrency [1]. However, nowadays, BC systems have a wide range of applications, such as IoT, insurance, healthcare, smart contracts, smart property, digital identity, digital content distribution, voting, notary systems, Botnet, P2P broadcast protocols, and many others [2]. BC system maintenance is based on democratic principles, which are reflected in consensus algorithms and the self-governing of the BC. On the other hand, the BC itself represents a reliable tool for democracy [3] that can be used in electronic voting and administration. Digital forensics is another interesting BC application proposed in [4]. In order to trace the chain of custody in digital forensics, it is very important to prove that nobody has been tampering with the evidence at any point of the investigation. BCs seem to be very suitable for the storage of forensic evidence as their immutability guarantees that digital evidence is collected, stored, and transmitted in a valid and legal way. More precisely, it is easy to detect when any inconsistency occurs and to identify who is responsible for it.
Several key concepts that have contributed to the success of the BC have been identified, such as the distributed nature of data, data integrity, transparency, auditability, programmability, immutability, and the necessity of achieving consensus [5,6]. On the other hand, the shortcomings of BC technology, especially the computing overhead, scaling, security, and privacy issues, must not be disregarded [7]. We are especially interested in two issues, the development of the new consensus protocol based on the proof-of-useful-work (PoUW) concept (to resolve the inefficient usage of resources) and the identification of malicious activities (as a tool to manage the security of BC systems). Access to BCs is realized via the Internet, by exchanging messages between participants (also referred to as agents, users, clients, customers, entities, and nodes). Therefore, BCs are always at risk, and their security has been addressed by numerous researchers from corresponding domains. On the other hand, the computing resources involved in BC maintenance are huge. Occasionally, disconnection or breakage of some devices could happen, but the main problem is the enormous amount of energy spent keeping this system in operation. Energy savings and increasing the efficiency of resource usage in BC have been considered in the recent literature; however, this is still a topic of great importance.
Our main contributions are the development of the new consensus protocol that we named the combinatorial optimization consensus protocol (COCP) and the identification of several challenges that should be resolved in order to implement a useful, secure, and efficient PoUW consensus protocol. Our COCP combines the BC and CO research fields, in accordance with the PoUW concept [8,9,10], with the aim of ensuring potential benefits with respect to energy consumption and security issues. Regarding the efficient use of energy, we propose to deal with the hard, real-life CO problem instances as a useful part of the consensus protocol. To resolve security issues, our COCP relies heavily on hashing and time-stamping. The main part of this paper is devoted to providing a detailed description of COCP and presenting a case study simulation. We explain the main steps involved in COCP, and provide a simulation using a part of the real-life BC network to illustrate the achieved benefits. In the Discussion section, we list the challenges identified and provide ways to resolve them.
In the remainder of this paper, we present basic facts about the BC systems and a review of the relevant literature, i.e., a survey of papers considering various aspects of the proof-of-useful-work consensus protocol in Section 2. Section 3 contains the proposed solution framework, with a primary focus on the possible execution scenarios, along with combinatorial optimization problems selected for the preliminary evaluation. The simulation that we performed is described in Section 4. In Section 5, a discussion about the proposed solution framework is provided. Finally, Section 6 contains a summary and conclusions of the work performed, as well as suggestions for future research.
2. Preliminaries and Related Work
2.1. BC Background
To explain the basics of the BC system, Figure 1 provides a schematic illustration of its organization. Data, referred to as “committed transactions”, published by the BC participants named basic users, are grouped together into blocks and stored in a list (chain) of blocks [6]. Each block contains several transactions and a hash value of the previous block to maintain consistency. The block structure is roughly divided into the block’s header and the block’s body. Transactions are stored in the body, whereas the block’s header contains various data required for maintaining the BC system. The most important field in the block’s header is the hash value of the previous block, which is crucial to maintaining the chain structure and preserving consistency. Other important fields are the miner identification, timestamp, nonce (if the PoW consensus protocol is applied), etc.
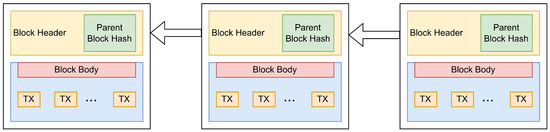
Figure 1.
Organization of the BC system.
New blocks are allowed to be added to the BC simultaneously by agents, called the miners, which gain a certain reward (e.g., an amount of cryptocurrency) for adding data. In order to add a new block to the BC, the miners must perform some tasks that are part of the block insertion mechanism called the consensus protocol. This protocol is responsible for maintaining the validity of transactions, as well as the integrity and security of the whole BC system. Although it is assumed that the miners who invested some resources in performing the required tasks are not interested in destroying the integrity of the BC system, an additional verification step is also included. More precisely, only blocks verified by the agreement (consensus) between a given number of agents called verifiers (selected among the participants) can be added to the chain. By performing these two steps of the consensus protocol (solving the required tasks and verifying the corresponding blocks), maintenance of the BC data is realized without the need for “trusted third parties”. The validity of a transaction should become common knowledge among all participants. Therefore, one of the crucial properties in the BC consensus protocol is the guarantee that the consensus of verifiers is achieved in every execution step and that all transactions occur in a trustworthy way. More precisely, the most important issues that the consensus protocol has to deal with are the reliability and security of the BC system.
A large number of consensus protocols are based on solving cryptographic puzzles related to the inversion of one-way functions (see, as an illustration, [11]). The main characteristic of these functions is the asymmetry between the calculation of their values and their arguments. More precisely, it is easy to calculate the function value for the given arguments; however, there are no efficient ways to find the arguments that correspond to a given function’s value (or a function’s values satisfying the required property). When the consensus protocol is based on solving a cryptographic puzzle, it is performed by employing computational resources, i.e., by performing some work. Therefore, these protocols are referred to as the proof-of-work (PoW).
Figure 2 provides a graphical representation of the PoW consensus protocol and the above defined terms. The classical PoW [6,12] works as follows: The data submitted by basic users are stored in the pool of transactions (see the left part of Figure 2). The miners select transactions from the pool and generate blocks that they want to add to the BC, as presented in the top right part of Figure 2. Usually, transactions are selected in a greedy manner, i.e., in such a way as to ensure the largest reward for the miner. The next step in executing the PoW is to solve the corresponding cryptographic puzzle, i.e., to find the unknown value called the nonce with the following property. Combined with the block content by means of the hash function, the nonce produces the resulting value that is less than a given threshold, i.e., the value that begins with a pre-specified number of zeros. It is well known that this puzzle is very hard; there is no better algorithm to solve it than to examine all the possible values for the nonce. Therefore, the miners expend huge amounts of computational power to properly guess the nonce value in order to publish the composed block. Once the miner announces its block and the corresponding nonce value, the verifiers check its validity and approve its addition to the BC (see the bottom right part of Figure 2). The corresponding miner receives the reward, which is marked by the dotted line connecting the “Block reward” rectangle with the green marked miner in the top right part of Figure 2.
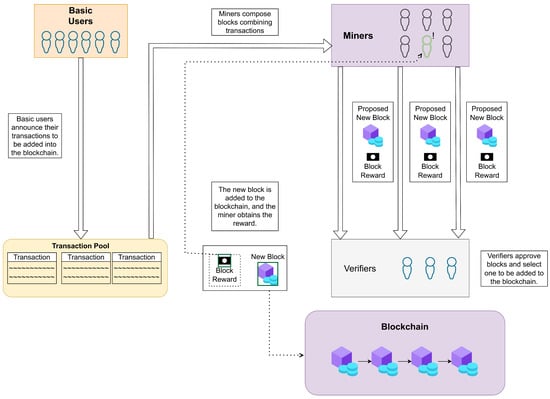
Figure 2.
Illustration of the classical PoW consensus protocol.
The described PoW represents a highly concurrent process. A number of miners are trying to add a new block (not necessarily the same one) simultaneously. All of them iteratively calculate the hash value for different nonce values until one of two criteria is satisfied: (i) the desired hash value is obtained, or (ii) a potentially new block for verification arrives. In the first case, the corresponding miner sends its block and the corresponding nonce value to others for verification, whereas the second case means that some other miner found the proper value for the nonce and its block will probably be accepted for inclusion in the BC. Consequently, only a single miner’s work is productive, whereas all the others merely waste their resources, time, and energy. In addition, transactions included in their blocks (and not in the accepted one) must be returned to the transaction pool and considered again.
There are other traditional BC consensus protocols [12,13]: proof-of-stake (PoS), proof-of-concept (PoCo), Byzantine fault tolerance (BFT), proof-of-authority (PoA), proof-of-activity (PoAc), proof-of-burn (PoB), proof-of-capacity (PoC), proof-of-elapsed-time (PoET), proof-of-importance (PoI), etc. In the systematic overview of consensus protocols presented in [14], BC consensus protocols are divided into two large groups, designated as popular consensus protocols and alternative protocols. The protocols in the popular group are PoW, delayed PoW, PoS, delegated PoS, PoA, PoI, the ripple protocol, practical BFT, delegated BFT, federated BFT, PoET, PoB, and PoC. After providing short descriptions of these protocols and a list of the BC platforms that use the popular BC consensus protocols, the authors consider alternative protocols. They divide these protocols into four categories, which are presented in Table 1, based on the requirements for the selection of a block publisher. Each of the alternative protocols is described and compared against the PoW consensus protocol, using the following metrics: throughput, scalability, security, energy consumption, and finality (the assurance or guarantee that transactions cannot be altered, reversed, or canceled after they are completed).

Table 1.
Categories of alternative consensus protocols presented in [14].
The execution of the consensus protocol appears as an overhead in the BC that should be paid to avoid the centralized verification paradigm. The overheads implied by the employed consensus protocol can be very large (with respect to the engaged memory or the running time, i.e., the energy consumption) and their minimization is an open topic of research. Therefore, to address the energy consumption overhead, we developed a new consensus protocol based on the PoUW paradigm [8,9,10,15], which involves solving some real-life CO problems instead of solving cryptographic puzzles.
Among the main requests required to be fulfilled in BC databases is the anonymity of the participants, i.e., to prevent the public availability of personally identifiable information (PII) of the BC participants. PII connects participants with their corresponding transactions [16]. Anonymity is achieved by means of encryption, which relies on two keys: public and private. Therefore, it is important to keep the private key unknown to the community. Although anonymity is a desirable feature from the viewpoint of participants, it can be exploited in order to hide malicious actions. BCs can be used as means of anonymizing transactions involving illegal activities that thus become difficult to trace [17,18]. Transactions of this kind are difficult to trace because generating new accounts and sharing data between them is a common occurrence, in a process called a peeling chain [19]. Therefore, it is possible for a single owner to possess several accounts. In this case, the owner is called an entity, which represents a person or an organization, which makes transactions via a BC. Although there is a slight possibility that one BC account may be shared by several people, that case can be ignored because it happens rarely. There is also a class of viruses, known as ransomware, that encrypt sensitive data in infected systems and demand a ransom before allowing the victim to decrypt the data. Some forms of ransomware may ask for a ransom to be paid using a BC, and these are known as crypto-ransomware [20]. Crypto-ransomware also follows the peeling chain pattern when spreading across the BC network. In light of all the issues mentioned above, BC users are subject to constant attacks focused on discovering patterns in the transaction history that could help adversaries to identify individual users. If an adversary is able to link transactions to their owner, the consequence is so-called deanonymization, i.e., the property of anonymity is broken. In order to minimize the threat to a user’s anonymity, all the risks related to a BC should be disclosed [21]. On the other hand, deanonymization allows for the discovery of malicious users and the prevention of attacks due to the abovementioned observation about the possibility of grouping users that exhibit similar behavior. In essence, deanonymization can be treated as a well-known classification/clustering problem. In this approach, the BC data can be modeled by means of a directed graph (DG) structure [22,23,24] called a transaction graph and generated using the publicly available BC data. The nodes of the DG denote participants, whereas directed edges represent transactions performed between them. A key issue in the clustering of the BC data is entity detection, where different addresses are connected to the same entity, i.e., we are actually dealing with the problem of community detection in directed graphs. This problem belongs to the CO class. Therefore, it can be considered as a useful part of the PoUW consensus protocol in a self-contained blockchain [25].
2.2. Related Work
In the recent literature, PoUW has already been established as a concept that aims to ensure the energy-efficient implementation of the BC consensus protocol [8,9,10,15]. Thus, the aim of our literature review is to briefly discuss the previous research on PoW and its drawbacks. In addition, we provide a detailed explanation of recent studies that have proposed how to turn PoW’s biggest drawback (namely, its uselessness) into a benefit for blockchain participants.
PoW [6,12] was the first consensus protocol used in relation to the Bitcoin cryptocurrency to ensure secure financial transactions between participants without the need for a trustful third party. It is a very secure and highly decentralized consensus protocol [11,14], as it explores cryptographic mechanisms involving encryption with asymmetric keys and hashing. However, the PoW approach has several major disadvantages. The first of them has already been mentioned: its enormous power consumption with completely useless resulting value [10,26]. Another drawback is the time-complexity of solving the hash-based cryptographic puzzle. The time required to complete the PoW task usually ranges from 10 to 20 min [27], which means that the PoW is not suitable for networks that require high transaction throughput per second [28].
Several alternative approaches, which use different hash functions, have been proposed in the recent literature, such as prime number verification [29], graph-theoretic proof-of-work [30], and proof-of-work based on the generalized birthday problem [31]. However, they all have the same drawbacks as the classical PoW. In the PoW based on the Collatz conjecture (PCC) [32], the running time does not increase exponentially with the number of blocks in the BC, as is the case with the classical PoW. However, PCC eliminates only the complexity issues of the PoW procedure; the problem of the usefulness of this algorithm still remains.
An example of a metaheuristic method being applied to the blockchain was presented in [33]. The authors proposed using a non-dominated sorting genetic algorithm II (NSGA-II) to improve the difficulty adjustment method of the proof-of-work consensus protocol. In particular, NSGA-II was used to optimize both the block interval and difficulty adjustment interval. Two objective functions were considered simultaneously: the standard deviations of the average block time and difficulty. The authors concluded that introducing NSGA-II into the difficulty adjustment method can help the blockchain to reach the desired difficulty faster, but it has some drawbacks, for instance, increasing the necessary processing power.
The proof of useful work concept, introduced in [10], tries to relate consensus protocol hardness to computational problems, such as orthogonal vectors. The authors provide a mathematical formalization of the PoUW and the properties that it should satisfy. They claim that, while keeping the basic properties of the classical PoW, the corresponding results are no longer energy-wasteful as long as problems of practical interest are considered. The main issue with their proposal is the requirement that the considered problem can be represented by polynomials and treated as orthogonal vectors.
The authors in [34] developed a hybrid scheme including a PoUW based on the traveling salesman problem (TSP) that operates in two rounds. In the first round, i.e., the hashcash stage, the classical PoW is executed using ASIC hardware in a deterministic time interval. In the second round, an instance of the NP-hard TSP is constructed based on the results from the first stage and solved. As the main advantage of this approach, the authors point to the efficient usage of the existing ASIC hardware, although the usefulness of the approach is not adequately elaborated. More studies have been dedicated to solving TSP [35,36]. In [37], the authors proposed the PoUW consensus protocol that performs machine learning (ML) model training as its useful component. Two sources of rewards are introduced for the miners: the standard reward for adding a new block and the reward offered by clients for training their ML models. By comparing cloud hourly fees and BC reward amounts, the authors showed that using the BC system for ML model training was more profitable for both clients and miners. Many works have aimed to develop new PoUWs based on the training of machine learning and deep learning models [37,38,39,40,41,42]. Authors have proposed using BC systems to train deep learning models as a part of the consensus protocol.
The hybrid approach to mining introduced in [43] combines hash value calculations (hashcash) with distributed problem solving (DPS). The main idea is that the user can submit a real-world problem for the miners to solve. A new block can be added to the chain either by solving submitted problems or by means of the hashcash process when real-world problems are not available. A modification of the PoW, named difficulty-based incentives for problem solving (DIPS), which gives incentives to miners who solve real-life problems of scientific interest, is described in [44]. When a better solution to a real-life problem is found, the difficulty of block hashing is reduced, making it easier to mine a new block. However, in that study, the exact method of submitting a new real-life problem is not provided; instead, the authors propose some ideas for submitting a new problem. One of these ideas includes choosing a set of privileged nodes that can submit a new problem. According to the second idea, every node has the right to submit a problem, and then all nodes vote on which problem to accept. The third idea for submitting problems enables any node to submit a problem, as long as that node invests a certain amount of tokens (coins). The weaknesses of these ideas and implementation issues are not discussed in this paper. On the other hand, a potential problem with the DIPS protocol as a whole is identified as the Bubka attack problem. Upon finding several successive solutions to a real-life problem, instead of using the best one, a miner could use all these solutions successively to hash several blocks in a row.
A more recent study related to the PoUW concept [15] was based on solving the problem of clustering a set of transportation requests sharing the same origin and destination. Each transportation request is specified by several key data and submitted to the pool of requests. Mining consists of grouping transportation requests into clusters so that all transportation requests belonging to one cluster can be performed by the same vessel. By combining transportation requests, the cost of each transportation request is reduced and the corresponding cost savings are used to reward the miner who solved the clustering problem. The block mining process starts after inserting a specified minimal number of transportation requests into the pool. This condition guarantees that the corresponding clustering problem is difficult enough to solve and that the solving time is not less than the expected rate of mining blocks. All transportation requests selected for clustering, as well as the corresponding determined clusters, are stored in the block’s header. The block’s body consists of other transactions submitted for storage in the BC. Although demonstrating obvious usefulness, this proposed approach does not specify the connection between the solved problem and the set of transactions forming a new block.
In all of the presented PoUW protocols, the main drawback of the classical PoW (the uselessness of energy consumption) has been addressed, and some other issues (such as integrity, security, and latency) have also been identified. Various approaches to resolving these issues have been proposed, the most prevalent being the solution of hard real-life CO problems and artificial neural network (ANN) training as the work to be completed within the new consensus protocol. These ideas ensure the maintenance of the benefits of the PoW and introduce two sources of rewards for the miners. The first source is the standard reward for adding a new block into the BC. The second source is a reward offered by the customers. They submit CO problem instances to be solved as a useful part of the PoUW consensus protocol and deposit some amount of cryptocurrency as a reward for the successful miner. The main drawback of all the surveyed papers is that only ideas have been presented, and their advantages discussed, and only some sporadic simulations have been described, mostly on a conceptual level. Only a few [8,9,10] have describing actual implementations and/or experimental evaluations and also provide theoretical proof of the security (under the required conditions) of their PoUW-based consensus protocols.
A relatively detailed implementation of the PoUW, named the proof-of-search method, is described in [9]. The author proposed this consensus protocol as a tool to search for good approximate solutions to any optimization problem. In that study, a special type of BC participant (client) is introduced. Their role is to submit instances of some optimization problem, together with the optimization method to be used for solving them, and an evaluation function is used by both the miners and the verifiers. The miners use the evaluation function to calculate the objective function values and to test whether the stopping criterion is fulfilled. Verifiers need this function to check if the provided solutions correspond to the announced objective function values and to confirm that the miners invested adequate work in the search process. The main idea is to code each visited solution and use it as a nonce in the classical PoW sense. In this system, the miners are forced to examine an adequate number of candidate solutions to prove that they invested work in mining a current block. The best-obtained solution (by all the miners) is kept and reported to the client, and a search process is performed until a proper nonce (one that provides a given number of zeros at the beginning of the block hash value) is discovered. The author analyzed the properties of the proposed approach, providing proof for its resistance to various types of malicious behavior. However, the complexity of the overall proof-of-search protocol seems to be too large, especially the introduction of intermediate mini-blocks. In addition, the protocol is focused on security and fairness issues, rather than the quality of the provided solutions. The requirement for clients to provide the solution method and evaluation function seems too restrictive. In such a case, a BC can be considered as a set of resources that is rented to interested clients for solving their instances.
Another formal description, including security proofs, of a PoUW-based consensus protocol—in this case named Ofelimos—is presented in [8]. In that study, the doubly parallel local search (DPLS) algorithm, crafted to suit implementation as the PoUW component of the adjusted PoW-based BC consensus protocol, is proposed. DPLS represents a general purpose stochastic local-search algorithm with a main component called the exploration algorithm, which is used to produce a set of points in a solution space based on the given input parameters. The consensus protocol proposed in [8] was designed to prevent users from picking exploration steps that are not complex enough and to disallow the creation of CO problem instances that would enable malicious users to mine faster than the honest miners by solving those instances. The protocol also has adjustable mining difficulty: it allows relatively fast publishing of new points in the DPLS algorithm and it has only a small overhead in preparing the execution of the exploration algorithm. After forming a block, a miner starts with a task similar to the standard PoW: generating a nonce value, and calculating the resulting hash value of the block. Each calculated hash value is used as a seed for a random number generator in the exploration algorithm of DPLS that the miner executes next. After the result of the exploration algorithm is found, the miner checks if the hash value of the block is below a certain threshold (based on the current mining difficulty), as this allows the block to be published. If the hash value is not below the threshold, the mining continues until a block is published. However, even if the block is not published, the miner publishes the result received from executing the exploration algorithm in the form of a special transaction, so that the result can be used for further execution of the DPLS. The authors also provide a detailed security and usefulness analysis and show how DPLS can be implemented for a variant of WalkSAT algorithm. However, some of the details are still not clear, for example, how the underlying optimization problems should be defined and published in the BC to be subjected to DPLS.
Based on the literature review presented here, we identified several issues that should be resolved in order to implement a useful, secure, and efficient PoUW consensus protocol. They are listed as challenges and described in Section 5, together with our proposal for how to address them.
3. Our Solution Framework
In this section we present a detailed description of COCP, the PoUW-based consensus protocol that we propose, explain how it can be incorporated into a BC network, and list the benefits of its utilization. This section also contains examples of CO problems and the corresponding solution methods that we have developed. These methods are used in our simulation described in Section 4.
3.1. Proposed PoUW Consensus Protocol
We propose to modify the classical PoW consensus protocol (shown in Figure 2) in such a way as to replace cryptographic puzzles with instances of hard CO problems that have real-life applications. The proposed COCP solution framework is illustrated in Figure 3, which is an extension of Figure 2 obtained by adding new components on its right side. A preliminary, brief description of our framework was presented in [45]. Here, we extend the development of the COCP, provide more details, and consider more challenges. To develop a successful PoUW protocol in the proposed COCP framework, we introduce a new type of participant, the problem publisher, client, or customer. These are individuals, organizations, or companies that join a BC system because they need its resources to provide software and hardware support for solving their real-life CO problems. The instances of these problems need to be specified to the system, and this specification must include the following important information:
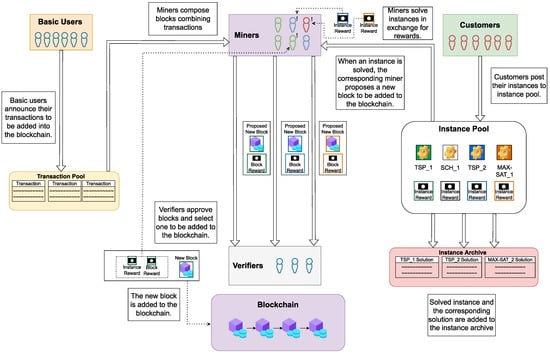
Figure 3.
The COCP solution framework.
- Customer identification;
- A timestamp;
- A valid address for CO problem instance data;
- The hash value of CO problem instance data;
- The solution threshold;
- The deadline for finding the solution; and
- The reward specification.
As the size of the problem definition may be large, and storing large data on BC systems is expensive, the CO problem instance specification does not contain the problem input data. Instead, a valid address that points to the location of the problem definition is provided. However, in order to prevent malicious behavior, the customer must also put a hash value of the instance data into the transaction. This way, one can easily detect if the instance is modified at any time after its publication. In addition to these two fields, a desired quality of the solution defined by the solution’s threshold, the deadline for finding the solution (optional), and the reward that will be given to the miner who solves the corresponding CO problem instance have to be specified. The pseudo-code for submitting a CO problem instance is presented in Algorithm 1. The reward offered by the customers for solving their instances is not specified in advance: only the minimum value is provided to discourage dishonest miners from committing fraud. Based on the input data specified by the customer, the hash value () is calculated, and it is verified whether or not the given instance i has already been solved (through the GetSolutions procedure). If at least one solution already exists, it is provided to the customer without the need to solve this instance. The only way to resubmit the same instance again is when the threshold value has been adjusted, i.e., when the customer wants a solution of higher quality. On the other hand, if there are no solutions for instance i, a transaction (t) is created that announces CO problem instance i to the BC. A timestamp, i.e., the time when instance becomes active, which is determined upon transaction t, is included in a block added to the BC. The value of the timestamp will be the same as the timestamp of the block that includes the submitted instance. The timestamp of the block is determined by the miner who formed the block, and this represents the unix time reported by the miner. Although it is difficult to verify that the time reported by the miner is correct, there are two conditions that the timestamp must meet. First, the timestamp of the block must be larger than the timestamp of its parent block. Second, the timestamp must not be too far in the future, i.e., it should be within the pre-specified time window of the current verifier’s unix time.
It should be noted that the CO problem instances could be published in at least two slightly different ways. The first involves a special kind of transaction that is published within the network and which enters the transaction pool. When these transactions are inserted in a block that becomes part of the BC network, the corresponding instances enter the instance pool. This is illustrated in the rightmost part of Figure 3. The existence of these new instances becomes common knowledge among all participants. The second method of publishing instances incorporates the use of smart contracts. Therefore, it is suitable for the BC systems that support them. In this case, the instance pool contains a set of special smart contracts at an address known to all participants. Instances can be accessed by interacting with the contract.
| Algorithm 1 Procedure for instance submission |
|
Published CO problem instances are located in the instance pool, which contains all instances that are still active. An active instance is a published instance for which the deadline has not passed and that still does not have a solution. Similarly to the connection between the block and the nonce value, it is necessary to establish the correspondence between the block and the active instance. We propose to accomplish this by means of the method presented in Algorithm 2. First, we reserve two fields from the block’s header (field1 and field2) for storing data related to the corresponding CO problem instance. When a block B to be mined is formed (repeat loop of Algorithm 2), the hash value, , of the block’s header (without the values in these two reserved fields) is calculated and it is used to select one among the active instances to be solved. We assume that the active instances in the pool (P) are enumerated (starting with 0) according to the same predefined criterion, for example, according to the increasing order of their deadlines. Note that the value of the deadline does not necessarily correspond to the hardness of the instance. The index i of the instance corresponding to block B is calculated by performing the modulo operation between and the number of instances in the pool, i.e., . If the enumeration of instances starts with 1, corresponds to the instance marked with . Once the miner determines index i, the instance needed to be solved for this particular block is and that should be common knowledge among all participants, especially the verifiers.
After selecting the corresponding CO problem instance i for block B, the miner executes the available solution method, trying to find a valid solution for instance i. The solution algorithm runs until one of the following events occurs (switch command of Algorithm 2):
- INTERRUPT: This means that another miner has already announced a new block and it is undergoing the verification process. If they are close to solving instance i, the miner may decide to continue mining for some short time period and, if successful, to announce the obtained valid solution for i and publish the composed block B. Even if B is not accepted for inclusion in BC, the miner could be rewarded for providing a valid solution for instance i.
- SOLVED: This indicates that the solution method succeeded in finding a valid solution for CO problem instance i, and the miner can announce it and publish block B.
- FAILED: This stands for the case when a solution method reaches the stopping criterion without providing a valid solution for instance i. In that case, the CO problem instance is returned to the instance pool for another attempt related to some future block.
Once the selected instance is solved, the miner is ready to announce a new block. To establish the correspondence between the composed block and the solved CO problem instance, the miner stores a pointer to the transaction, introducing the CO problem instance or smart contract that corresponds to the submitted instance in field1. This information enables all participants to access the data related to the solved instance.
| Algorithm 2 Procedure for block mining |
|
For security reasons and to save space, similarly to problem definitions (instance data), solutions are stored in the miner’s private location, which is predefined and known to all participants. In particular, field2 of the published block, the hash value of the instance, the data, and the hash value of the solution are stored in order to prevent malicious behavior (e.g., publishing a block and finding a solution later). However, both hash values (for instance and solution) are 256 bits long, also representing the maximum length of any field in the block’s header. Therefore, to store them in field2, the miner performs the bit-wise xor operation on the instance hash and the solution hash values. Knowing the instance hash (from the published instance’s data), it is easy to reconstruct the hash value of the solution.
Upon obtaining a valid solution for the considered CO problem instance, the miner stores it in a solution pool, together with the miner ID, with the content of field1 (pointing to address of the instance data), the hash value of the instance (), the objective function value (), and the hash value of a solution () corresponding to the considered instance. The role of the solution pool is to keep all valid solutions for each considered instance and to enable the identification and rewarding of the miner who found the best solution. The SolutionRetrieval procedure, presented in Algorithm 3, is used to determine if the solution of instance i has been obtained. It works in a loop that ends when at least one solution is reported or when the is met without a valid solution for instance i. By calling the procedure FindSolutions, the list of all valid solutions is created. It is then passed to the procedure FindBestSolution for the comparison of all valid solutions and the determination of the best among them. Data relevant for delivering the solution to the customer and rewarding the miner who found the best solution are returned. In the case in which no solution is reported, is empty and the SolutionRetrieval procedure checks whether the has been missed. If the deadline for solving instance i has passed, the customer is informed that the solution process failed and instance i is removed from the instance pool.
| Algorithm 3 Procedure for solution retrieval |
|
In the process of block verification (see Algorithm 4), the validity of all transactions is checked first. Next, it is confirmed that the solved instance i is the corresponding one for block B. The verifiers can access the instance data via the information from field1 and the solution from the miner’s private location. The verification part related to COCP consists of reconstructing the hash value of the solution from field2 by performing the bit-wise xor operation with the instance’s data hash. After this process, the verifier has all the data needed to perform the successful validation of the block. The hash value of the CO problem instance is calculated based on the instance data from the pool and compared with the corresponding hash value provided by the customer. On the other hand, the reconstructed hash of the solution is compared with the hash value calculated from the solution itself. If any pair of hashes does not contain the same values, the corresponding block cannot be validated and is discarded. In the next step of the verification process, the objective function value of the reported solution is calculated and compared with the solution quality provided by the miner. If these two do not match, block B is discarded as invalid. At the end of the verification process, the instance archive is checked to verify whether the miner solved the CO problem instance specified by this . If not, block B is discarded as invalid.
All solved instances are removed from the pool and new ones are included as soon as they are published. The solved instances are stored in an instance archive (as illustrated in the bottom rightmost part of Figure 3), together with the corresponding solutions and all other relevant data (minerID, timestamp, etc.). It may occur that the same instance is published again, and we should prevent both the wastage of resources in solving that instance again, as well as malicious behaviour by some miners trying to exploit the existing solution and add a new block without expending any effort. The role of the instance archive is to prevent this type of fraud, as it is easy to check if any newly submitted instance has already been archived.
| Algorithm 4 Procedure for block verification |
|
3.2. Benefits of COCP
As indicated in the literature, the main drawback of the classical PoW consensus protocol is that a large amount of computing power is expended in order to maintain a single block. Usually, several (sometimes even a quite large number of) miners compose blocks and try to add them simultaneously; however, only one will succeed. Therefore, the work of all the other miners is wasted. The transactions composing their blocks will be returned to the pool and eventually will be added to some other block(s). Such an unsuccessful mining event can happen more than once, increasing the amount of wasteful work even further. Our intention was to reduce the number of unnecessary computations as much as possible by proposing the above-described COCP, the PoUW-based consensus protocol. Although the transactions from discarded blocks are also returned to the transaction pool in COCP, for the next attempt to include them in block, a new CO problem instance will be considered.
In the classical PoW consensus protocol, miners with a larger computing capacity than others have a greater probability of adding blocks and thus earning a reward. Early backers of rising BC services or technologies are the backbone of the infrastructure and of its sustainability, reliability, and its potential success, but they do not necessarily have a large computing capacity. Once a BC network gains momentum, attracting new miners with larger computing capacities, the early backing miners might find themselves drowned out and cast aside from the rewarding process. In such a case, BC technologies may lose their early backers. Our COCP is designed in such a way as to provide incentives for early backers to re-join the mining process as we provide CO algorithms that can successfully run on standard hardware resources.
In addition, our COCP introduces new incentives for various types of participants. Customers, as new participants who join the network, benefit by having their problems solved. The miners who add a new block are now doubly rewarded: by the customer for solving the CO problem instance and, as before, for adding a block. The miners who solve the instance but who do not add blocks can still be rewarded by customers. Moreover, resources are expended for some useful work and thus the overall energy consumption is decreased, as the same amount of energy is used for mining a block and for solving one or more real-life CO problem instances.
Keeping in mind that the BC network is a highly dynamic distributed environment, we identified several possible scenarios that might occur when a consensus protocol is running and we describe them below.
Scenario 1. The miners create their own blocks, calculate the hash values of the block’s headers, and select the appropriate CO problem instances from the pool. The fastest miner who solves the corresponding instance publishes the created block and collects both rewards. All instances that were not solved are returned to the instance pool.
Scenario 2. It may happen that two or more miners solved their instances at about the same time and published their blocks, creating the situation that is known as a fork in BC systems. Forks are usually resolved in the synchronization phase. Only one of the blocks will pass both the verification and synchronization phases; however, customers will receive the solutions for all problems solved by the miners. In the case in which some miners solved the same CO problem instance, the best among the obtained solutions is provided to the corresponding customer and the miner who found that particular solution is rewarded.
Scenario 3. After a new block is published, some miners, believing that they are close to finding a solution, may continue working on their current instances for some short period of time. If they succeed in solving them, a fork may appear. After the verification and synchronization phase, it will be determined which block is to be included in the BC and how the rewards will be assigned to the miners.
Scenario 4. A group of miners can combine their computational power with the aim of solving the corresponding CO problem instance faster and splitting the reward. This is a common situation in the classical PoW consensus protocols and is known as a mining pool. We believe that it could be used in our COCP approach as well, but it is beyond the scope of this paper and is thus left to future works.
3.3. Some Examples of Optimization Problems
This section is devoted to describing the real-life CO problems utilized in our study. Some instances of scheduling, asymmetric vehicle routing, and maximum satisfiability problems represent the useful part of our COCP, which is tested on a small BC example in Section 4. All these problems are intensively studied in the relevant literature and various optimization methods (exact, heuristic, approximate, and metaheuristic) have been developed. We explore heuristic methods that are the results of our recent projects. At the end of the problem description, we provide a brief overview of the corresponding optimization method. We envision the ability to adopt any CO problem; however, algorithms to deal with them must be incorporated in the proposed COCP to ensure that the appropriate tools are available for the miners.
It is important to note that the benchmark instances for testing various optimization algorithms could also be considered as real-life CO problem instances: when developing their new optimization methods, scientists need to execute them (usually several times) on the corresponding benchmark sets in order to test their efficiency and undertake comparisons with the state-of-the-art results.
3.3.1. Scheduling Problems
Scheduling, generally speaking, deals with assigning tasks to resources in time. There are numerous variants of scheduling problems [46], each of them having an important role in modeling real-life tasks. Here, we describe two examples that we have been studying and for which we have developed efficient algorithms utilized to deal with large real-life instances.
Scheduling Independent Tasks for Identical Processors (P‖Cmax)
Here we revisit the problem of scheduling independent tasks on parallel processors [46,47,48,49] as it recently gained importance with respect to the efficient exploitation of high-performance computing resources, cloud computing, and massively parallel multiprocessor systems. We consider a case study involving -static scheduling of independent tasks on identical processors. The expression static means that the number of tasks and their duration (lengths and processing times) are known a priori. The problem objective is to minimize the time required to complete the execution of all tasks, i.e., makespan .
More specifically, let m be the total number of available identical processors and n the number of tasks to be executed. The problem consists of assigning tasks to processors and determining their starting times. All the tasks should be allocated for execution, each to exactly one processor. Task execution is performed in a non-preemptive way: once the task starts its execution, no interruption is allowed until completion. We denote by a given set of independent tasks, and by the set of identical processors. Each processor can engage only one task at a time. Let denote the processing time of task i (), which is known a priori and fixed, and let () represent the load of processor j, calculated as the sum of the processing times of all tasks assigned to processor j. The goal is to find a schedule of tasks on processors such that is minimized. can be formulated as an integer linear program (ILP) based on the assignment variables [50], on the arc-flow model [51], or in some other way [52], and it is known to be NP-hard in a strong sense [53]. Numerous exact [51], heuristic [54], and metaheuristic [47,55,56,57] algorithms have been developed for .
Several efficient heuristics, based on greedy iterative stochastic transformation (GIST), were proposed in [58]. These heuristics perform transformations of the current solution with the aim of improving it by rescheduling tasks to processors in such a way that either the lower bound is increased or the upper bound is decreased until they coincide or some predefined stopping criterion is satisfied. The best-performing subset of the proposed heuristics was used in our simulation described in Section 4.
Weighted Scheduling Problem with Deadlines and Release Times
Using Graham’s notation [59], this variant of the scheduling problem can be classified as . Besides the execution time , each task i is described by the release time , deadline , and the weight (price, reward) . The considered version is non-preemptive, implying that tasks cannot be split into several parts and have to be executed fully before the next task can start. The tasks cannot start before a certain number of time units have passed, specified by the release time (). Similarly, the tasks have to finish before the deadline (). The precedence relation between tasks can be enforced by specifying the appropriate release times and deadlines. In the literature, it is common to allow missing deadlines and release times by adding some penalty to the objective function value, but in our version of the problem, this is strictly prohibited; therefore, tasks that cannot be scheduled without violating the deadline and the release time constraints are omitted from the schedule entirely. This version of the problem is even more complex than the one with penalties, as it requires us to determine the best possible subset of tasks to be executed, without breaking any constraints, and maximizing the objective function value, which is defined as the sum of the weights of all scheduled tasks.
A mixed-integer linear programming (MILP) formulation of this problem was presented by Stanković et al. (2021) [60] and tested in the framework of the CPLEX exact solver. A metaheuristic approach based on the general variable neighborhood search (GVNS) method was proposed by Matijević et al. (2021) [61]. It explores five neighborhoods in the shaking phase and two neighborhoods in the variable neighborhood descent local improvement step. For the simulation, we explored GVNS, as it performs better than the MILP-based solvers.
3.3.2. Asymmetric Vehicle Routing Problem
The vehicle routing problem (VRP) asks “What is the optimal set of routes for an existing fleet of vehicles that need to serve a given set of customers?” and arises in many everyday situations related to the transportation of goods [62,63,64]. VRP was proposed in [65] as an abstraction of vehicle scheduling problems. Since then, the formulation of VRP has evolved in many directions based on imposed constraints and defined objective functions.
The asymmetric vehicle routing problem (AVRP) can be represented on a complete directed graph , where V is the set of vertices representing customers, and E is the set of edges connecting those customers. The goal is to minimize the total distance traveled by all of the vehicles. Each edge is associated with a non-negative weight , representing the distance between customers i and j. Aside from vertices representing customers, there are two more vertices and , corresponding to the origin and destination of each route (depots). Each vehicle starts from depot , serves a certain number of customers, and ends its route at depot . Each customer should be served by exactly one vehicle and should not be visited more than once. Each vertex representing a customer is associated with a non-negative weight , corresponding to the demand of that customer. Each vertex representing a customer is associated with a non-negative weight , corresponding to the weight of goods demanded by that particular customer. Vehicles are homogeneous, i.e., they all have the same capacity Q and average speed S. The total travel time of each route is limited and can be calculated by taking into consideration distances between customers, the speed of the vehicle, and the waiting time at each customer’s location, which is given as a parameter. The number of customers that can be served by each vehicle is also limited, with the idea of balancing the workload of each driver.
The above-described variant of AVRP was considered in [66,67,68]: an MILP formulation was developed and several local search-based metaheuristic methods were implemented. These methods include the multistart local search (MLS), greedy randomized adaptive search procedure (GRASP), and five variants of GVNS exploring three neighborhoods in different ways. In our COCP evaluation, we have utilized the best-performing GVNS.
3.3.3. Maximum Satisfiability Problem
Propositional satisfiability problems, known as SAT problems, are crucial in computational complexity theory. They provide a basis for determining the complexity of considered algorithms and have been applied in many scientific disciplines, such as mathematics, computer science, and even philosophy. Propositional formulas are constituted of basic building blocks, such as propositional (Boolean) variables and logical operators, for example, negation (¬), conjunction (∧), and disjunction (∨). Propositional formulas are used to articulate different statements that can have unique truth values (TRUE or FALSE). Propositional variables and their negation that appear in formulas are named literals. A formula, represented as a conjunction over disjunctions of its literals, is known as a conjunctive normal form (CNF). Each disjunction of literals in a CNF is referred to as a clause. SAT problems are defined as those in which we need to decide whether the given formula , including n Boolean variables , is satisfiable, i.e., whether there exists a valuation (truth assignment) of X for which formula is TRUE. This actually means that all clauses must be TRUE. Boolean variables can take the values TRUE (⊤) or FALSE (⊥). Therefore, in order to find the truth assignment that satisfies formula on n variables, in the worst case, we need to check valuations.
The maximum satisfiability problem (MAX-SAT) represents the optimization variant of SAT problem in which the objective is to find a model that maximizes the number of satisfied clauses. For a given formula in CNF, the goal is to find a truth assignment that satisfies as many clauses as possible.
The majority of researchers have adopted heuristic and metaheuristic approaches for tackling MAX-SAT as it belongs to the class of NP-hard problems [69]. It is a highly attractive research topic, as a large number of problems can be reduced to MAX-SAT, including variants of routing problems [70], protein sequence alignment [71], the max-clique problem [72], scheduling problems [73], software debugging problems [74], community detection problems [75], and many others. More examples can be found in [76].
In evaluating our COCP, we consider instances of MAX-SAT problem and address them using the sequential and parallel local search-based metaheuristics developed by L. Matijević and M. Todorović. The neighborhood is defined in a usual way: flipping the value of a propositional variable. Keeping in mind that evaluating the truth value of formula can be performed simultaneously for many truth assignments, they implemented parallel MLS and VNS metaheuristics to be executed on GPUs. In our simulation, we applied parallel MLS as it performed slightly better than parallel VNS.
All presented CO problems and the corresponding solution methods are presented in Figure 4. New problems or new variants of the same problem can be added to our COCP easily, as well as the corresponding solution methods. In addition, it is possible to add new (and potentially more efficient) solution methods for already existing CO problems. Then, miners would be able to select between different solution methods or to let the system invoke one of the available methods randomly.
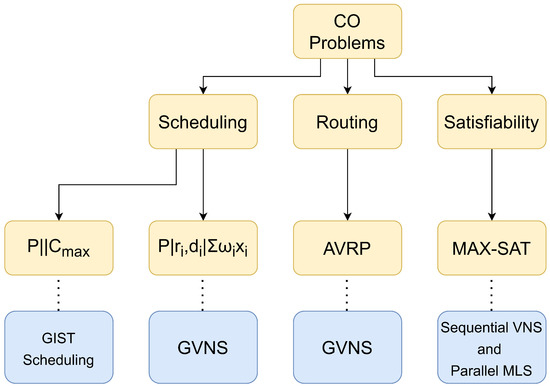
Figure 4.
Explored CO problems and corresponding solution methods.
4. Results: COCP Simulation
In this section we first describe one of the environments in which the proposed PoUW consensus protocol could be implemented, together with the selected simulation setup. To illustrate how our proposed PoUW-based consensus protocol (COCP) works, we performed simulations of the scenarios explained in Section 3.2 on a small example containing 11 blocks (denoted by B1, B2, …, B11) from the publicly available Ethereum test network Ropsten (https://ropsten.etherscan.io/ accessed on 17 May 2022). The headers of these 11 blocks are given in Appendix A.
In our simulation, we assume that it is necessary to add blocks B1–B11 in the same order as in the original sequence presented in Appendix A when executing COCP instead of the classical PoW-based consensus protocol. Although in each step the different miners can create (and even publish) different blocks, our goal was to propagate the corresponding current block from the example and to illustrate the direct benefits, as well as the side-benefits, of using our COCP. Moreover, in this simulation, we did not change the timestamp and the miner identification fields because they do not have a significant impact on the simulation results. Here, we consider all the implementation details of proposed COCP, but the comprehensive task of implementing a full-blown BC network that includes our COCP is beyond the scope of this paper.
4.1. Description of the Ethereum Platform
Ethereum represents an open distributed system, where anyone can join, participate in its functioning, and leave at any time. As in any other BC platform, every participant must have a local copy of the whole BC network, in order to prevent data loss and to maintain consistency and security. The participants in Ethereum can be basic users, verifiers, and miners with the roles already explained in Section 2. Ethereum uses “modified Merkle Patricia tries” to efficiently store transactions in blocks using their hash values. A trie, also called a Radix trie, Patricia trie, or prefix trie, is a data structure which is the fastest at finding common prefixes, simple to implement, requires a small memory, and which is thus used as a core data structure in data storage [77]. More details about the storage fundamentals of Ethereum can be found on (https://eth.wiki/ accessed on 2 June 2022).
As in other BC networks, each block in the Ethereum system consists of two main parts—the header and the body. The body of a block contains transactions and their receipts, which are processed and verified when the block is formed. The transactions and the receipts are stored in two separate trie structures. A third trie, representing the state of the system after executing transactions, is also part of the body. The header of a block contains various important data used by participants. The data stored in block’s header are given in Table 2. An example of a block’s header, taken from the Ethereum test network called Ropsten, is shown in Figure 5 in JSON format.

Table 2.
Data fields in Ethereum’s block header.

Figure 5.
An example of a block’s header.
The standard Ethereum network uses a well-known PoW consensus algorithm that is based on solving a simple yet heavily resource-demanding cryptographic puzzle. The goal of the miner is to find a certain number, the content of the nonce field of the block’s header, which yields a hash value of the block beginning with a number of zeroes specified in the difficulty field of the block. The described cryptographic puzzle actually represents the inversion of the so-called one-way function. Its value for the given arguments is easy to calculate; however, there is no efficient way to find the arguments that correspond to a given function’s value. The only way for the miner to determine the value of the nonce is by guessing. As we have already mentioned, the main drawback of this consensus algorithm is that a large quantity of computing power is used for solving a problem that has no application outside of mining a block. The role of the timestamp is important, especially in the verification process. The Ethereum whitepaper (https://ethereum.org/en/whitepaper/ accessed on 21 August 2022) states that the timestamp of the block needs to be larger than the timestamp of the parent block and smaller than the current unix time of the verifier, with allowed differences of 15 min. However, in the current implementation of the Geth client, this time difference is set to 15 s.
4.2. Simulation Setup
To specify CO problem instance data using transactions, a modification of Ethereum’s protocol is necessary in order to accommodate this new type of transaction. On the other hand, using a smart contract in Ethereum is straightforward.
For CO problem instances representing the useful part of our COCP, we selected:
- Nine instances of the problem (C_1_1, …, C_1_9);
- Ten instances of (Sched1, …, Sched10);
- Nine instances of AVRP (named EX__, where n denotes the number of customers and m stands for the number of vehicles); and
- Six examples of MAX-SAT (f600, f1000, f2000, hole8, hole10, pr150_75).
Keeping in mind that in our example we used Ethereum’s test network Ropsten, with a 10–15 s time interval between any two blocks, and we selected instances for which reasonable-quality solutions could be obtained in that amount of running time. The instances used came from companies that we worked with and from the libraries of benchmark instances for the considered CO problems from the literature.
We assumed that each mining step is performed by four miners on computers with the following characteristics: Intel Core i7-10750H CPU @ 2.60 GHz, 32 GB RAM and NVIDIA GeForce RTX 2060 with 6 GB GPU memory. The OS used on mining computers was Ubuntu 20.04, whereas the mining software was based on the latest version of the standard Ethereum Go client geth [78] and employed the same hash function keccak256 that is used by Ethereum’s PoW algorithm.
It is evident that the number of instances (34) was larger than the number of blocks in our example. This is because we wanted to make sure that all possible scenarios could be simulated by the proposed PoUW concept. Ensuring an adequate number of CO problem instances is of vital importance to ensure the correct functioning of our COCP. It is necessary that at least one instance of some CO problem is available each time the block is to be announced. Otherwise, i.e., in cases when the instance pool is empty, a hybrid variant, combining COCP with the PoW, PoS, or any other traditional consensus protocol, needs to be considered.
To establish the correspondence between the composed block and the solved CO problem instance, the two reserved fields were selected as follows: field1 was actually the nonce field, whereas field2 was selected to be mixHash. Thus, the mixHash field contained the result of the bit-wise xor operation on the CO problem instance hash and the solution hash values. To indicate the locations of input data, we simply inserted the hash value of the instance input data file name (without extension) into the nonce field. We needed to specify both these values to be able to calculate the hash value of the complete block that represented the connection between blocks in the BC network and which was stored in the header of the next added block using the parentHash field. In Appendix A, we present the changed values of the three specified fields (mixHash, nonce, and parentHash), colored in red.
4.3. Simulation Results
At the beginning of our simulation, we assumed that there were three published instances; they were enumerated starting with 0 in order to easily determine the instance that corresponded to the result of the modulo operation between (without mixHash and nonce values) and . Let the instance pool contain the following three active instances:
- 0.
- Ex_20_3
- 1.
- f1000
- 2.
- C_1_1
The instances are ordered by the publishing timestamp. We have neglected the deadlines here as the running times are reasonably small.
All four miners have created their blocks and started the mining process. However, as the number of instances is smaller than the number of miners, at least two of them must solve the same CO problem instance. Let us assume that all of them completed executions at approximately the same time, i.e., the second scenario described in Section 3.2 occurs. In addition, let us assume that block B1 is accepted for inclusion in the BC. When the operation is performed on the calculated hash value of B1, the result (2) suggests that instance C_1_1 should be considered for solving (see Figure 6). Therefore, the miner publishing B1 receives the reward coming from both sources: adding block B1 and solving instance C_1_1.
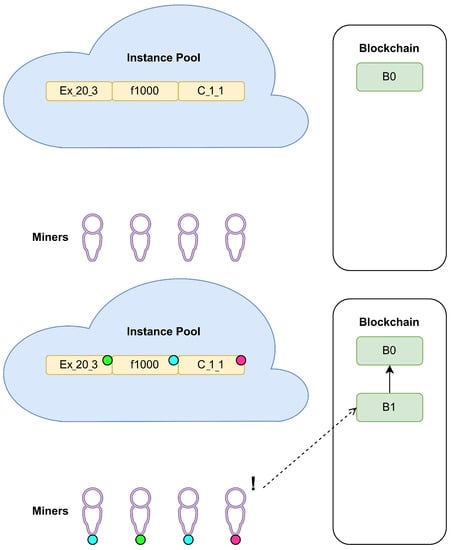
Figure 6.
An illustration of adding the first block to our BC example (B0 is a generic block required to establish BC network structure).
As the remaining instances are also solved, the rewards for their solutions should be given to the creditable miners. Please note that “solving an instance” means finding a solution that is better than the specified threshold. Suppose that instance f1000 was considered by two miners and that they provided different solutions. The miner who found a better solution would be rewarded. All instances are removed from the pool and, together with the solutions, moved to the instance archive.
While the miners were trying to add the first block, customers submitted six new instances.
- 0.
- C_1_3
- 1.
- f2000
- 2.
- Ex_22_2
- 3.
- C_1_4
- 4.
- Sched5
- 5.
- f600
For the inclusion of the second block, let us follow the first scenario. The fastest miner composed block B2 and calculated the block hash value (equal to 2), which pointed to the third available instance, Ex_22_2. After rewarding this miner, instance Ex_22_2 is moved from the pool to the archive, whereas the other considered instances are returned to the pool.
Before considering the third block, two new instances were published and the pool was composed of the following seven instances:
- 0.
- C_1_3
- 1.
- f2000
- 2.
- C_1_4
- 3.
- Sched5
- 4.
- f600
- 5.
- Sched4
- 6.
- Sched8
Let us assume that the second scenario is followed again and that four miners are considering three different instances. In addition, we assume that two miners are solving the instance f2000, corresponding to the target block B3, because . According to the second scenario, all miners found their solutions at the same time; all three instances (f2000, Sched5, and C_1_4) are regarded as solved and moved from the pool to the archive. However, for instance f2000, two different solutions are provided and, among the possible cases, we adopt the following assumptions: the miner who created B3 provided the worse solution and, after the block had been accepted, was rewarded only for adding the block to BC; the other miner (providing a solution of better quality) was rewarded for solving the CO problem instance.
After the beginning of the mining process for the fourth block, four new instances are submitted and the instance pool contains the following eight instances:
- 0.
- C_1_3
- 1.
- f600
- 2.
- Sched4
- 3.
- Sched8
- 4.
- pr150_75
- 5.
- hole10
- 6.
- Ex_25_3
- 7.
- C_1_9
Assuming the second scenario, the miners were able to solve two CO problem instances. The first one is pr150_75, which corresponds to B4, as the result of the operation applied to the block hash value is 4. The block B4 is verified and approved to be added to the BC. Therefore, a successful miner is rewarded from both sources. The second instance is Sched8, which was solved by another equally fast miner.
Having removed two instances and assuming that a new one is added, the content of our pool is now as follows:
- 0.
- C_1_3
- 1.
- f600
- 2.
- Sched4
- 3.
- hole10
- 4.
- Ex_25_3
- 5.
- C_1_9
- 6.
- Sched1
Assuming that the first scenario applies to the insertion of B5, the corresponding instance is the fifth one, as the result of the operation on the block hash value is four. The solved instance Ex_25_3 is removed from the pool and three new instances are added at the end of pool (Ex_19_2, C_1_7, and Sched7), increasing the number of active instances to nine.
- 0.
- C_1_3
- 1.
- f600
- 2.
- Sched4
- 3.
- hole10
- 4.
- C_1_9
- 5.
- Sched1
- 6.
- Ex_19_2
- 7.
- C_1_7
- 8.
- Sched7
For mining the sixth block, we assume the third scenario. Let the fastest miner solve instance Ex_19_2, and, although being aware of this information, let the two other miners decide to continue solving their instances. After only a couple of milliseconds, one of them manages to solve instance C_1_3, which, according to the operation (giving the result 0), happens to be the corresponding instance for block B6 (see the upper part of Figure 7). After the verification and synchronization process is completed, it is decided that B6 should be included in the BC. Appropriate rewards are provided to the miners and both instances are moved to the archive.
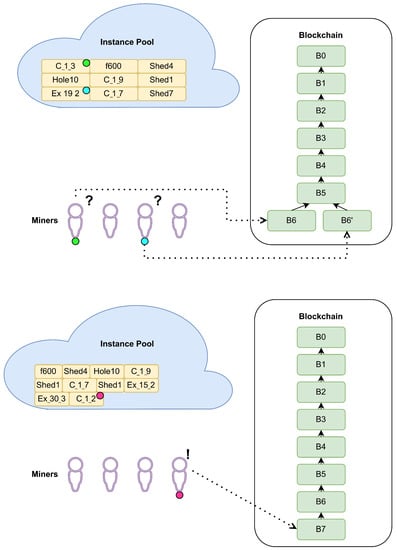
Figure 7.
Adding B6 and resolving the corresponding fork.
Before mining the seventh block, three new instances are submitted and the miners need to consider the following instance pool:
- 0.
- f600
- 1.
- Sched4
- 2.
- hole10
- 3.
- C_1_9
- 4.
- Sched1
- 5.
- C_1_7
- 6.
- Sched7
- 7.
- Ex_15_2
- 8.
- Ex_30_3
- 9.
- C_1_2
After the last instance (considering that ) is solved following the first scenario, block B7 is included in the considered BC network, as shown in the lower part of Figure 7.
In the next step, no instance is added to the pool and, before the eighth block is mined, the following instances are available in the pool:
- 0.
- f600
- 1.
- Sched4
- 2.
- hole10
- 3.
- C_1_9
- 4.
- Sched1
- 5.
- C_1_7
- 6.
- Sched7
- 7.
- Ex_15_2
- 8.
- Ex_30_3
According to scenario 2, four instances are solved at approximately the same time, C_1_9, corresponding to block B8 as . This instance resulted in both rewards being given to the miner who solved it, whereas the remaining three miners received rewards only for solving instances Sched4, Sched1, and Ex_15_2.
When the ninth block is to be mined, three instance are appended, increasing the pool size to 8:
- 0.
- f600
- 1.
- hole10
- 2.
- C_1_7
- 3.
- Sched7
- 4.
- Ex_30_3
- 5.
- Sched6
- 6.
- C_1_5
- 7.
- Sched10
In this case, we assume scenario 2 with the following outcome. The miner composing block B9 solved instance Sched7 (). The two other miners provided solutions for the instance f600, and the one reporting the better solution was rewarded. Finally, the fourth miner solved instance C_1_7, and all three instances were removed from the pool.
The next state of the instance pool is obtained by appending five new instances:
- 0.
- hole10
- 1.
- Ex_30_3
- 2.
- Sched6
- 3.
- C_1_5
- 4.
- Sched10
- 5.
- C_1_6
- 6.
- Sched2
- 7.
- Sched3
- 8.
- C_1_8
- 9.
- Sched9
Following scenario 3, the fastest miner solved instance C_1_6 as . With a slightly increased effort, two more instances (Sched6 and Ex_30_3) were solved; however, the miners collected rewards only from customers.
After the above-mentioned three instances are removed from the pool, for the mining of the last block, the following seven instances remain:
- 0.
- hole10
- 1.
- C_1_5
- 2.
- Sched10
- 3.
- Sched2
- 4.
- Sched3
- 5.
- C_1_8
- 6.
- Sched9
When mining the eleventh block, scenario 2 is applied: instance hole10 corresponds to block B11 (), whereas the solution for Sched2 is also provided without adding the corresponding block.
Meanwhile, four new instances are submitted in the pool, and our simulation of this small example is completed with the following nine active instances:
- 0.
- C_1_5
- 1.
- Sched10
- 2.
- Sched3
- 3.
- C_1_8
- 4.
- Sched9
- 5.
- Ex_26_2
- 6.
- Ex_35_3
- 7.
- hole8
- 8.
- Ex_31_2
However, in the real case, new blocks and new instances need to be created continuously.
5. Discussion
5.1. Comments on Simulation Results
In Table 3 we summarize the results and here we provide a point-by-point discussion of the takeaways of the simulation. Each row of Table 3 corresponds to the inclusion of one block into the BC. The block identification is presented in the first column. The state of an instance pool is given in the second column, whereas the third column contains the list of solved instances with the solution time, presented in brackets. The instance corresponding to the added block is presented in bold. The cumulative number of solved instances is given in the last column.

Table 3.
Summary of simulation results.
From the performed simulation, as summarized in Table 3, it can be seen that we solved 25 instances of various CO problems while adding the considered 11 blocks. Due to the fact that the times required for solving instances were almost negligible, their influence on the decision to accept the block were not the most significant. The time at which the miner started the mining process, as well as the duration of the verification and synchronization processes, were the dominant factors when deciding on the block to be included in the BC.
We cannot precisely compute the energy savings because we do not have knowledge about the computational power required to build (mine) the corresponding 11 blocks in the original part taken from the Ropsten test network. Moreover, the results that we presented might not be repeatable due to the distributed and stochastic nature of the mining process. However, the benefits of our approach are clearly evident from the fact that the employed resources enable not only the addition of new blocks, but also the solution of some real-life CO problem instances provided by customers.
The described process can be performed as long as there are instances to be solved and blocks to be added. In this simulation, we assumed that there was an adequate number of instances. Otherwise, the classical PoW or some other type of consensus protocol should be performed. It is always possible that some miners may prefer to execute the PoW process rather than the PoUW process, even if the pool of instances is not empty. Therefore, the hybrid variant may be an appropriate approach and, although it is out of the scope of this paper, we believe that its realization would be straightforward.
5.2. Challenges
In order to develop a successful PoUW consensus protocol, it is necessary to consider the challenges that we addressed throughout our work. Table 4 summarizes the challenges and we provide a point-by-point discussion below of the challenges and how each of them was resolved.

Table 4.
Summary of identified challenges.
- 1.
- Submission PrivilegesDescription: In some of the papers considering PoUW-based consensus protocols, there is a special type of user that can submit CO problem instances. They need to provide problem input data and incentives for the miners who solve them.Challenge resolution: We introduced a new category of users, customers, who pay to obtain high-quality solutions for the provided instances of real-life CO problems. Thus, we resolved challenge 1 regarding who is allowed to submit the CO problem instances. Customers can play any other role in the BC network; specifically, they could be considered basic users, because their payments should represent regular BC transactions.
- 2.
- Problem RangeDescription: The majority of prior papers considered a particular CO problem (e.g., TSP) for which the structure of the input data was known (i.e., the number of cities, distances between them, and optionally the pickup/delivery quantities, etc.). However, such an approach is very limited and the inclusion of various CO problems in these considerations may be more beneficial. On the other hand, in such a case, a proper user interface differentiating input data for distinct CO problems, as well as the corresponding solution methods, should be provided. In [8,10] the authors proposed the use of a generic solution framework that can accommodate numerous CO problems. This approach requires a pre-processing step in which the submitted CO problem instance is transformed into the form that is accepted by the generic framework.Challenge resolution: We envisioned that customers could submit instances of any CO problem of their choosing. The reasoning behind a resolution of challenge 2 in this manner is the fact that the number of clients requiring solutions for an instance of any particular problem may be negligible, whereas the number of CO problems and their variants is limitless for all practical purposes. In our COCP framework, CO problem instances are specified by a special kind of transaction or by a smart contract containing all the information necessary to decode which CO problem is to be considered and to select the appropriate solution method. We also envision the ease of appending new modules for different types or variants of CO problems. Expecting customers to provide algorithms for their CO problems (as is suggested in [9]) is reasonable only for scientific purposes. Otherwise, it is necessary to provide efficient solution methods as a part of the BC software system. Numerous optimization methods are available in open-source formats on the Internet.
- 3.
- Problem–Block CorrespondenceDescription: In the classical PoW, the nonce represents an adequate correspondence between the composed block and the work performed by the miner to publish it. When the PoUW is applied, this correspondence should be substituted by selecting an adequate submitted CO problem instance. It is important that the block structure refers to exactly one of the submitted instances. Some authors [8,10] use a nonce value (with the original meaning) to prove that a large number of solutions has been visited before an attempt to publish a composed block.Challenge resolution: When a pool of various instances is established, resolving challenge 3 involves choosing the instance that corresponds to the composed block, mimicking the connection between the hash value of a block and the nonce in the PoW-based consensus protocols. Only in a few papers in the literature is this correspondence problem mentioned; however, no adequate solution has been provided. The authors in [10] assumed that each instance has priority and the miners selected instances in accordance with that priority without specifying any more details. In [9] the authors suggested always dealing with a set of instances, rather than using only one. The authors also included mini-blocks that are put between actual blocks and each of them corresponds to one of the CO problem instances; however, the precise matching method is not provided.We resolved this challenge by performing a modulo operation between the hash value of the composed block and the number of instances currently available in the instance pool. Note that resolving this challenge also makes it very difficult, if not impossible, for a miner to choose instances to work on at will. The state of the instance pool at any moment should be common knowledge among all the BC participants. This is easy to ensure, bearing in mind that each instance has a timestamp marking the time of its submission. To ensure diversity in the block–instance correspondence, the number of instances in the pool has to be at least as large as the number of miners. This requirement is not strict: COCP can work correctly even if it is not fulfilled.
- 4.
- Ensuring UsefulnessDescription: The number of submitted CO problem instances must be as large as possible so that different blocks always correspond to different CO instances. In addition, the number of miners solving the same instance (during the process of mining a new block) decreases and the expected time for solving the corresponding CO problem instance increases. To estimate the number of required CO instances, we considered several use cases. The Bitcoin block insertion frequency is 10–15 min, and we require at least four to six instances per hour, i.e., 96–144 instances per day to ensure an instance for each inserted block. In some of the Ethereum BC systems, blocks are inserted every 10–15 s, and we need to provide 240–360 instances per hour. To the best of our knowledge, this problem has not been discussed in the relevant literature.Challenge resolution: The number of customers who would provide instances in a timely fashion is very important if we want COCP to perform useful work at all times. Customers such as delivery services (providing instances of various vehicle routing problems, especially in urban logistics), production companies, VLSI producers (who model the layout and connections between components through instances of the (MAX-)SAT problem), team builders or advertisers (who need to group their users into compact clusters/communities), and schedulers for cloud resources (especially when relatively small computing equipment has been rented for the execution of a large number of simple tasks), could jointly generate large numbers of instances. However, if we face a lack of CO problem instances we could generate classical cryptographic puzzles to represent CO problem instances and increase the instance pool.
- 5.
- Controlling HardnessDescription: It is very important to consider the trade-offs involved in keeping the complexities (i.e., the expected solution times) of all submitted CO problem instances very similar, even though it is very difficult to predict their complexities in advance. If miners obtain instances of lower complexity they might have a higher chance of solving the corresponding instance and obtaining an award. However, solving easy instances could be useful in some cases.Challenge resolution: In our study we assumed that both hard and easy instances were important for customers. Easy instances can be solved quickly and the solution could be provided to customers faster than if the instance was hard. The corresponding miners are rewarded accordingly. It may happen that some of the submitted CO problem instances are very hard, preventing the miners from solve them efficiently and thus introducing latency into the PoUW consensus protocol. However, in the PoUW it is not important to obtain an optimal solution of the considered CO instance. One of the input data corresponds to the solution threshold, i.e., the bound on the desired objective function value. For example, if we are addressing an instance of the TSP problem, the customer should specify the largest acceptable length of the resulting tour. As soon as the miner finds a solution with an objective function smaller than the given threshold, they can publish the corresponding block. If the instance is too hard and is not solved before another block is announced, it is returned to the instance pool for another solution attempt (as explained in Section 3.1). Solution methods are usually stochastic heuristics methods and each run may provide a different outcome. Each instance can be granted multiple solution attempts as long as its deadline is not passed. If the time required to obtain the desired quality solution is over the deadline, the instance is removed from the instance pool, and the customer may submit the instance again with an adjusted deadline value. To decrease the number of unusable instances, the optimization methods must be implemented in such a way as to accept the current best-known solution as an input parameter, i.e., to enable the continuation of the solution process. In such a way, it is possible to increase the time allowed to solve extremely hard instances. In general, NP-hard problems do not become easier when a good solution candidate is provided. However, in some cases it could help to solve them faster and make it possible to decrease the number of unusable instances.To be able to guarantee that the blocks are added in an approximately regular time interval, we set the stopping criterion of heuristic algorithms to the maximum CPU time, calculated in correspondence with the block insertion frequency. As the mining process is highly concurrent, we expect that at least one miner will be able to solve the instance within the given CPU time limit. However, if some of the instances are too easy, the corresponding blocks may be added more frequently. Therefore, we plan to include an instance pre-processing phase, in which an estimation of its hardness will be performed. This phase would enable us to balance the work of miners by requiring them to solve one hard instance or a group of several easy instances. The estimation of instance hardness is related to predicting the performance of stochastic heuristic algorithms. It is not an easy task; however, it has been studied by the CO research community and some results have already been published. It has been shown in the literature that stochastic (randomized) algorithms (solution methods based on a random number generator) exhibit exponential run-time distributions [79]. The question of predicting the performance of such algorithms is addressed by building so-called empirical hardness models, which take into account the parameters/features of the corresponding hard CO problem instances, as well as the algorithm’s parameter settings. A comprehensive review of different instance features and models can be found in [80]. The application of these methods in practice is a part of ongoing work.The lack of a pre-processing phase for the estimation of the instance hardness does not impede the proposed framework. Although some miners may need to solve easier instances, and some miners need to solve harder ones, the robustness of the system to this is the same as the robustness of the classic PoW regarding the luck of some miners.In order to prove that the miners invested a certain amount of work when executing the proof-of-solution consensus protocol, in [9] it was necessary to calculate the hash value of each solution and use it as a nonce in the classical PoW sense. This means that the miner had to evaluate as many solutions as was necessary to find the proper nonce value. In our approach, it is possible to use the number of objective function evaluations as the stopping criterion for the applied optimization method and to obtain a similar effect.
- 6.
- Efficient Hardware ExploitationDescription: In the classical PoW, the miners perform a large number of simple operations and they are equipped with suitable hardware resources. On the other hand, dealing with the selected CO problem instances in PoUW-based consensus protocols does not exploit hardware resources that are usually owned by a typical miner.Challenge resolution: Dealing with the selected CO problem usually does not require any special resources that are considered standard in the classical BC networks. Therefore, it may occur that the miners cannot engage their existing expensive hardware resources. In the literature, it has been suggested to implement a hybrid approach (involving both the PoW and the PoUW methods) and to allow miners to decide which consensus protocol they want to use. In order to increase their rewards, miners are motivated to use the PoUW approach (i.e., to select and solve an instance from the pool). We propose considering an alternative approach: To develop optimization algorithms suitable for execution on the hardware already owned by miners. For example, we developed a GPU-based metaheuristic approach to the MAX-SAT problem.
- 7.
- Data Management and Malicious BehaviorDescription: Some of the BC data security issues with respect to the malicious behavior of users include changing input or solution data and introducing confusion between an instance and its solution, stealing a solution from a successful miner, selfish mining, announcing a new block before obtaining a valid solution and hoping that the solution will be ready while the verifiers approve the block, and accessing instances and solutions from the archive.Challenge resolution: Regarding BC data security issues, we focused on the parts we introduced: input data and solution data for CO problem instances. Both data types can be very large and are thus not included in blocks of the BC system. Instead, they are stored in some public location that is accessible to everyone. For the input data, the location address is provided and included in the corresponding block via a transaction or via a smart contract. Upon finding a valid solution, the miner stores it in a private location, which is predefined and known to all participants. The name of the file containing the solution is the same as the name of a file with the instance input data and the solution file is always read-only. In addition to the input data location, the miner stores a pointer to the transaction or a smart contract that corresponds to the solved CO problem instance in the nonce field of the block’s header, enabling all participants to access its input data.The first example of data security issue involves preventing miners from performing selfish mining and other types of known frauds [81,82]. For example, miners could play the role of a customer and submit instances for which they already have high-quality solutions with the aim of composing and adding blocks to the BC without much effort. This is strongly discouraged by providing an adequate number of CO problem instances. Namely, when the number of instances in the pool is adequate, the effort needed to compose the block corresponding to any particular instance is very similar to the effort needed to solve the instance. Additionally, this is further discouraged as the malevolent miner must form a block that would provide a hash value that would pair up with the index of the instance that they posted, after applying the modulo operation. This is a difficult task to complete because the hash value of the block cannot be predicted and must always be calculated. In addition, the index of the problem may change over time because the content of the instance pool may be updated. It should also be noted that the malevolent miner cannot form the block in advance that pairs up with his instance, as he will not know the index of the instance until the instance enters the instance pool, which happens only when the transaction with the instance enters the BC. Moreover, the cost of announcing a CO problem instance is greater than the reward provided for its solution.The same argument holds for an attempt by a malicious miner to steal a solution from another miner and announce it as their own.The miner could try to announce a new block before obtaining a valid solution, hoping to obtain a valid solution before the verifiers approve the block. To prevent this security issue, the published block should contain both the hash value of the instance input data and of the solution in field2 (the mixHash field in our example).Some malicious users may try to change the input data of the CO problem instance and introduce confusion between instance and its solution. To prevent this security issue, a hash value of the problem data is stored in the transaction. Thus, any change can be detected by comparing this hash value with the one calculated from the file pointed by the location address.In the process of block verification, the verifiers access the instance data via the information provided in the field1 field and the solution obtained from the miner’s private location. Verification consists of reconstructing the hash value of the solution from field2 by performing the xor operation with the CO problem instance’s hash. Additionally, they check whether the miner ID corresponds to the miner ID associated with the solution saved in the instance archive. After this is completed, the verifier has all the data needed to validate the block. The hash value of the CO problem instance is calculated based on the instance data from the pool and compared with the corresponding hash value provided by the customer. On the other hand, the reconstructed hash of the solution is compared with the hash value calculated from the solution itself. If any pair of hashes does not contain the same values, we can detect malicious behavior and discard the corresponding block.To provide unhindered access to the solved CO problem instances and their solutions, the instance archive must be implemented in a distributed manner. Each instance and solution that are stored must be available at any time to the BC users because they need to perform mining and verification. There are already some distributed storage solutions that may be suitable for hosting the instance archive, such as SWARM (https://www.ethswarm.org/ accessed on 4 August 2022) and the InterPlanetary File System (https://ipfs.tech/ accessed on 4 August 2022). Both of these systems divide files into chunks and store multiple copies on various nodes, providing stable access to stored files that are resistant to tampering.
- 8.
- Increasing EfficiencyDescription: Distributed computing may significantly increase the efficiency of PoUW-based consensus protocols; however, this requires proper (parallel) optimization algorithms. Another type of distributed mining involves cooperation between miners in so-called pools of miners, specifically, a number of miners can team up in order to solve mining problems together and split the rewards accordingly. The main issue related to pools of miners considers the honesty of each pool member in maximally contributing toward the joint work. A dishonest miner could announce the solution as their own or even sell the solution to another mining pool.Challenge resolution: Distributed computing may significantly increase the efficiency of PoUW-based consensus protocols, however, this requires proper (parallel) optimization algorithms. Developing parallel optimization methods, both exact and heuristic, is a very fruitful field of research and the resulting algorithms can be efficiently used in COCP framework.Another type of distributed mining involves cooperation between the miners in so-called pools of miners, as considered in scenario 4: a group of miners can decide to work together and use their resources in order to find a solution to the mining problem and split the reward. These pools have an entity called a pool manager who forms a block and passes tasks to members of the pool for completion in order to mine the block. When the block is mined, the whole mining pool receives a reward which needs to be shared among its members based on the pool’s policy. Pools can have different policies, but they can be divided in two basic groups. One group consists of policies where the members of the pool receive payments immediately after completing a task given by the pool manager, whereas the policies of the other group split the reward of the mined block to the members based on the amount of the tasks they have solved. However, pool mining can have some drawbacks. First of all, the miners who join a pool must follow the decisions of the mining pool, and cannot make decisions by themselves when it comes to mining. Members of a pool also depend on the pool manager, who may be malicious, which may harm them. On the other hand, some of the members of the pool may exhibit malicious behavior, such as announcing the solution as their own or even selling the solution to another mining pool. Although this is a very important issue regarding the maintenance of the BC, it is outside the scope of our current research.
6. Conclusions
We have presented a new consensus protocol of the proof-of-useful-work (PoUW) type that is based on solving real-life instances of combinatorial optimization (CO) problems instead of traditional cryptographic puzzles. We named the protocol the combinatorial optimization consensus protocol (COCP). The main advantage of COCP is the efficient utilization of computing resources. The new type of blockchain user (entity), the customer, is introduced. These users can be organizations or companies that deal with optimization tasks in their everyday business.
We performed a simulation of a PoUW-based blockchain network to explore the COCP concept, using a small example consisting of 11 blocks from the publicly available Ethereum Ropsten network. The inclusion of each block was performed according to one of the possible scenarios that could occur during the block mining process. Our simulation illustrated the benefits of COCP over the classical PoW approach. As a result of our literature review and protocol implementation, we identified several challenges that should be resolved in order to implement a useful, secure, and efficient PoUW consensus protocol. We described these challenges, as well as the ways to resolve them.
In our future work, we plan to conduct a comprehensive implementation of an entire blockchain system that will include our consensus protocol and to increase its efficiency by designing a pool of miners so that miners can cooperate while solving combinatorial problems.
Author Contributions
Conceptualization, T.D., D.U. and D.R.; methodology, T.D., D.U., M.T. and D.R.; software, M.T. and L.M.; validation, T.D., T.J.K., D.U., M.T., L.M., Đ.J. and D.R.; formal analysis, M.T., T.D. and D.R.; investigation, M.T. and L.M.; resources, M.T., L.M. and D.R.; data curation, M.T. and L.M.; writing—original draft preparation, D.U., T.J.K., T.D. and D.R.; writing—review and editing, T.J.K., T.D., D.R. and Đ.J.; visualization, Đ.J.; supervision, T.D.; project administration, T.D.; funding acquisition, T.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded by the Serbian Ministry of Education, Science and Technological Development, Agreement No. 451-03-9/2021-14/200029 and by the Science Fund of Republic of Serbia, under the project “Advanced Artificial Intelligence Techniques for Analysis and Design of System Components Based on Trustworthy BlockChain Technology (AI4TrustBC)”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Instances of combinatorial optimization problems are available at https://github.com/frostymuaddib/symmetry-pouw-problems. All other data can be recovered from the article.
Acknowledgments
This project has been supported by Penn State Great Valley Big Data Lab. The authors would like to express their gratitude to the anonymous reviewers for their valuable comments and suggestions that helped us significantly improve our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and acronyms are used in this manuscript:
| ANN | Artificial neural network |
| ASIC | Application-specific integrated circuit |
| AVRP | Asymmetric vehicle routing problem |
| BC | BlockChain |
| BFT | Byzantine fault tolerance |
| CNF | Conjunctive normal form |
| CO | Combinatorial optimization |
| COCP | Combinatorial optimization consensus protocol |
| CPU | Central processing unit |
| DG | Directed graph |
| DIPS | Difficulty-based incentives for problem solving |
| DPLS | Doubly parallel local search |
| DPS | Distributed problem solving |
| GPU | Graphics processing unit |
| GRASP | Greedy randomized adaptive search procedure |
| GVNS | General variable neighborhood search |
| IoT | Internet-of-Things |
| MAX-SAT | Maximum satisfiability problem |
| MILP | Mixed integer linear programming |
| ML | Machine learning |
| MLS | Multistart local search |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| P2P | Peer-to-Peer |
| PCC | Proof-of-Collatz conjecture |
| PII | Personally identifiable information |
| PoA | Proof-of-authority |
| PoAc | Proof-of-activity |
| PoB | Proof-of-burn |
| PoC | Proof-of-capacity |
| PoCo | Proof-of-concept |
| PoET | Proof-of-elapsed-time |
| PoI | Proof-of-importance |
| PoS | Proof-of-stake |
| PoS | Proof-of-stake |
| PoUW | Proof-of-useful-work |
| PoW | Proof-of-work |
| TSP | Traveling salesman problem |
| VLSI | Very-large-scale integration |
| VRP | Vehicle routing problem |
Appendix A. The Considered BC Example
The eleven original consecutive blocks obtained from Ethereum’s test network Ropsten, given in the JSON format. The red color indicates the changed values of the corresponding fields received for the same blocks when they were mined in the proposed COCP.

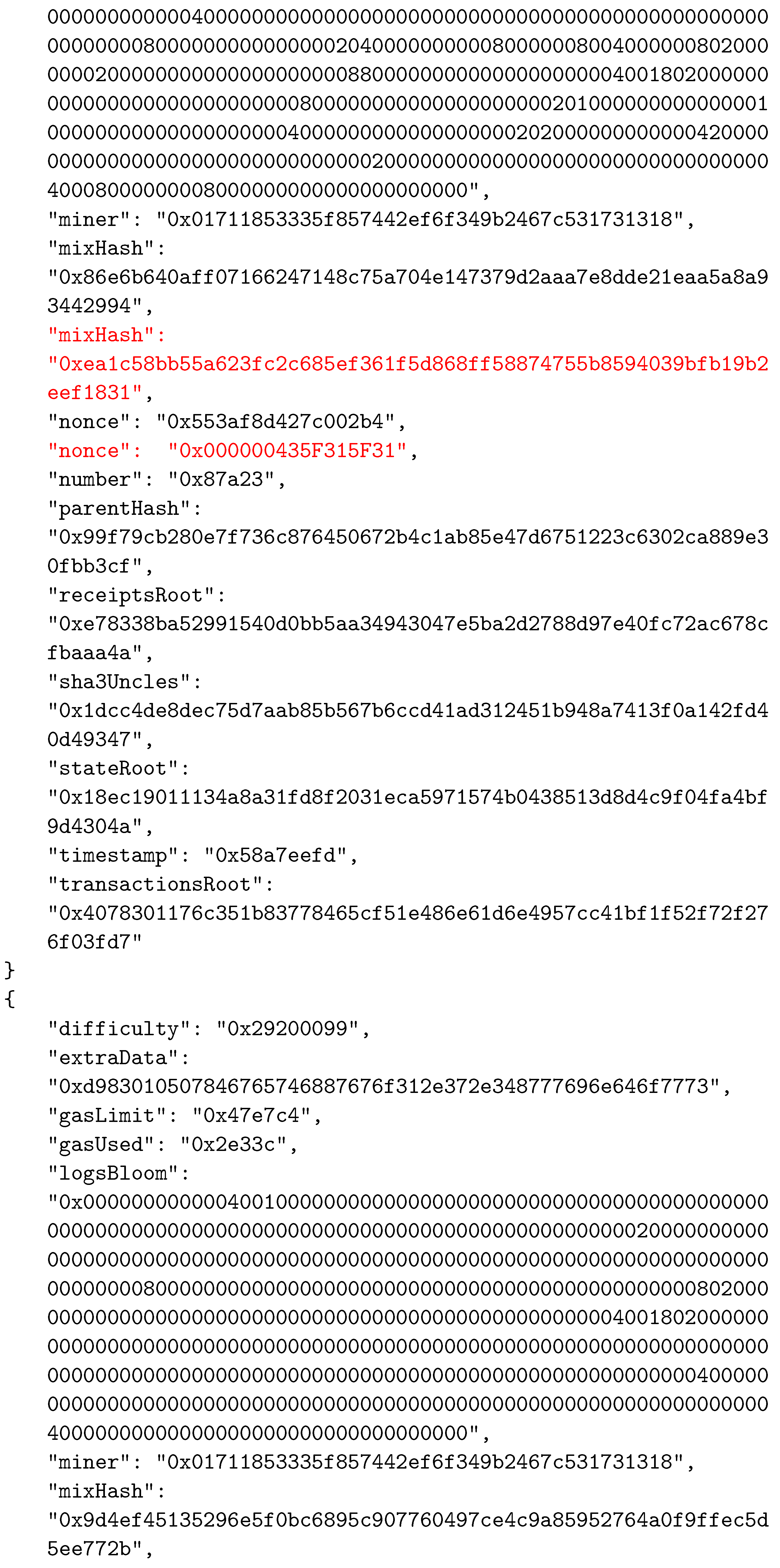

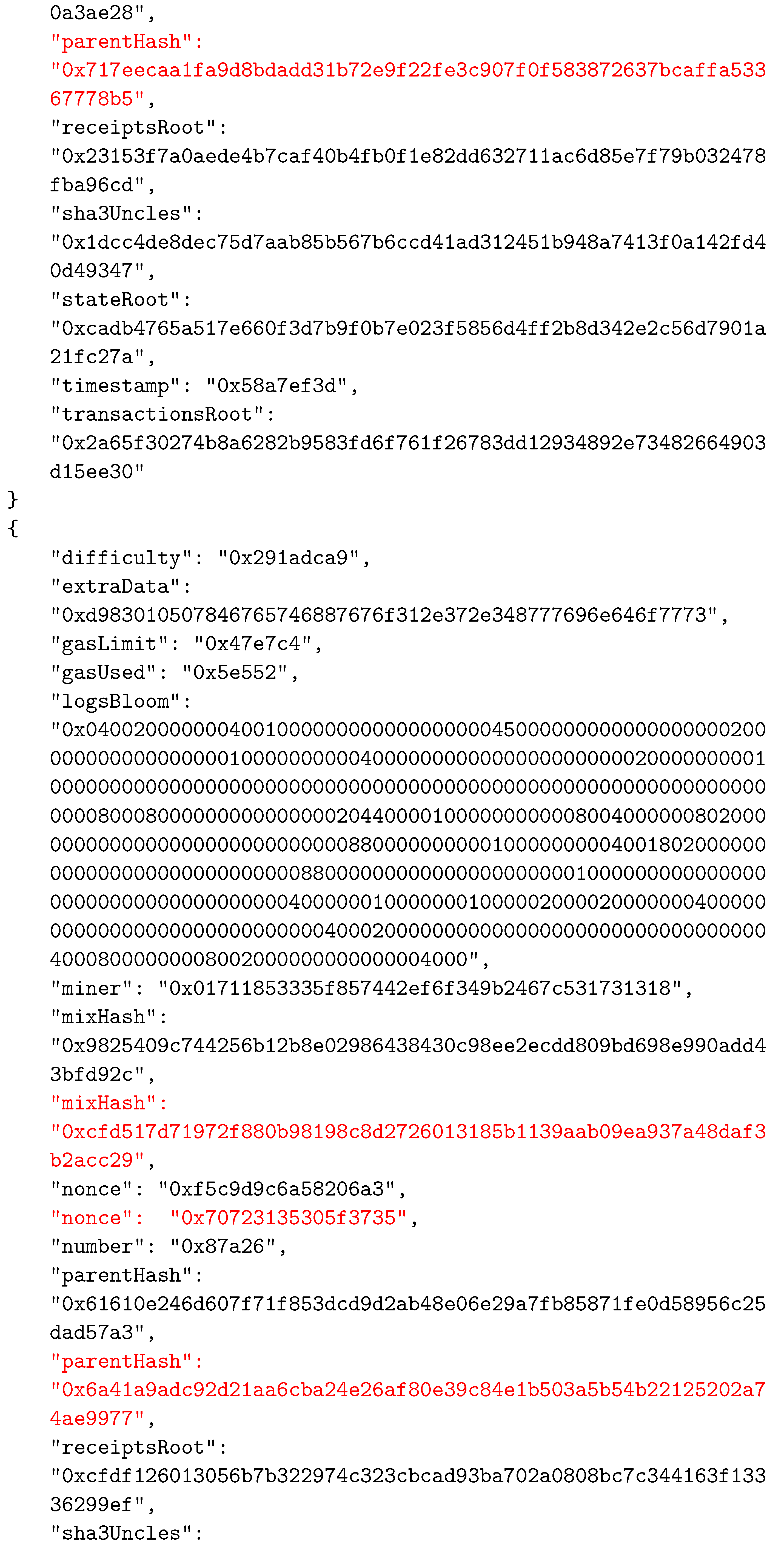
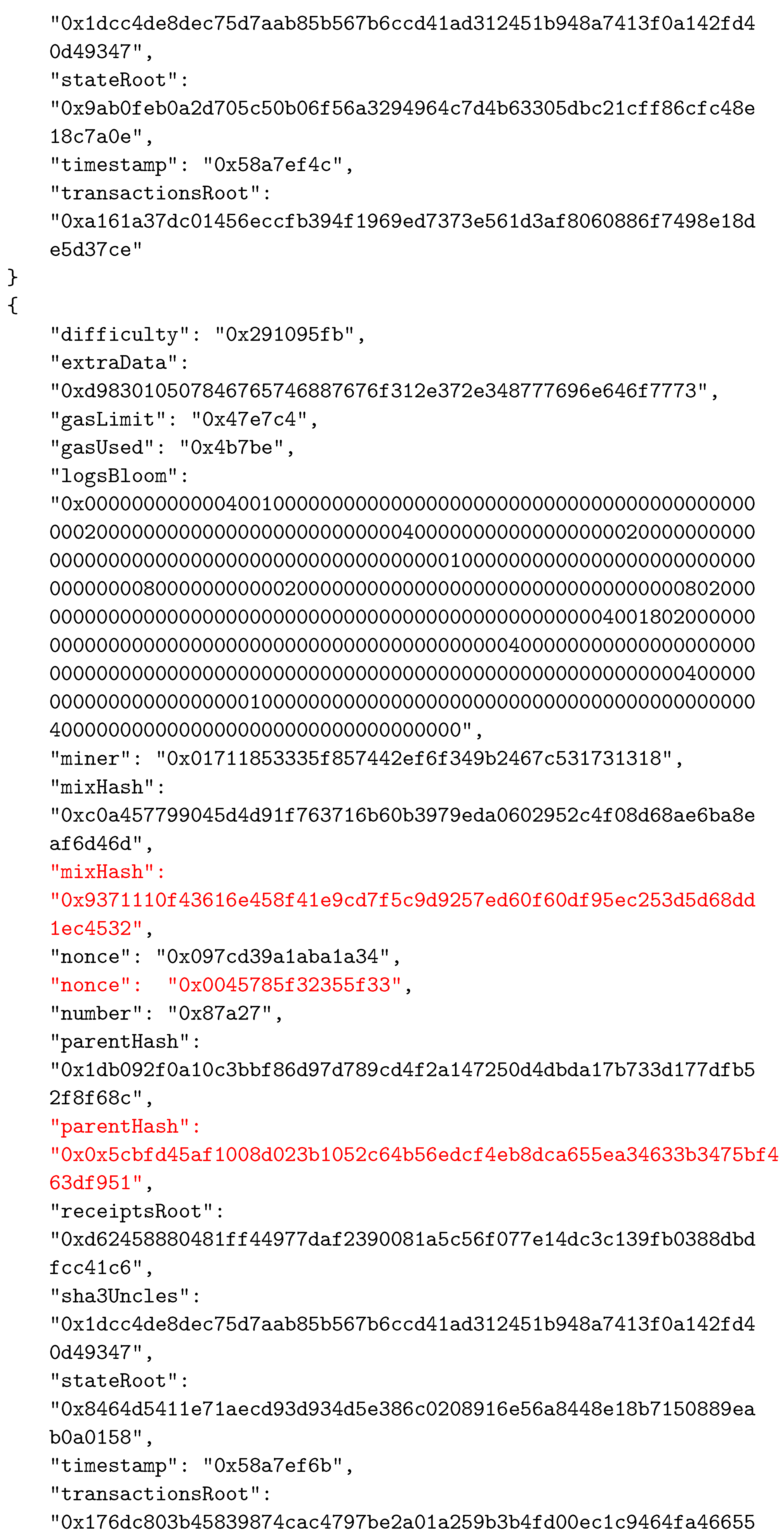
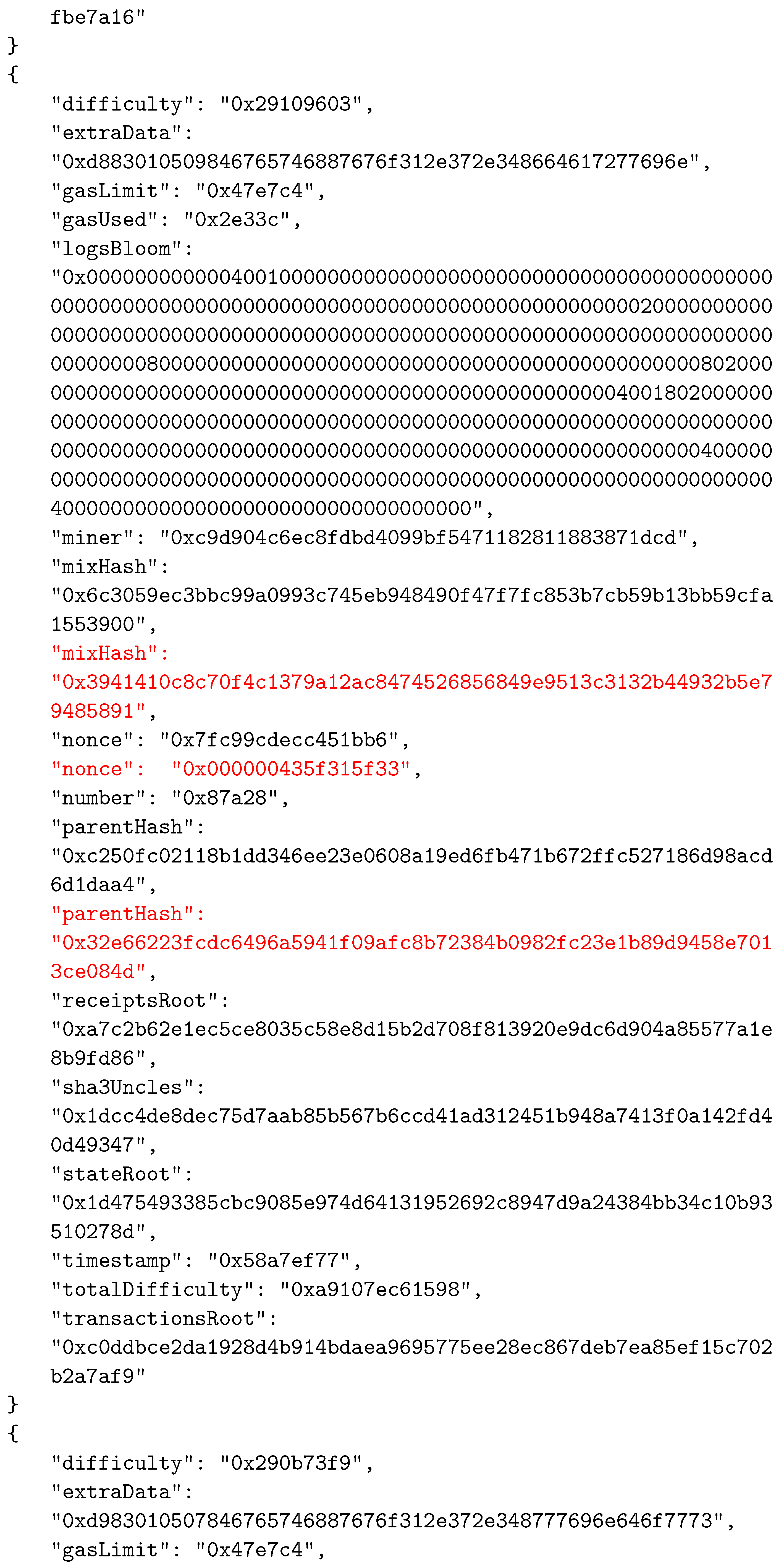

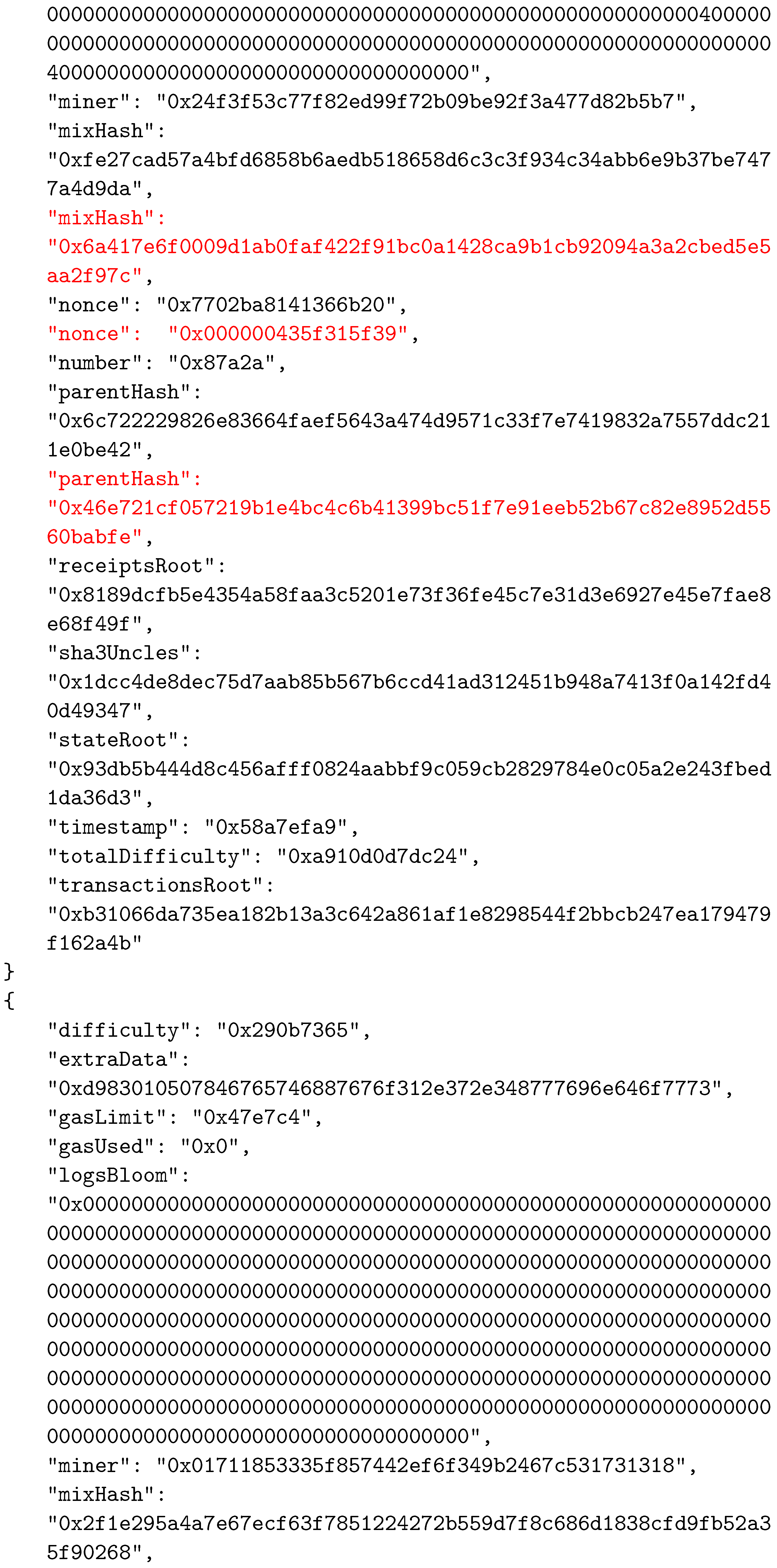
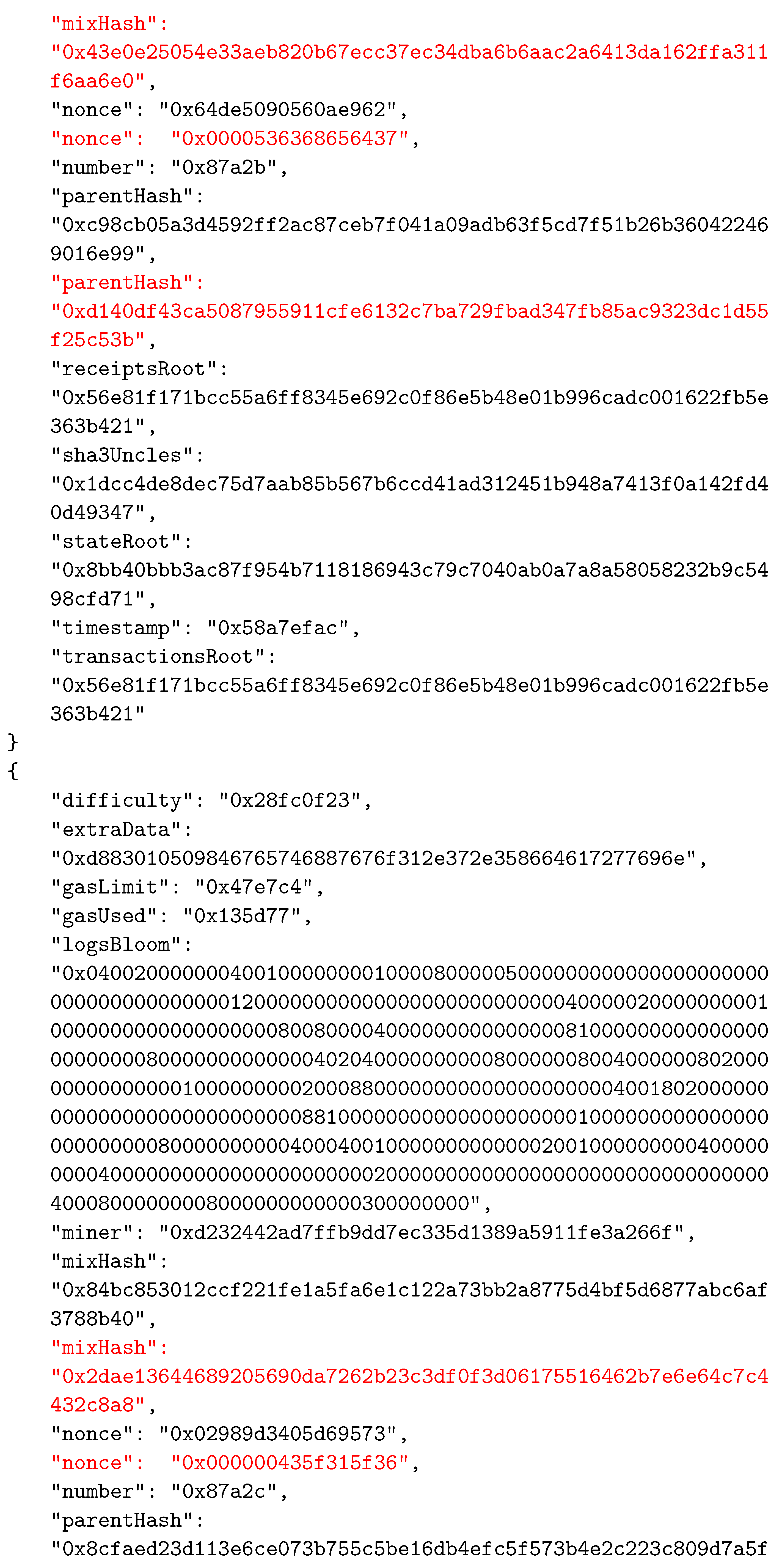
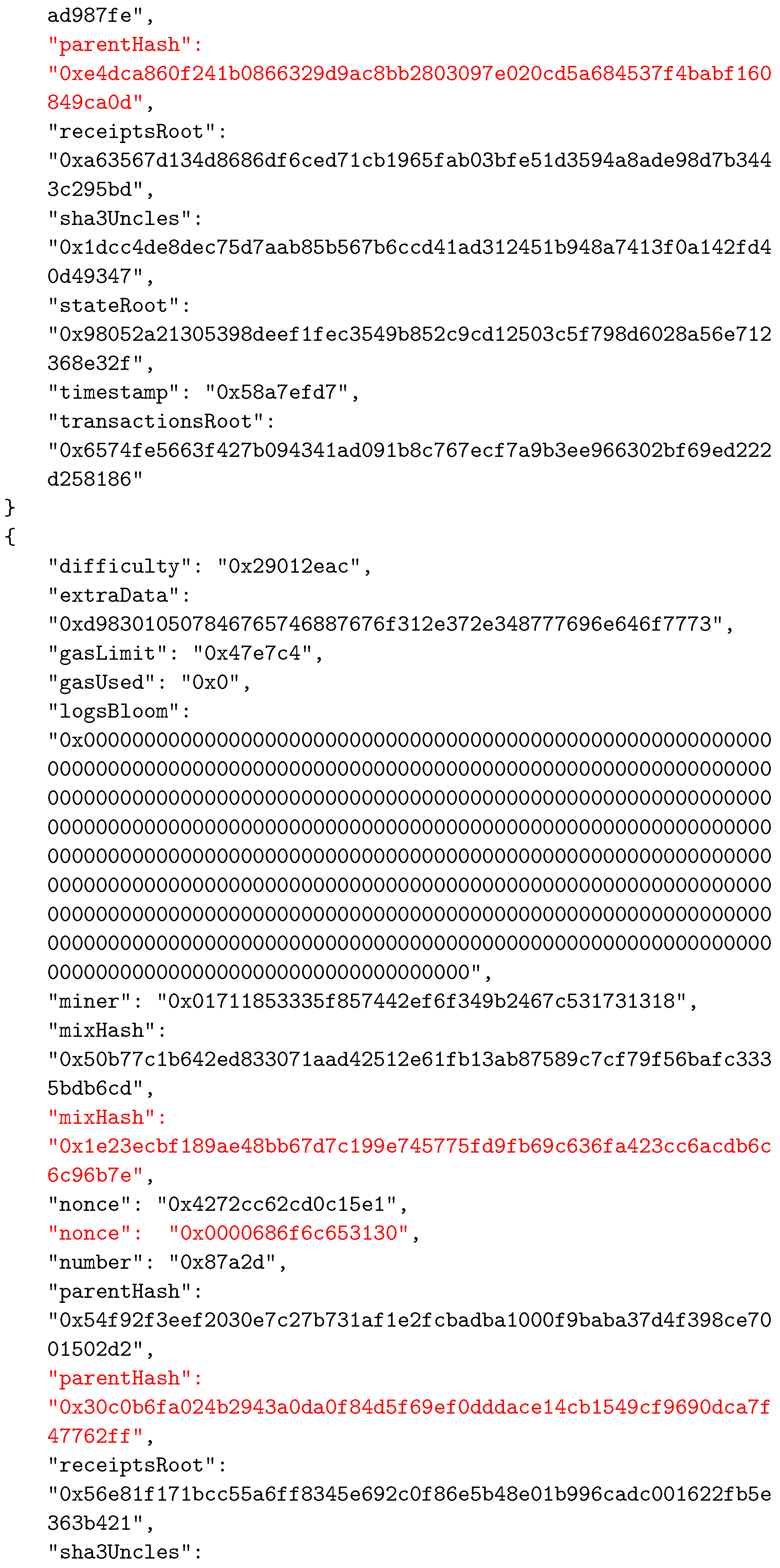

References
- Nakamoto, S. Bitcoin: A Peer-To-Peer Electronic Cash System. 2008. Available online: https://nakamotoinstitute.org/bitcoin/ (accessed on 12 May 2022).
- Yli-Huumo, J.; Ko, D.; Choi, S.; Park, S.; Smolander, K. Where is current research on blockchain technology?—A systematic review. PLoS ONE 2016, 11, e0163477. [Google Scholar] [CrossRef] [PubMed]
- Erbguth, J. Literature Review on Blockchain and Democracy. Available online: https://www.academia.edu/39122357/_Blockchain_and_democracy_by_J%C3%B6rn_Erbguth (accessed on 19 May 2022).
- Ali, M.; Ismail, A.; Elgohary, H.; Darwish, S.; Mesbah, S. A Procedure for Tracing Chain of Custody in Digital Image Forensics: A Paradigm Based on Grey Hash and Blockchain. Symmetry 2022, 14, 334. [Google Scholar] [CrossRef]
- Treiblmaier, H. Toward more rigorous blockchain research: Recommendations for writing blockchain case studies. In Blockchain and Distributed Ledger Technology Use Cases; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–31. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An overview of blockchain technology: Architecture, consensus, and future trends. In Proceedings of the IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar]
- McGinn, D.; McIlwraith, D.; Guo, Y. Towards open data blockchain analytics: A Bitcoin perspective. R. Soc. Open Sci. 2018, 5, 180298. [Google Scholar] [CrossRef] [PubMed]
- Fitzi, M.; Kiayias, A.; Panagiotakos, G.; Russell, A. Ofelimos: Combinatorial Optimization via Proof-of-Useful-WorknA Provably Secure Blockchain Protocol. IACR Cryptology ePrint Archive. 2021. Available online: https://eprint.iacr.org/2021/1379.pdf (accessed on 14 May 2022).
- Shibata, N. Proof-of-search: Combining blockchain consensus formation with solving optimization problems. IEEE Access 2019, 7, 172994–173006. [Google Scholar] [CrossRef]
- Ball, M.; Rosen, A.; Sabin, M.; Vasudevan, P.N. Proofs of Useful Work. IACR Cryptology ePrint Archive. 2017. Available online: https://eprint.iacr.org/2017/203.pdf (accessed on 4 June 2022).
- Mihaljević, M.J. A Security Enhanced Encryption Scheme and Evaluation of Its Cryptographic Security. Entropy 2019, 21, 701. [Google Scholar] [CrossRef]
- Bamakan, S.M.H.; Motavali, A.; Bondarti, A.B. A survey of blockchain consensus algorithms performance evaluation criteria. Expert Syst. Appl. 2020, 154, 113385. [Google Scholar] [CrossRef]
- Salah, K.; Rehman, M.H.U.; Nizamuddin, N.; Al-Fuqaha, A. Blockchain for AI: Review and open research challenges. IEEE Access 2019, 7, 10127–10149. [Google Scholar] [CrossRef]
- Oyinloye, D.P.; Teh, J.S.; Jamil, N.; Alawida, M. Blockchain Consensus: An Overview of Alternative Protocols. Symmetry 2021, 13, 1363. [Google Scholar] [CrossRef]
- Haouari, M.; Mhiri, M.; El-Masri, M.; Al-Yafi, K. A novel proof of useful work for a blockchain storing transportation transactions. Inf. Process. Manag. 2022, 59, 102749. [Google Scholar] [CrossRef]
- Turner, A.; Irwin, A.S.M. Bitcoin transactions: A digital discovery of illicit activity on the blockchain. J. Financ. Crime 2018, 25, 109–130. [Google Scholar] [CrossRef]
- FBI. Bitcoin Virtual Currency: Unique Features Present Distinct Challenges for Deterring Illicit Activity; Technical Report; Federal Bureau of Investigation, Report from the: Directorate of Intelligence; Cyber Intelligence Section and Criminal Intelligence Section: Washington, DC, USA, 2012. [Google Scholar]
- Raeesi, R. The Silk Road, Bitcoins and the global prohibition regime on the international trade in illicit drugs: Can this storm be weathered? Glendon J. Int. Stud. D’ÉTudes Int. Glendon 2015, 2, 8. [Google Scholar]
- Meiklejohn, S.; Pomarole, M.; Jordan, G.; Levchenko, K.; McCoy, D.; Voelker, G.M.; Savage, S. A fistful of bitcoins: Characterizing payments among men with no names. In Proceedings of the 2013 Conference on Internet Measurement Conference, Barcelona, Spain, 23–25 October 2013; pp. 127–140. [Google Scholar]
- Gonzalez, D.; Hayajneh, T. Detection and prevention of crypto-ransomware. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 472–478. [Google Scholar]
- Reid, F.; Harrigan, M. An Analysis of Anonymity in the Bitcoin System. In Security and Privacy in Social Networks; Springer: Berlin/Heidelberg, Germany, 2013; pp. 197–223. [Google Scholar]
- Chawathe, S.S. Clustering blockchain data. In Clustering Methods for Big Data Analytics; Springer: Cham, Switzerland, 2019; pp. 43–72. [Google Scholar]
- Ober, M.; Katzenbeisser, S.; Hamacher, K. Structure and anonymity of the bitcoin transaction graph. Future Internet 2013, 5, 237–250. [Google Scholar] [CrossRef]
- Otte, P.; de Vos, M.; Pouwelse, J. TrustChain: A Sybil-resistant scalable blockchain. Future Gener. Comput. Syst. 2020, 107, 770–780. [Google Scholar] [CrossRef]
- Ramljak, D.; Davidović, T.; Urošević, D.; Jakšić Krüger, T.; Matijević, L.; Todorović, M.; Jovanović, D. Combinatorial optimization for self contained blockchain: An example of useful synergy. In Proceedings of the XLVIII Symposium on Operational Research (SYM-OP-IS 2021), Banja Koviljača, Serbia, 20–23 September 2021; pp. 285–290. [Google Scholar]
- Drescher, D. Blockchain Basics: A Non-Technical Introduction in 25 Steps; Apress: New York, NY, USA, 2017. [Google Scholar]
- Lasla, N.; Alsahan, L.; Abdallah, M.; Younis, M. Green-PoW: An energy-efficient blockchain proof-of-work consensus algorithm. arXiv 2020, arXiv:2007.04086. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, Z.; Feng, D.; Zhang, S.; Zhang, L.; Peng, M.; Li, Y. Performance analysis and comparison of PoW, PoS and DAG based blockchains. Digit. Commun. Netw. 2020, 6, 480–485. [Google Scholar] [CrossRef]
- King, S. Primecoin: Cryptocurrency with Prime Number Proof-of-Work. 2013. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.694.5890&rep=rep1&type=pdf (accessed on 12 June 2022).
- Tromp, J. Cuckoo cycle: A memory bound graph-theoretic proof-of-work. In Proceedings of the International Conference on Financial Cryptography and Data Security, San Juan, Puerto Rico, 26–30 January 2015; pp. 49–62. [Google Scholar]
- Biryukov, A.; Khovratovich, D. Equihash: Asymmetric proof-of-work based on the generalized birthday problem. Ledger 2017, 2, 1–30. [Google Scholar] [CrossRef]
- Aljassas, H.M.A.; Sasi, S. Performance evaluation of proof-of-work and collatz conjecture consensus algorithms. In Proceedings of the 2nd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 1–3 May 2019; pp. 1–6. [Google Scholar]
- Chin, Z.H.; Yap, T.T.V.; Tan, I.K.T. Genetic-Algorithm-Inspired Difficulty Adjustment for Proof-of-Work Blockchains. Symmetry 2022, 14, 609. [Google Scholar] [CrossRef]
- Loe, A.F.; Quaglia, E.A. Conquering generals: An NP-hard proof of useful work. In Proceedings of the 1st Workshop on Cryptocurrencies and Blockchains for Distributed Systems, Munich, Germany, 15 June 2018; pp. 54–59. [Google Scholar]
- Syafruddin, W.A.; Dadkhah, S.; Köppen, M. Blockchain Scheme Based on Evolutionary Proof of Work. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 771–776. [Google Scholar]
- Li, W. Adapting Blockchain Technology for Scientific Computing. arXiv 2018, arXiv:1804.08230. [Google Scholar]
- Lihu, A.; Du, J.; Barjaktarevic, I.; Gerzanics, P.; Harvilla, M. A Proof of Useful Work for Artificial Intelligence on the Blockchain. arXiv 2020, arXiv:2001.09244. [Google Scholar]
- Chenli, C.; Li, B.; Shi, Y.; Jung, T. Energy-recycling blockchain with proof-of-deep-learning. In Proceedings of the 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Seoul, Korea, 14–17 May 2019; pp. 19–23. [Google Scholar]
- Li, B.; Chenli, C.; Xu, X.; Shi, Y.; Jung, T. DLBC: A Deep Learning-Based Consensus in Blockchains for Deep Learning Services. arXiv 2020, arXiv:1904.07349v2. [Google Scholar]
- Li, B.; Chenli, C.; Xu, X.; Jung, T.; Shi, Y. Exploiting computation power of blockchain for biomedical image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019; pp. 2802–2811. [Google Scholar]
- Qiu, C.; Wang, X.; Yao, H.; Du, J.; Yu, F.R.; Guo, S. Networking Integrated Cloud-Edge-End in IoT: A Blockchain-Assisted Collective Q-Learning Approach. IEEE Internet Things J. 2020, 8, 12694–12704. [Google Scholar] [CrossRef]
- Baldominos, A.; Saez, Y. Coin. AI: A proof-of-useful-work scheme for blockchain-based distributed deep learning. Entropy 2019, 21, 723. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, K.; Goharshady, A.K.; Pourdamghani, A. Hybrid mining: Exploiting blockchain’s computational power for distributed problem solving. In Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, Limassol, Cyprus, 8–12 April 2019; pp. 374–381. [Google Scholar]
- Philippopoulos, P.; Ricottone, A.; Oliver, C.G. Difficulty Scaling in Proof of Work for Decentralized Problem Solving. arXiv 2019, arXiv:1911.00435. [Google Scholar] [CrossRef]
- Davidović, T.; Todorović, M.; Ramljak, D.; Jakšić Krüger, T.; Matijević, L.; Jovanović, D.; Urošević, D. COCP: Blockchain Proof-of-Useful-Work Leveraging Real-Life Applications. In Proceedings of the International Conference on Blockchain Computing and Applications (BCCA 2022), San Antonio, TX, USA, 5–7 September 2022. [Google Scholar]
- Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Davidović, T.; Šelmić, M.; Teodorović, D.; Ramljak, D. Bee colony optimization for scheduling independent tasks to identical processors. J. Heuristics 2012, 18, 549–569. [Google Scholar] [CrossRef]
- Frachtenberg, E.; Schwiegelshohn, U. Preface. In Proceedings of the 15th Internation Workshop, JSSPP 2010, Job Scheduling Strategies for Parallel Processing, Atlanta, GA, USA, 23 April 2010; pp. V–VII. [Google Scholar]
- Graham, R.L. Bounds on multiprocessing timing anomalies. SIAM J. Appl. Math. 1969, 17, 416–429. [Google Scholar] [CrossRef]
- Mokotoff, E. An exact algorithm for the identical parallel machine scheduling problem. Eur. J. Oper. Res. 2004, 152, 758–769. [Google Scholar] [CrossRef]
- Mrad, M.; Souayah, N. An Arc-Flow Model for the Makespan Minimization Problem on Identical Parallel Machines. IEEE Access 2018, 6, 5300–5307. [Google Scholar] [CrossRef]
- Unlu, Y.; Mason, S.J. Evaluation of mixed integer programming formulations for non-preemptive parallel machine scheduling problems. Comput. Ind. Eng. 2010, 58, 785–800. [Google Scholar] [CrossRef]
- Fanjul-Peyro, L.; Ruiz, R. Iterated greedy local search methods for unrelated parallel machine scheduling. Eur. J. Oper. Res. 2010, 207, 55–69. [Google Scholar] [CrossRef]
- Paletta, G.; Ruiz-Torres, A.J. Partial solutions and multifit algorithm for multiprocessor scheduling. J. Math. Model. Algorithms Oper. Res. 2015, 14, 125–143. [Google Scholar] [CrossRef]
- Alharkan, I.; Bamatraf, K.; Noman, M.A.; Kaid, H.; Nasr, E.S.A.; El-Tamimi, A.M. An order effect of neighborhood structures in variable neighborhood search algorithm for minimizing the makespan in an identical parallel machine scheduling. Math. Probl. Eng. 2018, 2018, 3586731. [Google Scholar] [CrossRef]
- Laha, D.; Gupta, J.N. An improved cuckoo search algorithm for scheduling jobs on identical parallel machines. Comput. IE 2018, 126, 348–360. [Google Scholar] [CrossRef]
- Kamaraj, S.; Saravanan, M. Optimisation of identical parallel machine scheduling problem. Int. J. Rapid Manuf. 2019, 8, 123–132. [Google Scholar] [CrossRef]
- Ostojić, D.; Davidović, T.; Jakšić Krüger, T.; Ramljak, D. Comparative Analysis of Heuristic Approaches to P||Cmax. In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems, ICORES 2021, Online, 4–6 February 2021; pp. 352–359. [Google Scholar]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. In Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 5, pp. 287–326. [Google Scholar]
- Stanković, U.; Matijević, L.; Davidović, T. Mathematical Models for the Weighted Scheduling Problem with Deadlines and Release Times. In Proceedings of the XLVIII Symposium on Operational Research (SYM-OP-IS 2021), Banja Koviljača, Serbia, 20–23 September 2021; pp. 327–332. [Google Scholar]
- Matijević, L.; Stanković, U.; Davidović, T. General Variable Neighborhood Search for the Weighted Scheduling Problem with Deadlines and Release Times. In Proceedings of the XLVIII Symposium on Operational Research (SYM-OP-IS 2021), Banja Koviljača, Serbia, 20–23 September 2021; pp. 207–212. [Google Scholar]
- Golden, B.L.; Raghavan, S.; Wasil, E.A. The Vehicle Routing Problem: Latest Advances and NEW Challenges; Springer: Berlin/Heidelberg, Germany, 2008; Volume 43. [Google Scholar]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Ilin, V.; Matijević, L.; Davidović, T.; Pardalos, P.M. Asymmetric Capacitated Vehicle Routing Problem with Time Window. In Proceedings of the XLV Symposium on Operations Research (SYM-OP-IS 2018), Zlatibor, Serbia, 16–19 September 2018; pp. 174–179. [Google Scholar]
- Matijević, L.; Davidović, T.; Ilin, V.; Pardalos, P.M. General Variable Neighborhood Search for Asymmetric Vehicle Routing Problem. In Proceedings of the XLVI Symposium on Operations Research (SYM-OP-IS 2019), Kladovo, Serbia, 15–18 September 2019. [Google Scholar]
- Matijević, L.; Ilin, V.; Davidović, T.; Jakšić Krüger, T.; Pardalos, P.M. Asymmetric Vehicle Routing Problem with Time and Capacity Constraints: Exact and Heuristic approaches. 2020; submitted. [Google Scholar]
- Kilani, Y.; Bsoul, M.; Alsarhan, A.; Al-Khasawneh, A. A survey of the satisfiability-problems solving algorithms. Int. J. Adv. Intell. Paradig. 2013, 5, 233–256. [Google Scholar] [CrossRef]
- Xu, H.; Rutenbar, R.A.; Sakallah, K. sub-SAT: A formulation for relaxed boolean satisfiability with applications in routing. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2003, 22, 814–820. [Google Scholar] [CrossRef]
- Strickland, D.M.; Barnes, E.; Sokol, J.S. Optimal protein structure alignment using maximum cliques. Oper. Res. 2005, 53, 389–402. [Google Scholar] [CrossRef]
- Li, C.M.; Quan, Z. An efficient branch-and-bound algorithm based on maxsat for the maximum clique problem. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010. [Google Scholar]
- Vasquez, M.; Hao, J.K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite. Comput. Optim. Appl. 2001, 20, 137–157. [Google Scholar] [CrossRef]
- Jose, M.; Majumdar, R. Bug-Assist: Assisting fault localization in ANSI-C programs. In Proceedings of the International Conference on Computer Aided Verification, Snowbird, UT, USA, 14–20 July 2011; pp. 504–509. [Google Scholar]
- Jabbour, S.; Mhadhbi, N.; Raddaoui, B.; Sais, L. SAT-based models for overlapping community detection in networks. Computing 2020, 102, 1275–1299. [Google Scholar] [CrossRef]
- Morgado, A.; Heras, F.; Liffiton, M.; Planes, J.; Marques-Silva, J. Iterative and core-guided MaxSAT solving: A survey and assessment. Constraints 2013, 18, 478–534. [Google Scholar] [CrossRef]
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger Berlin Version b8ffc51. 2022. Available online: https://ethereum.github.io/yellowpaper/paper.pdf (accessed on 6 May 2022).
- Go Ethereum: Official Go Implementation of the Ethereum Protocol. Available online: https://geth.ethereum.org/ (accessed on 23 May 2022).
- Hutter, F.; Hamadi, Y.; Hoos, H.H.; Leyton-Brown, K. Performance prediction and automated tuning of randomized and parametric algorithms. In Proceedings of the 12th International Conference on Principles and Practice of Constraint Programming—CP 2006, Nantes, France, 25–29 September 2006; pp. 213–228. [Google Scholar]
- Hutter, F.; Xu, L.; Hoos, H.H.; Leyton-Brown, K. Algorithm runtime prediction: Methods & evaluation. Artif. Intell. 2014, 206, 79–111. [Google Scholar]
- Shalini, S.; Santhi, H. A survey on various attacks in bitcoin and cryptocurrency. In Proceedings of the 2019 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 4–6 April 2019; pp. 220–224. [Google Scholar]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.A.; Nyang, D.; Mohaisen, A. Overview of attack surfaces in blockchain. In Blockchain for Distributed Systems Security; John Wiley & Sons: Hoboken, NJ, USA, 2019; pp. 51–66. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).