Optimizing the Routing of Urban Logistics by Context-Based Social Network and Multi-Criteria Decision Analysis

Abstract

The proper vehicle-route selection is a key challenge affecting the quality of urban logistics since any delay may cause disasters. This study proposes a novel approach of using symmetry/asymmetry traffic context data and multi-criteria decision analysis to optimize vehicle-route selection as part of urban-logistical planning. The traffic context data are collected from official urban transportation databases and metadata of Google Maps route planning to construct a context-based social network. The traffic features and routing criteria have symmetry/asymmetry properties to influence the decision of path selection. Multi-criteria decision analysis can generate a ranking of candidate paths based on an evaluation of traffic data in context-based social networks to recommend to the deliveryman. The deliveryman can select a reasonable path for delivering products according to the ranking of candidate paths. A case study demonstrates the steps of the proposed approach. Experimental results show that the precision is 79.65%, recall is 80.70%, and F1-score is 80.17%, thus proving the vehicle-route recommendation effectiveness. The contribution of this work is to optimize traffic-routing solutions for improved urban logistics in smart cities. It helps deliverymen send products as soon as possible to customers to retain quality, especially in cold-chain logistics.

1. Introduction

In order to satisfy various needs of life, people obtain products in different ways, such as shopping in physical stores or purchasing items on the internet. The rapid development of information and communication technologies has led to many business models for selling products to consumers, such as e-commerce and mobile commerce [1]. In order to make e-commerce run smoothly, stakeholders have established a logistics supply chain ecosystem. In the urban logistics areas, logistics services have always played an important part in delivering products to customers. Information systems that are part of the logistics services industry can enable participants to add, modify, delete, and query orders through convenient and efficient interfaces on computers and mobile and other portable devices. Logistics services can also take advantage of the internet to avoid problems regarding product availability caused by time and space constraints. An effective information system can accelerate and enhance product-status verification and tracking. Participants can obtain a product’s delivery status through web interfaces from tracking distribution centers and transit stations. Portable devices such as smartphones, tablets, and personal digital assistants (PDAs) also offer greater convenience to users accessing the system. In fact, the supply chain ecosystem for mobile commerce is even more convenient than PC-based e-commerce. In addition, artificial intelligence technology is in full swing [2,3] and can be used to analyze massive amounts of data to help make forecasts and recommendations. In short, the application of communications technologies will play a key role in making urban logistics more efficient.

However, there are challenges in the development of new and enhanced urban logistics services. Customers expect these services to consistently deliver products on time, even during peak traffic periods. This puts a strain on logistics systems. Delivering high volumes of products during periods of heavy traffic congestion can cause delays. These delays could, in turn, hold up deliveries of products at other times, putting the system at risk of spinning out of control. For example, the freshness of expensive ingredients is a key factor for restaurants to keep customers’ loyalty, since any delay may cause disasters. Therefore, how to retain the freshness of ingredients in cold-chain logistics becomes an important issue. Proper traffic-route analysis and planning are designed to avoid these problems and improve delivery services [4,5,6]. Currently, mapping services such as Google Maps and Apple Maps have spurred the development of location-based social networks (LBSNs) [7].

A delivery service’s point-of-interest (POI) becomes a specific map location on these networks. How to find the appropriate traffic route to a specific POI that meets the deliveryman’s expectations is becoming an important challenge. The deliveryman must choose from among various candidate routes which have varying levels of congestion and other road conditions. Determining the best path for the deliveryman to a specific POI based on the huge amount of symmetry/asymmetry traffic-routing information available on location-based social networks is a research topic worth exploring [8,9,10]. The criteria for selecting a recommended route play an important role in the decision-making analysis process. A multiple criteria decision-making (MCDM) method evaluates a range of criteria [11,12] to construct a mechanism to arrive at a recommended route from among various candidate routes.

This paper proposes a novel approach for using symmetry/asymmetry traffic context data and multi-criteria decision analysis to optimize traffic-route selection for urban logistics. All potential routes from the deliveryman’s point of origin to his point-of-interest are collected and identified as candidate paths. The multi-criteria decision analysis generates a ranking of candidate paths based on the evaluation of symmetry/asymmetry contextual traffic data. Then, a recommended traffic route is provided to the deliveryman. We collect symmetry/asymmetry traffic context data from official urban transportation databases and metadata of Google Map route planning to construct a context-based social network. The deliveryman can ultimately select the optimal path to deliver his products according to the context-based social network. The path recommendation is made by rankings produced by the following multi-criteria decision analysis methods [11,12]: TOPSIS, VIKOR, ELECTRE, PROMETHEE, and SAW. These methods help to demonstrate the effectiveness of the proposed approach to optimizing the vehicle traffic-routing solution for urban logistics in smart cities. To sum up, the main contributions of this paper are as follows.

• To solve the product delivery delay problems in the urban logistics areas, this work proposes a novel approach of using symmetry/asymmetry traffic context data and multi-criteria decision analysis to optimize vehicle-route selection as part of urban-logistical planning.
• The paper uses data mining technologies to process the traffic context data from official urban transportation databases and metadata of Google Maps route planning in order to construct a context-based social network. Since the traffic features and routing criteria have symmetry/asymmetry properties to influence the decision of path selection, we adopt multi-criteria decision analysis to generate a ranking of candidate paths based on an evaluation of traffic data in context-based social networks to recommend to the deliveryman. The deliveryman can select a reasonable path for delivering products according to the ranking of candidate paths.
• The experimental results show that the work’s precision is 79.65%, recall is 80.70%, and F1-score is 80.17% in order to prove the vehicle-route recommendation effectiveness. It helps deliverymen send products as soon as possible to customers to retain the quality, especially in cold-chain logistics. The paper optimizes traffic-routing solutions for improved service quality of urban logistics in smart cities.

The remainder of this paper is organized as follows: Section 2 introduces related research. Section 3 presents our proposed approach to optimize path selection. We discuss a case study in Section 4. The experiment results and relevant discussions are shown in Section 5. Finally, Section 6 presents our conclusions.

2. Related Work

This section introduces related research about two topics associated with this study: points-of-interest recommendations in location-based social networks and multi-criteria decision analysis.

2.1. Points-of-Interest (POI) Recommendations in Location-Based Social Networks (LBSNs)

The emergence of geotagging services, such as Foursquare and Instagram, has prompted people to post a variety of contributed photos, tags, time, and location information on the internet. In recent years, location-based social networks (LBSNs) have become a hot topic for researchers. Users can share their location and activities with friends through “check-ins” on websites and apps [10,13]. LBSNs show the digital versions of historical catalogs which summarize and synthesize ratings and reviews provided by amateurs or expert reviewers [14]. The network will recommend attractions according to the user’s current location. When the user frequently checks in and signs into the LBSN, network operators will often also provide special offers or services as rewards. LBSNs originally only appeared in basic location-sharing platforms, such as Flickr and Foursquare, but their presence has expanded. The geographic characteristics of the LBSN directly relate to the relationship between physical and virtual network worlds and create a rich ecosystem [13,15]. Wei et al. [4] proposed a concept in which a tourism solution plan can be inferred by the user’s personal tourism experience and point-of-interest (POI). Yu et al. [16] used a location-based social network to propose a personalized travel-recommendation method. The data collected from the LBSN was used to simulate users and their geographic location information, and a collaborative filtering method was used to recommend the most suitable travel destination for them. Abeer et al. [17] presented a comparative analysis of three matrix factorization algorithms on location-based social networks and used two performance metrics for evaluation.

Points-of-interest (POI) are mainly used to designate information about a landmark or attraction on a map, including tourist attractions, such as monuments, local, state, and national parks, etc.; or commercial establishments, such as cinemas, department stores, restaurants, convenience stores, gas stations, hospitals and clinics, government agencies, transportation facilities, etc. The POI information can be used to introduce the name and related information of the landmark. Therefore, POI content should include this information and more, such as the category of points-of-interest the landmark or attraction belongs to, as well as longitude, latitude, and possibly altitude of the entry. This information is displayed on an electronic map. This enables users to quickly find the relevant information they need. Research into POI recommendation systems has flourished in recent years [18,19,20]. This is different from traditional recommendation systems because POI recommendation systems also rely on geographic proximity data, a high frequency of data updates, and influence of social contacts on separate networks. The POI recommendation systems also face some challenges, including physical limitations, complex associations, and, at times, a wide diversity of information they must handle. When implemented properly, POI recommendation systems can satisfy user preferences for new information using the intelligence of the LBSN, including providing users with proximity-based advertising and offers.

According to the research literature, POI recommendation systems of late have gradually become a new trend among recommendation systems in general. Safavi et al. [21] provides a systematic review focusing on recent research on POI recommendation systems. Griesner et al. [22] described how matrix decomposition provides support for POI recommendations. They proposed a GeoMF-TD method that factors in geographic and time dependencies to the matrix decomposition. Cheng et al. [23] observed two features in the registration order for the POI recommendation systems, including personalized Markov chains and region localization. They proposed a new matrix decomposition method, FPMC-LR, incorporating the Markov chains and local regions. The new method solved the time relationship issue neglected in the sign-in so that users can obtain a set of consecutive POI recommendation itineraries. Feng et al. [24] proposed a personalized ranking metric embedding method, PRME, to simulate a personalized checking-in sequence. They further developed a PRME-G model combined with time series information, personal preferences, and geographical influences to improve the system’s recommendation performance. Han et al. [25] proposed a novel method of geographic proportional dispersion, which recommended various POIs located around the user’s activity area, so that the distribution of each subpoint of interest can be related to the user’s activity area. Liu et al. [26] proposed a new category-aware POI recommendation model using the user’s location-category preference to improve the accuracy of the recommendation. Their model uses matrix decomposition to predict the user’s category preferences and then analyzes the user’s geographic preferences in their respective categories. Hu et al. [27] proposed a translation-based knowledge graph enhanced multi-task learning framework (TransMKR) for the POI recommendation. It enhances the expressive ability of POI data and alleviates the problem of data sparsity. Hossein et al. [28] proposed a linear-regression-based fusion of POI contexts that effectively finds the best combination of contexts for each user or group of users from their historical interactions. This suggested that appropriate context fusion is an essential element of an accurate, fair, and transparent POI recommendation system. Liu et al. [29] proposed a real-time preference mining model (RTPM) which is based on LSTM to recommend the next POI with time restrictions. RTPM does not utilize users’ attributes and their current locations for recommendations, which makes great contributions to users’ privacy protection. Pablo et al. [14] presented a systematic review focused on the research conducted in the last 10 years about the topic of “point-of-interest recommender systems based on location-based social networks”. They discussed and categorized the algorithms and evaluation methodologies used in these works and pointed out the opportunities and challenges that remain open in the field.

2.2. Multi-Criteria Decision Analysis (MCDA)

Multi-criteria decision analysis (MCDA) is a process of solving a problem based on multiple criteria [30]. In other words, MCDA is an analytical method that helps users select a reasonable target matching the user’s ideals, based on assessment of multiple criteria. Performing assessments to optimize the recommendation process is a viable approach to maintain quality. There are two types of multi-criteria decision analysis [11,12]. One is multi-objective decision-making (MODM), and the other is multi-attribute decision-making (MADM). Multi-objective decision-making consists of a set of restricted conditions, with the optimal solution obtained for several objective functions. Multi-attribute decision-making considers multiple attributes (criteria) with which to evaluate alternatives, and the best option is determined by evaluating the pros and cons of the results.

General multi-criteria decision analysis methods [11,12] include the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), ELimination and Choice Translating Reality (ELECTRE), Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE), Simple Additive Weighting (SAW), and Analytic Hierarchy Process (AHP). The VIKOR method [11,12] uses the concept of a compromise solution to solve the problem of ranking candidate solutions based on how close they approach the ideal. VIKOR is an optimal method for arriving at a compromise solution. At first, it defines two important ideal solutions. One is the positive ideal solution (PIS), and the other is the negative ideal solution (NIS). It calculates the proximity between each candidate solution’s criteria and the ideal. The ranking order is produced based on the proximity to the best solution. An advantage of the VIKOR method is that it can maximize a group’s benefits and minimize disagreements. The decision-maker agrees to a compromise solution.

There are adaptations of the general multi-criteria decision methods, as well. For example, Liou and Chuang [31] proposed a hybrid multi-criteria decision method to select an outsourcing provider. They used the DEMATEL method to construct a relationship between standards and used the ANP method to make sure of the weight. Then, they used the VIKOR method to calculate a ranked list of outsourcing providers. Tadić et al. [32] chose a new hybrid multi-criteria decision model integrating the DEMATEL, ANP, and VIKOR methods to help the city of Belgrade, Serbia to solve a city logistics problem. Liu et al. [33] used a multi-criteria decision model to promote a service connecting a municipal subway system with an airport. They used the DANP and VIKOR methods to evaluate and choose the best routes to promote the development of tourism.

3. Problem Definition

This section introduces some problems in urban logistics. To solve the issues, we propose a novel systematic framework to optimize traffic-route selection. The system framework is functional modularity. This work uses a utility model to formalize the candidate paths and discovers a selection order via the multi-criteria decision method. We use the confusion matrix to evaluate the deliverymen’s feedback to prove the proposed system framework’s effectiveness.

3.1. Routing Problems in Urban Logistics

In urban logistics, logistics services have always played an important part in delivering products to customers. However, this work lists three problems with the development of new and enhanced urban logistics services.

Problem Definition 1:

Customers expect these services to consistently deliver products on time, even during peak traffic periods. Delivering high volumes of products during periods of heavy traffic congestion can cause delays. These delays could, in turn, hold up deliveries of products at other times, putting the delivery schedule at risk of spinning out of control. How to find the appropriate traffic route to a specific POI that meets the deliveryman’s expectations is the first problem.

Problem Definition 2:

Determining the best path for the deliveryman to a specific POI based on the huge amount of symmetry/asymmetry traffic-routing information available on location-based social networks becomes a challenge. The deliveryman must choose from among various candidate routes which have varying levels of congestion and other road conditions. How to select the best path for the deliveryman to deliver products to customers is the second problem.

Problem Definition 3:

The application of information and communications technologies plays a key role in making urban logistics more efficient. How to design a novel systematic framework to optimize the traffic-route selection and recommend a reasonable routing path for the deliveryman is the third problem.

Problem Definition 4:

How to prove the proposed novel systematic framework’s effectiveness is the fourth problem.

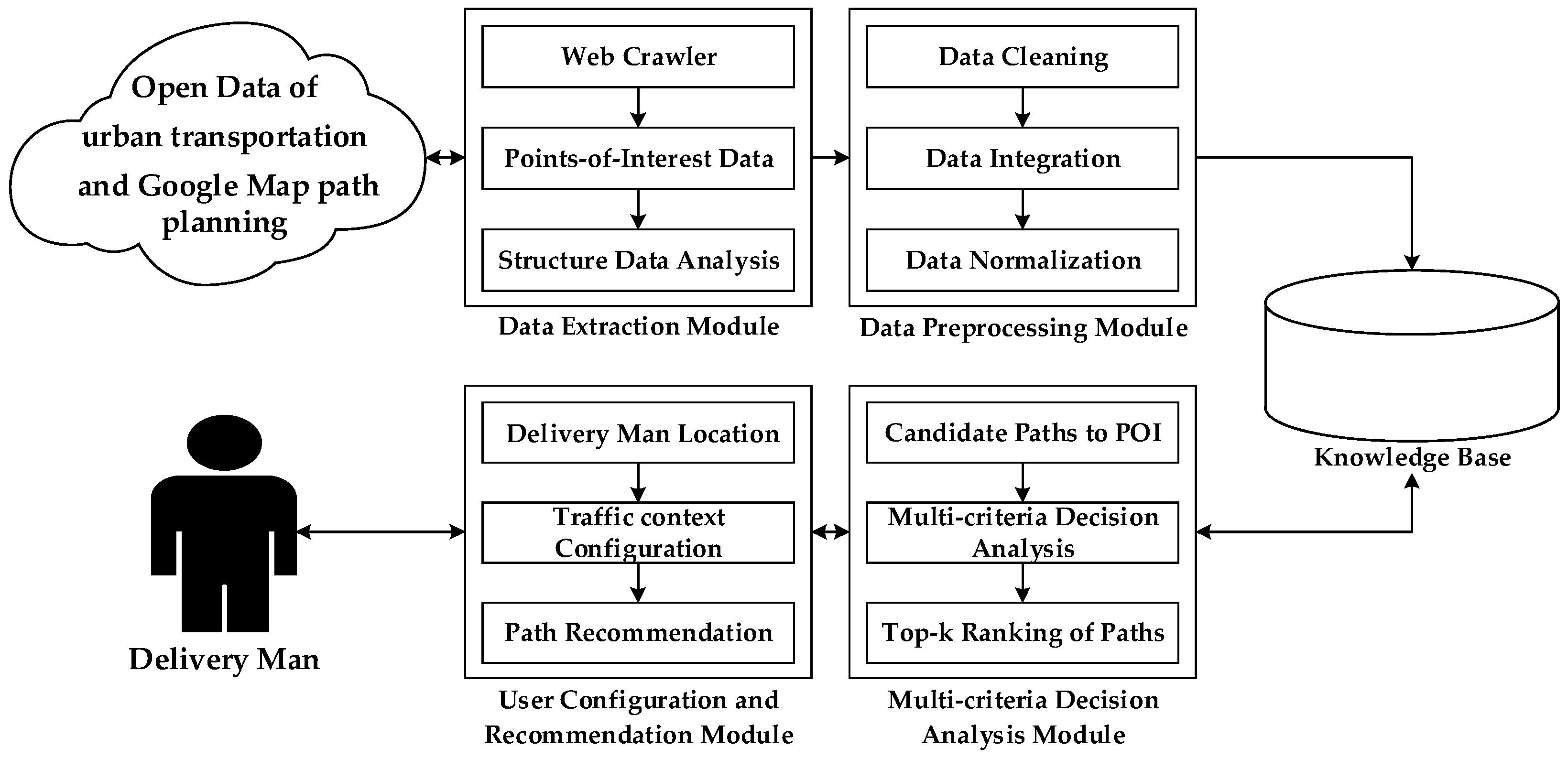
3.2. A Novel System to Optimize Traffic-Route Selection in Urban Logistics

To improve the urban logistics problems mentioned above, this paper proposes a novel system framework [18] as shown in Figure 1. According to the data mining methodology, we design the data extraction module for data collection. The data preprocessing module is used for data cleaning, transformation, and integration, to construct a symmetry/asymmetry context-based social network. In the data analysis model, the multi-criteria decision analysis module is designed by TOPSIS, VIKOR, ELECTRE, PROMETHEE, and SAW methodologies. In the knowledge representation, the user configuration and recommendation module is implemented as a web/app-based application as the user interface. The proposed system framework, along with a resulting knowledge base, is designed by the relational database methodology. The algorithm of each module is presented as follows.

The data extraction module collects the symmetry/asymmetry information on the logistics destination, referred to as points-of-interest (POI), which is required by the deliveryman. It also analyzes the relevant symmetry/asymmetry information through the proposed system. The information about the POIs provided in the cloud server, i.e., official open data, Google Maps, and urban transportation servers, is collected from web pages. Then, this information, for example, the POI description and relevant attributes, is extracted through the JavaScript Object Notation (JSON) lightweight data-interchange format from web pages to be stored in the knowledge base. The pseudocode is shown in the data extraction algorithm.

Data extraction algorithm: collects the symmetry/asymmetry information on the logistics destination, referred to as points-of-interest (POI), which is required by the deliveryman. Parameter definition is shown as follows.
OpenDataUrl	The URL of open data website.
UrbantransportationUrl	The URL of urban transportation website.
GoogleMapUrl	The URL of Google Maps website.
POI	Data extraction from cloud servers.
urlSet	A URL set of the open data websites.
POISet	A set of the POI.
POIInformation	Information on POI.
POIData	A set of POI data.
JSONKey	The key of JSON.
JSONKeySet	A set of JSONKey.
Input: OpenDataUrl, UrbantransportationUrl, GoogleMapUrl Output: POIData DataExtraction (OpenDataUrl, UrbantransportationUrl, GoogleMapUrl) { urlSet ≡ Analysis of OpenDataUrl, UrbantransportationUrl, and GoogleMapUrl; while (urlSet.Url is not empty) { POI ≡ Get web page content form urlSet.Url; POISet add the POI;    } while (POISet is not empty)    {        while (JSONKeySet.JSONKey is not empty)        {           Get JSONKey messages to store in the POIInformation;        }        Add the POIInformation to the POIData;    }    return POIData; }

In the data preprocessing module, the proposed system uses data mining techniques to analyze the POI description and relevant symmetry/asymmetry attributes to remove meaningless information. It includes data cleaning, data integration, and data normalization processes of the POI obtained by the data extraction module. Data preprocessing executes the non-symbol, stemming, and stop-word removal tasks to prevent interference in a context-based social network construction. The information on points-of-interest after data cleaning may contain duplicate attribute values in the data set. This type of data will be difficult to analyze because of its inconsistency. Therefore, in the data integration process, the data will be merged. The information for POIs processed through data integration may include attribute values of different scopes and sizes, which will affect the subsequent analysis, so the data normalization process will be executed. The pseudocode is shown in the data preprocessing algorithm.

Data preprocessing algorithm: analyzes the POI description and relevant symmetry/asymmetry attributes to remove meaningless information. Parameter definition is shown as follows.
POIData	A set of POI data.
DCPOIDataSet	A set of POI data after data cleaning.
DCPOIData	POI data after data cleaning.
UrbantransportationData	Urban transportation POI data after data cleaning.
GoogleMapData	Google Maps POI data after data cleaning.
DIPOIDataSet	A set of POI data after data integration.
DIPOIData	Symmetry/asymmetry POI data after data integration.
Input: POIData  Output: DIPOIDataSet DataPreprocessing(POIData) { while (POIData is not empty) { if (POIData is duplicate)       {           DCPOIDataSet ≡ POIData delete duplicate data;       } } while (DCPOIDataSet.DCPOIData.GoogleMapData is not empty) {       DIPOIDataSet ≡ Combination of UrbantransportationData and GoogleMapData; } return DIPOIDataSet; }

After executing the data preprocessing module, a set of normalized symmetry/asymmetry POI data is produced. Then, we use the normalized symmetry/asymmetry POI data set with the traffic context criteria defined by the AHP method, including the average speed, degree of congestion, distance, and personal interest of the driver to construct a context-based social network. A logistics destination is defined as a point-of-interest near a deliveryman location. All traffic paths from the deliveryman location to the POI are collected and identified as candidate paths.

The multi-criteria decision analysis (MCDA) module is the core of the recommendation mechanism. The MCDA generates a ranking of candidate paths based on the evaluation of criteria in the context of traffic conditions. After MCDA, the system recommends a reasonable traffic path from the deliveryman location to the logistics destination. The user-configuration module obtains the context information, including deliveryman locations and the current traffic-routing context of candidate paths. The deliveryman can also configure preferences related to personal interest. In addition, he can set up the logistics destination in the system for delivering products and send feedback to help improve the system for the next recommendation. The pseudocode is shown in the multi-criteria decision analysis algorithm.

Multi-criteria decision analysis algorithm: generates a ranking of candidate paths based on the evaluation of criteria in the context of traffic conditions. Parameter definition is shown as follows.
CandidatePathSet	A data set of the candidate path with traffic context values regarding issues for a deliveryman.
RCandidatePathSet	A data set of the candidate path with normalized traffic context values.
WeightSet	A criteria weight set by the deliveryman configuration.
RankingOrder	Ranking order from use of a multi-criteria decision method.
MCDACandidatePathSet	A data set of the paths from use of multi-criteria decision analysis.
Input: CandidatePathSet, WeightSet Output: MCDACandidatePathSet MultiCriteriaDecisionAnalysis (CandidatePathSet, WeightSet) { switch { case TOPSIS: RankingOrder ≡ TOPSIS(RCandidatePathSet, WeightSet); case VIKOR: RankingOrder ≡ VIKOR(RCandidatePathSet, WeightSet); case ELECTRE: RankingOrder ≡ ELECTRE(RCandidatePathSet, WeightSet); case PROMETHEE: RankingOrder ≡ PROMETHEE(RCandidatePathSet, WeightSet); case SAW: RankingOrder ≡ SAW(RCandidatePathSet, WeightSet); } return the MCDACandidatePathSet based on the RankingOrder; }

Then, we introduce the proposed approach to optimize the path selection of a recommendation system, including using a utility-based reputation model [34,35,36] and the VIKOR method of multi-criteria decision analysis [11,12].

3.3. Utility Model for Candidate Paths

This work adapted a utility-based reputation model [34,35,36] to formalize a traffic-routing path’s quality of service (QoS) items in order to enforce the utility model. This item is determined based on the Analytic Hierarchy Process (AHP) [11,12] to identify the criteria of traffic context. The AHP method is applied to decision-making problems with multiple evaluation criteria and multiple objectives under uncertain circumstances. The hierarchical analysis rule is to gather the opinions of experts and to express complex decision-making problems with a simple and clear hierarchical structure. The first layer is the goal, which is the purpose of solving the problem, while the second layer is the criteria. Then, various measures are undertaken, while taking guidelines under consideration. Finally, the third layer is an alternative to solving the problem.

Traffic-routing path formalization is an initial task in the proposed approach. A utility-based reputation model [34,35,36] is used to formalize the context items of a path. Let $P=\left\{p_1, p_2,\dots ,p_n\right\}$ denote the set of paths, and $p\in P$. Each path has associated context items of interest, denoted by set $CI$, of which $ci$ is interest for monitoring and $ci\in CI$. Function $E:P\times CI\to R$ denotes the expected utility of path $p$ for the context item $ci$ that it monitors, where $R$ denotes real numbers. Notation $e{v}_{p,ci}$ represents the expectation of path p regarding context item $ci$. After the formalized process of a specific-interest issue, a utility model is used to represent user consideration with path selection. Let $U_{p,ci}$ denote the utility value of path $p$ for the context item $ci$. Each feature value $e{v}_{p,ci}$ is normalized to a utility value $U_{p,ci} :R$. Each expected value $U_{p,ci}$ of a specific-interest context item ci of a path $p$ is used to build a comparative utility vector $p_i$, as shown in Equation (1).

$$p_i=\left(U_{p_i,c{i}_1}, U_{p_i,c{i}_2}, \dots ,U_{p_i,c{i}_n}\right),i=\left\{1,2,\dots ,n\right\}$$

(1)

Once the traffic-routing path formalization is complete and a relational utility model is applied, the path will obtain the expected value of the status item of interest. Based on various status items of interest, selecting the most suitable path from a large number of candidates requires multi-criteria decision analysis.

3.4. Discovering a Selection Order via the VIKOR Method

Multi-criteria decision analysis [11,12] is an analytical method that can help a user make a selection decision by evaluating each candidate in terms of multiple criteria. The multi-criteria decision analysis task uses the initial set of candidate paths (initial matrix $P$). The candidate paths’ feature vectors will be used to construct a normalization candidate path set (normalized matrix $P^{\prime }$) as the input object in the multi-criteria decision analysis algorithm. Another input object is a criteria weight set (weight matrix $W$) configured by a user. We use eight steps to discover the selection order of paths using the VIKOR method [11,12]. The criterion value is normalized to form a normalized candidate path set for multi-criteria decision analysis. The formal weights of the criteria form a criteria weight set for the multi-criteria decision analysis.

• Step 1: Construct the initial matrix $P$, as shown in Equation (2).

  $$P={\left[p_{ij}\right]}_{m\times n}=\left[\begin{array}{c}\begin{array}{ccc}{U}_{p_1,c{i}_1}& \dots & U_{p_1,c{i}_j}\\ ⋮& \ddots & ⋮\end{array}\\ \begin{array}{ccc}{U}_{p_i,c{i}_1}& \dots & U_{p_i,c{i}_j}\\ ⋮& \ddots & ⋮\end{array}\\ \begin{array}{ccc}{U}_{p_m,c{i}_1}& \dots & U_{p_m,c{i}_j}\end{array}\end{array}\begin{array}{c}\begin{array}{cc}\dots & U_{p_1,c{i}_n}\\ \ddots & ⋮\end{array}\\ \begin{array}{cc}\dots & U_{p_i,c{i}_n}\\ \ddots & ⋮\end{array}\\ \begin{array}{cc} \dots & U_{p_m,c{i}_n}\end{array}\end{array}\right]$$

  (2)

  where $m$ indicates the number of candidate paths, $n$ indicates the number of candidate path context items.
• Step 2: Calculate the column vector by Equation (3) and normalize the matrix $P$ to obtain a normalized matrix $P^{\prime }$.

  $$P^{\prime }={\left[p_{ij}\right]}_{m\times n}, f_{ij}=\frac{p_{ij}}{\sqrt{{{\displaystyle \sum }}_{i=1}^m{p}_{ij}^2}}$$

  (3)
• Step 3: Determine the ideal $f_i^{*}$ value by Equation (4) and the worst $f_i^{-}$ value by Equation (5). If the $i$th function represents a benefit then:

  $$f_i^{*}=\left\{\left(ma{x}_j f_{ij}\parallel i\in I_1\right), \left(mi{n}_j f_{ij}\parallel i\in I_2\right)\right\}$$

  (4)

  $$f_i^{-}=\left\{\left(mi{n}_j f_{ij}\parallel i\in I_1\right), \left(ma{x}_j f_{ij}\parallel i\in I_2\right)\right\}$$

  (5)
• Step 4: Set the weight of the evaluation criteria by Equation (6). The weight matrix $W$ is configured by the user in this work.

  $$W={\left[\begin{array}{ccc}{w}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & w_n\end{array}\right]}_{n\times n}$$

  (6)
• Step 5: Calculate the group utility $S_i$ of candidate path $i$ by Equation (7) and the individual regret $R_i$ of candidate path $i$ by Equation (8) where $w_j$ are the weights of criteria, expressing their relative importance.

  $$S_i={{\displaystyle \sum }}_j^n W_j\left(f_j^{*}-f_{ij}\right)/\left(f_j^{*}-f_j^{-}\right)$$

  (7)

  $$R_i=Ma{x}_j\left[W_j\left(f_j^{*}-f_{ij}\right)/\left(f_j^{*}-f_j^{-}\right)\right]$$

  (8)
• Step 6: Compute the values $Q_i$ by Equation (9) where $v$ is introduced as weight of the strategy of the maximum group utility, here $v$ = 0.5.

  $$Q_i=v\left(S_j-S^{*}\right)/\left(S^{-}-S^{*}\right)+\left(1-v\right)\left(R_j-R^{*}\right)/\left(R^{-}-R^{*}\right)$$

  (9)
• Step 7: Rank the candidate paths, sorting by the values $S$, R, and $Q$, in decreasing order. The results are three ranking lists.
• Step 8: Propose as a compromise solution the candidate path ($a^{\prime }$) which is ranked the best by the measure $Q$ (minimum) if the following two conditions are satisfied:

• Condition 1: Acceptable advantage.
  • where $a^{″}$ is the candidate path with the second position in the ranking list by $Q$; $DQ=1/\left(J-1\right)$; $J$ is the number of candidate paths.
• Condition 2: Acceptable stability in decision-making.
  • Candidate path $a^{\prime }$ must also be the best ranked by $S$ and/or $R$. This compromise solution is stable within a decision-making process, which could be: “voting by majority rule” (when $v>0.5$ is needed), or “by consensus” $v\approx 0.5$, or “with veto” ($v<0.5$). Here, $v$ is the weight of the decision-making strategy of the maximum group utility.

If one of the conditions is not satisfied, then a set of compromise solutions is proposed, which consists of: candidate paths $a^{\prime }$ and $a^{″}$ only if Condition 2 is not satisfied, or candidate paths $a^{\prime }$, $a^{″}$,…, $a^{\left(M\right)}$ if Condition 1 is not satisfied; and $a^{\left(M\right)}$ is determined by the relation $Q(a^{\left(M\right)})-Q\left(a^{\prime }\right)<DQ$ for maximum $M$ (the positions of these candidate paths are “in closeness”).

The best candidate path, ranked by $Q$, is the one with the minimum value of $Q$. The main ranking result is the compromise ranking list of candidate paths, and the compromise solution with the “advantage rate”.

3.5. Evaluation of System Framework

We use the confusion matrix to evaluate the deliverymen’s feedback. The confusion matrix includes four elements: True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). TP means that our predicted positive is true. TN means that our predicted negative is true. FP means that our predicted positive is false. FN means that our predicted negative is false. Then, this work uses the precision calculated by Equation (10), the recall calculated by Equation (11), and the F1-score calculated by Equation (12) to evaluate the proposed system framework’s effectiveness.

$$\mathrm{Precision}=\frac{TP}{TP+FP}\times 100\%$$

(10)

$$\mathrm{Recall}=\frac{TP}{TP+FN}\times 100\%$$

(11)

$$\mathrm{F}1-\mathrm{score}=\frac{2\times precision\times Recall}{precision+Recall}\times 100\%$$

(12)

4. Case Study on Traffic-Routing Recommendation for Deliverymen

Based on the open data collected from the Taichung City Bus Station Information system in Taiwan, R.O.C., and metadata of Google Maps route planning, we obtained a symmetry/asymmetry data set that includes 19,192 points-of-interest. Removing the duplicate data reduced the size of the data set to 12,452 POIs [18]. We developed traffic context criteria, as defined by the AHP method, including average speed, degree of congestion, distance, and driver personal interest to construct a context-based social network. In other words, each traffic path included context metadata for multi-criteria decision analysis, including the above criteria. The deliveryman first configured an initial location. Then, the multi-criteria decision analysis was performed to produce a ranked order of candidate paths and to generate a recommended route to a POI. Finally, the results of the traffic-route selection for several deliveryman POIs were generated. An example of initial POI to destination POI is shown in Figure 2 [18,19]. The traffic routing of urban-logistical planning includes seven POIs and six adaptive routing paths.

We conducted a study that included ten candidate paths to demonstrate eight steps of the multi-criteria decision analysis, with the VIKOR method. The expected context items included the average speed, degree of congestion, distance, and the driver’s personal level of interest, defined by the AHP method.

Table 1. Candidate paths from deliveryman to logistics destination.

Path No	Average Speed (Kilometer/Hour)	Congestion Degree (1 to 10)	Distance (Kilometer)	Personal Interest (1 to 10)
P01	33	6	2.08	5
P02	42	2	1.65	7
P03	30	8	1.79	4
P04	44	2	2.62	6
P05	25	8	1.74	8
P06	46	3	4.02	2
P07	38	4	1.24	4
P08	43	6	3.58	6
P09	46	3	1.93	7
P10	52	1	3.90	8

shows each traffic context item’s corresponding value.

The eight steps were used to discover the selection order of paths using the VIKOR method [11,12]. A criterion value is normalized to form a normalized candidate path data set for multi-criteria decision analysis. As per this suggestion, in this case study, we invited 10 deliverymen to provide weighted values for each criterion. The average weighted value of each criterion was used to set the formal weighting. The formal weights of the criteria were set at: average speed = 0.3, congestion degree = 0.2, distance = 0.1, and driver interest = 0.4. This weight set would be used for the multi-criteria decision analysis.

• Step 1: Construct the initial matrix $P$ where 10 indicates the number of candidate paths and 4 indicates the number of candidate path items.

  $$P=\left[\begin{array}{cccc}33& 6& 2.08& 5\\ 42& 2& 1.65& 7\\ 30& 8& 1.79& 4\\ 44& 2& 2.62& 6\\ 25& 4& 1.74& 8\\ 46& 3& 4.02& 2\\ 38& 4& 1.24& 4\\ 43& 6& 3.58& 6\\ 46& 9& 1.93& 7\\ 52& 1& 3.9& 8\end{array}\right]$$
• Step 2: Calculate the column vector by Equation (3) and normalize the matrix $P$ to obtain a normalized matrix $P^{\prime }$.

  $$P^{\prime }=\left[\begin{array}{cccc}0.25627& 0.38490& 0.24933& 0.26389\\ 0.32654& 0.12830& 0.19779& 0.36945\\ 0.23325& 0.51320& 0.21457& 0.21111\\ 0.34209& 0.12830& 0.31406& 0.31667\\ 0.19437& 0.51320& 0.20858& 0.42222\\ 0.35764& 0.19245& 0.48188& 0.10556\\ 0.29544& 0.25660& 0.14864& 0.21111\\ 0.33432& 0.38490& 0.42914& 0.31667\\ 0.35764& 0.19245& 0.23135& 0.36945\\ 0.40429& 0.06415& 0.46750& 0.42222\end{array}\right]$$
• Step 3: Determine the ideal $f_i^{*}$ value by Equation (4) and the worst $f_i^{-}$ value by Equation (5). If the $i$th function represents a benefit, then:

  $$\begin{array}{c}{f}_i^{*}=\left\{\left(0.40429, 0.06415, 0.14864, 0.42222\right)\right\} \\ f_i^{-}=\left\{\left(0.19437, 0.51320, 0.48188, 0.10556\right)\right\}\end{array}$$
• Step 4: Set the weight of the evaluation criteria by Equation (6). The weight matrix $W$ is configured by the user in this work.

  $$W=\left[\begin{array}{cccc}0.3& 0& 0& 0\\ 0& 0.2& 0& 0\\ 0& 0& 0.1& 0\\ 0& 0& 0& 0.4\end{array}\right]$$
• Step 5: Calculate the group utility $S_i$ of candidate path $i$ by Equation (7) and the individual regret $R_i$ of candidate path $i$ by Equation (8) where $w_j$ are the weights of criteria, expressing their relative importance.

  $$\begin{array}{c}{S}_1=0.58418 S_2=0.22109 S_3=0.73089 S_4=0.30043 S_5=0.51799\\ S_6=0.62381 S_7=0.50794 S_8=0.46036 S_9=0.21529 S_{10}=0.09568\\ R_1=0.21111 R_2=0.11111 R_3=0.26667 R_4=0.13333 R_5=0.30000\\ R_6=0.40000 R_7=0.26667 R_8=0.14286 R_9=0.06667 R_{10}=0.09568 \end{array}$$
• Step 6: Compute the values $Q_i$ by Equation (9) where $v$ is introduced as the weight of the strategy of the maximum group utility, here $v$ = 0.5.

  $$\begin{array}{l}{S}^{*}=Mi{n}_j S_j=0.09568, S^{-}=Ma{x}_j S_j=0.58418,\\ R^{*}=Mi{n}_j R_j=0.09568, R^{-}=Ma{x}_j R_j=0.21111, v=0.5\\ Q_1=0.60118 Q_2=0.16538 Q_3=0.80000 Q_4=0.26116 Q_5=0.68242\\ Q_6=0.91571 Q_7=0.62451 Q_8=0.40134 Q_9=0.09415 Q_{10}=0.04352 \end{array}$$
• Step 7: Rank the candidate paths, sorting by the values S, R, and Q, in decreasing order. The results are three ranking lists.
• Step 8: Propose as a compromise solution the candidate path ($a^{\prime }$), which is ranked the best by the measure $Q$ (minimum) if the following two conditions are satisfied: in the case study, the top-k ranking order “P10→P09→P02→P04→P08→P01→P07→P05→P03→P06” is produced. The traffic path P10 is a reasonable path for the deliveryman because its ranking order is the first.

The experiment describes how a VIKOR method was used to analyze candidate traffic routes. A utility model formalizes the expected utility items in the path to compile an expected utility matrix, which presents the expected utility items as the criteria of traffic context to be evaluated. In Steps 1 through 8, the method discovers the ranking order of candidate paths in order to select a suitable traffic-routing path.

5. Experimental Results

This section illustrates the results of our experiment, including rankings of candidate traffic routes produced by various MCDA methods, as well as evaluation and discussion of the results.

5.1. Path Rankings from Different MCDA Methods

Based on the results of experiments that were part of our previous research [37], we compared the mean average precision (MAP) for a decision-maker selecting a reasonable multi-criteria decision analysis method from among various MCDA methods. Our experiment ranked the following MCDA methods based on their mean average precision (MAP) scores: ELECTRE (MAP: 46%), TOPSIS (MAP: 56%), VIKOR (MAP: 56%), PROMETHEE (MAP: 50%), and SAW (MAP: 46%). The mean average precision of the VIKOR method is good, and it can be chosen to carry out the decision-making analysis process of a recommendation system.

In this work, we explored traffic-route recommendation effectiveness and how the proposed approach works with the various multi-criteria decision analysis methods mentioned above.

Table 2. Candidate path ranking order output from our experiments with five MCDA methods.

MCDA Method	Candidate Path Ranking Order
TOPSIS	P10→P02→P09→P04→P05→P08→P07→P01→P06→P03
VIKOR	P10→P09→P02→P04→P08→P01→P07→P05→P03→P06
ELECTRE	P02→P10→P09→P04→{P05, P08}→P07→P01→P06→P03
PROMETHEE	P10→P02→P09→P04→P07→P05→P08→P06→P01→P03
SAW	P10→P02→P09→P04→P07→P08→P05→P01→P06→P03

shows the rankings of the 10 candidate traffic routes using the five MCDA methods. The results of the experiment indicate that “P10” may be the first choice of a deliveryman selecting the best traffic path. Note that the candidate paths enclosed in brackets, “{…}” mean that the indicated paths have an equal ranking order.

5.2. Evaluations and Discussions

Based on open data collected from the Taichung City Bus Station Information system in Taiwan, R.O.C., and metadata of Google Maps route planning, we obtained a data set that includes 19,192 POIs. Removing the duplicate data reduced the size of the data set to 12,452 POIs. We developed traffic context criteria, as defined by the AHP method, including average speed, degree of congestion, distance, and driver personal interest, to construct a context-based social network. Our previous research [37] found that the TOPSIS, VIKOR, and PROMETHEE methods perform better than the ELECTRE and SAW methods. The mean average precision of the VIKOR method is good, and it can be chosen to carry out the decision-making analysis process of a recommendation system. In addition, evaluation of the case study indicated that the proposed approach adapted from the VIKOR method can be implemented most effectively. Table 2 indicates that a reasonable traffic route is “P10” for a deliveryman. In our review of the literature, García et al. [38] recommended a target that satisfied the user’s preferences based on his or her configuration. Overall, our work used multi-criteria decision analysis to obtain a ranking of candidate paths and the approach was effective at recommending an appropriate path to the deliveryman. Lin et al. [39] recommended use of a web service via collaborative filtering and quality-of-service considerations. Our own work recommended a reasonable path based on multiple context criteria that a deliveryman would focus on. The quality of the service is the key concern when determining the most appropriate path from a set of candidates. We collected the ten deliverymen’s feedback and used the confusion matrix to evaluate. Experimental results show that the precision is 79.65%, recall is 80.70%, and F1-score is 80.17% in order to prove the vehicle-route recommendation effectiveness.

6. Conclusions

In the urban logistics areas, the proper vehicle-route selection is a key challenge affecting its quality. The main problem is any delay may cause disasters, especially in cold-chain logistics. This study uses information and communication technology to design an approach to optimize traffic-route selection as part of urban-logistical planning. A context-based social network is constructed to provide symmetry/asymmetry traffic context items: the average speed, degree of congestion, distance, and deliveryman personal interest, as defined by the AHP method of multi-criteria decision analysis. A deliveryman can select a reasonable path to transport products based on recommended rankings of candidate routes from multi-criteria decision analysis. Based on the experiment results, we believe that the contribution of this work is actually to optimize traffic-route selection as part of urban-logistical planning in smart cities. To sum up, the main contributions of this paper are as follows.

• To solve the product delivery delay problems in the urban logistics areas, this work proposes a novel systematic framework of using symmetry/asymmetry traffic context data and multi-criteria decision analysis to optimize vehicle-route selection as part of urban-logistical planning.
• The paper uses data mining technologies to process the huge amount of traffic context data from official urban transportation databases and metadata of Google Maps route planning in order to construct a context-based social network. Since the traffic features and routing criteria have symmetry/asymmetry properties to influence the decision of path selection, we adopt multi-criteria decision analysis to generate a ranking of candidate paths based on an evaluation of traffic data in context-based social networks to recommend to the deliveryman. The deliveryman can select a reasonable path for delivering products according to the ranking of candidate paths.
• The experimental results show the path recommendation of the work’s precision is 79.65%, recall is 80.70%, and F1-score is 80.17% to prove the vehicle-route recommendation effectiveness. It helps deliverymen send products as soon as possible to customers to retain the quality, especially in cold-chain logistics. The paper optimizes traffic-routing solutions for improved service quality of urban logistics in smart cities.

The limitations of this work are as follows.

• Expiry of collected data may cause the recommendation to have unexpected results. The open data in official urban transportation databases may update regularly but not immediately.
• If the traffic features are not contained in official urban transportation databases and metadata of Google Maps route planning, we cannot design the comprehensive criteria to evaluate, e.g., weather influence, traffic incidents, temporary road construction, etc. This work cannot handle complex real-time traffic features.
• This work does not consider the adaptive mechanism to adjust the weight configuration of criteria in multi-criteria decision analysis. The weight configuration of criteria may influence the path recommendation.

In future work, we intend to investigate the following issues:

• As for now, the proposed approach is functional modularity but it lacks the space and time complexity analysis of each algorithm to identify its pros and cons.
• Using more comprehensive criteria with symmetry/asymmetry concepts, such as traffic status, logistics vehicle, deliverymen habits, and customer requirement features, in an effort to analyze usage scenarios more realistically.
• The human emotional analysis and deep learning models can be explored to strengthen the effectiveness of the proposed approach.
• Using the unified theory of acceptance and use of technology (UTAUT) to verify the user acceptance of this paper’s novel approach.