Abstract
Load balancing is a very important concept in cloud computing. In this work, studies are conducted on workload traces at Los Alamos National Lab (LANL). The jobs in this trace are asymmetric in nature as most of them have small time limit. Two hybrid algorithms, a Genetic Algorithm combined with First Come First Serve (GA_FCFS) and Genetic Algorithm combined with Round Robin (GA_RR), are proposed here. The results obtained are compared with the existing First Come First Serve (FCFS), Round Robin (RR) and Genetic Algorithm (GA). Makespan and Resource Utilization are used for the comparison of results. In terms of Makespan, it is observed that GA_RR outperforms the other methods for all the batch sizes. Although the performance of GA_FCFS is much better than that of the other three well-established algorithms FCFS, RR and GA, it is still worse than that of the GA_RR algorithm for all the cases. GA_RR performs best in terms of Resource Utilization also and GA_FCFS is a close competitor. Overall, GA_RR outperforms all the other algorithms.
1. Introduction
The usage of the internet has grown tremendously in our day and age, and consumer needs are changing radically. A lot of computational resources are required to meet the needs of a wide range of clients. Through outsourcing, resources are made available to clients as a service in cloud computing (see Figure 1) [1,2].
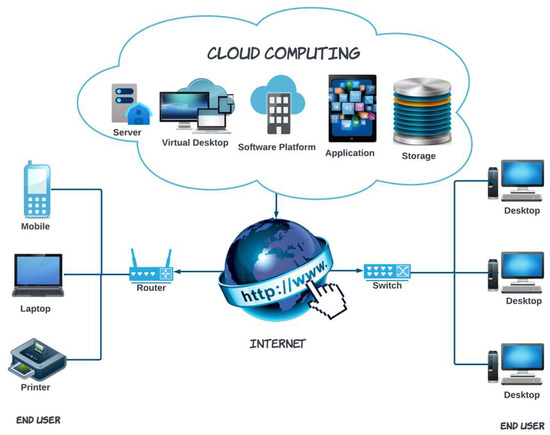
Figure 1.
Cloud Architecture.
Due to the distributed nature and flexibility of cloud resources, clients receive flawless services. Virtual machines, often known as VMs, are shared resources that are virtualized [3], and they replicate a physical server to provide isolated hardware and software. Cloud users and cloud service providers [4] are the two key stakeholder groups, and cloud service providers must guarantee they achieve the highest level of client satisfaction by offering on-demand services [4].
Requests from clients are viewed as jobs that need to be allocated to the relevant virtual machine (VM). Task scheduling is therefore among the most crucial elements of cloud computing. Numerous Quality of Service criteria have to be assessed to ascertain the extent of appropriate scheduling [5]. The computational QoS criteria of maximum resource use, shortest makespan, and high throughput have a substantial impact on task scheduling. The optimization of job scheduling is aided by the improvement of these indicators. Resource usage is enhanced by load balancing [3], which equally distributes the load among various resources. Client requests are considered tasks that must be meticulously scheduled [3,6].
The concept of load balancing is used to prevent cloud resources from being overused or underused. Due to inadequate load balancing [3,7], the cloud system loses computing capacity as some resources remain inactive for an extended period of time. Idle resources are to be blamed for rising financial losses [7,8] and increasing CO2 emissions. Better load balancing can help enhance makespan, and throughput thus benefits equally the client and the cloud service provider. In cloud computing, schedulers define the mapping of various jobs that arrive at far-off data centers. The best mapping occurs when tasks are sent to the best machine for the job since different jobs have distinct computational requirements. Task scheduling is categorized as an NP-hard problem [9] as varied task mapping is attainable on heterogeneous virtual machines. In service-oriented clouds, Service Level Agreements [10] (SLAs) are used to negotiate services among service providers and customers. Static schedulers can be quite beneficial in this situation because the needs of the client are already known [11]. Meta-heuristic [1] and Heuristic schedulers [3,10] are employed in this field to determine the best scheduling. Because of its diversity, meta-heuristics can best achieve the goal of improving results while examining a wide search space of potential solutions. Meta-heuristics are better optimization approaches because they search for a solution iteratively and have the ability to become more efficient over time [12,13]. Heuristics, on the other hand, frequently draw hasty conclusions based on limited evidence. It is common practice to explore and make use of the probable mapping search space using schedulers with meta-heuristics [1]. The most prevalent meta-heuristics techniques used in cloud computing (CC) for job scheduling are Symbiotic Organism Search (SOS), Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Ant Colony Algorithm (ACO), etc. Owing to excellent search capabilities, GA-based schedulers have been employed for task scheduling [14,15,16].
In order to increase throughput, makespan and load balancing in task scheduling, hybrid schedulers have recently become available. Numerous hybridization strategies for schedulers can use Modified Genetic Algorithm (MGA) [15] combined with the Greedy approach (MGGS) to direct the optimization process [11,17,18]. The amount of load balancing is calculated as a fitness criterion. Effectively balancing the load in a cloud setting can be beneficial to the Cloud service provider (CSP) and high throughput with improved makespan can be beneficial for both the user and the CSP. In order to attain both load balancing and a shorter makespan, multi-objective optimization is needed [1].
In this work, the real workload traces at Los Alamos National Lab (LANL) are considered. These jobs terminate in three different states: they can either be successful, may be cancelled or may time out. A job may be cancelled either by the user or due to some hardware or software failure. Users provide a time limit for each submitted job and usually try to keep this value small as smaller jobs are assigned priority by the scheduler. If the user-provided time limit is reached before the execution is completed, the jobs time out. This trace is asymmetrical in nature as most of the jobs are of smaller size.
Therefore, the main objective of this work is to develop an algorithm which works well for asymmetrical jobs and attempts to reduce the makespan along with optimizing the energy requirement. The significant contributions are as follows:
- Two hybrid algorithms based on Genetic Algorithm for multi-objective optimization for reducing makespan and energy optimization are proposed.
- The flowchart for the algorithms is presented and the algorithms are simulated using CloudSim simulator.
- Experiments are performed for FCFS, RR, GA, GA_FCFS and GA_RR algorithms for the real workload traces at Los Alamos National Lab (LANL).
The remaining paper is arranged as follows. Section 2 includes a review of the literature. Section 3 describes the proposed research methodology. Section 4 describes in detail the proposed Hybrid Genetic algorithm. The results obtained are discussed in Section 5. Section 6 enlists the conclusions drawn from the work.
2. Literature Review
In cloud computing, several solutions have been developed to address a range of task scheduling challenges. In this domain, heuristics and meta-heuristics have been employed. Makespan is the most commonly used parameter for the evaluation of any algorithm. Apart from it, load balancing and resource utilization are also frequently used. The following are some of the heuristic approaches and meta-heuristic approaches found in the literature.
2.1. Heuristic Approaches
To address a specific issue, heuristic algorithms are developed. Heuristics do not examine all or a portion of all possible solutions in optimization problems, which often have an extensive range of potential answers. Because a heuristic solution often has a mathematical formulation at its core, heuristics are frequently employed in optimization. The below portion explores the algorithms in which the heuristics are employed to develop the possible solution to the problem.
To evenly distribute workloads between various VMs, Min-Min Load Balanced Algorithm (MMLB) was developed [17]. It employs a classic Min-Min approach where a job is assigned to a certain Virtual machine that has the fastest completion time. Following the classic Min-Min approach, MMLB’s second stage remaps overburdened virtual machine tasks to underloaded virtual machines. The completion time of each individual VM is used to determine whether a VM is overloaded or underloaded. In an overloaded virtual machine, the shortest job is moved to the virtual machine where it will finish in the lowest amount of time. While determining whether a VM is overloaded, we do not consider the actual load, and hence there is still room for enhancement in load balancing.
Travelling Salesman Algorithm for Cloudlet Scheduling TSCS [1,19] is based on the well-known travelling salesman method incorporating three different stages. By creating clusters for each one of the available VM, the vast size problem is scaled down to a reasonable level in the initial clustering phase. Each cluster obtains cloudlets that are either lesser than or equal to the full load of the cluster. In the next step, the issue is subsequently shifted to the Traveling Salesman Problem (TSP) domain. The closest neighbor strategy is used in the third phase; based on Cluster Execution Time, cloudlets are assigned to virtual machines. Like adjacent neighbours, each node is accessed; hence, TSCS is better suited to situations when we have a lesser number of clusters.
In order to boost efficiency while reducing energy use, a heuristic known as the Energy-efficient Task Scheduling Algorithm (ETSA) was introduced in [20]. The use of resources is considered to be a significant barrier to raising energy consumption. The first phase of ETSA, which consists of three parts, determines the estimated time of completion and the resource busy period. The tasks are then mapped to VMs in the third and final step after the second step choose the finest VM according to the timings predicted in the first step. However, because resource consumption occurs primarily on the basis of time, it cannot drastically improve resource use.
In [21], a probabilistic load-balancing scheduler with two stages was presented. Non-descending order of size is used to arrange the tasks. The second stage involves allocating tasks to virtual machines. The subsequent tasks are mapped to VMs with the lowest starting load, and the primary load is revised after the assignment.
A Resource-Aware Load Balancing Algorithm (RALBA) [3] determines a VM’s proportion of the available processing power and distributes tasks in accordance with that share. It is divided into two stages: spill and fill schedulers. In this stage, any VM may be given a choice from a pool of jobs based on its portion of the workload. The biggest task is mapped to the VM with the maximum VM share. In the second stage of RALBA, the remaining jobs are mapped based on their earliest completion time.
2.2. Meta-Heuristics Approaches
In the case of NP-hard problems, Meta-Heuristics for Cloud Scheduling optimization techniques are used to investigate a huge search space of potential solutions [1]. Although they are problem-independent, meta-heuristics are altered for use in optimization problems.
In Longest Cloudlet to Fastest Processor (LCFP) algorithm in the initial stage of population generation, a random number is assigned [12]. For finding the optimal solution with a better makespan, the randomness and the properties of the Heuristic are merged to obtain a more diverse population.
By combining Max-Min and Min-Min in GA, the Load Balancing Aware Genetic Algorithm (LAGA) tried to improve the issue of load balancing [15]. Using the algorithms Max-Min and Min-Min, LAGA creates only one chromosome. The major goal of combining Min-Min and Max-Min is to combine the benefits of both strategies in order to enhance makespan and other response times. However, in order to improve load balancing, the fitness function takes into account the overall time required by resources.
A redesigned GA with improved Max-Min was proposed in [22]. By using improved Max-Min, the virtual machine with the least processing power is subjected to the maximum workload. The norm for choosing the largest task, on the other hand, is established on average execution time. During the population initialization stage, improved Max-Min is used for a better makespan.
For improved makespan, GA with Tournament Selection (TS-GA) algorithm was presented in [13], and it performed much better than the round-robin heuristic in terms of resource consumption and makespan. Random Make Genetic Optimizer (RMGO) algorithm was suggested to improve load balancing in [23]. In RMGO, Suffrage, Min-Min and Max-Min are three heuristics that are used to initialize the population. Even though the fitness function excludes the need for load balancing, RMGO shows significant improvement in makespan and load balancing.
Adaptable Incremental Genetic Algorithm (AIGA) [4] has adaptive crossover and mutation possibilities. The chances are determined by the fitness of the best chromosome, the number of iterations and the size of the population. When compared to regular GA, AIGA offers enhanced performance. To optimize resource use, the Improved Genetic Algorithm (IGA) [24] takes into account idle resources and monitors them. Tasks are allocated to all the idle resources till no more idle resource is found. The remaining tasks are assigned to resources according to their minimum projected completion time. In IGA, fitness is calculated based on resource consumption.
For enhancing the makespan and load balancing, a hybrid GA called Modified Genetic Algorithm (MGA) paired with Greedy Approach (MGGS) [14] was proposed. Although MGGS considers makespan to be a chromosome’s fitness criterion, greedy strategy, a load balancing procedure, is activated on chromosomes to prevent overuse of the available resources. Load balancing is achieved by ordering virtual machines according to their execution time. To activate load balancing, the shortest job allocated to the VM with the longest finishing time is mapped to a virtual machine with the shortest execution time. This process is repeated till the VM with the shortest execution time becomes the VM with the longest execution time. Although this algorithm enhances load balancing, it is computationally expensive.
A scheduler based just on GA, Efficient Task Allocation based on Genetic Algorithms (ETA-GA) [25], was proposed to decrease failure in network delay and improve makespan. The GA parameters are reflected in order to fine-tune the objective function. However, in the case of ETA-GA, the chances of selecting the best chromosome are highest, which could lead to a discrepancy between exploration and exploitation. Two meta-heuristics were combined in Ant Colony Optimization with Hybrid Genetic Algorithm HGA-ACO [26], Ant Colony Optimization and Hybrid Genetic Algorithm. A queue of jobs is monitored by a utility scheduler and is arranged according to memory and execution time. The utility scheduler selects the best chromosomes, which are then delivered to ACO, where the final chromosomes are subjected to mutation and crossover. This method employs two completely working meta-heuristics.
A Hybrid-Particle Swarm Optimization (H-PSO) [27] was presented in this method. In PSO, a method called differential evolution is employed for upgrading the velocity. Hybrid PSO defines a multi-objective fitness function that includes makespan and use of resources. To enhance the PSO’s performance, the Shortest Job to Fastest Processor (SJFP) heuristic was incorporated in [28]. SJFP is only used during the population initialization phase. SJF technique outplays GA and PSO with regard to makespan. In [29], an enhanced PSO was proposed for optimizing resource use. As stated by the author, PSO’s traditional convergence speed can be increased by adding Simulated Annealing (SA) with it, which also results in better resource usage. Personal worst is introduced in the enhanced version, which is identical to PSO’s traditional personal best. Merging SA into regular PSO improves the goal of better resource usage
To attain improved load balancing, the honeybee model is combined with PSO [9]. The degree of load balancing between VMs is calculated by means of a statistical measure of standard deviation. In this strategy, attaining honey from an empty origin is similar to overloading. The load is later moved from overloaded VMs to underloaded VMs. To improve the makespan, Discrete Symbiotic Organism Search DSOS [30] approach has been proposed. Three processes—mutualism, commensalism, and parasitism—are used to illustrate the symbiotic interdependence of animals. The DSOS performs better than a number of PSO versions when their respective performances are compared.
In [31], Deep Reinforcement Learning with Long Short-Term Memory (DRL-LSTM) approach was suggested to gain an understanding of optimal scheduling policy on the basis of response. In this technique, task execution is examined, and the model is then taught to obtain enhanced resource use. In comparison to other strategies that address time-sensitive tasks, DRL-LSTM improves prediction accuracy and resource utilization.
A job scheduler based on supervised Artificial Neural Network (ANN) [32] was proposed to reduce energy consumption, leading to better resource usage. The training set is created by applying GA. A back-propagation ANN is used to normalize both the energy consumption and job completion times in order to determine the mapping. Based on training data, the scheduler displays an enhancement in precision.
The approach that the authors proposed in [33] makes use of load-balancing methods, new genetic operators, and updated genetic operators. To maximise resource efficiency at execution time, the algorithm described in this study makes use of a load-balancing routine. The findings show that the suggested algorithm executes task scheduling with the least amount of time and money spent when compared to other algorithms of this field. In [34], the author suggests three major contributions: first. a Heterogeneous Initialized Load Balancing (HILB) method is suggested. Second, combining the HILB and genetic algorithm to create a Hybrid Load Balance based on Genetic Algorithm (HLBGA) is proposed. Finally, GA is performed using a newly developed fitness function that minimizes the load deviation. While using cloud resources, the suggested approach is applied in both homogeneous and heterogeneous resource scenarios.
In [35], Multi-resource Load Balancing Algorithm (MrLBA) is proposed. The suggested technique, which is based on Ant Colony Optimization (ACO), targets makespan and cost while maintaining a well-balanced system. By maintaining a balanced load across resources, MrLBA decreases execution time and cost while making efficient use of the available resources. To manage cloud resources, state-action-reward-state-action learning and genetic algorithms are combined in [36]. The intelligent agents schedule the tasks in the first phase by investigating the workflow while they are learning. The resource provisioning stage follows with the assignment of each resource to an agent and attempts to maximize its consumption during the learning process of its related agent. The suggested method’s agents are brought together using a genetic algorithm, which also achieves global optimization. The approach shortens the makespan and improves load balancing and resource consumption. An improved ant-lion optimization (ALO) approach hybridized with particle swarm optimisation (PSO) technique is proposed in [37] to optimize a workflow scheduling specifically for the cloud. The goal of the research is to improve workflow scheduling. Evaluation criteria for enhancement processes include cost, makespan and load. According to the results, the suggested technique reduces costs by 10% for PSO, 20% for ALO, 9.8% for GA-PSO, 12% for GA and 30% for RR. The proposed solution decreases load balancing and makespan by 10% compared to ALO, 8% compared to GA-PSO, 35% compared to RR, 45% compared to GA and 20% compared to PSO.
3. Proposed Research Approach
One of the main concerns in cloud computing is task scheduling. The diverse nature of tasks requires heavy computing demands. Virtual machines (VMs) require task scheduling. Quality of Service (QoS) metrics are essential for load balancing and scheduling makespan. In order to increase makespan and load balancing, this research presents a revolutionary load balancer. The architecture of Genetic Algorithm-based hybrid algorithms GA_FCFS and GA_RR is discussed in this section. The logic for combining heuristics to improve load balancing is discussed.
3.1. Task Scheduling
Task scheduling, which is an important part of cloud computing, seeks to maximize the usage of virtual machines (VMs) whilst cutting datacenter operational expenditures, which results in considerable improvements in QoS parameters and general performance [6]. The job of the scheduler is to decide on the resources that are to be allocated to a system. In the cloud, there are three major entities. Overall, the client is the user who must accomplish a task on one hand. On other hand, the resource provider makes infrastructure available for the transfer or storage of data as well as the execution of programs [4]. The broker is in charge of managing customer data on resources and coordinating the execution of applications among clients and resource providers [38].
The scheduler defines a mapping scheme once tasks arrive in data centers. A cloud broker receives a mapping scheme, which is then used to assign jobs to virtual machines. Figure 2 depicts a cloud environment in which the scheduler determines an appropriate mapping for incoming jobs.
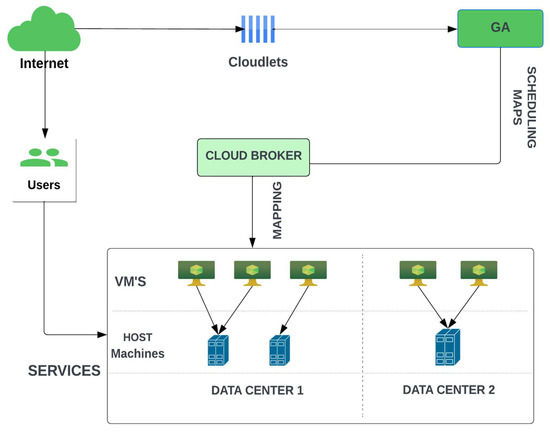
Figure 2.
Cloud Environment.
The challenge of task scheduling is to efficiently assign, plan and distribute a wide variety of jobs to a large number of virtual machines while completing all the tasks in a short period of time [39,40]. As demonstrated in Equation (1), the cloud environment depicted as CS (Cloud System) consists of () physical machines (PM) and () virtual machines on each physical machine.
where PMi (i = 1, 2,…, ) represents the physical machines working in the cloud, demonstrated in Equation (2):
in which VMk (k = 1, 2,…, ) denotes the virtual machine (VM). stands for the entire quantity of VMs, and for cloud’s kth virtual machine device. The criteria in Equation (3) are used to define the characteristics of the kth VM:
where idk is the identifier of the VM, userIdk is the identifier of the user whose job has been assigned to the VM, mipsk is the processing power of the physical machine in million instructions per second, pesNumberk is the identifier of the physical machine on which the VM exists, ramk is the size of RAM, bwk is the bandwidth of the VM, sizek is the VM size in MB and vmmk is the virtual machine manager [41,42].
CS = [PM1, PM2, ………, PMi, ……., PMNpm],
PM = [VM1, VM2, ………, VMk, ………, VMNvm],
VMk = [idk, userIdk, mipsk, pesNumberk, ramk, bwk, sizek, vmmk],
Tasks or cloudlets are defined as given in Equation (4):
where represents the total number of tasks submitted by the client.
virtual machine’s completion time, , is the amount of time spent in executing the current task after the previous task was completed on the given machine. It is given by the Equation (5):
where i (in the range of 1 to m) stands for the total number of virtual machines [40,43,44], and j (in the range of 1 to n) stands for the total number of tasks.
3.2. Performance Parameters
3.2.1. Makespan
The duration of time required to complete all jobs is known as the makespan. In other words, the length of time between the start and finish of a sequence of tasks is known as the makespan. If the makespan value is low, the scheduler is offering virtual machines the best and most efficient planning stages for jobs. However, the scheduler does not provide devices with the best and most effective task-planning steps if the makespan has a larger value [40]. Equation (6) determines the makespan:
3.2.2. Resource Utilization (Ru)
Resource Utilization [45] is a performance statistic or metric that is employed to calculate how well resources and devices are being used. A high price or value for utilization indicates that the service provider makes the utmost profit. It can be calculated using Equation (7) below:
4. Hybrid Genetic Algorithms
In this work, two hybrid algorithms based on Genetic Algorithms, GA_FCFS and GA_RR, are proposed. These algorithms take 20 chromosomes in the initial population, but instead of generating all these chromosomes randomly, they generate 19 chromosomes randomly, take the last chromosome using First Come First Serve (FCFS) in the GA_FCFS algorithm, and take the last chromosome using Round Robin (RR) in the GA_RR algorithm.
4.1. Task-Scheduling Policies
4.1.1. Time-Shared
Time-shared can be explained as a policy in which multiple jobs are allocated to a processor where the allocated job runs for some period of time before being preempted to allow other jobs to run [45,46]. In other words, time sharing means the central processor is made available to each entity in turn for a set amount of time and that entity is interrupted when the allotted time has elapsed, and the next entity then starts its execution.
4.1.2. Space-Shared
The concept of space-shared is that the resource is distributed among different entities at the same time [47,48].
Each of these entities holds its share of resources and executes till completion.
The scheduling policies used in this work are as specified below:
- Cloudlet Scheduler—Space-Shared;
- VM Scheduler—Time-Shared;
- PE to VM scheduling in host—Space-Shared.
4.2. Proposed Algorithms
In this work, we suggest two hybrid algorithms based on Genetic Algorithm for targeting the problem of load balancing. The reason for using the Genetic Algorithm is that the data that are mostly available for the job scheduling problem suffer from three main problems: availability and diversity, workload variability and effect of accuracy on final performance [49,50]. A lot of research is being conducted in the domain of machine learning for load balancing, but due to these limitations, it has not been a great success till now.
The flowchart for the proposed hybrid algorithm after fine-tuning the GA parameters is depicted in Figure 3, and its various components are discussed below. We arrived at the values of various parameters used in the Genetic Algorithm by using the ANalysis Of VAriance (ANOVA) statistical technique.
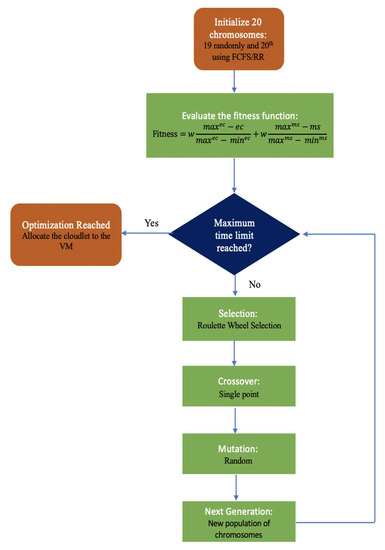
Figure 3.
Flowchart for the proposed GA_FCFS and GA_RR algorithms.
4.2.1. Parameter Tuning in Genetic Algorithm
The performance of Genetic Algorithm depends on its parameters (Population size, Mutation Probability, Crossover Probability, etc.). In this work, the Analysis of the variance (ANOVA) is used as the statistical technique for fine-tuning the GA parameters. This technique analyses the variations in mean to determine the effect of one or more than one quantitative or qualitative variables (factors) on any quantitative response. Then, the values of Sum of Squares, Degree of Freedom, Mean Square, F-ratio, Significance Level (p-level) and F-critical are determined. For the null hypothesis to hold true, the obtained p-level should be less than or equal to a threshold value (p-value). In this work, the threshold value (p-value) was taken as 0.05. This means that if the p-level obtained for any factor is less than 0.05, then the various values of that factor are statistically significant with a confidence level of 95%.
The variables (factors) used in this work for carrying out the statistical test using ANOVA are Number of Iterations, Crossover Probability, Mutation Probability, Type of Crossover, Type of Mutation and Type of Selection. The values of these factors are listed in Table 1.

Table 1.
Variables used in ANOVA.
Two-factor ANOVA was used in this work for carrying out the statistical analysis for each of the factors separately. The implementation was carried out in Microsoft Excel and the results obtained for each factor are depicted in Table 2 below.

Table 2.
ANOVA table for the analysis of effect of various factors in Genetic Algorithm using the fitness function.
The fitness function normalized in the range of [0, 1] was used for the comparison of the results. As can be seen from Table 2, the significance level (p-level) for type of crossover and type of mutation is greater than 0.05. This means that these factors are not having significant impact on our results. On the other hand, the number of iterations, crossover probability, mutation probability and the type of selection have higher value of F-Ratio and lower value of significance level (p-level). Hence, these factors have greater relevance.
Once the importance of these factors was established, further analysis was carried out for each of these factors using Duncan’s Multiple Range Test. In this test, comparisons are made for each value of a particular factor to determine which value has the maximum impact. This helps to determine the influence of these factors on the performance of the Genetic Algorithm. The results obtained from this statistical method for each factor are depicted in Table 3.

Table 3.
Duncan’s Multiple Range Test results for various factors in Genetic Algorithm using the fitness function.
Based on the results obtained from ANOVA, it was observed that the Number of iterations has significant impact on the execution of GA, and the MRT table shows that the value of 1000 yields significantly different result. Hence, this value was considered for further investigation.
The variable Crossover Probability has significant impact as established by ANOVA, and for this, the MRT table shows that the value 0.8 provides a significantly different result and hence this value was considered for further evaluation of the algorithm. Mutation Probability also has a significant impact on the working of the algorithm, and from the MRT table, it can be seen that the values 0.1 and 0.01 are yielding significantly different results. Out of these two values, 0.01 provides minimum mean, and hence it is the optimum value for further investigation.
Although Type of Crossover and Type of Mutation did not have any significant impact as was concluded for ANOVA, Single Point Crossover and Bit Flip Mutation were considered in this work as they are providing better mean value. As far as the Type of Selection is concerned, Roulette wheel method provides significantly different result, and hence it is considered for the rest of the calculations.
Therefore, the final values for the various factors obtained from ANOVA and Duncan’s MRT test are given in Table 4.

Table 4.
Final Values of the variables.
The detailed description of the steps of the Algorithms 1–5 is given below.
4.2.2. Encoding
The scheduler has to map a number of jobs after receiving them as input in batch mode. Chromosomes exist in GA, and they must be correctly encoded in order to represent the job scheduling issue. Task scheduling can use GA in a variety of ways. Discrete encoding, also referred to as real number encoding, is used in this work. A vector of 1n dimensions is generated through discrete encoding where n represents the total number of tasks. It indicates that there is a corresponding value of genes that reflects the VM number for every task/job. Genes only have single allele, and the total number of VMs (m) is their allele range.
It is assumed there are six tasks represented by T1, T2, T3, T4, T5, and T6. Three virtual machines (R1, R2, and R3) must be assigned to tasks. We let the chromosome be v = 3, 2, 3, 1, 2, 2. This indicates that T1 is allocated to R3. The corresponding , , , , and values are assigned to T2, T3, T4, T5, and T6. There are three task pools since there are three VMs. R1 only receives one job in the mapping defined for chromosome v, so the pool {}, { , } and = {}. The aim of GA_FCFS and GA_RR is to identify a chromosome that represents a mapping that is best suited for achieving better and improved makespan and resource utilization.
Proposed Hybrid Virtual Machine Allocation policy for load balancing
| Algorithm 1: Hybrid Virtual Machine Allocation Algorithm |
| Input: |
| -Cloudlet list: The tasks to be assigned to the VMs; |
| -VM list: The total number of virtual machines; |
| -Host list: Total number of hosts in the datacenter; |
| -GA parameters: Selection, Crossover, Mutation. |
| Output: |
| -VM allocation list. |
| Method: |
| -Read the workload traces from Los Alamos National Lab (LANL); |
| -Create a container for storing the virtual machines; |
| -Create VMs with parameters (id, userId, mips, pesNumber, ram, bw, size, vmm) with space shared scheduling policy for cloudlets; |
| -Create a container for storing the cloudlets; |
| -Read Cloudlets from the workload traces. |
| Main program: |
| Step1: Initialize the CloudSim package before creating any entity; |
| Step 2: Create Datacenters; |
| Step 3: Create Datacenter Broker; |
| Step 4: Create VMs and send them to broker along with the cloudlets: Sort the cloudlets based on their completion time; Sort the VMs based on their MIPS value; Assign longest task to fastest processor. |
| Hybrid Genetic Algorithm: Step 1: Initial Population Generate the initial population of 20 chromosomes: Generate 19 chromosomes randomly; Take the 20th chromosome using FCFS. |
| Step 2: Fitness Function Makespan and energy consumption are used for calculating the fitness function: |
| Step 3: Selection Use roulette wheel selection. |
| Step 4: Crossover Use single-point crossover. |
| Step 5: Mutation Carry out the mutation operation. |
| Step 6: Check the termination criteria If time <1,000,000 ms, Go back to step 2. Else Print the final allocation and the makespan. |
4.2.3. Fitness Function
The fitness of the solution is calculated with the minimum and maximum values of energy consumption and makespan. The weight factor is used for each parameter. In the experiments of this article, an equal weight, i.e., 0.5 was used for all parameters. Equation (8) is used to calculate the fitness value.
| Algorithm 2: Fitness Function |
| Initialize: k = −1, w1 = 0 |
| make[] = no_cloudlets |
| makespans[] = no_chromosomes |
| for i = 0 to no_chromosomes do |
| makespans[i] = 0 ec[i] = 0 |
| for i= 0 to no_VMs do |
| make[i] = 0 |
| for m = 0 to no_chromosomes do |
| k++ |
| for q= 0 to no_VMs do |
| for n = 0 to no_cloudlets do |
| if a[m][n] == q |
| make[w1] = make[w1] + etc[n][q] |
| w1++ |
| w1 = 0 |
| makespans[k] = maximum[make] ec[k] =maximum[ec] |
| for w = 0 to no_chromosomes do |
| makespans2[w] = (makespans[w] + maximum[ec])/2 |
4.2.4. Selection Operator
GA_FCFS and GA_RR incorporate the proportionate selection operator with a few simple changes. A roulette wheel spin is an analogy for proportionate selection, with the size of the pie indicating the value of a particular chromosome across the entire population. Every chromosome has a chance to be chosen in a typical proportionate selection operator. The best chromosomes, however, can be selected more often than others since they have high proportions.
The final chromosome to be included is chosen using the selection operator, and there may be further possibilities to choose the healthiest of those obtained with previous methods. Through the selection operator, two chromosomes are chosen, and they then take part in the production of offspring. If the same two chromosomes are selected as parents repeatedly, the selection mechanism has to be re-performed in order to select a different pair.
| Algorithm 3: Selection |
| total_fitness = 0 |
| for w = 0 to no_chromosomes do total_fitness+=makespans[w] |
| current_min_makespan = makespans2[0] |
| for w = 0 to no_chromosomes do if (current_min_makespan > makespans2[w]) current_min_makespan = makespans2[w] |
| throughput = no_cloudlets/current_min_makespan |
| current_min_makespan = current_min_makespan + (1/throughput) |
| Initialize count, count_same, ind, countm to 0 |
| while (!(abs_value(min_makespan) == abs_value(current_min_makespan) && count_same == 3)) do for m = 0 to no_chromosomes do for n = 0 no_cloudlets do final_matrix[m][n] = b[m][n] for = 0 to no_chromosomes do final_makespans2[q] = makespans2[q]; min_makespan = total_fitness |
4.2.5. Crossover Operator
Single-point crossover is implemented in both the hybrid algorithms proposed in this work. For this, a pair of chromosomes is selected, and their values are swapped from a particular point known as the crossover point. The offspring generated after crossover is again evaluated using the fitness function. The crossover probability is taken as 0.8 in this work.
| Algorithm 4: Crossover |
| Initialize temp1 = 0 |
| for m = 0 to no_chromosomes do |
| for n = 0; o = no_VMs to n < no_VMs && o < no_cloudlets do temp1 = b[m][n] b[m][n] = b[m + 1][o] b[m + 1][o] = temp1 end for m = m+2 end for |
4.2.6. Mutation Operator
The genetic algorithm uses a mutation operator to ensure that the optimization is not stuck in some local minima. For this, few values of the chromosomes are taken randomly and flipped. Our algorithms use arbitrary readjustment with a mutation rate of 0.01.
In this case, k is the population size.
| Algorithm 5: Mutation |
| for m = 0 to no_chromosomes do |
| b[m][rand.nextInt(no_VMs] = rand.nextInt(no_VMs) |
| end for |
5. Results of the Experiment
In this section, the details of the dataset and the experimental setup are described. Additionally, the benchmark approaches are described, followed by the findings and any relevant comments.
5.1. Experimental Setup
For experimentation, the cloud-based environment is simulated using CloudSim 3.0.3 [43]. Settings similar to the benchmark procedures are used for all the experiments. As a stopping condition, the number of iterations for all the meta-heuristic procedures is fixed at 1000. In CloudSim, two data centers were established. There is a total of 14 VMs and 2 host computers in each data center. The host computers have 200 GBs of RAM. Each machine, including the hosts, runs a Linux operating system. These devices have a 100,000 Mbps bandwidth. For testing, CloudSim’s time-sharing VM scheduling mechanism is employed. The VM, Host and Datacenter characteristics are summarized in Table 5.

Table 5.
Host, VM and Datacenter Characteristics.
Real workload traces from Los Alamos National Lab (LANL) were used in this experiment. The results were obtained for batches of 100, 200, 300, 400, 500, 600, 700, 800, 900 and 1000 cloudlets extracted from the real-time data.
5.2. Benchmark Techniques
The results of the three existing algorithms, First Come First Serve (FCFS), Round Robin (RR), and Genetic Algorithm (GA), are compared with those of the newly proposed algorithms. In this work, a hybrid of the Genetic Algorithm with the other two algorithms was proposed and the results were compared. The proposed algorithm takes 20 chromosomes in the initial population, but instead of generating all these chromosomes randomly, it generates 19 chromosomes randomly and takes the last chromosome using FCFS in the GA_FCFS algorithm and selects the last chromosome using Round Robin (RR) in the GA_RR algorithm. The crossover probability in GA was taken as 0.8 and the mutation probability was 0.01.
Table 6 shows the results obtained for all five algorithms in terms of resource utilization and makespan.

Table 6.
Makespan and resource utilization.
Figure 4 shows the results obtained for the makespan for different batch sizes of our workload. In this figure, the x-axis depicts the number of cloudlets and the y-axis depicts the makespan in seconds. It provides a comparison of makespan for the five algorithms, FCFS, RR, GA, GA_FCFS and GA_RR. It can be seen from this figure that GA_RR outperforms the other methods for all the batch sizes. Although the performance of GA_FCFS is much better than that of the other three well-established algorithms, FCFS, RR and GA, it is still worse than that of the GA_RR algorithm for all the cases. Interestingly, it can be seen that although First Come First Serve (FCFS) performs better than RR for batch size less than or equal to 500, RR outperforms it for larger batch sizes. On average, GA_FCFS outperforms FCFS, RR and GA by 57.01%, 57.05% and 38.33%, respectively. Similarly, GA_RR outperforms FCFS, RR and GA by 63.07%, 62.95% and 48.09%, respectively. Both these results are depicted graphically in Figure 5.
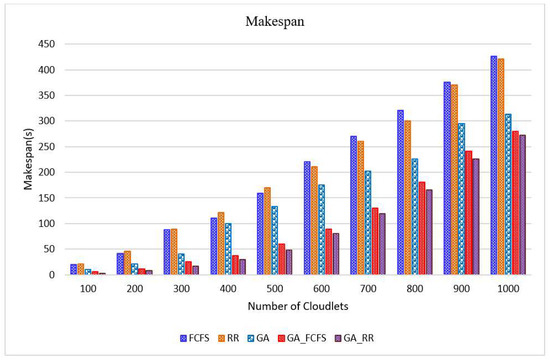
Figure 4.
Makespan obtained for various algorithms for different numbers of cloudlets.
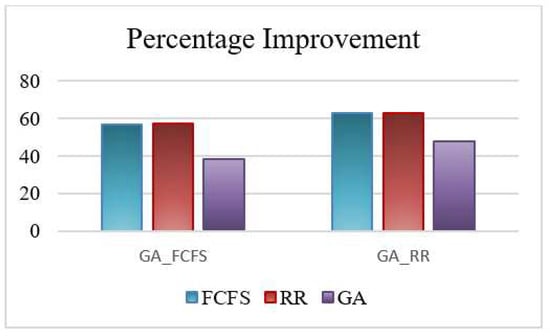
Figure 5.
Percentage Improvement of GA_FCFS and GA_RR based on Makespan.
The average resource utilization ratio is an important parameter which provides the measure of how well resources and devices are being used. It also signifies the amount of load balancing for any algorithm. It is a very important QoS parameter and its value lies in the range of 0 to 1. Figure 6 shows the average resource utilization (RU) for the existing and proposed algorithms. In this figure, the x-axis denotes the number of cloudlets and the y-axis signifies the resource utilization. As can be seen from the figure, GA_RR performs best in terms of this parameter and GA_FCFS is also a close competitor. Both these algorithms perform much better compared to the FCFS, RR and GA. The average improvement in GA_FCFS is 66.25%, 60.84% and 26.32%, respectively, compared to FCFS, RR and GA algorithms. Similarly, the average improvement in GA_RR is 69.01%, 64.00% and 32.46%, respectively, compared with FCFS, RR and GA algorithms. This is depicted in Figure 7 below. Overall, GA_RR outperforms all the other algorithms. The reason for the hybrid algorithms performance being better than that of the standard algorithms is that the hybrid GA converges better and faster towards the optimal solution compared to the other algorithms under study.
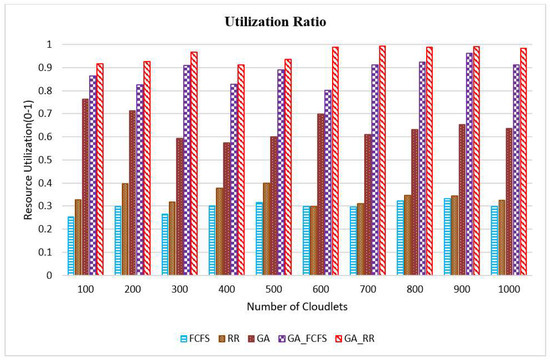
Figure 6.
Resource Utilization for the algorithms for different number of cloudlets.
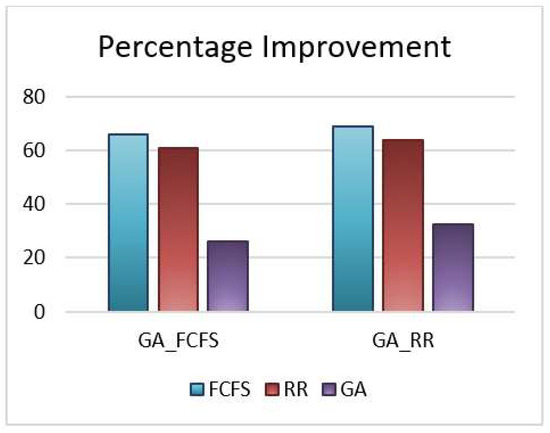
Figure 7.
Percentage Improvement of GA_FCFS and GA_RR based on Resource Utilization.
Another parameter used for the efficiency measurement of the proposed algorithms and its comparison with the existing algorithms is the throughput which is the number of tasks executed per unit of time. This value depends on the makespan obtained. As can be seen from Figure 8, GA_RR outperforms all the other algorithms and GA_FCFS, is the next best to it. The reason for better throughput is that GA_RR converges faster towards the optimal solution.
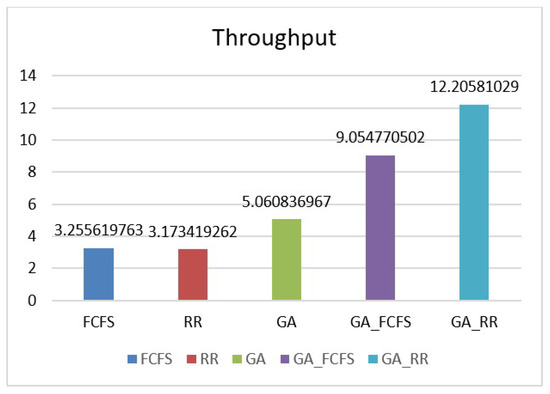
Figure 8.
Average throughput of all the algorithms.
6. Discussion
Two hybrid algorithms, GA_FCFS and GA_RR, are proposed in this work. The first part of this work consists of tuning of parameters in genetic algorithms. The detailed analysis for the same is presented in Section 4.2 using analysis of variance (ANOVA) and Duncan’s Multiple Range Tests (DMRT). The parameter value of 1000 for number of iterations, 0.8 for Crossover Probability, 0.01 for Mutation Probability, Single-Point for Crossover, Bit Flip for mutation and Roulette Wheel for selection were determined to be the best values. Hence. these values are used for further analysis.
The workload traces that are studied in this work are asymmetrical in nature and for this workload, it was determined that First Come First Serve (FCFS) algorithm is not good in terms of makespan, resource utilization as well as throughput. Round Robin (RR) performs a bit better compared to FCFS, but the improvement is not significant in terms of all the three parameters. Genetic algorithm (GA) shows significant improvement in terms of all the three makespan parameters, resource utilization and throughput. This improvement is greater in terms of makespan as the number of cloudlets increases, but is less significant in terms of resource utilization as the number of cloudlets increases. The two proposed hybrid algorithms show significant improvement in terms of all the three parameters. After evaluating the performance of all the algorithms, we discover that GA_RR is the most suitable algorithm for optimizing the makespan, resource utilization and the throughput.
7. Conclusions
The use of cloud computing in a number of domains has increased manyfold in recent years. Since the number of users is very large in cloud computing, there are several issues associated with it. Some of these issues are resource utilization, energy consumption, makespan and load balancing. In order to decrease the makespan and improve load balancing, this research presents a revolutionary load balancer. When some of the resources are left idle, insufficient load balancing might result in an overhead of less resource usage. The suggested technique incorporates a load-balancing mechanism that takes into account the real load, measured in million instructions assigned to VMs. In this method, a load balancer allocates a task to a server in real time based on the goal. Experimental studies are conducted on workload traces at Los Alamos National Lab (LANL). Two hybrid algorithms, a Genetic Algorithm combined with First Come First Serve (GA_FCFS) and Genetic Algorithm combined with Round Robin (GA_RR), are proposed in this work. The implementation is carried out on CloudSim 3.0.3 installed into eclipse. The results are compared with those of the existing First Come First Serve (FCFS), Round Robin (RR) and Genetic Algorithm (GA). Makespan and Resource Utilization are used for the comparison of results. The results obtained show that the performance of GA_RR is best followed by GA_FCFS. These hybrid algorithms provide better results compared to the standard algorithm because they explore the search space in a better manner compared to standard GA.
In this paper, the energy requirement of the data center and CPU is only considered. However, in real life, other resources also consume some energy. This is one of the limitations of the work carried out here. Another limitation is that we take a simple weighted function to solve the multi-objective optimization problem. In the future, some other technique for multi-objective optimization can be employed.
Author Contributions
Conceptualization: I.N., S.N. and F.S.; Methodology: I.N., S.N., F.S. and P.A.; Software: I.N., F.S. and S.N.; Validation: F.S., S.N., J.A. and B.A.; Formal analysis: S.N., P.A. and J.A.; Initial draft: F.S. and I.N.; Review and editing: S.N., I.N. and J.A.; Supervision: S.N., P.A. and B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Research data can be obtained from the corresponding author upon request.
Acknowledgments
We would like to acknowledge the contributions made by Khalid Imam Rehmani during the formal analysis, review and editing of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gulbaz, R.; Siddiqui, A.B.; Anjum, N.; Alotaibi, A.A.; Althobaiti, T.; Ramzan, N. Balancer genetic algorithm—A novel task scheduling optimization approach in cloud computing. Appl. Sci. 2021, 11, 6244. [Google Scholar] [CrossRef]
- Abdullahi, M.; Ngadi, M.A.; Dishing, S.I.; Ahmad, B.I.E. An efficient symbiotic organisms search algorithm with chaotic optimization strategy for multi-objective task scheduling problems in cloud computing environment. J. Netw. Comput. Appl. 2019, 133, 60–74. [Google Scholar] [CrossRef]
- Hussain, A.; Aleem, M.; Khan, A.; Iqbal, M.A.; Islam, M.A. RALBA: A computation-aware load balancing scheduler for cloud computing. Clust. Comput. 2018, 21, 1667–1680. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Siu, S.W.; Song, W.; Guan, S.S.U. Adaptive incremental genetic algorithm for task scheduling in cloud environments. Symmetry 2018, 10, 168. [Google Scholar] [CrossRef]
- Yiqiu, F.; Xia, X.; Junwei, G. Cloud computing task scheduling algorithm based on improved genetic algorithm. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2017; pp. 852–856. [Google Scholar]
- Wang, Y.; Zuo, X. An effective cloud workflow scheduling approach combining PSO and idle time slot-aware rules. IEEE/CAA J. Autom. Sin. 2021, 8, 1079–1094. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, X.; Zhao, X. Task scheduling based on multi-objective genetic algorithm in cloud computing. J. Inf. Comput. Sci. 2015, 12, 1429–1438. [Google Scholar] [CrossRef]
- Mansouri, N.; Zade, B.M.H.; Javidi, M.M. Hybrid task scheduling strategy for cloud computing by modified particle swarm optimization and fuzzy theory. Comput. Ind. Eng. 2019, 130, 597–633. [Google Scholar] [CrossRef]
- Ebadifard, F.; Babamir, S.M. A PSO-based task scheduling algorithm improved using a load-balancing technique for the cloud computing environment. Concurr. Comput. Pract. Exp. 2018, 30, e4368. [Google Scholar] [CrossRef]
- Hussain, A.; Aleem, M.; Iqbal, M.A.; Islam, M.A. SLA-RALBA: Cost-efficient and resource-aware load balancing algorithm for cloud computing. J. Supercomput. 2019, 75, 6777–6803. [Google Scholar] [CrossRef]
- Singh, R.M.; Paul, S.; Kumar, A. Task scheduling in cloud computing. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 7940–7944. [Google Scholar]
- Kaur, S.; Verma, A. An efficient approach to genetic algorithm for task scheduling in cloud computing environment. Int. J. Inf. Technol. Comput. Sci. (IJITCS) 2012, 4, 74–79. [Google Scholar] [CrossRef]
- Hamad, S.A.; Omara, F.A. Genetic-based task scheduling algorithm in cloud computing environment. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 550–556. [Google Scholar]
- Zhou, Z.; Li, F.; Zhu, H.; Xie, H.; Abawajy, J.H.; Chowdhury, M.U. An improved genetic algorithm using greedy strategy toward task scheduling optimization in cloud environments. Neural Comput. Appl. 2020, 32, 1531–1541. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, G.Y.; Gong, Y.J.; Zhang, J. Load balance aware genetic algorithm for task scheduling in cloud computing. In Proceedings of the Simulated Evolution and Learning: 10th International Conference, SEAL 2014, Dunedin, New Zealand, 15–18 December 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 644–655. [Google Scholar]
- Javanmardi, S.; Shojafar, M.; Amendola, D.; Cordeschi, N.; Liu, H.; Abraham, A. Hybrid job scheduling algorithm for cloud computing environment. In Proceedings of the Fifth International Conference on Innovations in Bio-Inspired Computing and Applications IBICA 2014, Ostrava, Czech Republic, 23–25 June 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 43–52. [Google Scholar]
- Patel, G.; Mehta, R.; Bhoi, U. Enhanced load balanced min-min algorithm for static meta task scheduling in cloud computing. Procedia Comput. Sci. 2015, 57, 545–553. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions. IEEE Trans. Evol. Comput. 2018, 23, 718–731. [Google Scholar] [CrossRef]
- Nasr, A.A.; El-Bahnasawy, N.A.; Attiya, G.; El-Sayed, A. Using the TSP solution strategy for cloudlet scheduling in cloud computing. J. Netw. Syst. Manag. 2019, 27, 366–387. [Google Scholar] [CrossRef]
- Panda, S.K.; Jana, P.K. An energy-efficient task scheduling algorithm for heterogeneous cloud computing systems. Clust. Comput. 2019, 22, 509–527. [Google Scholar] [CrossRef]
- Panda, S.K.; Jana, P.K. Load balanced task scheduling for cloud computing: A probabilistic approach. Knowl. Inf. Syst. 2019, 61, 1607–1631. [Google Scholar] [CrossRef]
- Singh, S.; Kalra, M. Scheduling of independent tasks in cloud computing using modified genetic algorithm. In Proceedings of the 2014 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 565–569. [Google Scholar]
- Mohamad, Z.; Mahmoud, A.A.; Nik, W.N.S.W.; Mohamed, M.A.; Deris, M.M. A genetic algorithm for optimal job scheduling and load balancing in cloud computing. Int. J. Eng. Technol. 2018, 7, 290–294. [Google Scholar]
- Kaur, S.; Sengupta, J. Load balancing using improved genetic algorithm (iga) in cloud computing. Int. J. Adv. Res. Comput. Eng. Technol. IJARCET 2017, 6, 1229–1233. [Google Scholar]
- Rekha, P.M.; Dakshayini, M. Efficient task allocation approach using genetic algorithm for cloud environment. Clust. Comput. 2019, 22, 1241–1251. [Google Scholar] [CrossRef]
- Senthil Kumar, A.M.; Venkatesan, M. Multi-objective task scheduling using hybrid genetic-ant colony optimization algorithm in cloud environment. Wirel. Pers. Commun. 2019, 107, 1835–1848. [Google Scholar] [CrossRef]
- Krishnasamy, K. Task scheduling algorithm based on Hybrid Particle Swarm Optimization in cloud computing environment. J. Theor. Appl. Inf. Technol. 2013, 55. [Google Scholar]
- Abdi, S.; Motamedi, S.A.; Sharifian, S. Task scheduling using modified PSO algorithm in cloud computing environment. In Proceedings of the International Conference on Machine Learning, Electrical and Mechanical Engineering, Athens, Greece, 8–9 April 2023; Volume 4, No. 1. pp. 8–12. [Google Scholar]
- Kaur, G.; Sharma, E.S. Optimized utilization of resources using improved particle swarm optimization based task scheduling algorithms in cloud computing. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 110–115. [Google Scholar]
- Abdullahi, M.; Ngadi, M.A. Symbiotic organism search optimization based task scheduling in cloud computing environment. Future Gener. Comput. Syst. 2016, 56, 640–650. [Google Scholar] [CrossRef]
- Rjoub, G.; Bentahar, J.; Abdel Wahab, O.; Saleh Bataineh, A. Deep and reinforcement learning for automated task scheduling in large-scale cloud computing systems. Concurr. Comput. Pract. Exp. 2021, 33, e5919. [Google Scholar] [CrossRef]
- Sharma, M.; Garg, R. An artificial neural network based approach for energy efficient task scheduling in cloud data centers. Sustain. Comput. Inform. Syst. 2020, 26, 100373. [Google Scholar] [CrossRef]
- Iranmanesh, A.; Naji, H.R. DCHG-TS: A deadline-constrained and cost-effective hybrid genetic algorithm for scientific workflow scheduling in cloud computing. Clust. Comput. 2021, 24, 667–681. [Google Scholar] [CrossRef]
- Saber, W.; Moussa, W.; Ghuniem, A.M.; Rizk, R. Hybrid load balance based on genetic algorithm in cloud environment. Int. J. Electr. Comput. Eng. 2021, 11, 2477–2489. [Google Scholar] [CrossRef]
- Muteeh, A.; Sardaraz, M.; Tahir, M. MrLBA: Multi-resource load balancing algorithm for cloud computing using ant colony optimization. Clust. Comput. 2021, 24, 3135–3145. [Google Scholar] [CrossRef]
- Asghari, A.; Sohrabi, M.K.; Yaghmaee, F. Task scheduling, resource provisioning, and load balancing on scientific workflows using parallel SARSA reinforcement learning agents and genetic algorithm. J. Supercomput. 2021, 77, 2800–2828. [Google Scholar] [CrossRef]
- Kakkottakath Valappil Thekkepuryil, J.; Suseelan, D.P.; Keerikkattil, P.M. An effective meta-heuristic based multi-objective hybrid optimization method for workflow scheduling in cloud computing environment. Clust. Comput. 2021, 24, 2367–2384. [Google Scholar] [CrossRef]
- Aziza, H.; Krichen, S. Bi-objective decision support system for task-scheduling based on genetic algorithm in cloud computing. Computing 2018, 100, 65–91. [Google Scholar] [CrossRef]
- Mohammadi, A.; Rezvani, M.H. A novel optimized approach for resource reservation in cloud computing using producer–consumer theory of microeconomics. J. Supercomput. 2019, 75, 7391–7425. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. A novel hybrid antlion optimization algorithm for multi-objective task scheduling problems in cloud computing environments. Clust. Comput. 2021, 24, 205–223. [Google Scholar] [CrossRef]
- Dai, Y.; Lou, Y.; Lu, X. A task scheduling algorithm based on genetic algorithm and ant colony optimization algorithm with multi-QoS constraints in cloud computing. In Proceedings of the 2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics, Washington, DC, USA, 26–27 August 2015; Volume 2, pp. 428–431. [Google Scholar]
- Sundarrajan, R.; Vasudevan, V. An optimization algorithm for task scheduling in cloud computing based on multi-purpose cuckoo seek algorithm. In Proceedings of the Theoretical Computer Science and Discrete Mathematics: First International Conference, ICTCSDM 2016, Krishnankoil, India, 19–21 December 2016; Revised Selected Papers 1. Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 415–424. [Google Scholar]
- Mapetu, J.P.B.; Chen, Z.; Kong, L. Low-time complexity and low-cost binary particle swarm optimization algorithm for task scheduling and load balancing in cloud computing. Appl. Intell. 2019, 49, 3308–3330. [Google Scholar] [CrossRef]
- Varshney, S.; Singh, S. An optimal bi-objective particle swarm optimization algorithm for task scheduling in cloud computing. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 780–784. [Google Scholar]
- Saranu, K.A.; Jaganathan, S. Intensified Scheduling Algorithm for Virtual Machine Tasks in Cloud Computing. In Artificial Intelligence and Evolutionary Algorithms in Engineering Systems: Proceedings of ICAEES 2014, Volume 2; Springer: Chennai, India, 2015; pp. 283–290. [Google Scholar]
- Downey, A.B. Predicting queue times on space-sharing parallel computers. In Proceedings of the 11th International Parallel Processing Symposium, Genva, Switzerland, 1–5 April 1997; pp. 209–218. [Google Scholar]
- Calheiros, R.N.; Ranjan, R.; Beloglazov, A.; De Rose, C.A.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Exp. 2011, 41, 23–50. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1925; Volume 22, No. 5; pp. 700–725. [Google Scholar]
- Kuchnik, M.; Park, J.W.; Cranor, C.; Moore, E.; DeBardeleben, N.; Amvrosiadis, G. This is why ML-driven cluster scheduling remains widely impractical. Tech. Rep. 2019. Available online: https://www.pdl.cmu.edu/ftp/CloudComputing/CMU-PDL-19-103.pdf (accessed on 25 April 2023).
- Naaz, S.; Alam, A.; Biswas, R. Load balancing algorithms for peer to peer and client server distributed environments. Int. J. Comput. Appl. 2012, 47, 17–21. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).