Abstract
In this study, a high-order compact finite difference method is used to solve boundary value problems with Robin boundary conditions. The norm is to use a first-order finite difference scheme to approximate Neumann and Robin boundary conditions, but that compromises the accuracy of the entire scheme. As a result, new higher-order finite difference schemes for approximating Robin boundary conditions are developed in this work. Six examples for testing the applicability and performance of the method are considered. Convergence analysis is provided, and it is consistent with the numerical results. The results are compared with the exact solutions and published results from other methods. The method produces highly accurate results, which are displayed in tables and graphs.
1. Introduction
Boundary value problems (BVPs) are paramount in the modeling of several real-life problems with diverse applications. Boundary conditions of different types often accompany these problems. Dirichlet boundary conditions are the most common and more straightforward to implement. The Neumann boundary conditions are also not too complicated to deal with. On the other hand, the implementation of Robin boundary conditions poses significant difficulties to many researchers. As a result, BVPs with Robin boundary conditions have not received much attention. The Robin boundary condition, also referred to as the third-type boundary condition, was named after Victor Gustave Robin, who was behind its inception [1]. The Robin boundary condition is a linear combination of the solution and its derivative at the boundary point. It arises in diverse physical situations.
If a differential equation is to be solved over a domain , where denotes the domain’s boundary, the Robin boundary condition is:
on the boundary. Our focus, in this work, is to solve second-order boundary value problems of the form
subject to the Robin boundary conditions
where , and are constants.
Numerous approximation methods have been developed and implemented to solve Equation (2). They include the homotopy perturbation method [2], homotopy analysis method [3], Adomian decomposition method [4], variational iteration method [5], spectral method [6], shooting method [7], and finite differences [8], to name a few. The Robin boundary conditions have not been covered that extensively because they are difficult to deal with. Some of the methods that have been utilized to solve Equation (2) with Robin boundary conditions include the diagonal block method [9], modified Adomian decomposition method [10], Bernoulli polynomials [11], the compact finite difference method [12].
Compact finite difference schemes (CFDSs) have gained popularity in the field of numerical approximations in recent years. In [13], Lele gave an in-depth description of CFDSs for various applications such as interpolation, filtering, and evaluating derivatives. They have been applied to solve differential equations such as Poisson’s equation [14], Burger’s equation [15,16], American option pricing problems [17], Navier–Stokes equation [18], integro-differential equation [19,20], Korteweg–de Vries equation [21], Black–Scholes equation [22,23], dynamical systems [24,25], and many more [26,27,28,29,30]. Their main advantage is that, with few grid points, they attain very high-order accuracy.
In this work, we use the higher-order compact finite difference schemes to solve two-point boundary value problems with Robin boundary conditions. Usually, when finite difference methods are used to solve differential equations subjected to Neumann or Robin boundary conditions, the first-order finite difference formula is used to approximate the derivative in the boundary condition, even if a higher-order method is being used to solve the equation. The disadvantage with that is that the overall accuracy is compromised because of the lower-order approximation at the boundaries. Hence, we develop new higher-order finite difference schemes to approximate the Robin boundary conditions in this work. This enhances the overall accuracy. We consider some examples of boundary value problems that are subjected to Robin boundary conditions to test the applicability and accuracy of the new schemes.
The rest of the paper is laid out as follows. In Section 2, we discuss the quasilinearization technique. In Section 3, we present the derivations of the sixth-order compact finite difference schemes. In Section 4 we discuss the development of CFDSs with Robin boundary conditions. We discuss the convergence of method in Section 5. The results and discussion are presented in Section 6, followed by the conclusions in Section 7.
2. Quasilinearization
Before applying the CFDM, we need to linearize Equation (2) first. To this end, we use the quasilinearization (QLM) technique that was introduced by Bellman and Kalaba [31]. The QLM reduces the nonlinear BVP into a sequence of linear BVPs, which we solve iteratively until a set tolerance level is reached.
We expand the nonlinear function in Equation (2) using Taylor’s series up to the first-order terms, to obtain
where
3. Compact Finite Difference Schemes at Interior Nodes
In this section, we present the derivations of the sixth-order compact finite difference schemes for approximating first and second derivatives. We consider a function defined on , where a and b are arbitrary constants. We discretize the domain into N number of nodes with a uniform step size and nodes
3.1. First Derivative Approximation
The general formula for approximating first derivatives is given by
where and is the truncation error. A and are constants to be determined. The values of these constants are obtained by expanding both sides of Equation (9) using the Taylor series expansion about and matching the coefficients of , with for a sixth-order accurate scheme. That results in six algebraic equations that are solved to obtain the following constants:
Therefore, the scheme for approximating the first derivative is given by
The first unmatched coefficients of the Taylor series expansion are used to determine the truncation error, which is given by
3.2. Second Derivative Approximation
The general formula for approximating second derivatives is given by
with being the truncation error. Similarly, the values of these constants are obtained by expanding both sides of Equation (13) using the Taylor series expansion about and matching the coefficients of , with for a sixth-order-accurate scheme. That results in six algebraic equations that are solved to obtain the following constants:
Therefore, the scheme for approximating the second derivative is given by
Similarly, the first unmatched coefficients of the Taylor series expansion are used to determine the truncation error, which is given by
4. Compact Finite Difference Schemes for Robin Boundary Conditions
In this section, we develop sixth-order compact finite difference schemes for approximating first and second derivatives for arbitrary functions with Robin boundary conditions. To accommodate the Robin boundary conditions and maintain a sixth-order accuracy at the boundaries, the schemes are adjusted appropriately. To that end, we use one-sided compact finite difference schemes, specifically for the points , and . The derivatives at the interior points are approximated using Equations (11) and (15).
4.1. First Derivative Approximation
We start by illustrating how the sixth-order compact schemes are formulated for first derivative approximations at the boundaries. The one-sided schemes for the first derivative at the boundary points are given as follows:
At , we have
The constants are obtained in a similar manner as in the previous section, and they are
The truncation error is
At , we have
with the constants obtained as
and
At , we have
where
and
Finally, at , we have
Here, the constants are
and
The sixth-order-accurate compact finite difference approximation for approximating the first derivative of an arbitrary function with the Robin boundary condition is obtained by combining Equation (11) with Equations (17), (20), (23), and (26), and is given by
where
and
The first derivative is therefore approximated by
where and
4.2. Second Derivative Approximation
The one-sided schemes for the second derivative at the boundary points are given as follows:
At , we have
The constants are obtained in a similar manner as in the previous section, and they are given as
and
At , we have
where the constants are
and
At , we have
and the constants are
and
Lastly, at , we have
The constants are
and
The sixth-order-accurate compact finite difference approximation for approximating the second derivative of an arbitrary function with the Robin boundary condition is obtained by combining Equation (15) with Equations (33), (36), (39), and (42) and is given by
where
The second derivative is therefore approximated by
where and .
5. Convergence
In this section, we discuss the convergence of the proposed method described in Section 4 to solve Equation (5).
Theorem 1.
Let and be vectors of the numerical solution and exact solution obtained by solving the linear system (5), respectively. Then, provided , we have
where
Proof.
The exact solution, , of Equation (5) is given by
where and . The approximate solution, Y, of Equation (5) is given by
We can write and as
where
Multiplying Equation (61) by , we obtain
We then multiply Equation (62) by to obtain
Recall that if is a subordinate matrix norm and B is any matrix such that , then the matrix is invertible and
Now, if , then
is invertible, and it follows that the norm of E is
□
6. Numerical Examples
In this section, we consider several examples to highlight the applicability and high accuracy of the proposed algorithm in solving two-point boundary value problems subjected to Robin boundary conditions. To check the accuracy, we compute the maximum absolute error () between the exact and numerical solutions, i.e.,
where and represent the CFDM solution and exact solution at the grid point , respectively. In addition, we compute the numerical rate of convergence, which is defined as
where and are absolute errors corresponding to grids with step size and , respectively. We compare our results with published results obtained using other methods.
Example 1.
Consider the linear boundary value problem:
with boundary conditions:
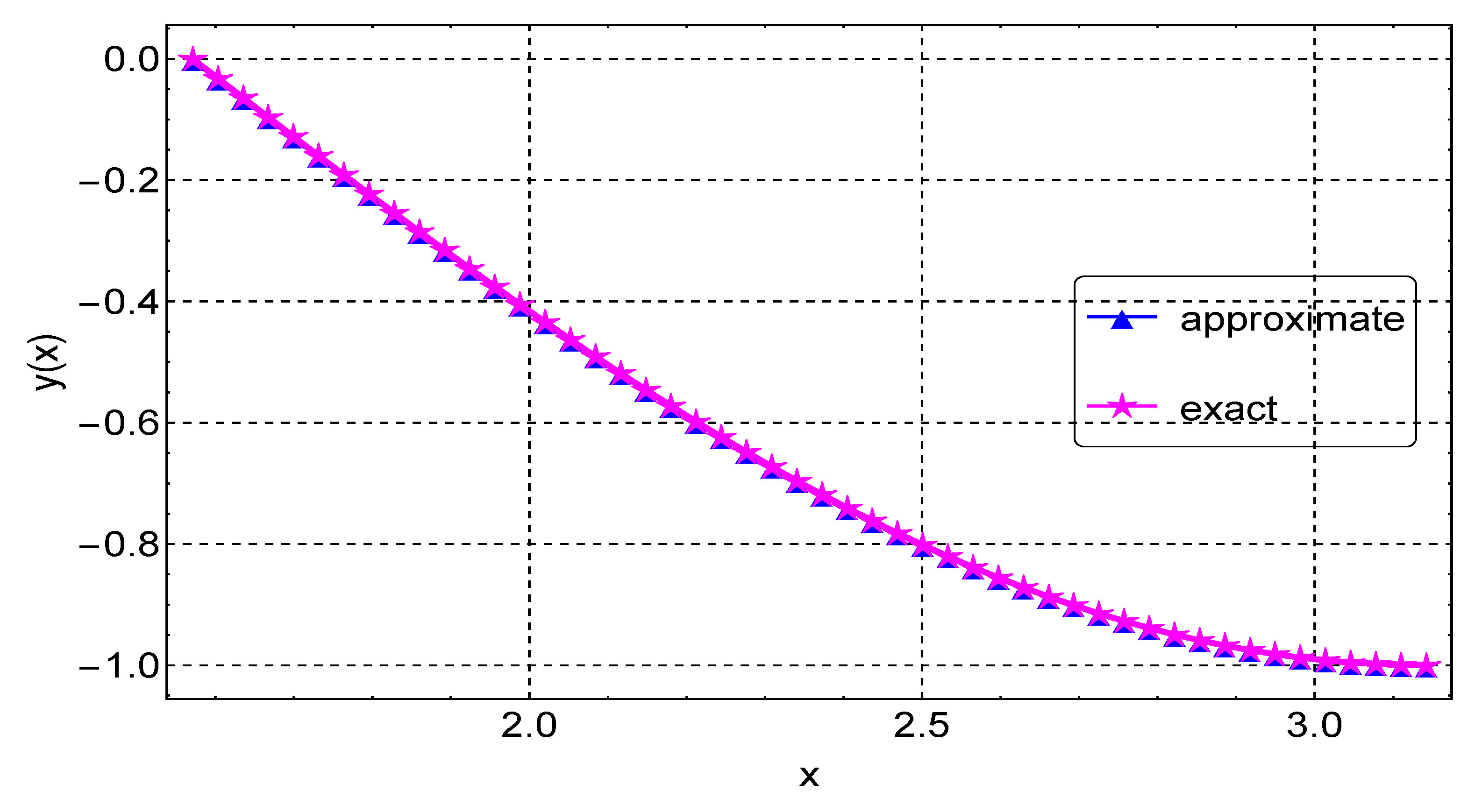
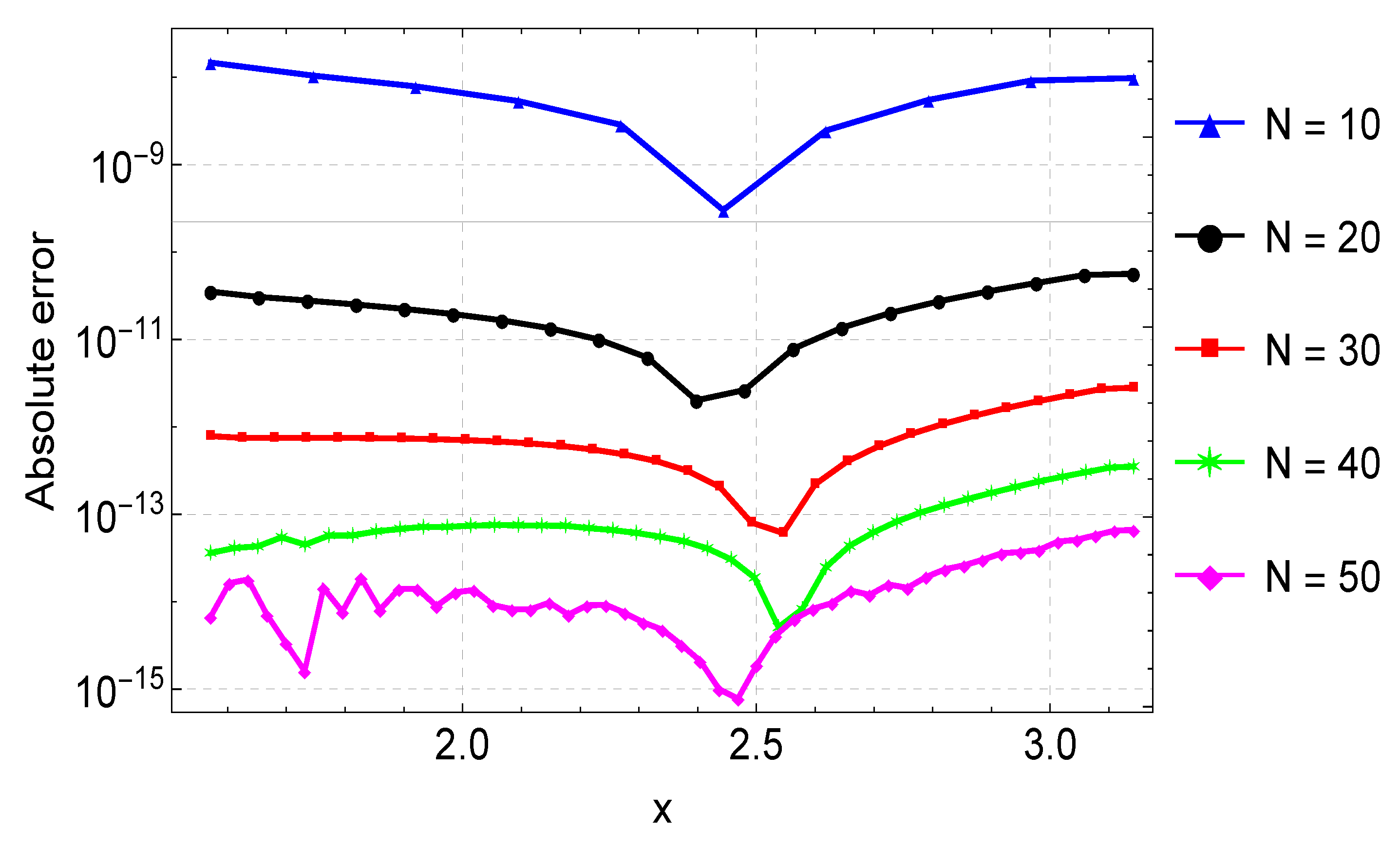
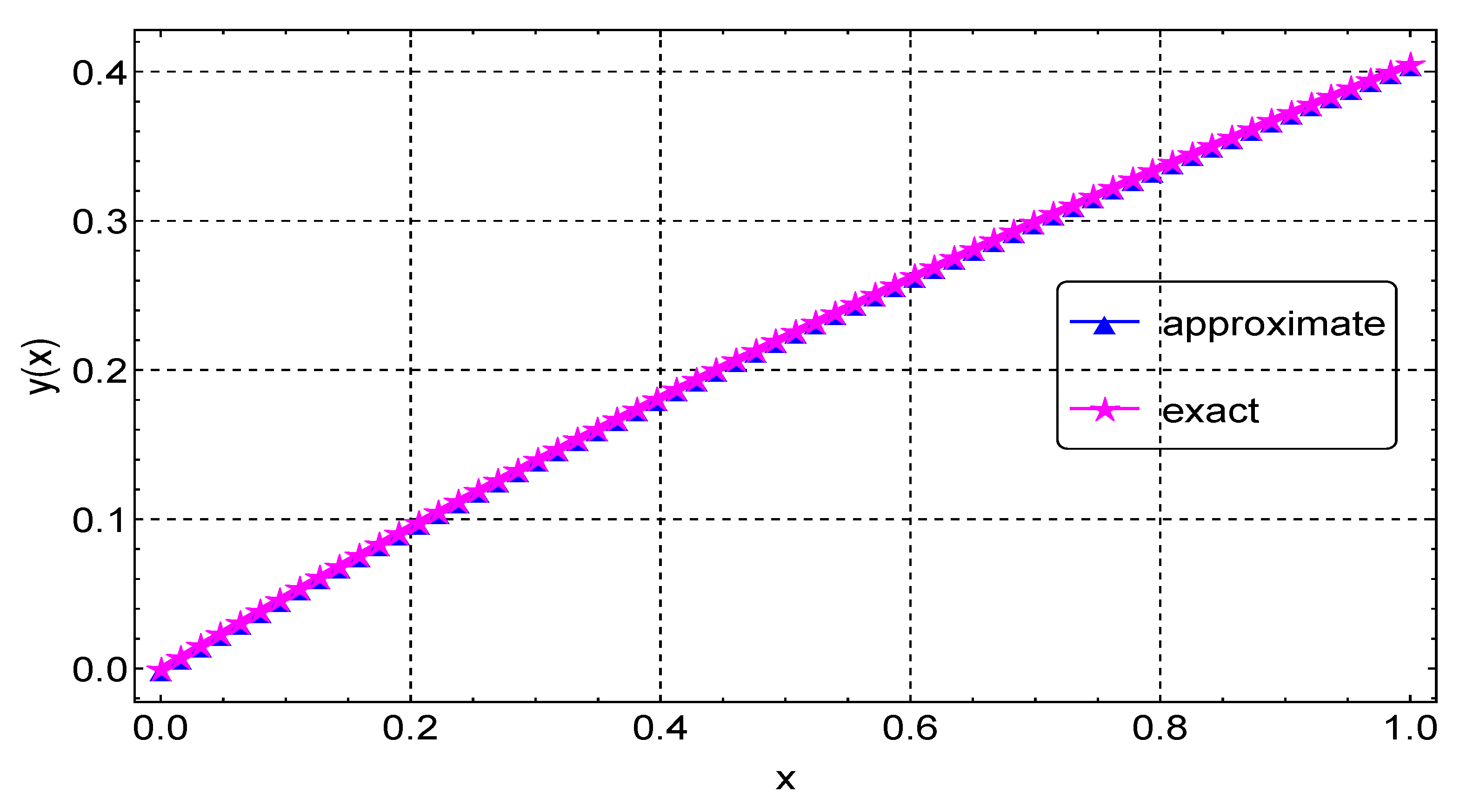
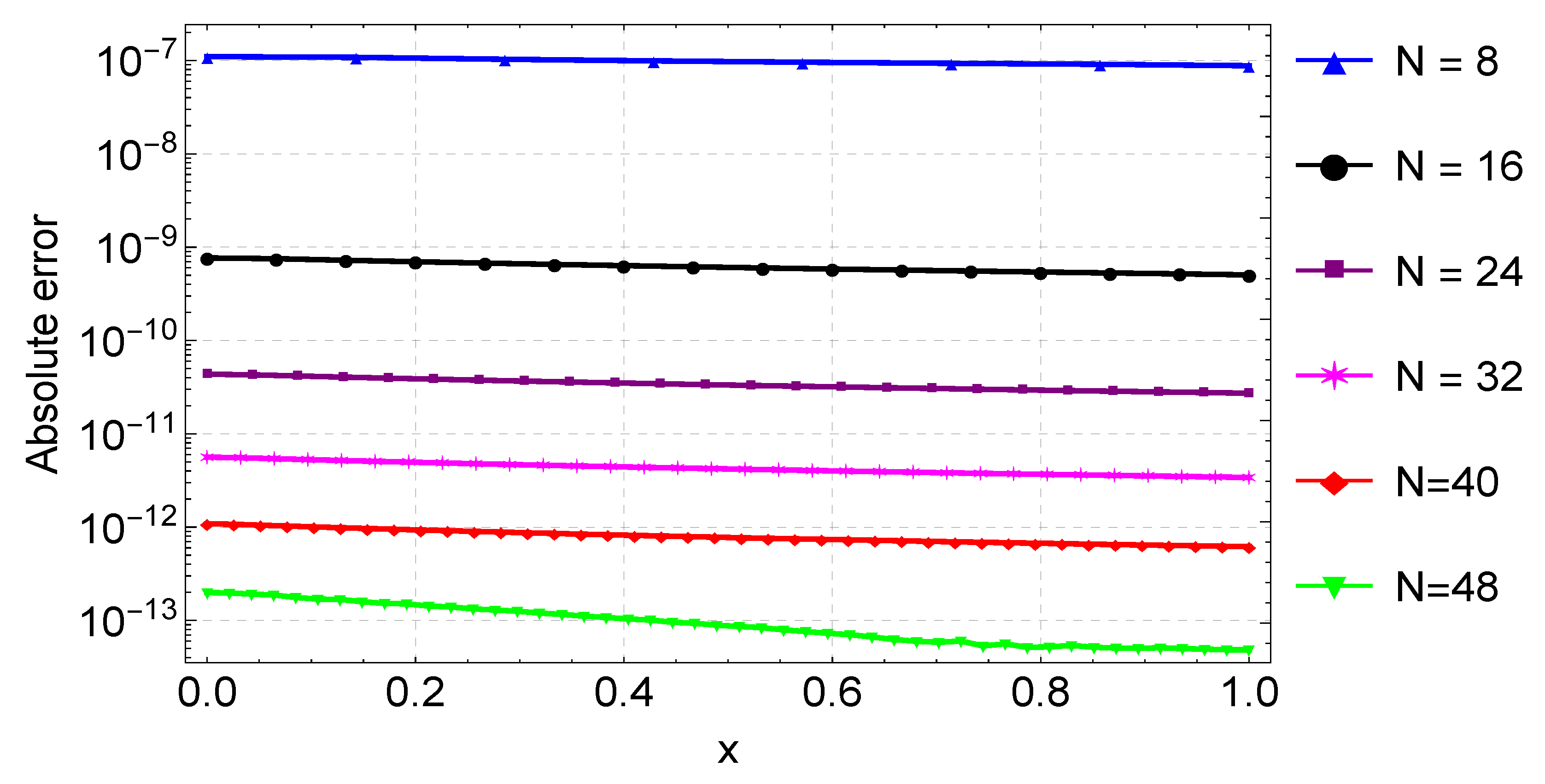
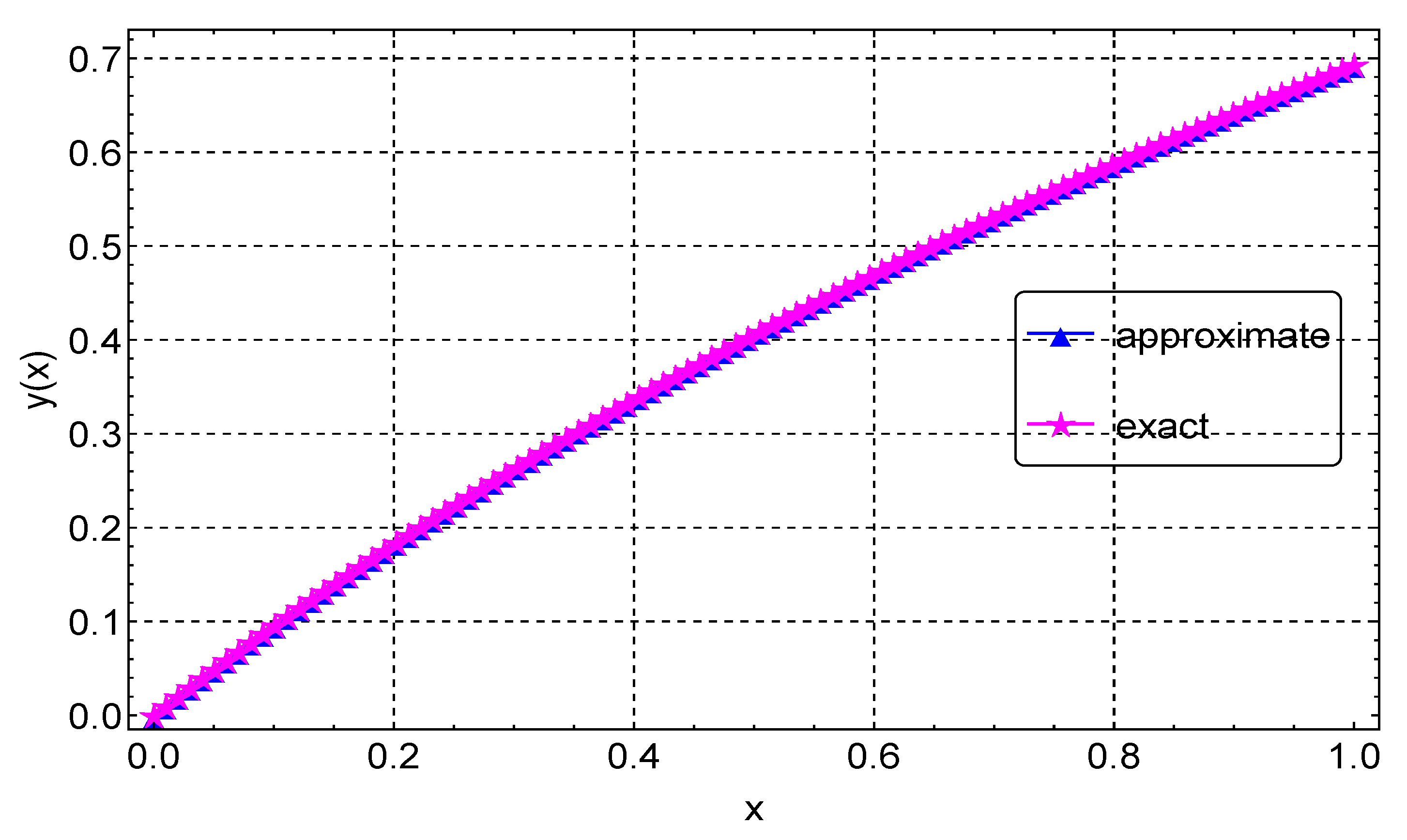
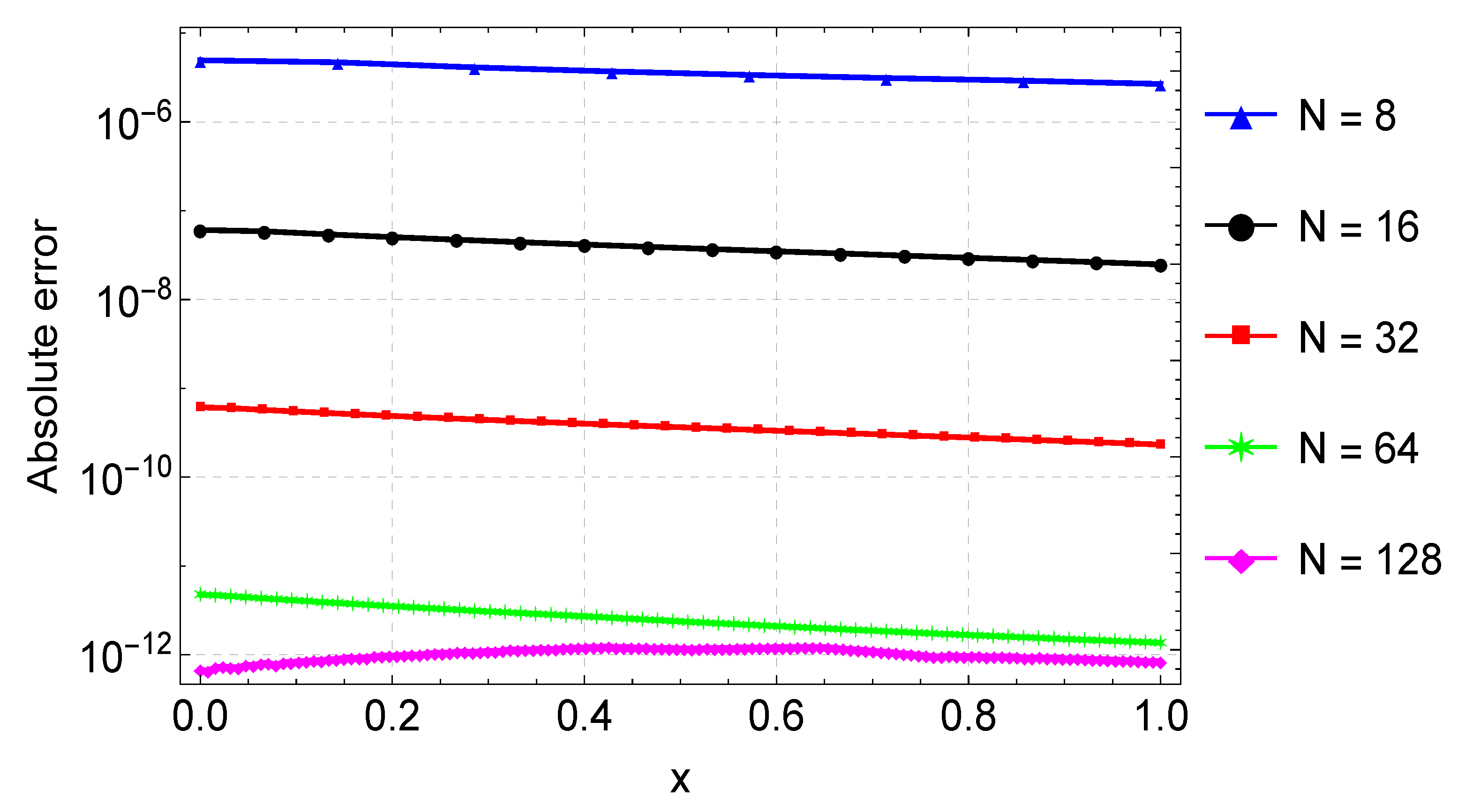
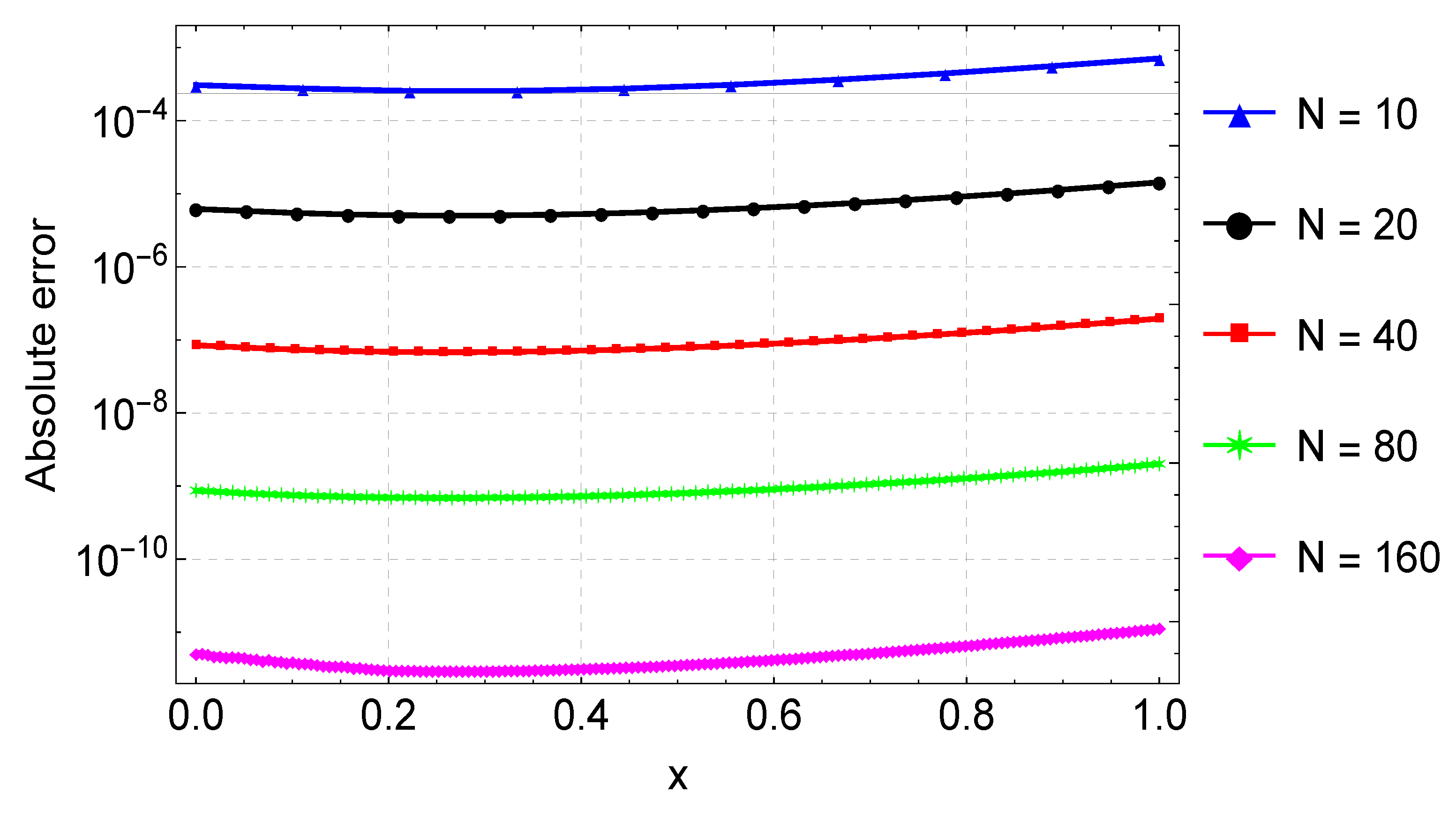
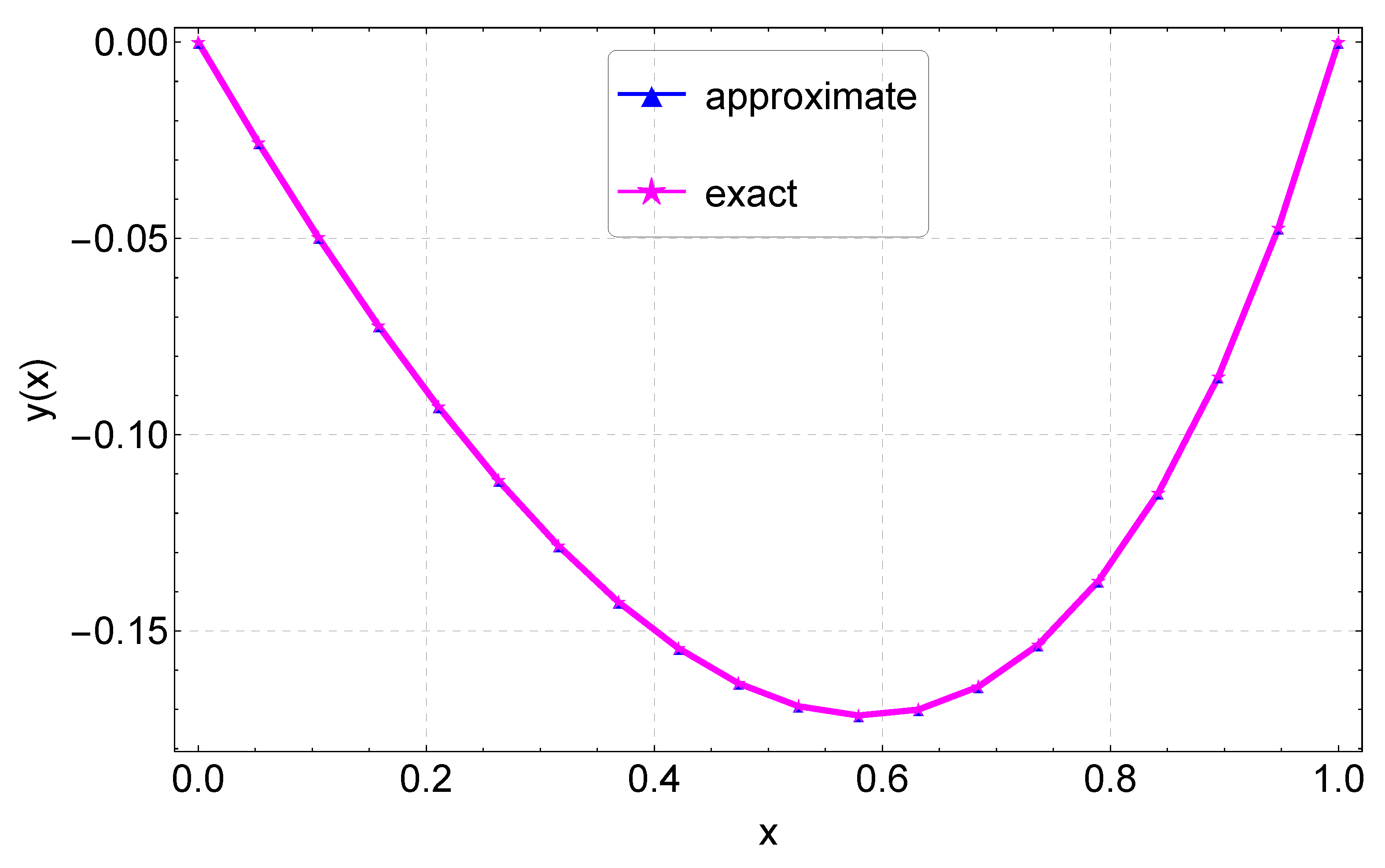
We present the results of Example 1 in Table 1. We display the maximum absolute error computed using different values of grid points N. In this example, we obtain the maximum accuracy, with an error of about , when . When compared to the results in [9,11], our results are much more accurate. For instance, with a step size , the error in [9] is about , but our error is about , with a slightly larger step size. Our results are also better compared to the results of [11] obtained using Bernoulli polynomials. The agreement between the exact and numerical solutions is depicted in Figure 1, with the errors from the different values of N again shown in Figure 2.

Table 1.
Maximum absolute error () for Example 1.
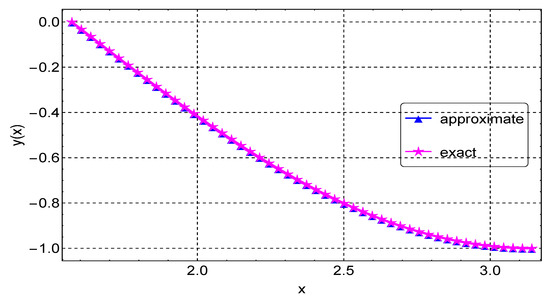
Figure 1.
Exact and approximate solution plots for Example 1.
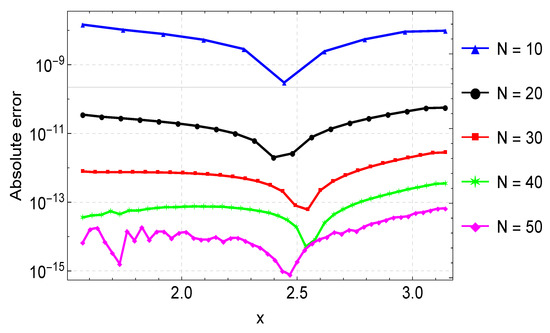
Figure 2.
Error plots for the approximation of Example 1 for varying values of N.
Example 2.
Consider the nonlinear second-order boundary value problem:
with boundary conditions:
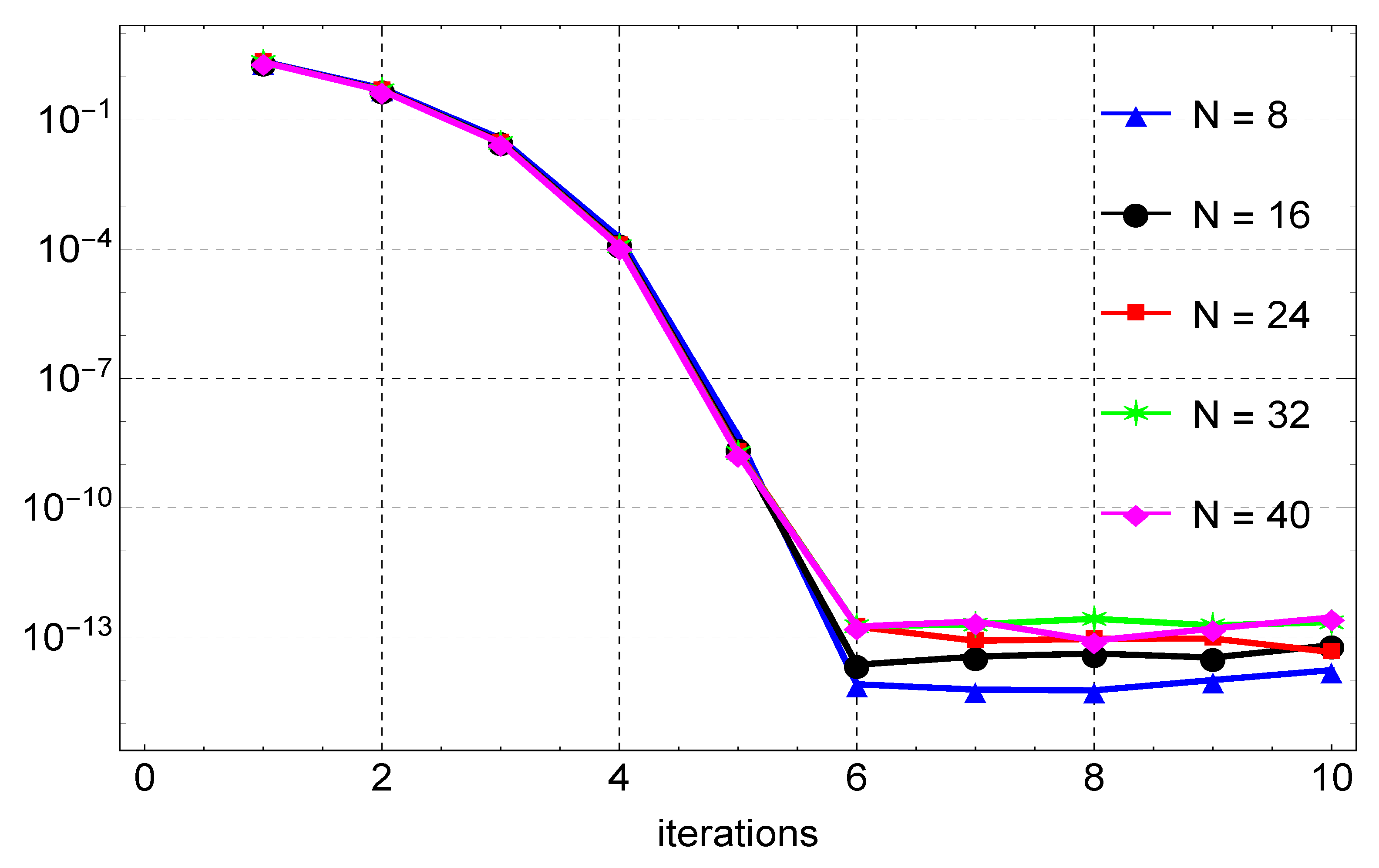
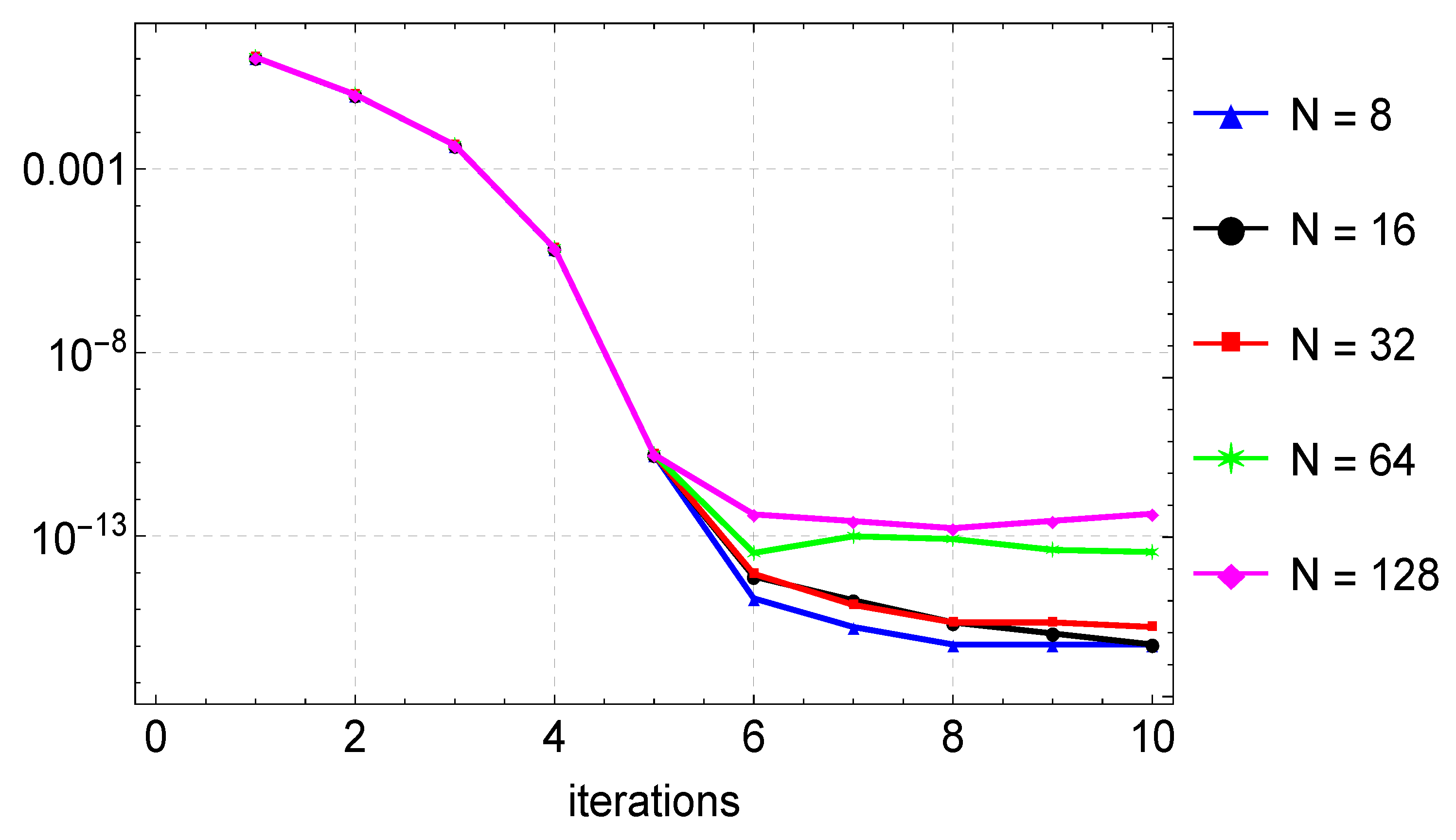
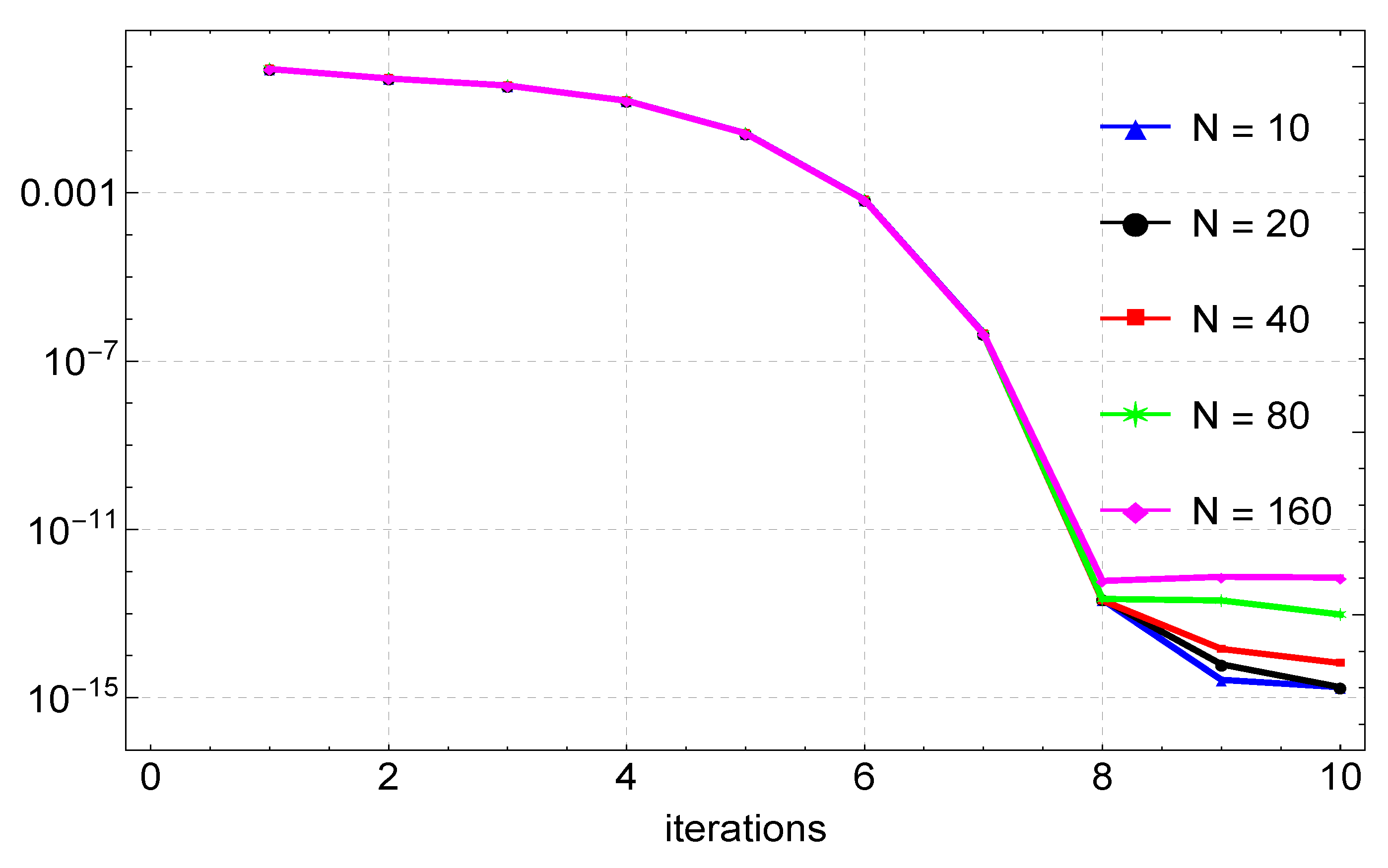
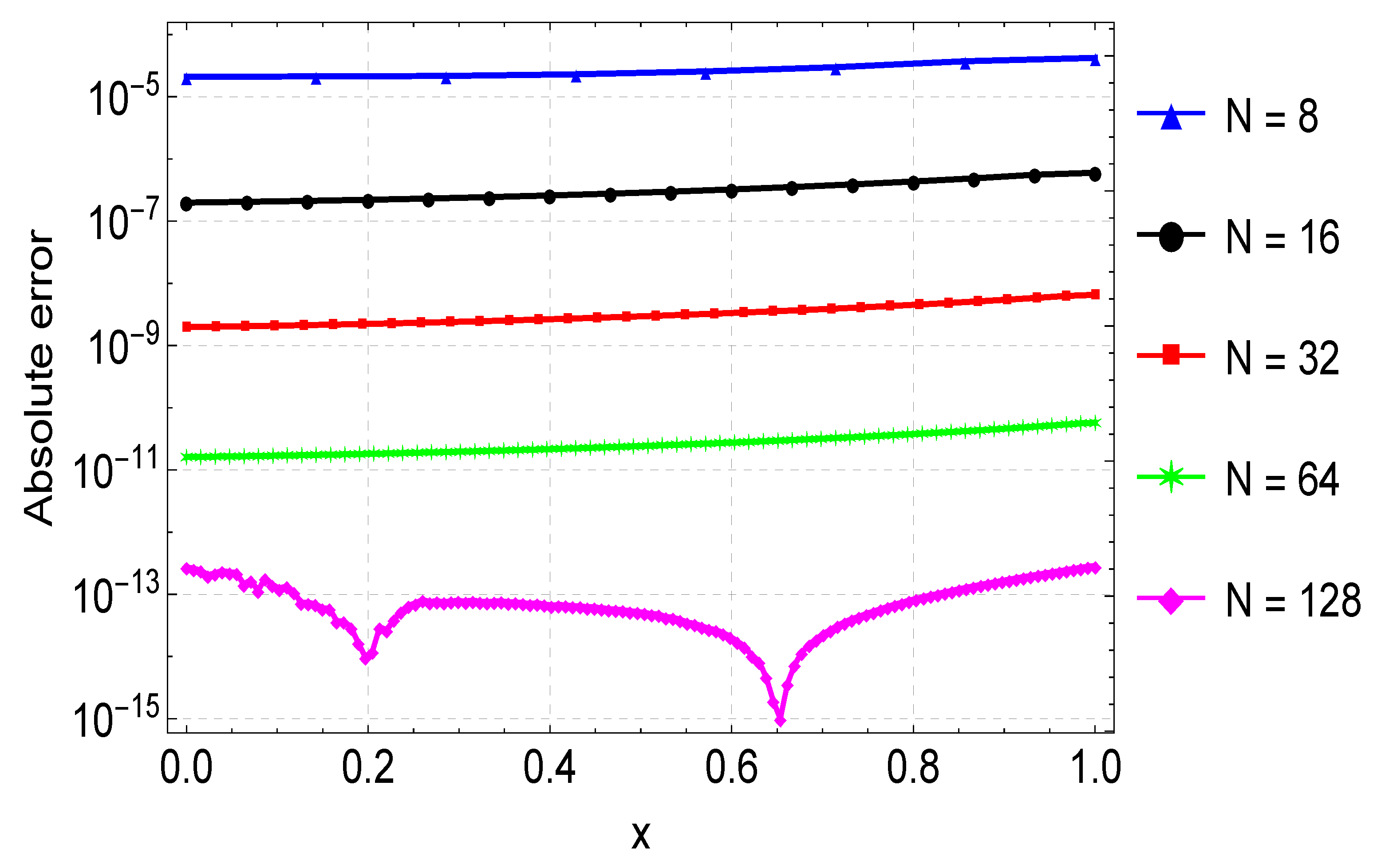
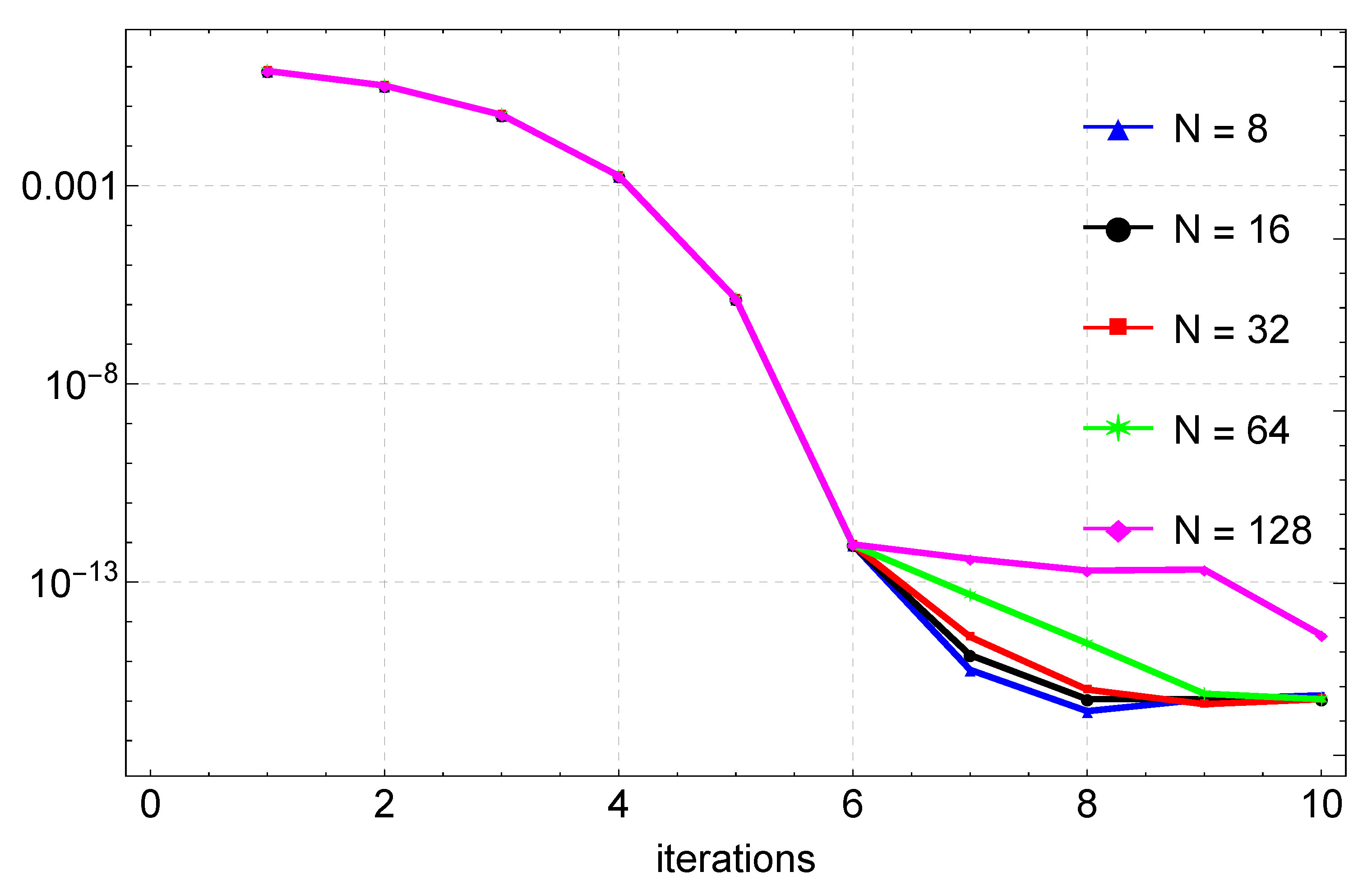
Figure 3 depicts the solution of Example 2. A good agreement between the exact and the numerical solution can be observed. In this example, gives the maximum error of about , and this is shown in Table 2. Again, when compared to the results in [9], the method shows remarkable accuracy on a slightly larger step size than in [9]. The errors are also shown in Figure 4 for the different values of N. Figure 5 shows that six iterations of the quasilinearization are required to reach full convergence.
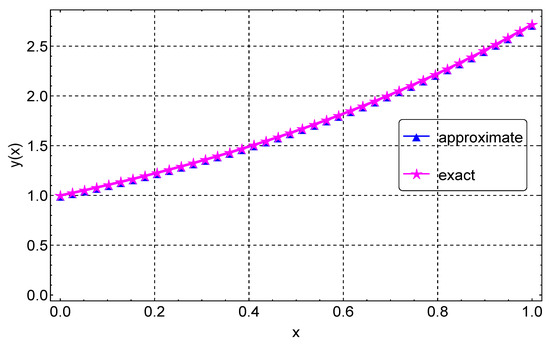
Figure 3.
Exact and approximate solution plots for Example 2.

Table 2.
Maximum absolute error () and ROC for Example 2.
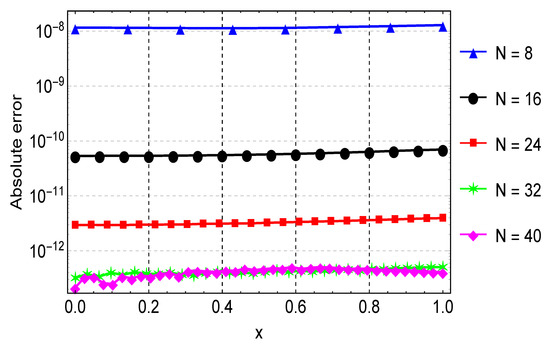
Figure 4.
Error plots for the approximation of Example 2 for varying values of N.
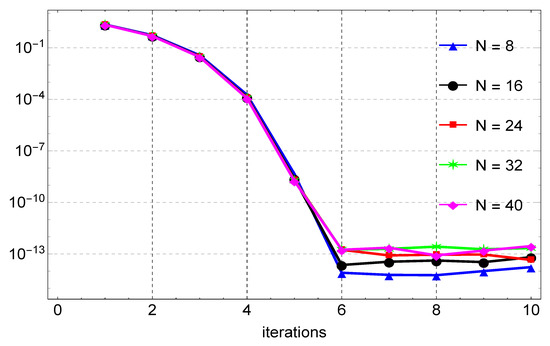
Figure 5.
Convergence plots for the approximation of Example 2 for varying values of N.
Example 3.
Consider the nonlinear second-order boundary value problem:
with boundary conditions:
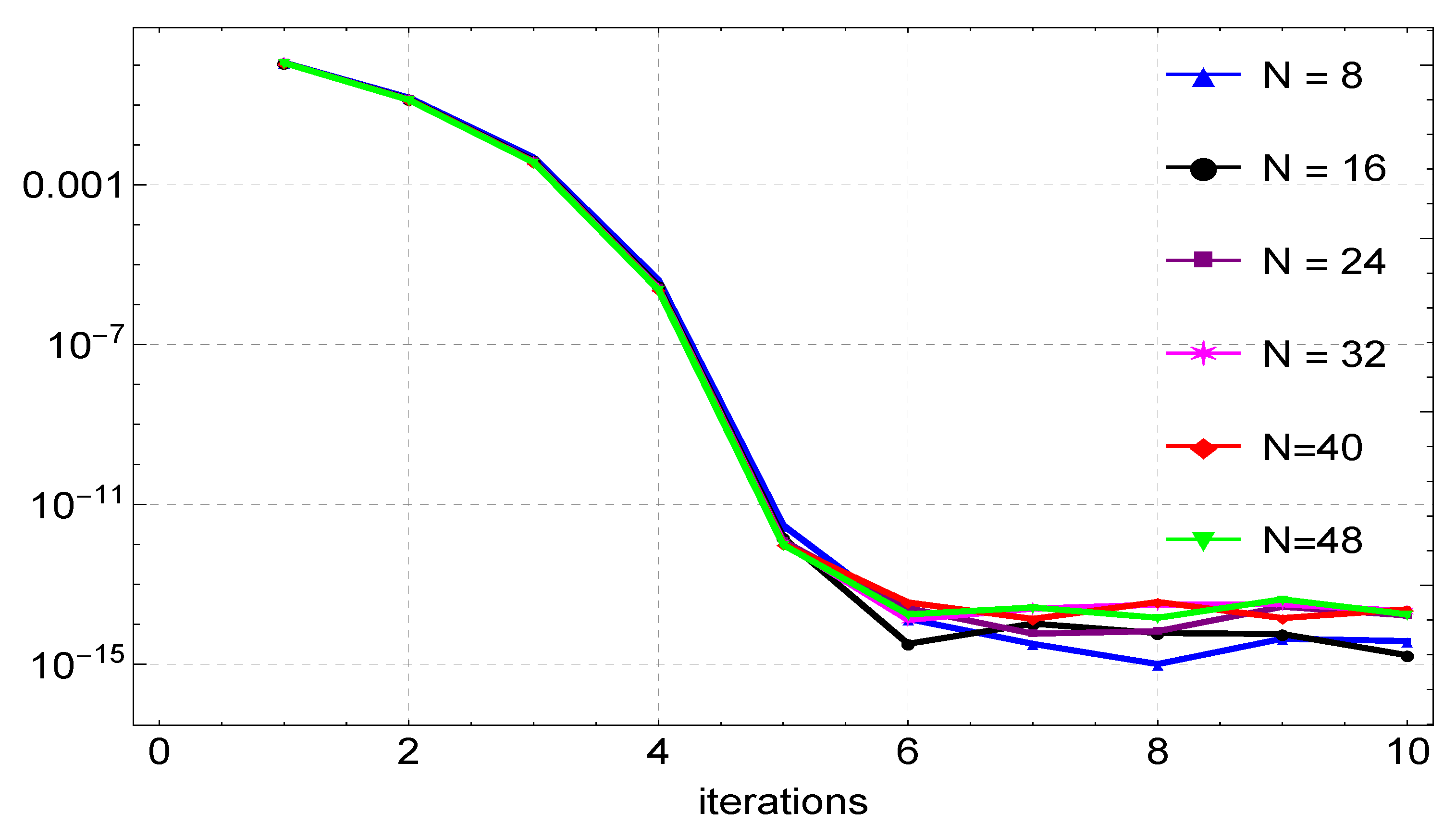
The results of Example 3 are similar to those of the previous examples. Figure 6 shows the plots of the exact and numerical solution, which are in good agreement. The maximum absolute error, computational times, and rates of convergence (ROCs) are presented in Table 3, with results from Nasir et al. [9] included. As shown in the table, the proposed method gives accurate results with fewer grid points compared to the results in [9]. Plots of the maximum absolute errors for various values of N are shown in Figure 7. Finally, Figure 8 shows the convergence plots for the various N values. It can be seen from the plot that the method reaches full convergence after six iterations.
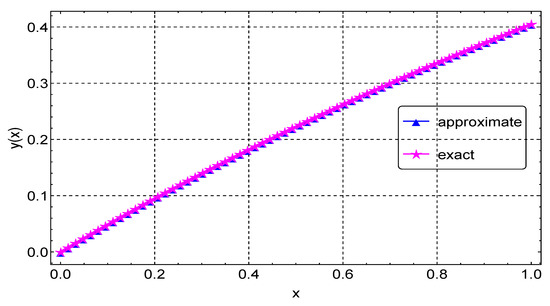
Figure 6.
Exact and approximate solution plots for Example 3.

Table 3.
Maximum absolute error () and ROC for Example 3.
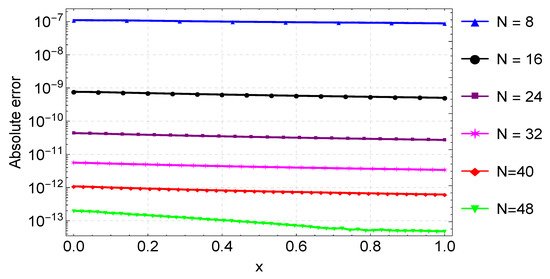
Figure 7.
Error plots for the approximation of Example 3 for varying values of N.
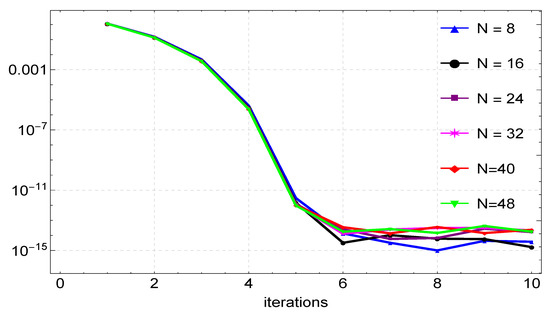
Figure 8.
Convergence plots for the approximation of Example 3 for varying values of N.
Example 4.
Consider the nonlinear second-order boundary value problem:
with boundary conditions:
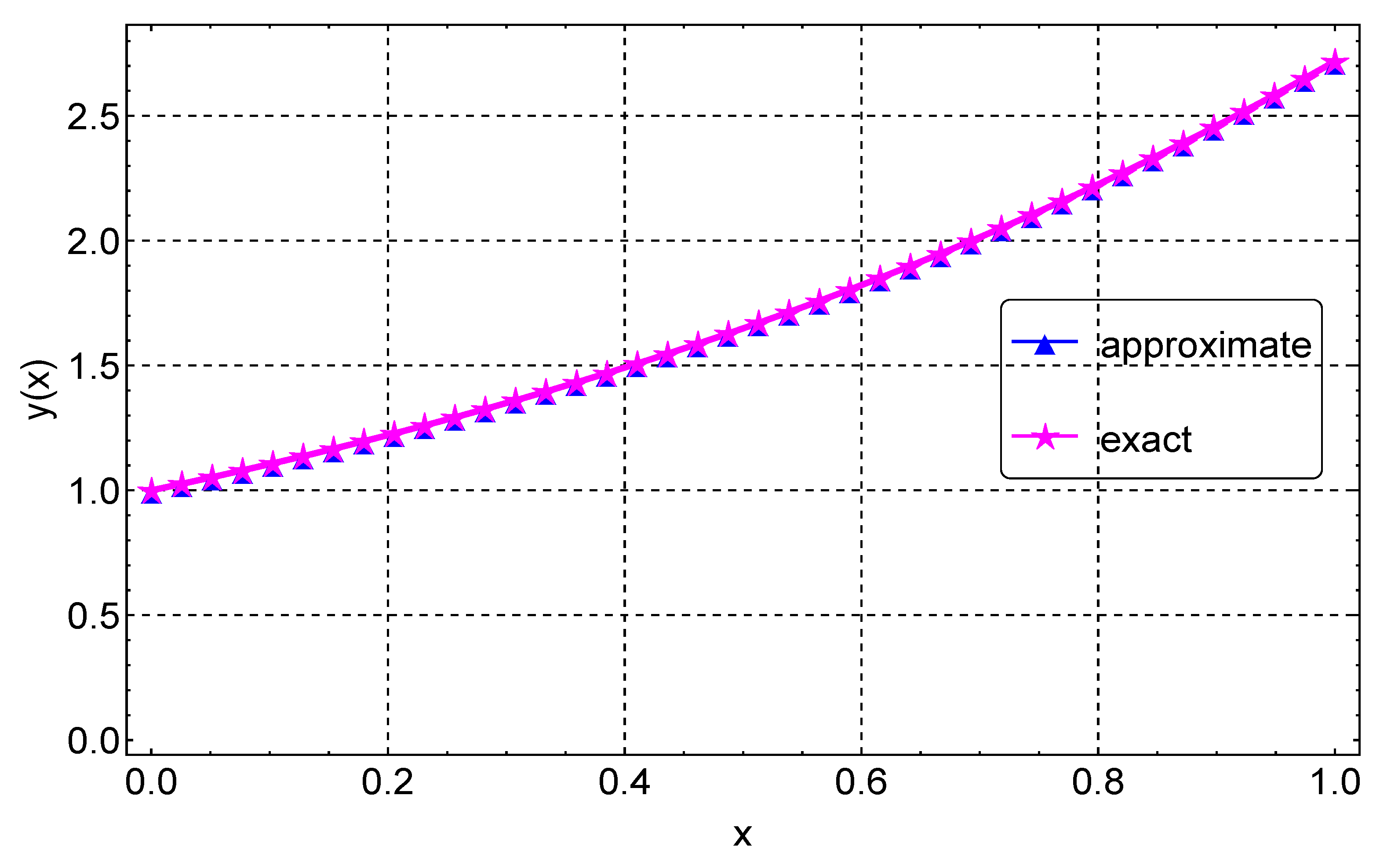
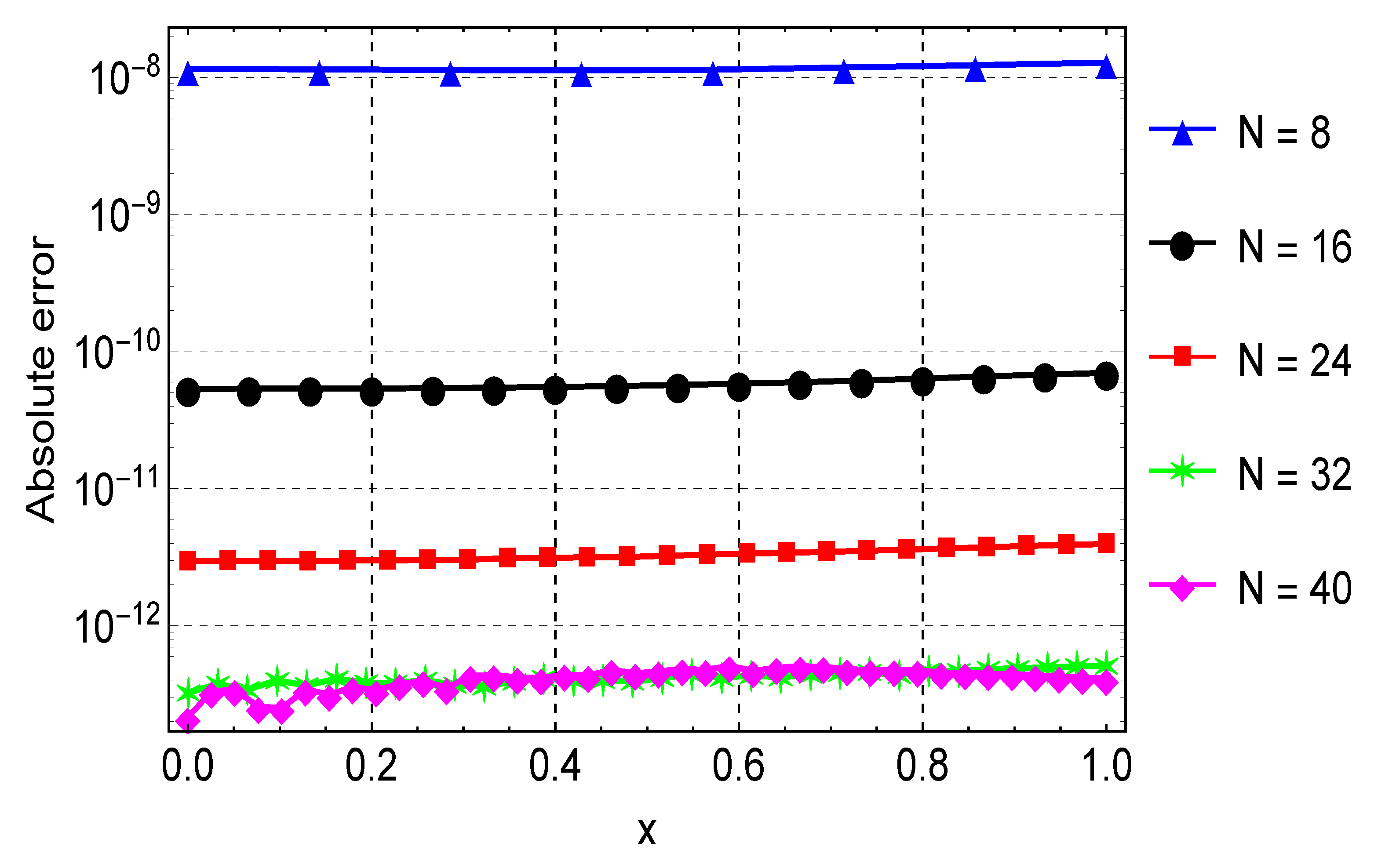
For Example 4, we also compute the approximate solution using the proposed CFDM for various values of N. Likewise, the error norm, rates of convergence, and computational times are presented in Table 4. As shown in the table, for , the CFDM has an error of about , whereas in [9], the error is for . This comparison confirms that the CFDM gives accurate results with fewer grid points. A graphical comparison of the CFDM results and the exact solution is shown in Figure 9. Plots of the absolute errors for various N values is shown in Figure 10. Lastly, Figure 11 shows the convergence plots for the various N values. The plot indicates the method reaches full convergences after six iterations.

Table 4.
Maximum absolute error () and ROC for Example 4.
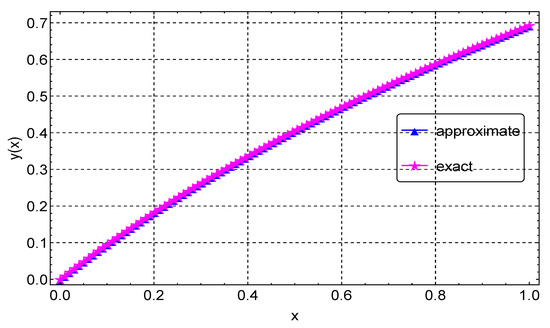
Figure 9.
Exact and approximate solution plots for Example 4.
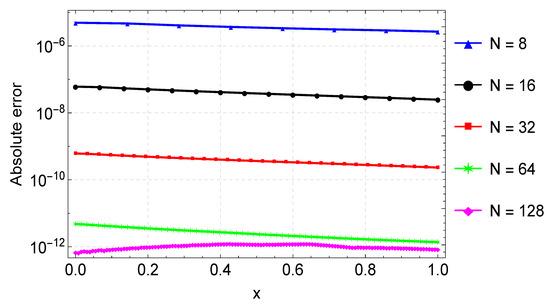
Figure 10.
Error plots for the approximation of Example 4 for varying values of N.
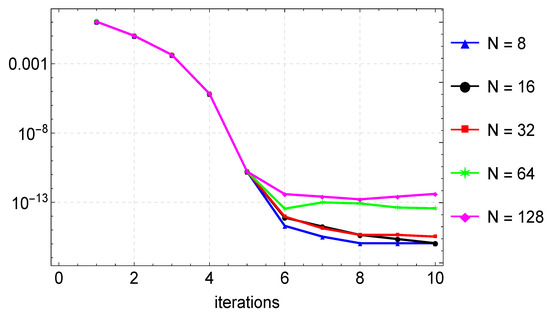
Figure 11.
Convergence plots for the approximation of Example 4 for varying values of N.
Example 5.
Consider the nonlinear second-order boundary value problem:
with boundary conditions:
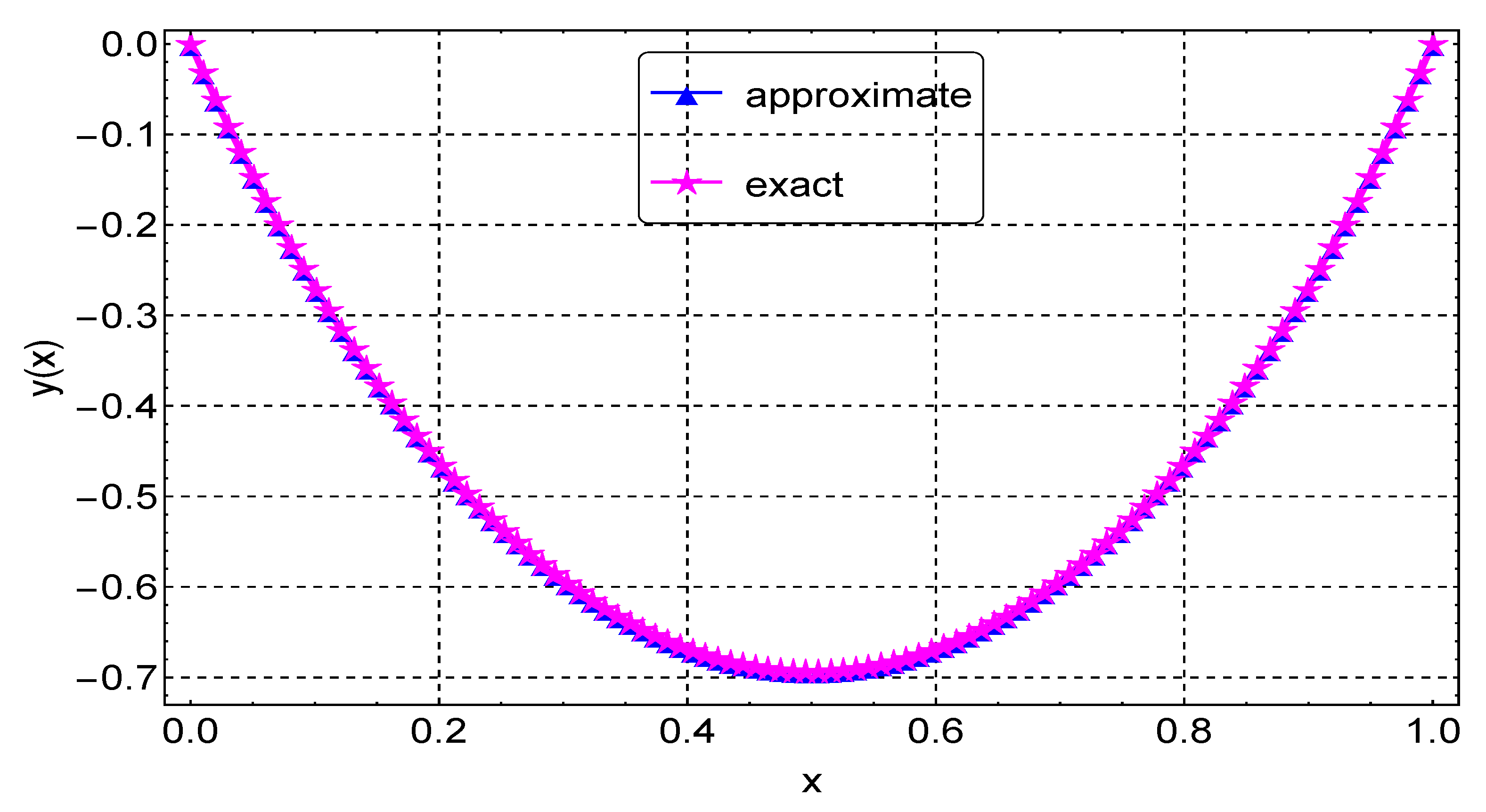
Likewise, in Example 5, we estimate the solution of the nonlinear differential equation using the CFDM for various values of N. The error norm, rates of convergence, and execution times of the proposed method are presented in Table 5, with results from Nasir et al. [9]. The table indicates that the CFDM achieves accuracy on a slightly larger step size than in [9]. A graphical comparison of the CFDM results and the exact solution is shown in Figure 12. The errors for various values of N are shown in Figure 13. Lastly, convergence plots for the different N values are depicted in Figure 14, depicting that the method reaches full convergence after about 6 to 8 iterations, depending on the value of N.

Table 5.
Maximum absolute error () and ROC for Example 5.
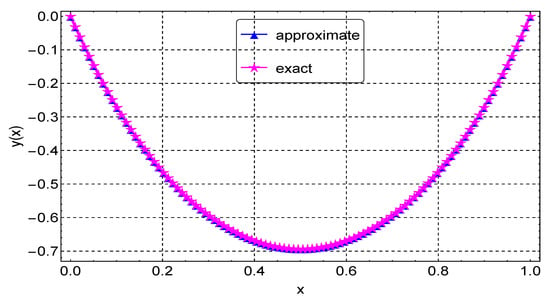
Figure 12.
Exact and approximate solution plots for Example 5.
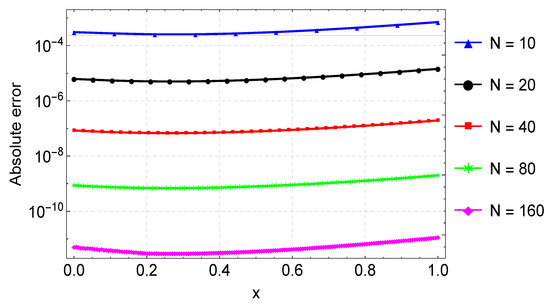
Figure 13.
Error plots for the approximation of Example 5 for varying values of N.
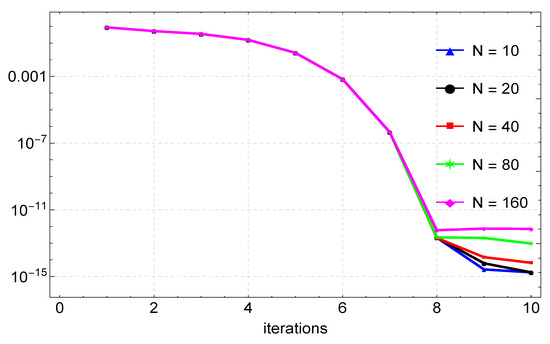
Figure 14.
Convergence plots for the approximation of Example 5 for varying values of N.
Example 6.
Consider the nonlinear second-order boundary value problem:
with boundary conditions:
Lastly, a graphical comparison of the CFDM results and the exact solution is shown in Figure 15. The maximum absolute errors of Example 6 obtained using various values of N are displayed in Table 6 and also shown in Figure 16. We observe that with the same step size, we obtain better accuracy than the results in [32,34]. Lastly, convergence plots for the different N values are depicted in Figure 17, depicting that the method reaches full convergence after 8 or 9 iterations, depending on the value of N used.
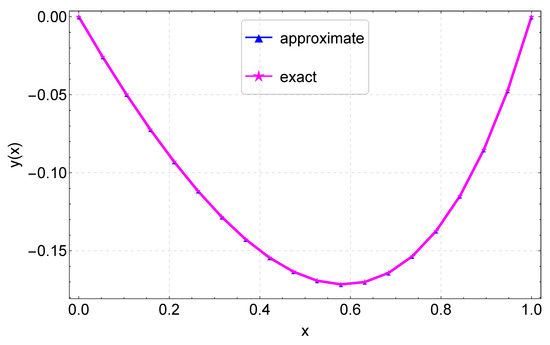
Figure 15.
Exact and approximate solution plots for Example 6.

Table 6.
Maximum absolute error () and ROC for Example 6.
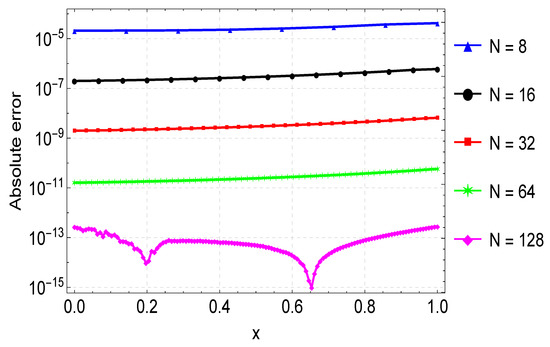
Figure 16.
Error plots for the approximation of Example 6 for varying values of N.
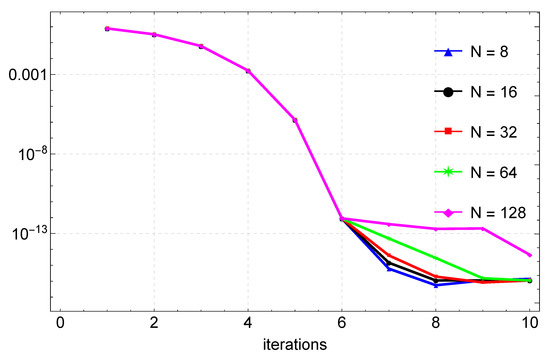
Figure 17.
Convergence plots for the approximation of Example 6 for varying values of N.
7. Conclusions
In this paper, we presented a highly accurate compact finite difference method (CFDM) to solve both linear and nonlinear second-order boundary value problems subjected to Robin boundary conditions. The method utilizes sixth-order compact finite difference schemes. We successfully developed new sixth-order schemes to approximate the Robin boundary conditions, and this leads to a highly accurate method, as shown by the results. Nonlinear equations were first linearized using the quasilinearization (QLM) technique. Convergence of the CFDM was established by using the properties of the standard matrix norm. By computing the absolute error norm, and rates of convergence, the high accuracy of the CFDM was confirmed by comparing its numerical results against the numerical results of the diagonal block method presented in Nasir et al. [9] and Majid et al. [34], symmetric spline [32], Bernoulli polynomials [11], and quintic B-spline collocation [33]. We also observed that the CFDM approximate solution is in excellent agreement with the exact solution in all of the considered examples. Numerical results further confirmed that the rate of convergence of the presented CFDM is seven, consistent with the theoretical approximation.
We conclude that to solve linear and nonlinear boundary value problems subject to Robin boundary conditions, the CFDM is highly accurate and computationally efficient and a dependable method to utilize.
Author Contributions
Conceptualization, P.D. and S.S.; methodology, J.M.; software, J.M.; validation, J.M., P.D. and S.S.; investigation, J.M.; writing—original draft preparation, J.M.; writing—review and editing, P.D. and S.S.; supervision, P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Okereki, M.; Keates, S. Finite Element Applications. A Practical Guide to the FEM Process; Springer: New York, NY, USA, 2018. [Google Scholar]
- Chun, C.; Sakthivel, R. Homotopy perturbation technique for solving two-point boundary value problems–Comparison with other methods. Comput. Phys. Commun. 2010, 181, 1021–1024. [Google Scholar] [CrossRef]
- Hassan, H.N.; El-Tawil, M.A. An efficient analytic approach for solving two-point nonlinear boundary value problems by homotopy analysis method. Math. Methods Appl. Sci. 2011, 34, 977–989. [Google Scholar] [CrossRef]
- Jang, B. Two-point boundary value problems by the extended Adomian decomposition method. J. Comput. Appl. Math. 2008, 219, 253–262. [Google Scholar] [CrossRef]
- Lu, J. Variational iteration method for solving two-point boundary value problems. J. Comput. Appl. Math. 2007, 207, 92–95. [Google Scholar] [CrossRef]
- Egidi, N.; Maponi, P. A spectral method for the solution of boundary value problems. Appl. Math. Comput. 2021, 409, 125812. [Google Scholar] [CrossRef]
- Ibraheem, K.I.; Khalaf, B.M. Shooting neural networks algorithm for solving boundary value problems in ODEs. Appl. Appl. Math. 2011, 6, 187–200. [Google Scholar]
- Chawla, M.M.; Subramanian, R.; Sathi, H.L. A fourth order method for a singular two-point boundary value problem. BIT Numer. Math. 1988, 28, 88–97. [Google Scholar] [CrossRef]
- Nasir, N.M.; Majid, Z.A.; Ismail, F.; Bachok, N. Diagonal Block Method for Solving Two-Point Boundary Value Problems with Robin Boundary Conditions. Math. Probl. Eng. 2018, 2018, 2056834. [Google Scholar]
- Duan, J.; Rach, R.; Wazwaz, A.; Chaolu, T.; Wang, Z. A new modified Adomian decomposition method and its multistage form for solving nonlinear boundary value problems with Robin boundary conditions. Appl. Math. Model. 2013, 37, 8687–8708. [Google Scholar] [CrossRef]
- Islam, M.S.; Shirin, A. Numerical Solutions of a Class of Second Order Boundary Value Problems on Using Bernoulli Polynomials. Appl. Math. 2011, 2011, 1059–1067. [Google Scholar] [CrossRef]
- Roul, P.; Goura, V.M.K.P.; Agarwal, R. A compact finite difference method for a general class of nonlinear singular boundary value problems with Neumann and Robin boundary conditions. Appl. Math. Comput. 2019, 350, 283–304. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Gupta, M.M.; Kouatchou, J.; Zhang, J. Comparison of second-and fourth-order discretizations for multigrid Poisson solvers. J. Comput. Phys. 1997, 132, 226–232. [Google Scholar] [CrossRef]
- Sari, M.; Gürarslan, G. A sixth-order compact finite difference scheme to the numerical solutions of Burgers’ equation. Appl. Math. Comput. 2009, 208, 475–483. [Google Scholar] [CrossRef]
- Liao, W. An implicit fourth-order compact finite difference scheme for one-dimensional Burgers’ equation. Appl. Math. Comput. 2008, 206, 755–764. [Google Scholar] [CrossRef]
- Zhao, J.; Davison, M.; Corless, R.M. Compact finite difference method for American option pricing. J. Comput. Appl. Math. 2007, 206, 306–321. [Google Scholar] [CrossRef]
- Shah, A.; Yuan, L.; Khan, A. Upwind compact finite difference scheme for time-accurate solution of the incompressible Navier–Stokes equations. Appl. Math. Comput. 2010, 214, 320–3213. [Google Scholar] [CrossRef]
- Zhao, J.; Corless, R.M. Compact finite difference method for integro-differential equations. Appl. Math. Comput. 2006, 177, 271–288. [Google Scholar] [CrossRef]
- Zhao, J. Compact finite difference methods for high order integro-differential equations. Appl. Math. Comput. 2013, 221, 66–78. [Google Scholar] [CrossRef]
- Li, J.; Visbal, M.R. High-order compact schemes for nonlinear dispersive waves. J. Sci. Comput. 2006, 26, 1–23. [Google Scholar] [CrossRef]
- Düring, B.; Fournié, M.; Jüngel, A. High order compact finite difference schemes for a nonlinear Black–Scholes equation. Int. J. Theor. Appl. Financ. 2003, 6, 767–789. [Google Scholar] [CrossRef]
- Fournie, M. High Order Compact Finite Difference Schemes for a Nonlinear Black–Scholes Equation; University of Konstanz Center of Finance and Econometrics Discussion Paper, 01/07; University of Konstanz, Center of Finance and Econometrics (CoFE): Konstanz, Germany, 2001. [Google Scholar]
- Mathale, D.; Dlamini, P.G.; Khumalo, M. Compact finite difference relaxation method for chaotic and hyperchaotic initial value systems. Comput. Appl. Math. 2018, 37, 5187–5202. [Google Scholar] [CrossRef]
- Kouagou, J.N.; Dlamini, P.G.; Simelane, S.M. On the multi-domain compact finite difference relaxation method for high dimensional chaos: The nine-dimensional Lorenz system. Alex. Eng. J. 2020, 59, 2617–2625. [Google Scholar] [CrossRef]
- Dlamini, P.G.; Khumalo, M. A new compact finite difference quasilinearization method for nonlinear evolution partial differential equations. Open Math. 2017, 15, 1450–1462. [Google Scholar] [CrossRef]
- Zhao, J. Highly accurate compact mixed methods for two point boundary value problems. Appl. Math. Comput. 2007, 188, 1402–1418. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, T.; Corless, R.M. Convergence of the compact finite difference method for second-order elliptic equations. Appl. Math. Comput. 2006, 182, 1454–1469. [Google Scholar] [CrossRef]
- Pettigrew, M.F.; Rasmussen, H.A. Compact method for second-order boundary value problems on nonuniform grids. Comput. Math. Appl. 1996, 31, 1–16. [Google Scholar] [CrossRef][Green Version]
- Holsapple, R.; Venkataraman, R.; Doman, D. New, fast numerical method for solving two-point boundary-value problems. J. Guid. Control. Dyn. 2004, 27, 301–304. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier: New York, NY, USA, 1965. [Google Scholar]
- Bhatta, S.K.; Sastri, K.S. Symmetric spline procedures for boundary value problems with mixed boundary conditions. J. Comput. Appl. Math. 1993, 45, 237–250. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. Quintic B-spline collocation method for second order mixed boundary value problem. Comput. Phys. Commun. 2012, 183, 913–921. [Google Scholar] [CrossRef]
- Majid, Z.A.; Nasir, N.M.; Ismail, F.; Bachok, N. Two point diagonally block method for solving boundary value problems with Robin boundary conditions. Malays. J. Math. Sci. 2019, 13, 1–14. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).