Security Enhanced Symmetric Key Encryption Employing an Integer Code for the Erasure Channel
Abstract
:1. Introduction
2. Related Work and Background on the Security-Enhanced Encryption Scheme
2.1. Related Work and Our Goals
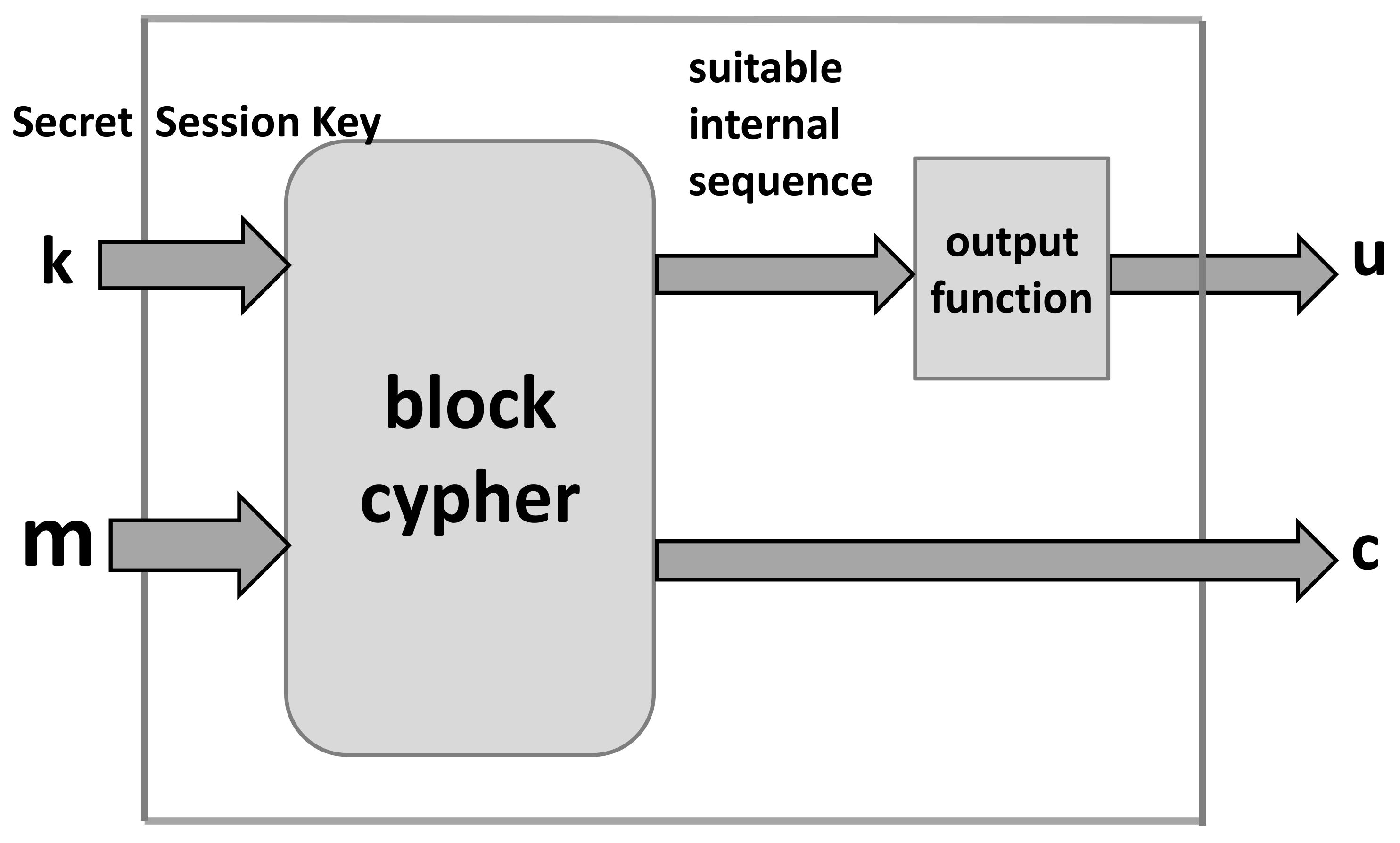
2.2. Main Background
3. Integer Codes Correcting One Erasure per Data Byte
3.1. Scenario of Employment
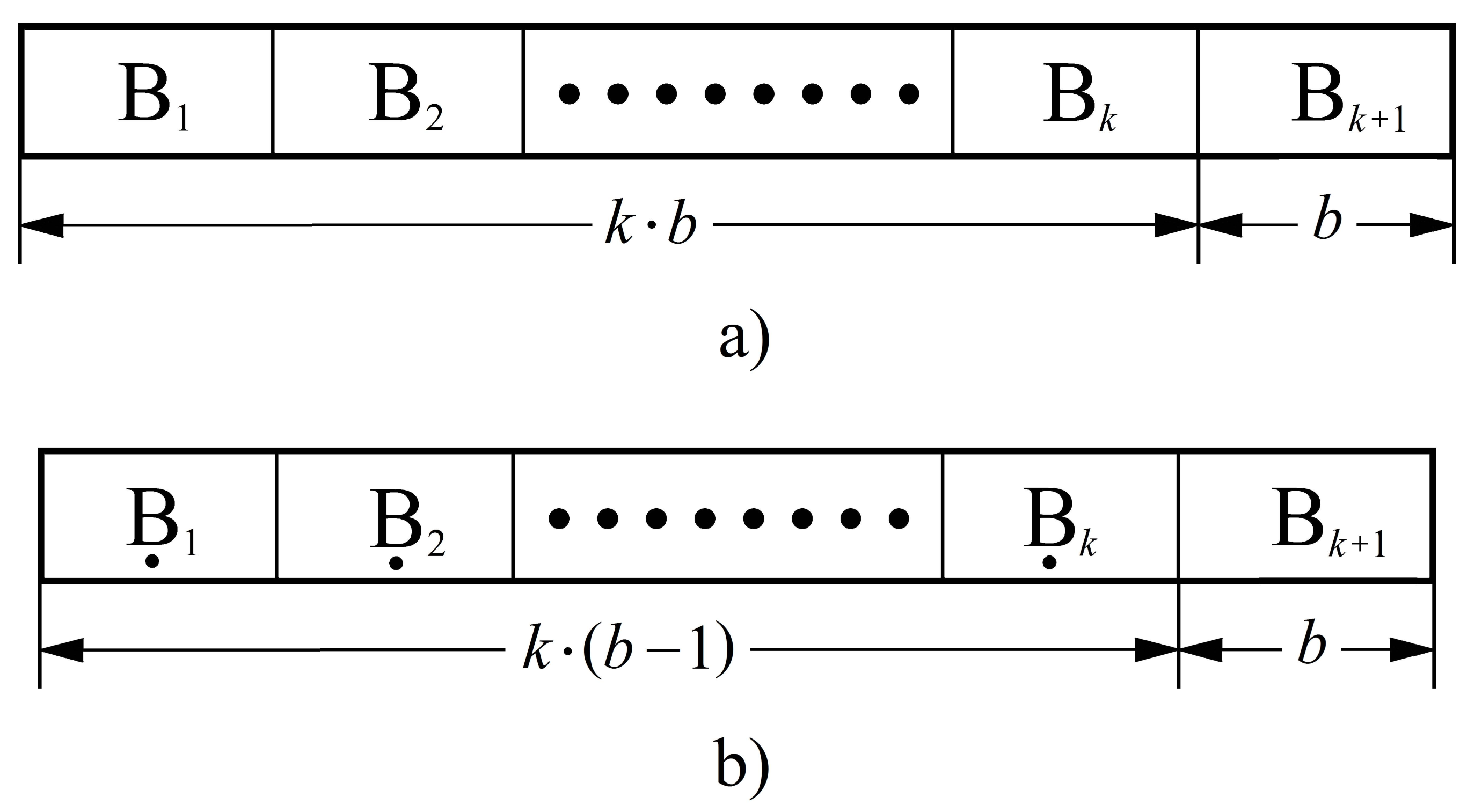
3.2. Code Construction
3.3. The Pseudocodes and Illustrative Examples
3.4. Evaluation Issues
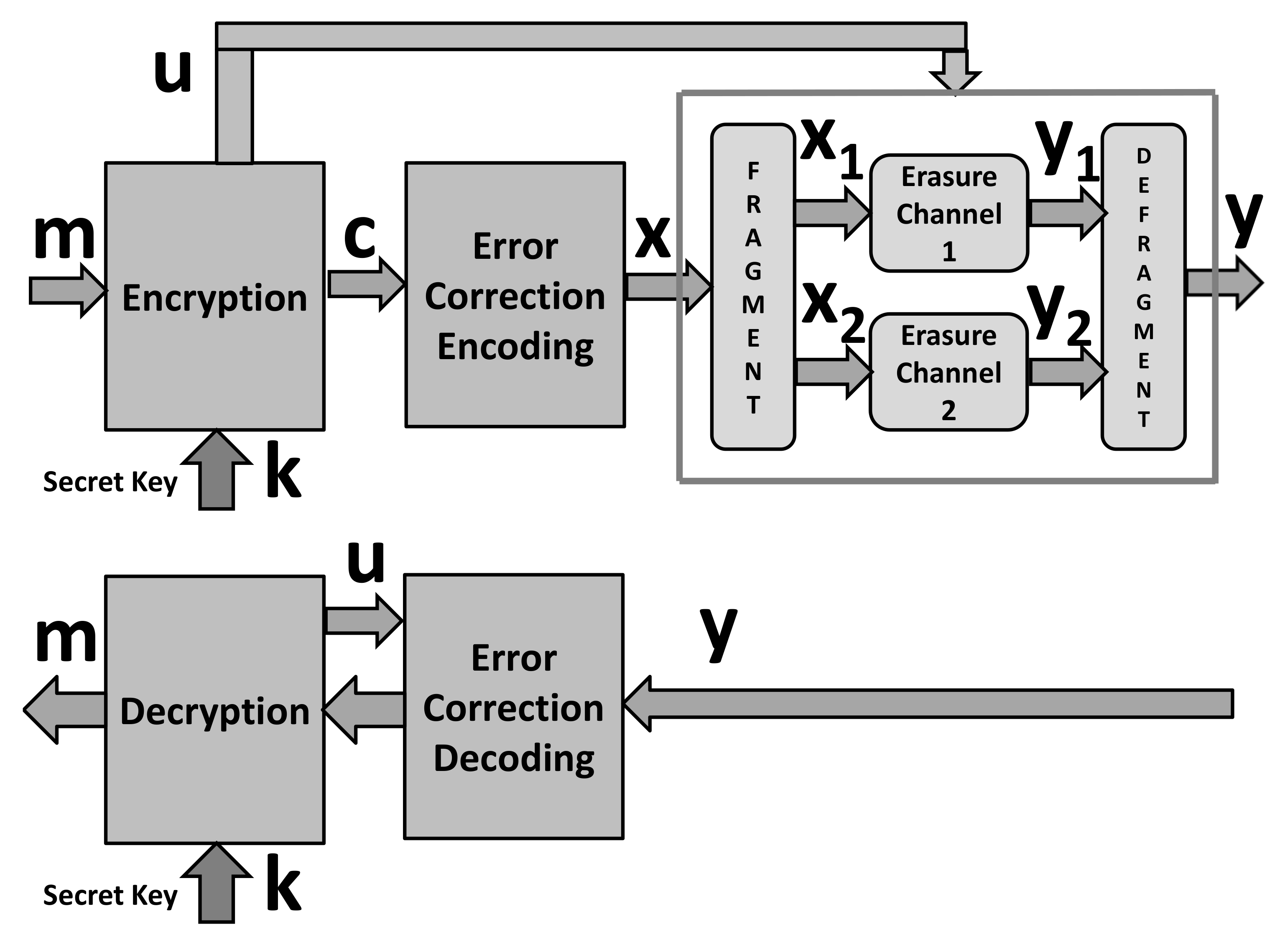
4. Security-Enhanced Encryption Scheme
- Input: b-bit byte , of the codeword and the parameter and the vector . If the considered byte is the check-byte, preset .
- if : do i = 1, b
- -
- = ? if = i
- -
- otherwise
- if : do i = 1, b
- -
- Output: b-bit byte
5. Security Evaluation of the Enhanced Encryption
5.1. Security Notation
- 1.
- The adversary chooses a pair of messages of the same length n and passes them on to the encryption system for encrypting.
- 2.
- A bit is chosen uniformly at random, and only one of the two messages , precisely , is encrypted into ciphertext and returned to .
- 3.
- Upon observing , and without knowledge of b, the adversary outputs a bit .
- 4.
- The experiment output is defined to be 1 if , and 0 otherwise; if the experiment output is 1, denoted shortly as the event , we say that has succeeded.
5.2. Evaluation of the Security Gain
6. Implementation Complexity of the Components for Enhancement
6.1. Time Complexity of the Encoding and Decoding Procedures
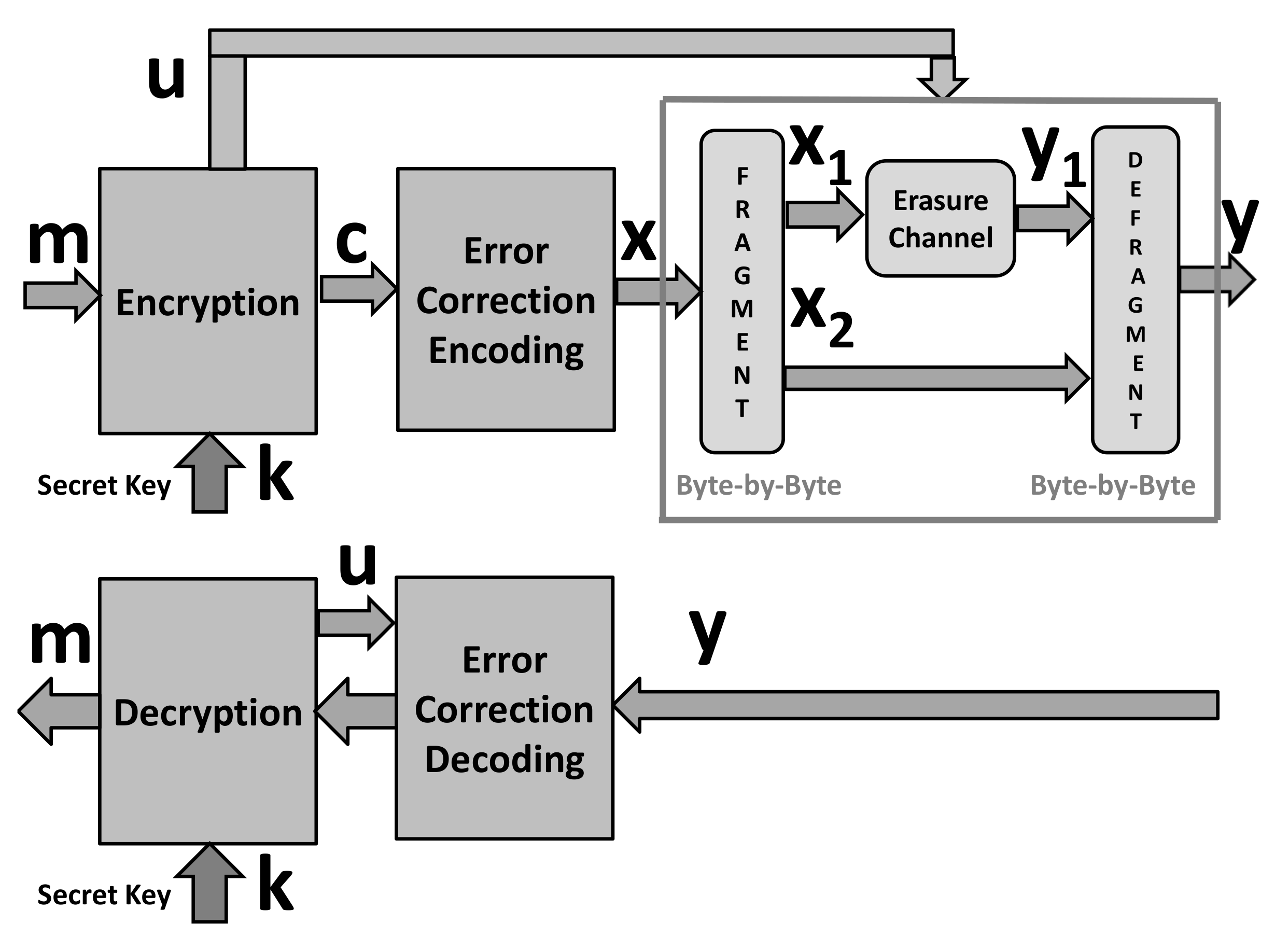
6.2. Implementation Complexity of Simulated Channel with Synchronization Errors
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mihaljević, M.J.; Wang, L.; Xu, S. An Approach for Security Enhancement of Certain Encryption Schemes Employing Error Correction Coding and Simulated Synchronization Errors. Entropy 2022, 24, 406. [Google Scholar] [CrossRef] [PubMed]
- Rivest, R.; Sherman, T. RandomizedEncryption Techniques. In Advances in Cryptology: Proceedings of CRYPTO ’82; Plemum: New York, NY, USA, 1983; pp. 145–163. [Google Scholar]
- Willett, M. Deliberate noise in a moderncryptographic system. IEEE Trans. Inform. Theory 1980, 26, 102–104. [Google Scholar] [CrossRef]
- Esmaeili, M.; Dakhilalian, M.; Gulliver, T.A. New secure channel coding scheme based on randomly punctured quasi-cyclic-low density parity check codes. IET Commun. 2014, 8, 2556–2562. [Google Scholar] [CrossRef]
- Esmaeili, M.; Gulliver, T.A. Joint channel coding-cryptography based on random insertions and deletions in quasi-cyclic-low-density parity check codes. IET Commun. 2015, 9, 1555–1560. [Google Scholar] [CrossRef]
- Esmaeili, M.; Gulliver, T.A. A Secure Code Based Cryptosystem via Random Insertions, Deletions, and Errors. IEEE Commun. Lett. 2016, 20, 870–873. [Google Scholar] [CrossRef]
- Hooshmand, R.; Aref, M.R.; Eghlidos, T. Physical layer encryption scheme using finite-length polar codes. IET Commun. 2015, 9, 1857–1866. [Google Scholar] [CrossRef]
- Hooshmand, R.; Aref, M.R. Efficient Polar Code-Based Physical Layer Encryption Scheme. IEEE Wirel. Commun. Lett. 2017, 6, 710–713. [Google Scholar] [CrossRef]
- Lu, X.; Lei, J.; Li, W.; Lai, K.; Pan, Z. Physical Layer Encryption Algorithm Based on Polar Codes and Chaotic Sequences. IEEE Access 2018, 4, 4380–4390. [Google Scholar] [CrossRef]
- Stuart, C.M.; Spandana, K.; Dhanaraj, K.J.; Pattathil, D.P. Design and implementation of hardwareefficient modified Rao–Nam scheme with high security for wireless sensor networks. J. Inf. Secur. Appl. 2016, 29, 65–79. [Google Scholar]
- An, C.; Liu, Y.; Lu, X. Evolution of the Polar Code-Based Encryption Schemes. In Proceedings of the 2021 IEEE Globecom Workshops, Madrid, Spain, 7–11 December 2021. [Google Scholar]
- Bagheri, K.; Eghlidos, T.; Sadeghi, M.R.; Panario, D.; Khodaiemehr, H. A Joint Encryption, Channel Coding and Modulation Scheme Using QC-LDPC Lattice-Codes. IEEE Trans. Commun. 2020, 68, 4673–4693. [Google Scholar] [CrossRef]
- Hooshmand, R.; Shooshtari, M.K.; Aref, M.R. Secret key cryptosystem based on polar codes over Binary Erasure Channel. In Proceedings of the 2013 10th International ISC Conference on Information Security and Cryptology (ISCISC), Yazd, Iran, 29–30 August 2013. [Google Scholar]
- Rajagopalan, A.; Thangaraj, A.; Agrawal, S. Wiretap Polar Codes in Encryption Schemes Based on Learning with Errors Problem. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018. [Google Scholar]
- Rao, T.R.N.; Nam, K.-H. Private-key algebraic-code encryptions. IEEE Trans. Inf. Theory 1989, 35, 829–833. [Google Scholar] [CrossRef]
- Khiabani, Y.S.; Wei, S.; Yuan, J.; Wang, J. Enhancement of Secrecy of Block Ciphered Systems by Deliberate Noise. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1604–1613. [Google Scholar] [CrossRef]
- Mihaljević, M.J.; Imai, H. An approach for stream ciphers design based on joint computing over random and secret data. Computing 2009, 85, 153–168. [Google Scholar] [CrossRef]
- Mihaljević, M.J.; Kavčić, A.; Matsuura, K. An Encryption Technique for Provably Secure Transmission from a High Performance Computing Entity to a Tiny One. Math. Probl. Eng. 2016, 2016, 7920495. [Google Scholar] [CrossRef]
- Mihaljevic, M.J.; Oggier, F. Security Evaluation and Design Elements for a Class of Randomized Encryptions. IET Inf. Secur. 2019, 13, 36–47. [Google Scholar] [CrossRef]
- Mihaljevic, M.J. A Security Enhanced Encryption Scheme and Evaluation of Its Cryptographic Security. Entropy 2019, 21, 11. [Google Scholar] [CrossRef]
- Oggier, F.; Mihaljević, M.J. An Information-Theoretic Security Evaluation of a Class of Randomized Encryption Schemes. IEEE Trans. Inf. Forensics Secur. 2014, 9, 158–168. [Google Scholar] [CrossRef]
- Wei, S.; Wang, J.; Yin, R.; Yuan, J. Trade-Off Between Security and Performance in Block Ciphered Systems With Erroneous Ciphertexts. IEEE Trans. Inf. Forensics Secur. 2013, 8, 636–645. [Google Scholar] [CrossRef]
- Applebaum, B.; Cash, D.; Peikert, C.; Sahai, A. Fast Cryptographic Primitives and Circular-Secure Encryption Based on Hard Learning Problems. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2009; Volume 5677, pp. 595–618. [Google Scholar]
- Gilbert, H.; Robshaw, M.J.B.; Seurin, Y. How to Encrypt with the LPN Problem. ICALP 2008, Part II. Lect. Notes Comput. Sci. 2008, 5126, 679–690. [Google Scholar]
- Arıkan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Thomas, E.K.; Tan, V.Y.F.; Vardy, A.; Motani, M. Polar coding for the binary erasure channel with deletions. IEEE Commun. Lett. 2017, 21, 710–713. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, Y.-S.; No, J.-S. Ciphertext-Only Attack on Linear Feedback Shift Register-Based Esmaeili-Gulliver Cryptosystem. IEEE Commun. Lett. 2017, 21, 971–974. [Google Scholar] [CrossRef]
- Wang, J.; Mu, J.; Wei, S.; Jiang, C.; Beaulieu, N.C. Statistical Characterization of Decryption Errors in Block-Ciphered Systems. IEEE Trans. Commun. 2015, 63, 4363–4376. [Google Scholar] [CrossRef]
- Yap, W.-S.; Heng, S.-H.; Goi, B.-M. Security analysis of M-DES and key-based coded permutation ciphers in wireless channels. IET Commun. 2018, 12, 1230–1235. [Google Scholar] [CrossRef]
- Rybin, P.; Andreev, K.; Zyablov, V. Error Exponents of LDPC Codes under Low-Complexity Decoding. Entropy 2021, 23, 253. [Google Scholar] [CrossRef]
- Trofimiuk, G.; Iakuba, N.; Rets, S.; Ivanov, K.; Trifonov, P. Fast Block Sequential Decoding of Polar Codes. IEEE Trans. Veh. Technol. 2020, 69, 10988–10999. [Google Scholar] [CrossRef]
- Lin, S.-J.; Al-Naffouri, T.Y.; Han, Y.S.; Chung, W.-H. Novel Polynomial Basis with Fast Fourier Transform and Its Application to Reed–Solomon Erasure Codes. IEEE Trans. Inf. Theory 2016, 62, 6284–6299. [Google Scholar] [CrossRef]
- Radonjic, A. (Perfect) Integer Codes Correcting Single Errors. IEEE Commun. Lett. 2018, 22, 17–20. [Google Scholar] [CrossRef]
- Radonjic, A.; Vujicic, V. Integer Codes Correcting Burst and Random Asymmetric Errors within a Byte. J. Franklin Inst. 2018, 355, 981–996. [Google Scholar] [CrossRef]
- Radonjic, A.; Vujicic, V. Integer Codes Correcting Sparse Byte Errors. Cryptogr. Commun. 2019, 11, 1069–1077. [Google Scholar] [CrossRef]
- Radonjic, A. Integer Codes Correcting Double Errors and Triple-Adjacent Errors within a Byte. IEEE Trans. Very Large Scale Integr. Syst. 2020, 8, 1901–1908. [Google Scholar] [CrossRef]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; CRC Press: Boca Ratton, FL, USA, 2007. [Google Scholar]
- Tebbe, D.L.; Dwyer, S.J., III. Uncertainty and the Probability of Error. IEEE Trans. Inf. Theory 1968, IT-24, 516–518. [Google Scholar] [CrossRef]
- Feder, M.; Merhav, N. Relations between entropy and error probability. IEEE Trans. Inf. Theory 1994, 40, 259–266. [Google Scholar] [CrossRef]
- Rahmati, M.; Duman, T.M. Upper Bounds on the Capacity of Deletion Channels Using Channel Fragmentation. IEEE Trans. Inf. Theory 2015, 61, 146–156. [Google Scholar] [CrossRef]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Efficient Erasure Correcting Codes. IEEE Trans. Inf. Theory 2001, 47, 569–584. [Google Scholar] [CrossRef]
- Pishro-Nik, H.; Fekri, F. On Decoding of Low-Density Parity-Check Codes Over the Binary Erasure Channel. IEEE Trans. Inf. Theory 2004, 50, 439–454. [Google Scholar] [CrossRef]

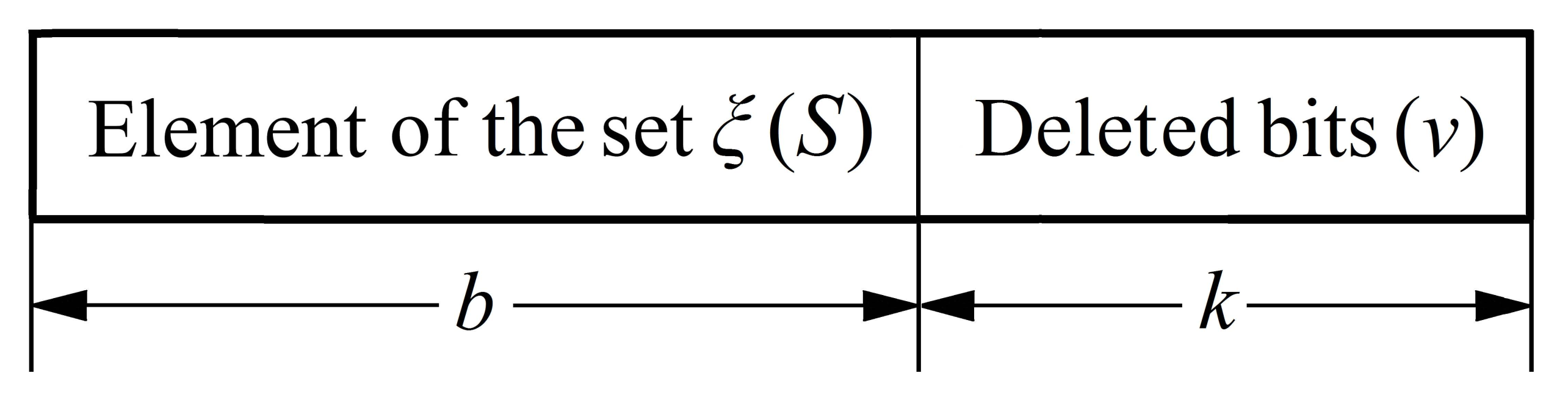



| s | v | s | v | s | v | ||||||||||||||
| 1 | 3 | 0 | 0 | 1 | 1 | 6 | 13 | 0 | 1 | 1 | 0 | 11 | 23 | 1 | 1 | 0 | 1 | ||
| 2 | 5 | 1 | 0 | 1 | 0 | 7 | 14 | 0 | 0 | 0 | 1 | 12 | 24 | 0 | 1 | 0 | 0 | ||
| 3 | 7 | 0 | 1 | 0 | 1 | 8 | 16 | 1 | 0 | 0 | 0 | 13 | 27 | 0 | 1 | 1 | 1 | ||
| 4 | 9 | 1 | 1 | 0 | 0 | 9 | 19 | 1 | 0 | 1 | 1 | 14 | 29 | 1 | 1 | 1 | 0 | ||
| 5 | 12 | 1 | 1 | 1 | 1 | 10 | 20 | 0 | 0 | 1 | 0 | 15 | 30 | 1 | 0 | 0 | 1 | ||
| s | v | s | v | s | v | ||||||||||||||
| 1 | 2 | 1 | 0 | 1 | 1 | 6 | 12 | 1 | 1 | 0 | 0 | 11 | 21 | 1 | 1 | 0 | 1 | ||
| 2 | 4 | 0 | 1 | 0 | 0 | 7 | 13 | 0 | 1 | 0 | 1 | 12 | 24 | 1 | 0 | 1 | 0 | ||
| 3 | 6 | 1 | 1 | 1 | 1 | 8 | 16 | 0 | 0 | 1 | 0 | 13 | 25 | 0 | 0 | 1 | 1 | ||
| 4 | 8 | 1 | 0 | 0 | 0 | 9 | 17 | 1 | 0 | 0 | 1 | 14 | 28 | 1 | 1 | 1 | 0 | ||
| 5 | 9 | 0 | 0 | 0 | 1 | 10 | 20 | 0 | 1 | 1 | 0 | 15 | 29 | 0 | 1 | 1 | 1 | ||
| Upper Bound on | Upper Bound on | Upper Bound on | Upper Bound on | |
|---|---|---|---|---|
| for | for | for | for | |
| 1.00 | 0.7440 | 0.8333 | 0.8929 | 0.9417 |
| 0.95 | 0.7563 | 0.8433 | 0.8985 | 0.9447 |
| 0.90 | 0.7703 | 0.8535 | 0.9043 | 0.9477 |
| 0.85 | 0.7860 | 0.8640 | 0.9100 | 0.9507 |
| 0.80 | 0.8032 | 0.8748 | 0.9159 | 0.9537 |
| 0.75 | 0.8221 | 0.8859 | 0.9218 | 0.9567 |
| 0.70 | 0.8424 | 0.8973 | 0.9278 | 0.9598 |
| 0.65 | 0.8641 | 0.9089 | 0.9339 | 0.9629 |
| 0.60 | 0.8872 | 0.9208 | 0.9400 | 0.9660 |
| 0.55 | 0.9116 | 0.9330 | 0.9461 | 0.9691 |
| 0.50 | 0.9373 | 0.9454 | 0.9523 | 0.9722 |
| Upper Bound on | Upper Bound on | Upper Bound on | |
|---|---|---|---|
| for | for | for | |
| 1.00 | 0.9062 | 0.8906 | 0.9453 |
| 0.95 | 0.9119 | 0.8963 | 0.9483 |
| 0.90 | 0.9176 | 0.9020 | 0.9513 |
| 0.85 | 0.9234 | 0.9078 | 0.9543 |
| 0.80 | 0.9293 | 0.9137 | 0.9573 |
| 0.75 | 0.9352 | 0.9196 | 0.9604 |
| 0.70 | 0.9412 | 0.9256 | 0.9634 |
| 0.65 | 0.9472 | 0.9316 | 0.9665 |
| 0.60 | 0.9533 | 0.9377 | 0.9696 |
| 0.55 | 0.9595 | 0.9439 | 0.9727 |
| 0.50 | 0.9657 | 0.9501 | 0.9758 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihaljević, M.J.; Radonjić, A.; Wang, L.; Xu, S. Security Enhanced Symmetric Key Encryption Employing an Integer Code for the Erasure Channel. Symmetry 2022, 14, 1709. https://doi.org/10.3390/sym14081709
Mihaljević MJ, Radonjić A, Wang L, Xu S. Security Enhanced Symmetric Key Encryption Employing an Integer Code for the Erasure Channel. Symmetry. 2022; 14(8):1709. https://doi.org/10.3390/sym14081709
Chicago/Turabian StyleMihaljević, Miodrag J., Aleksandar Radonjić, Lianhai Wang, and Shujiang Xu. 2022. "Security Enhanced Symmetric Key Encryption Employing an Integer Code for the Erasure Channel" Symmetry 14, no. 8: 1709. https://doi.org/10.3390/sym14081709
APA StyleMihaljević, M. J., Radonjić, A., Wang, L., & Xu, S. (2022). Security Enhanced Symmetric Key Encryption Employing an Integer Code for the Erasure Channel. Symmetry, 14(8), 1709. https://doi.org/10.3390/sym14081709






