Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel
Abstract
:1. Introduction
2. Preliminaries
3. Methodology
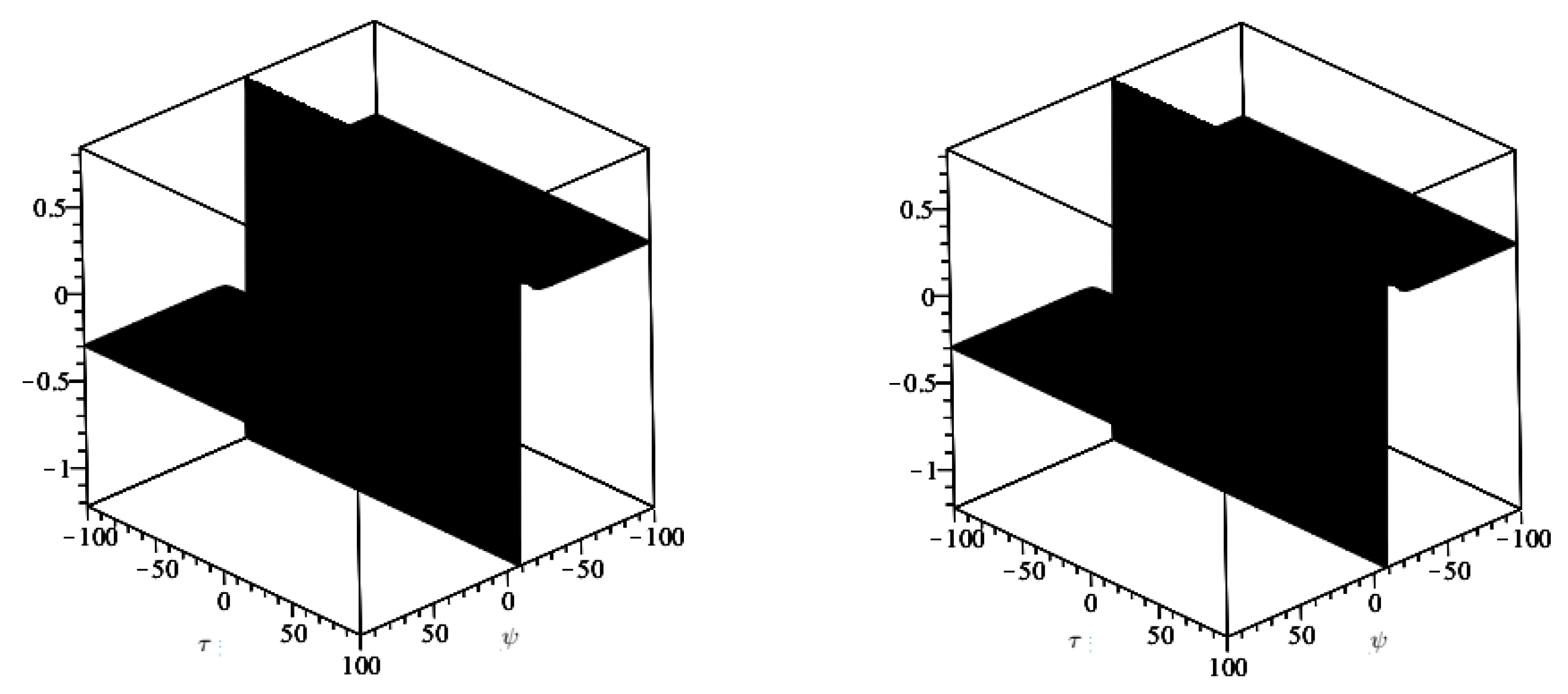
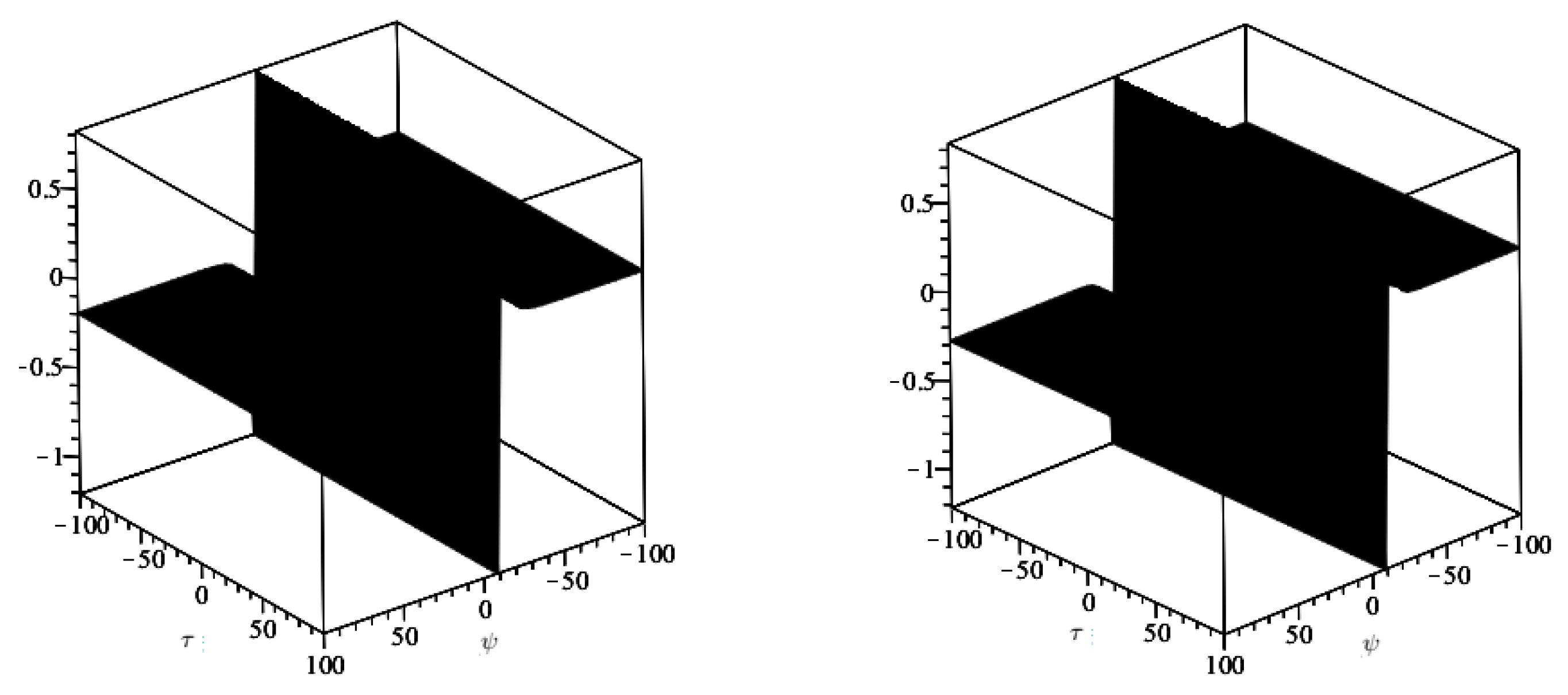
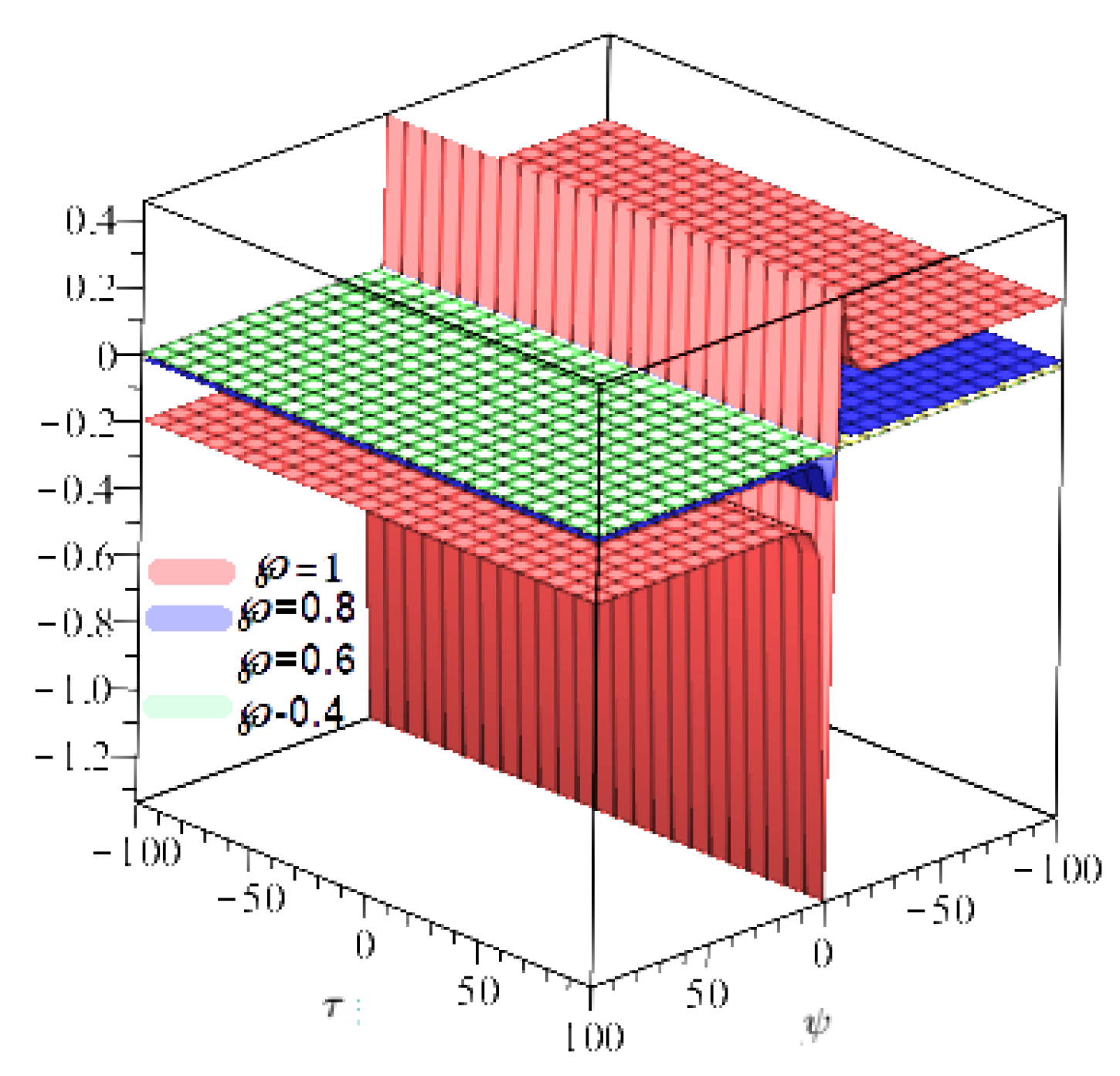
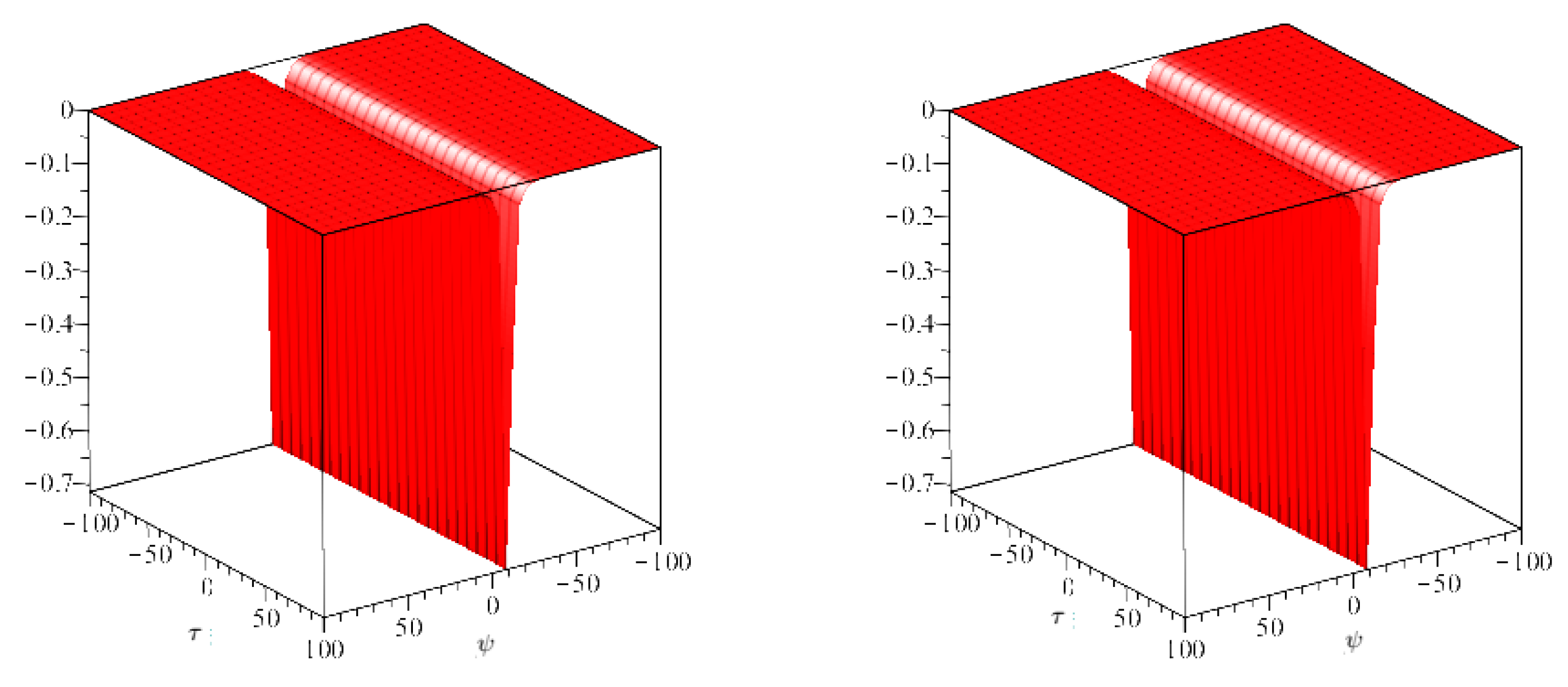
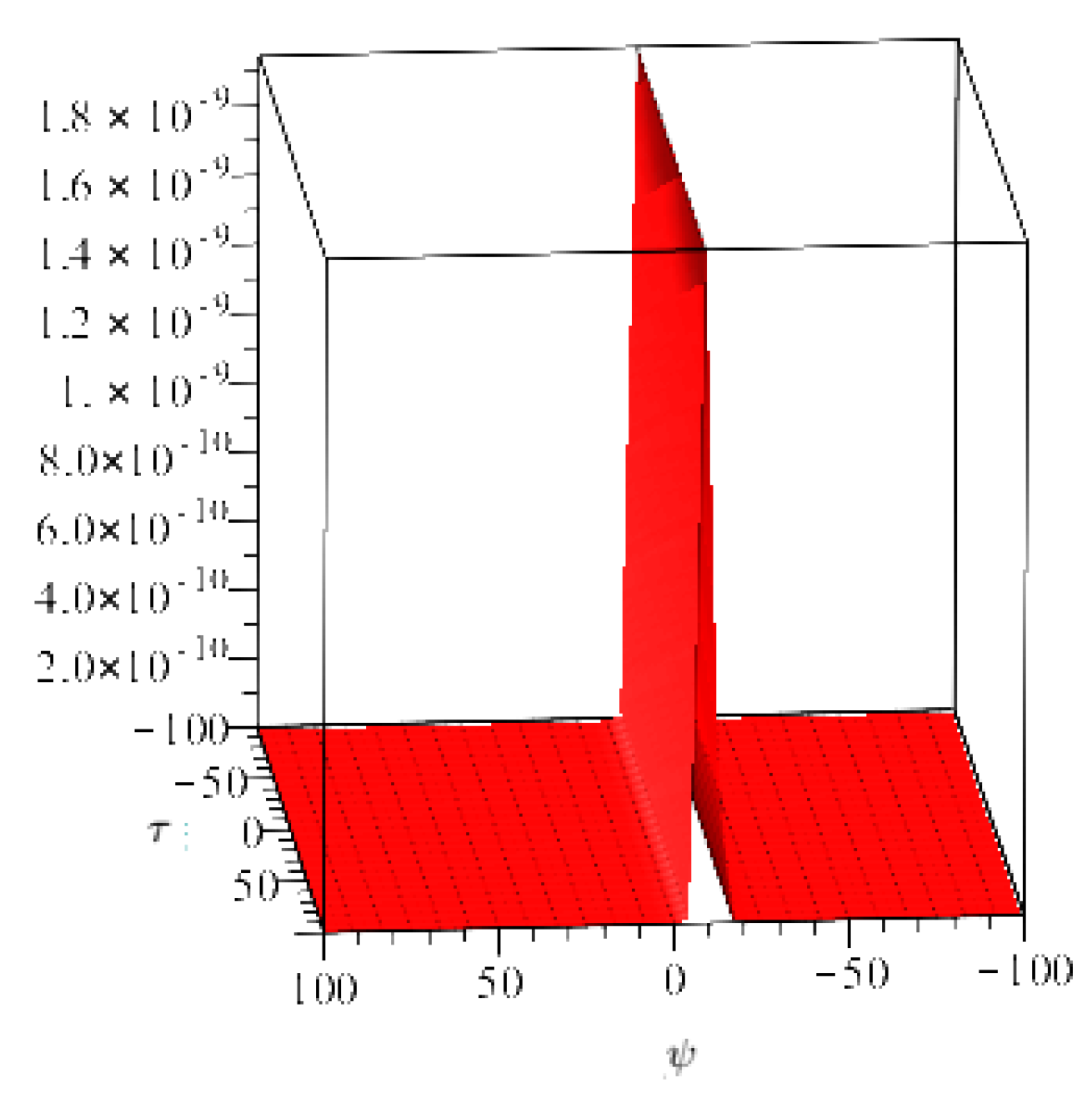
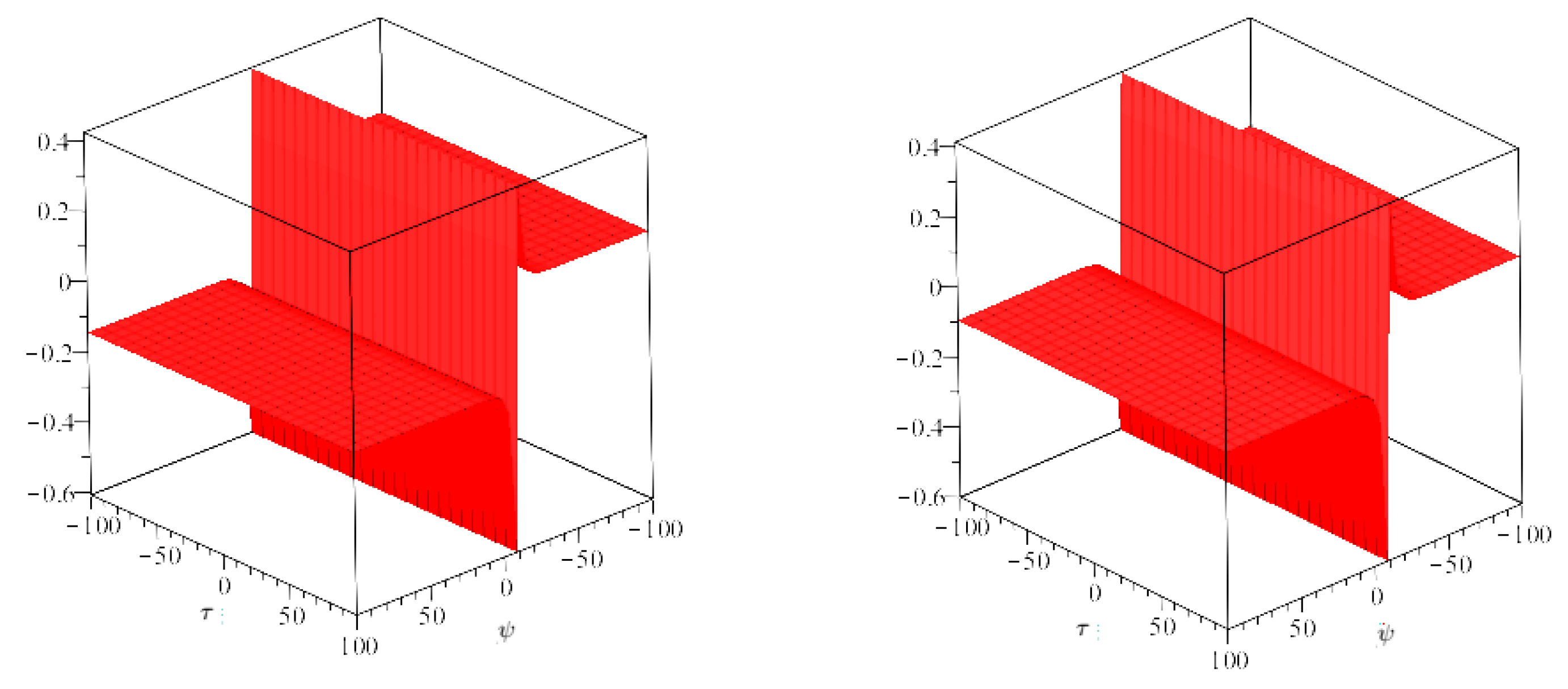
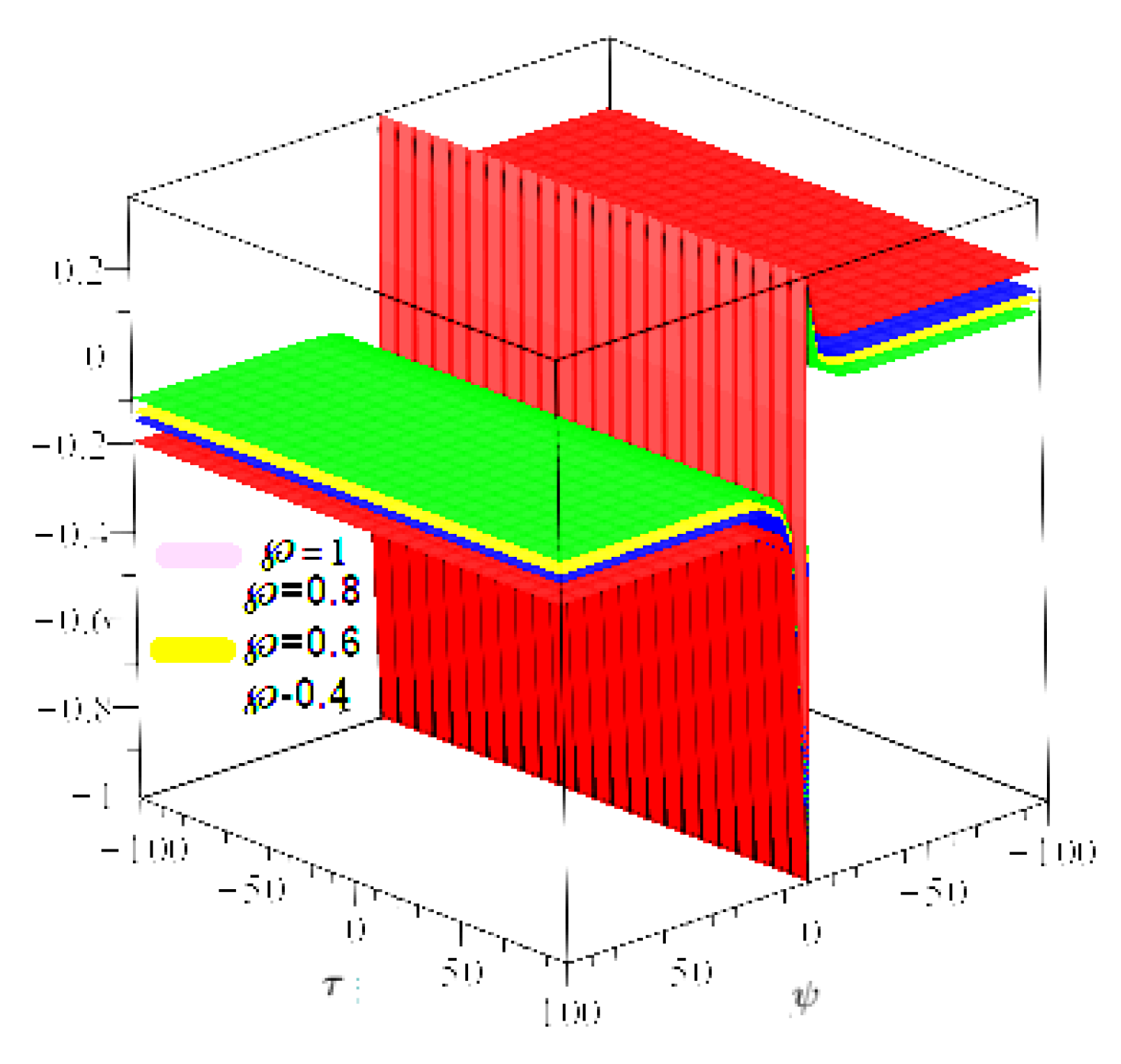
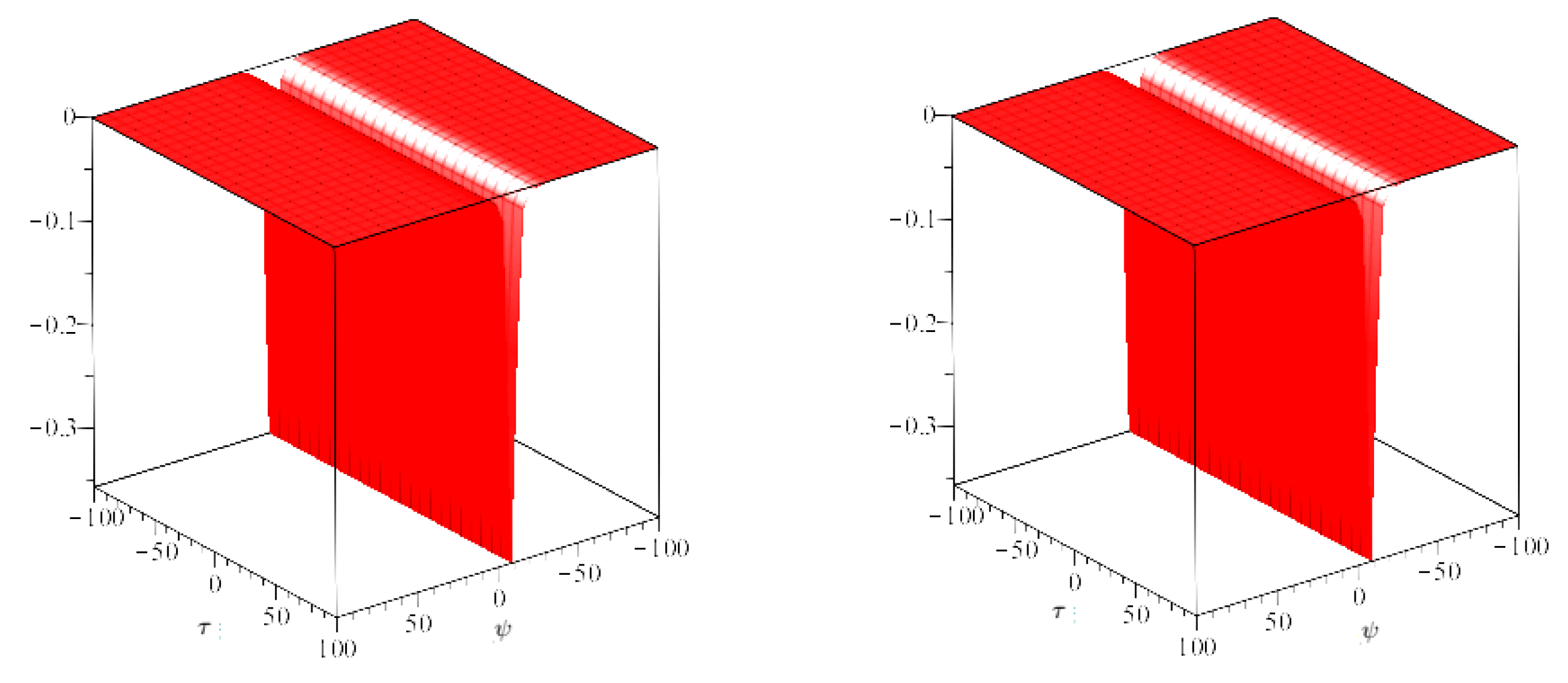
4. Numerical Examples
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Khan, H.; Kumam, P.; Baleanu, D.; Arif, M. An efficient analytical technique, for the solution of fractional-order telegraph equations. Mathematics 2019, 7, 426. [Google Scholar] [CrossRef]
- Kiryakova, S.V. Multiple (multiindex) Mittag-Leffler functions and relations to generalized fractional calculus. J. Comput. Appl. Math. 2000, 118, 441–452. [Google Scholar] [CrossRef]
- Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. The analytical investigation of time-fractional multi-dimensional Navier-Stokes equation. Alex. Eng. J. 2020, 59, 2941–2956. [Google Scholar] [CrossRef]
- Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. Analytical solutions of (2+ time fractional order) dimensional physical models, using modified decomposition method. Appl. Sci. 2019, 10, 122. [Google Scholar] [CrossRef]
- Momani, S.; Shawagfeh, N.T. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, Y. Variational Formulation of the Stress-Strain Problem in Capillary-Porous Materials with Fractal Structure. In Proceedings of the 2020 IEEE 15th International Conference on Computer Sciences and Information Technologies (CSIT), Zbarazh, Ukraine, 23–26 September 2020; Volume 1, pp. 1–4. [Google Scholar]
- Shymanskyi, V.; Sokolovskyy, Y. Finite Element Calculation of the Linear Elasticity Problem for Biomaterials with Fractal Structure. Open Bioinform. J. 2021, 14, 114–122. [Google Scholar] [CrossRef]
- Siryk, S.V.; Salnikov, N.N. Numerical solution of Burgers equation by Petrov-Galerkin method with adaptive weighting functions. J. Autom. Inf. Sci. 2012, 44, 50–67. [Google Scholar] [CrossRef]
- Roos, H.-G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; 604p. [Google Scholar]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Salnikov, N.N.; Siryk, S.V. Construction of Weight Functions of the Petrov-Galerkin Method for Convection-Diffusion-Reaction Equations in the Three-Dimensional Case. Cybern. Syst. Anal. 2014, 50, 805–814. [Google Scholar] [CrossRef]
- John, V.; Knobloch, P.; Novo, J. Finite elements for scalar convection-dominated equations and incompressible flow problems: A never ending story? Comput. Vis. Sci. 2018, 19, 47–63. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proc. R. Soc. Lond. Ser. A 1967, 299, 6–25. [Google Scholar]
- Broer, L.J.F. Approximate equations for long water waves. Appl. Sci. Res. 1975, 31, 377–395. [Google Scholar] [CrossRef]
- Kaup, D.J. A higher-order water-wave equation and the method for solving it. Prog. Theor. Phys. 1975, 54, 396–408. [Google Scholar] [CrossRef]
- Saha Ray, S. A novel method for travelling wave solutions of fractional Whitham-Broer-Kaup, fractional modified Boussinesq and fractional approximate long wave equations in shallow water. Math. Methods Appl. Sci. 2015, 38, 1352–1368. [Google Scholar] [CrossRef]
- Shah, N.; Alyousef, H.; El-Tantawy, S.; Chung, J. Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, P.L.F. Modified Boussinesq equations and associated parabolic models for water wave propagation. J. Fluid Mech. 1995, 288, 351–381. [Google Scholar] [CrossRef]
- Khater, M.M.; Kumar, D. New exact solutions for the time fractional coupled Boussinesq-Burger equation and approximate long water wave equation in shallow water. J. Ocean Eng. Sci. 2017, 2, 223–228. [Google Scholar] [CrossRef]
- Nuruddeen, R.I. Elzaki decomposition method and its applications in solving linear and nonlinear Schrodinger equations. Sohag J. Math. 2017, 4, 1–5. [Google Scholar] [CrossRef]
- Naeem, M.; Azhar, O.F.; Zidan, A.M.; Nonlaopon, K.; Shah, R. Numerical analysis of fractional-order parabolic equations via Elzaki transform. J. Funct. Spaces 2021, 2021, 3484482. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, R.; Khan, H.; Arif, M. Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions. Math. Methods Appl. Sci. 2020, 43, 199–212. [Google Scholar] [CrossRef]
- Elzaki, T.M.; Alkhateeb, S.A. Modification of Sumudu transform Elzaki transform and Adomian decomposition method. Appl. Math. Sci. 2015, 9, 603–611. [Google Scholar] [CrossRef]
- Shah, R.; Kumam, P.; Arif, M. An analytical technique to solve the system of nonlinear fractional partial differential equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgul, A.; Mahariq, I.; Kafle, J. A comparative analysis of the fractional-order coupled Korteweg-De Vries equations with the Mittag-Leffler law. J. Math. 2022, 2022, 8876149. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Alderremy, A.A.; Elzaki, T.M.; Chamekh, M. New transform iterative method for solving some Klein-Gordon equations. Results Phys. 2018, 10, 655–659. [Google Scholar] [CrossRef]
- Kim, H. The time shifting theorem and the convolution for Elzaki transform. Int. J. Pure Appl. Math. 2013, 87, 261–271. [Google Scholar] [CrossRef]


| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | −0.244849 | −0.244844 | −0.244810 | −0.244701 | −0.2445699 | |
| 0.4 | −0.252178 | −0.252154 | −0.252140 | −0.252122 | −0.252119 | |
| 0.2 | 0.6 | −0.249632 | −0.249608 | −0.249595 | −0.249577 | −0.249574 |
| 0.8 | −0.247212 | −0.247188 | −0.247176 | −0.247158 | −0.247155 | |
| 1 | −0.244911 | −0.244888 | −0.244876 | −0.244859 | −0.244855 | |
| 0.2 | −0.254864 | −0.254850 | −0.254838 | −0.254818 | −0.254812 | |
| 0.4 | −0.252183 | −0.252169 | −0.252158 | −0.252138 | −0.252132 | |
| 0.4 | 0.6 | −0.249637 | −0.249623 | −0.249612 | −0.249593 | −0.249586 |
| 0.8 | −0.247217 | −0.247203 | −0.247193 | −0.247174 | −0.247167 | |
| 1 | −0.244915 | −0.244902 | −0.244892 | −0.244874 | −0.244866 | |
| 0.2 | −0.254868 | −0.254861 | −0.254853 | −0.254835 | −0.254826 | |
| 0.4 | −0.252187 | −0.252180 | −0.252172 | −0.252154 | −0.252145 | |
| 0.6 | 0.6 | −0.249640 | −0.249634 | −0.249626 | −0.249609 | −0.249599 |
| 0.8 | −0.247220 | −0.247214 | −0.247206 | −0.247189 | −0.247178 | |
| 1 | −0.244918 | −0.244912 | −0.244905 | −0.244889 | −0.244877 | |
| 0.2 | −0.254874 | −0.254870 | −0.254866 | −0.254851 | −0.254840 | |
| 0.4 | −0.252192 | −0.252189 | −0.252185 | −0.252171 | −0.252158 | |
| 0.8 | 0.6 | −0.249644 | −0.249642 | −0.249638 | −0.249624 | −0.249611 |
| 0.8 | −0.247226 | −0.247222 | −0.247218 | −0.247204 | −0.247190 | |
| 1 | −0.244923 | −0.244921 | −0.244917 | −0.244904 | −0.244889 | |
| 0.2 | −0.254882 | −0.254879 | −0.254878 | −0.254868 | −0.254854 | |
| 0.4 | −0.252199 | −0.252197 | −0.252196 | −0.252187 | −0.252171 | |
| 1 | 0.6 | −0.249654 | −0.249650 | −0.249649 | −0.249640 | −0.249623 |
| 0.8 | −0.247234 | −0.247230 | −0.247229 | −0.247220 | −0.247202 | |
| 1 | −0.244932 | −0.244928 | −0.244927 | −0.244919 | −0.244900 |
| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | −0.013760 | −0.013754 | −0.013751 | −0.013747 | −0.013747 | |
| 0.4 | −0.013066 | −0.013061 | −0.013058 | −0.013055 | −0.013055 | |
| 0.2 | 0.6 | −0.012414 | −0.012410 | −0.012407 | −0.012404 | −0.012404 |
| 0.8 | −0.011801 | −0.011796 | −0.011794 | −0.011791 | −0.011791 | |
| 1 | −0.011223 | −0.011219 | −0.011217 | −0.011213 | −0.011213 | |
| 0.2 | −0.013761 | −0.013758 | −0.013755 | −0.013751 | −0.013751 | |
| 0.4 | −0.013067 | −0.013064 | −0.013062 | −0.013058 | −0.013058 | |
| 0.4 | 0.6 | −0.012415 | −0.012413 | −0.012411 | −0.012407 | −0.012407 |
| 0.8 | −0.011802 | −0.011799 | −0.011797 | −0.011794 | −0.011794 | |
| 1 | −0.011224 | −0.011221 | −0.011220 | −0.011216 | −0.011216 | |
| 0.2 | −0.013762 | −0.013760 | −0.013758 | −0.013754 | −0.013754 | |
| 0.4 | −0.013068 | −0.013067 | −0.013065 | −0.013061 | −0.013061 | |
| 0.6 | 0.6 | −0.012416 | −0.012415 | −0.012413 | −0.012410 | −0.012410 |
| 0.8 | −0.011803 | −0.011801 | −0.011800 | −0.011797 | −0.011797 | |
| 1 | −0.011225 | −0.011223 | −0.011222 | −0.011219 | −0.011219 | |
| 0.2 | −0.013764 | −0.013762 | −0.013761 | −0.013758 | −0.013758 | |
| 0.4 | −0.013071 | −0.013069 | −0.013068 | −0.013065 | −0.013065 | |
| 0.8 | 0.6 | −0.012419 | −0.012417 | −0.012416 | −0.012413 | −0.012413 |
| 0.8 | −0.011805 | −0.011803 | −0.011802 | −0.011800 | −0.011800 | |
| 1 | −0.011228 | −0.011225 | −0.011224 | −0.011222 | −0.011222 | |
| 0.2 | −0.013768 | −0.013766 | −0.013764 | −0.013762 | −0.013762 | |
| 0.4 | −0.013074 | −0.013071 | −0.013070 | −0.013068 | −0.013068 | |
| 1 | 0.6 | −0.012422 | −0.012420 | −0.012418 | −0.012416 | −0.012416 |
| 0.8 | −0.011808 | −0.011806 | −0.011804 | −0.011803 | −0.011803 | |
| 1 | −0.011230 | −0.011228 | −0.011226 | −0.011225 | −0.011225 |
| (Approx) | ||||||
|---|---|---|---|---|---|---|
| 0.2 | −0.124923 | −0.124912 | −0.124907 | −0.124899 | −0.124899 | |
| 0.4 | −0.123582 | −0.123572 | −0.123567 | −0.123559 | −0.123559 | |
| 0.2 | 0.6 | −0.122308 | −0.122299 | −0.122294 | −0.122287 | −0.122287 |
| 0.8 | −0.121098 | −0.121089 | −0.121084 | −0.121077 | −0.121077 | |
| 1 | −0.119947 | −0.119938 | −0.119934 | −0.119927 | −0.119927 | |
| 0.2 | −0.124925 | −0.124919 | −0.124914 | −0.124906 | −0.124906 | |
| 0.4 | −0.123584 | −0.123578 | −0.123574 | −0.123566 | −0.123566 | |
| 0.4 | 0.6 | −0.122310 | −0.122305 | −0.122300 | −0.122293 | −0.122293 |
| 0.8 | −0.121100 | −0.121094 | −0.121090 | −0.121083 | −0.121083 | |
| 1 | −0.119948 | −0.119943 | −0.119940 | −0.119933 | −0.119933 | |
| 0.2 | −0.124926 | −0.124924 | −0.124920 | −0.124913 | −0.124913 | |
| 0.4 | −0.123585 | −0.123583 | −0.123580 | −0.123572 | −0.123572 | |
| 0.6 | 0.6 | −0.122311 | −0.122309 | −0.122306 | −0.122299 | −0.122299 |
| 0.8 | −0.121101 | −0.121098 | −0.121096 | −0.121089 | −0.121089 | |
| 1 | −0.119950 | −0.119947 | −0.119945 | −0.119938 | −0.119938 | |
| 0.2 | −0.124927 | −0.124928 | −0.124926 | −0.124920 | −0.124920 | |
| 0.4 | −0.123588 | −0.123586 | −0.123585 | −0.123579 | −0.123579 | |
| 0.8 | 0.6 | −0.122315 | −0.122312 | −0.122311 | −0.122305 | −0.122305 |
| 0.8 | −0.121104 | −0.121102 | −0.121100 | −0.121095 | −0.121095 | |
| 1 | −0.119953 | −0.119950 | −0.119949 | −0.119944 | −0.119944 | |
| 0.2 | −0.124935 | −0.124933 | −0.124931 | −0.124927 | −0.124927 | |
| 0.4 | −0.123592 | −0.123590 | −0.123589 | −0.123585 | −0.123585 | |
| 1 | 0.6 | −0.122319 | −0.122316 | −0.122315 | −0.122311 | −0.122311 |
| 0.8 | −0.121107 | −0.121106 | −0.121104 | −0.121101 | −0.121101 | |
| 1 | −0.119958 | −0.119955 | −0.119953 | −0.119950 | −0.119950 |
| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | −0.006880 | −0.006877 | −0.006875 | −0.006873 | −0.006873 | |
| 0.4 | −0.006533 | −0.006530 | −0.006529 | −0.006527 | −0.006527 | |
| 0.2 | 0.6 | −0.006207 | −0.006205 | −0.006203 | −0.006202 | −0.006202 |
| 0.8 | −0.005900 | −0.005898 | −0.005897 | −0.005895 | −0.005895 | |
| 1 | −0.005611 | −0.005609 | −0.005608 | −0.005606 | −0.005606 | |
| 0.2 | −0.006880 | −0.006879 | −0.006877 | −0.006875 | −0.006875 | |
| 0.4 | −0.006533 | −0.006532 | −0.006531 | −0.006529 | −0.006529 | |
| 0.4 | 0.6 | −0.006207 | −0.006206 | −0.006205 | −0.006203 | −0.006203 |
| 0.8 | −0.005901 | −0.005899 | −0.005898 | −0.005897 | −0.005897 | |
| 1 | −0.005612 | −0.005610 | −0.005610 | −0.005608 | −0.005608 | |
| 0.2 | −0.006881 | −0.006880 | −0.006879 | −0.006877 | −0.006877 | |
| 0.4 | −0.006534 | −0.006533 | −0.006532 | −0.006530 | −0.006530 | |
| 0.6 | 0.6 | −0.006208 | −0.006207 | −0.006206 | −0.006205 | −0.006205 |
| 0.8 | −0.005901 | −0.005900 | −0.005900 | −0.005898 | −0.005898 | |
| 1 | −0.005612 | −0.005611 | −0.005611 | −0.005609 | −0.005609 | |
| 0.2 | −0.006881 | −0.006881 | −0.006880 | −0.006879 | −0.006879 | |
| 0.4 | −0.006534 | −0.006534 | −0.006534 | −0.006532 | −0.006532 | |
| 0.8 | 0.6 | −0.006208 | −0.006208 | −0.006208 | −0.006206 | −0.006206 |
| 0.8 | −0.005901 | −0.005901 | −0.005901 | −0.005900 | −0.005900 | |
| 1 | −0.005612 | −0.005612 | −0.005612 | −0.005611 | −0.005611 | |
| 0.2 | −0.006881 | −0.006882 | −0.006882 | −0.006881 | −0.006881 | |
| 0.4 | −0.006534 | −0.006535 | −0.006535 | −0.006534 | −0.006534 | |
| 1 | 0.6 | −0.006208 | −0.006209 | −0.006209 | −0.006208 | −0.006208 |
| 0.8 | −0.005901 | −0.005902 | −0.005902 | −0.005901 | −0.005901 | |
| 1 | −0.005612 | −0.005613 | −0.005613 | −0.005612 | −0.005612 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alderremy, A.A. Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel. Symmetry 2022, 14, 1632. https://doi.org/10.3390/sym14081632
Alderremy AA. Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel. Symmetry. 2022; 14(8):1632. https://doi.org/10.3390/sym14081632
Chicago/Turabian StyleAlderremy, Aisha Abdullah. 2022. "Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel" Symmetry 14, no. 8: 1632. https://doi.org/10.3390/sym14081632
APA StyleAlderremy, A. A. (2022). Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel. Symmetry, 14(8), 1632. https://doi.org/10.3390/sym14081632





