A DVA-Beam Element for Dynamic Simulation of DVA-Beam System: Modeling, Validation and Application

Abstract

The dynamic vibration absorber (DVA) has a broad application background in slender structure vibration reduction, such as in machine gun systems, micro actuators, and so on. Rapid modeling and simulation of the DVA-beam system are of great importance for dynamic performance, evaluation, and finally, the structural design. The primary motivation for this paper is to present a reliable and convenient technique for the modeling and computation of the DVA-beam system. A novel DVA-beam element, which consists of a beam segment and a DVA, is presented. In this element, the DVA position can be arbitrarily allocated, whether on the beam node or within the beam domain. In this way, the beam can be modeled with a few elements to save on computing costs and maintain ideal modeling accuracy. An element deactivating method, which endows the DVA-beam element with the ability to simulate a bare beam and a DVA-beam structure simultaneously, is proposed. Some numerical examples were carried out to validate the reliability of the DVA-beam element in addressing different kinds of boundary conditions by comparing the beam tip responses with those simulated by ADAMS software, and good agreements were observed. Finally, two DVA optimization examples were conducted to investigate the effectiveness and applicability of the DVA-beam element in engineering optimization. The performance was impressive.

1. Introduction

Suppression of undesired beam vibrations is an essential issue in mechanical systems, such as in machine gun barrels [1,2,3,4,5], miniature actuators [6,7,8,9,10], machine tools, and other engineering systems, see, e.g., [11,12,13] and references therein. Among various vibration suppression methods, the dynamic vibration absorber (DVA) is promising for its reliability, efficiency, and low cost [14]. Generally, a DVA consists of mass-spring-damper systems and is attached to the primary structure to suppress its vibration. To design the DVA parameters of a specific system, the most widely used method is structural optimization based on dynamic simulations. Additionally, the literature on DVA optimal designs is abundant; see, e.g., [15,16,17,18,19,20,21,22,23], to cite a few. According to the different optimization criteria, DVA optimization can be classified into H_∞ optimization [24,25], H₂ optimization [26,27], and stability maximization [28,29] optimization et. al., a good review can be found in [27]. In DVA optimization, the mass, spring stiffness, damper coefficient, and DVA position are always the main design parameters.

In reviewing the literature, we found that research on DVA-beam systems is still rare. In [14], a finite element model of a simply supported beam with two DVAs attached is established, in which the damping effect is neglected. A combination of active and passive confinement techniques is adopted to suppress the beam vibration. In [15], a translational-rotational combined DVA is designed to suppress the beam vibration under point or distributed harmonic excitation. They derived the motion equations using a finite element method (FEM) and assumed the DVA was allocated on the element node for simplicity. Samani et al. [30,31] derived the dynamic model of a beam with nonlinear DVAs attached using the assumed mode method (AMM), and the random optimization technique was used to obtain the optimal DVA parameters. They found that, under some circumstances, DVAs with nonlinear stiffness were more effective than the linear ones in reducing the maximum beam deflection. Since the AMM adopts the eigenfunctions of the beam structure under certain boundary conditions to derive the motion equations, the adaptability of the AMM to different boundary conditions is unsatisfactory. From this point of view, the FEM is more convenient than the AMM in engineering applications. For that, the different kinds of boundary conditions can be easily simulated by changing the constraints of the element nodes in the FEM. However, in previous literature, the DVA was assumed to be allocated on the beam element node. This means the DVA position can only be optimized step by step, and the step size depends on the beam element length. The beam span should be meshed into enough elements to accurately determine the optimal DVA position. This will increase the computational cost and make the optimization time too long. This is why there is little literature dealing with DVA position optimization over the slender beam span.

To this end, a novel DVA-beam element, which is composed of a bare beam segment and a DVA, is developed in our paper. In a DVA-beam element, the DVA mass, spring stiffness, damper coefficient, and DVA position of each DVA-beam element are all parametric. Using this element, the DVA-beam system can be modeled with a few elements to save computational cost, while maintaining an ideal computational accuracy. An element deactivating method is presented, which enables the DVA-beam element to simulate a common beam element. This makes the dynamic modeling of the DVA-beam system more convenient, because only one kind of element is needed. All these characteristics make the DVA optimal design more convenient in real applications.

In Section 2, the DVA-beam element is introduced first. The element motion equations are derived using the Euler-Lagrange equation. A standard MATLAB function, which can return the elementary matrix directly, is compiled and given in Appendix A. The assembly method of the global motion equations is introduced. In Section 3, we present a feasible DVA deactivating method. In Section 4, some suggestions are given for the selection of deactivating coefficients with some numerical examples. The accuracy of the DVA-beam element in addressing different boundary conditions is investigated by comparing the beam tip responses with those simulated by ADAMS software. Finally, two DVA optimization examples are conducted to show the effectiveness of the DVA-beam technique in engineering applications.

2. System Description and Problem Formulation

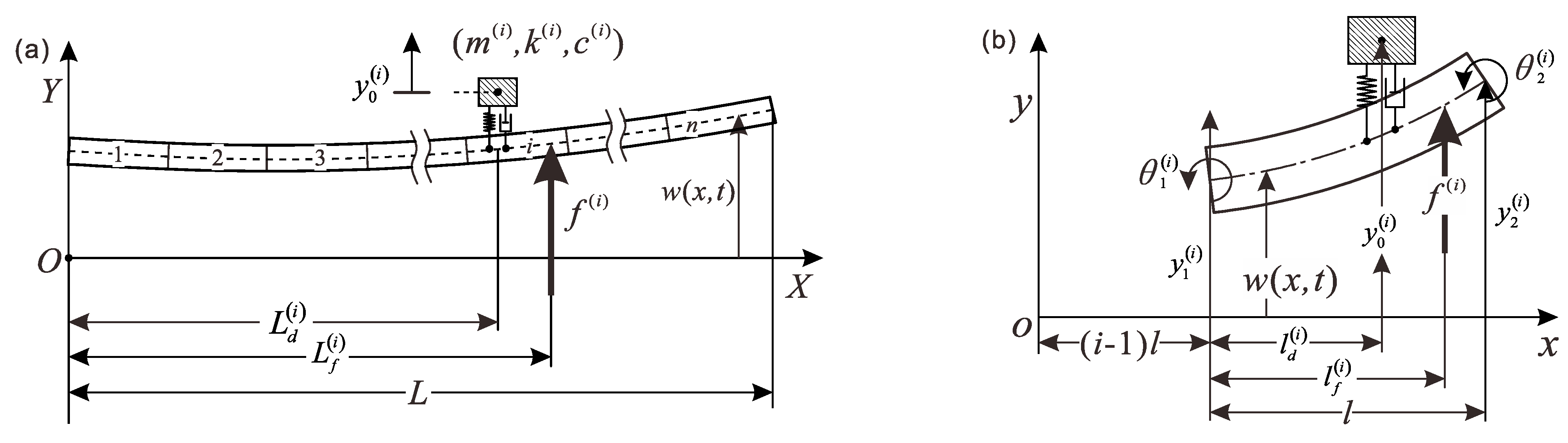
2.1. DVA-Beam Element

Consider a uniform beam with a DVA attached, as illustrated in Figure 1a. The beam has a total length of L and the transverse deflection is represented by w(x, t). The whole beam span is divided into n elements with a uniform element length l = L/n, and an element is exhibited in Figure 1b. It should be noted that a beam element contains only one DVA, and this kind of element is named a DVA-beam element in our paper. Each DVA-beam element has a set of parameters, which are the DVA displacement $y_0^{\left(i\right)}$, mass $m^{\left(i\right)}$, damping coefficient $c^{\left(i\right)}$, stiffness $k^{\left(i\right)}$, and the DVA position in element $l_d^{\left(i\right)}$. Additionally, i denotes the element number starting from the left hand of the beam to the right hand. In order to simulate the beam structure subject to external excitation, an external force $f^{\left(i\right)}$ applied to the beam at $l_f^{\left(i\right)}$ in the element is considered. Additionally, we have

$$\{\begin{array}{l}{l}_f^{\left(i\right)}=L_f^{\left(i\right)}-\left(i-1\right)l\\ l_d^{\left(i\right)}=L_d^{\left(i\right)}-\left(i-1\right)l\end{array}$$

(1)

assumed the stiffness of the spring is linear and neglected the hysteresis characteristics of the spring. The kinetic energy $T_i$ and potential energy $U_i$ of the i-th element are given as

$$T^{\left(i\right)}=\frac{1}{2}\rho A{\displaystyle {\int }_0^l{\dot{w}}^{2}dx}+\frac{1}{2}{m}^{\left(i\right)}{\dot{y}}_0^{\left(i\right)}{}^2$$

(2)

$$U^{\left(i\right)}=\frac{1}{2}EI{\displaystyle {\int }_0^l{w^{″}}^{2}dx}+\frac{1}{2}{k}^{\left(i\right)}{\left(y_0^{\left(i\right)}-{w|}_{l_d^{\left(i\right)}}\right)}^2$$

(3)

where $\rho$, $A$, $E$, and $I$ represent the beam mass density, cross-section area, Young’s modulus, and area moment of inertia, respectively. The dot and prime denote the differentiation with respect to time and the X coordinate, respectively.

Unlike a common beam element, the DVA-beam element contains five degrees of freedom, which are $y_0^{\left(i\right)}$, $y_1^{\left(i\right)}$, ${\theta }_1^{\left(i\right)}$, $y_2^{\left(i\right)}$, and ${\theta }_2^{\left(i\right)}$, respectively, as shown in Figure 1b. Where $y_1^{\left(i\right)}$, $y_2^{\left(i\right)}$ and ${\theta }_1^{\left(i\right)}$, ${\theta }_2^{\left(i\right)}$ are nodal displacement and slope freedoms respectively. $y_0^{\left(i\right)}$ denotes the rigid-body displacement of DVA.

Using the finite element discretization, the beam transverse deflection $w$ and DVA displacement $y_0^{\left(i\right)}$ could be expressed in the form of a nodal displacement vector ${\mathbf{q}}^{\left(i\right)}$ as

$$\{\begin{array}{l}w={\mathbf{N}}_1{\mathbf{q}}^{\left(i\right)}\\ y_0^{\left(i\right)}={\mathbf{N}}_2{\mathbf{q}}^{\left(i\right)}\end{array}$$

(4)

where

$$\{\begin{array}{l}{\mathbf{N}}_1={\left[\begin{array}{c}1-\frac{3x^2}{l^2}+\frac{2x^3}{l^3}\\ x-\frac{2x^2}{l}+\frac{x^3}{l^2}\\ 0\\ \frac{3x^2}{l^2}-\frac{2x^3}{l^3}\\ -\frac{x^2}{l}+\frac{x^3}{l^2}\end{array}\right]}^T\\ {\mathbf{N}}_2=\left[\begin{array}{ccccc}0& 0& 1& 0& 0\end{array}\right]\end{array}$$

(5)

$${\mathbf{q}}^{\left(i\right)}={\left[\begin{array}{ccccc}{y}_1^{\left(i\right)}& {\theta }_1^{\left(i\right)}& y_0^{\left(i\right)}& y_2^{\left(i\right)}& {\theta }_2^{\left(i\right)}\end{array}\right]}^T$$

(6)

$$T^{\left(i\right)}=\frac{1}{2}{\dot{\mathbf{q}}}^{\left(i\right)T}{\mathbf{m}}_1^{\left(i\right)}{\dot{\mathbf{q}}}^{\left(i\right)}+\frac{1}{2}{\dot{\mathbf{q}}}^{\left(i\right)T}{\mathbf{m}}_2^{\left(i\right)}{\dot{\mathbf{q}}}^{\left(i\right)}$$

(7)

$$U^{\left(i\right)}=\frac{1}{2}{\mathbf{q}}^{\left(i\right)T}{\mathbf{k}}_1^{\left(i\right)}{\mathbf{q}}^{\left(i\right)}+\frac{1}{2}{\mathbf{q}}^{\left(i\right)T}{\mathbf{k}}_2^{\left(i\right)}{\mathbf{q}}^{\left(i\right)}$$

(8)

where

$$\{\begin{array}{l}{\mathbf{m}}_1^{\left(i\right)}=\rho A{\displaystyle {\int }_0^l{\mathbf{N}}_1^T{\mathbf{N}}_{1}dx}\\ {\mathbf{m}}_2^{\left(i\right)}=m^{\left(i\right)}{\mathbf{N}}_2^T{\mathbf{N}}_2\\ {\mathbf{k}}_1^{\left(i\right)}=EI{\displaystyle {\int }_0^l{\mathbf{N}}_1^{″T}{\mathbf{N}}_1^{″}dx}\\ {\mathbf{k}}_2^{\left(i\right)}=k\left({\mathbf{N}}_2^T{\mathbf{N}}_2+{{\mathbf{N}}_1^T|}_{l_d^{\left(i\right)}}{{\mathbf{N}}_1|}_{l_d^{\left(i\right)}}-{\mathbf{N}}_2^T{{\mathbf{N}}_1|}_{l_d^{\left(i\right)}}-{{\mathbf{N}}_1^T|}_{l_d^{\left(i\right)}}{\mathbf{N}}_2\right)\end{array}$$

(9)

where ${\mathbf{m}}_1^{\left(i\right)}$, ${\mathbf{m}}_2^{\left(i\right)}$, ${\mathbf{k}}_1^{\left(i\right)}$, and ${\mathbf{k}}_2^{\left(i\right)}$ are all 5th order symmetry matrices.

2.2. Motion Equations and Assembling

Upon substituting the discretized kinetic energy and potential energy expressions, which are Equations (7) and (8), into the Euler-Lagrange equation, one could obtain the following element motion equations

$${\mathbf{m}}^{\left(i\right)}{\ddot{\mathbf{q}}}^{\left(i\right)}+{\mathbf{k}}^{\left(i\right)}{\mathbf{q}}^{\left(i\right)}={\mathbf{f}}^{\left(i\right)}$$

(10)

where

$$\{\begin{array}{l}{\mathbf{m}}^{\left(i\right)}={\mathbf{m}}_1^{\left(i\right)}+{\mathbf{m}}_2^{\left(i\right)}\\ {\mathbf{k}}^{\left(i\right)}={\mathbf{k}}_1^{\left(i\right)}+{\mathbf{k}}_2^{\left(i\right)}\end{array},$$

(11)

and

$${\mathbf{f}}^{\left(i\right)}=-c^{\left(i\right)}\left({\mathbf{N}}_2{\dot{\mathbf{q}}}^{\left(i\right)}-{{\mathbf{N}}_1|}_{l_d^{\left(i\right)}}{\dot{\mathbf{q}}}^{\left(i\right)}\right)\otimes {\mathbf{N}}_2^T+c^{\left(i\right)}\left({\mathbf{N}}_2{\dot{\mathbf{q}}}^{\left(i\right)}-{{\mathbf{N}}_1|}_{l_d^{\left(i\right)}}{\dot{\mathbf{q}}}^{\left(i\right)}\right)\otimes {{\mathbf{N}}_1^T|}_{l_d^{\left(i\right)}}+f^{\left(i\right)}\otimes {{\mathbf{N}}_1^T|}_{l_f^{\left(i\right)}}$$

(12)

is generalized force vector. To take structural damping effects into consideration, the Rayleigh’s proportional damping model is adopted here. The element damping matrix ${\mathbf{c}}^{\left(i\right)}$ is expressed as

$${\mathbf{c}}^{\left(i\right)}=\alpha {\mathbf{m}}_1^{\left(i\right)}+\beta {\mathbf{k}}_1^{\left(i\right)}$$

(13)

where α and $\beta$ are two damping coefficients. According to Equations (10) and (13), the damped DVA-beam element motion equation is obtained as

$${\mathbf{m}}^{\left(i\right)}{\ddot{\mathbf{q}}}^{\left(i\right)}+{\mathbf{c}}^{\left(i\right)}{\dot{\mathbf{q}}}^{\left(i\right)}+{\mathbf{k}}^{\left(i\right)}{\mathbf{q}}^{\left(i\right)}={\mathbf{f}}^{\left(i\right)}$$

(14)

The explicit formulations of the $m^{\left(i\right)}$, $c^{\left(i\right)}$, $k^{\left(i\right)}$, and $f^{\left(i\right)}$ are derived and complied into a standard MATLAB function, which could be found in the Appendix A. This code could return the elementary matrix directly once the desired parameters are given. Finally, the global motion equation

$$\mathbf{M}\ddot{\mathbf{q}}+\mathbf{C}\dot{\mathbf{q}}+\mathbf{Kq}=\mathbf{F}$$

(15)

can be obtained by assembling the element motion equation, Equation (14), according to the following assembling rules.

$$\{\begin{array}{l}\mathbf{M}={\displaystyle \sum _{i=1}^n\left(\mathbf{M}\left(3i-2:3i+2,3i-2:3i+2\right)+{\mathbf{m}}^{\left(i\right)}\right)}\\ \mathbf{C}={\displaystyle \sum _{i=1}^n\left(\mathbf{C}\left(3i-2:3i+2,3i-2:3i+2\right)+{\mathbf{c}}^{\left(i\right)}\right)}\\ \mathbf{K}={\displaystyle \sum _{i=1}^n\left(\mathbf{K}\left(3i-2:3i+2,3i-2:3i+2\right)+{\mathbf{k}}^{\left(i\right)}\right)}\\ \mathbf{q}={\displaystyle \sum _{i=1}^n\left(\mathbf{q}\left(3i-2:3i+2,1\right)+{\mathbf{q}}^{\left(i\right)}\right)}\\ \mathbf{F}={\displaystyle \sum _{i=1}^n\left(\mathbf{F}\left(3i-2:3i+2,1\right)+{\mathbf{f}}^{\left(i\right)}\right)}\end{array}$$

(16)

To better illustrate Equation (16), the assembling rules are exhibited graphically in Figure 2, where the black filled part denotes the rigid-body freedom of the DVA. Additionally, the section-line filled part denotes the element nodal freedoms, through which the elementary motion equations are assembled together. These matrices, therefore, are symmetric. The global motion equations are a set of second-order ordinary differential equations. In the following, the accurate Runge–Kutta method is adopted to integrate the motion equations and obtain the system responses. The boundary conditions for the motion equations could be applied by modifying the element of $\mathbf{F}$.

3. DVA Effect Deactivating Method

Generally, the DVA-beam system could be modeled by a combination of common beam elements and the presented DVA-beam element. However, a common beam element can also be simulated by a DVA-beam element as long as its DVA effect is deactivated. In this way, the dynamic simulation of the DVA-beam system will be much easier, for that only one kind of element is needed, and the results will be regularly structured and suitable for post-processing. This characteristic is particularly important in an optimization problem, since some undesired errors may occur during the evaluation of the objective functions using an irregular result structure. Therefore, in this section, we present a feasible DVA deactivating method.

Theoretically, to deactivate the DVA effect, the DVA mass $m^{\left(i\right)}=0$ is required. However, this can result in a singular global mass matrix $\mathbf{M}$. Therefore, a feasible way to deactivate the DVA effect is to adjust the DVA mass $m^{\left(i\right)}$ to be small enough, and the DVA stiffness $k^{\left(i\right)}$ to be large enough, while the DVA damping coefficient $c^{\left(i\right)}=0$. For convenience, the DVA mass $m^{\left(i\right)}$ is set proportional to the beam element mass, $\rho Al$, by introducing a deactivating coefficient $a_m$ as

$$m^{\left(i\right)}=a_m\rho Al$$

(17)

As the deactivating coefficient tends to be zero, the effect of the DVA’s inertia force on beam dynamics will be negligible, and the DVA-beam element will work as a common beam element. Note that in the deactivated DVA-beam element, the DVA mass is given by Equation (17), and stiffness should be large enough, generally 1 × 10⁶ N/m will be sufficient. While in the active DVA-beam element, the DVA mass, damping, and stiffness are their actual values. The selection of the deactivating coefficient a_m will be discussed in Section 4.1.

4. Results and Discussion

To validate the presented DVA-beam element, some numerical examples are performed in this section. The obtained dynamic responses will be compared to those simulated by ADAMS 2020, which is a famous dynamic simulation software of MSC company in the Los Angeles, USA. In modeling the DVA-beam system using ADAMS, the flexible beam should be generated first as a separate *.mnf file. In our work, the Ansys software is adopted to establish a finite element model of the beam structure and generate the *.mnf file. Then, the *.mnf file is imported into the ADAMS environment to establish the rigid-flexible dynamic model, as shown in Figure 3. In modeling, the DVA and the beam can only be coupled together at the predefined coupling points. If not otherwise specified, the beam parameters are: $E$ = 2.1 GPa, I = 1.33 × 10⁻⁸ m⁴, $\rho$ = 7900 kg/m³, $A$ = 4 × 10⁻⁴ m², and $L$ = 1.5 m.

4.1. Selection of Deactivating Coefficient

In the following, the DVA-beam element will be adopted to model the DVA-beam system. The total beam span is divided into three ($n=3$) DVA-beam elements, i.e., the elements’ length $l$ = 0.5 m.

Here we first discuss the selection of the deactivating coefficient $a_m$. The DVAs in this section are all assumed to be allocated at the right-side nodes, i.e., $l_d^{\left(i\right)}$ = 0.5 m. The stiffness $k^{\left(i\right)}$ = 1 × 10⁶ N/m and the damping coefficient $c^{\left(i\right)}$ = 0 N·m/s. An initial tip deflection, 5 mm, is given to the beam at the initial moment, and the initial displacements of each node are plotted in Figure 4. The node number starts from the left hand of the beam to the right hand. The initial conditions can be obtained by applying a certain static force to the beam’s tip and mapping the resulting static nodal displacement according to the given initial tip deflection.

In this subsection, all the DVAs’ masses are given by Equation (17). We then vary the deactivating coefficient $a_m$ from 1 × 10⁻⁶ to 0.1. In the simulations, the beam will vibrate freely, and the transverse tip deflections for different $a_m$ are compared in Figure 5a, an enlarged view is displayed in Figure 5b. It can be observed that as $a_m$ decreases from 0.1 to 1 × 10⁻⁶, the effects of DVA vanish gradually. When $a_m$ = 1 × 10⁻⁶, the tip deflection histories almost coincide with those simulated by ADAMS, in which the DVA is not considered. It indicates that the presented DVA deactivating method is feasible. It could be observed that as $a_m$ decreases from 0.01 to 1 × 10⁻⁶, it produces little difference in beam dynamic behavior. Hence, to deactivate the DVA effect, $a_m\le 0.01$ is advisable.

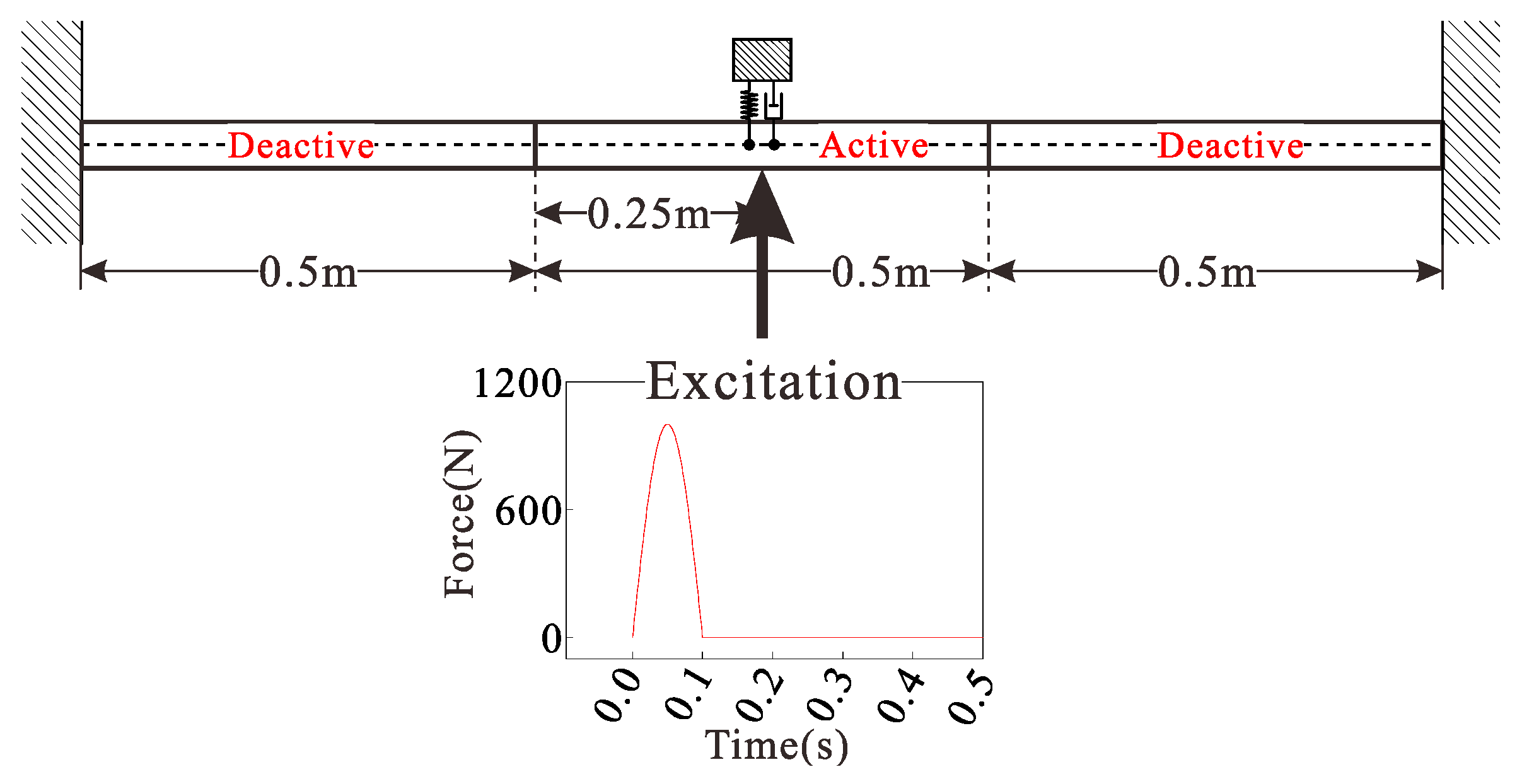
4.2. Validation of the Reliability of the DVA-Beam Element

In this subsection, we investigate the computational accuracy of the DVA-beam element under different boundary conditions. First, we consider a cantilever beam with one DVA attached. An initial tip deflection, 5 mm, is given to the beam at the initial moment, and the beam will vibrate freely as time goes on. As mentioned above, the DVA-beam element allows the DVA to be arbitrarily allocated, whether on the element node or in the element domain. To show its effectiveness, we investigated the beam dynamics with one DVA attached at different positions, as illustrated in Figure 6. In positions 1 and 3, the DVA is attached at the element node, while in positions 2 and 4, the DVA is attached in the element domain. For the elements without a DVA attached, the DVA effect is deactivated using the method introduced in Section 3 and Section 4.1. While in an active DVA-beam element, if not otherwise specified, the DVA stiffness $k^{\left(i\right)}$ = 200 N/m, damping coefficient $c^{\left(i\right)}$ = 5 N·m/s, and mass $m^{\left(i\right)}$ = 0.1 Kg is considered.

Figure 7 compares the time histories of the beam tip deflection (the solid line and ●) and DVA’s relative displacement (the dotted line and $▲$), which were obtained from the DVA-beam technique and ADAMS software, respectively. By comparison, it can be observed that the results of all four examples simulated by the DVA-beam technique agree well with those obtained by ADAMS software. In addition, the closer the DVA is attached to the beam’s tip, the beam vibration decreases faster and the DVA’s peak vibration amplitude becomes larger. It reveals that the DVA absorbs more vibration energy from the beam structure under the present circumstances.

To show the adaptability of the DVA-beam element under different boundary conditions, it is adopted to address a clamped-clamped beam problem, and the physical model is depicted in Figure 8, a DVA is attached at the beam midspan. In this example, an external half-sine impact excitation, $f^{\left(i\right)}=1000\sin \left(10\pi t\right)$, for 0 ≤ t ≤ 0.1 s, is applied to the beam’s midspan. The initial displacement and velocity of all element nodes are set to zero. After computation, the dynamic responses of the beam’s midspan and DVA displacement are compared in Figure 9. After the excitation disappears, the beam will vibrate freely, and the displacement of the beam’s midspan will decrease gradually to zero. The results obtained by the DVA-beam element are still in good agreement with those simulated by ADAMS. This indicates that the DVA-beam element is reliable for different kinds of boundary conditions, making it convenient to be applied in engineering practices.

In some circumstances, several DVAs will be attached to a slender beam structure simultaneously to achieve better performance. Therefore, the ability of a technique to simulate the multi-DVAs-beam system is an important factor in engineering. In fact, it is easy to simulate the multi-DVAs-beam system using the DVA-beam technique by activating the DVA effect where the element has a DVA attached. While the DVA effects are all deactivated in the bare beam region. To show the effectiveness of the DVA-beam technique, we attached multiple DVAs to a slender cantilever beam simultaneously, as shown in Figure 10. Here we consider the beam vibrates freely, and an initial tip deflection, 5 mm, is given to the beam at the initial moment. The dynamic responses simulated by the DVA-beam technique and ADAMS software are compared in Figure 11. As the excitation disappears, the DVA-beam system vibrates freely. Under the action of the DVAs, the tip displacement decreases gradually. Figure 11b reveals that the amplitude of DVA1 is larger than that of DVA2, which conforms to the physical behavior of the DVA-beam system. It can be observed that the two DVAs work together orderly, and the response curves are still consistent with those simulated by ADAMS. This indicates that the DVA-beam element is reliable in addressing the multi-DVAs-beam system problem.

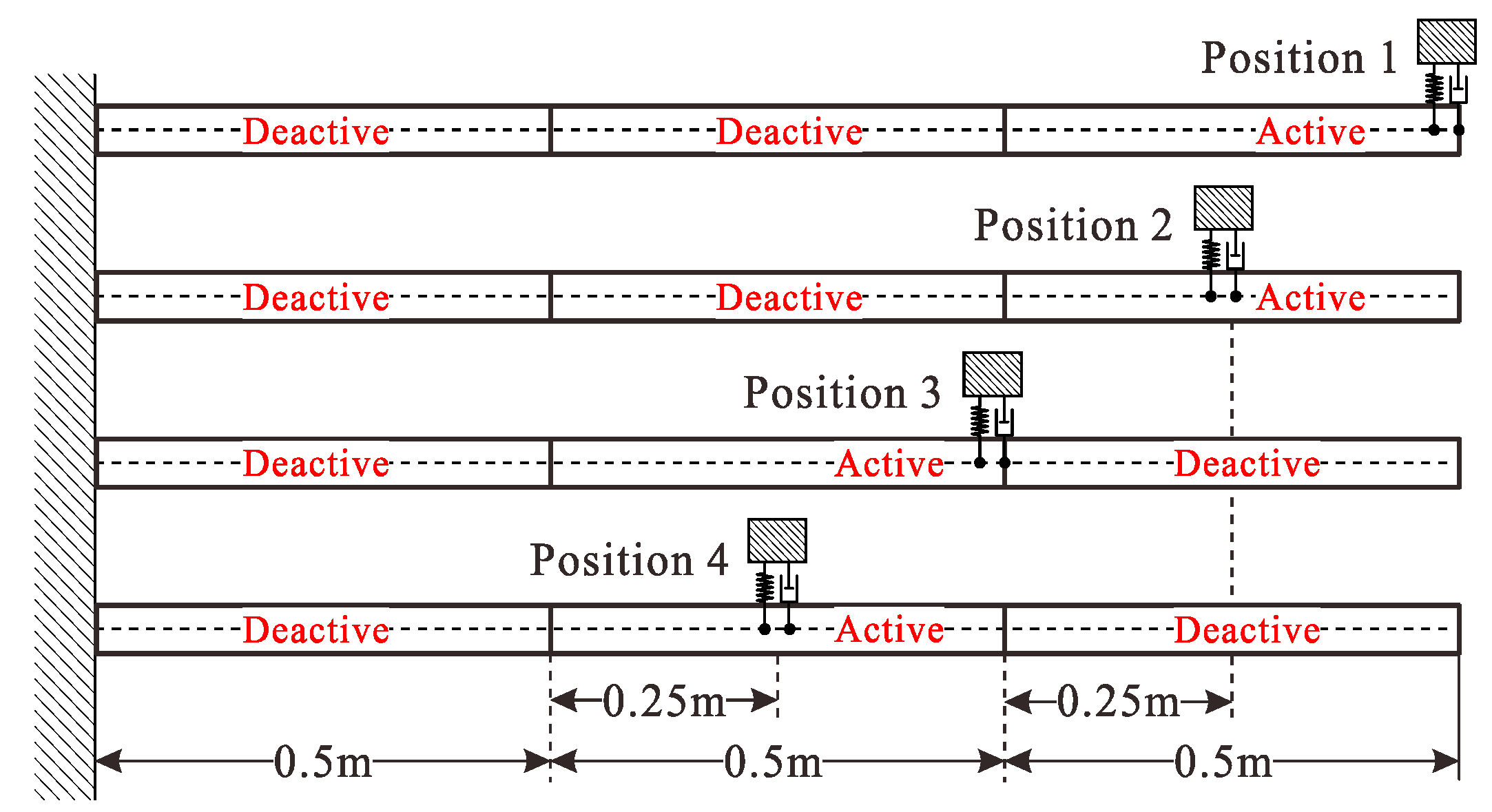
4.3. Application Examples: DVA Optimal Design

In designing DVA applications, the most important aspect is to obtain the DVA parameters, i.e., $m^{\left(i\right)}$, $c^{\left(i\right)}$, and $k^{\left(i\right)}$ as well as the DVA-beam position $L_d^{\left(i\right)}$ in the beam span, to achieve the desired performance. To accomplish this task, the DVA-beam technique will be adopted to conduct DVA parameter optimization in this subsection. Additionally, the main purpose of the optimization is to reduce the vibration of the beam.

For convenience, the DVA-beam position $L_d^{\left(i\right)}$ is represented by $l_d^{\left(i\right)}$ and $i$ according to

$$\{\begin{array}{l}i=\lceil L_d^{\left(i\right)}/l\rceil \\ l_d^{\left(i\right)}=L_d^{\left(i\right)}-\left(i-1\right)l\end{array}$$

(18)

where $i$ denotes the number of the element, in which the DVA is allocated. $\lceil \rceil$ denotes the ceiling operator. Finally, the design variables of the DVA optimization problem are $m^{\left(i\right)}$, $c^{\left(i\right)}$, $k^{\left(i\right)}$, $l_d^{\left(i\right)}$, and $i$. The design space for these variables can be given according to the design requirements, engineering experience, or trial and error. In our work, the design spaces are given as

$$\{\begin{array}{l}0.1 \le m^{\left(i\right)}\le 1.5 \mathrm{kg}\\ 0 \le c^{\left(i\right)}\le 100 \mathrm{N}\cdot \mathrm{m}/\mathrm{s}\\ 10 \le k^{\left(i\right)}\le 1000 \mathrm{N}/\mathrm{m}\\ 0 \le l_d^{\left(i\right)}\le 0.5 \mathrm{m}\\ i\in \left\{1,2,3\right\}\end{array}$$

(19)

Note that the design space is only for the active DVA-beam element. In other elements, the DVA effect is deactivated. The objective function is the root mean square (RMS) value of the beam tip deflection over all time domains.

$$obj=\mathrm{RMS}\left(w\left(L,t\right)\right)$$

(20)

The physical meaning of minimizing the RMS value of the beam tip deflection is that the beam tip has the minimum vibration amplitude over a certain time span. In this circumstance, the DVA parameters are optimal. In the following, a random optimization technique is adopted to seek these optimal parameters. In the following random optimizations, 2000 samples are generated uniformly in the design space. Then, the dynamic computations are performed based on each sample. After all the computations are completed, some intuitive distributions of the objective function with respect to each design variable will be obtained, from which we can obtain the optimal parameters directly.

First, we consider a cantilever beam vibrating freely, which can be regarded as a residual vibration resulting from external unwanted excitation. The task of the DVA in this condition is to suppress the residual vibration of the beam as soon as possible. For convenience, an initial static tip deflection, 5 mm, is given to the beam tip in the dynamic simulations. The dynamic response of the tip deflection is computed and plotted in Figure 12f, the dotted line, and the corresponding RMS value is 2.9966 mm.

Then the random optimization is carried out to obtain the distributions of the objective function with respect to each design variable. The intuitive distributions of the objective function with respect to each design variable are plotted in Figure 12a–e. From these distributions, the optimal parameter set can be easily determined, i.e., $m^{\left(i\right)}$ = 1.38 kg, $c^{\left(i\right)}$ = 19.03 N·m/s, $k^{\left(i\right)}$ = 576.05 N/m, $l_d^{\left(i\right)}$ = 0.48 m, and $i$ = 3. Where, $i$ = 3 means that, in the current load conditions, the DVA should be allocated to the third beam element. The corresponding RMS value of the tip deflection is 0.615 mm, with a reduction of 79.5%. To determine the effectiveness of the optimal DVA parameters, the tip dynamic response is then computed based on the optimal parameters and compared in Figure 12f, the solid line. By comparison, we found that the vibration of the optimal DVA-beam system decreases rapidly. Approximately 0.5 s later, the tip vibration is almost eliminated. This confirms the effectiveness of the optimally designed DVA.

In the following, we investigate the reliability of the DVA-beam technique in forced vibration optimization problems. For convenience, a harmonic excitation, $f=5\sin \left(10\pi t\right)$, is applied to the beam tip. It should be noted that in engineering, the frequency and amplitude of external excitation may not be exactly the same as we considered above. The main purpose here is to investigate the reliability of the DVA-beam technique in addressing a certain forced vibration optimization. The actual frequency and amplitude of external excitation should be consistent with the practical problem. For a bare beam, the tip dynamic response is computed and plotted in Figure 13f, the dotted line, and the RMS value of the tip deflection is 2.4240 mm. After the optimization, the intuitive distributions of the objective function with respect to each design variable are plotted in Figure 13a–e. From these figures, we can obtain the optimal parameters: $m^{\left(i\right)}$ = 1.39 kg, $c^{\left(i\right)}$ = 91.42 N·m/s, $k^{\left(i\right)}$ = 925.86 N/m, $l_d^{\left(i\right)}$ = 0.45 m, and $i$ = 3. Additionally, the corresponding objective function is 0.6591 mm, which is reduced by 72.8%. Based on the optimal parameters, the response of the tip deflection is computed and compared in Figure 13f, the solid line. Since the external excitation acts all the time, the beam will vibrate constantly. Comparing Figure 12e and Figure 13e, it could be observed that for the cantilever DVA-beam system, allocating the DVA to the beam tip is most effective for vibration reduction. This phenomenon is consistent with the actual engineering experience. It is nice to find that the vibration amplitude of the optimal DVA-beam system is greatly reduced. This further reveals that the DVA-beam element has good reliability and applicability. In addition, for the vibration reduction problem, it is recommended to adopt the RMS value of the corresponding response as the objective function.

5. Conclusions

A novel DVA-beam element, which consists of a beam segment and a DVA, is presented in our paper. In this element, the DVA position can be arbitrarily allocated, regardless of being allocated on the beam nodes or in the beam domain. The DVA mass, spring stiffness, damper coefficient, and DVA position of each DVA-beam element are all parametric. A standard MATLAB function is given in Appendix A, which can return the elementary matrix directly once the desired parameters are given. A common beam element can also be simulated by the DVA-beam element by deactivating the element’s DVA effect. These characteristics make it extremely convenient for DVA optimization and other potential applications. A feasible DVA deactivating method is then presented by introducing a deactivating coefficient $a_m$, some numerical examples indicate that to deactivate the DVA effect, $a_m\le 0.01$ is advisable.

The reliability of the DVA-beam element in addressing different kinds of boundary conditions was investigated by comparing the beam tip responses with those simulated by ADAMS software; good agreements were observed. The DVA-beam element can also accurately simulate the dynamic responses of the multi-DVA-beam system. We can confirm that the presented element has good adaptability to different kinds of boundary conditions. Two DVA optimization examples were conducted aiming at reducing the beam vibrations using the DVA-beam technique. The results reveal that the DVA-beam element is reliable in optimization applications.

Future work will focus on the real-time computing aspect of the DVA-beam technique to enhance its portability on embedded microcontroller platforms.