Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Analysis
2.2. Machine Learning Models
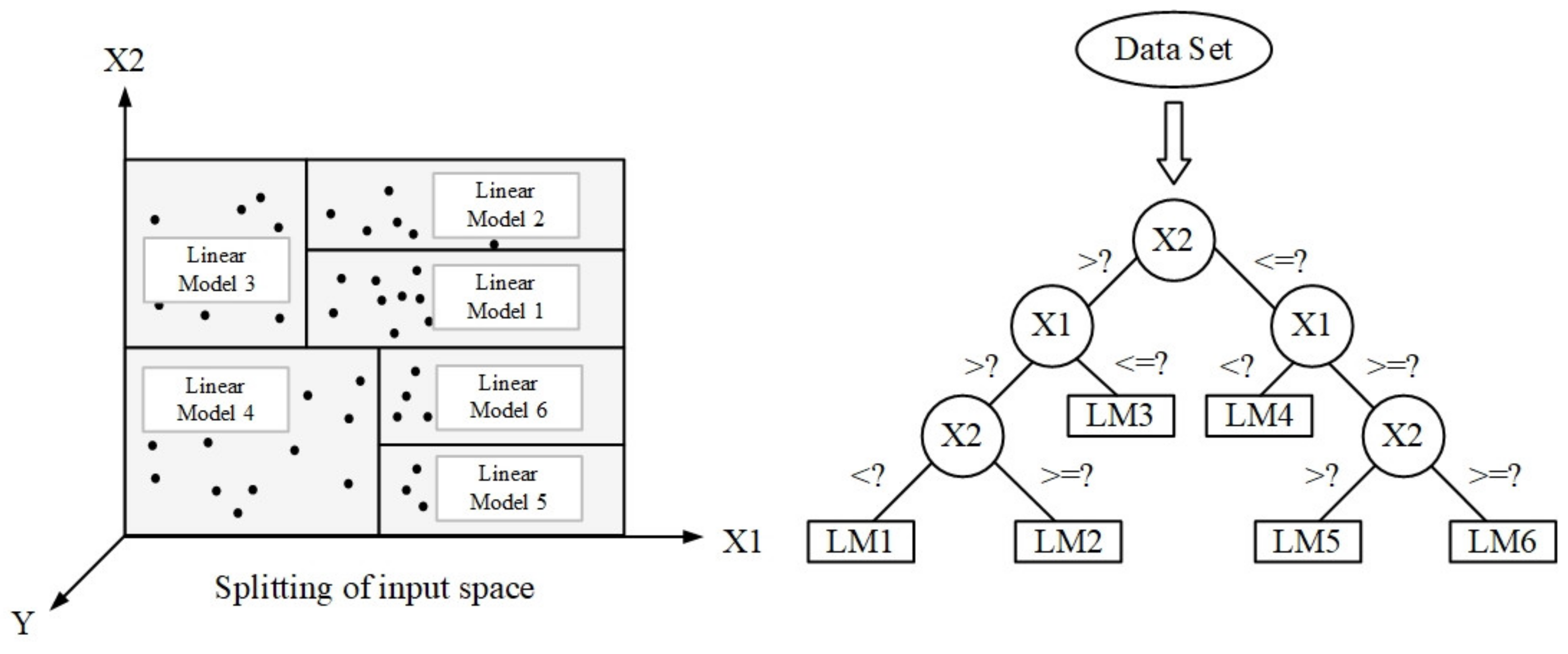
2.2.1. M5 Model Tree
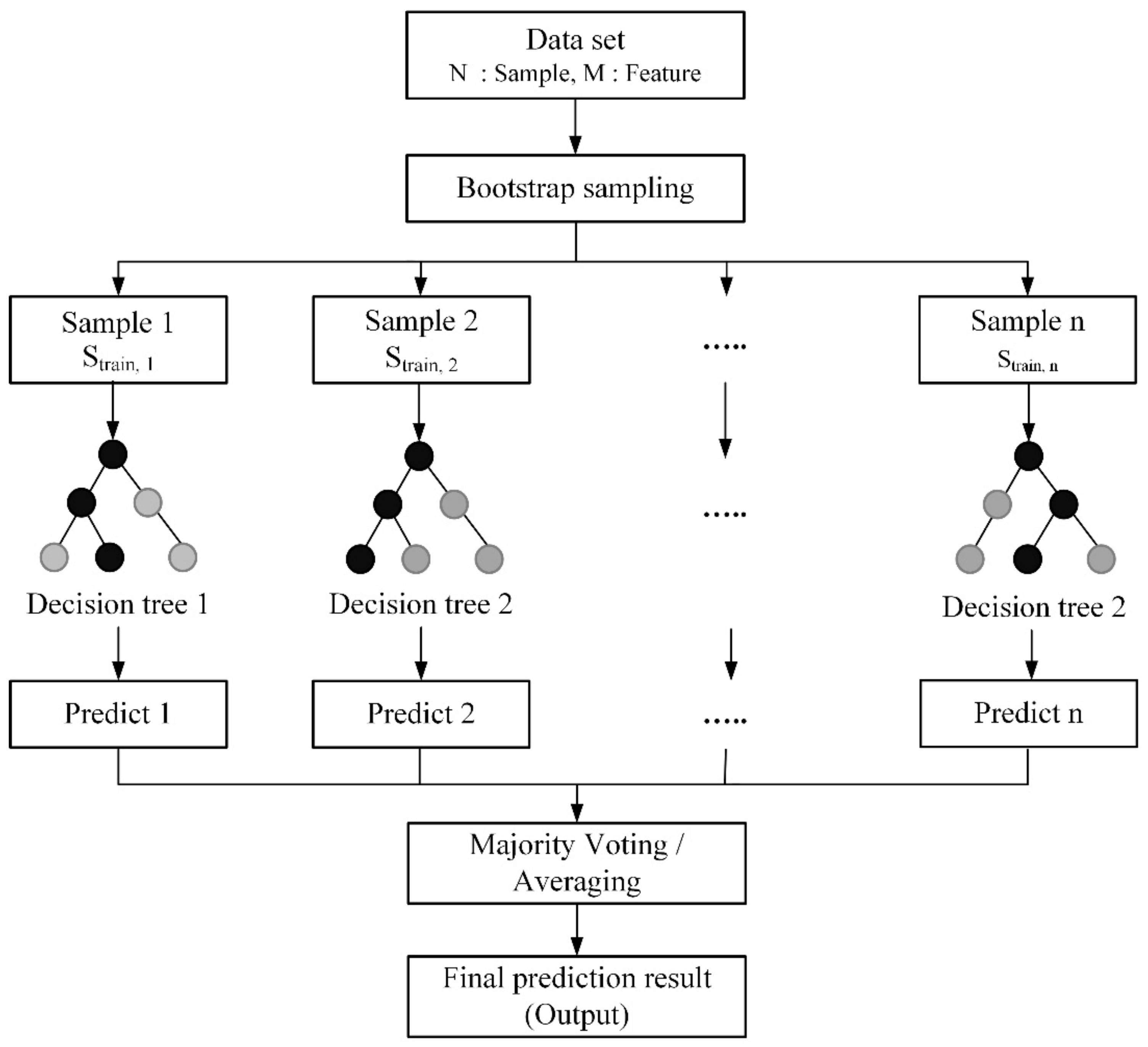
2.2.2. Random Forest
2.2.3. Support Vector Regression
- Linear kernel
- Polynomial kernel
- RBF kernel

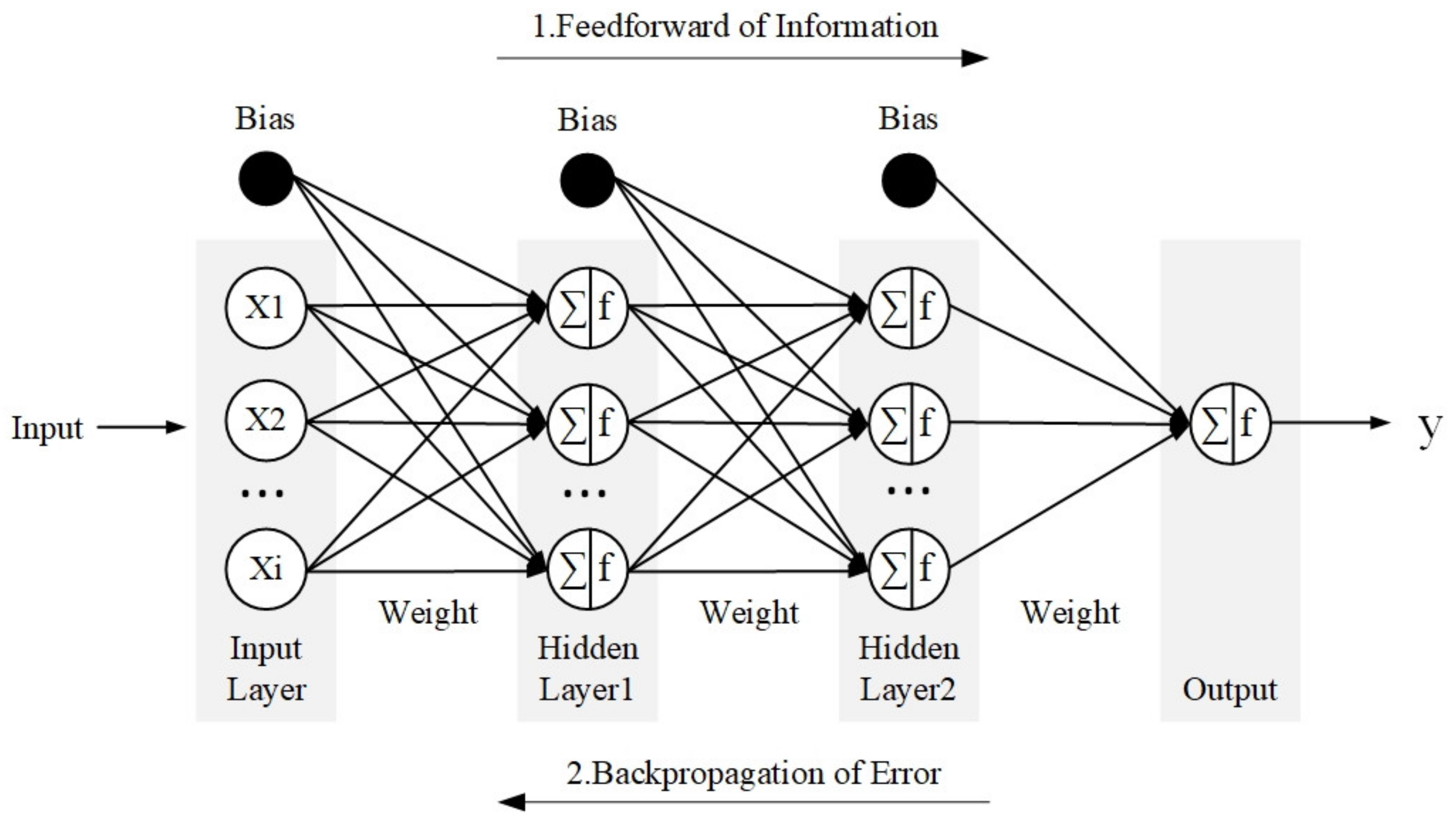
2.2.4. Multilayer Perceptron
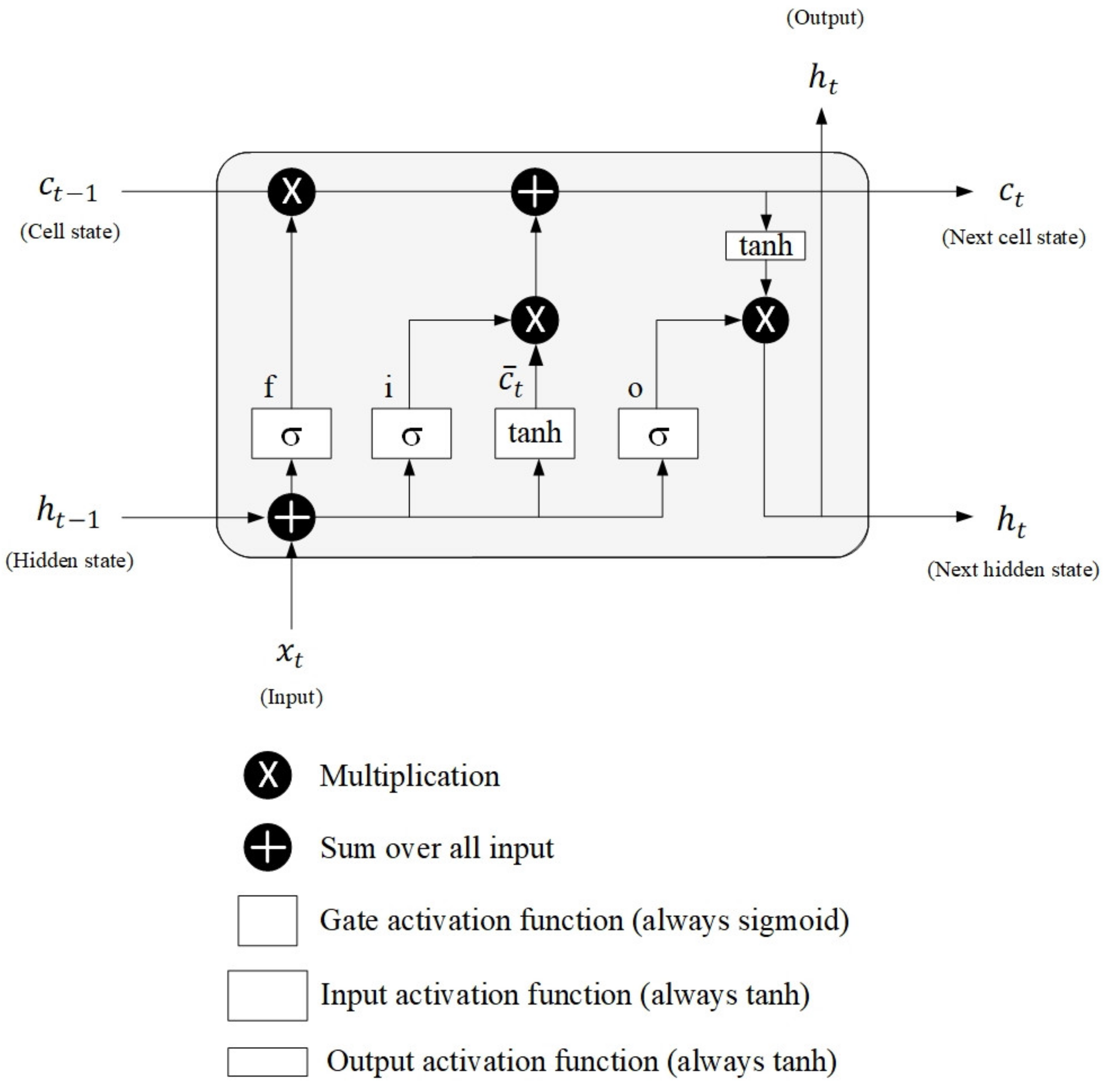
2.2.5. Long-Short Term Memory
- Forget gate
- Input gate
- Cell state candidate
- Cell state
- Output gate
- Hidden state
2.3. Model Development
- Scenario1: ML models with large-scale climate and meteorological variables as inputs.
- Scenario2: ML models with only meteorological variables as inputs.
- Scenario3: ML models with only rainfall variables as an input.
2.4. Model Performance Evaluation
3. Results and Discussion
3.1. Input Selection
3.2. Tuning Hyperparameters for Machine Learning Methods
3.2.1. M5 Model Tree
3.2.2. Random Forrest
3.2.3. Support Vector Regression
3.2.4. Multilayer Perceptron
3.2.5. Long Short-Term Memory
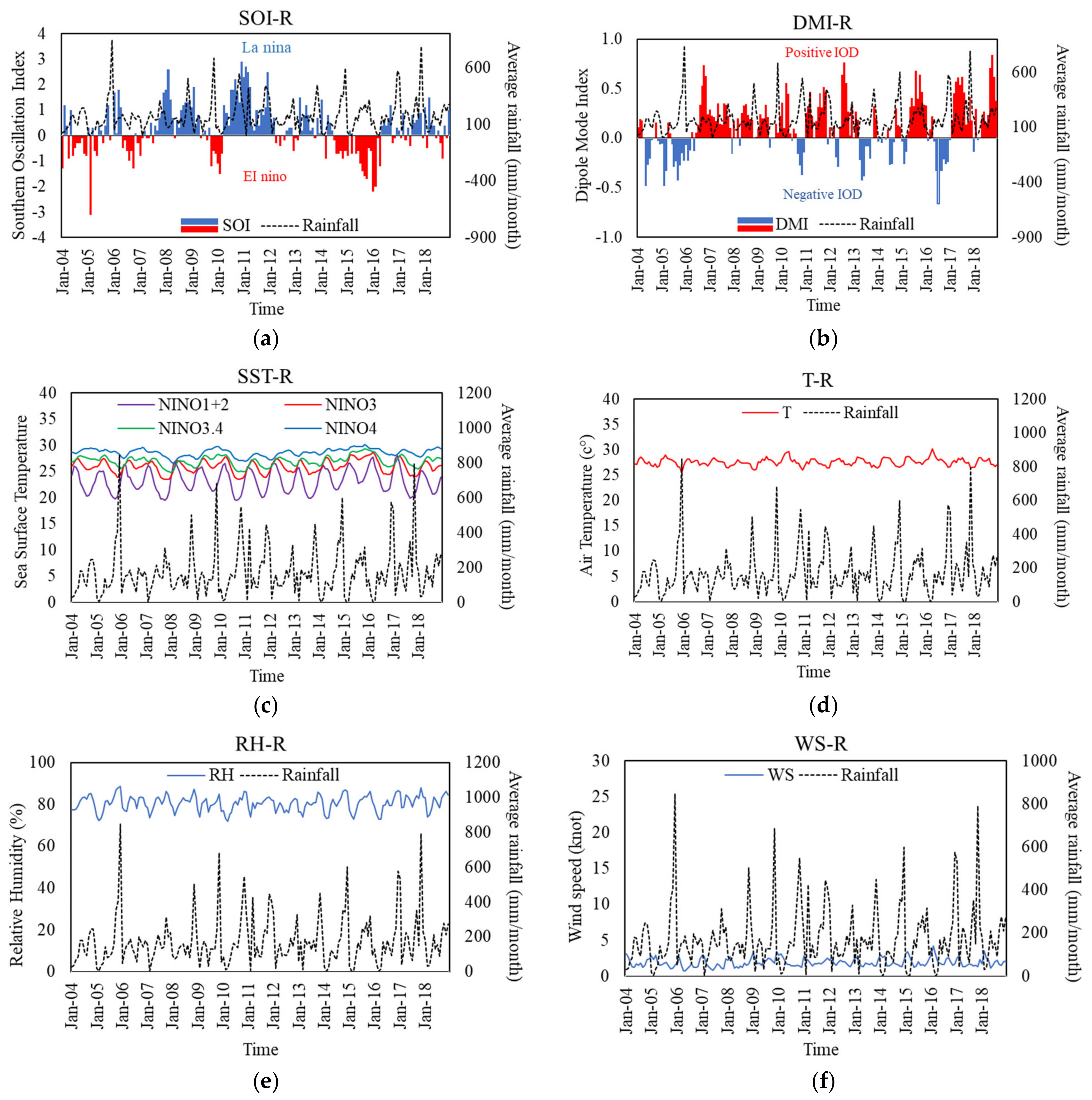
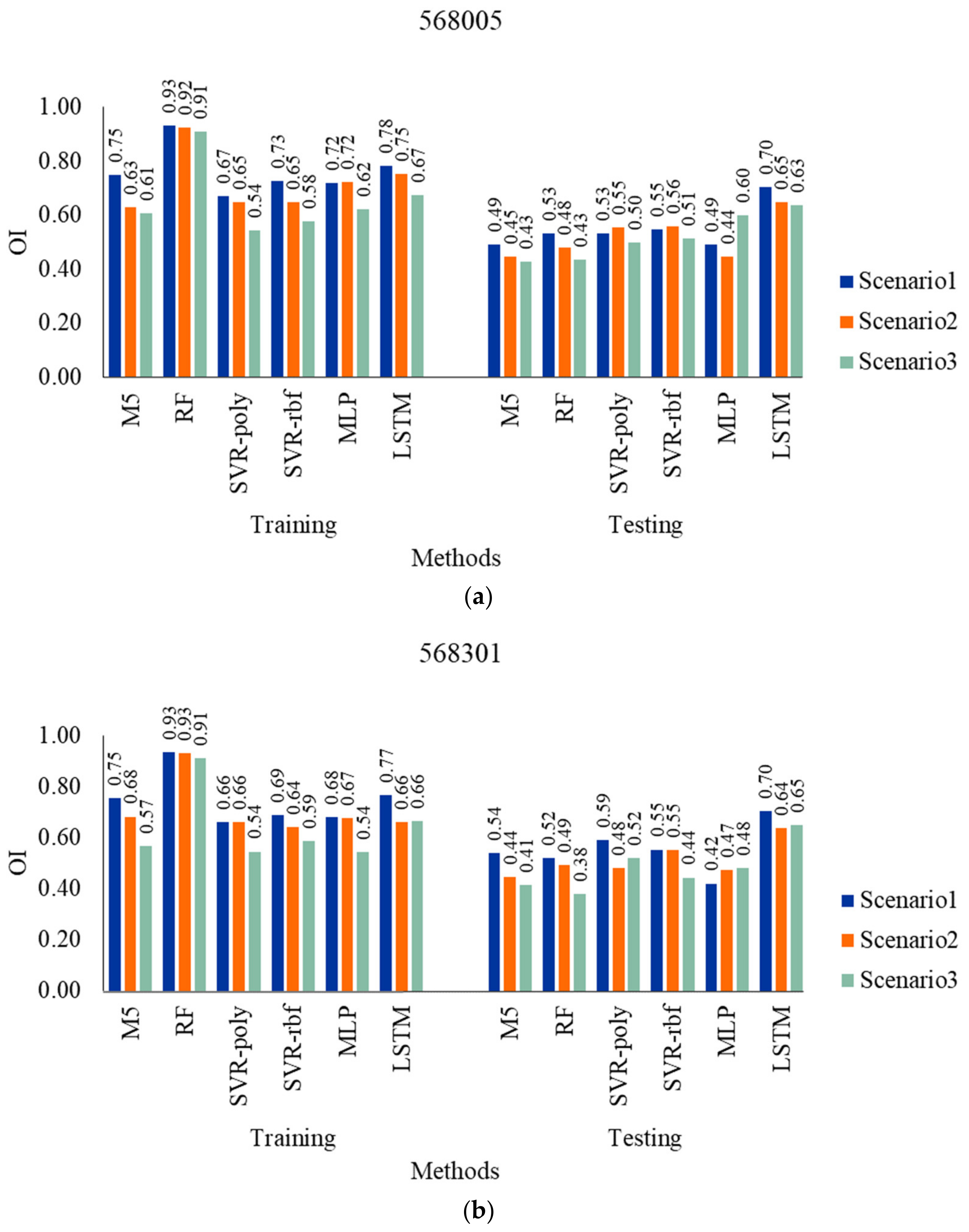
3.3. Influence of Climate Variables on Monthly Rainfall and Model Performance Comparison
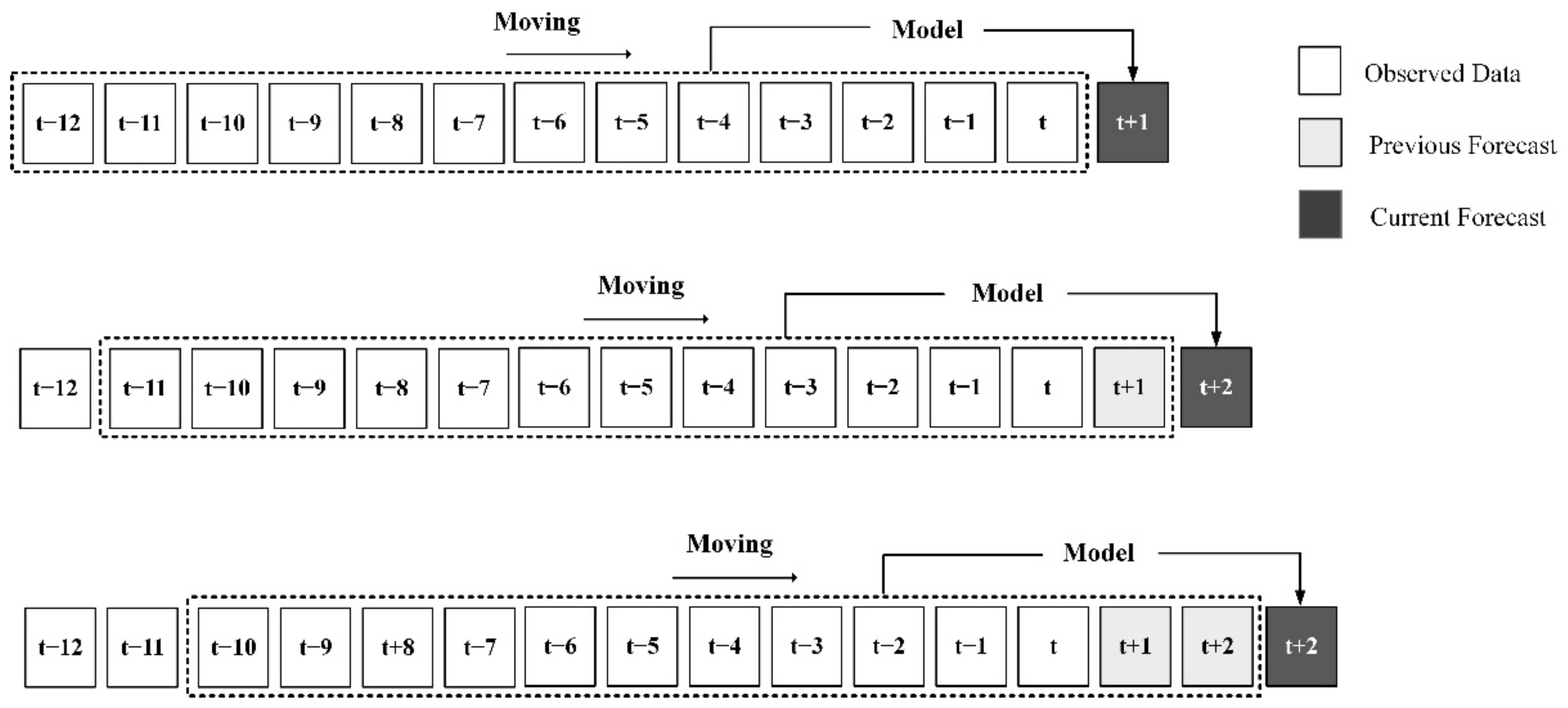
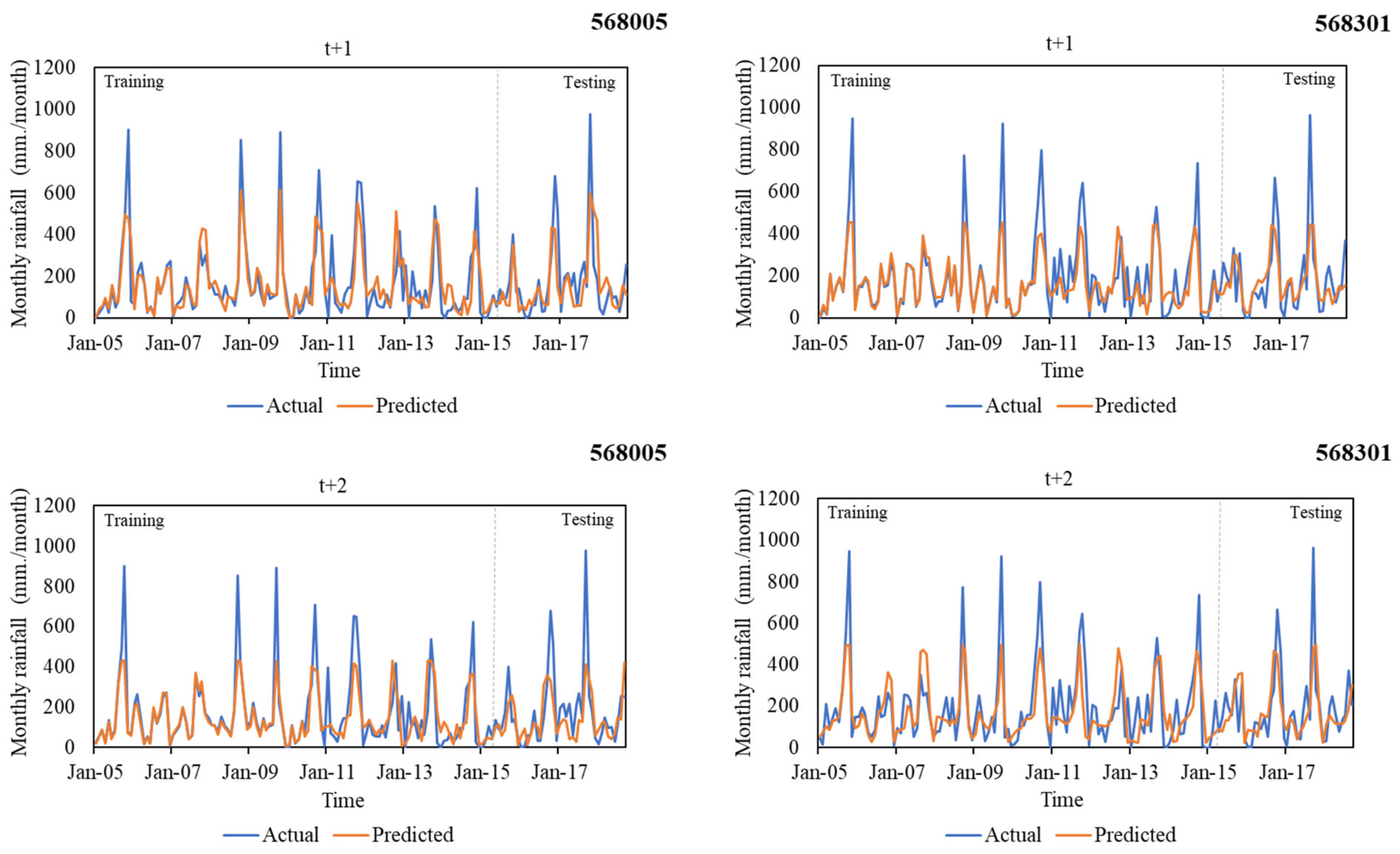
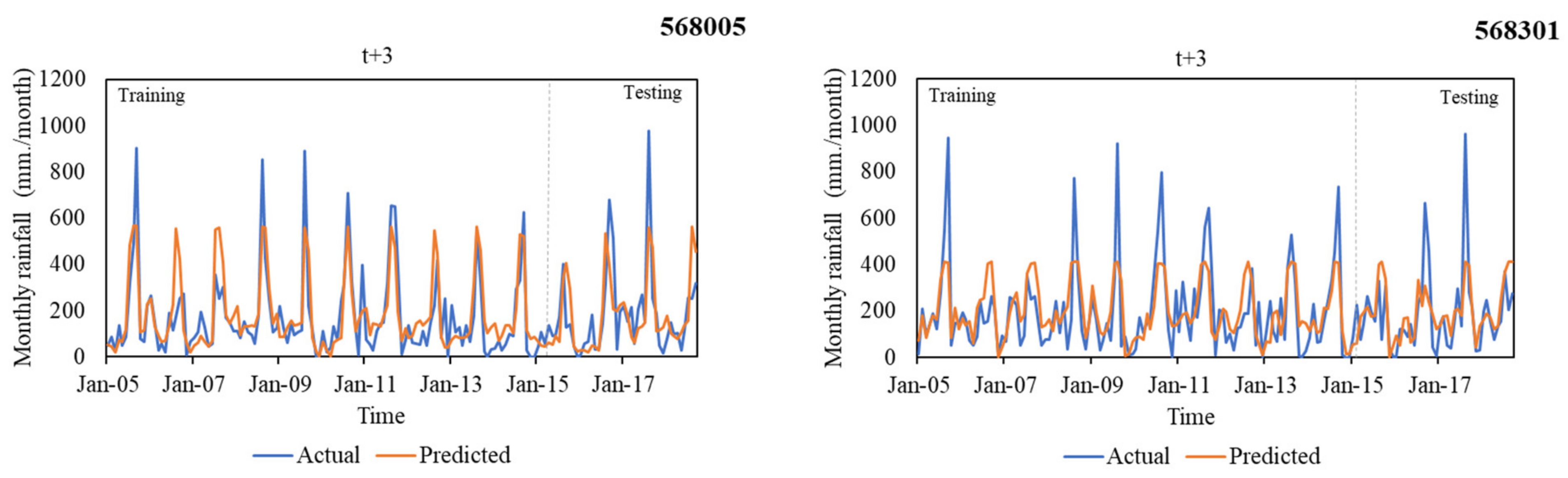
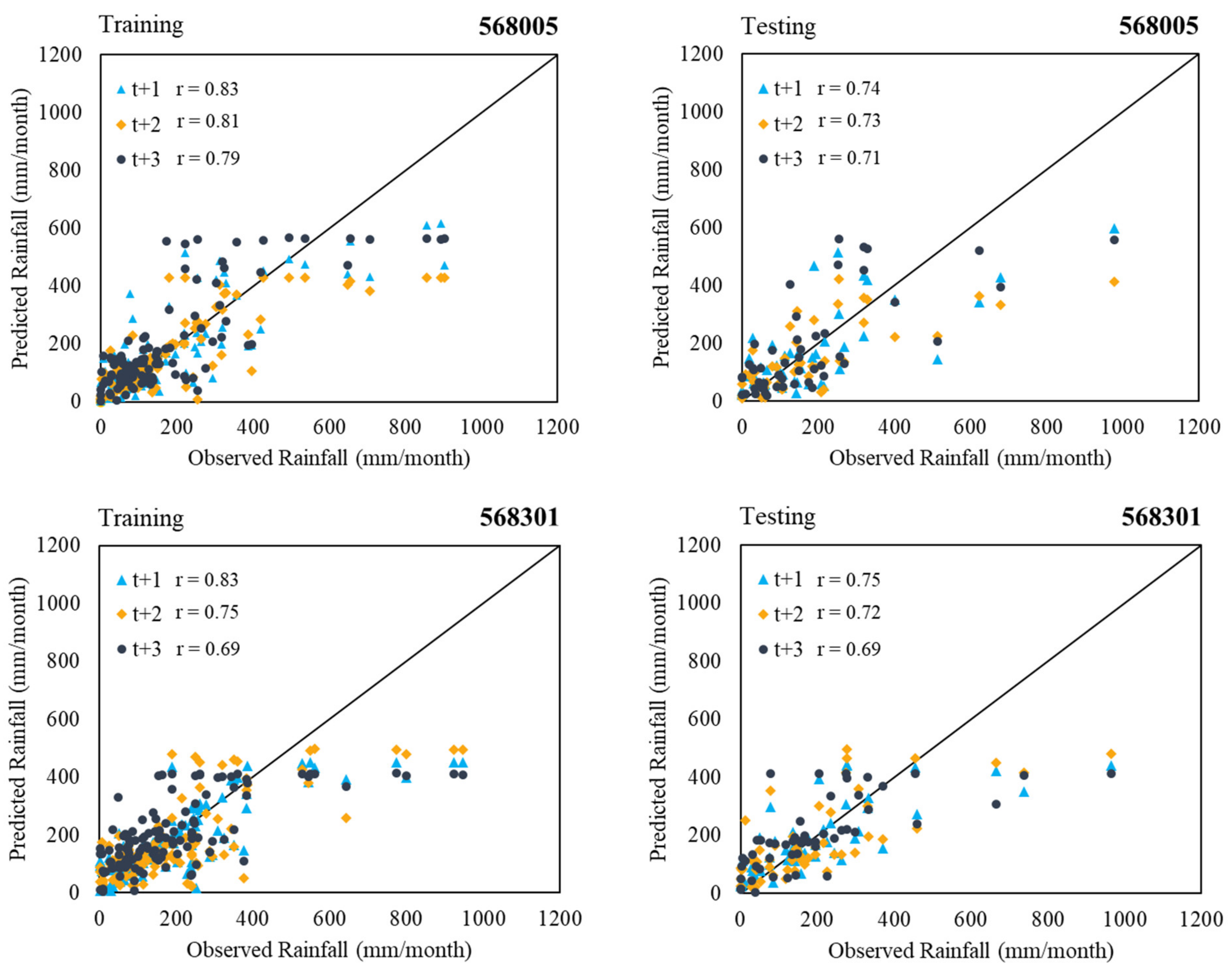
3.4. Multi-Month-Ahead Rainfall Predicting
4. Conclusions
- (1)
- The most relevant input variables for monthly rainfall prediction in the Thale Sap Songkhla basin, Thailand, were large-scale climate variables (i.e., SOI, DMI, and SST) and meteorological variables (i.e., air temperature: T; relative humidity: RH; and wind speed: WS).
- (2)
- Among large-scale climate variables (i.e., SOI, DMI, and SST), SST had the most influence on monthly rainfall prediction in the Thale Sap Songkhla basin, Thailand, followed by SOI and DMI, respectively. In addition, the developed models with SST as input variables provided the best model performance in most models.
- (3)
- The investigated results of the applicability of six ML techniques (i.e., M5, RF, SVR with polynomial and RBF kernels, MLP, and LSTM) in the multiple-month-ahead prediction of rainfall using small data sets revealed that the LSTM model provided the best performance for both gauged stations. In addition, it provided the predictive rainfall models for two rain gauged stations with the acceptable average performance: r (0.74), MAE (86.31 mm), RMSE (129.11 mm), and OI (0.70) for 1 month ahead, r (0.72), MAE (91.39 mm), RMSE (133.66 mm), and OI (0.68) for 2 months ahead, and r (0.70), MAE (94.17 mm), RMSE (137.22 mm), and OI (0.66) for 3 months ahead.
- (4)
- This research benefits farmer’s plantation plans and water-related agencies for irrigated water allocation plans and long-term flood forecasting. The proposed approach could be used for monthly rainfall prediction at all rainfall stations in this river basin.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babel, M.; Sirisena, T.; Singhrattna, N. Incorporating large-scale atmospheric variables in long-term seasonal rainfall forecasting using artificial neural networks: An application to the Ping Basin in Thailand. Hydrol. Res. 2017, 48, 867–882. [Google Scholar] [CrossRef][Green Version]
- Sharma, A.; Goyal, M.K. Bayesian network model for monthly rainfall forecast. In Proceedings of the 2015 IEEE International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Kolkata, India, 20–22 November 2015; pp. 241–246. [Google Scholar]
- Hasan, N.; Nath, N.C.; Rasel, R.I. A support vector regression model for forecasting rainfall. In Proceedings of the 2015 2nd international conference on electrical information and communication technologies (EICT), Khulna, Bangladesh, 10–12 December 2015; pp. 554–559. [Google Scholar]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414-415, 284–293. [Google Scholar] [CrossRef]
- Taweesin, K.; Seeboonruang, U.; Saraphirom, P. The influence of climate variability effects on groundwater time series in the lower central plains of Thailand. Water 2018, 10, 290. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Singhrattna, N.; Rajagopalan, B.; Kumar, K.K.; Clark, M. Interannual and interdecadal variability of Thailand summer monsoon season. J. Clim. 2005, 18, 1697–1708. [Google Scholar] [CrossRef]
- Haq, D.Z.; Novitasari, D.C.R.; Hamid, A.; Ulinnuha, N.; Farida, Y.; Nugraheni, R.D.; Nariswari, R.; Rohayani, H.; Pramulya, R.; Widjayanto, A. Long short-term memory algorithm for rainfall prediction based on El-Nino and IOD data. Procedia Comput. Sci. 2021, 179, 829–837. [Google Scholar] [CrossRef]
- Maass, M.; Ahedo-Hernández, R.l.; Araiza, S.; Verduzco, A.; Martínez-Yrízar, A.; Jaramillo, V.c.J.; Parker, G.; Pascual, F.n.; García-Méndez, G.; Sarukhán, J. Long-term (33 years) rainfall and runoff dynamics in a tropical dry forest ecosystem in western Mexico: Management implications under extreme hydrometeorological events. For. Ecol. Manag. 2018, 426, 7–17. [Google Scholar] [CrossRef]
- Islam, F.; Imteaz, M.A. Development of prediction model for forecasting rainfall in Western Australia using lagged climate indices. Int. J. Water 2019, 13, 248–268. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Li, J.; Qiao, Z.; Cao, J. Improved Medium- and Long-Term Runoff Forecasting Using a Multimodel Approach in the Yellow River Headwaters Region Based on Large-Scale and Local-Scale Climate Information. Water 2017, 9, 608. [Google Scholar] [CrossRef]
- Weekaew, J.; Ditthakit, P.; Kittiphattanabawon, N. Reservoir Inflow Time Series Forecasting Using Regression Model with Climate Indices; Springer: Cham, Switzerland, 2021; pp. 127–136. [Google Scholar] [CrossRef]
- Limsakul, A. Impacts of El Niño-Southern Oscillation (ENSO) on rice production in Thailand during 1961–2016. Environ. Nat. Resour. J. 2019, 17, 30–42. [Google Scholar] [CrossRef]
- Kirtphaiboon, S.; Wongwises, P.; Limsakul, A.; Sooktawee, S.; Humphries, U. Rainfall variability over Thailand related to the El Nino-Southern Oscillation (ENSO). Sustain. Energy Environ. 2014, 5, 37–42. [Google Scholar]
- Bridhikitti, A. Connections of ENSO/IOD and aerosols with Thai rainfall anomalies and associated implications for local rainfall forecasts. Int. J. Climatol. 2013, 33, 2836–2845. [Google Scholar] [CrossRef]
- Wikarmpapraharn, C.; Kositsakulchai, E. Relationship between ENSO and rainfall in the Central Plain of Thailand. Agric. Nat. Resour. 2010, 44, 744–755. [Google Scholar]
- Chang, T.; Talei, A.; Chua, L.; Alaghmand, S. The Impact of Training Data Sequence on the Performance of Neuro-Fuzzy Rainfall-Runoff Models with Online Learning. Water 2018, 11, 52. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Venkatesan, E.; Mahindrakar, A.B. Forecasting floods using extreme gradient boosting-a new approach. Int. J. Civ. Eng. 2019, 10, 1336–1346. [Google Scholar]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Jaiswal, R.; Ali, S.; Bharti, B. Comparative evaluation of conceptual and physical rainfall–runoff models. Appl. Water Sci. 2020, 10, 48. [Google Scholar] [CrossRef]
- Chen, Y.; Ren, Q.; Huang, F.; Xu, H.; Cluckie, I. Liuxihe Model and its modeling to river basin flood. J. Hydrol. Eng. 2011, 16, 33–50. [Google Scholar] [CrossRef]
- Lee, H.; McIntyre, N.; Wheater, H.; Young, A. Selection of conceptual models for regionalisation of the rainfall-runoff relationship. J. Hydrol. 2005, 312, 125–147. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Pandhiani, S.M.; Sihag, P.; Shabri, A.B.; Singh, B.; Pham, Q.B. Time-Series Prediction of Streamflows of Malaysian Rivers Using Data-Driven Techniques. J. Irrig. Drain. Eng. 2020, 146, 04020013. [Google Scholar] [CrossRef]
- Okkan, U.; Serbes, Z.A. Rainfall-runoff modeling using least squares support vector machines. Environmetrics 2012, 23, 549–564. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Cirilo, J.A.; Verçosa, L.F.d.M.; Gomes, M.M.d.A.; Feitoza, M.A.B.; Ferraz, G.d.F.; Silva, B.d.M. Development and application of a rainfall-runoff model for semi-arid regions. Rbrh 2020, 25, e15. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types; EPA/600/R-17/482; U.S. Environmental Protection Agency: Washington, DC, USA, 2017; pp. 1–29.
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Alizadeh, A.; Rajabi, A.; Shabanlou, S.; Yaghoubi, B.; Yosefvand, F. Modeling long-term rainfall-runoff time series through wavelet-weighted regularization extreme learning machine. Earth Sci. Inform. 2021, 14, 1047–1063. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. Short-term flood forecasting with a neurofuzzy model. Water Resour. Res. 2005, 41, W04004. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Mohamadi, S.; Sheikh Khozani, Z.; Ehteram, M.; Ahmed, A.N.; El-Shafie, A. Rainfall prediction using multiple inclusive models and large climate indices. Environ. Sci. Pollut. Res. 2022, 29, 1–38. [Google Scholar] [CrossRef]
- Mohammadi, B.; Moazenzadeh, R.; Christian, K.; Duan, Z. Improving streamflow simulation by combining hydrological process-driven and artificial intelligence-based models. Environ. Sci. Pollut. Res. 2021, 28, 65752–65768. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Mohammadi, B.; Pham, Q.B.; Adarsh, S.; Balkhair, K.S.; Rahman, K.U.; Linh, N.T.T.; Tri, D.Q. A novel approach for predicting daily pan evaporation in the coastal regions of Iran using support vector regression coupled with krill herd algorithm model. Theor. Appl. Climatol. 2020, 142, 349–367. [Google Scholar] [CrossRef]
- Heng, S.Y.; Ridwan, W.M.; Kumar, P.; Ahmed, A.N.; Fai, C.M.; Birima, A.H.; El-Shafie, A. Artificial neural network model with different backpropagation algorithms and meteorological data for solar radiation prediction. Sci. Rep. 2022, 12, 10457. [Google Scholar] [CrossRef] [PubMed]
- Achite, M.; Banadkooki, F.B.; Ehteram, M.; Bouharira, A.; Ahmed, A.N.; Elshafie, A. Exploring Bayesian model averaging with multiple ANNs for meteorological drought forecasts. Stoch. Environ. Res. Risk Assess. 2022, 36, 1835–1860. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Banadkooki, F.B.; Ehteram, M.; Ahmed, A.N.; El-Shafie, A. Combining autoregressive integrated moving average with Long Short-Term Memory neural network and optimisation algorithms for predicting ground water level. J. Clean. Prod. 2022, 348, 131224. [Google Scholar] [CrossRef]
- Hung, N.Q.; Babel, M.S.; Weesakul, S.; Tripathi, N. An artificial neural network model for rainfall forecasting in Bangkok, Thailand. Hydrol. Earth Syst. Sci. 2009, 13, 1413–1425. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Chen, S.-Y.; Kuo, C.-M.; Tseng, H.-W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Mekanik, F.; Imteaz, M.; Gato-Trinidad, S.; Elmahdi, A. Multiple regression and Artificial Neural Network for long-term rainfall forecasting using large scale climate modes. J. Hydrol. 2013, 503, 11–21. [Google Scholar] [CrossRef]
- Ridwan, W.M.; Sapitang, M.; Aziz, A.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Rainfall forecasting model using machine learning methods: Case study Terengganu, Malaysia. Ain Shams Eng. J. 2021, 12, 1651–1663. [Google Scholar] [CrossRef]
- Mislan, M.; Haviluddin, H.; Hardwinarto, S.; Sumaryono, S.; Aipassa, M. Rainfall monthly prediction based on artificial neural network: A case study in Tenggarong Station, East Kalimantan-Indonesia. Procedia Comput. Sci. 2015, 59, 142–151. [Google Scholar] [CrossRef]
- Zhang, X.; Mohanty, S.N.; Parida, A.K.; Pani, S.K.; Dong, B.; Cheng, X. Annual and non-monsoon rainfall prediction modelling using SVR-MLP: An empirical study from Odisha. IEEE Access 2020, 8, 30223–30233. [Google Scholar] [CrossRef]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Kişi, Ö. Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for forecasting precipitation based on large-scale climate signals. Hydrol. Sci. J. 2016, 61, 1001–1009. [Google Scholar] [CrossRef]
- Aswin, S.; Geetha, P.; Vinayakumar, R. Deep learning models for the prediction of rainfall. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 3–5 April 2018; pp. 657–661. [Google Scholar]
- Chen, C.; Zhang, Q.; Kashani, M.H.; Jun, C.; Bateni, S.M.; Band, S.S.; Dash, S.S.; Chau, K.-W. Forecast of rainfall distribution based on fixed sliding window long short-term memory. Eng. Appl. Comput. Fluid Mech. 2022, 16, 248–261. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Samui, P.; Jha, R.K. Forecasting monthly precipitation using sequential modelling. Hydrol. Sci. J. 2019, 64, 690–700. [Google Scholar] [CrossRef]
- Ditthakit, P.; Pinthong, S.; Salaeh, N.; Binnui, F.; Khwanchum, L.; Pham, Q.B. Using machine learning methods for supporting GR2M model in runoff estimation in an ungauged basin. Sci. Rep. 2021, 11, 19955. [Google Scholar] [CrossRef]
- Perea, R.G.; Ballesteros, R.; Ortega, J.F.; Moreno, M.Á. Water and energy demand forecasting in large-scale water distribution networks for irrigation using open data and machine learning algorithms. Comput. Electron. Agric. 2021, 188, 106327. [Google Scholar] [CrossRef]
- Vilanova, R.S.; Zanetti, S.S.; Cecílio, R.A. Assessing combinations of artificial neural networks input/output parameters to better simulate daily streamflow: Case of Brazilian Atlantic Rainforest watersheds. Comput. Electron. Agric. 2019, 167, 105080. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Khadr, M.; Elshemy, M. Data-driven modeling for water quality prediction case study: The drains system associated with Manzala Lake, Egypt. Ain Shams Eng. J. 2017, 8, 549–557. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2018, 1168, 022022. [Google Scholar] [CrossRef]
- Kanchan, P.; Shardoor, N.K. Rainfall Analysis and Forecasting Using Deep Learning Technique. J. Inform. Electr. Electron. Eng. 2021, 2, 142–151. [Google Scholar] [CrossRef]
- Tao, L.; He, X.; Li, J.; Yang, D. A multiscale long short-term memory model with attention mechanism for improving monthly precipitation prediction. J. Hydrol. 2021, 602, 126815. [Google Scholar] [CrossRef]
- Tongal, H.; Berndtsson, R. Impact of complexity on daily and multi-step forecasting of streamflow with chaotic, stochastic, and black-box models. Stoch. Environ. Res. Risk Assess. 2017, 31, 661–682. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network based rainfall–runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Solomatine, D.P.; Xue, Y. M5 model trees and neural networks: Application to flood forecasting in the upper reach of the Huai River in China. J. Hydrol. Eng. 2004, 9, 491–501. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Park, M.; Jung, D.; Lee, S.; Park, S. Heatwave Damage Prediction Using Random Forest Model in Korea. Appl. Sci. 2020, 10, 8237. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 1995. [Google Scholar]
- Caraka, R.E.; Bakar, S.A.; Tahmid, M. Rainfall forecasting multi kernel support vector regression seasonal autoregressive integrated moving average (MKSVR-SARIMA). In Proceedings of the AIP Conference Proceedings, Selangor, Malaysia, 4–6 April 2018; p. 020014. [Google Scholar]
- Yu, P.-S.; Chen, S.-T.; Chang, I.-F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Chandra, A.; Suaib, M.; Beg, D. Web spam classification using supervised artificial neural network algorithms. Adv. Comput. Intell. Int. J. ACII 2015, 2, 21–30. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Zhu, H.; Zeng, H.; Liu, J.; Zhang, X. Logish: A new nonlinear nonmonotonic activation function for convolutional neural network. Neurocomputing 2021, 458, 490–499. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Zadeh, H.A.; Isazadeh, M.; Terzi, O. A comparative study of artificial neural network (MLP, RBF) and support vector machine models for river flow prediction. Environ. Earth Sci. 2016, 75, 476. [Google Scholar] [CrossRef]
- Mandal, T.; Jothiprakash, V. Short-term rainfall prediction using ANN and MT techniques. ISH J. Hydraul. Eng. 2012, 18, 20–26. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Pei, S.; Qin, H.; Yao, L.; Liu, Y.; Wang, C.; Zhou, J. Multi-step ahead short-term load forecasting using hybrid feature selection and improved long short-term memory network. Energies 2020, 13, 4121. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Sarzaeim, P.; Bozorg-Haddad, O.; Bozorgi, A.; Loáiciga, H.A. Runoff Projection under Climate Change Conditions with Data-Mining Methods. J. Irrig. Drain. Eng. 2017, 143, 04017026. [Google Scholar] [CrossRef]
- Dehghani, M.; Salehi, S.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Ghamisi, P. Spatial analysis of seasonal precipitation over Iran: Co-variation with climate indices. ISPRS Int. J. Geo-Inf. 2020, 9, 73. [Google Scholar] [CrossRef]
- Sein, Z.M.M.; Ogwang, B.; Ongoma, V.; Ogou, F.K.; Batebana, K. Inter-annual variability of May-October rainfall over Myanmar in relation to IOD and ENSO. J. Environ. Agric. Sci. 2015, 4, 28–36. [Google Scholar]
- Bae, J.H.; Han, J.; Lee, D.; Yang, J.E.; Kim, J.; Lim, K.J.; Neff, J.C.; Jang, W.S. Evaluation of sediment trapping efficiency of vegetative filter strips using machine learning models. Sustainability 2019, 11, 7212. [Google Scholar] [CrossRef]
- Parashar, N.; Khan, J.; Aslfattahi, N.; Saidur, R.; Yahya, S.M. Prediction of the Dynamic Viscosity of MXene/Palm Oil Nanofluid Using Support Vector Regression. In Recent Trends in Thermal Engineering; Springer: Singapore, 2022; pp. 49–55. [Google Scholar]
- Armstrong, J.S. Evaluating forecasting methods. In Principles of Forecasting; Springer: Boston, MA, USA, 2001; pp. 443–472. [Google Scholar]
- Ritter, A.; Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Liyew, C.M.; Melese, H.A. Machine learning techniques to predict daily rainfall amount. J. Big Data 2021, 8, 153. [Google Scholar] [CrossRef]
- Cheng, H.; Tan, P.-N.; Gao, J.; Scripps, J. Multistep-ahead time series prediction. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Singapore, 9–12 April 2006; pp. 765–774. [Google Scholar]
- Ghamariadyan, M.; Imteaz, M.A. Monthly rainfall forecasting using temperature and climate indices through a hybrid method in Queensland, Australia. J. Hydrometeorol. 2021, 22, 1259–1273. [Google Scholar] [CrossRef]


| Data | Statistical Value | |||||
|---|---|---|---|---|---|---|
| Max | Min | Avg | SD | Kurt | Skew | |
| Meteorological | ||||||
| Rainfall (mm) | 977.60 | 0.00 | 179.03 | 179.89 | 5.51 | 2.16 |
| Air temperature (C) | 30.00 | 25.40 | 0.66 | 0.81 | 0.21 | 0.16 |
| Relative humidity (%) | 89.75 | 70.00 | 79.62 | 3.97 | −0.30 | 0.24 |
| Wind speed (Knot) | 4.50 | 0.40 | 1.88 | 0.78 | 0.06 | 0.59 |
| Large-scale climate variables | ||||||
| SOI | 2.90 | −3.10 | 0.24 | 0.97 | 0.62 | 0.09 |
| DMI | 0.84 | −0.66 | 0.12 | 0.28 | −0.14 | 0.07 |
| SST | ||||||
| −NINO1 + 2 | 28.10 | 19.50 | 23.22 | 2.16 | −1.09 | 0.11 |
| −NINO3 | 28.74 | 23.48 | 25.96 | 1.24 | −0.78 | −0.07 |
| −NINO3.4 | 29.42 | 24.86 | 27.03 | 0.99 | −0.37 | −0.06 |
| −NINO4 | 30.13 | 26.62 | 28.65 | 0.74 | −0.40 | −0.48 |
| Models | Hyperparameters | Sensitive | Start | End | Rang of RRSE |
|---|---|---|---|---|---|
| M5 | batchSize | No | 100 | 1000 | 85.15–99.46 |
| minNumInstances | Yes | 4.00 | 30.00 | ||
| numDecimalPlaces | No | 4.00 | 4.00 | ||
| RF | batchSize | No | 100 | 1000 | 78.93–96.02 |
| numIteration | Yes | 100 | 1000 | ||
| numExecutionSlots | No | 1.00 | 1.00 | ||
| SVR-poly | c | Yes | 0.1 | 50 | 80.57–94.16 |
| epsilonParameter | Yes | 0.0001 | 0.1 | ||
| exponent | Yes | 1.00 | 1.00 | ||
| SVR-rbf | c | Yes | 0.1 | 100 | 74.72–94.70 |
| epsilonParameter | Yes | 0.0001 | 0.1 | ||
| gramma | Yes | 0.01 | 0.5 | ||
| MLP | hiddenLayers | Yes | * | * | 84.87–115.76 |
| learningRate | Yes | 0.1 | 0.5 | ||
| momentum | Yes | 0.1 | 0.5 | ||
| trainingTime | Yes | 100 | 1000 | ||
| LSTM | Rate | Yes | 0.1 | 0.9 | N/A |
| Momentum | No | 0.1 | 0.9 | ||
| Epoch | Yes | 500 | 1000 | ||
| Progress Frequency | Yes | 10 | 100 | ||
| Normalization Layer | Yes | N/A | N/A | ||
| LSTM Layer Activation (tanH) | Yes | 40 | 80 | ||
| Dense Layer1 Activation (tanH) | Yes | 10 | 50 | ||
| Dense Layer2 Activation (Relu) | Yes | 10 | 50 | ||
| Output Layer Activation (Relu) | Yes | 1 | 1 |
| Stations | Methods | Performance Criteria | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | ||||||||
| r | MAE (mm) | RMSE (mm) | OI | r | MAE (mm) | RMSE (mm) | OI | ||
| 568005 | M5 | 0.79 | 75.47 | 111.80 | 0.75 | 0.49 | 127.27 | 172.38 | 0.49 |
| RF | 0.98 | 33.17 | 51.24 | 0.93 | 0.53 | 124.70 | 164.50 | 0.53 | |
| SVR-poly | 0.74 | 71.01 | 130.19 | 0.67 | 0.56 | 114.67 | 164.49 | 0.53 | |
| SVR-rbf | 0.78 | 76.04 | 116.97 | 0.73 | 0.55 | 116.95 | 161.66 | 0.55 | |
| MLP | 0.76 | 77.38 | 118.39 | 0.72 | 0.57 | 128.97 | 172.72 | 0.49 | |
| LSTM * | 0.83 | 64.91 | 102.37 | 0.78 | 0.74 | 88.63 | 128.11 | 0.70 | |
| 568301 | M5 | 0.80 | 82.69 | 111.44 | 0.75 | 0.53 | 119.46 | 165.80 | 0.54 |
| RF | 0.98 | 36.30 | 50.84 | 0.93 | 0.52 | 126.14 | 169.74 | 0.52 | |
| SVR-poly | 0.71 | 89.10 | 133.20 | 0.66 | 0.60 | 102.96 | 155.41 | 0.59 | |
| SVR-rbf | 0.74 | 89.77 | 126.90 | 0.69 | 0.53 | 112.78 | 163.12 | 0.55 | |
| MLP | 0.73 | 94.93 | 128.89 | 0.68 | 0.46 | 144.55 | 188.16 | 0.42 | |
| LSTM * | 0.83 | 59.97 | 108.13 | 0.77 | 0.75 | 83.99 | 130.09 | 0.70 | |
| Stations | Lead-Time (Month) | Performance Criteria | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | ||||||||
| r | MAE (mm) | RMSE (mm) | OI | r | MAE (mm) | RMSE (mm) | OI | ||
| 568005 | 1 | 0.83 | 64.91 | 102.37 | 0.78 | 0.74 | 88.63 | 128.11 | 0.70 |
| 2 | 0.81 | 58.26 | 110.27 | 0.75 | 0.73 | 89.03 | 134.23 | 0.68 | |
| 3 | 0.79 | 78.79 | 112.18 | 0.75 | 0.71 | 96.48 | 134.74 | 0.67 | |
| 568301 | 1 | 0.83 | 59.97 | 108.13 | 0.77 | 0.75 | 83.99 | 130.09 | 0.70 |
| 2 | 0.75 | 85.02 | 122.21 | 0.71 | 0.72 | 93.75 | 133.09 | 0.69 | |
| 3 | 0.69 | 93.20 | 132.26 | 0.67 | 0.69 | 91.87 | 139.71 | 0.66 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salaeh, N.; Ditthakit, P.; Pinthong, S.; Hasan, M.A.; Islam, S.; Mohammadi, B.; Linh, N.T.T. Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand. Symmetry 2022, 14, 1599. https://doi.org/10.3390/sym14081599
Salaeh N, Ditthakit P, Pinthong S, Hasan MA, Islam S, Mohammadi B, Linh NTT. Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand. Symmetry. 2022; 14(8):1599. https://doi.org/10.3390/sym14081599
Chicago/Turabian StyleSalaeh, Nureehan, Pakorn Ditthakit, Sirimon Pinthong, Mohd Abul Hasan, Saiful Islam, Babak Mohammadi, and Nguyen Thi Thuy Linh. 2022. "Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand" Symmetry 14, no. 8: 1599. https://doi.org/10.3390/sym14081599
APA StyleSalaeh, N., Ditthakit, P., Pinthong, S., Hasan, M. A., Islam, S., Mohammadi, B., & Linh, N. T. T. (2022). Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand. Symmetry, 14(8), 1599. https://doi.org/10.3390/sym14081599







