Collision Forgery Attack on the AES-OTR Algorithm under Quantum Computing

Abstract

In recent years, some general cryptographic technologies have been widely used in network platforms related to the national economy and people’s livelihood, effectively curbing network security risks and maintaining the orderly operation and normal order of society. However, due to the fast development and considerable benefits of quantum computing, the classical cryptosystem faces serious security threats, so it is crucial to analyze and assess the anti-quantum computing ability of cryptographic algorithms under the quantum security model, to enhance or perfect the design defects of related algorithms. However, the current design and research of anti-quantum cryptography primarily focus on the cryptographic structure or working mode under the quantum security model, and there is a lack of quantum security analysis on instantiated cryptographic algorithms. This paper investigates the security of AES-OTR, one of the third-round algorithms in the CAESAR competition, under the Q2 model. The periodic functions of the associated data were constructed by forging the associated data according to the parallel and serial structure characteristics of the AES-OTR algorithm in processing the associated data, and the periodic functions of the associated data were constructed multiple times based on the Simon quantum algorithm. By using the collision pair, two collision forgery attacks on the AES-OTR algorithm can be successfully implemented, and the period s is obtained by solving with a probability close to 1. The attacks in this paper caused a significant threat to the security of the AES-OTR algorithm.

1. Introduction

1.1. Background

The field of modern cryptography has changed dramatically since the quantum computer [1] was proposed in 1980. Research on quantum-resistant cryptosystems is also being accelerated internationally to meet the need of the post-quantum cryptography era. In 2016, the National Institute of Standards and Technology (NIST) publicly solicited quantum-resistant cryptographic algorithms worldwide and planned to formulate preliminary standards for quantum-resistant cryptography in 2022 to promote the standardization of quantum-resistant cryptographic algorithms. The security of some common block cipher structures and working modes has been demonstrated [2,3,4]. Recently, Chinese experts and scholars have conducted extensive cross-studies on the security analysis of cryptographic algorithm patterns and structures and the evaluation of attack resources under the quantum security model [5,6,7].

Quantum algorithms employ the coherence and superposition of quantum to accelerate computing and achieve parallel computing. Currently, commonly used quantum algorithms include the Shor algorithm [8], Simon algorithm [9], and Grover algorithm [10]. Among them, the Shor algorithm can solve large integer factorization and discrete logarithm problems in polynomial time, which seriously affect the security of RSA and Diffie–Hellman public-key cryptosystems. In the security analysis of symmetric cryptographic algorithms, Simon and Grover quantum search algorithms are often employed. The Grover algorithm is employed to search for a specific element from n unclassified elements. Since Simon’s algorithm is the simplest algorithm for determining the nontrivial periods, this study primarily uses the Simon algorithm.

Recently, based on the Simon and Grover algorithm, security analysis approaches such as quantum differential and linear analysis [11], quantum correlated key attack [12,13], and quantum sliding attack [14] have been proposed and applied. According to the work of Zhandry [15], the standard security model (Q1 model) and the quantum security model (Q2 model) are the two models for the quantum analysis of current cryptographic algorithms. In the Q1 model, the adversary can only collect and query data in a traditional way and employs quantum computers to process and calculate the data. In the Q2 model, the adversary queries the random oracle machine by constructing a quantum superposition state and uses the quantum computer to receive the corresponding quantum superposition state output. For example, Soukharev et al. [16] proposed the quantum security models INT-PTXT (plaintext integrity under quantum attack) and INT-qCTXT (ciphertext integrity under quantum attack) for authentication and encryption under the Q2 model.

1.2. Related Work

In 2014, NIST launched the Competition for Authenticated Encryption: Security, Applicability and Robustness (CAESAR) [17] for the global collection of authenticated encryption schemes, aiming to develop new and more efficient authenticated encryption schemes that are more secure than the Advanced Encryption Standard Galois/Counter Mode [18], and combine security, applicability, and robustness. The AES-OTR algorithm [19] is one of the candidate algorithms to enter the CAESAR competition’s third round. AES-OTR is an authenticated encryption algorithm that combines the AES algorithm [20] with the OTR mode of operation [21]. The OTR operation mode is extensively employed in the design of authentication encryption algorithms such as AEZ [22] and ESTATE [23] due to low computational complexity, parallelism, and inverse freedom. Its authentication part function, AFE, is a variant of PMAC [24]. In the case of a known pair of plaintext and s + 1 (s > 0) pair of plaintexts, Zheng et al. [25] proposed a traditional forgery attack on the AES-OTR algorithm by reusing associated data and public message codes. The probability of a successful attack was computed as ${(m-1)}^2\cdot 2^{-(n+2)}$ and $s^2(s+1)\cdot 2^{\frac{m-1}{2}-n}$ (where m is the length of the blocks and n is the number of the blocks), and the possibility of forgery was proved. Since AES-OTR is the fastest algorithm implemented in hardware in the CAESAR competition, it is crucial to evaluate the performance of its high-speed applications. For the first time, Banik et al. [26] employed an 8-bit serial AES circuit to compactly implement three authenticated encryption algorithms, CLOC [27], SILC [28], and AES-OTR [19]. Ueno et al. [29] parallelized the encryption core part of AES into the Feistel network’s data path corresponding to the OTR algorithm and proposed a scalable AES-OTR hardware architecture with a smaller area and higher throughput quantity. The actual efficiency of the AES-OTR hardware implementation is assessed using FPGA and ASIC, and authentication and encryption can be completed with low energy consumption. Mancillas [30] established the AES-OTR algorithm’s superiority in high-speed and ultra-high-speed authentication and encryption applications, demonstrating that when the underlying algorithm is AES and has certain requirements for hardware speed, AES-OTR outperforms the OCB structure.

The AES-OTR authentication encryption algorithm processes associated data in two structures: serial and parallel. This study employs the relative independence between the AES-OTR algorithm’s modules to deal with the associated data’s parallel and serial structural characteristics. The data’s collision form is constructed and combined with the Simon quantum algorithm to solve the collision period, the AES-OTR algorithm’s collision forgery attack under quantum computing is proposed, and its feasibility and efficiency are verified.

2. AES-OTR Algorithm Description

2.1. Basic Symbols

First, some symbols in the AES-OTR authentication encryption algorithm are explained. ${\left\{0,1\right\}}^{\mathrm{n}}$ and ${\left\{0,1\right\}}^{*}$ represent the binary strings of n bits and indefinite lengths, respectively, and $\epsilon$ represents an empty string. A set of strings of length $\left|M\right|$ represented as $P\stackrel{128}{\to }\left(P\left[1\right]\parallel P\left[2\right]\parallel \cdots \parallel P\left[m-r\right]\parallel \cdots \parallel P\left[m\right]\right)$ ($P\in {\left\{0,1\right\}}^{*}$), indicating that the string P is divided into m blocks with a block-length of 128 bits, and $0^r$ is employed to represent a sequence of r zero characters. Representing the first bits of the string, $P\in {\left\{0,1\right\}}^{\ast }$ as $ms{b}_a\left(P\right)$. Furthermore, $\left|P\left[i\right]\right|=128$ when $1\le i\le m-1$, and $\left|P\left[i\right]\right|\le 128$ when $i=m$. Thus, when the processed data’s length is not a multiple of the 128-bit packet’s length, it must be padded according to the following rules, referred to as

$$\underset{\_}{P}=pa{d}_{128}\left(P\right)\leftarrow \{\begin{array}{cc}P\parallel 1\parallel 0^{128-1-\left(\left|P\right|\mathrm{mod}128\right)}& if\left|P\right|>0\\ \epsilon & if\left|P\right|=0\end{array}$$

(1)

The AES-OTR algorithm’s encryption authentication part is $E\left(K,N,AD,M\right)=\left(C,Tag\right)$, corresponding to ${\left\{0,1\right\}}^k\times {\left\{0,1\right\}}^n\times {\left\{0,1\right\}}^{\ast }\times {\left\{0,1\right\}}^{\ast }\to {\left\{0,1\right\}}^{\ast }\times {\left\{0,1\right\}}^t$, and k represents the size of the key K; n represents the size of the public message code N (Nonce); t represents the size of the generated Tag; and AD, M, and C represent the variable length’s associated with data, plaintext, and ciphertext, respectively. The decryption and verification part can be expressed as $D\left(K,N,AD,C,T\right)=\left(M,\perp \right)$ if the verification is successful, where the plaintext M is output; otherwise, the output $\perp$ shows that the verification fails.

2.2. Plaintext Encryption

Assuming an n-variable encrypted Boolean function $E_k:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, an authentication encryption scheme based on an OTR operation mode is denoted by $OTR\left[E,\tau \right]$, and AES-OTR’s encryption and decryption functions are represented as $OTR-{\epsilon }_{E,\tau }$ and $OTR-{\epsilon }_{D,\tau }$, respectively. The plaintext and ciphertext are firstly processed in two blocks when encrypting and decrypting after two rounds of Feistel permutation, and different input masks are employed in each round’s underlying function. Figure 1 and Figure 2 show the encryption-processing procedures for the first m − 1 blocks and the m-th block, respectively, assuming that m plaintext blocks are processed.

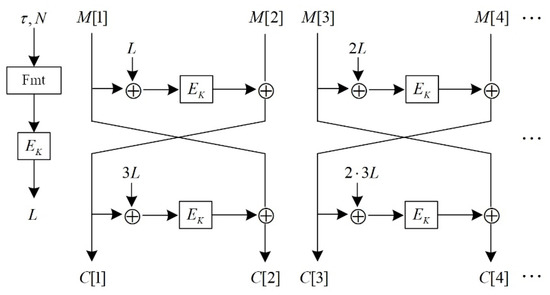
Figure 1. AES-OTR algorithm handles plaintext blocks other than the last block.

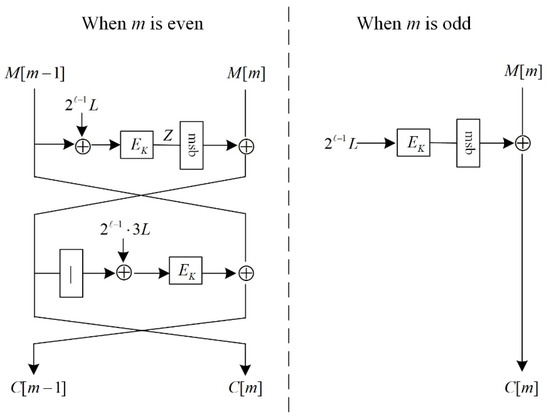
Figure 2. AES-OTR processing the last plaintext block.

The generation of the parameter L in the process can be expressed as $E_k\left(Format\left(\tau ,N\right)\right)\to L$. It is crucial to distinguish between odd-numbered and even-numbered blocks since the plaintext is to be grouped in pairs. If the plaintext pair of the encrypted pair of odd-numbered and even-numbered blocks is represented as $M\stackrel{128}{\to }\left(M\left[1\right]\parallel M\left[2\right]\parallel \cdots \parallel M[\ell ]\right)$, then for $i<\ell$, after encryption processing, the plaintext pair $M\left[i\right]=\left(M\left[2i-1\right]\parallel M\left[2i\right]\right)$ of the i-th pair of odd-numbered and even-numbered blocks can be expressed as

$$\{\begin{array}{l}C\left[2i-1\right]=E_k\left(2^{i-1}L\oplus M\left[2i-1\right]\oplus M\left[2i\right]\right)\\ C\left[2i\right]=E_k\left(2^{i-1}3L\oplus C\left[2i-1\right]\oplus M\left[2i-1\right]\right)\end{array}$$

(2)

It is essential to judge the parity of the last plaintext block’s index number m when processing the last plaintext block so that different structures are employed for encryption processing. Figure 2 shows the schematic diagram. According to the definition of reference [31], the specific expression of the multiple function 2X is as follows:

$$2X=\{\begin{array}{cc}X\ll 1& if ms{b}_1\left(X\right)=0\\ \left(X\ll 1\right)\oplus 0^{120}10000111& if ms{b}_1\left(X\right)=1\end{array}$$

(3)

where $X\ll 1$ represents the left cyclic shift of 1 bit of string X.

2.3. Associated Data Processing

When AES-OTR processes the associated data, it first divides the associated data into 128-bit blocks, represented as $AD\stackrel{128}{\to }\left(AD\left[1\right]\parallel AD\left[2\right]\parallel \cdots \parallel AD\left[a\right]\right)$, and $A{D}_i$ represents the i-th associated data block. When the last block is less than 128 bits, it must be padded to 128 bits, which is expressed as $\underset{\_}{A{D}_a}$ or $pa{d}_{128}\left(A{D}_i\right)$. AES-OTR employs both parallel and serial structures to process the associated data and finally generate TA. Figure 3 and Figure 4 show the structure diagrams.

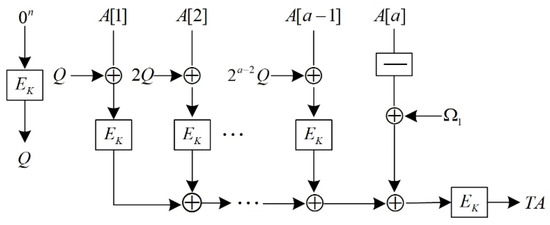
Figure 3. AES-OTR processes the associated data in parallel.

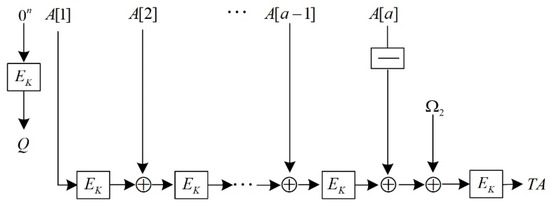
Figure 4. AES-OTR processes the associated data in serial.

As shown in Figure 3, according to whether the last associated data block needs to be padded, the value of the input mask ${\Omega }_1$ is as follows:

$${\Omega }_1=\{\begin{array}{cc}{2}^{a-1}3Q& when\left|A\left[a\right]\right|\ne 128\\ 2^{a-1}{3}^{2}Q& when\left|A\left[a\right]\right|=128\end{array}$$

(4)

As shown in Figure 4, according to whether the last associated data block needs to be padded, the value of the input mask ${\Omega }_2$ is as follows:

$${\Omega }_2=\{\begin{array}{cc}2Q& when\left|A\left[a\right]\right|\ne 128\\ 4Q& when\left|A\left[a\right]\right|=128\end{array}$$

(5)

2.4. Tag Generation Process

Figure 5 shows the tag generation process. The intermediate value TE is obtained by employing the input mask to encrypt the checksum, and then the XOR operation is performed using the TA obtained in the associated data processing; finally, the Tag is obtained to complete the authentication. The checksum’s expression in the process is related to the parity of the plaintext block m. When m is an even number,

$$\{\begin{array}{l}\Sigma =M\left[2\right]\oplus M\left[4\right]\oplus \cdots \oplus M\left[m-2\right]\oplus Z\oplus C\left[m\right]\\ Z\leftarrow E\left(L\oplus M\left[m-1\right]\right)\\ L^{\ast }=2^{l-1}L\oplus \delta \end{array}$$

(6)

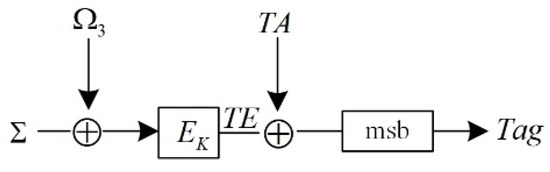
Figure 5. The generation process of AES-OTR’s Tag.

When m is odd,

$$\{\begin{array}{l}\Sigma =M\left[2\right]\oplus M\left[4\right]\oplus \cdots M\left[m-1\right]\oplus C\left[m\right]\\ L^{\ast }=2^{l-1}L\end{array}$$

(7)

As shown in Figure 5, according to whether the last plaintext block needs to be padded, the value of the input mask ${\Omega }_3$ is as follows:

$${\Omega }_3=\{\begin{array}{cc}{3}^2{L}^{\ast }& when\left|M\left[m\right]\right|\ne 128\\ 7L^{\ast }& when\left|M\left[m\right]\right|=128\end{array}$$

(8)

3. Collision Forgery Attack Based on Quantum Computing

For the collision forgery attack under quantum computing for the AES-OTR cryptographic algorithm, it is crucial to first construct a periodic function that satisfies the Simon assumption according to the cryptographic algorithm’s structural characteristics, and then employ the Simon algorithm to search and solve to obtain s, and realize the collision forgery attack after recovering the period. Algorithm 1 shows the analysis idea of this study. This section explains the qubit, Hadamard transform, $U_f$ transform, quantum parallelism, and Simon quantum algorithm in turn.

Algorithm 1 Collision Forgery Attack on AES-OTR Algorithm under Quantum Computing

1: Investigating the two structural characteristics of the authentication encryption algorithm AES-OTR serial and parallel processing of the associated data, and forging the associated data; 2: Determining the periodic function f of the associated data; $3:\mathrm{Solving}\mathrm{the}\mathrm{period},s,\mathrm{using}\mathrm{the}\mathrm{Simon}\mathrm{quantum}\mathrm{algorithm}\mathrm{so}\mathrm{that}f\left(x\oplus s\right)=f\left(x\right)$; 4: The two groups of the associated data A and B are processed, and the generated authentication tag $Ta{g}_A$$\mathrm{and}Ta{g}_B$$\mathrm{are}\mathrm{computed},\mathrm{where}B=A\oplus s$$,\mathrm{the}\mathrm{resulting}\mathrm{collision}\mathrm{is}Ta{g}_B=Ta{g}_A$, and the forgery attack is completed.

3.1. Qubit

The classical bit is the fundamental unit of classical computation, with a certain 0 or 1, representing a low level and high level, respectively. Qubits, unlike classical bits, are indeterminate. The superposition state of the qubit $|\psi ⟩$ is the squared probability $|0⟩$ of $\alpha$ plus the squared probability $|1⟩$ of $\beta$ that can be represented by a linear combination as $|\psi ⟩=\alpha |0⟩+\beta |1⟩=\left[\begin{array}{cc}\alpha & \beta \end{array}\right]$. Where, $\alpha$ and $\beta$ are complex numbers, and ${\alpha }^2+{\beta }^2=1$.

3.2. Hadamard Transform

The quantum logic gate circuit, the single-quantum Hadamard gate converts $|0⟩$ into $|+⟩$ and $|1⟩$ into $|-⟩$$|-⟩$ in the quantum logic gate circuit, which can be expressed as $H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$. Each qubit is transformed between $|0⟩$ and $|+⟩$ and between $|1⟩$ and $|-⟩$ for multi-qubit Hadamard gates. This n-bit Hadamard gate can be represented by a matrix as

$$H^{\otimes n}|y⟩=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\otimes \cdots \otimes \frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]=2^{-\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle {\sum }_{x\in {\left\{0,1\right\}}^n}{(-1)}^{x\cdot y}|x⟩}$$

(9)

where $\otimes$ is the tensor product and $\cdot$ is the inner product.

3.3. Transform and Quantum Parallelism

If $|x⟩$ is the n-qubit data register, $|y⟩$ is the n-qubit destination register. Defining an n-variable encrypted Boolean function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, when the adversary computes f(x), it is equivalent to applying $U_f$ transformation to $|x⟩|y⟩$, which can be expressed as $U_f|x⟩|y⟩=|x⟩|f(x)\oplus y⟩$. Similarly, when the adversary applies the $U_f$ transformation to the input superposition state ${\displaystyle {\sum }_{x,y}{\lambda }_{x,y}|x⟩}|y⟩$, the resulting output superposition state is

$$U_f{\displaystyle {\sum }_{x,y}{\lambda }_{x,y}|x⟩|y⟩={\displaystyle {\sum }_{x,y}{\lambda }_{x,y}|x⟩|f(x)\oplus y⟩}}$$

(10)

Thus, the quantum computer can simultaneously realize the mapping of different x values to f(x) through one $U_f$ transformation; that is, quantum parallelism is realized.

3.4. Simon Quantum Algorithm

Given an n-variable Boolean function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, for any $(x,y)\in {\left\{0,1\right\}}^n$, there is a nontrivial period s, such that $f(x)=f(y)\iff x\oplus y=\left\{0^n,s\right\}$, where $x\ne y$, then how to solve the value of s is the Simon problem.

However, the condition of the function f in the Simon problem is rather harsh, and according to [32], the Simon assumption’s condition can usually be relaxed appropriately. For an n-variable Boolean function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, it is generally assumed that for any $x\in {\left\{0,1\right\}}^n$, there is always a $s\in {\left\{0,1\right\}}^n$ such that $f(x\oplus s)=f(x)$. Under these conditions, this study completes the construction of the periodic function f, so that the collision forgery attack under the AES-OTR algorithm’s quantum computing is investigated.

The Simon algorithm, as the simplest algorithm for determining quantum periods, queries the relevant cryptosystem’s quantum superposition state in the form of $|x⟩|0⟩\mapsto |x⟩|f(x)⟩$. Through $O\left(n\right)$ sub-quantum query, the function’s nontrivial period s can be searched for, while the traditional query approach’s complexity is $O\left({\sqrt{2}}^n\right)$. Simon’s algorithm achieves an exponential speedup compared to traditional approaches. The details of Simon’s algorithm(Algorithm 2) are shown below.

Algorithm 2 Simon Algorithm

$\mathrm{Set}f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ $\mathrm{Input}:\begin{array}{ccc}n,& U_f:& |x⟩|0⟩\mapsto |x⟩|f(x)⟩\end{array}$ $\mathrm{Output}:\begin{array}{cc}y,& y\cdot s=0\end{array}$ 1: Initializing the state of the quantum registers of the two n-dimensional vectors to ${|0⟩}^n{|0⟩}^n$; 2: Applying the Hadamard transform into the first register to obtain the superposition state: $2^{-\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle {\sum }_{x\in {\left\{0,1\right\}}^n}|x⟩|0⟩}$; 3: Applying the $U_f$ transformation to the superposition state in the previous step to obtain $2^{-\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle {\sum }_{x\in {\left\{0,1\right\}}^n}|x⟩|f(x)⟩}$; 4: If f(z) is obtained by measuring the second register, the first register will have the following collision: $\frac{1}{\sqrt{2}}\left(|z⟩+|z\oplus s⟩\right)$; 5: Performing the Hadamard transform on the first n qubits again to obtain $2^{-\raisebox{1ex}{$(n+1)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\displaystyle {\sum }_{y\in {\left\{0,1\right\}}^n}\left[{\left(-1\right)}^{y\cdot z}\left(1+{\left(-1\right)}^{y\cdot s}\right)\right]}|y⟩$; 6: Repeating the above steps n − 1 times to obtain n − 1 linear equations, solve the equation system, and obtain the nontrivial period s.

4. Construction of the Collision Form of AES-OTR

4.1. Collision Form When Processing AD Parallelly

Figure 6 shows the process of constructing a collision form for parallel processing of the associated data. First, it is assumed that there is an existing set of associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel A\left[2\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$. Since the attack approach proposed in this study has nothing to do with whether the last associated data block needs to be filled, for the convenience of explanation, the following assumes that the last associated data block is exactly 128 bits; i.e., it has not been padded. When processing the associated data in parallel, set the intermediate variables obtained after the first a−1-linked data packets are encrypted with AES to be $X\left[1\right]\parallel X\left[2\right]\parallel \cdots \parallel X\left[a-1\right]$ in turn; then, the intermediate variables and output expressions of the associated data processing are as follows:

$$\{\begin{array}{l}X\left[1\right]=E_k\left(A\left[1\right]\oplus Q\right)\\ X\left[2\right]=E_k\left(A\left[2\right]\oplus 2Q\right)\\ \begin{array}{ccc}& ⋮& \end{array}\\ X\left[a-1\right]=E_k\left(A\left[a-1\right]\oplus 2^{a-2}Q\right)\end{array}$$

(11)

$$T{A}_A=E_k\left(X\left[1\right]\oplus X\left[2\right]\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)$$

(12)

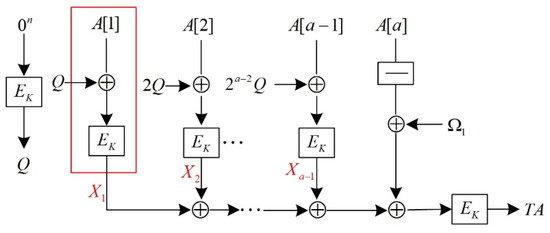
Figure 6. Constructing a collision form for parallel processing of the associated data.

As shown in the above formula, to output the final TA value, the intermediate variable $X\left[i\right]\left(1\le i\le a-1\right)$ must undergo a series of XOR operations in a linear form. Furthermore, under the same set of K and Nonce, the output E_k is only related to the input associated data blocks. Thus, a set of collisions can be constructed by conducting a suitable linear transformation on the associated data blocks so that the final input value $E_k$ remains unchanged.

When the first two associated data blocks $A\left[1\right]$ and $A\left[2\right]$ are employed as forged objects, let the forged two new associated data blocks be $B\left[1\right]$ and $B\left[2\right]$, where $B\left[1\right]=A\left[2\right]\oplus 3Q$ and $B\left[2\right]=A\left[1\right]\oplus 3Q$; then, the forged block of associated data is $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$. The intermediate variables obtained are $Y\left[1\right]\parallel Y\left[2\right]\parallel \cdots \parallel X\left[a-1\right]$ after the first a − 1-associated data blocks are encrypted with AES. Thus, after processing the first two associated data blocks, the obtained intermediate variable expressions are as follows:

$$\begin{array}{ll}Y\left[1\right]& =E_k\left(B\left[1\right]\oplus Q\right)\\ & =E_k\left(A\left[2\right]\oplus 3Q\oplus Q\right)\\ & =E_k\left(A\left[2\right]\oplus Q\right)\\ & =X\left[2\right]\end{array}$$

(13)

$$\begin{array}{ll}Y\left[2\right]& =E_k\left(B\left[2\right]\oplus Q\right)\\ & =E_k\left(A\left[1\right]\oplus 3Q\oplus Q\right)\\ & =E_k\left(A\left[1\right]\oplus Q\right)\\ & =X\left[1\right]\end{array}$$

(14)

Therefore, after the associated data processing, there is the following output:

$$\begin{array}{ll}T{A}_B& =E_k\left(Y\left[1\right]\oplus Y\left[2\right]\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ & =E_k\left(X\left[2\right]\oplus X\left[1\right]\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ & =T{A}_A\end{array}$$

(15)

When generating the Tag, $Tag=msb\left(TA\oplus TE\right)$; thus, for the associated data A there is

$$\begin{array}{ll}Ta{g}_A& =msb\left(T{A}_A\oplus TE\right)\\ & =msb\left(T{A}_B\oplus TE\right)\\ & =Ta{g}_B\end{array}$$

(16)

Thus, for $Ta{g}_A=Ta{g}_B$, forgery verification is completed. We can further extend the above approach. For a set of known associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel \cdots \parallel A\left[p\right]\parallel \cdots \parallel A\left[q\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$, process the first a−1-associated data blocks, and the obtained intermediate variables and final output are recorded as follows:

$$\{\begin{array}{l}X\left[1\right]=E_k\left(A\left[1\right]\oplus Q\right)\\ \begin{array}{ccc}& ⋮& \end{array}\\ X\left[p\right]=E_k\left(A\left[p\right]\oplus 2^{p-1}Q\right)\\ \begin{array}{ccc}& ⋮& \end{array}\\ X\left[q\right]=E_k\left(A\left[q\right]\oplus 2^{q-1}Q\right)\\ \begin{array}{ccc}& ⋮& \end{array}\\ X\left[a-1\right]=E_k\left(A\left[a-1\right]\oplus 2^{a-2}Q\right)\end{array}$$

(17)

$$T{A}_A=E_k\left(X\left[1\right]\oplus \cdots \oplus X\left[p\right]\oplus \cdots \oplus X\left[q\right]\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)$$

(18)

Arbitrarily selecting two associated data blocks $A\left[p\right]$ and $A\left[q\right]$ $\left(1\le p<q\le a-1\right)$ as the forgery objects, and setting the forged two new associated data blocks as $B\left[p\right]$ and $B\left[q\right]$, where $B\left[p\right]=A\left[q\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q$ and $B\left[q\right]=A\left[p\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q$, then the associated data’s re-forged block can be expressed as $B\stackrel{128}{\to }\left[A\left[1\right]\parallel \cdots \parallel B\left[p\right]\parallel \cdots \parallel B\left[q\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$. After the first a−1-associated data blocks are encrypted with AES, the intermediate variables obtained are in turn $X\left[1\right]\parallel \cdots \parallel Y\left[p\right]\parallel \cdots \parallel Y\left[q\right]\cdots X\left[a-1\right]$. Thus, after processing the two associated data blocks of $B\left[p\right]$ and $B\left[q\right]$, the obtained intermediate variable expression is as follows:

$$\begin{array}{ll}Y\left[p\right]& =E_k\left(B\left[p\right]\oplus 2^{p-1}Q\right)\\ & =E_k\left(A\left[q\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q\oplus 2^{p-1}Q\right)\\ & =E_k\left(A\left[q\right]\oplus 2^{q-1}Q\right)\\ & =X\left[q\right]\end{array}$$

(19)

$$\begin{array}{ll}Y\left[q\right]& =E_k\left(B\left[q\right]\oplus 2^{q-1}Q\right)\\ & =E_k\left(A\left[p\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q\oplus 2^{q-1}Q\right)\\ & =E_k\left(A\left[p\right]\oplus 2^{p-1}Q\right)\\ & =X\left[p\right]\end{array}$$

(20)

Therefore, after the associated data processing, there is the following output:

$$\begin{array}{ll}T{A}_B& =E_k\left(X\left[1\right]\oplus \cdots \oplus Y\left[p\right]\oplus \cdots \oplus Y\left[q\right]\oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ & =E_k\left(X\left[1\right]\oplus \cdots \oplus X\left[q\right]\oplus \cdots \oplus X\left[p\right]\oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ & =T{A}_A\end{array}$$

(21)

When generating the Tag, $Tag=msb\left(TA\oplus TE\right)$; thus, for the associated data A there is

$$\begin{array}{ll}Ta{g}_A& =msb\left(T{A}_A\oplus TE\right)\\ & =msb\left(T{A}_B\oplus TE\right)\\ & =Ta{g}_B\end{array}$$

(22)

Thus, $Ta{g}_A=Ta{g}_B$, and the same message authentication code is generated; the forgery verification thus is completed. Next, we can implement the collision forgery attack of the AES-OTR algorithm under quantum computing using the two sets of collision pairs arbitrarily forged above when processing the associated data in parallel.

4.2. Collision Form When Processing AD Serially

Figure 7 shows the process of constructing a collision form for serial processing of the associated data. It is assumed that a set of associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel A\left[2\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$ is known to the adversary for the structural analysis when serially processing the associated data, as described in Section 4.1. Denoting the intermediate variables before the AES encryption processing operation of the first a-associated data block as $X\left[1\right]\parallel X\left[2\right]\parallel \cdots \parallel X\left[a-1\right]\parallel X\left[a\right]$ in turn, then the output expressions of the intermediate variables and associated data processing are as follows:

$$\{\begin{array}{l}X\left[1\right]=A\left[1\right]\\ X\left[2\right]=E_k\left(X\left[1\right]\right)\oplus A\left[2\right]\\ X\left[3\right]=E_k\left(X\left[2\right]\right)\oplus A\left[3\right]\\ \begin{array}{ccc}& ⋮& \end{array}\\ X\left[a-1\right]=E_k\left(X\left[a-2\right]\right)\oplus A\left[a-1\right]\\ X\left[a\right]=E_k\left(X\left[a-1\right]\right)\oplus A\left[a\right]\oplus 4Q\end{array}$$

(23)

$$T{A}_A=E_k\left(X\left[a\right]\right)$$

(24)

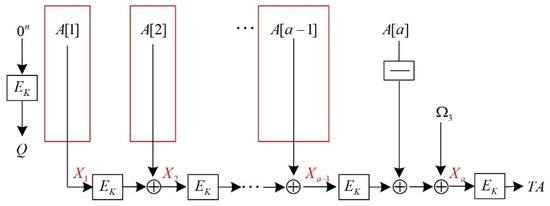
Figure 7. Constructing a collision form for serial processing of associated data.

As shown in the above formula, when serially processing the associated data, the final output value TA is only related to the intermediate variable $X\left[a\right]$; thus, the associated data blocks can be appropriately transformed during forgery so that the intermediate variable $X\left[a-1\right]$ and the associated data block $A\left[a\right]$ are unaffected. Furthermore, under the same set of K and Nonce, the output $E_k$ is only related to the input-associated data blocks. Thus, by appropriately transforming the associated data blocks, the input value of the final $E_k$ can be kept unchanged, thereby constructing a set of collisions.

If starting from the third intermediate variable as the attack target, setting the intermediate variables before each associated data block performs the AES encryption processing operation as $Y\left[1\right]\parallel Y\left[2\right]\parallel \cdots \parallel Y\left[a-1\right]$ in turn, and the forged new block of associated data is $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel B\left[a-1\right]\right]$, where

$$\{\begin{array}{l}B\left[1\right]=X\left[2\right]=E_k\left(A\left[1\right]\right)\oplus A\left[2\right]\\ B\left[2\right]=A\left[3\right]\\ B\left[3\right]=A\left[4\right]\\ \begin{array}{ccc}& ⋮& \end{array}\\ B\left[a-1\right]=A\left[a\right]\oplus 4Q\end{array}$$

(25)

Thus, after processing the forged new associated data blocks, the obtained intermediate variables and the final output expression are as follows:

$$\{\begin{array}{l}Y\left[1\right]=B\left[1\right]\\ Y\left[2\right]=E_k\left(B\left[1\right]\right)\oplus B\left[2\right]=E_k\left(E_k\left(A\left[1\right]\right)\oplus A\left[2\right]\right)\oplus B\left[2\right]\\ =E_k\left(X\left[2\right]\right)\oplus A\left[3\right]=X\left[3\right]\\ Y\left[3\right]=E_k\left(Y\left[2\right]\right)\oplus B\left[3\right]=E_k\left(X\left[3\right]\right)\oplus A\left[4\right]=X\left[4\right]\\ \begin{array}{ccc}& ⋮& \end{array}\\ Y\left[a-1\right]=E_k\left(X\left[a-1\right]\right)\oplus A\left[a\right]\oplus 4Q=X\left[a\right]\end{array}$$

(26)

$$T{A}_B=E_k\left(Y\left[a-1\right]\right)=E_k\left(X\left[a\right]\right)=T{A}_A$$

(27)

When generating the Tag, $Tag=msb\left(TA\oplus TE\right)$; thus, for the associated data A there is

$$\begin{array}{ll}Ta{g}_A& =msb\left(T{A}_A\oplus TE\right)\\ & =msb\left(T{A}_B\oplus TE\right)\\ & =Ta{g}_B\end{array}$$

(28)

Therefore, $Ta{g}_A=Ta{g}_B$, and forgery verification is completed. We can further extend the above approach. For a set of known associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel \cdots \parallel A\left[p\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$, starting from the p-th intermediate variable as the attack target, and setting the intermediate variables before each associated data block performs the AES encryption processing operation as $Y\left[1\right]\parallel Y\left[2\right]\parallel \cdots \parallel Y\left[a-p+2\right]$, where $\left(2\le p\le a\right)$, and the associated data’s forged new set is $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel B\left[a-p+2\right]\right]$, where

$$\{\begin{array}{l}B\left[1\right]=X\left[p-1\right]=E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]\\ B\left[2\right]=A\left[p\right]\\ B\left[3\right]=A\left[p+1\right]\\ \begin{array}{ccc}& ⋮& \end{array}\\ B\left[a-p+2\right]=A\left[a\right]\oplus 4Q\end{array}$$

(29)

The corresponding intermediate variables and final output expressions are as follows:

$$\{\begin{array}{l}Y\left[1\right]=B\left[1\right]\\ Y\left[2\right]=E_k\left(B\left[1\right]\right)\oplus B\left[2\right]=E_k\left(E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]\right)\oplus B\left[2\right]\\ =E_k\left(X\left[p-1\right]\right)\oplus A\left[p\right]=X\left[p\right]\\ Y\left[3\right]=E_k\left(Y\left[2\right]\right)\oplus B\left[3\right]=E_k\left(X\left[p\right]\right)\oplus A\left[p+1\right]=X\left[p+1\right]\\ \begin{array}{ccc}& ⋮& \end{array}\\ Y\left[a-p+2\right]=E_k\left(X\left[a-1\right]\right)\oplus A\left[a\right]\oplus 4Q=X\left[a\right]\end{array}$$

(30)

$$T{A}_B=E_k\left(Y\left[a-p+2\right]\right)=E_k\left(X\left[a\right]\right)=T{A}_A$$

(31)

Similarly, $Ta{g}_A=Ta{g}_B$ can be proven, and the forgery verification can be completed again. Thus, we can achieve the AES-OTR algorithm’s collision forgery attack under quantum computing using the above two blocks of forged collision pairs when serially processing the associated data.

5. Collision Forgery Attack on AES-OTR

Assuming that the encryption oracle machine is represented as $E_k:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$, and $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ is an n-variable Boolean function, the block cipher algorithm $E_k:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ must be employed to complete the function’s construction to obtain a periodic function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ related to the input. Whether the external variable b is introduced or not, the periodic function’s construction primarily has the following two forms:

$$f_1:x\mapsto p\left(\tilde{E}\left(x\right)+\tilde{E}\left(x\oplus s\right)\right)$$

(32)

$$f_2:b,x\mapsto \{\begin{array}{cc}\tilde{E}\left(x\right),& b=0\hfill \\ \tilde{E}\left(x\oplus s\right),& b=1\hfill \end{array}$$

(33)

Among them, $\tilde{E}\left(x\right)$ is a function constructed by the block cipher algorithm $E_k:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$. From the expression, the period in $f_1$ is s, and the period in $f_2$ is $1\parallel s$. The solution of the nontrivial period s is performed using Simon’s quantum algorithm. Figure 8 shows the quantum circuit diagram of Simon’s algorithm.

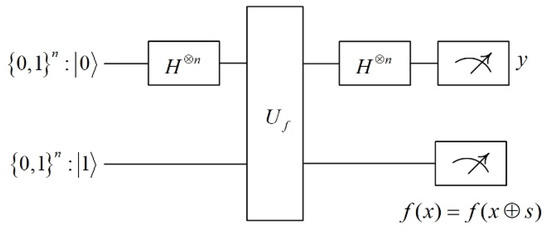
Figure 8. Quantum circuit diagram of Simon’s algorithm.

This section employs the Simon quantum algorithm to perform a collision forgery attack on the AES-OTR authentication encryption algorithm under quantum computing. Thus, we must first construct a periodic function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ that satisfies the Simon problem’s condition. Given a certain set of K and Nonce, we construct $f_N:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n$ using an arbitrary constant $\delta \in {\left\{0,1\right\}}^{128}$. Section 4.1 and Section 4.2 of this study describe the construction of the collision form for processing associated data in parallel and serially, respectively. The following uses parallel processing of associated data as an example to conduct a collision forgery attack on the AES-OTR algorithm under quantum computing.

Assuming an existing set of associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel A\left[2\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$, when two new associated data blocks $B\left[1\right]$ and $B\left[2\right]$ are employed to forge the associated data blocks $A\left[1\right]$ and $A\left[2\right]$, respectively, the forged new associated data is represented as $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$, where $B\left[1\right]=A\left[2\right]\oplus 3Q$ and $B\left[2\right]=A\left[1\right]\oplus 3Q$. Then, for the input $x\in {\left\{0,1\right\}}^{128}$, bring it into the process of parallel processing of associated data, there is

$$\begin{array}{l}{f}_N\left(x\right)=E_k\left(x\parallel x\oplus \delta \right)\\ =E_k\left(Y\left[1\right]\oplus Y\left[2\right]\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ =E_k\left(E_k\left(B\left[1\right]\oplus Q\right)\oplus E_k\left(B\left[2\right]\oplus Q\right)\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\\ =E_k\left(E_k\left(A\left[2\right]\oplus Q\right)\oplus E_k\left(A\left[1\right]\oplus Q\right)\oplus \cdots \oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\right)\end{array}$$

(34)

Expanding on this basis, arbitrarily selecting two associated data blocks $A\left[p\right]$ and $A\left[q\right]$ $\left(1\le p<q\le a-1\right)$ as forged objects, and setting the forged two new associated data blocks as $B\left[p\right]$ and $B\left[q\right]$, where $B\left[p\right]=A\left[q\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q$ and $B\left[q\right]=A\left[p\right]\oplus 2^{p-1}Q\oplus 2^{q-1}Q$, then the re-forged block of associated data can be represented as $B\stackrel{128}{\to }\left[A\left[1\right]\parallel \cdots \parallel B\left[p\right]\parallel \cdots \parallel B\left[q\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$. Thus, bringing the input $x\in {\left\{0,1\right\}}^{128}$ into the process of parallel processing of associated data, there is

$$\begin{array}{l}{f}_N\left(x\right)=E_k\left(x\parallel x\oplus \delta \right)\\ =E_k\left(\left(\begin{array}{l}X\left[1\right]\oplus \cdots \oplus Y\left[p\right]\oplus \cdots \oplus Y\left[q\right]\oplus \\ X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\end{array}\right)\right)\\ =E_k\left(\begin{array}{l}X\left[1\right]\oplus \cdots \oplus E_k\left(B\left[p\right]\oplus 2^{p-1}Q\right)\oplus \cdots \\ \oplus E_k\left(B\left[q\right]\oplus 2^{q-1}Q\right)\oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\end{array}\right)\\ =E_k\left(\begin{array}{l}X\left[1\right]\oplus \cdots \oplus E_k\left(A\left[q\right]\oplus 2^{q-1}Q\right)\oplus \cdots \\ \oplus E_k\left(A\left[p\right]\oplus 2^{p-1}Q\right)\oplus X\left[a-1\right]\oplus A\left[a\right]\oplus 2^{a-1}{3}^{2}Q\end{array}\right)\end{array}$$

(35)

According to the construction of the collision form in parallel processing of associated data in Section 4.1, we can find that when $s=\delta \oplus 2^{p-1}Q\oplus 2^{q-1}$ the constructed function $f_N$ satisfies $f_N\left(x\right)=f_N\left(x\oplus s\right)$. Thus, for a certain set of K and Nonce, $\left(x\oplus s\oplus \delta \parallel x\oplus s\right)$ and $\left(x\parallel x\oplus \delta \right)$ will generate the same authentication Tag.

Thus, by using the Simon quantum algorithm to search out the period $s=\delta \oplus 2^{p-1}Q\oplus 2^{q-1}$, the authentication Tag’s forgery can be completed, and the time complexity is close to 1. Therefore, the collision forgery attack on the AES-OTR algorithm is completed under quantum computing. The proposed attack approach’s success rate is analyzed as follows.

For the Simon algorithm with suitable commitments, [33] presents the following theorem:

Theorem 1.

If $\epsilon (f,s)\le p_0<1$, then after cn queries, the Simon quantum algorithm returns s with a probability of $p\ge 1-{\left(2{(\frac{1+p_0}{2})}^c\right)}^n$. Then, when $c\ge \frac{3}{1-p_0}$, there is

$$\begin{array}{ll}p& \ge 1-{\left(2{(\frac{1+p_0}{2})}^c\right)}^n\\ & =1-{\left(2{(1-\frac{1-p_0}{2})}^c\right)}^n\\ & \ge 1-{\left(2e^{-\frac{3}{2}}\right)}^n\approx 1-{0.446}^n\end{array}$$

(36)

Thus, the Simon algorithm computes s with a probability close to 1 when the number of queries is large enough, indicating that the approach is feasible and efficient.

Similarly, the collision forgery attack on the AES-OTR algorithm under quantum computing can be completed again by combining the construction of the collision form when serially processing associated data in Section 4.2. The following uses serial processing of the associated data as an example to conduct a collision forgery attack on the AES-OTR algorithm under quantum computing.

Setting the intermediate variables before each associated data block performs the AES encryption processing operation as $Y\left[1\right]\parallel Y\left[2\right]\parallel \cdots \parallel Y\left[a-1\right]$ in turn, and the forged new block of associated data is $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel B\left[a-1\right]\right]$, where $B\left[1\right]=X\left[2\right]=E_k\left(A\left[1\right]\right)\oplus A\left[2\right]$,$B\left[2\right]=A\left[3\right]$, $B\left[3\right]=A\left[4\right]$, …, and $B\left[a-1\right]=A\left[a\right]\oplus 4Q$. Then, for the input $x\in {\left\{0,1\right\}}^{128}$, bring it into the process of serial processing of the associated data, and due to $Y\left[1\right]=B\left[1\right]$, $\begin{array}{l}Y\left[2\right]=E_k\left(B\left[1\right]\right)\oplus B\left[2\right]=E_k\left(E_k\left(A\left[1\right]\right)\oplus A\left[2\right]\right)\oplus B\left[2\right]\\ =E_k\left(X\left[2\right]\right)\oplus A\left[3\right]=X\left[3\right]\end{array}$,$Y\left[3\right]=X\left[4\right]$, there is

$$f_N\left(x\right)=E_k\left(x\parallel x\oplus \delta \right)=E_k\left(Y\left[a-1\right]\right)=E_k\left(X\left[a-1\right]\oplus A\left[a\right]\oplus 4Q\right)$$

(37)

Expanding on this basis, For a set of known associated data $A\stackrel{128}{\to }\left[A\left[1\right]\parallel \cdots \parallel A\left[p\right]\parallel \cdots \parallel A\left[a-1\right]\parallel A\left[a\right]\right]$, starting from the p-th intermediate variable as the attack target, and setting the intermediate variables before each associated data block performs the AES encryption processing operation as $Y\left[1\right]\parallel Y\left[2\right]\parallel \cdots \parallel Y\left[a-p+2\right]$, where $\left(2\le p\le a\right)$, the associated data’s forged new set is $B\stackrel{128}{\to }\left[B\left[1\right]\parallel B\left[2\right]\parallel \cdots \parallel B\left[a-p+2\right]\right]$, where $B\left[1\right]=X\left[p-1\right]=E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]$, $B\left[2\right]=A\left[p\right]$, $B\left[3\right]=A\left[p+1\right]$, …, $B\left[a-p+2\right]=A\left[a\right]\oplus 4Q$. Thus, bringing the input $x\in {\left\{0,1\right\}}^{128}$ into the process of serial processing of the associated data, due to $Y\left[1\right]=B\left[1\right]$, $Y\left[2\right]=E_k\left(B\left[1\right]\right)\oplus B\left[2\right]=E_k\left(E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]\right)\oplus B\left[2\right]=X\left[p\right]$, $Y\left[3\right]=X\left[p+1\right]$, there is

$$f_N\left(x\right)=E_k\left(x\parallel x\oplus \delta \right)=E_k\left(Y\left[a-p+2\right]\right)=E_k\left(X\left[a-1\right]\right)\oplus A\left[a\right]\oplus 4Q$$

(38)

According to the construction of the collision form in serial processing of associated data in Section 4.2, we can find that when $s=\delta \oplus E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]$ the constructed function $f_N$ satisfies $f_N\left(x\right)=f_N\left(x\oplus s\right)$. Thus, for a certain set of K and Nonce, $\left(x\oplus s\oplus \delta \parallel x\oplus s\right)$ and $\left(x\parallel x\oplus \delta \right)$ will generate the same authentication Tag.

Thus, by using the Simon quantum algorithm to search out the period $s=\delta \oplus E_k\left(X\left[p-2\right]\right)\oplus A\left[p-1\right]$, the authentication Tag’s forgery can be completed, and the time complexity is close to 1. Therefore, the collision forgery attack on the AES-OTR algorithm is completed under quantum computing. Furthermore, when the number of queries is large enough, the Simon algorithm calculates s with a probability close to 1.

For the two structures of parallel and serial processing of associated data, both use the pre-constructed collision form, and then use the Simon quantum algorithm to attack. Therefore, the two methods are more or less the same. However, a detailed analysis reveals that this operation is more efficient and feasible for parallel processing of associated data. When serially processing associated data, more data blocks need to be processed, and the operation is more cumbersome, so the efficiency is not good. This is also the direction we need to improve in the next step. At the same time, it also shows that for the structure of serial processing of associated data, the security is higher during encryption and decryption.

6. Conclusions and Future Work

This study proposes a collision forgery attack on the AES-OTR algorithm under quantum computing by making full use of the relative independence between different modules of the AES-OTR authentication encryption algorithm, the characteristics of parallel and serial structures in associated data processing, and the simplicity of intermediate variable generation. It is demonstrated that the AES-OTR algorithm faces a serious threat when the associated data and Nonce are reused. The periodic function f of the associated data is constructed by analyzing the collision form of the associated data, and is combined with the Simon quantum algorithm to solve the collision period s with a success rate close to 1, so that $f_N\left(x\right)=f_N\left(x\oplus s\right)$; then, when employing the fake associated data to process, the same authentication Tag is generated. The effect of monitoring or tampering is achieved without being discovered by a third party, which has good feasibility and efficiency.

To address the cryptographic crisis in the post-quantum era, current anti-quantum cryptography design and research primarily focus on the cryptographic structure or working mode under the quantum security model, excluding quantum security analysis of instantiated cryptographic algorithms. In this study, the research on collision forgery attacks under quantum computing of AES-OTR helps enrich the security analysis of specific authentication encryption algorithms, thus offering ideas for enhancing the design scheme of related quantum-resistant cryptographic algorithms. The next stage is to develop a polynomial time quantum discriminator with as many rounds as possible. In addition to employing the Simon algorithm to search for the period s, the Grover algorithm can also be combined to enhance the exhaustive search key’s speed to realize the quantum key recovery attack.