Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis
Abstract
1. Introduction
- (1)
- The negative Poisson’s ratio calculation formula of a re-entrant structure with a negative Poisson’s ratio was derived.
- (2)
- The Lagrange equation was used to model the honeycomb base, and a uniform mass matrix was introduced to simplify the calculation.
- (3)
- The vibration level difference was adopted to analyze the vibration isolation performance of the honeycomb base more intuitively, and the finite element COMSOL software was used for the analysis and for verification.
2. The Numerical Modeling
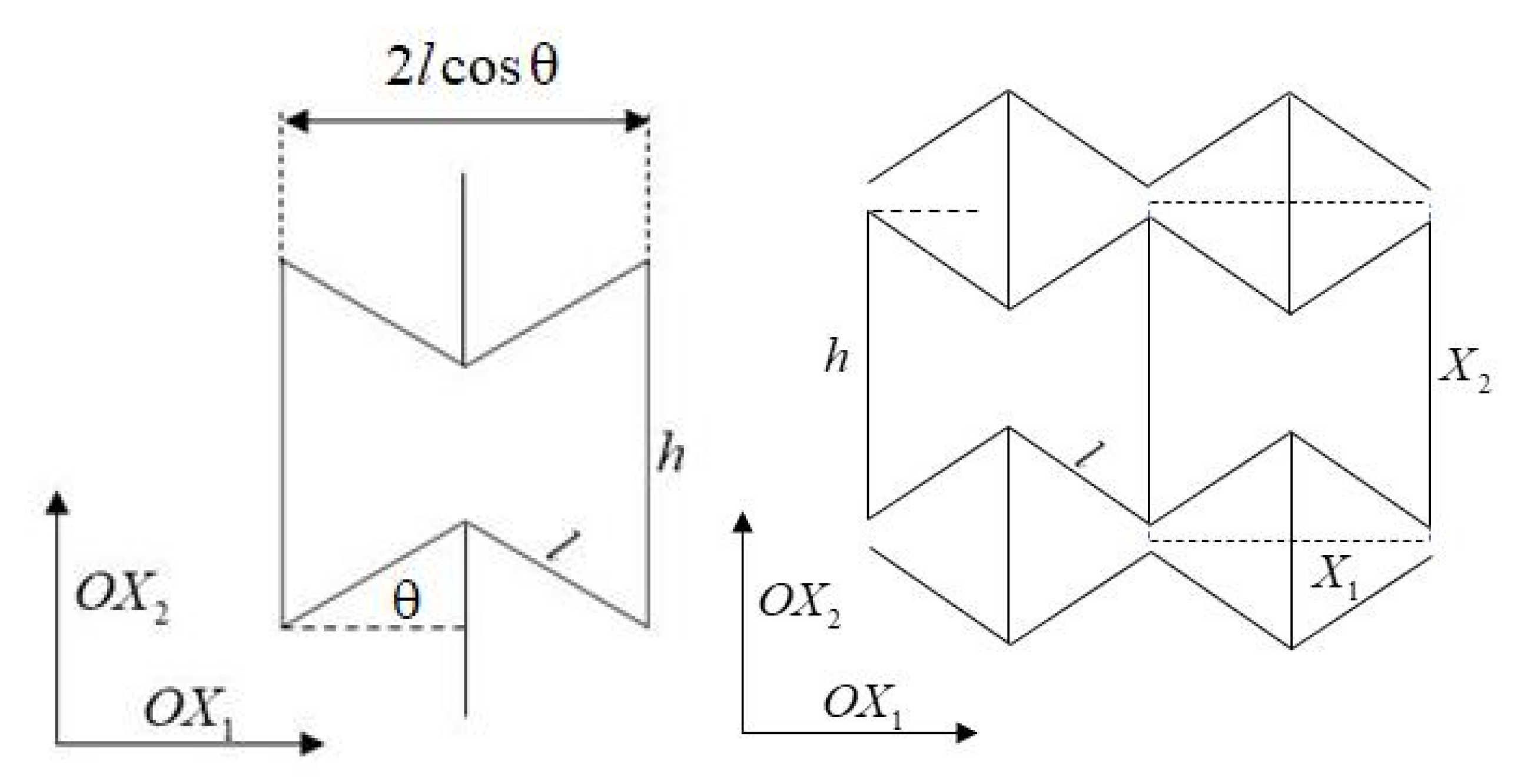
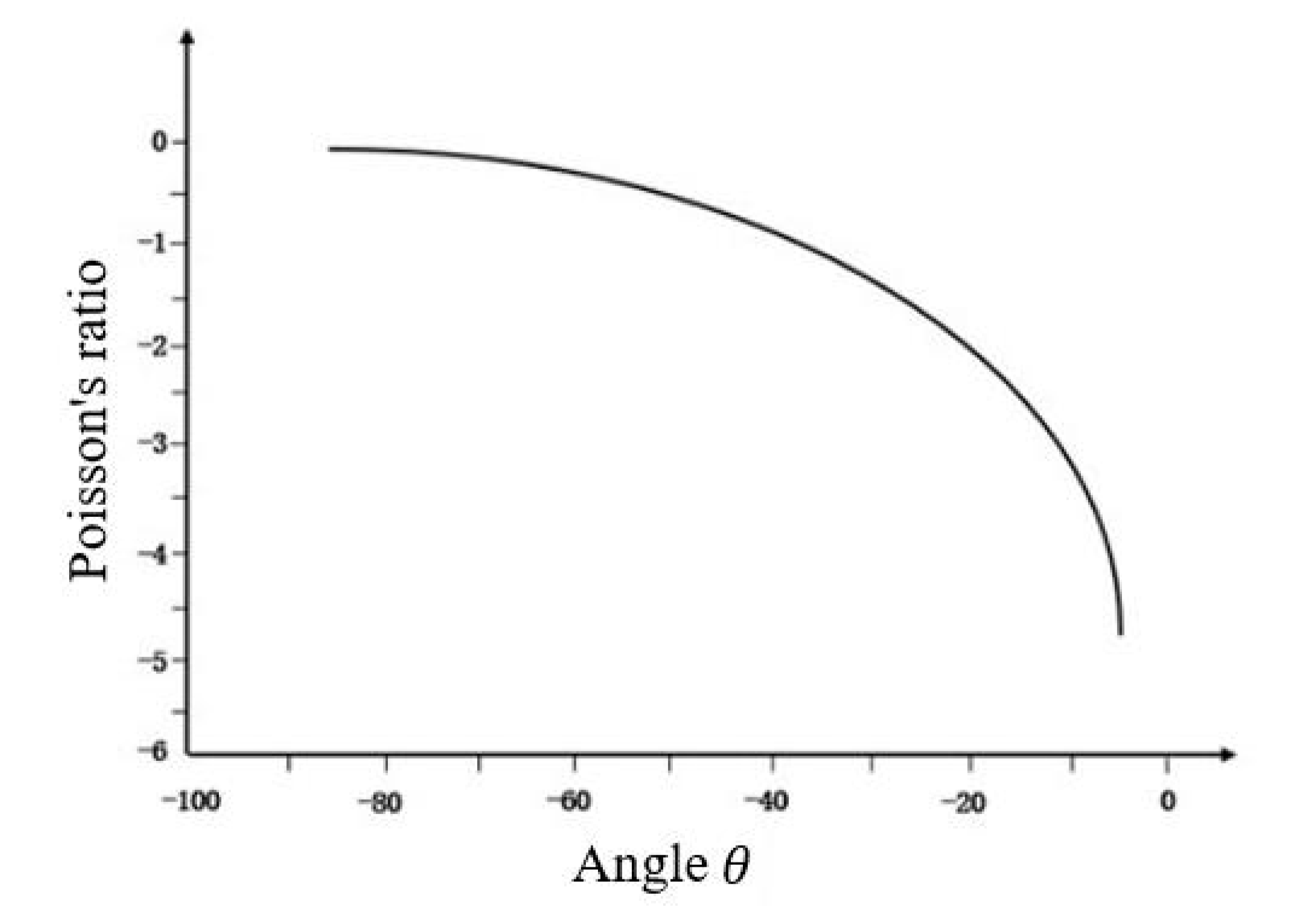
2.1. Theoretical Derivation of Poisson’s Ratio
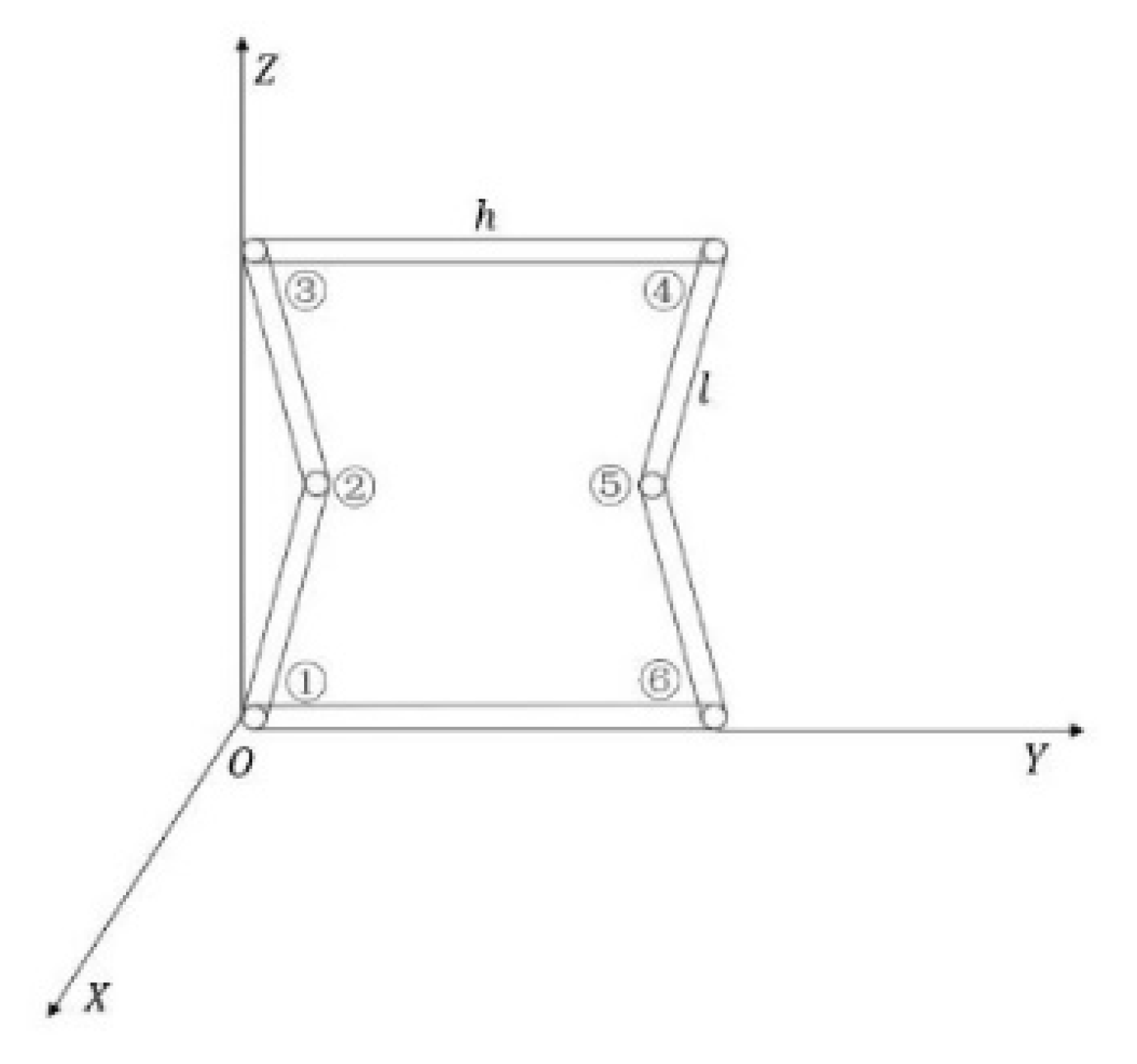
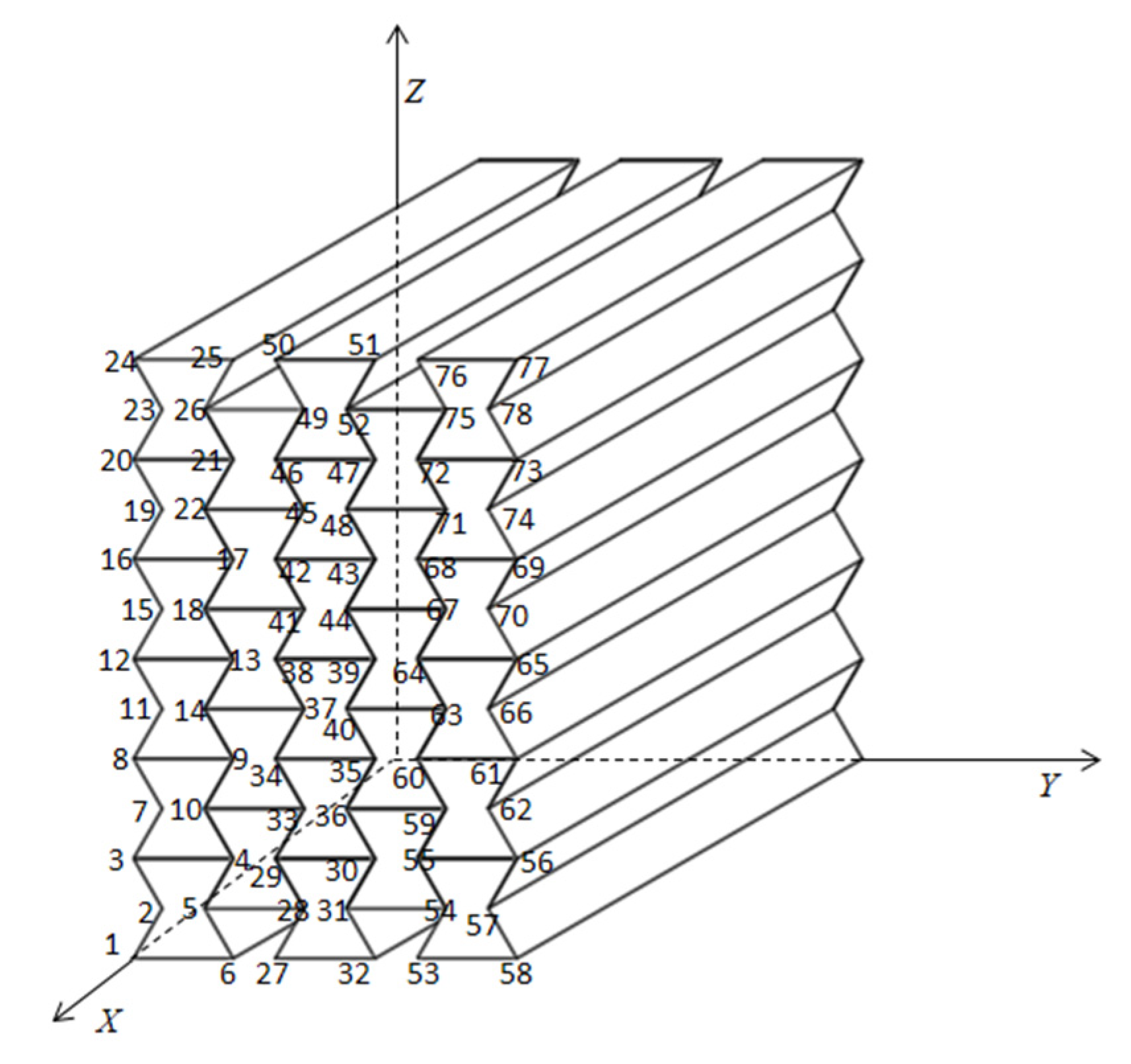
2.2. Honeycomb Base Modeling
3. Numerical Results Analysis
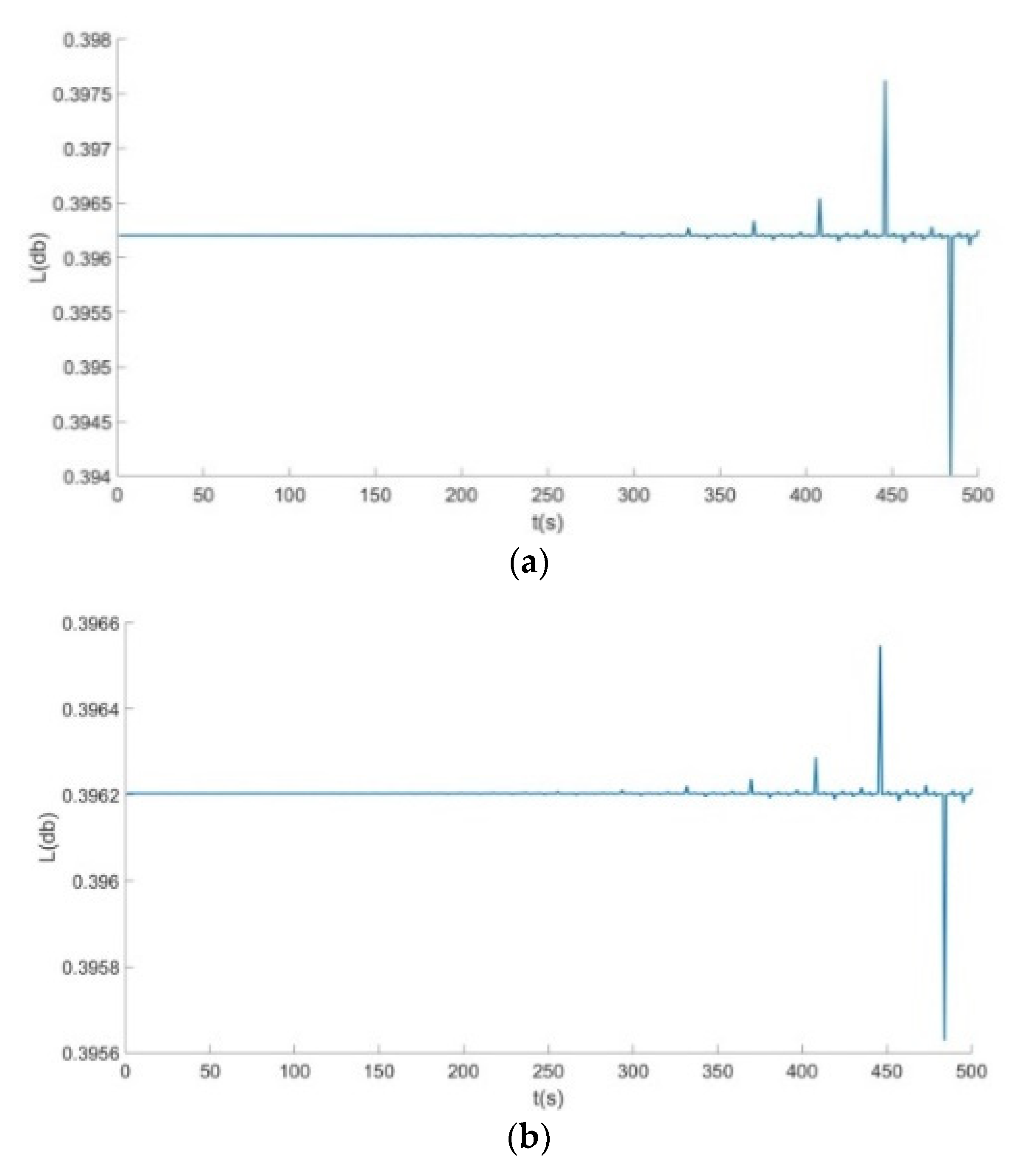
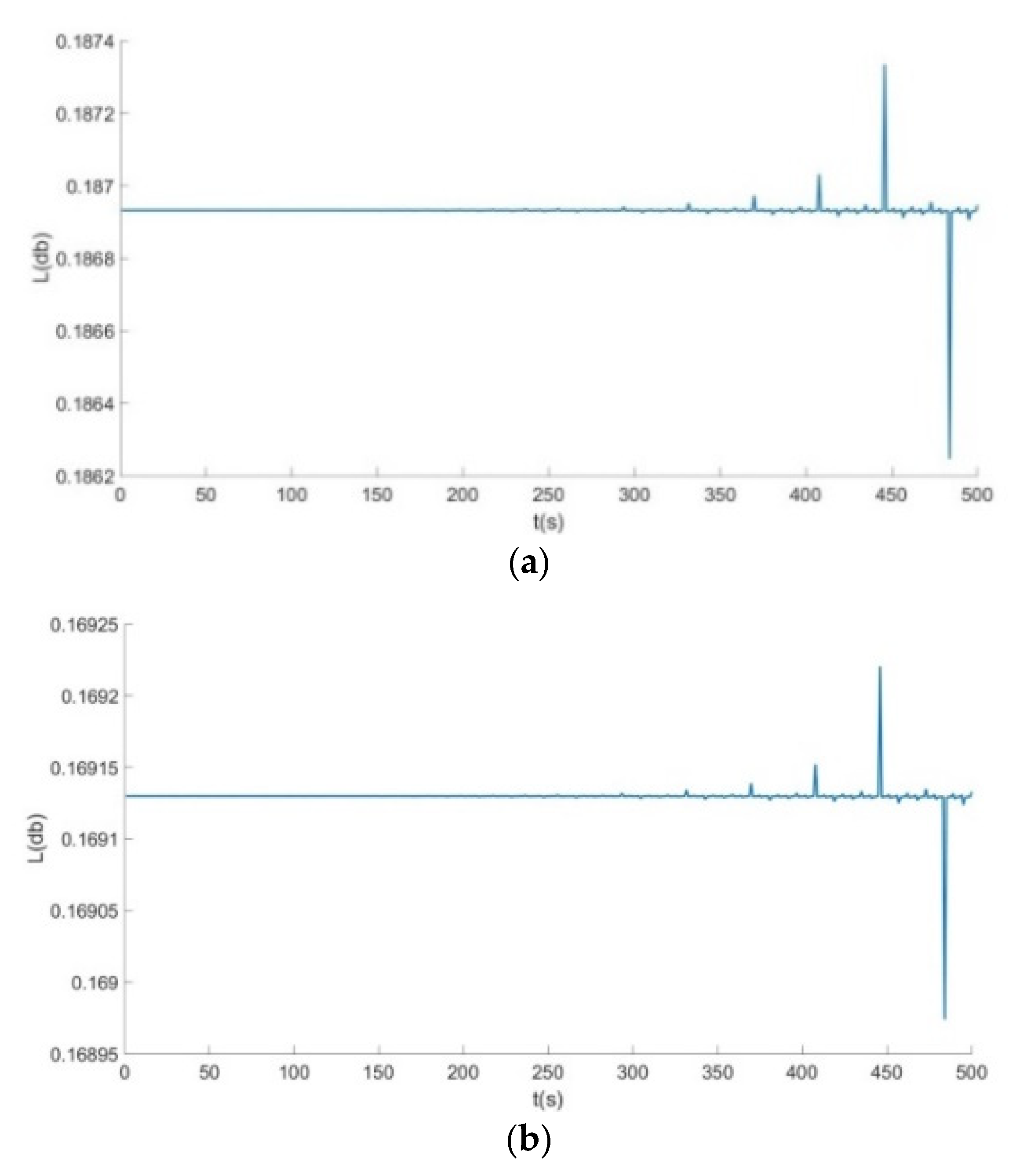
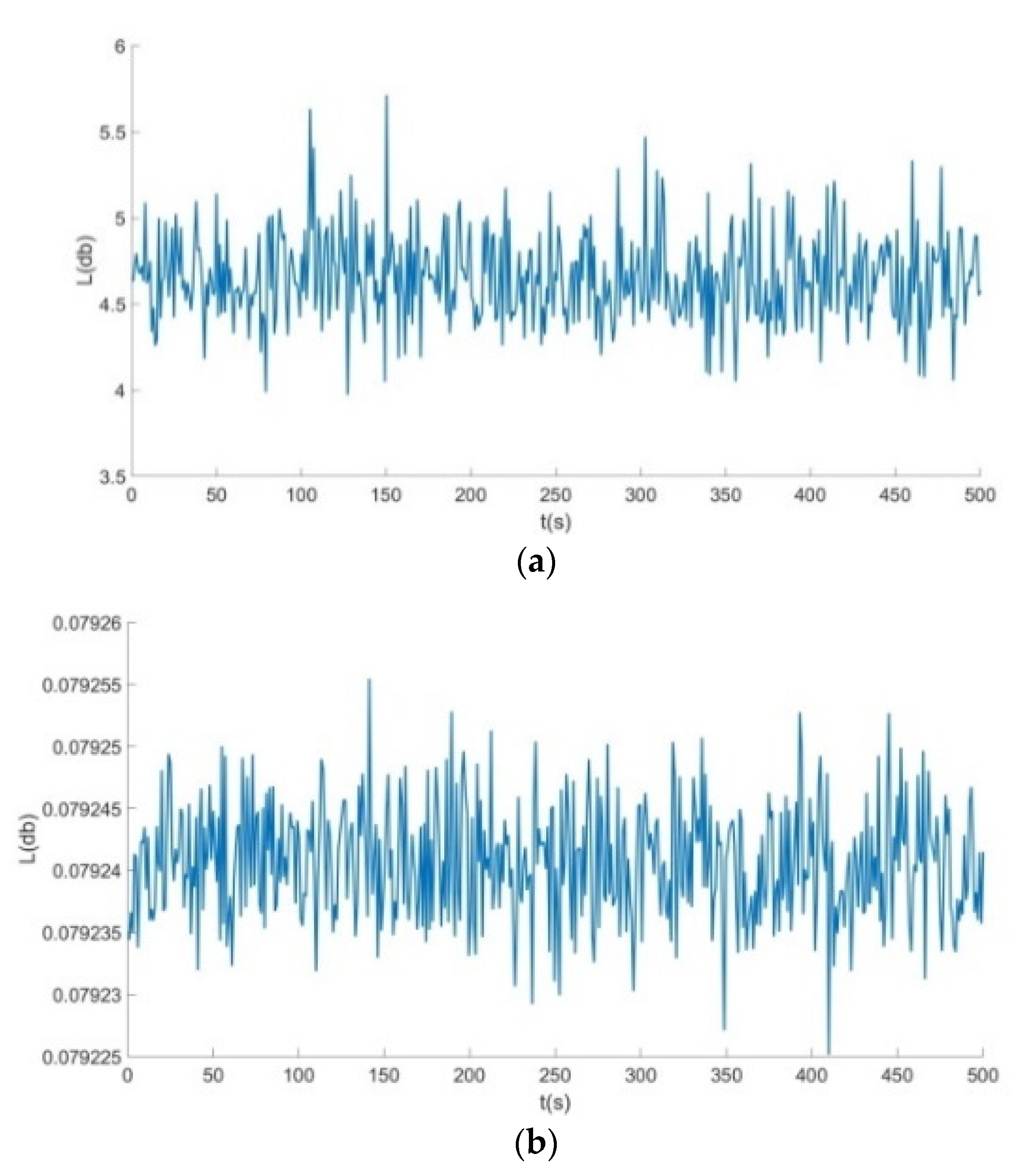
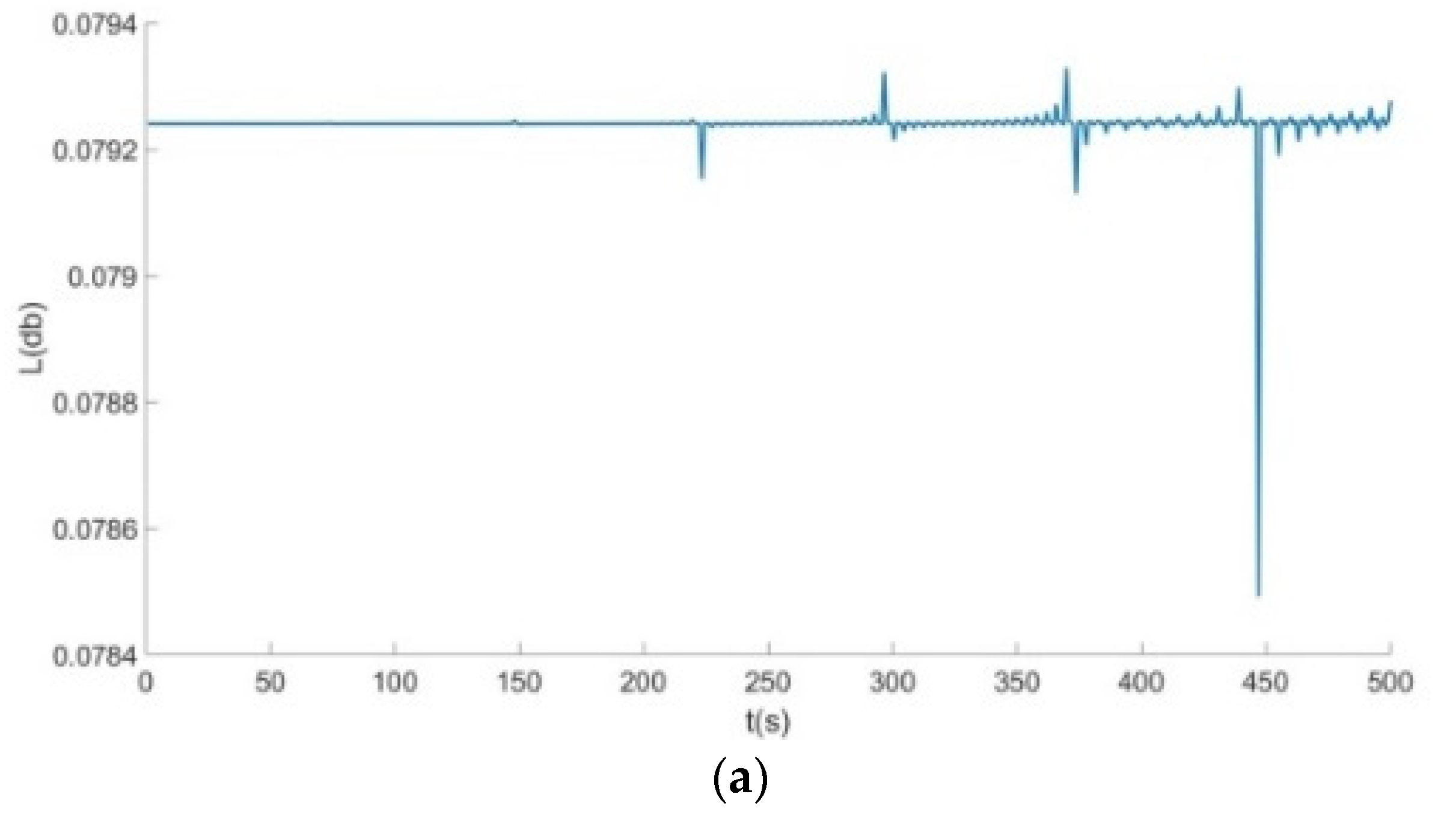
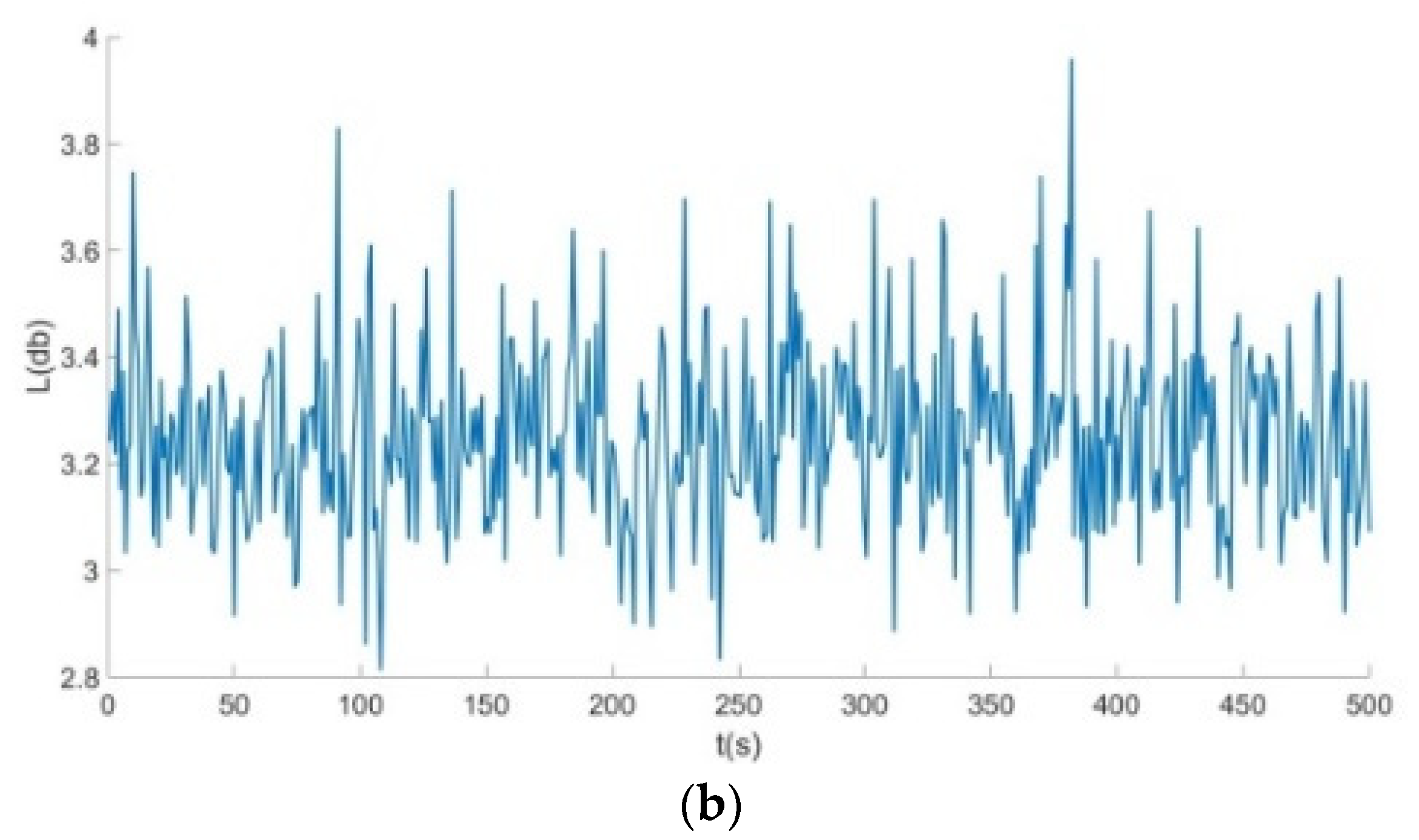
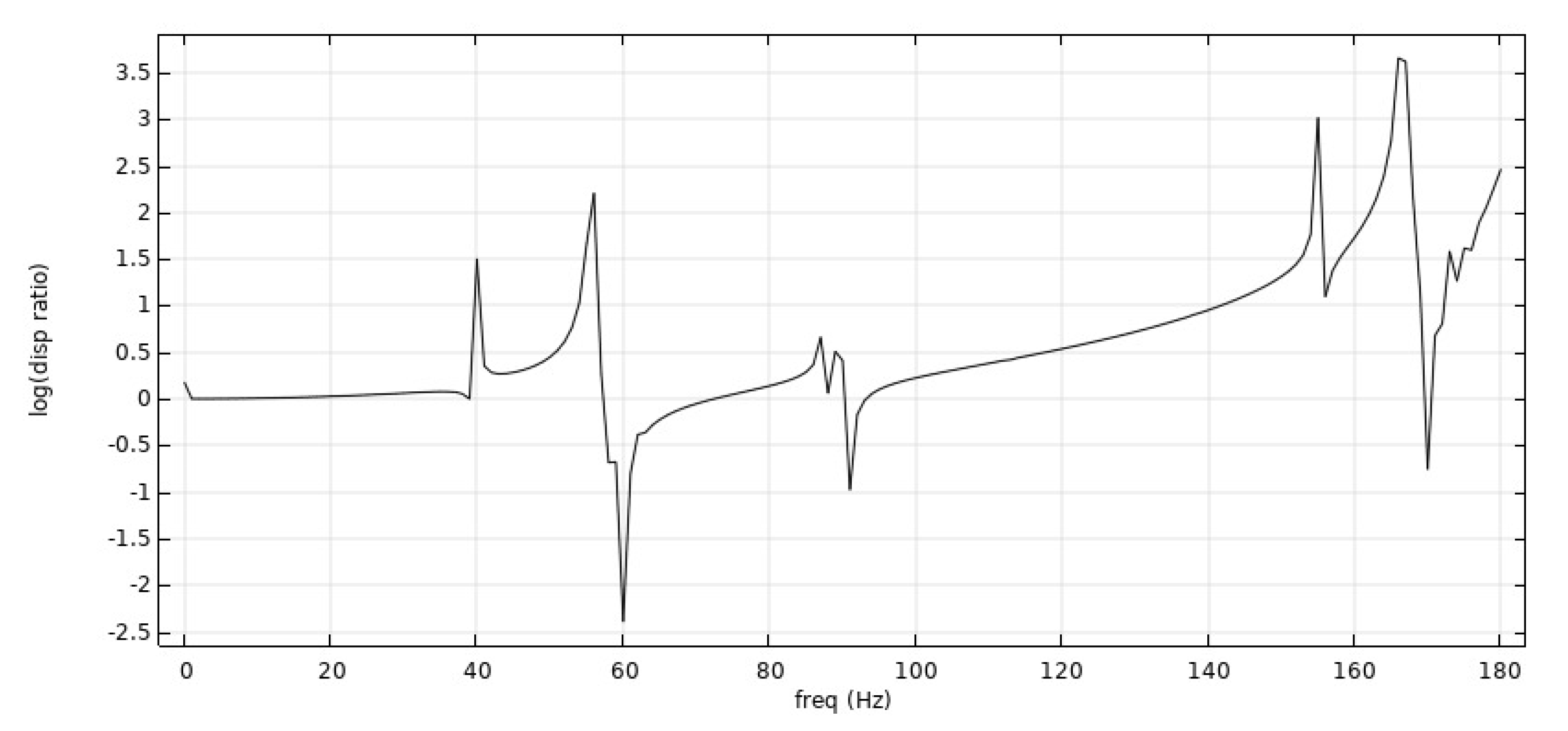
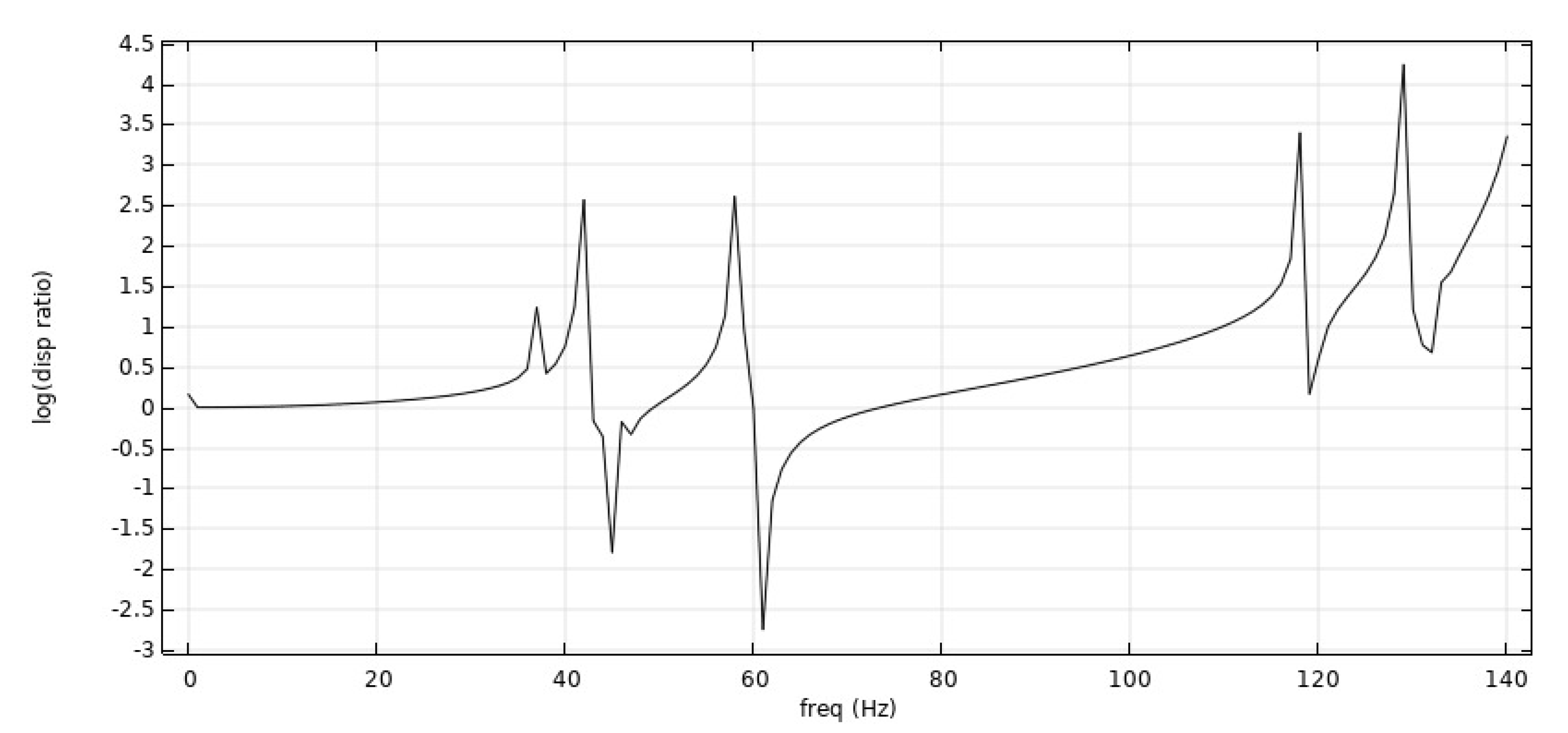
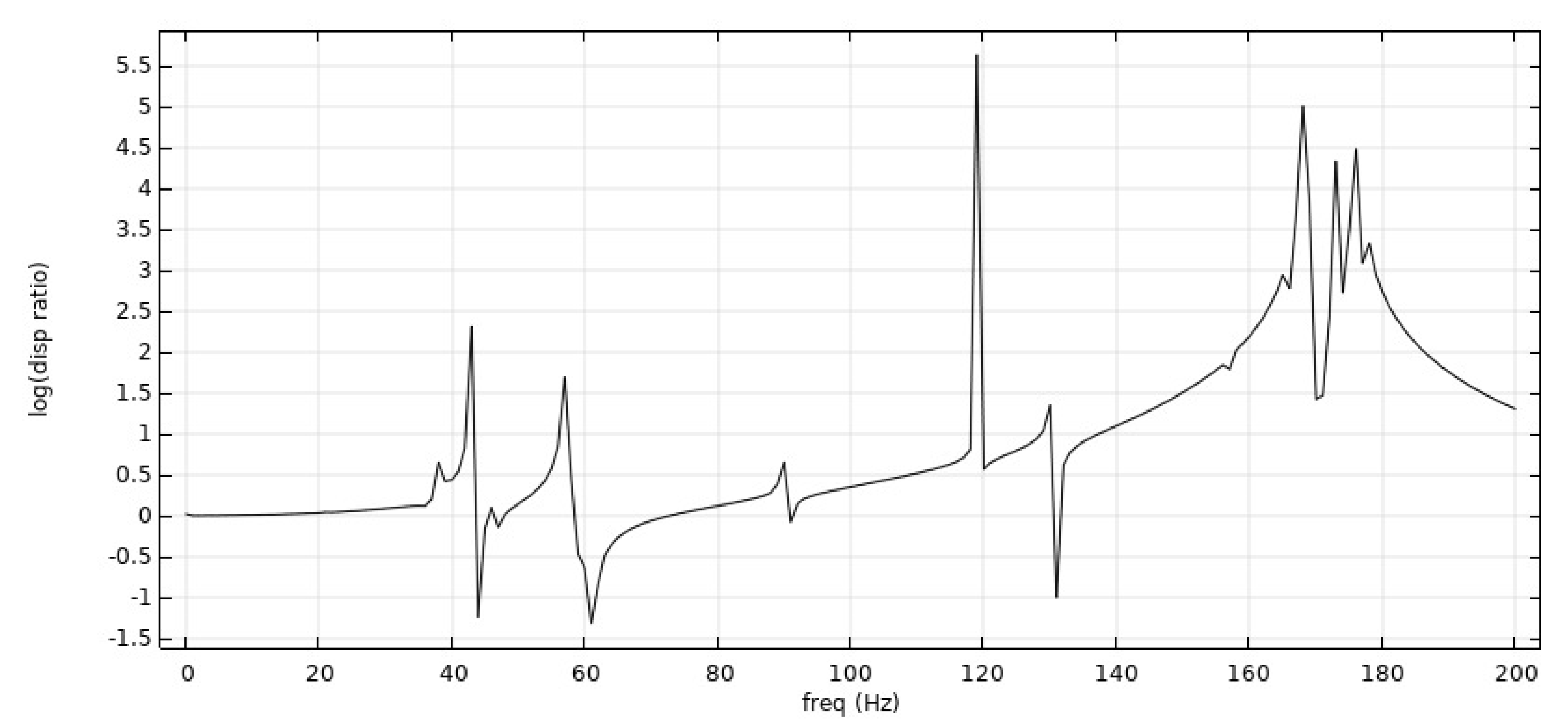
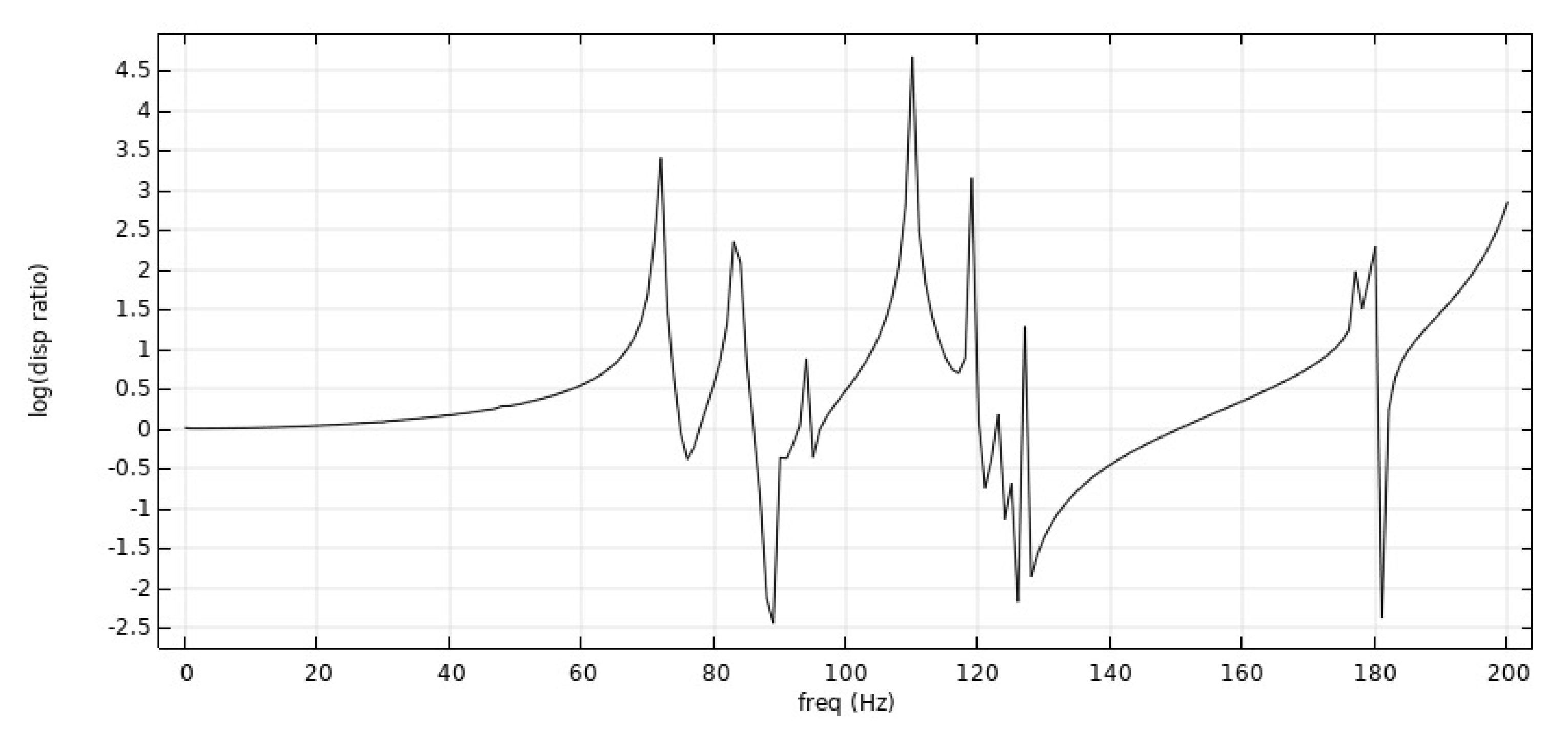
- From Figure 6, Figure 7 and Figure 8: when the Poisson’s ratio of the re-entrant structure was and the wall thickness was , the honeycomb base had a better damping effect on the external excitation frequency of 60 Hz, but it had no obvious damping effects on the external excitation frequencies of 10 Hz and 120 Hz. When the wall thickness of the re-entrant structure was , the honeycomb base had an obvious damping effect on the external excitation frequency of 110 Hz, but it had no obvious damping effect on the low frequency of 10 Hz and the intermediate frequency of 60 Hz.
- From Figure 9, Figure 10 and Figure 11: when the Poisson’s ratio of the re-entrant structure was and the wall thickness was , the honeycomb base had a better damping effect on the external excitation frequency of 60 Hz, but it had no obvious damping effects on the external excitation frequencies of 10 Hz and 120 Hz. When the wall thickness of the re-entrant structure was , the honeycomb base had an obvious damping effect on the external excitation frequency of 110 Hz, but it had no obvious damping effect on the low frequency of 10 Hz and the intermediate frequency of 60 Hz.
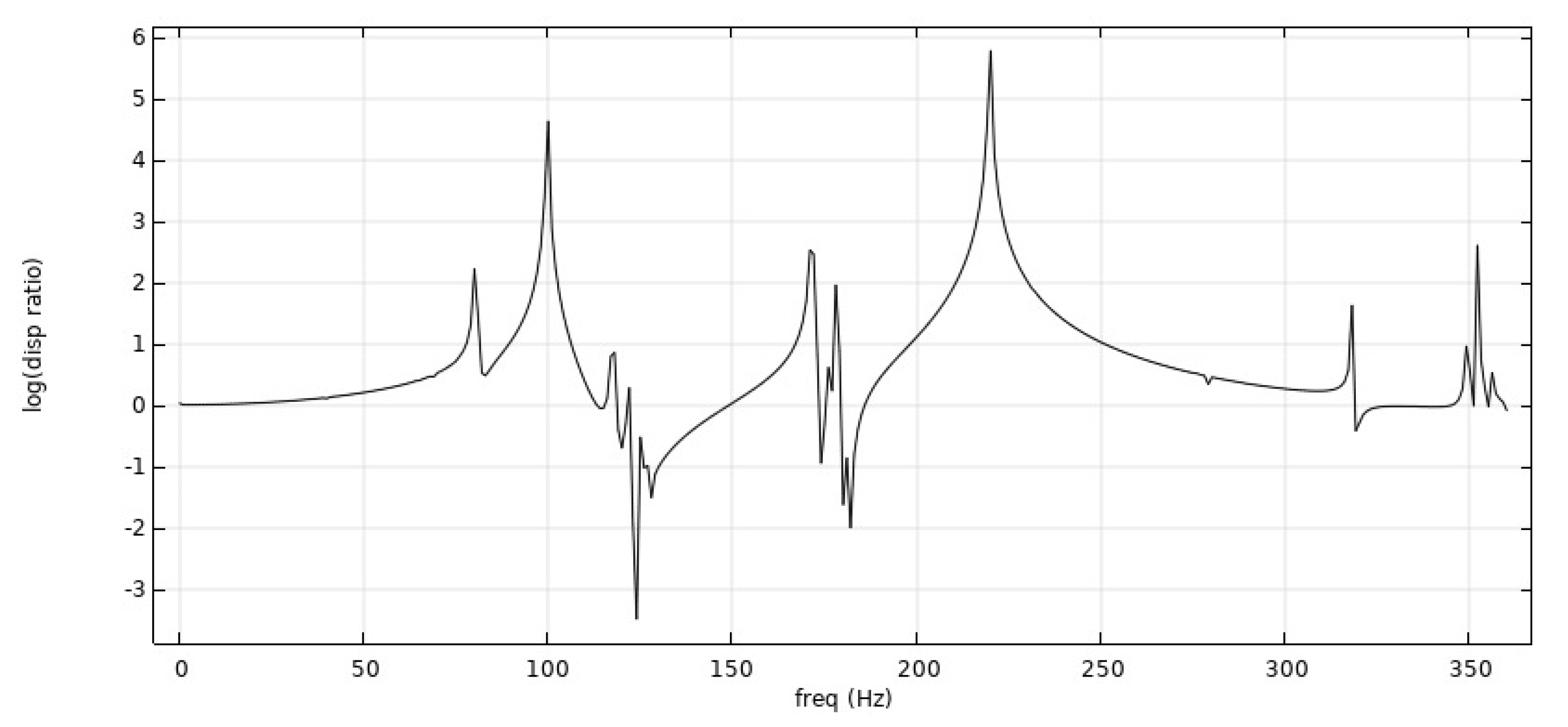
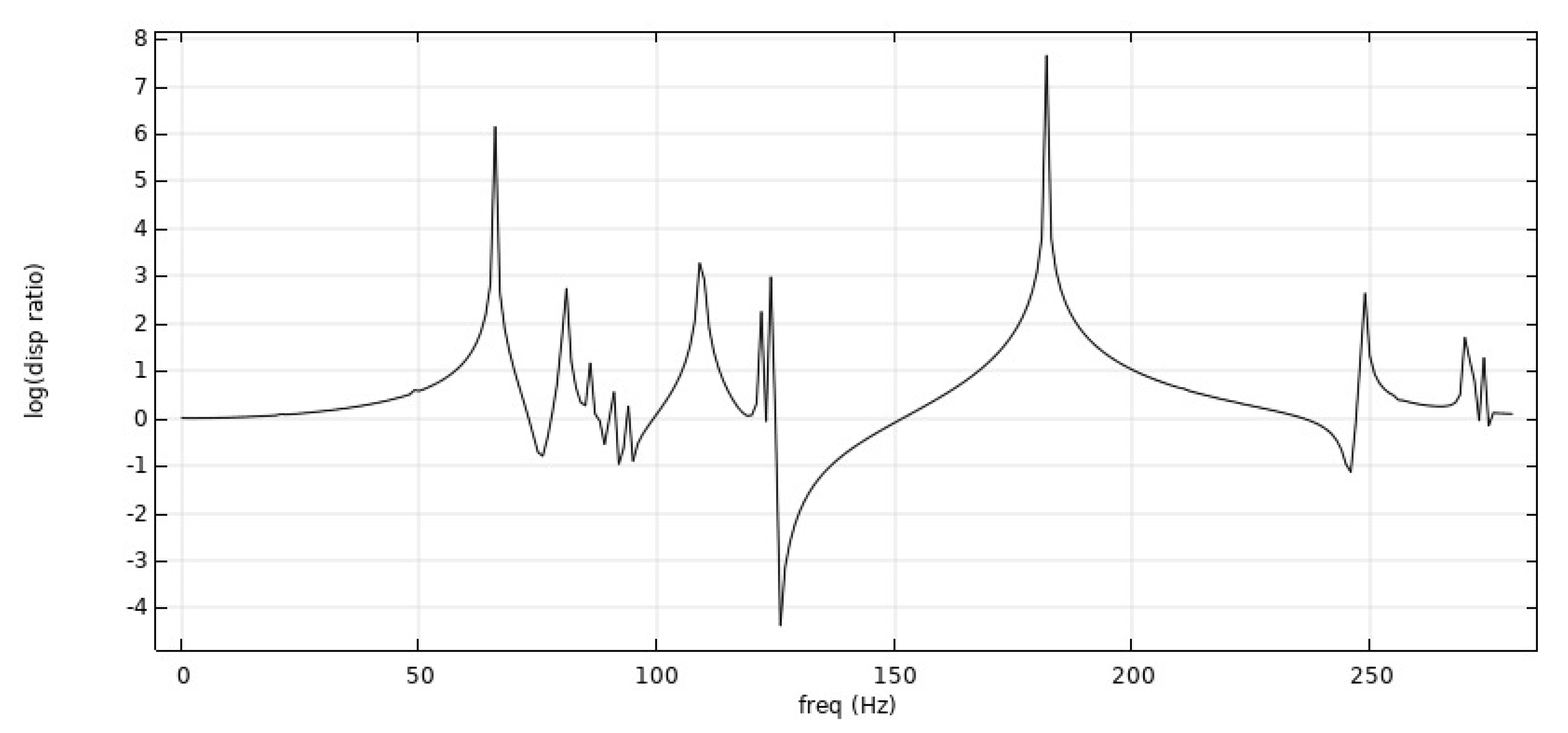
- From Figure 12, Figure 13 and Figure 14: when the re-entrant structure with mixed Poisson’s ratios was used to form the honeycomb base and when the wall thickness of the re-entrant structure was , the honeycomb base had a better damping effect on the external excitation frequency of 60 Hz, but it had no obvious damping effects on the external excitation frequencies of 10 Hz and 110 Hz. When the wall thickness of the re-entrant structure was , the honeycomb base had an obvious damping effect on the external excitation frequency of 120 Hz, but it had no obvious damping effect on the low frequency of 10 Hz and the middle frequency of 60 Hz.
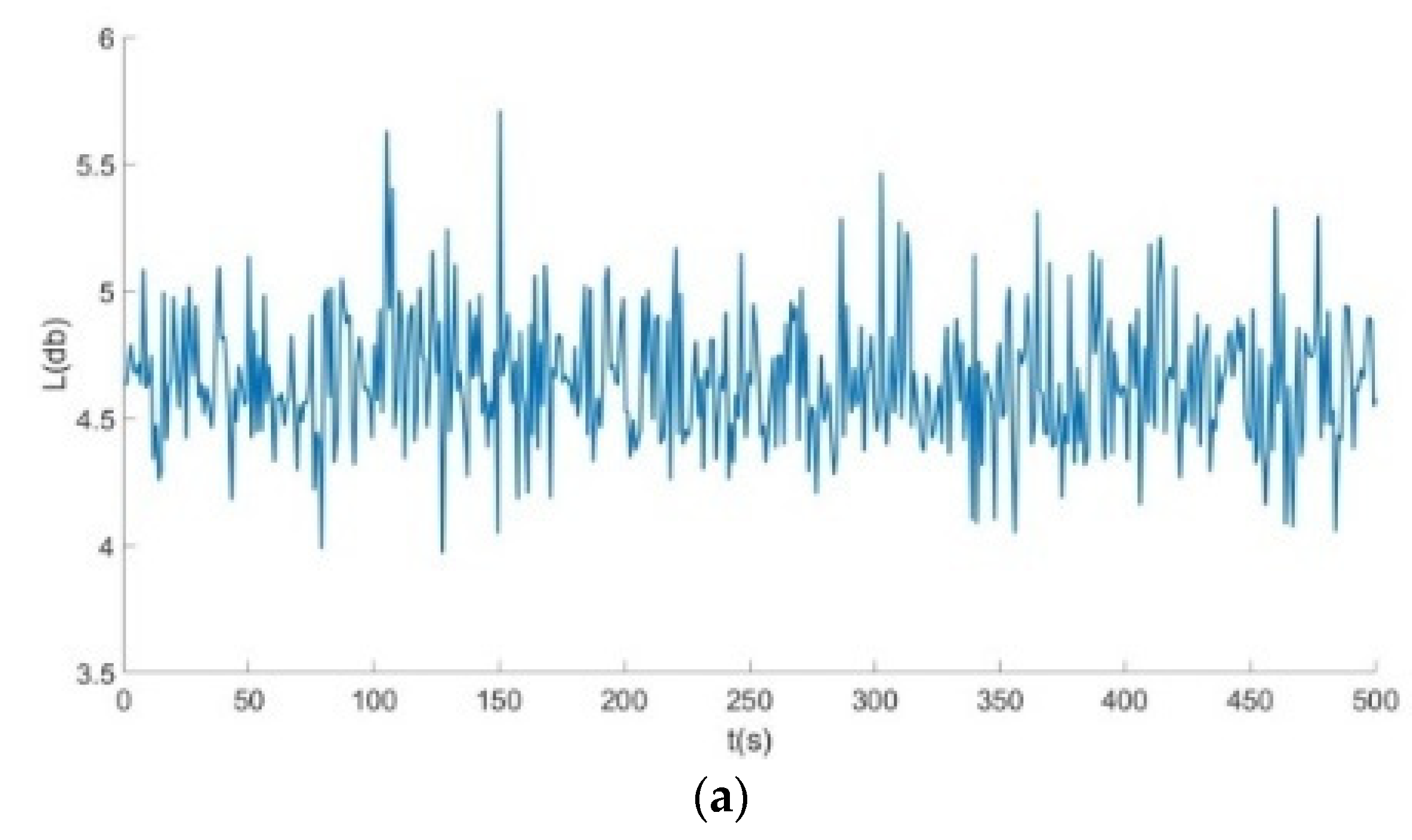
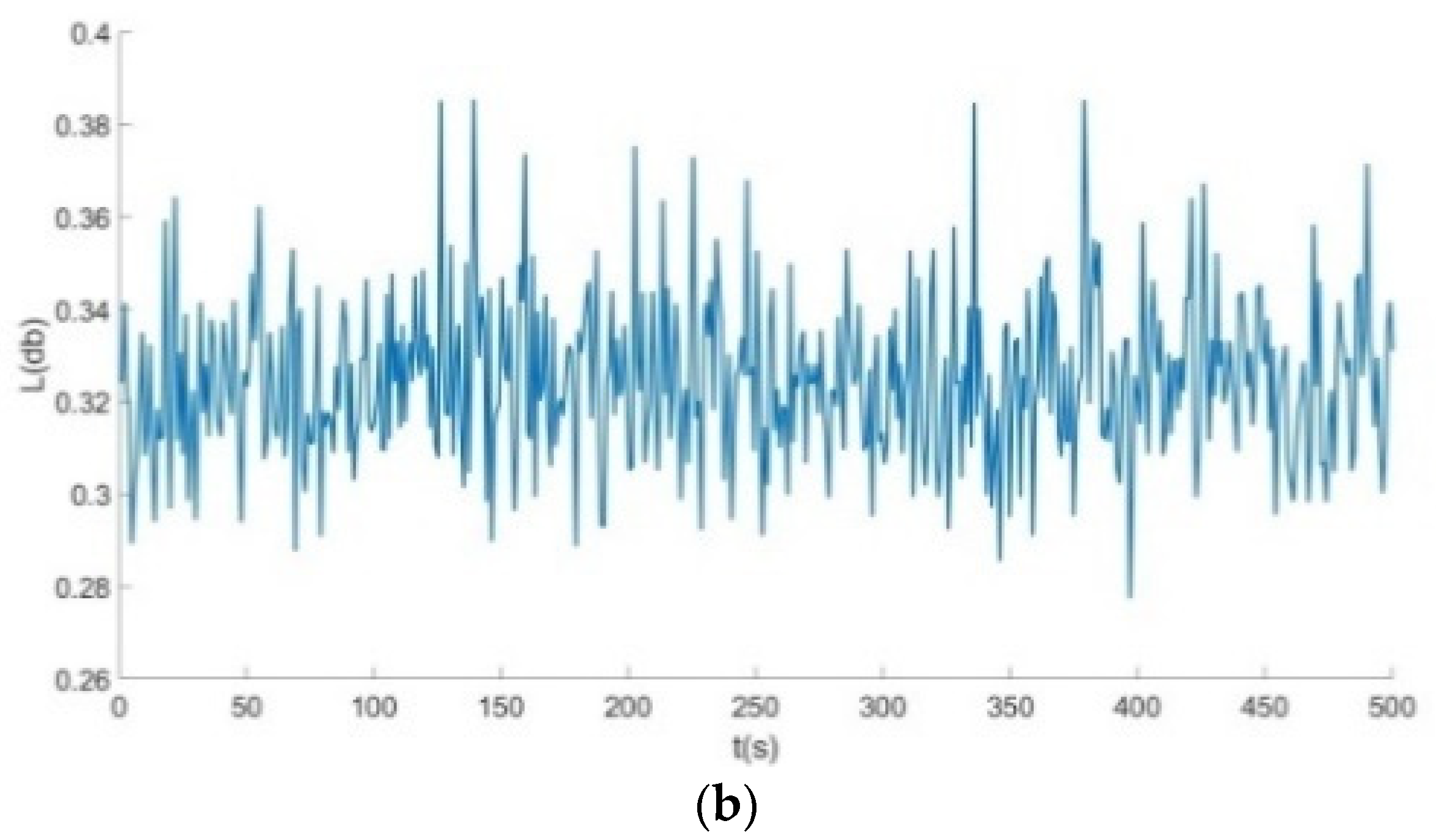
- By comparing the frequency response curves of the honeycomb base with different wall thicknesses of the re-entrant structure, we concluded that when the wall thickness was , the isolation frequency of the honeycomb base to external excitation was mainly concentrated on the relative high frequency. For example, when the Poisson’s ratio was , and the wall thickness was , the isolation frequency of the honeycomb base to external excitation was near a high frequency of 125 Hz. When Poisson’s ratio was , the vibration isolation frequency of the honeycomb base to external excitation was 125 Hz–150 Hz. When the honeycomb was laid with two different Poisson’s ratios, the vibration isolation frequency of the honeycomb base to external excitation was 70 Hz–90 Hz, 120 Hz–150 Hz and 180 Hz. In contrast, when the wall thickness of the re-entrant structure was , the vibration isolation frequency of the honeycomb base was mainly concentrated between 45 Hz–70 Hz.
- By analyzing the frequency response curves of the re-entrant hexagonal honeycomb structure with different Poisson’s ratios, we concluded that when Poisson’s ratio was , the vibration isolation performance of honeycomb base was better than that of the honeycomb base when Poisson’s ratio was .
- The method of laying the re-entrant structure with different Poisson’s ratios was adopted. By analyzing the corresponding frequency response curve, we concluded that the vibration isolation of the honeycomb base composed of re-entrant structures with different Poisson’s ratios to external excitation had a wider frequency band.
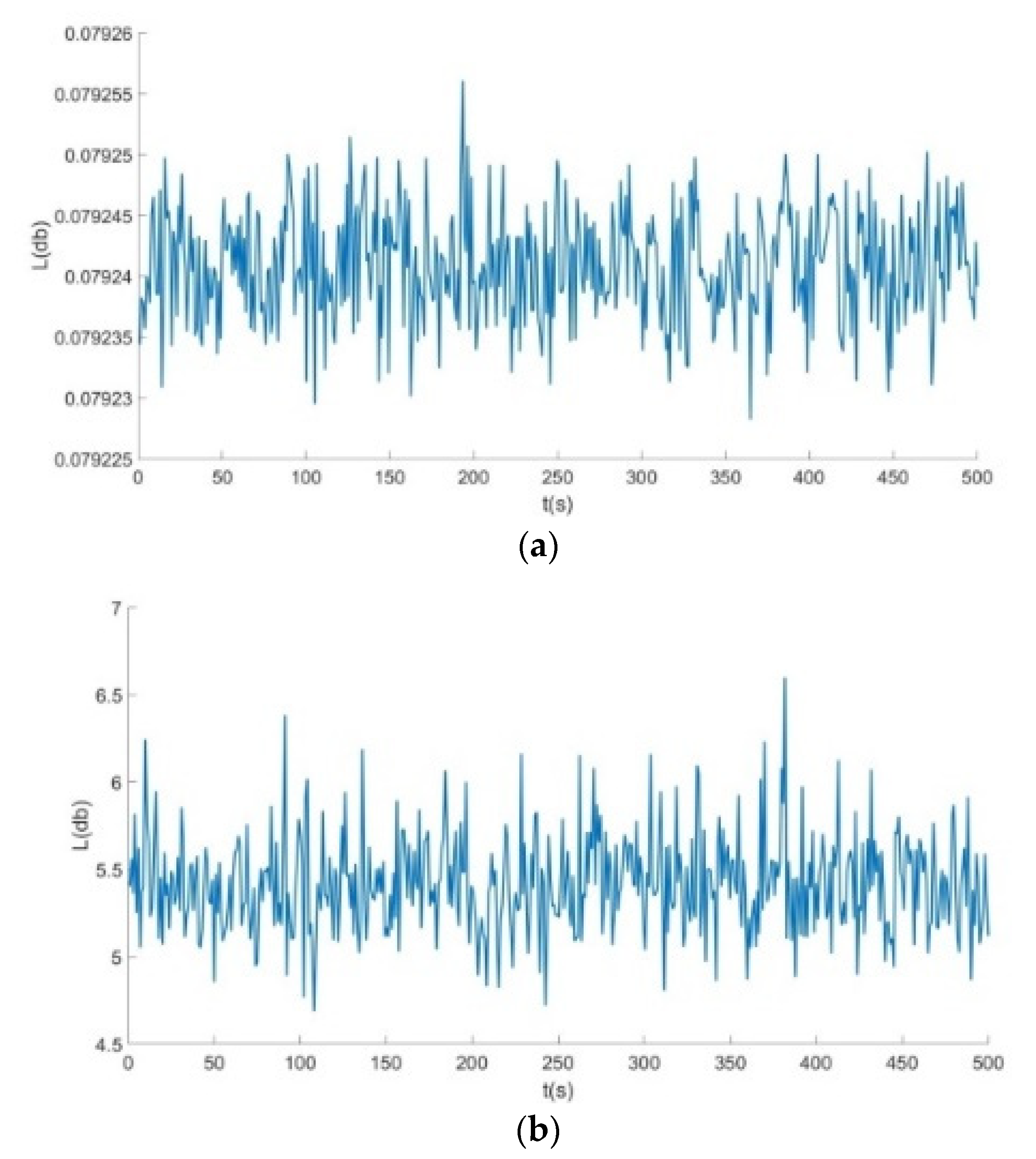
- By analyzing the results obtained using the Lagrange equation, we obtained the vibration isolation performance data and analyzed the honeycomb base by modeling the Lagrange equation, which was basically consistent with the results of the finite element analysis. Furthermore, this demonstrates the correctness and effectiveness of modeling and analyzing vibration isolation performance using the Lagrange method.
4. Conclusions
- By comparing the vibration level difference results of the honeycomb base composed of re-entrant structures with different Poisson’s ratios, we concluded that when the wall thickness of the re-entrant structure was , the honeycomb base had a better damping effect on the external excitation frequency of 60 Hz, but it had no obvious damping effects on the external excitation frequencies of 10 Hz and 120 Hz. When the wall thickness of the re-entrant structure was , the honeycomb base had an obvious damping effect on the external excitation at the high frequency of 110 Hz, but it had no obvious damping effect on the external excitation at the low frequency of 10 Hz and the intermediate frequency of 60 Hz.
- By comparing the frequency response curves of the honeycomb base with different wall thicknesses of the re-entrant structure, we concluded that when the wall thickness was , the isolation frequency of the honeycomb base to external excitation was mainly concentrated on the relative high frequency. In contrast, when the wall thickness of the re-entrant structure was , the vibration isolation frequency of the honeycomb base was more concentrated between 45 Hz–70 Hz. The method of laying the re-entrant structure with different Poisson’s ratios was adopted. By analyzing the corresponding frequency response curve, we concluded that the vibration isolation of the honeycomb base composed of re-entrant structures with different Poisson’s ratios to external excitation had a wider frequency band.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hu, F.W.; Cheng, J.J. Reviews on metamaterials manufacturing via 3D printing. Ind. Technol. Innov. 2017, 4, 15–19. [Google Scholar]
- Liu, W.W. Mechanics of Materials I; Higher Education Press: Beijing, China, 2004. [Google Scholar]
- Shi, W.; Yang, W.; Li, Z.M. Advances in negative Poisson’s ratio materials. Polym. Bull. 2003, 6, 48–57. [Google Scholar]
- Jiang, J.S.; Kim, Y.; Park, H.S. Auxetic nanomaterials, precent progress and future development. Appl. Phys. Rev. 2016, 3, 41101. [Google Scholar] [CrossRef]
- Critchley, R.; Corni, I.; Wharton, J.A.F.; Walsh, C.; Wood, R.J.K.; Stokes, K.R. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status Solidi 2013, 250, 1963–1982. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, K.L. Auxetic materials, the positive side of being negative. Eng. Sci. Educ. J. 2000, 9, 148. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496. [Google Scholar] [CrossRef]
- Hassan, M.R.; Scarpa, F.; Mohamed, N.A. In-plane Tensile Behavior of Shape Memory Alloy Honeycombs with Positive and Negative Poisson’s Ratio. J. Intell. Mater. Syst. Struct. 2009, 20, 897–905. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S. The Mechanics of two-dimensional cellular materials. Proc. R. Soc. A 1982, 382, 25–42. [Google Scholar]
- Fozdar, D.Y.; Soman, P.; Lee, J.W. Three-dimensional polymer constructs exhibiting a tunable negative Poisson’s ratio. Adv. Funct. Mater. 2011, 21, 2712–2720. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids, Structure and Properties; Cambridge University Press: London, UK, 1997. [Google Scholar]
- Scarpa, F.; Panayiotou, P.; Tomlinson, G. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. J. Strain Anal. Eng. Des. 2000, 35, 383–388. [Google Scholar] [CrossRef]
- Alderson, K.L.; Alderson, A.; Smart, G. Auxetic polypropylene fibres, Part 1 Manufacture and character isation. Plast. Rubber Compos. 2013, 31, 344–349. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic Materials and Structures; Springer: Singapore, 2015. [Google Scholar]
- Wang, X.L.; Stronge, W.J. Micropolar theory for two-dimensional stresses in elastic honeycomb. Proc. R. Soc. A 1999, 455, 2091–2116. [Google Scholar] [CrossRef]
- Sanami, M.; Ravirala, N.; Alderson, K.; Alderson, A. Auxetic materials for sports applications. Procedia Eng. 2014, 72, 453–458. [Google Scholar] [CrossRef]
- Banerjee, S.; Bhaskar, A. Free vibration of cellular structures using continuum modes. J. Sound Vib. 2005, 287, 77–100. [Google Scholar] [CrossRef][Green Version]
- Ruzzene, M.; Scarpa, F.L. Control of wave propagation in sandwich beams with auxetic core. J. Intell. Mater. Syst. Struct. 2003, 14, 443–453. [Google Scholar] [CrossRef]
- Idczak, E.; Strek, T. Computational modelling of vibrations transmission loss of auxetic lattice structure. Vib. Phys. Syst. 2016, 27, 123–128. [Google Scholar]
- Ma, Y.; Scarpa, F.; Zhang, D.; Zhu, B.; Jie, H. A nonlinear auxetic structural vibration damper with metal rubber particles. Smart Mater. Struct. 2013, 22, 084012. [Google Scholar]
- Grujicic, M.; Galgalikar, R.; Snipes, J.S. Multi-physics modeling of the fabrication and dynamic performance of all-metal auxetic-hexagonal sandwich-structures. Mater. Des. 2013, 51, 113–130. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C.Q. Analyses on the In-Plane Impact Resistance of Auxetic Double Arrowhead Honeycombs. J. Appl. Mech. 2015, 82, 51007. [Google Scholar] [CrossRef]
- Ingrole, A.; Hao, A.; Liang, R. Design and modeling of auxetic and hybrid honeycomb structures for in-plane property enhancement. Mater. Des. 2016, 117, 72–83. [Google Scholar] [CrossRef]
- Schultz, J.; Griese, D.; Shankar, P.; Summers, J.D.; Thompson, L. Optimization of honeycomb cellular meso-structures for high speed impact energy absorption. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011. [Google Scholar]
- Yu, Y.; Shen, H.S. A Comparison of Nonlinear Bending and Vibration of Hybrid Metal/CNTRC Laminated Beams with Positive and Negative Poisson’s Ratios. Int. J. Struct. Stab. Dyn. 2020, 20, 2043007. [Google Scholar] [CrossRef]
- Lv, W.; Li, D.; Dong, L. Study on blast resistance of a composite sandwich panel with isotropic foam core with negative Poisson’s ratio. Int. J. Mech. Sci. 2021, 191, 106105. [Google Scholar] [CrossRef]
- Pan, K.; Ding, J.Y.; Dong, H.W.; Zhang, B.B. Discrete variational method of multi-body system dynamics cased on center of gravity interpolation. J. Qingdao Univ. (Nat. Sci. Ed.) 2017, 30, 77–82. [Google Scholar]

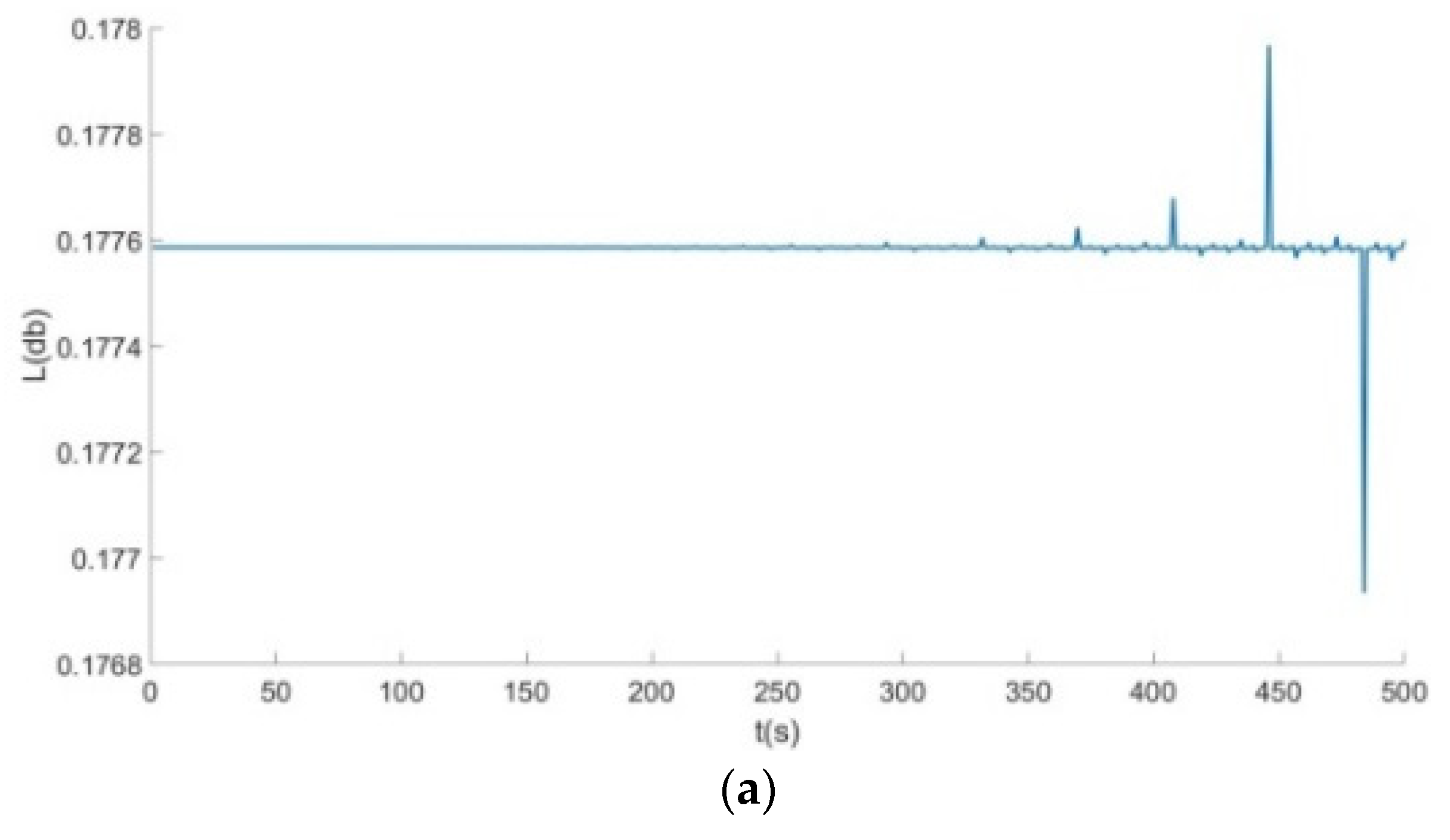
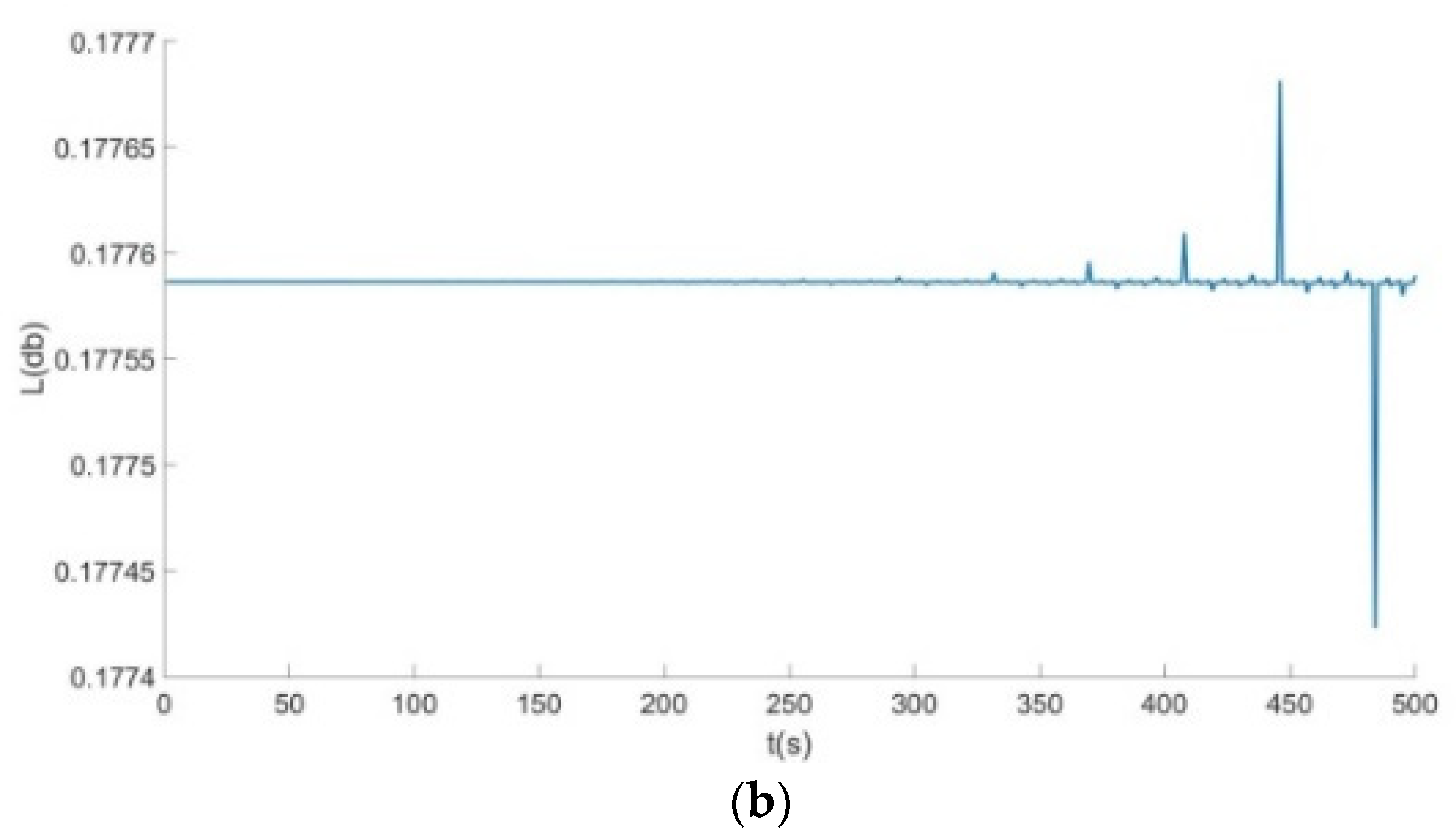
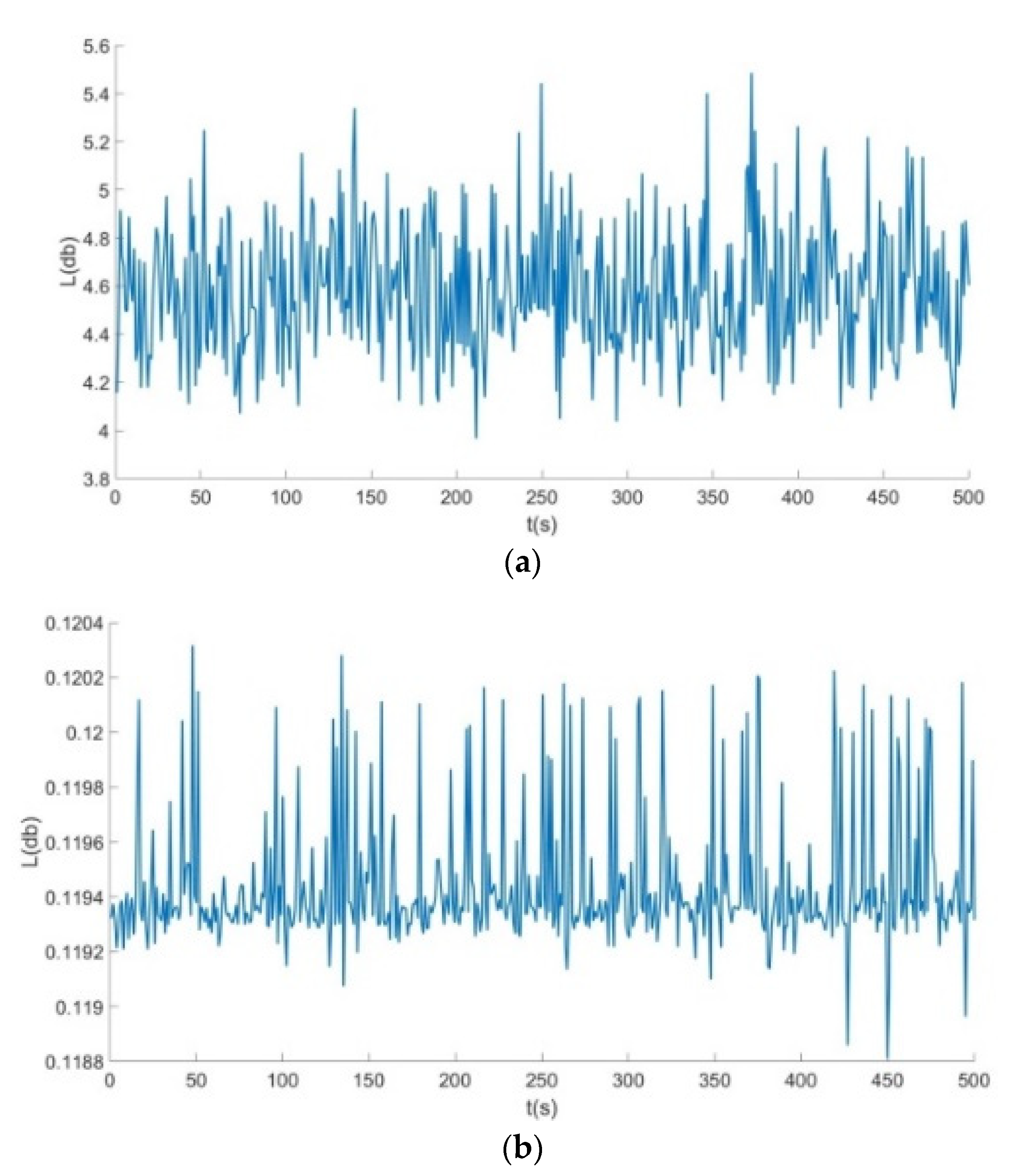
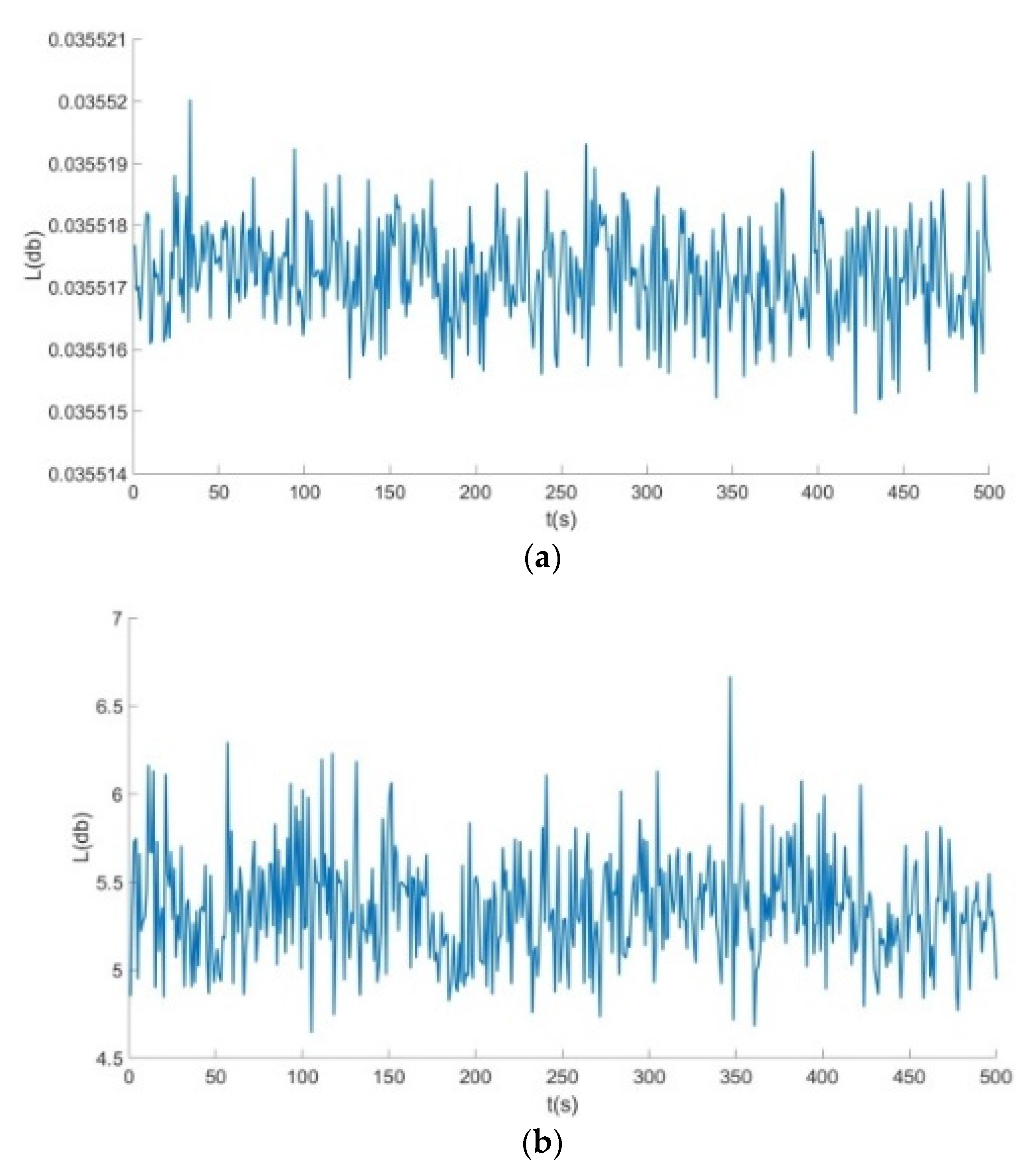
| 0.1776 | 4.6000 | 0.0355 | |
| 0.1776 | 0.1196 | 5.5000 |
| 0.3963 | 4.7000 | 0.0792 | |
| 0.3962 | 0.3300 | 5.5000 |
| 0.1869 | 4.7500 | 0.0792 | |
| 0.1691 | 0.0792 | 3.3500 |
| Vibration Isolation Frequency | |||
|---|---|---|---|
| 60 Hz, 90 Hz–170 Hz | 40 Hz–60 Hz | 45 Hz–70 Hz | |
| 125 Hz | 75 Hz, 125 Hz | 70 Hz–90 Hz, 120 Hz–150 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, K.; Zhang, W.; Ding, J. Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis. Symmetry 2022, 14, 1356. https://doi.org/10.3390/sym14071356
Pan K, Zhang W, Ding J. Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis. Symmetry. 2022; 14(7):1356. https://doi.org/10.3390/sym14071356
Chicago/Turabian StylePan, Kun, Wei Zhang, and Jieyu Ding. 2022. "Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis" Symmetry 14, no. 7: 1356. https://doi.org/10.3390/sym14071356
APA StylePan, K., Zhang, W., & Ding, J. (2022). Negative Poisson’s Ratio Re-Entrant Base Modeling and Vibration Isolation Performance Analysis. Symmetry, 14(7), 1356. https://doi.org/10.3390/sym14071356







