Impact of Buoyancy and Stagnation-Point Flow of Water Conveying Ag-MgO Hybrid Nanoparticles in a Vertical Contracting/Expanding Riga Wedge

Abstract

Riga surface can be utilized to reduce the pressure drag and the friction of the submarine by stopping the separation of the boundary layer as well as by moderating turbulence production. Therefore, the current symmetry of the work investigates the slip impacts on mixed convection flow containing water-based hybrid Ag-MgO nanoparticles over a vertical expanding/contracting Riga wedge. In this analysis, a flat surface, wedge, and stagnation point are also discussed. A Riga surface is an actuator that contains electromagnetic where a span-wise array associated with the permanent magnets and irregular electrodes accumulated on a smooth surface. A Lorentz force is incorporated parallel to the surface produced by this array which eases exponentially normal to the surface. Based on the considered flow symmetry, the physical scenario is initially modeled in the appearance of partial differential equations which are then rehabilitated into a system of ordinary differential equations by utilizing the pertinent similarity variables. A bvp4c solver is engaged to acquire the numerical solution. The flow symmetry and the influences of pertaining parameters involved in the problem are investigated and are enclosed in graphical form. The findings confirm that the velocity reduces, and temperature enhances due to nanoparticle volume fraction. A modified Hartmann number increases the velocity and diminishes the temperature. Moreover, the suction parameter enhances the velocity profiles and reduces the dimensionless temperature profiles. The heat transfer gradually increases by diminishing the contracting parameter and increasing the expanding parameter.

1. Introduction

Technologies in modern science identify the significant role of a new kind of fluids in heat transfer due to uplifting requirements of energy and are signified as Nanofluid. The thermal conductivity of regular fluids is vital in the mechanism of heat transfer features. As the materials of non-metallic such as ethylene, glycol, oil, and water have less thermal conductivity compared to materials of metallic such as aluminum, silver, diamond, gold, copper, etc. To boost the thermal conductivity of these regular fluids, the oxides and metallic materials are scattered into these fluids. The selection of a combination of regular fluid particles depends on applications for which the nanofluids are deliberated. They have numerous applications in biomedical and engineering such as the cooling process in industries, cancer therapy, etc. Choi figure [1] proposed the word nanofluid by comprising the tiny particles of size 1–100 nm into the regular fluids. Gorla et al. [2] inspected the heat transport fluids containing nanofluid through a circular cylinder in a stretching motion. Similar research has been carried out by Fakour [3] by considering the fluid flow in a porous channel with a magnetic field. Makinde and Aziz [4] examined numerically the fluid flow from a heated stretched surface induced by nanofluid with the aid of the RK technique. Akber et al. [5] scrutinized the magnetic flow involving nanofluid incorporated the Brownian motion in peristalsis. The bi-phase couple stress flow of nanofluid was numerically inspected by Zeeshan et al. [6]. Recently, Khan et al. [7] discussed the impact of entropy on the nonlinear radiative flow of ethylene-glycol and water-based gamma-Al₂O₃ particles through a vertical stretched surface with mixed convection and viscous dissipation. The features of heat transport and entropy impact induced by a non-Newtonian nanofluid past an expandable linearly irregular medium are investigated by Jamshed et al. [8]. Jamshed et al. [9] inspected the thermal characteristics of Casson fluid containing nanoparticles through a parabolic solar trough collector. They scrutinized that the thermal efficiency enhances up to 18.5% in the presence of nanofluid. Some recent developments on the performance of nanofluid in the heat transfer enhancement are summarized in refs. [10,11,12].

Recently, to enhance the heat transfer properties, scientists and researchers are mixing two or more nanoparticles into the regular fluid to achieve superior thermal conductivity namely called hybrid nanofluid (HyNF). To generate a HyNF, a two-step technique is widely utilized by scholars and researchers due to its capability and the cost of effectiveness on a large usual scale. Turcu et al. [13] were the first anticipate the synthesis of the Fe₂O₃/MWCNTs hybrid nanofluid. The different features and techniques containing hybrid nanofluid were examined by Nine et al. [14]. Huang et al. [15] scrutinized the heat transport features and nanofluids’ pressure drop involving Al₂O₃/MWCNTs hybrid nanofluid. The impact of nonlinear radiation on the 3D rotated flow of Cu-Al₂O₃ hybrid nanocomposites past a stretched surface with unsteady thermal conductivity was scrutinized by Usman et al. [16]. Waini et al. [17] surveyed the time-dependent flow with characteristics of heat transport over a continuous porous shrinkable/stretchable curved sheet induced by a hybrid nanofluid and multiple solutions were found by using the bvp4c technique.

The significant features of the magnetic field are found in several fields such as geophysics, astrophysics, flow meters, MHD generators, thermal nuclear reactor, etc. The extensively utilized fluids as liquid metals, electrolytes, plasma, and several others depending on the application of electric and magnetic fields. The liquids are not consistently good electricity conductors, even though their conductivity can be uplifted by employing an electric field via an external agent. Alternatively, the Riga plate is an electro-magnetic actuator containing electrodes and magnet pairs displayed in a specific form that was initiated by Gailitis and Lielausis [18]. Pantokratoras and Magyari [19] involvedlow electrical conductivity to inspect the fluid flow through a Riga surface. Hayat et al. [20] examined the erratic thick Riga surface contained in the fluid flow of nanofluid affected via heat generation/absorption properties. Ahmad et al. [21] explored the impact of zero mass flux and convective heating on flow moving through a Riga plate with nanofluid. The bvp4c and shooting techniques were employed to acquire the numerical results. The bio-convection influence of nanofluid from an erratic thick Riga surface within the domain flow was investigated by Iqbal et al. [22]. Ganesh et al. [23] explored the electro-magneto flow of nanofluid containing gamma aluminum particles from a Riga stretchable plate. Zaib et al. [24] obtain multiple solutions of the radiative flow of micropolar fluid involving alloy particles through a Riga surface with buoyancy influences. Recently, Khatun et al. [25] investigated the impact of EMHD on radiative flow over an infinitely wide or long permeable vertical Riga surface induced in a rotating system.

The boundary-layer flow and heat transport via wedge-shaped surface has achieved great interest in recent years. This is credited to its several applications in the engineering and chemical industry such as in the geothermal industries and aerodynamics field. Historically, Falkner and Skan [26] were the first who suggested this kind of flow. In recent times, these equations are presently signified as the equation of Falkner-Skan (F-S). Afterward, a parameter known as the Hartree pressure gradient was introduced by Hartree [27] in the F-S equation. Riley and Weidman [28] have obtained dual solutions of the F-S flow through a stretched sheet. Awad [29] discussed the heat transfer characteristics through a rotating disc to investigate the Prandtl number of fluids by employing an asymptotic model. Afterward, the works on the F-S flow were carried out by various researchers with different aspects as described in Refs. [30,31,32,33,34].

All of the preceding studies progressed their discussions under the assumption of no-slip boundary conditions. One of the core themes of Navier–Stokes hypothesis is the no-slip boundary condition (the supposition that a fluid conforms to a solid wall). However, in some cases, this condition does not apply. Slip effects can arise on the elongating boundary once the liquid is particulate, such as suspensions, emulsions, polymer solutions, and foams. Boundary slip fluids have significant technological applications, such as polishing internal cavities and artificial heart valves. The no-slip condition is modified by Navier’s partial slip condition for several coated surfaces that prevent adherence, such as Teflon, where the slip velocity is dependent on the local shear stress. However, experiments indicate that the slip velocity is also affected by the normal stress. Andersson [35] inspected the impact of slip on the flow through a stretchable sheet. The features of the slip effect on the flow and heat transport past a stretchable oscillatory sheet were examined by Abbas et al. [36]. Turkyilmazoglu [37] obtained double solutions of slip flow of the viscoelastic fluid from a stretchable sheet. The features of heat transfer induced by an exponential stretchable sheet with slip, radiation, and magnetic effects were investigated by Mukhopadhyay [38]. Baranovskii and Artemov [39] inspected the influence of Navier’s wall slip by considering the Oldroyd fluid. Khan et al. [40] investigated multiple slips’ impacts on the axisymmetric flow of buoyant fluid through a stretched sheet with radiation and magnetic fields. A mathematical model specifying the viscous flow of a non-uniformly fluid from a heated confined domain subject to the slip condition was examined by Baranovskii and Domnich [41]. Recently, Khan et al. [42] examined the partial slip impact on magneto flow of Sisko fluid induced by gold particles past a permeable radiative surface and found double solutions.

In contrast with the previous studies, this one considers the mixed convective flow of a hybrid nanofluid embedded with slip effects past a contracting/expanding Riga wedge. In addition, the Riga surface can be utilized to reduce the pressure drag and the friction of the submarine by stopping the separation of the boundary layer as well as by moderating turbulence production. Thus, the novelty of the present exploration is to examine single-phase flow, mass suction/injection, and thermal analysis of particulate the slip effect on buoyancy flow near a stagnation point involving Ag-MgO hybrid nanoparticles over a contracting/expanding Riga wedge. Outcomes of the three dissimilar cases of flow symmetry namely, stagnation-point, wedge, and the flat plate have been discussed. A bvp4c technique is utilized to obtain the numerical solution of the transformed PDEs. A comparison is also made with existing solutions available in the literature to certify the current outcomes.

2. Mathematical Background of the Problem

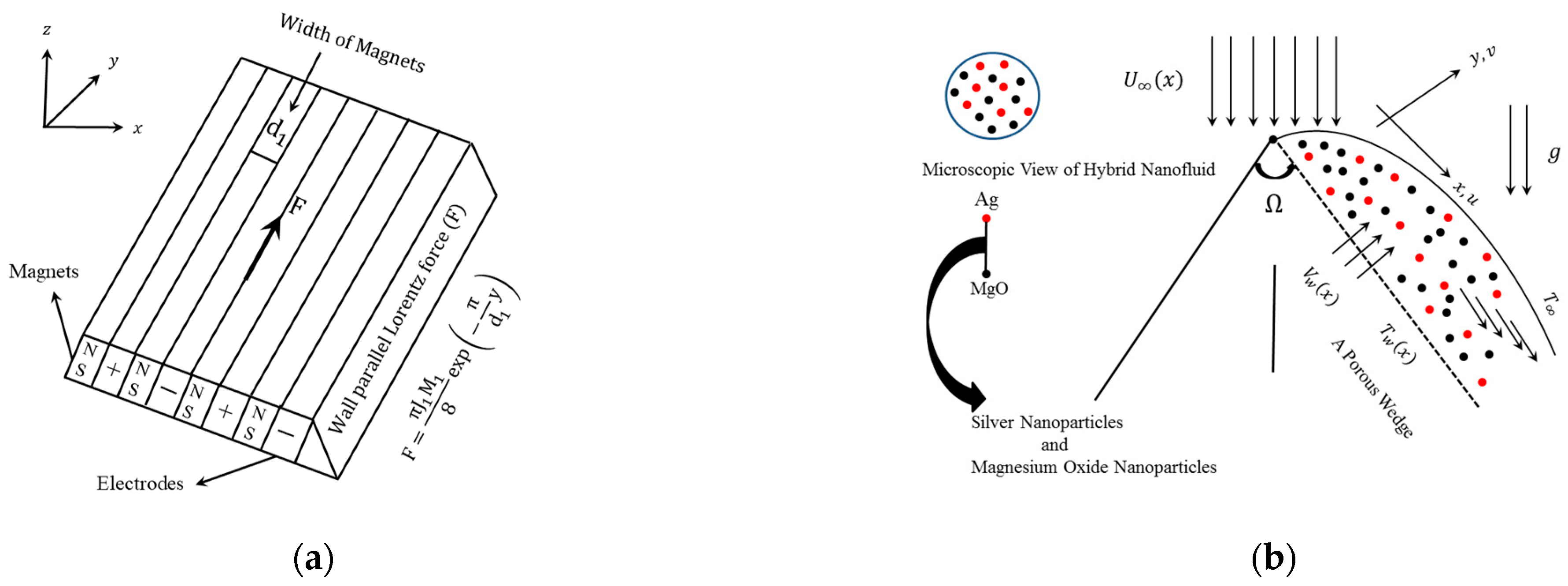
Let us assume a steady, two-dimensional, boundary layer flow of a hybrid nanofluid over a vertical permeable contracting/expanding Riga wedge in the presence of slip and the combined effect of the free and forced convection. The water-based Ag-MgO hybrid nanofluid and heat transfer schematic flow configurations of the current model are more clearly manifested along with the Cartesian coordinate system for the three different geometries are demonstrated in Figure 1a,b. It is more precious to mention that the three different geometries surfaces such as stagnation point, wedge, and flat plate are treated as Riga plates for the considered flow symmetry. Moreover, it is presumed that the thermophysical properties are constant, but the density differences caused by temperature gradients are taken into account. It is presumed that the contracting and expanding vertical wedge has a variable velocity, $U_w(x)$, while the velocity at the free stream is dignified by $U_{\infty }(x)$. Whereas $T_w(x)$ signifies the variable temperature at the wall surface of the wedge, while the ambient or free stream takes the constant value and is denoted by $T_{\infty }$. Far away from the surface of the wedge plate, both the Newtonian absorbing fluid and the surrounding fluid are maintained at a uniform temperature $T_{\infty }$. Moreover, at the cooled surface condition when the variable temperature is less than the ambient temperature such as $T_w<T_{\infty }$ corresponds to the buoyancy opposing flow at the heated surface condition when the variable temperature is superior to the free-stream temperature such as $T_w>T_{\infty }$ corresponds to the buoyancy assisting flow. It is further assumed that the mass flux velocity is denoted by $V_w\left(x\right)$, where $V_w\left(x\right)>0$ corresponds to blowing or injection and $V_w\left(x\right)<0$ corresponds to suction. Under the aforementioned stated proviso, the requisite leading governing equations following are as follows:

Continuity Equation,

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

Momentum Equation,

$$\begin{array}{l}u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=U_{\infty }\frac{d{U}_{\infty }}{dx}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\left(\frac{{\partial }^{2}u}{\partial y^2}\right)+\frac{\pi J_1{M}_1}{8{\rho }_{hnf}}\exp \left(-\frac{\pi }{d_1}y\right)\\ +\frac{g{\left({\beta }_T\rho \right)}_{hnf}}{{\rho }_{hnf}}\left(T-T_{\infty }\right)\cos \left(\frac{\mathsf{\Omega }}{2}\right)\end{array}$$

(2)

Temperature Equation,

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho c_p\right)}_{hnf}}\left(\frac{{\partial }^{2}T}{\partial y^2}\right),$$

(3)

whereas, $u$ and $v$ are the components of velocity along with the corresponding $x$- and $y$-axis directions, respectively, $J_1$ is an employed current density in electrodes, $T$ is the HyNF temperature, $d_1$ represents the width of magnet and electrodes, $g$ is the acceleration due to gravity, and $M_1$ dignify the magnetization of the permanent magnets. Further, mathematical symbols in the above governing Equations (1)–(3) manifest the hybrid nanofluid such as ${\mu }_{hnf}$ corresponds to the dynamic or absolute viscosity, ${\rho }_{hnf}$ corresponds the density, $k_{hnf}$ corresponds the thermal conductivity, ${\left({\beta }_T\rho \right)}_{hnf}$ corresponds the thermal expansion coefficient, and ${\left(c_p\rho \right)}_{hnf}$ corresponds the specific heat coefficient.

2.1. Physical Boundary Conditions

The suitable boundary conditions for the current literature are as follows:

$$\begin{array}{l}u\left(x,y=0\right)=U_w\left(x\right)+{\gamma }_1\left(x\right){\mu }_f\frac{\partial u}{\partial y},u\left(x,y\to \infty \right)\to U_{\infty }\left(x\right),\\ T\left(x,y=0\right)=T_w\left(x\right)+{\gamma }_2\left(x\right){\mu }_f\frac{\partial T}{\partial y},T\left(x,y\to \infty \right)\to T_{\infty },\\ v\left(x,y=0\right)=V_w\left(x\right).\end{array}\}$$

(4)

At the surface of the Riga wedge, the velocity and temperature slips signify as ${\gamma }_1\left(x\right)$ and ${\gamma }_2\left(x\right)$, respectively. We suppose here that $U_w\left(x\right)$, ${\gamma }_1\left(x\right)$, $V_w\left(x\right)$, ${\gamma }_2\left(x\right)$, $T_w\left(x\right)$ and $U_{\infty }\left(x\right)$ have the following mathematical form,

$$\begin{gathered} U_w\left(x\right)=b{x}^m,{\gamma }_1\left(x\right)=\frac{Ax}{{\lambda }_0{\mu }_f},V_w\left(x\right)=\left(\frac{{\alpha }^{*}}{x}\right){\lambda }_0\left(\frac{m+1}{2}{f}_w\right),{\gamma }_2\left(x\right)=\frac{Bx}{{\lambda }_0{\mu }_f}, \\ {T}_w\left(x\right)=T_{\infty }+T_{0}x,U_{\infty }\left(x\right)=c{x}^m \end{gathered}$$

(5)

where, $T_0$ and $c$ are positive arbitrary constants, while the other positive arbitrary constants such as $A$ and $B$ are the slip parameters, and $b>0$ investigates the expanding surface of the Riga wedge plate while $b<0$ investigating the contracting surface. The HP (Hartree pressure) gradient can be mathematically expressed as $m={\beta }_1/\left(2-{\beta }_1\right)$, where ${\beta }_1$ is the corresponding HPG parameter which joins to $\pi {\beta }_1=\mathsf{\Omega }$ and $\mathsf{\Omega }$ is the entire angle of the wedge surface of the Riga plate. 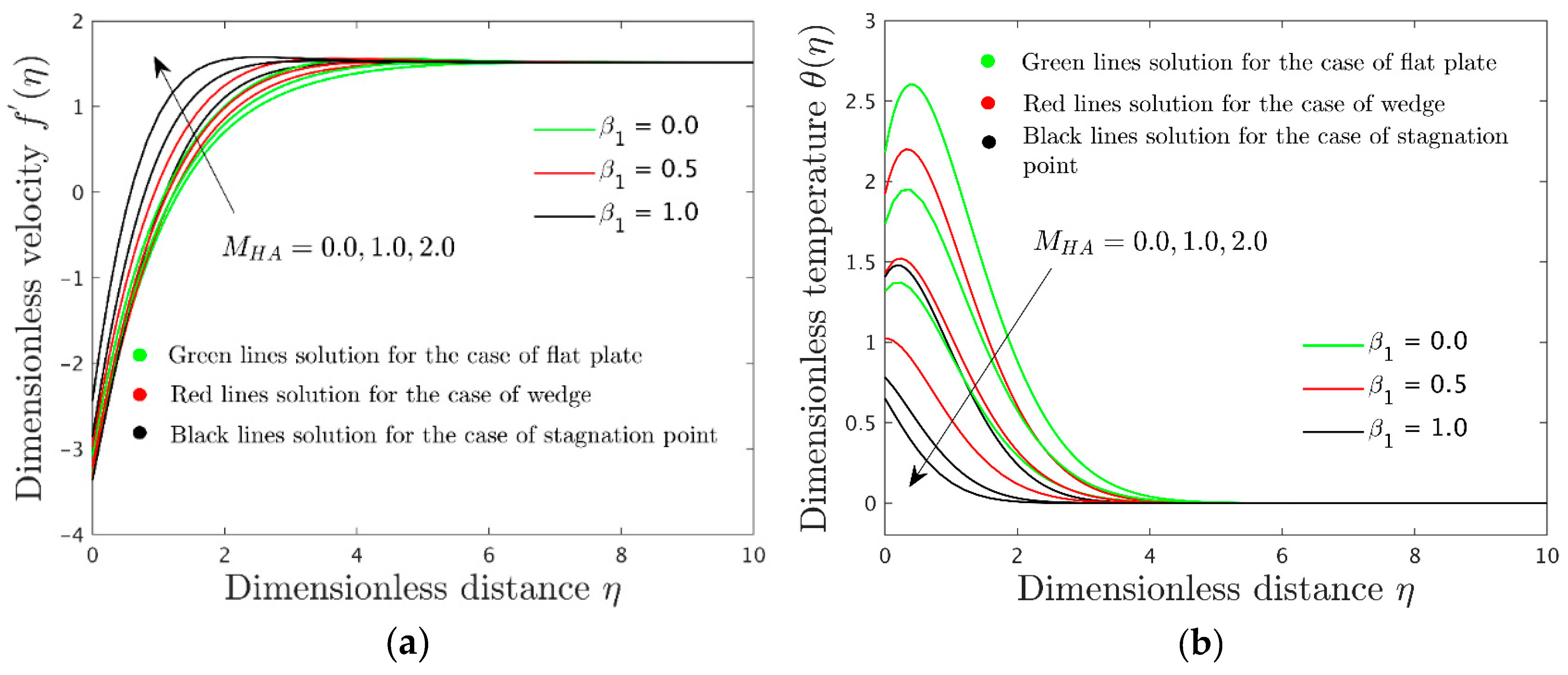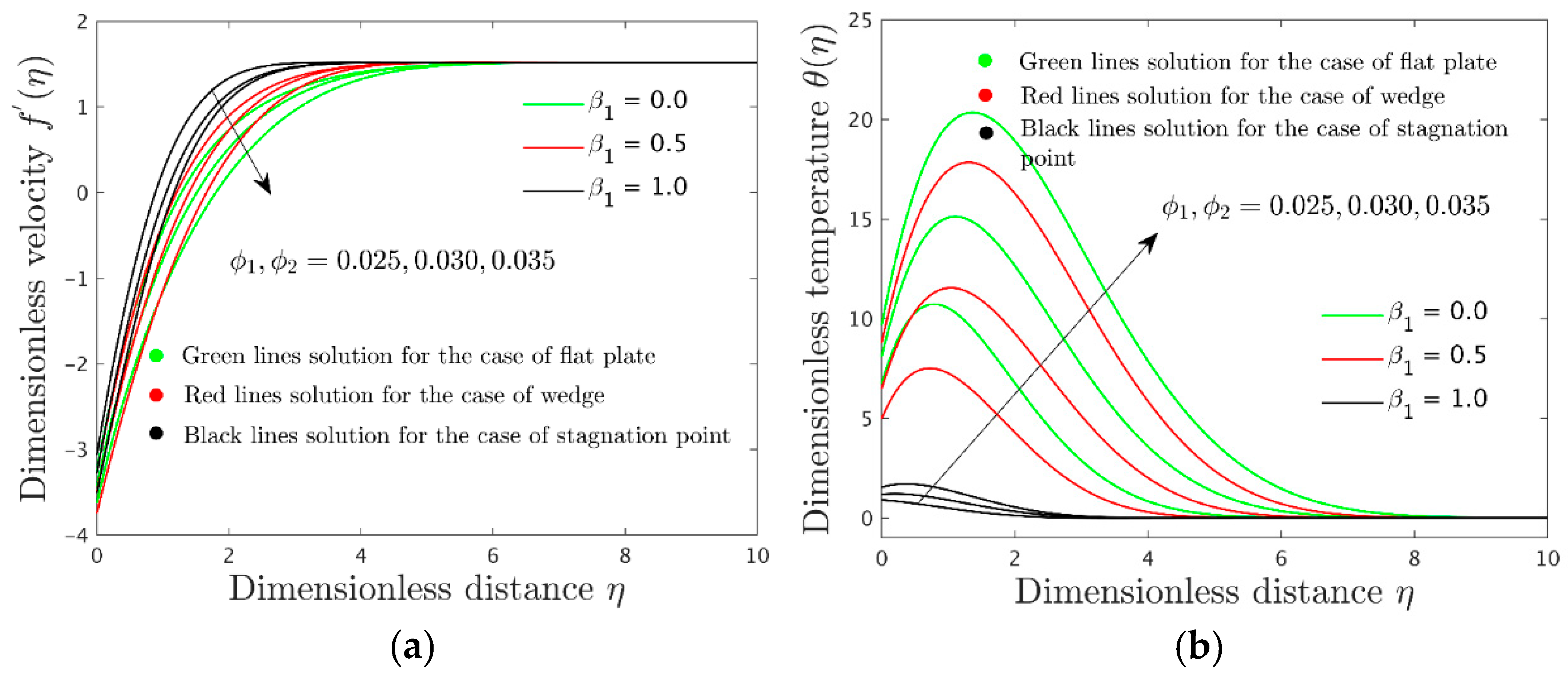The HPG parameter ${\beta }_1$ for the particular selected values 0.0, 0.5, and 1 correspond to the flow geometry of a flat plate, wedge, and stagnation point, respectively. In addition, the references of Lin and Lin [43] and Basha et al. [44] have demarcated the parameter ${\lambda }_0=\sqrt{{\mathrm{Re}}_x}{\delta }_0$ which can be best fit and pertinent for any fluid Prandtl number (Pr), ${\delta }_0=\sqrt{\mathrm{Pr}}{\left(1+\mathrm{Pr}\right)}^{-E}$, $E=1/6$ and ${\mathrm{Re}}_x=U_{\infty }x/{\nu }_f$ is called the local Reynolds number.

2.2. Model Relative Expression and Thermo-Physical Data of the Hybrid Nanofluid

In this section, it is retained our investigation only for the hybrid nanofluid. Two distinct types of nanocomposites namely silver (Ag) and magnesium oxide (MgO) have been opted along with the water base fluid to form the corresponding hybrid nanofluid. To procure the fluid flow symmetry characteristics precisely, hence, it is bounded the upcoming governing equations exercising the thermophysical properties as demonstrated by various researchers such as Takabi and Salehi [45], Acharya et al. [46], and Khan et al. [47]. The thermophysical data of the tiny nanoparticles and regular base fluid and the relative expression of the HyNF formulations are portrayed in Table 1 and Table 2, respectively.

Table 1. Thermophysical data of tiny nanoparticles and base fluid [44].

Physical Properties	Water	Ag	MgO
$c_p$ (J/Kg K)	4179	235	955
$\rho$ (Kg/m3)	997.1	10,500	3560
${\beta }_T\times {10}^{-5}$ (1/K)	21	1.89	1.05
$k$ (W/mK)	0.613	429	45
Pr	6.2	-	-

Table 1. Thermophysical data of tiny nanoparticles and base fluid [44].

Physical Properties	Water	Ag	MgO
$c_p$ (J/Kg K)	4179	235	955
$\rho$ (Kg/m3)	997.1	10,500	3560
${\beta }_T\times {10}^{-5}$ (1/K)	21	1.89	1.05
$k$ (W/mK)	0.613	429	45
Pr	6.2	-	-

Table 2. Thermophysical properties of the water-based Ag-MgO hybrid nanofluid [44,45].

Properties	Hybrid Nanofluid
Dynamic viscosity	${\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}$
Thermal expansion	${\left({\beta }_T\rho \right)}_{hnf}=\left[\left(1-{\varphi }_1\right){\left({\beta }_T\rho \right)}_f+{\varphi }_1{\left({\beta }_T\rho \right)}_{s_1}\right]\left(1-{\varphi }_2\right)+{\varphi }_2{\left({\beta }_T\rho \right)}_{s_2}$
Thermal conductivity	$\begin{array}{l}{k}_{hnf}=\frac{\left(k_{s_2}+2k_{nf}\right)-2{\varphi }_1\left(k_{nf}-k_{s_2}\right)}{\left(k_{s_2}+2k_{nf}\right)+{\varphi }_2\left(k_{nf}-k_{s_2}\right)}\\ \mathrm{with}{k}_{nf}=\frac{\left(2k_f+k_{s_1}\right)-2{\varphi }_1\left(k_f-k_{s_1}\right)}{\left(2k_f+k_{s_1}\right)+{\varphi }_2\left(k_f-k_{s_1}\right)}\times k_f\end{array}$
Density	${\rho }_{hnf}=\left[{\varphi }_1{\rho }_{s_2}+\left\{{\varphi }_1{\rho }_{s_1}+\left(1-{\varphi }_1\right){\rho }_f\right\}\left(1-{\varphi }_2\right)\right]$
Heat capacity	${\left(\rho c_p\right)}_{hnf}=\left[\left(1-{\varphi }_1\right){\left(\rho c_p\right)}_f+{\varphi }_1{\left(\rho c_p\right)}_{s_1}\right]\left(1-{\varphi }_2\right)+{\varphi }_2{\left(\rho c_p\right)}_{s_2}$

Table 2. Thermophysical properties of the water-based Ag-MgO hybrid nanofluid [44,45].

Properties	Hybrid Nanofluid
Dynamic viscosity	${\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}$
Thermal expansion	${\left({\beta }_T\rho \right)}_{hnf}=\left[\left(1-{\varphi }_1\right){\left({\beta }_T\rho \right)}_f+{\varphi }_1{\left({\beta }_T\rho \right)}_{s_1}\right]\left(1-{\varphi }_2\right)+{\varphi }_2{\left({\beta }_T\rho \right)}_{s_2}$
Thermal conductivity	$\begin{array}{l}{k}_{hnf}=\frac{\left(k_{s_2}+2k_{nf}\right)-2{\varphi }_1\left(k_{nf}-k_{s_2}\right)}{\left(k_{s_2}+2k_{nf}\right)+{\varphi }_2\left(k_{nf}-k_{s_2}\right)}\\ \mathrm{with}{k}_{nf}=\frac{\left(2k_f+k_{s_1}\right)-2{\varphi }_1\left(k_f-k_{s_1}\right)}{\left(2k_f+k_{s_1}\right)+{\varphi }_2\left(k_f-k_{s_1}\right)}\times k_f\end{array}$
Density	${\rho }_{hnf}=\left[{\varphi }_1{\rho }_{s_2}+\left\{{\varphi }_1{\rho }_{s_1}+\left(1-{\varphi }_1\right){\rho }_f\right\}\left(1-{\varphi }_2\right)\right]$
Heat capacity	${\left(\rho c_p\right)}_{hnf}=\left[\left(1-{\varphi }_1\right){\left(\rho c_p\right)}_f+{\varphi }_1{\left(\rho c_p\right)}_{s_1}\right]\left(1-{\varphi }_2\right)+{\varphi }_2{\left(\rho c_p\right)}_{s_2}$

where the subscripts $nf,hnf,f,s_1,s_2,{\varphi }_1$, and ${\varphi }_2$ indicate the respective nanofluid, hybrid nanofluid, and the regular base fluid, $s_1$ and $s_2$ designate Ag and MgO nanoparticles, respectively, ${\varphi }_1$ and ${\varphi }_2$ signify the solid nanoparticles volume fraction. In addition, $k_s$ and $k_f$ correspond to the thermal conductivity of the solid nanoparticles andbase fluid, respectively, ${\mu }_f$ is the dynamic viscosity of the base fluid, ${\rho }_s$ and ${\rho }_f$ correspond the density of the solid nanoparticles and the base fluid, ${\left({\beta }_T\right)}_f$ and ${\left({\beta }_T\right)}_s$ correspond the thermal expansion of the carrier-based fluid and solid nanoparticles, ${\left(\rho c_p\right)}_f$ and ${\left(\rho c_p\right)}_s$ called the specific heat capacity of the carrier-based fluid and solid nanoparticles, respectively.

2.3. Similarity Transformations

Following Basha et al. [44], the appropriate self-similarity transformation to change our model into a dimensionless form. Let us introduce the requisite similarity transformation which can be demarcated as follow:

$$\begin{array}{l}\eta ={\lambda }_0\frac{y}{x},\psi \left(x,y\right)={\lambda }_0{\alpha }^{*}f\left(\eta \right),u=f^{\prime }\frac{c{x}^m}{{\left(1+\mathrm{Pr}\right)}^{2E}},\mathrm{Pr}=\frac{{\nu }_f}{{\alpha }^{*}},{\alpha }^{*}=\frac{k_f}{{\left(\rho c_p\right)}_f}\\ v=-{\lambda }_0\left(\frac{{\alpha }^{*}}{x}\right)\left[\frac{m+1}{2}f\left(\eta \right)+\eta \frac{m-1}{2}{f}^{\prime }\left(\eta \right)\right],T=T_{0}x\theta \left(\eta \right)+T_{\infty },\end{array}$$

(6)

where $\eta \left(x,y\right)$ the pseudo-similarity variable, $\psi \left(x,y\right)$ the stream function, ${\nu }_f$ the kinematic viscosity, and ${\alpha }^{*}$ the thermal diffusivity.

Now, implementing the aforementioned transformation (6) into PDE’s Equations (2) and (3) along with the appropriate boundary stipulations (4) which can take place in the following dimensionless form as:

$$\begin{array}{l}\frac{{\mu }_d}{{\rho }_d}\mathrm{Pr}{f}^{‴}+\left(\frac{m+1}{2}\right){ff}^{″}+m\left({\left(1+\mathrm{Pr}\right)}^{4E}-{f^{\prime }}^2\right)+\frac{{\left(\rho {\beta }_T\right)}_d}{{\rho }_d}{\lambda }_{MC}\theta \cos \left(\frac{\mathsf{\Omega }}{2}\right)\\ +\frac{M_{HA}}{{\rho }_d}{\left(1+\mathrm{Pr}\right)}^{4n}\exp \left(\frac{-\eta {\alpha }_{HA}{\left(1+\mathrm{Pr}\right)}^E}{\sqrt{\mathrm{Pr}}}\right)=0,\\ \end{array}$$

(7)

$$\frac{k_d}{{\left(\rho c_p\right)}_d}{\theta }^{″}+\left(\frac{m+1}{2}\right)f{\theta }^{\prime }-\theta f^{\prime }=0,$$

(8)

where the prime signifies the change with respect to $\eta$. In which,

$${\mu }_d=\frac{{\mu }_{hnf}}{{\mu }_f},{\rho }_d=\frac{{\rho }_{hnf}}{{\rho }_f},k_d=\frac{k_{hnf}}{k_f},{\left(\rho {\beta }_T\right)}_d=\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\left(\rho {\beta }_T\right)}_f},{\left(\rho c_p\right)}_d=\frac{{\left(\rho c_p\right)}_{hnf}}{{\left(\rho c_p\right)}_f}$$

(9)

Similarly, the boundary stipulations are written in the dimensionless form as:

$$\begin{array}{l}\mathrm{At}\hspace{0.17em}\hspace{0.17em}\eta =0:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}^{\prime }\left(0\right)={\lambda }_T{\left(1+\mathrm{Pr}\right)}^{2E}+A{f}^{″}\left(0\right),\hspace{0.17em}f\left(0\right)=f_w,\hspace{0.17em}\theta \left(0\right)=B{\theta }^{\prime }\left(0\right)+1,\\ \mathrm{As}\hspace{0.17em}\hspace{0.17em}\eta \to \infty :\hspace{0.17em}\hspace{0.17em}{f}^{\prime }\left(\eta \right)\to {\left(1+\mathrm{Pr}\right)}^{2E},\hspace{0.17em}\theta \left(\eta \right)\to 0.\end{array}\}$$

(10)

The parameters involved in the current investigation are the following, the modified Hartmann number, the exponent parameter, and the mixed convection or buoyancy parameter that are demonstrated as follows:

$${\alpha }_{HA}=\frac{\pi }{d_1}\sqrt{\frac{{\nu }_{f}x}{U_{\infty }\left(x\right)}},M_{HA}=\frac{\pi j_1{M}_{1}x}{8U_{\infty }^2\left(x\right)},{\lambda }_{MC}=\frac{G{r}_x}{{\mathrm{Re}}_x^2}$$

(11)

where $G{r}_x=x^3\left(T_w-T_{\infty }\right)g{\left({\beta }_T\right)}_f/{\nu }_f^2$ the Grashof number and ${\mathrm{Re}}_x=U_{\infty }\left(x\right)x/{\nu }_f$ the local Reynolds number. To exist the similarity solution for Equations (7) and (8) along with the boundary stipulations (10), it is assumed (see Nasir et al. [48]):

$$d_1=x{d}_1^{*},M_1=x^{2m-1}{M}_1^{*}\mathrm{and}{\beta }_T=x^{2m-2}{\beta }_T^{*}$$

(12)

where $d_1^{*}$ represents the characteristic width of magnet and electrodes, $M_1^{*}$ dignify the characteristic magnetization of the permanent magnets, and ${\beta }_T^{*}$ is the constant thermal expansion coefficient. Now utilizing Equation (12) into Equation (11) to acquire the required dimensionless parameters in the following form as follow,

$${\alpha }_{HA}=\frac{\pi }{d_1^{*}\sqrt{{\mathrm{Re}}_x}},M_{HA}=\frac{\pi j_1{M}_1^{*}}{8c^2},{\lambda }_{MC}=\frac{g{T}_0{\beta }_T^{*}}{c^2}$$

(13)

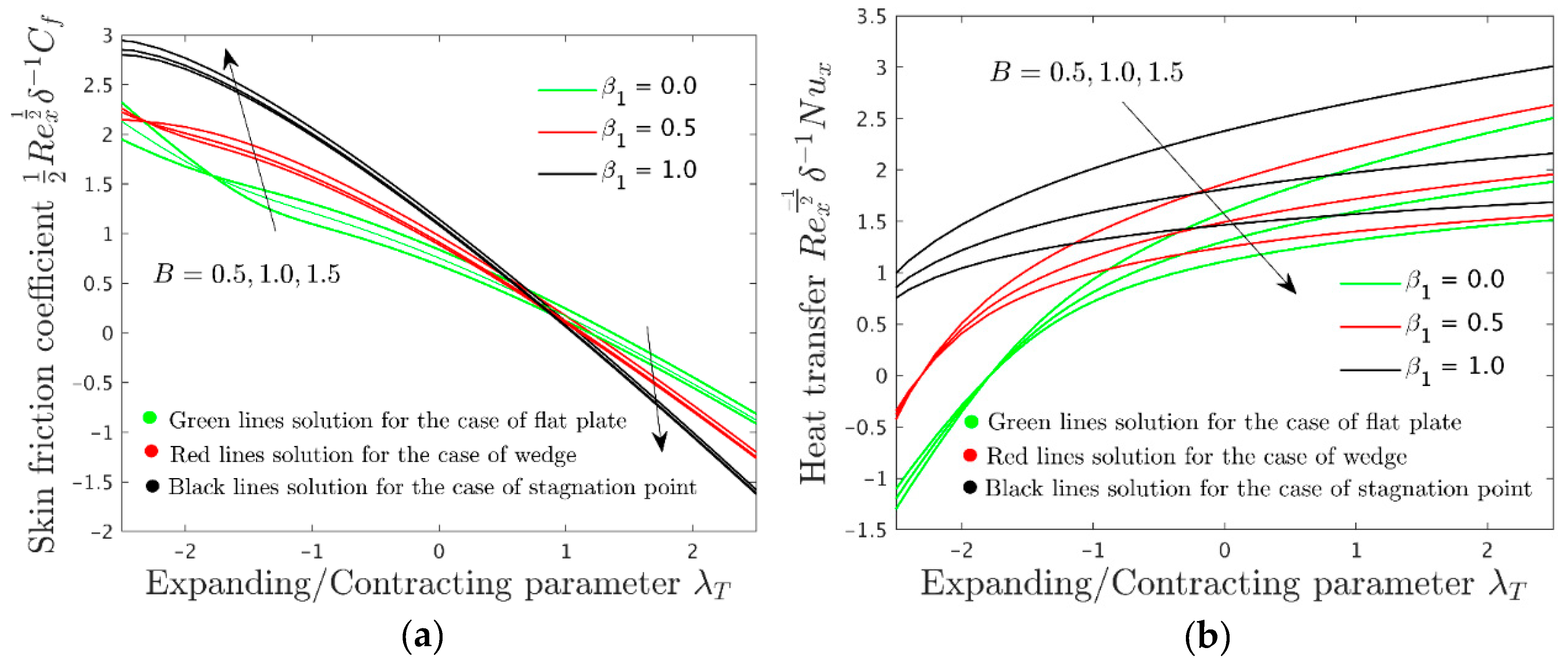
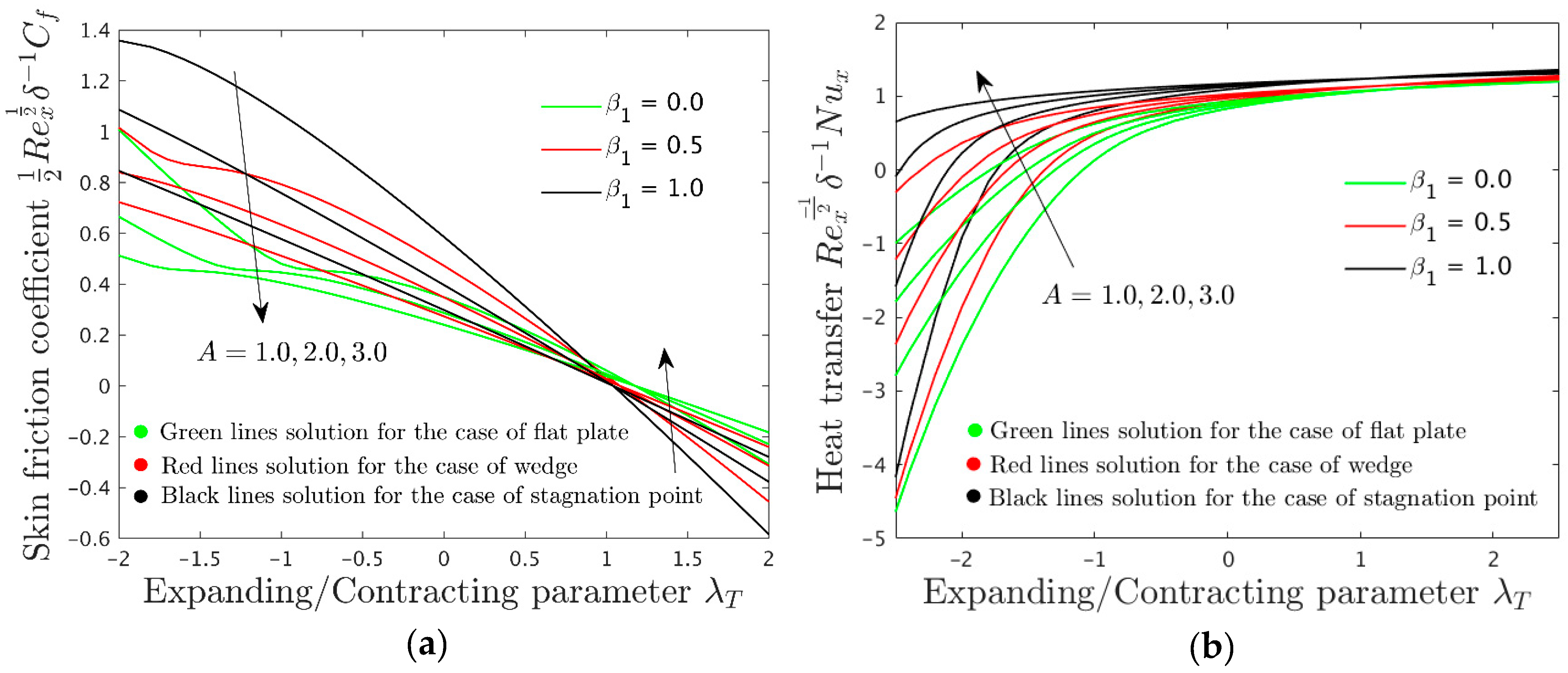
Note that the supposition of Equation (12) is important for Equation (7) to be independent or free of the variable $x$. In addition, ${\lambda }_T=b/c$ the contracting/extending surface of the wedge parameter, and ${\lambda }_T>0$ corresponds to the extending surface of the wedge and ${\lambda }_T<0$ corresponds to the contracting surface of the wedge while $f_w$ standing for the suction and injection parameter.

2.4. Engineering Physical Quantities of Interest

The gradients or physical quantities which are crucial in engineering and physics for the fluid flow symmetry behavior as well as for the practical purposes to design equipment at the nanoscale and micro-level are the friction factor $C_f$, and the heat transfer $N{u}_x$, which are demarcated as,

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}_{\infty }^2\left(x\right)}\mathrm{and}N{u}_x=\frac{q_{w}x}{k_f\left(T_w\left(x\right)-T_{\infty }\right)}$$

(14)

whereas in (14), ${\tau }_w$ corresponds to the wall shear stress along the surface of the Riga wedge and $q_w$ is the wall heat flux of the contracting and expanding surface of the Riga wedge, and are mathematically given by,

$${\tau }_w={{\mu }_{hnf}\frac{\partial u}{\partial y}|}_{y=0}\mathrm{and}{q}_w={-k_{hnf}\frac{\partial T}{\partial y}|}_{y=0}$$

(15)

Substituting the dimensionless variables as in (6) into (14) along with (15), we achieved the following dimensionless form of the friction factor:

$$\frac{1}{2}{\mathrm{Re}}_x^{\frac{1}{2}}{\delta }^{-1}{C}_f=\frac{{\mu }_d}{{\left(1+\mathrm{Pr}\right)}^{2E}}{f}^{″}\left(0\right),$$

(16)

and reduced form of the heat transfer,

$${\mathrm{Re}}_x^{-\frac{1}{2}}{\delta }^{-1}N{u}_x=-k_d{\theta }^{\prime }\left(0\right),$$

(17)

where ${\mathrm{Re}}_x$ corresponds the local Reynolds number.

3. Methodology of the Considered Numerical Solution

3.1. Single Solution through bvp4c Technique

The set of highly non-linear dimensionless Equations (7) and (8) along with the boundary stipulations (10) are very challenging and therefore, they cannot be solved exactly or analytically. Therefore, these achievable equations in the dimensionless form along with the associated boundary stipulations (10) have been resolved numerically using the colocation formula such as the bvp4c. This code is built-in software in MATLAB that gives the solution exercising the well-known 3-stage Lobatto IIIA formula [7,24,33] which is also based on the finite difference scheme. For the working process of the bvp4c package, first, introduce the new variables and with the help of them, we can receive the set of first-order equations from the leading dimensionless equations. The package required some appropriate initial guesses to obtain a better solution. Moreover, the boundary stipulations at $\eta$ tends to infinity are substituted via those at $\eta ={\eta }_{\infty }$. The interior iteration procedure is completed with an asymptotically convergence criterion along with the accuracy up to 10⁻⁶ level error tolerance in all cases.

3.2. Confirmation of the Existing Numerical Code

For the authentication, validation, and accuracy of the existing bvp4c code, results have compared the output of the heat transfer for the flow of stagnation point and wedge along with Lin and Lin [43] and Basha et al. [44] for the special case of taking the constant temperature at the corresponding surface of the Riga wedge, $T\left(x,y=0\right)=T_w$, the expanding/contracting wedge parameter ${\lambda }_T=1$, and neglecting the inspiration of the nanoparticles volume fraction, mass suction, slip parameters and modified Hartmann number. The heat transfers numerical values and the percentage errors for the aforementioned conditions are enlisted in

Table 3. Comparison of the heat transfer numerical outcome values for the limiting case of $T\left(x,y=0\right)=T_w$ and ${\lambda }_T=1$ in the absence of ${\varphi }_1={\varphi }_2=f_w=A=B=M_{HA}=0$. (Error % is calculated with reference to [43]).

$\mathbf{Pr}$	Stagnation Point				Wedge
	Ref. [43]	Ref. [44]	Current Solution	Error %	Ref. [43]	Ref. [44]	Current Solution	Error %
0.01	0.76098	0.76098	0.76099567	0.002	0.61437	0.61440	0.61439867	0.004
0.1	0.70524	0.70524	0.70523953	0.000	0.55922	0.55926	0.55925644	0.006
1.0	0.64032	0.64032	0.64031945	0.000	0.49396	0.49401	0.49421435	0.051
10	0.63136	0.63192	0.63191758	0.088	0.47703	0.47824	0.47819435	0.243

which shows an excellent sound and agreement with the available literature.

4. Results and Discussion

This segment of the work is committed to explore the outcomes of requisite factors for the water-based Ag-MgO hybrid nanofluid on velocity profile, temperature distribution, friction factor, and heat transfer for the solution of three different flow geometries (a flat plate, stagnation point, and wedge). For the considered flow symmetry, the effects of various constraints are exhibited through graphical pictures as well as tabular forms. Hence, the values have incorporated the numerical fixed values of the constraints in our whole simulation as $0.2\le M_{HA}\le 2.0,$ $0.025\le {\varphi }_1\le 0.035,$ $0.5\le {\lambda }_{MC}\le 1.0,$ $0.025\le {\varphi }_2\le 0.035,$ $-5.5\le {\lambda }_T\le 2.5,$ $1.0\le {\alpha }_{HA}\le 2.0,$ $1.0\le A\le 3.0,$ $0.1\le B\le 0.5,$ and $1.0\le f_w\le 3.0$. In addition, for a flat plate, wedge, and stagnation point the following particular values of ${\beta }_1$ are taken such as 0, 0.5, and 1.0, which correspond to the angle $\mathsf{\Omega }=0°,90°,180°$, respectively. The solution behavior of the three different geometries is shown graphically in Figure 2a,b, Figure 3a,b, Figure 4a,b, Figure 5a,b, Figure 6a,b and Figure 7a,b. In addition, the whole calculation of the current literature was carried out for the case of buoyancy assisting flow.

4.1. Effect of the Modified Hartmann Number on Dimensionless Velocity and Temperature Distribution Profiles

The effects of the modified Hartmann number $M_{HA}$ on the velocity and temperature distribution profiles of the three different geometries for the H₂O-based Ag-MgO hybrid nanofluid are shown in Figure 2a,b, respectively. It is clear that when the flow along with the flat plate, wedge flow, and stagnation point flow is considered the velocity is higher and the temperature is lower. A similar tendency of the velocity and temperature is detected with the upsurge of the modified Hartmann number. In this regard, the higher value of $M_{HA}$ diminishes the momentum boundary layer and thickens the thermal boundary layer. Physically, the external electric field is increased due to the higher values of M_HA, which creates the wall Lorentz or drag force parallel to the Riga stagnation point, flat plate, and the wedge. As a consequence, the stronger magnetic field causes an improvement in flow dimensionless velocity, and thus the temperature distribution of the fluid decreases.

Figure 2. (a) Influence of $M_{HA}$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Influence of $M_{HA}$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Figure 2. (a) Influence of $M_{HA}$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Influence of $M_{HA}$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$.

4.2. Effect of the Solid Nanoparticle Volume Fractions on Dimensionless Velocity and Temperature Distribution Profiles

The velocity and temperature profiles for the H₂O-based Ag-MgO hybrid nanofluid due to varying the volume fraction of nanoparticles are presented in Figure 3a,b, respectively. It is found that the velocity decreases and the temperature increase for higher values of ${\varphi }_1$ and ${\varphi }_2$. Conversely, the dimensionless velocity increases, and profiles of temperature decrease according to the flat plate, wedge flow, and stagnation point flow irrespective of ${\varphi }_1$ and ${\varphi }_2$. Since the thermophysical features of the hybrid nanofluid are altered with the inclusion of nanoparticles and it is heavier, hence the velocity of the fluid diminishes.

Figure 3. (a) Influence of ${\varphi }_1$ and ${\varphi }_2$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$. (b) Influence of ${\varphi }_1$ and ${\varphi }_2$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$.

Figure 3. (a) Influence of ${\varphi }_1$ and ${\varphi }_2$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$. (b) Influence of ${\varphi }_1$ and ${\varphi }_2$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$.

4.3. Effect of the Suction Parameter on Dimensionless Velocity and Dimensionless Temperature Distribution Profiles

In Figure 4a,b, the influence of the suction parameter $f_w$ on dimensionless velocity and dimensionless temperature for the H₂O-based Ag-MgO hybrid nanofluid are illustrated, respectively. With the increase of $f_w$, the profiles of dimensionless velocity for the hybrid nanofluid increase but its temperature decreases. Whatever the choice of the suction parameter is considered the highest velocity is for a stagnation point and the lowest velocity is for a flat plate. The contrary trend is observed in the phenomenon of temperature. As the suction of fluid through the surface accelerates the flow velocity hence the cold fluid particles come close to the surface. For this reason, the aforesaid characteristics are identified.

Figure 4. (a) Influence of $f_w$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, and ${\varphi }_2=0.025$. (b) Influence of $f_w$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, and ${\varphi }_2=0.025$.

Figure 4. (a) Influence of $f_w$ on dimensionless velocity ($f^{\prime }\left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, and ${\varphi }_2=0.025$. (b) Influence of $f_w$ on dimensionless temperature distribution ($\theta \left(\eta \right)$) for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-5.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, and ${\varphi }_2=0.025$.

4.4. Influence of the Solid Nanoparticle Volume Fractions on Shear Stress and Heat Transfer

The influences of the volume fraction of nanoparticles on the skin friction coefficient and heat transfer for the H₂O-based Ag-MgO hybrid nanofluid against the expanding/contracting parameter are exhibited in Figure 5a,b respectively. It is more clearly observable from these figures that the local skin friction coefficient augments for ${\mathsf{\lambda }}_T\le 1$ and shrinkages for ${\mathsf{\lambda }}_T\ge 1$. Due to the increase of the values of ${\varphi }_1$ and ${\varphi }_2$ it also increases in the range ${\mathsf{\lambda }}_T\le 1$, but a decreasing behavior is seen in the range ${\mathsf{\lambda }}_T\ge 1$. In contrast, the heat transfer gradually increases by diminishing the contracting parameter and increasing the expanding parameter. Moreover, for larger values of ${\varphi }_1$ and ${\varphi }_2$ the heat transfer increases which eventually uplifts the thermal conductvity.

Figure 5. (a) Deviation of local skin friction coefficient for several values of ${\varphi }_1$ and ${\varphi }_2$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$. (b) Deviation of the heat transfer for several values of ${\varphi }_1$ and ${\varphi }_2$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$.

Figure 5. (a) Deviation of local skin friction coefficient for several values of ${\varphi }_1$ and ${\varphi }_2$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$. (b) Deviation of the heat transfer for several values of ${\varphi }_1$ and ${\varphi }_2$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $B=0.5$, $\mathrm{Pr}=6.2$, $A=2.0$, $E=1/6$, $f_w=1.0$, and $M_{HA}=0.2$.

4.5. Effect of the Temperature and Velocity Slip Constraint on Friction Factor and Nusselt Number

The modifications in the friction factor and Nusselt number for varying temperature slip parameter $B$ for the water-based Ag-MgO hybrid nanoparticles are elucidated in Figure 6a,b, respectively. With the rising value of $B$, the skin friction coefficient is found to increase for ${\mathsf{\lambda }}_T\le 1$ and decrease for ${\mathsf{\lambda }}_T\ge 1$. Contrary to this, the heat transport augments by decreasing the contracting parameter and increasing the expanding parameter.

Figure 6. (a) Deviation of skin friction coefficient for several values of $B$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Deviation of Nusselt number for several values of $B$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Figure 6. (a) Deviation of skin friction coefficient for several values of $B$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Deviation of Nusselt number for several values of $B$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$.

The variations of A on the friction drag and the rate of heat transfer are highlighted in Figure 7a,b, respectively while numerical values are presented in

Table 4. Numerical values of the Shear Stress for the three different geometries varying the mixed convection parameter, velocity slip parameter, mass suction parameter, and dimensionless exponent parameter while the rest are fixed.

${\mathit{\lambda }}_{\mathit{M}\mathit{C}}$	${\mathit{f}}_{\mathit{w}}$	$\mathit{A}$	${\mathit{\alpha }}_{\mathit{H}\mathit{A}}$	$\left(1/2\right){\mathbf{Re}}_{\mathit{x}}^{1/2}{\mathit{\delta }}^{-1}{\mathit{C}}_{\mathit{f}}$
				${\mathit{\beta }}_1=0.0$	${\mathit{\beta }}_1=0.5$	${\mathit{\beta }}_1=1.0$
0.5	1.0	2.0	1.0	1.2585	1.2525	1.3191
0.7	-	-	-	1.2653	1.2621	1.3562
1.0	-	-	-	1.2751	1.2758	1.3935
0.5	1.0	2.0	1.0	1.2585	1.2525	1.3191
-	2.0	-		1.2592	1.2467	1.5943
-	3.0	-	-	1.2428	1.2462	1.7214
0.5	1.0	1.0	1.0	2.0146	1.9988	1.9761
-	-	2.0	-	1.2585	1.2525	1.3191
-	-	3.0	-	0.9277	0.9405	1.2118
0.5	1.0	2.0	1.0	1.2585	1.2525	1.3191
-	-	-	1.5	1.2593	1.2528	1.3047
-	-	-	2.0	1.2595	1.2527	1.2970

. As the value of A is increased a shrinkage in the skin friction coefficient is seen in the range ${\mathsf{\lambda }}_T\le 1$ and it is increased for ${\mathsf{\lambda }}_T\ge 1$. Oppositely, the heat transfer always increases for ${\mathsf{\lambda }}_T\ge -2.5$ due to the increase of A. However, in the case of expanding parameter, that is ${\mathsf{\lambda }}_T\ge 1$, the heat transfer is changed a little bit.

Figure 7. (a) Deviation of skin friction coefficient for several values of $A$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $B=0.5$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Deviation of heat transfer for several values of $A$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $B=0.5$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Figure 7. (a) Deviation of skin friction coefficient for several values of $A$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $B=0.5$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$. (b) Deviation of heat transfer for several values of $A$ against ${\mathsf{\lambda }}_T$ for the three different cases of geometry such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation point (${\beta }_1=1.0$) when ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $B=0.5$, $E=1/6$, $M_{HA}=0.2$, $f_w=1.0$, and ${\varphi }_2=0.025$.

4.6. The Computational Values of the Shear Stress and Nusselt Number for the Flow Geometries of the Wedge, Flat Plate, and Stagnation Point Due to the Effect of Various Varying Parameters

In Table 4 and

Table 5. Numerical values of the heat transfer for the three different geometries varying the mixed convection parameter, temperature slip parameter, mass suction parameter, and dimensionless exponent parameter while the rest are fixed.

${\mathit{\lambda }}_{\mathit{M}\mathit{C}}$	${\mathit{f}}_{\mathit{w}}$	$\mathit{B}$	${\mathit{\alpha }}_{\mathit{H}\mathit{A}}$	${\mathbf{Re}}_{\mathit{x}}^{-\frac{1}{2}}{\mathit{\delta }}^{-1}\mathit{N}{\mathit{u}}_{\mathit{x}}$
				${\mathit{\beta }}_1=0.0$	${\mathit{\beta }}_1=0.5$	${\mathit{\beta }}_1=1.0$
0.5	1.0	0.5	1.0	−13.2431	−9.2025	−1.2299
0.7	-	-	-	−9.3317	−6.3996	−0.5940
1.0	-	-	-	−6.3905	−4.2928	−0.2116
0.5	1.0	0.5	1.0	−13.2431	−9.2025	−1.2299
-	2.0	-	-	−12.0503	−5.8362	0.9478
-	3.0	-	-	−9.9226	−0.7498	1.2777
0.5	1.0	0.1	1.0	−14.3720	−11.2200	−4.9021
-	-	0.3	-	−14.1125	−10.2073	−1.6997
-	-	0.5	-	−13.2431	−9.2025	−1.2299
0.5	1.0	0.5	1.0	−13.2431	−9.2025	−1.2299
-	-	-	1.5	−13.5935	−9.5456	−1.6407
-	-	-	2.0	−13.8065	−9.7651	−1.9222

, the influences of $f_w$, ${\mathsf{\lambda }}_{MC}$, and ${\alpha }_{HA}$ on the skin friction coefficient (SFC) and heat transfer are illustrated. It is evident from the numerical values that when ${\mathsf{\lambda }}_{MC}$ is increased to 0.5, 0.7, and 1.0, the SFC grows but the heat transfer diminishes. This is because the higher value of ${\mathsf{\lambda }}_{MC}$ induces a larger buoyancy force and consequently the upward flow velocity becomes stronger and the SFC increases. In addition to, for higher values of ${\alpha }_{HA}$, the skin friction for flat plate increases whereas that for stagnation point decreases. Contrary to this, the heat transfer is higher for larger ${\alpha }_{HA}$. An increase in $f_w$ reduces the skin friction coefficient for the stagnation point and wedge, however, the heat transfer for the flat plate and wedge.

4.7. Grid Sensitivity Analysis

The grid independence test has been carried out and the values of the dimensionless velocity $f^{\prime }\left(\eta \right)$ and dimensionless temperature distribution $\theta \left(\eta \right)$ for the following different flow geometries such as flat plate (${\beta }_1=0.0$), wedge (${\beta }_1=0.5$) and stagnation-point (${\beta }_1=1.0$) are presented in

Table 6. Grid sensitivity analysis for the case of flat plate (${\beta }_1=0.0$) when ${\lambda }_T=-3.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $M_{HA}=0.2$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Function	$\mathit{h}$	$\mathit{\eta }$
		0.5	2.0	4.0	6.0	8.0	10.0
$f^{\prime }\left(\eta \right)$	50.0	−1.4733	0.2943	1.2159	1.6600	1.8729	1.9310
	75.0	−1.4923	0.2982	1.2124	1.6595	1.8728	1.9310
	100.0	−1.4920	0.2918	1.2123	1.6593	1.8728	1.9310
$\theta \left(\eta \right)$	50.0	10.7621	7.0693	0.8839	0.0192	0.0000	0.0000
	75.0	10.7265	7.0450	0.8993	0.0194	0.0000	0.0000
	100.0	10.7270	7.0854	0.8998	0.0194	0.0000	0.0000

,

Table 7. Grid sensitivity analysis for the case of wedge (${\beta }_1=0.5$) when ${\lambda }_T=-3.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $M_{HA}=0.2$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Function	$\mathit{h}$	$\mathit{\eta }$
		0.5	2.0	4.0	6.0	8.0	10.0
$f^{\prime }\left(\eta \right)$	50.0	−1.3034	0.5428	1.6202	1.8929	1.9287	1.9310
	75.0	−1.4938	0.5613	1.6189	1.8921	1.9287	1.9310
	100.0	−1.4506	0.5551	1.6183	1.8916	1.9287	1.9310
$\theta \left(\eta \right)$	50.0	6.4723	3.5353	0.1865	0.0003	0.0000	0.0000
	75.0	6.3718	3.4750	0.1884	0.0003	0.0000	0.0000
	100.0	6.4017	3.4954	0.1893	0.0003	0.0000	0.0000

and

Table 8. Grid sensitivity analysis for the case of stagnation point (${\beta }_1=1.0$) when ${\lambda }_T=-3.5$, ${\lambda }_{MC}=0.5$, ${\alpha }_{HA}=2.0$, $M_{HA}=0.2$, $B=0.5$, $\mathrm{Pr}=6.2$, ${\varphi }_1=0.025$, $A=2.0$, $E=1/6$, $f_w=1.0$, and ${\varphi }_2=0.025$.

Function	$\mathit{h}$	$\mathit{\eta }$
		0.5	2.0	4.0	6.0	8.0	10.0
$f^{\prime }\left(\eta \right)$	50.0	−1.2187	0.8625	1.8086	1.9250	1.9309	1.9310
	75.0	−1.2258	0.8811	1.8024	1.9250	1.9309	1.9310
	100.0	−1.2449	0.8748	1.8020	1.9249	1.9309	1.9310
$\theta \left(\eta \right)$	50.0	2.1522	0.7952	0.0091	0.0000	0.0000	0.0000
	75.0	2.1530	0.7758	0.0103	0.0000	0.0000	0.0000
	100.0	2.1594	0.7823	0.0104	0.0000	0.0000	0.0000

, respectively. It is performed basically here for the three different values of the grid or step sizes such as 50.0, 75.0, and 100.0 while all the other parameters are taking to be fixed. In addition, from the output of the numerical tables, it is seen that the results are in good agreement.

5. Conclusions

Here, it has been presented the influences of the H₂O-based Ag-MgO hybrid nanofluid on the combined effect of free and forced convection near a stagnation point in a contracting/expanding Riga wedge along with the significant impacts of slip. The key findings of the present flow symmetry investigation are listed as follows.

• The dimensionless velocity profile and momentum boundary layer width is enhancing due to greater values of $M_{HA}$ and $f_w$ for the dynamics of flow cases such as stagnation point, flat plate, and wedge, while the temperature shows the opposite behavior.
• It is established that the dimensionless velocity profiles declines and the temperature uplifts forthe higher volume fraction of nanoparticles.
• The stagnation point case has a larger velocity profile as compared to the flat plate and wedge cases, while the temperature profile is larger for the case of the flat plate than for the stagnation point and wedge.
• The outcomes indicate that the local SFC upsurges for the range of ${\mathsf{\lambda }}_T\le 1$ and decreases for the range of ${\mathsf{\lambda }}_T\ge 1$ owing to the higher nanoparticles volume fraction and the temperature slip parameter. Instead, the heat transfer rate is increasing for the larger contracting parameter and decreasesfor the expanding parameter owed to the advanced values of the hybrid nanoparticles while the change tendency is detected for the temperature slip parameter.
• With the higher values of the velocity slip parameter, a decrease in the skin friction coefficient is seen in the range ${\mathsf{\lambda }}_T\le 1$ and it is increased for ${\mathsf{\lambda }}_T\ge 1$ while the heat transfer rate is increased.
• The skin friction coefficient is increased with the percentage of 0.540%, 0.766%, 2.812%, 0.063%, 0.023%, and 0.030% for the values of the mixed convection parameter, and the values of the dimensionless exponent parameter, respectively. In addition, the shear stress is reduced due to the higher impact of suction and velocity slip parameter with the percentage of 0.738%, 0.463%, and 7.3835 and 37.531%, 37.337%, and 33.247%, respectively.

The existing work can be expanded in a variety of ways, such as analyzing various aspects such as buoyancy flow in conjunction with motile microorganisms or different effects such as thermal stratification, which is very effective in pool-type reactor systems.