Abstract
In the paper, we determine the period of an n-dimensional nonlinear dynamical system by using a derived formula in an (n + 1)-dimensional augmented space. To form a periodic motion, the periodic conditions in the state space and nonlinear first-order differential equations constitute a special periodic problem within a time interval with an unknown length. Two periodic problems are considered: (a) boundary values are given and (b) boundary values are unknown. By using the shape functions, a boundary shape function method (BSFM) is devised to obtain an initial value problem with the initial values of the new variables given. The unknown terminal values of the new variables and period are determined by two iterative algorithms for the case (a) and one iterative algorithm for the case (b). The periodic solutions obtained from the BSFM satisfy the periodic conditions automatically. For the numerical example, the computed order of convergence displays the merit of the BSFM. For the sake of comparison, the iterative algorithms based on the shooting method for cases (a) and (b) were developed by directly implementing the Poincaré map into the fictitious time-integration method to determine the period. The BSFM is better than the shooting method in terms of convergence speed, accuracy, and stability.
1. Introduction
The study of nonlinear ordinary differential equations (ODEs) is highly important for many practical applications, since the most dynamical phenomena in our real world are described by nonlinear ODEs. In the last few decades, considerable attention was focused on the periodic solutions of nonlinear oscillators [1], which are ubiquitous in every area of science concerned with oscillatory phenomena, not only in the areas of mechanics and physics, but also in other disciplines involving engineering applications.
Computational methods have been developed for determining the periodic solutions of nonlinear ODEs, such as the linearized Lindstedt–Poincaré method [2], the harmonic balance method [3,4,5], the variational iteration method [6,7], the homotopy perturbation method [8,9,10], the parameter-expanding method [11], the exp-function method [12], the differential transform method [13], and the optimal scale polynomial interpolation technique [14]. Dai et al. [15,16] employed a simple time-domain collocation method to solve nonlinear oscillatory problems. Khan et al. [17] solved the periodic solutions of a nonlinear Duffing oscillator quickly by using the modified harmonic balance method with optimal scales and the optimally scaled polynomial-Fourier-series method. Viswanath [18] developed a method to compute high-precision periodic orbits of nonlinear dynamical systems based on the linearized Lindstedt–Poincaré method.
The periodic problems of nonlinear dynamical systems involve complicated situations. Not all nonlinear dynamical systems allow periodic motions; even if periodic motion is present in a nonlinear dynamical system, not all the initial points necessarily possess a periodic orbit to emanate from it. In practice, the periodic conditions are the basic requirements of the numerical method for determining the unknown period of a system, but for many nonlinear dynamical systems, the periodic conditions are highly unsuitable, since most of the initial points do not lead to periodic orbits in the state space. For most nonlinear dynamical systems, the periods are unknown, and the determination of these periods and periodic solutions is a difficult issue. Although AUTO, COCO, or MATCONT can be used to solve the periodic problems of nonlinear ODEs, new and efficient methods are still important to solve this complex periodic problem.
The idea of the boundary shape function (BSF) was first introduced by Liu and Chang [19] to find the periodic solutions of nonlinear jerk equations, and by Liu et al. [20] to solve the optimal control problems of nonlinear Duffing oscillators. Since the methods of the BSF are versatile, they have been successfully applied to solving boundary value problems. However, the current problems with unknown period and periodic boundary values in the n-dimensional space are more difficult to solve.
This paper is structured as follows. In Section 2, a novel formula is derived in an (n + 1)-dimensional augmented space for n-dimensional first-order ODEs to compute the period. For the two cases considered in Section 3, we derive two sets of shape functions. In Section 4, we introduce new variables whose initial values are given, such that the periodic problem is framed as an initial value problem, and three iterative algorithms, based on the boundary shape function method (BSFM), to account for different periodic problems. Seven numerical examples are given in Section 5 to test the proposed new iterative algorithms’ ability to solve the periodic problems of nonlinear ODEs. The periodic problem for the non-autonomous system of nonlinear ODEs is discussed in Section 6, where the periodic solutions of the forced Duffing oscillator are given. Finally, we draw some conclusions in Section 7.
2. Nonlinear First-Order ODEs and Period
We can transform any n-th order ODE into a system of n first-order ODEs in the state space. Here, we consider the periodic problem of n first-order ODEs:
The extension to a non-autonomous system of n first-order ODEs is discussed in Section 6. In terms of , it follows from Equation (1) that
When is an unknown constant, there are two periodic boundary conditions to be considered:
For the case (a), are given, such that there is only one unknown period T to be determined. For the case (b), are not given, such that n + 1 unknown values and T are to be determined. In (a) and (b), the common parts are termed periodic conditions in the state space. Equations (2) and (3) or (4) constitute periodic problems in the state space. It is apparent that the periodic problem (b) is more difficult than the periodic problem (a).
It must be emphasized that periodic solutions may not exist for some ODEs, and that there may be infinitely more periodic solutions for others, such as the Lorenz dynamical system. Therefore, the periodic problem we consider here must be present in at least one periodic motion in the state space, but it may be that not all initial points permit the periodic motion. Hence, the periodic problem with case (b) is proposed to seek such a periodic motion in the state space, with both period and initial point being unknown. Some ODEs permit periodic motions for most initial points, and the period depends on the given initial point. Hence, the periodic problem with case (a) is proposed for seeking the unknown period of such a periodic motion in the state space. Notice that the periodicity condition in Equations (3) and (4) is, in essence, the Poincaré map of the sought periodic orbit, also known as the first return map.
In order to evaluate the period T in Equation (2), we introduce a supplementary variable by considering its evolution:
where is a given initial value and the index is one integer among . Taking the product of to the I-th equation, and using Equation (5), Equation (2) with and the following formula:
we can obtain
which is integrated by using Equations (3) and (4) with ,
We can choose a suitable index and some suitable values of to cause
such that the period can be computed from Equation (8) by
which expresses the period in an (n + 1)-dimensional augmented space .
3. Shape Functions
According to [19], two sets of shape functions are derived to solve the periodic problem of Equation (1) for the two cases (a) and (b) in Equations (3) and (4).
Theorem 1.
For case (a), we take two shape functions by
For any function ,
Satisfy the periodic conditions in Equation (3).
Proof.
Inserting into Equation (12), leads to
Upon using and from Equation (11), which becomes
Thus, we prove the first part of Equation (3). Similarly, inserting into Equation (12) and using and from Equation (11) yields
Thus, the second part of Equation (3) is proven. □
Theorem 2.
For the case (b), we let the shape functions be
where are constant parameters. For any function ,
Satisfy the periodic conditions in Equation (4).
Proof.
It follows from Equation (14) after inserting and that
Subtracting the first by the second yields
which, with the aid of Equation (13), becomes
The proof is ended. □
4. Iterative Algorithms
4.1. First BSFM Iterative Algorithm
From Theorem 1, for case (a), we transform the periodic problem into the initial value problem with the help of the shape functions. For this iterative algorithm, we can consider the variable transformation from to a new variable by
where
Equation (2) in terms of is presented by a new system of first-order ODEs:
where
are constants. Upon knowing and giving as the initial values, Equation (17) can be integrated to obtain .
In terms of . in Equation (15), in Equation (10) reads as
which by letting
yields
Next, our task is to use Equations (20)–(22) to determine the unknown period .
Here, in the function are unknown constants, which are denoted by . The first BSFM iterative algorithm for Equation (1) of the case (a) is given as follows: (i) Give , , , , , , , and , and (ii) for , with steps, we integrate n + 3 first-order ODEs involving Equation (17) and
where the first equation is derived from Equations (5) and (15), and the last two equations are derived from Equations (20) and (21), with initial values obtained by inserting . Take
where is given. The iteration is terminated until
4.2. Second BSFM Iterative Algorithm
Next, we come to a more difficult periodic problem of Equations (2) and (4). The second BSFM iterative algorithm for solving Equation (1) of case (b) is similar to that in Section 4.1, merely replacing by
We can obtain
where are the convergent values of the sequence , , and Equation (25) is obtained from Equation (14) by inserting . and using .
For case (b), we can insert Equation (25) with for into Equation (23) to accelerate the speed of convergence of the computation of .
4.3. Third BSFM Iterative Algorithm
Theorem 1 is modified to the following for case (a) in Equation (3):
Theorem 3.
For any functions , given by Equation (14) satisfy the periodic conditions (3) for the case (a), if are given by
where and . Moreover, we have
Proof.
In Theorem 2, has been proven for given by Equation (14); hence, we merely need to prove that given by Equation (14) satisfy , if the condition (26) holds. Inserting into Equation (14), leads to
Using Equation (13), which becomes
Inserting Equation (26) for , it changes to
Hence, we prove in Equation (3). Equation (27) follows from Equation (26) directly.
From Theorem 3, we can either specify by Equation (26) or specify by Equation (27). For the latter, are obtained upon giving and , and we can reduce the n + 1 unknown constants from to since it is the only unknown constant to be determined. Accordingly, we can develop the third BSFM iterative algorithm for Equation (1) of case (a): (i) Give , , , , , , initial guess of , , and , and compute , by Equation (27). (ii) For , integrate Equation (17) with given by Equation (24) and
Take
If converges according to
then the iteration is terminated. □
In the iterative algorithms of the above three BSFMs, the initial guesses of , are required in the variable transformations from to ; however, the iterative algorithms are not sensitive to , , of which , are taken for all testing examples.
4.4. Shooting Method
Let be a vector. If is located on a periodic orbit with the minimal period , then the Poincaré map is given by [21]:
where is a flow of the dynamical system emanating from the initial point . The shooting method has been described in [21], wherein the Poincaré map was solved by the Newton–Raphson iterative scheme. However, the initial guesses of and must be close to the actual values and the Jacobian must be known or approximated.
We can observe that the vector periodicity condition in Equation (28) is equivalent to a scalar equation:
where is the Euclidean norm. Instead of solving Equation (28), we can solve Equation (29) in the newly developed shooting method.
The shooting method to solve Equations (2) and (3) requires adjustment of an unknown period , such that after integrating Equation (2) with the given initial conditions , the integrated results of can match in Equation (3). Let
be an implicit function of and we solve
To obtain the period .
By introducing a fictitious time variable, , Equation (31) is recast to a first-order ODE [22]:
Integrating it for solving , yields
where is a fictitious time increment and . The iterations in Equation (33) can be terminated if . The above method is termed the fictitious time-integration method [22].
For the periodic problem in Equations (2) and (4), we can develop the following shooting method: (i) Give initial guesses of and , , , , and . (ii) For , integrate Equation (2) and take
If converge with
then stop. For the periodic problem (a), in Equation (34) is replaced by the given .
Remark 1.
In the shooting method,in Equation (2) orin Equation (1) are obtained with a guessed value of the period. In the first BSFM,in Equation (17) is obtained with definite initial valuesbeing given. For the shooting method, it is not guaranteed thatin Equation (2) satisfy the right boundary conditions; however, when we insertinto Equation (12), Theorem 1 guarantees thatsatisfy the right boundary conditions.
5. Testing through Examples
In summary, we have developed three iterative algorithms based on the BSFM to determine the period and periodic solution of n-dimensional nonlinear dynamical system. For case (a), we developed two algorithms, namely the first (Theorem 1) and third BSFM (Theorem 3) iterative algorithms, based on either two shape functions in Equation (11) or n shape functions in Equation (13). For case (b), we developed one iterative algorithm, namely the second BSFM (Theorem 2), based on the shape functions in Equation (13). Below are examples through which the performance of these iterative algorithms is evaluated.
For solving a scalar equation iteratively, the numerically computed order of convergence (COC) is approximated by [23,24]:
where is a solution of and the sequence are generated from an iterative scheme. In the computation of COC, we store the values of and take where is the number of iterations for the convergence. Indeed, COC consists of a sequence of numbers, where , , and .
For the first BSFM to solve the periodic problem, we can generate the sequence . We define
where is the number of iterations for satisfying the convergence criterion, and we take , instead of the exact values, which are in general unknown. For the other two BSFMs, the processes to compute COC(k) and ACOC are the same.
5.1. Example 1
Next, the first BSFM is used to solve a two-dimensional predator–prey equation of Lotka–Volterra type [25]:
where is the population of predator and is the population of prey. The system is conserved by
whose level set is a periodic orbit. For any given initial point with and , a periodic orbit is passed through .
Under the parameters , , , , , and , the first BSFM is convergent with 7 iterations. is obtained and the errors of the periodic conditions are and . In Table 1, the sequences of COC(n) are listed, whose average is ACOC = 1.6638. This reveals that the current iterative algorithm is rapidly, with high performance.

Table 1.
The sequence of COC(n) when applying the first BSFM to example 1.
For the sake of comparison, the shooting method in Section 4.4 is applied with , , , , , and , which is convergent with 23 iterations. is obtained and the errors of the periodic conditions are and . The shooting method with ACOC = 0.9679 is more slowly convergent than the first BSFM; moreover, the first BSFM is more accurate than the shooting method to preserve the periodic conditions.
Under the parameters , , , , , and , the first BSFM is convergent with 16 iterations, as shown in Figure 1a by solid line. is obtained, and , and are shown in Figure 1b by solid line. In this case, ACOC = 1.468 is reduced, which shows that the parameter is better than . If , , , and other parameters are unchanged, the first BSFM is convergent with 76 iterations and the error in the order . ACOC = 14.85 is large than 2. That is, if the increases, it is not easy to search for the solution under a large step size. From the above results, we can state that the BSFM obtained through the different initial guess values, I, , and can approximate the same periodic T. This means that the BSFM can avoid the multi-solutions problem.
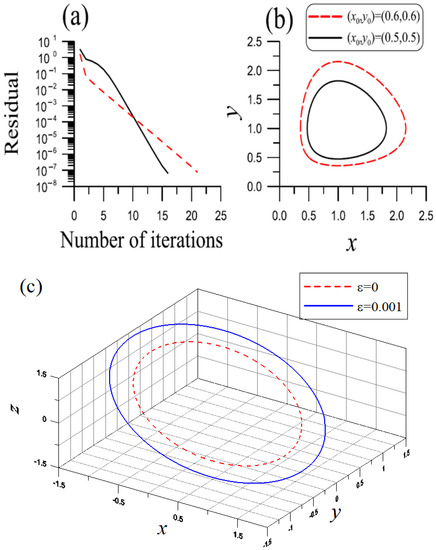
Figure 1.
Showing (a) convergence rates and (b) periodic orbits for example 1 and (c) two periodic orbits for example 2.
If we change some parameters to and and other parameters are unchanged, which is convergent with 21 iterations, as shown in Figure 1a by dashed line, is obtained with the error in the order , as shown in Figure 1b by dashed line. Rothe [26] developed a formula to compute the period of Lotka–Volterra system; however, the result is complicated and is not as accurate.
5.2. Example 2
It is known that
possess a periodic solution for arbitrary nonzero initial values with a period when .
Under the parameters , , , , , , , , , , and , the first BSFM is convergent with 28 iterations. is obtained with the error in the order of compared to the exact period . As shown in Figure 1c by dashed line, the orbit constructed is good, with the error of the periodic conditions.
Next, we consider a perturbed example with , which is solved by the second BSFM with , , , , , , , and . The number of iterations is seven under . , , , and are obtained with the errors of , , and . The periodic orbit is shown in Figure 1c by solid line. For this problem, COC(n) = 1.649 is obtained, which reveals that the second BSFM is rapidly convergent.
The shooting method in Section 4.4 is used to solve this problem with case (b), where we take the initial guesses to be , , , and , and the other parameters are , , , and . The shooting method is convergent with 45 iterations. is obtained with the errors , , and . The shooting method is more slowly convergent than the second BSFM; moreover, the second BSFM is more accurate than the shooting method at preserving the periodic conditions. We find that the shooting method is unstable in its sensitivity to the initial guesses. For instance, with the initial guesses of , , and , the shooting method is divergent.
5.3. Example 3
We consider a jerk equation [27,28]:
which has a periodic solution for certain nonzero initial values.
Under the parameters , , , , , , , , , , and , the second BSFM obtains with the absolute error in the order compared to the period obtained by the harmonic balance method [28]. , and are obtained and the periodic conditions are satisfied well with the error in the order as shown in Figure 2a by solid line.

Figure 2.
For example 3: (a) two periodic orbits. For example 4: (b) a periodic orbit. For example 5: (c) a periodic orbit.
With , , , , , and , the third BSFM based on Equation (26) is convergent with 25 iterations under . is obtained with the error in the order , as shown in Figure 2a by dashed line.
5.4. Example 4
We consider Chen’s system [29]:
Under the parameters , , , , , , , , , , and , the first BSFM is convergent with 13 iterations under . is obtained and, as shown in Figure 2b, the orbit to preserve the periodic conditions is good, with error of .
5.5. Example 5
We consider Lorenz’s system [30,31]:
As mentioned in [31], for non-standard parameters with the Lorenz system no longer displays chaotic dynamics. Especially for the initial values of , Tucker [31] found a periodic orbit with .
Under the parameters , , , , and , the first BSFM is convergent with 5 iterations under . is obtained with the error in the order of , as shown in Figure 2c. ACOC = 1.5764 is obtained to show that the first BSFM is very rapidly convergent.
5.6. Example 6
We consider the Euler equation of a rigid body motion [25,32]:
Under the parameters , , and , and the initial values , , and , the period is computed from the elliptic integral, which is .
With , , , , , and , the third BSFM based on Equation (27) is convergent with 34 iterations under , as shown in Figure 3a. is obtained, of which the error is , as shown in Figure 3b.
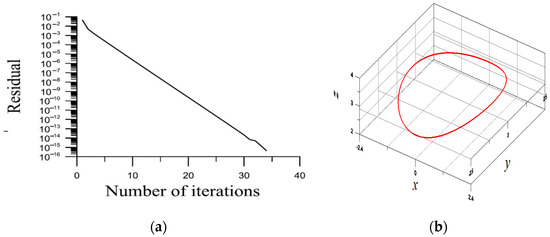
Figure 3.
For example 6: (a) convergence rate and (b) a periodic orbit.
5.7. Example 7
We consider a more difficult four-dimensional ODE [33]:
Under the parameters , . or , , , , , , , and , the orbit tends to be periodic in the steady state after , as shown in Figure 4a by dashed line, where and . The transient trajectory emanating from the initial point , , , and is not plotted in the figure.

Figure 4.
For example 7 of the four-dimensional ODEs comparing the periodic solution in the steady state obtained by the RK4 and the one obtained from the third BSFM: (a) and (b) .
With , , , , and , the third BSFM to solve this problem with is convergent with 58 iterations under . is obtained with the errors of the periodic conditions being . The periodic orbit, shown by solid line in Figure 4a, coincides with that obtained by the RK4.
For , we change some parameters to , , and , and the number of iterations reduces to 14. is obtained and the periodic conditions feature an error in the order . As shown in Figure 4b by solid line, the periodic orbit obtained from the third BSFM almost coincides with that obtained by the RK4, as shown by dashed line.
6. Non-Autonomous Dynamical System
For the n-dimensional non-autonomous dynamical system, we can consider
where the period is determined by
For the two cases in Equations (3) and (4), the numerical processes of these three BSFM iterative algorithms are the same.
Finally, we consider a more difficult forced Duffing equation:
which can be recast to
where , and , , and are to be determined. Under certain parameters, there are periodic motions in the phase plane [34].
Under the parameters , , , = 1, and , the orbit tends to be periodic in the steady state after , as shown in Figure 5a by solid line. The transient trajectory emanating from the initial point is not plotted in the figure. With , , , , , , and , the third BSFM is used to solve this problem, with its initial values obtained from the RK4 to a final time . is obtained with the periodic conditions with errors in the order .
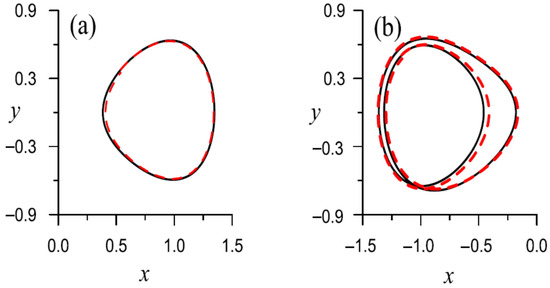
Figure 5.
For the forced Duffing oscillators solved by the third BSFM, comparing results in the phase plane by dashed line with that computed by RK4 to the steady state as shown by solid line: (a) periodic orbit and (b) -subharmonic motion.
With , the orbit tends to be -subharmonic in the steady state after , as shown in Figure 5b by solid line. The transient trajectory emanating from the initial point is not plotted in the figure. With , , , , , and , we apply the third BSFM to solve this problem, with its initial values obtained from the RK4 to a final time . is obtained with the error of the periodic conditions. On the other hand, with , , , , , and , the second BSFM solves the problem for case (b). In Table 2, we list , , , , , and the number of iterations (NIs) for different initial guess of .

Table 2.
For the forced Duffing equation, the periodic data obtained from the second BSFM for different .
In Figure 6, we show the periodic orbits in the phase plane from shorter to longer periods listed in Table 2. It can be seen that 1/2-subharmonic motions with different periods in (a) , (b) , (c) , and (d) , 1/3-subharmonic motion in (e) , and 1/4-subharmonic motion in (f) .
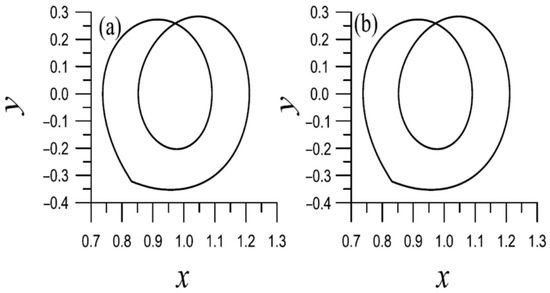
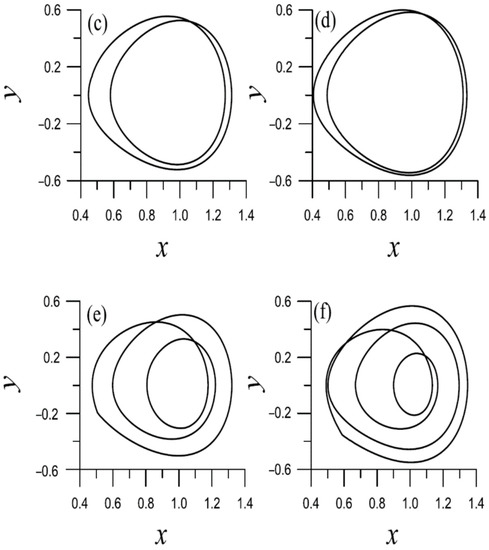
Figure 6.
For the forced Duffing oscillators solved by the second BSFM, showing periodic orbits in the phase plane from shorter to longer periods. The first four in (a–d) are 1/2-subharmonic motions, (e) is a 1/3-subharmonic motion, and (f) is a 1/4-subharmonic motion.
7. Conclusions
We normalized a nonlinear dynamical system with an unknown period that appeared in ODEs and derived an extra formula to compute the period in the augmented space, with its evolution being one variable in the nonlinear ODEs of the dynamical system. The novelties of the present paper include the methods based on the derived shape functions for the two considered cases, which transformed the periodic problem of the nonlinear dynamical system to the initial value problem for new variables. The period, the derived formula, and the terminal values of the new variables were determined iteratively. Based on the BSFM, three novel iterative algorithms were developed, and eight numerical examples were tested to confirm the high performance of the BSFMs, in which, for most of the examples, the COC was much larger than one for a few iterations. The numerical result shows that the accuracy and convergence speed is better than with the shooting method. For solving numerical procedures, the presented BSFM is easy to implement and easy to program when determining the period and periodic solution of the nonlinear dynamical system, which features no initial values. Again, we transformed the n-dimensional periodic conditions into an equivalent nonlinear scalar equation and derived an iteration formula to determine the period based on the fictitious time-integration method (FTIM). The BSFM is better than the FTIM in terms of accuracy and convergence speed. Hence, the proposed algorithm is accurate and convergent, and better than the traditional harmonic balance method, shooting method, and FTIM for nonlinear dynamic systems.
Author Contributions
C.-S.L. contributed to the conception and supervision of the work (conceptualization, resources, methodology, writing—original draft), collected and analyzed the data, and interpreted the results. C.-W.C. contributed to the design and supervision of the work (data collection, investigation, project administration, software), and validated and visualized the data. Y.-W.C. contributed to the validation of the work (writing—review and editing, validating and visualizing the data) and the funding acquisition. Y.-S.C. contributed to the writing of the work (review and editing, software, project administration). All authors have read and agreed to the published version of the manuscript.
Funding
The corresponding authors would like to thank the Ministry of Science and Technology, Taiwan for their financial support (grant number MOST 110-2221-E-019-044).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
References
- Farkas, M. Periodic Motions; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Liu, C.S.; Chen, Y.W. A simplified Lindstedt-Poincaré method for saving computational cost to determine higher order nonlinear free vibrations. Mathematics 2021, 9, 3070. [Google Scholar] [CrossRef]
- Donescu, P.; Virgin, L.N.; Wu, J.J. Periodic solutions of an unsymmetric oscillator including a comprehensive study of their stability characteristics. J. Sound Vib. 1996, 192, 959–976. [Google Scholar] [CrossRef]
- Wu, B.S.; Sun, W.P.; Lim, C.W. An analytical approximate technique for a class of strongly non-linear oscillators. Int. J. Non-Linear Mech. 2006, 41, 766–774. [Google Scholar] [CrossRef]
- Liu, L.; Thomas, J.P.; Dowell, E.H.; Attar, P.; Hall, K.C. A comparison of classical and high dimension harmonic balance approaches for a Duffing oscillator. J. Comput. Phys. 2006, 215, 298–320. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method—A kind of non-linear analytic technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Öziş, T.; Yildirim, A. A study of nonlinear oscillators with u1/3 force by He’s variational iteration method. J. Sound Vib. 2007, 306, 372–376. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Shou, D.H. The homotopy perturbation method for nonlinear oscillators. Comput. Math. Appl. 2009, 58, 2456–2459. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.S. Linearized homotopy perturbation method for two nonlinear problems of Duffing equations. J. Math. Research 2021, 13, 10–19. [Google Scholar] [CrossRef]
- Köroğlu, C.; Öziş, T. Applications of parameter-expanding method to nonlinear oscillators in which the restoring force is inversely proportional to the dependent variable or in form of rational function of dependent variable. Comput. Model. Eng. Sci. 2011, 75, 223–234. [Google Scholar] [CrossRef]
- He, J.H.; Abdou, A. New periodic solutions for nonlinear evolution equations using exp-function method. Chaos Soliton Fract. 2007, 34, 1421–1429. [Google Scholar] [CrossRef]
- Chu, H.P.; Lo, C.Y. Application of the differential transform method for solving periodic solutions of strongly non-linear oscillators. Comput. Model. Eng. Sci. 2011, 77, 161–172. [Google Scholar] [CrossRef]
- Yue, X.K.; Dai, H.H.; Liu, C.S. Optimal scale polynomial interpolation technique for obtaining periodic solutions to the Duffing oscillator. Nonlinear Dyn. 2014; 77, 1455–1468. [Google Scholar] [CrossRef]
- Dai, H.H.; Schnoor, M.; Atluri, S.N. A simple collocation scheme for obtaining the periodic solutions of the duffing equation, and its equivalence to the high dimensional harmonic balance method: Subharmonic oscillations. Comput. Model. Eng. Sci. 2012, 84, 459–497. [Google Scholar]
- Dai, H.H.; Yue, X.K.; Yuan, J.P. A time domain collocation method for obtaining the third superharmonic solutions to the duffing oscillator. Nonlinear Dyn. 2013, 73, 593–609. [Google Scholar] [CrossRef]
- Khan, N.A.; Liu, C.S.; Riaz, F. An optimally scaled polynomial-Fourier-series method for the numerical solution of the Duffing oscillator. Int. J. Appl. Nonlinear Sci. 2016, 2, 290–310. [Google Scholar] [CrossRef]
- Viswanath, D. The Lindstedt-Poincaré technique as an algorithm for computing periodic orbits. SIAM Rev. 2001, 43, 478–495. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.S.; Chang, J.R. The periods and periodic solutions of nonlinear jerk equations solved by an iterative algorithm based on a shape function method. Appl. Math. Lett. 2020, 102, 106151. [Google Scholar] [CrossRef]
- Liu, C.S.; Kuo, C.L.; Chang, J.R. Solving the optimal control problems of nonlinear Duffing oscillators by using an iterative shape functions method. Comput. Model. Eng. Sci. 2020, 122, 33–48. [Google Scholar] [CrossRef]
- Parker, T.S.; Chua, L.O. Practical Numerical Algorithms for Chaotic Systems; Springer: New York, NY, USA, 1989. [Google Scholar] [CrossRef]
- Liu, C.S.; Atluri, S.N. A novel time integration method for solving a large system of non-linear algebraic equations. Comput. Model. Eng. Sci. 2008, 31, 71–83. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Liu, C.S.; Hong, H.K.; Lee, T.L. A splitting method to solve a single nonlinear equation with derivative-free iterative schemes. Math. Comput. Simul. 2021, 190, 837–847. [Google Scholar] [CrossRef]
- Liu, C.S. Preserving constraints of differential equations by numerical methods based on integrating factors. Comput. Model. Eng. Sci. 2006, 12, 83–107. [Google Scholar] [CrossRef]
- Rothe, F. The periods of the Volterra-Lotka system. J. Reine Angew Math. 1985, 355, 129–138. [Google Scholar] [CrossRef]
- Mulholland, R.J. Non-linear oscillations of a third order differential equation. Int. J. Non-linear Mech. 1971, 6, 279–294. [Google Scholar] [CrossRef]
- Gottlieb, H.P.W. Harmonic balance approach to limit cycles for nonlinear jerk equations. J. Sound Vib. 2006, 297, 243–250. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifur. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley and Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Tucker, W. Computing accurate Poincaré maps. Physica D 2002, 171, 127–137. [Google Scholar] [CrossRef]
- Calvo, M.; Laburta, M.P.; Montijano, J.I.; Rández, L. Error growth in the numerical integration of periodic orbits. Math. Comput. Simul. 2011, 81, 2646–2661. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Liu, C.S. Cone of non-linear dynamical system and group preserving schemes. Int. J. Non-Linear Mech. 2001, 36, 1047–1068. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).