Abstract
In this work, we investigate the effects of a geometrically generated early dark energy era on the energy spectrum of the primordial gravitational waves. The early dark energy era, which we choose to have a constant equation of state parameter w, is synergistically generated by an appropriate gravity in the presence of matter and radiation perfect fluids. As we demonstrate, the predicted signal for the energy spectrum of the primordial gravitational waves is amplified and can be detectable, for various reheating temperatures, especially for large reheating temperatures. The signal amplitude depends on the duration of the early dark energy era and on the value of the dark energy equation of state parameter, with the latter affecting more crucially the amplification. Specifically, the amplification occurs when the equation of state parameter approaches the de Sitter value . Regarding the duration of the early dark energy era, we find that the largest amplification occurs when the early dark energy era commences at temperature eV until eV. Moreover, we study a similar scenario in which amplification occurs, where the early dark energy era commences at eV and lasts until the temperature is increased by eV. The discovery of primordial gravitational waves will reveal if several symmetries in the Universe exist or not so this work is important toward revealing the primordial gravitational waves.
1. Introduction
One of the solutions proposed in the literature for solving the -tension problem is the existence of an early dark energy era [1,2,3,4,5]. If such an era is observed, then this could eliminate the -tension problem. In this work, the focus is on the effects of an early dark energy era on the energy spectrum of the primordial gravitational waves generated by an gravity. Specifically we shall assume that an gravity is the underlying geometric source that drives inflation, the early dark energy era, and the late-time acceleration era, the commonly known dark energy era. In our approach, inflation will be controlled by a vacuum gravity, while the early and ordinary dark energy era will synergistically be controlled by appropriate gravity terms and radiation and cold dark matter fluids. Our aim is to see, in a quantitative way, the direct effect of a geometrically generated early dark energy era on the primordial gravitational waves energy spectrum. For our analysis, we shall use the theoretically predicted energy spectrum which appears in many studies, see, for example, Refs. [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] and references therein, and we shall numerically evaluate the effects of the gravity on the general relativistic waveform. We shall use a WKB approach developed in [29] and we shall investigate the amount of amplification caused by an early dark energy era, which is generated by an gravity in the presence of perfect matter and radiation fluids. The early dark energy era is described by a constant equation of state (EoS) parameter w, and we shall find which gravity can generate such an evolution in the presence of matter and radiation perfect fluids. Then, we shall calculate the overall amplification factor of the general relativistic energy spectrum of the primordial gravitational waves. Our results will be confronted with the sensitivity curves of future interferometric experiments, such as the LISA laser interferometer space antenna [62,63], the DECIGO [64,65], the Einstein Telescope [66], the future BBO (Big Bang Observatory) [67,68], and also the non-interferometric experiments Square Kilometer Array (SKA) [69] and the NANOGrav collaboration [70,71]. As we shall demonstrate, the general relativistic energy spectrum is amplified by the presence of an gravity-generated early dark energy era, only if several conditions hold true. Specifically, the duration of the early dark energy era plays an important role, and also the value of the EoS parameter w also crucially affects the results. As we show, in most of the cases we studied, the energy spectrum signal is amplified due to this gravity-generated early dark energy era. As a conclusion, we point out that a detection of a stochastic gravitational wave signal in future interferometric experiments may have many possible explanations, and the early dark energy realized by an f(R) gravity is one of these explanations. Also such a discovery might highlight several unrevealed symmetries of the Universe, such as supersymmetry.
2. Gravity Realization of Inflation and Subsequent Eras
The standard approach for realizing various cosmological eras in Einstein–Hilbert cosmology is usually performed by using perfect matter fluids. The latter dominate the evolution at a certain point, and the corresponding era is controlled by those fluids, for example, the radiation domination era is controlled by the radiation fluid, the energy density of which redshifts as , where a is the scale factor of a flat Friedmann–Robertson–Walker (FRW) metric. Additionally for the matter domination era, the matter perfect fluid dominates the evolution, which describes non-baryonic non-relativistic matter and its energy density redshifts as . Apart from the three standard evolution eras that we usually assume that the Universe underwent, that is, the inflationary, radiation and matter domination, and dark energy era, we basically do not know the behavior of our Universe post-inflationary. We have hints for the post-inflationary era, but no proofs. This era is a mysterious era, and it commences with the reheating era, which is the beginning of the radiation era, and it is believed that the reheating era smoothly deforms to the radiation era. Remarkably, we also lack knowledge of what happened from the reheating era up to the matter domination era, and before the recombination era. Thus, the question is: What do we know? We know very well the physics beyond the recombination era up to the present day. The recombination era is basically where the last scattering surface of the CMB photons was formed, and from this era until present day, we understand the physics relatively well.
Thus, for the epoch before the recombination era, we have no measured data, only at last scattering and beyond, so let us assume that an early dark energy era is realized before the recombination and specifically from the matter–radiation equality redshift until some final redshift in the past, deeply in the matter domination era . In this work, we shall assume that this final redshift is a free variable and we shall investigate what would be the effect of an early dark energy era on the spectrum of the primordial gravitational waves, focusing on modes which were subhorizon modes immediately after the inflationary era and during the first stages of the reheating era. Additionally, regarding the early dark energy era itself, we shall assume that it is described by a constant EoS parameter, and, more importantly, it is not realized by some perfect matter fluid, but it is realized geometrically, by some dominant form of gravity for the whole early dark energy era. It is also natural to assume that controls the inflationary and the late dark energy era, as follows:
with being the curvature scale of inflation, which is calculated primordially when the modes exit the horizon at the first time, so at the beginning of inflation. Additionally, the curvature scale is the curvature scale at the recombination, is the curvature scale when the early dark energy era commences, is the curvature at matter radiation equality, and is the curvature scale at present day, so it is basically identical to the cosmological constant. Note that according to our scenario, the era between the curvature scales is not described by modified gravity, so modified gravity affects, post-inflationary, the evolution after .
The exact forms of and will be specified shortly on the basis of phenomenological viability. Regarding the function , this in conjunction with the matter and radiation perfect fluids will synergistically generate the early dark energy era with a constant EoS parameter w, and we shall find that shortly. The function will realize the dark energy era, at late-times, so some appropriate form of this will be used in order to provide a viable dark energy era phenomenology. In order to find the exact forms of the gravity, we consider the gravitational action with perfect matter fluids present:
with , with G being Newton’s constant, and stands for the reduced Planck mass. In the metric formalism, the field equations are
with being the energy momentum tensor of the matter and radiation perfect fluids, and furthermore . For a flat FRW spacetime, in which case the line element reads
the field equations become
with , standing for the cold dark matter energy density and radiation energy density, respectively.
Now let us proceed to the core of our analysis and we assume that the Universe goes through an intermediate early dark energy era, with a constant EoS parameter w, thus , where and are the Universe’s total pressure and energy density. The early dark energy era will be assumed to last from , so from the matter radiation equality, until a redshift , which will be a free parameter in our analysis. During the early dark energy era, lasting from up to , the scale factor of the Universe is
with being the scale factor at the redshift . It is easy to find which geometrical theory can realize the cosmology (5) synergistically in the presence of matter and radiation perfect fluids. In order to do so, we shall apply the formalism of Ref. [72], so we use the e-foldings number as a dynamical variable; thus, we have
where is some initial value of the scale factor. Using the e-foldings number N, the Friedmann equation takes the form
where . Introducing the auxiliary function, , the Ricci scalar is written as follows:
Eventually, the Friedman equation becomes
where and . By solving the above equation, one obtains the gravity which realizes the given scale factor of interest, which in our case is that of Equation (5). Let us now proceed to find the explicit form of the gravity which realizes the scale factor (5). For the scale factor (5), becomes
and we took for simplicity. Upon combining Equations (8) and (10), we obtain
The above, in conjunction with the following,
affect the Friedmann Equation (9), which becomes
where the index “i” takes values , with indicating radiation and indicating cold dark matter perfect fluids. In addition, the parameters and , , and A are defined in the following way:
By solving (13) we will obtain the gravity which generates the early dark energy era, which was denoted previously, so the solution is
where are simple integration constants, and also and are
with . Let us now specify the late time era, and we shall choose a convenient gravity which is known to provide a viable late-time phenomenology. We shall choose the one used in Ref. [51], which is known to be a viable dark energy gravity model, which is
where is , and also denotes the cold dark matter energy density at present day. Furthermore, the parameter is chosen, , is an arbitrary dimensionless parameter, and is the cosmological constant. Hence, the Universe’s evolution is controlled during inflation by an model, while from and up to by given in Equation (15), and at late times by given in Equation (17). In principle, it is not hard to find such a phenomenological model, for example, such a phenomenological model would look similar to
It should be noted that the above model is not the only one that can reproduce the phenomenology we want to describe; it is one example, but certainly not the only one. We just quote one example for completeness. With regard to the early dark energy era, we shall consider three cases for values of the EoS parameter, described below:
Scenarios I and II basically describe the limiting cases of accelerating expansion, nearly a de Sitter one (Scenario I) and nearly accelerating (Scenario II, slightly smaller EoS parameter compared to the value of the EoS parameter for which non-accelerating nor decelerating cosmology occurs, namely ). Finally, for Scenario III, the EoS parameter takes an intermediate value for the sake of completeness.
Let us now proceed to the evaluation of the observational indices relevant to the calculation of the energy spectrum of the primordial gravitational waves. Specifically, we shall calculate the tensor-to-scalar ratio and the tensor spectral index. We shall be interested in modes with, which is the pivot scale used in Planck. For gravity, the tensor spectral index is [51,73,74]
and the tensor-to-scalar ratio is [51,73,74]
with being the first slow-roll index . For the gravity we have ; hence
and the corresponding tensor-to-scalar ratio is
In the next section we shall evaluate numerically the energy spectrum of the primordial gravitational waves at present day, for all the modes that became subhorizon during the early stages of the reheating era. We are interested in short wavelength modes with Mpc, or equivalently with wavenumbers Mpc−1 up to Mpc−1, which corresponds to the frequency range Hz.
3. Primordial Gravitational Wave Energy Spectrum: The Effects of an Early Dark Energy Phase
In the next ten years, several space interferometers will provide observational data on whether the theoretically predicted stochastic gravitational wave background exists or not. Already in the literature, the theoretical predictions for the stochastic background of primordial gravitational waves are intensively studied, see Refs. [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] and references therein.
In this paper, the focus is to investigate the effect of an gravity-realized early dark energy era, with constant EoS parameter w, which commences at the matter–radiation equality and stretches up to a final redshift , which shall be a free variable for the moment. Our main assumption is that , but we shall allow for other higher values for completeness in order to see the effect on the energy spectrum of the primordial gravitational waves. Let us note that the choice of is arbitrary, it just indicates the end of the early dark energy era. This is the maximum redshift which we will allow the upper redshift limit of the early dark energy era to be.
Let us discuss more the duration of the early dark energy era, and as we stated we shall assume that it starts around the matter–radiation equality at redshift , so at a temperature eV [75], and it ends at which will be assumed in the range , which corresponds to a temperature range eV [75]. In terms of the temperature, the early dark energy era does not go deeply in the radiation domination era, and specifically we shall assume that it lasts from eV up to eV; however, we shall extend the duration up to eV.
The procedure to extract the overall effect of the gravity on the primordial gravitational waves is based on a WKB method which applies on the modes that became subhorizon just after the inflationary era ended, so during the reheating era. For a pictorial representation of the subhorizon modes, see Figure 1. The WKB method was developed in Refs. [29,30] and relies on the calculation of the parameter , defined as
and the modified gravity effect on the waveform is
where is the waveform with which corresponds to the general relativity case, and also the quantity is defined as
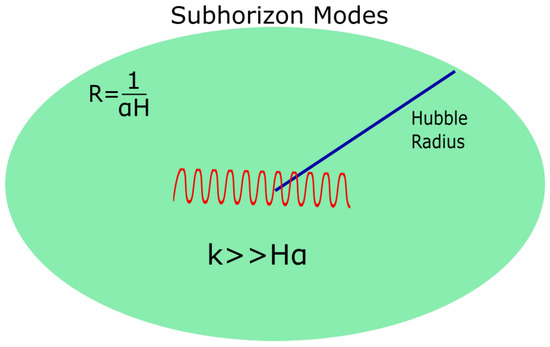
Figure 1.
Subhorizon inflationary modes which, during the inflationary era, were at subhorizon scales, and have the smallest wavelength. These are the first that reenter the horizon after the end of the inflationary era and during the early stages of the reheating era. The subhorizon modes will be probed by future space interferometers.
The primordial gravity waves energy density including the gravity effects is [9,21,22,29,30,32,51],
with Mpc−1 being CMB pivot scale. Additionally, denotes the tensor spectral index and r denotes the tensor-to-scalar ratio. The calculation of the quantity is the main aim hereafter, for the redshift ranges , and , and to see the overall amplification or damping on the energy spectrum. Thus, the quantity that needs to be calculated is
with and being calculated for and , respectively, and with varying in the range . Let us now present our analysis for the three different scenarios we defined in the previous section. For the scenarios II and III, the overall amplification factors are nearly zero; hence, the predicted energy spectrum of the primordial gravitational waves is undetectable. Just for the sake of being precise, for scenario II, the parameter is and these results apply for both the redshift ranges and . In addition, the first integral for all scenarios is of the order for all the scenarios. The only non-trivial result occurs only for the Scenario I, in which case we obtain and , so in both cases, amplification occurs for the energy spectrum. In Figure 2 and Figure 3, we plot the gravity -scaled energy spectrum as a function of the frequency, and specifically Figure 2 corresponds to the case for which the early dark energy era lasts up to and Figure 3 for . In both the plots, we also included the sensitivity curves of most of the future interferometer experiments, and the predicted energy spectrum is presented for three distinct reheating temperatures, for GeV (purple curve), for GeV (red curve), and GeV (blue curve).
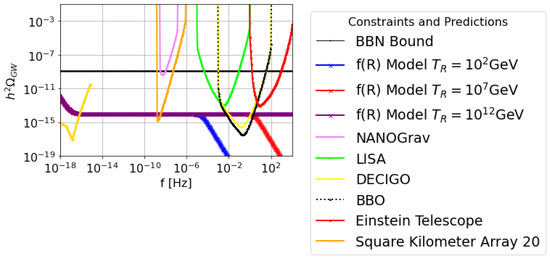
Figure 2.
The -scaled gravitational wave energy spectrum for the early dark energy w-era generated by gravity, for the Scenario I for , with reheating temperatures GeV (purple), to GeV (red) and to (blue) GeV.
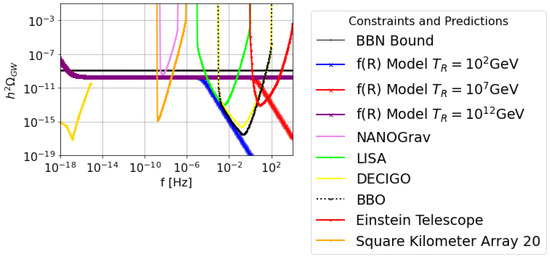
Figure 3.
The -scaled gravitational wave energy spectrum for the early dark energy w-era generated by gravity, for Scenario I for , with reheating temperatures GeV (purple), to GeV (red) and to (blue) GeV.
As it is obvious from both Figure 2 and Figure 3, the signals corresponding to the gravity models are detectable from most future experiments. Specifically, for the case with , the gravity signal will be detected by the SKA experiment for all reheating temperatures, and by the DECIGO and BBO experiments for reheating temperatures GeV and GeV. As for the case with , in which case the early dark energy era lasts slightly longer compared to the standard scenarios in the literature, the signal will be detected by all the experiments, except for the case with reheating temperature GeV, which will be detected only by the SKA and NANOGrav experiments. Let us also note that if the early dark energy era commences earlier, for example at the recombination with , and lasts until , similar results are obtained. Indeed, in this case we obtain , and in Figure 4 we plot the -scaled energy spectrum for this case. As it can be seen, the signal will be detected by all the future experiments, except for the low reheating temperature scenario. As an overall comment for all the cases we studied in this section, it seems that the signal of gravity gravitational waves depends on the duration of the early dark energy era, and for a good possibility of detection, the eras between which the early dark energy era occurs must have a temperature difference approximately of the order eV. We also need to comment on an important issue: since our WKB approach affects the subhorizon modes during reheating, the figures we presented must be looked at with caution for small frequencies, because these modes were superhorizon during reheating. Hence, our results are valid for frequencies starting from the NANOGrav until the Einstein Telescope.
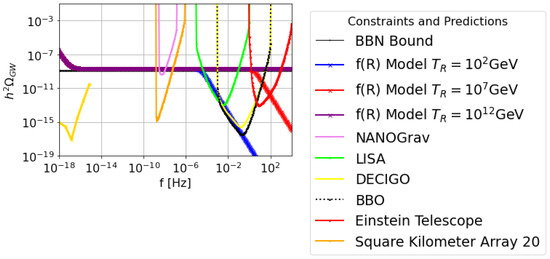
Figure 4.
The -scaled gravitational wave energy spectrum for the early dark energy w-era generated by gravity, for Scenario I for and for starting redshift of the early dark energy era , with reheating temperatures GeV (purple), to GeV (red) and to (blue) GeV.
Before closing this section, an important comment is in order. In standard contexts of the Starobinsky inflationary scenario, the signal of the primordial gravitational waves is undetectable. This has to do with the fact that the tensor spectral index for the standard Starobinsky inflation is negative, and thus, the energy spectrum of the primordial gravitational waves generated is significantly lower than the sensitivity curves of most future gravitational waves experiments. This result, however, is mainly based on a standard post-inflationary evolution, which includes the reheating, radiation domination, and matter domination eras. However, with this work, we aimed to show in a quantitative way that a geometrically generated early dark energy era which occurs just before recombination can amplify the energy spectrum significantly. By geometrically generated, we mean that the origin of this era is an gravity in the presence of matter and radiation perfect fluids. The reason for this amplification is an overall amplifying factor appearing in front of Equation (27). This factor takes into account the WKB effects of the modified gravity beyond the inflationary era. The gravitational waves still redshift as radiation but their energy spectrum is amplified, and this amplification is a direct modified gravity effect, due to the fact that the evolution equation contains a WKB overall factor. In most studies known for the Starobinsky inflation predictions for primordial gravitational waves, this post-inflationary amplification is absent, due to the fact that the post-inflationary evolution comprises the reheating, radiation domination, and matter domination eras. In our case, post-inflationary there are non-trivial effects generated by the gravity geometrically generated early dark energy era. To show in a simple and brief way this issue, in the presence of a non-trivial modified gravity, the evolution equation for tensor perturbations is described by the following equation of the tensor perturbation :
where is, in our case, given in Equation (24). If post-inflationary the evolution is the standard one, then the solution to the above equation is described by the one appearing in Equation (25) without the factor ; thus, . In our case though, the amplifying factor is non-trivial and as we showed numerically by evaluating in Equation (26) for a constant EoS parameter early dark energy era generated by gravity in the presence of matter and radiation perfect fluids, the amplification is significant.
Furthermore, we need to clarify that the epochs before the early dark energy era are not affected at all in our framework. The only effect of the early dark energy era is contained in the amplifying factor in Equation (27). The post-inflationary epochs in between inflation and the early dark energy era are contained in Equation (27), and even the era of BBN is contained there. The BBN bounds are also taken into consideration in Figure 2, Figure 3 and Figure 4, corresponding to a straight solid black line.
4. Conclusions
In this work, we investigated quantitatively the effect of a geometrically generated early dark energy era on the energy spectrum of the primordial gravitational waves. Specifically the early dark energy era is generated by an appropriate gravity in the presence of matter and radiation perfect fluids. The main assumption we made is that gravity generates the inflationary era, specifically, an gravity, the late-time acceleration era, and also the early dark energy era. As we showed, the energy spectrum of the primordial gravitational waves is significantly amplified in a detectable way, and the signal can be detected by most of the future gravitational waves experiments that will search for stochastic gravitational waves. Our analysis indicates that the amplification of the signal depends on two crucial parameters, the value of the dark energy EoS parameter w and the duration of the early dark energy era. As we showed, the amplification occurs only when the EoS parameter of the early dark energy era is close to the de Sitter value, and we specifically studied the case . In addition, the duration of the early dark energy era affects the amplification. We assumed that the early dark energy era started at up to and we also considered the case in which the early dark energy era started at up to . In both cases, the amplification is significant for and for large reheating temperatures. In conclusion, the scenario we described in this paper indicates one certain thing: if a stochastic gravitational wave signal is detected in future gravitational waves experiments, the source of this signal is far from being certain, since several scenarios might lead to such a spectrum.
Author Contributions
Investigation, E.C.L.; Supervision, V.K.O.; Writing—review & editing, V.K.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Niedermann, F.; Sloth, M.S. Resolving the Hubble tension with new early dark energy. Phys. Rev. D 2020, 102, 063527. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D 2016, 94, 103523. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Unifying inflation with early and late dark energy epochs in axion F(R) gravity. Phys. Rev. D 2021, 103, 044036. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying Inflation with Early and Late-time Dark Energy in F(R) Gravity. Phys. Dark Univ. 2020, 29, 100602. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kovetz, E.D. The Quest for B Modes from Inflationary Gravitational Waves. Ann. Rev. Astron. Astrophys. 2016, 54, 227. [Google Scholar] [CrossRef]
- Denissenya, M.; Linder, E.V. Gravity’s Islands: Parametrizing Horndeski Stability. J. Cosmol. Astropart. Phys. 2018, 11, 010. [Google Scholar] [CrossRef]
- Turner, M.S.; White, M.J.; Lidsey, J.E. Tensor perturbations in inflationary models as a probe of cosmology. Phys. Rev. D 1993, 48, 4613–4622. [Google Scholar] [CrossRef]
- Boyle, A.L.; Steinhardt, P.J. Probing the early universe with inflationary gravitational waves. Phys. Rev. D 2008, 77, 063504. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, Y.; Zhao, W.; Chen, Y. Relic gravitational waves in the accelerating Universe. Class. Quant. Grav. 2005, 22, 1383. [Google Scholar] [CrossRef]
- Schutz, B.F.; Ricci, F. Gravitational Waves, Sources, and Detectors. arXiv 2010, arXiv:1005.4735. [Google Scholar]
- Sathyaprakash, S.B.; Schutz, F.B. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Rel. 2009, 12, 2. [Google Scholar] [CrossRef]
- Caprini, C.; Figueroa, D.G. Cosmological Backgrounds of Gravitational Waves. Class. Quant. Grav. 2018, 35, 163001. [Google Scholar] [CrossRef]
- Arutyunov, G.; Heinze, M.; Medina-Rincon, D. Superintegrability of Geodesic Motion on the Sausage Model. J. Phys. A 2017, 50, 244002. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Chiba, T.; Sugiyama, N. Precision calculations of the gravitational wave background spectrum from inflation. Phys. Rev. D 2009, 79, 103501. [Google Scholar] [CrossRef]
- Clarke, T.J.; Copeland, E.J.; Moss, A. Constraints on primordial gravitational waves from the Cosmic Microwave Background. J. Cosmol. Astropart. Phys. 2020, 10, 002. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Takahashi, T.; Yokoyama, S. Blue-tilted Tensor Spectrum and Thermal History of the Universe. J. Cosmol. Astropart. Phys. 2015, 2, 003. [Google Scholar] [CrossRef]
- Nakayama, K.; Yokoyama, J. Gravitational Wave Background and Non-Gaussianity as a Probe of the Curvaton Scenario. J. Cosmol. Astropart. Phys. 2010, 1, 010. [Google Scholar] [CrossRef]
- Smith, T.L.; Kamionkowski, M.; Cooray, A. Direct detection of the inflationary gravitational wave background. Phys. Rev. D 2006, 73, 023504. [Google Scholar] [CrossRef]
- Giovannini, M. Thermal history of the plasma and high-frequency Gravitons. Class. Quant. Grav. 2009, 26, 045004. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhao, W.; Zhang, Y.; Zhu, Z.H. Detecting Relic Gravitational Waves by Pulsar Timing Arrays: Effects of Cosmic Phase Transitions and Relativistic Free-Streaming Gases. Phys. Rev. D 2016, 93, 024031. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y.; You, X.P.; Zhu, Z.H. Constraints of relic gravitational waves by pulsar timing arrays: Forecasts for the FAST and SKA projects. Phys. Rev. D 2013, 87, 124012. [Google Scholar] [CrossRef]
- Vagnozzi, S. Implications of the NANOGrav results for inflation. Mon. Not. R. Astron. Soc. 2021, 502, L11–L15. [Google Scholar] [CrossRef]
- Watanabe, Y.; Komatsu, E. Improved Calculation of the Primordial Gravitational Wave Spectrum in the Standard Model. Phys. Rev. D 2006, 73, 123515. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837–2851. [Google Scholar] [CrossRef]
- Giarè, W.; Renzi, F. Propagating speed of primordial gravitational waves. Phys. Rev. D 2020, 102, 083530. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Takahashi, T.; Yokoyama, S. Blue-tilted inflationary tensor spectrum and reheating in the light of NANOGrav results. J. Cosmol. Astropart. Phys. 2021, 1, 071. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y. Relic gravitational waves and their detection. Phys. Rev. D 2006, 74, 043503. [Google Scholar] [CrossRef]
- Nishizawa, A. Generalized framework for testing gravity with gravitational-wave propagation. I. Formulation. Phys. Rev. D 2018, 97, 104037. [Google Scholar] [CrossRef]
- Arai, S.; Nishizawa, A. Generalized framework for testing gravity with gravitational-wave propagation. II. Constraints on Horndeski theory. Phys. Rev. D 2018, 97, 104038. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I. Maximal freedom at minimum cost: Linear large-scale structure in general modifications of gravity. J. Cosmol. Astropart. Phys. 2014, 7, 050. [Google Scholar] [CrossRef]
- Nunes, C.R.; Alves, S.E.M.; de Araujo, N.C.J. Primordial gravitational waves in Horndeski gravity. Phys. Rev. D 2019, 99, 084022. [Google Scholar] [CrossRef]
- D’Agostino, R.; Nunes, R.C. Probing observational bounds on scalar-tensor theories from standard sirens. Phys. Rev. D 2019, 100, 044041. [Google Scholar] [CrossRef]
- Mitra, A.; Mifsud, J.; Mota, D.F.; Parkinson, D. Cosmology with the Einstein Telescope: No Slip Gravity Model and Redshift Specifications. Mon. Not. R. Astron. Soc. 2021, 502, 5563–5575. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Nakayama, K.; Saito, S. Prospects for determination of thermal history after inflation with future gravitational wave detectors. Phys. Rev. D 2011, 84, 123513. [Google Scholar] [CrossRef]
- Campeti, P.; Komatsu, E.; Poletti, D.; Baccigalupi, C. Measuring the spectrum of primordial gravitational waves with CMB, PTA and Laser Interferometers. J. Cosmol. Astropart. Phys. 2021, 1, 012. [Google Scholar] [CrossRef]
- Nishizawa, A.; Motohashi, H. Constraint on reheating after f(R) inflation from gravitational waves. Phys. Rev. D 2014, 89, 063541. [Google Scholar] [CrossRef]
- Zhao, W. Improved calculation of relic gravitational waves. Chin. Phys. 2007, 16, 2894–2902. [Google Scholar] [CrossRef][Green Version]
- Cheng, W.; Qian, T.; Yu, Q.; Zhou, H.; Zhou, Y.R. Gravitational Wave from Axion-like Particle Inflation. arXiv 2021, arXiv:2107.04242. [Google Scholar]
- Nishizawa, A.; Yagi, K.; Taruya, A.; Tanaka, T. Cosmology with space-based gravitational-wave detectors—Dark energy and primordial gravitational waves. Phys. Rev. D 2012, 85, 044047. [Google Scholar] [CrossRef]
- Chongchitnan, S.; Efstathiou, G. Prospects for direct detection of primordial gravitational waves. Phys. Rev. D 2006, 73, 083511. [Google Scholar] [CrossRef]
- Lasky, P.D.; Mingarelli, C.M.F.; Smith, T.L.; Giblin, J.T.; Reardon, D.J.; Caldwell, R.; Bailes, M.; Bhat, N.D.R.; Burke-Spolaor, S.; Coles, W.; et al. Gravitational-wave cosmology across 29 decades in frequency. Phys. Rev. X 2016, 6, 011035. [Google Scholar] [CrossRef]
- Guzzetti, M.C.; Bartolo, N.; Liguori, M.; Matarrese, S. Gravitational waves from inflation. Riv. Nuovo Cim. 2016, 39, 399–495. [Google Scholar] [CrossRef]
- Ben-Dayan, I.; Keating, B.; Leon, D.; Wolfson, I. Constraints on scalar and tensor spectra from Neff. J. Cosmol. Astropart. Phys. 2019, 6, 007. [Google Scholar] [CrossRef]
- Nakayama, K.; Saito, S.; Suwa, Y.; Yokoyama, J. Probing reheating temperature of the universe with gravitational wave background. J. Cosmol. Astropart. Phys. 2008, 6, 020. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Nojiri, S.; Odintsov, S.D. Evolution of gravitons in accelerating cosmologies: The case of extended gravity. Phys. Rev. D 2017, 95, 083524. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Nojiri, S.; Odintsov, S.D. f(R) gravity constrained by PPN parameters and stochastic background of gravitational waves. Gen. Rel. Grav. 2009, 41, 2313–2344. [Google Scholar] [CrossRef]
- Capozziello, S.; Corda, C.; De Laurentis, F.M. Massive gravitational waves from f(R) theories of gravity: Potential detection with LISA. Phys. Lett. B 2008, 669, 255–259. [Google Scholar] [CrossRef]
- Cai, R.G.; Fu, C.; Yu, W.W. Parity violation in stochastic gravitational wave background from inflation. arXiv 2021, arXiv:2112.04794. [Google Scholar]
- Cai, R.G.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Fronimos, F.P. Quantitative predictions for f(R) gravity primordial gravitational waves. Phys. Dark Univ. 2022, 35, 100950. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Vagnozzi, S. Primordial gravitational waves from NANOGrav: A broken power-law approach. Phys. Rev. D 2022, 105, 043520. [Google Scholar] [CrossRef]
- Lin, J.; Gao, S.; Gong, Y.; Lu, Y.; Wang, Z.; Zhang, F. Primordial black holes and scalar induced secondary gravitational waves from Higgs inflation with non-canonical kinetic term. arXiv 2021, arXiv:2111.01362. [Google Scholar]
- Zhang, F.; Lin, J.; Lu, Y. Double-peaked inflation model: Scalar induced gravitational waves and primordial-black-hole suppression from primordial non-Gaussianity. Phys. Rev. D 2021, 104, 063515. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Pre-inflationary bounce effects on primordial gravitational waves of f(R) gravity. Phys. Lett. B 2022, 824, 136817. [Google Scholar] [CrossRef]
- Pritchard, J.R.; Kamionkowski, M. Cosmic microwave background fluctuations from gravitational waves: An Analytic approach. Ann. Phys. 2005, 318, 2–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, W.; Xia, T.; Yuan, Y. Analytic approach to the CMB polarizations generated by relic gravitational waves. Phys. Rev. D 2006, 74, 083006. [Google Scholar] [CrossRef]
- Baskaran, D.; Grishchuk, L.P.; Polnarev, A.G. Imprints of Relic Gravitational Waves in Cosmic Microwave Background Radiation. Phys. Rev. D 2006, 74, 083008. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Primordial gravitational waves predictions for GW170817-compatible Einstein–Gauss–Bonnet theory. Astropart. Phys. 2022, 141, 102718. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Myrzakulov, R. Spectrum of Primordial Gravitational Waves in Modified Gravities: A Short Overview. Symmetry 2022, 14, 729. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Amplification of Primordial Gravitational Waves by a Geometrically Driven non-canonical Reheating Era. arXiv 2022, arXiv:2203.10599. [Google Scholar] [CrossRef]
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Smith, T.L.; Caldwell, R. LISA for Cosmologists: Calculating the Signal-to-Noise Ratio for Stochastic and Deterministic Sources. Phys. Rev. D 2019, 100, 104055. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. arXiv 2020, arXiv:2006.13545. [Google Scholar] [CrossRef]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity Studies for Third-Generation Gravitational Wave Observatories. Class. Quant. Grav. 2011, 28, 094013. [Google Scholar] [CrossRef]
- Crowder, J.; Cornish, J.N. Beyond LISA: Exploring future gravitational wave missions. Phys. Rev. D 2005, 72, 083005. [Google Scholar] [CrossRef]
- Smith, T.L.; Caldwell, R. Sensitivity to a Frequency-Dependent Circular Polarization in an Isotropic Stochastic Gravitational Wave Background. Phys. Rev. D 2017, 95, 044036. [Google Scholar] [CrossRef]
- Weltman, A.; Bull, P.; Camera, S.; Kelley, K.; Padmanabhan, H.; Pritchard, J.; Raccanelli, A.; Riemer-Sørensen, S.; Shao, L.; Andrianomena, S.; et al. Fundamental physics with the Square Kilometre Array. Publ. Astron. Soc. Austral. 2020, 37, e002. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Cordes, J.M.; et al. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Pol, N.S.; Taylor, S.R.; Kelley, L.Z.; Vigeland, S.J.; Simon, J.; Chen, S.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Brazier, A.; et al. Astrophysics Milestones for Pulsar Timing Array Gravitational Wave Detection. arXiv 2020, arXiv:2010.11950. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cosmological reconstruction of realistic modified F(R) gravities. Phys. Lett. B 2009, 681, 74. [Google Scholar] [CrossRef]
- Nojiri SOdintsov SD Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary attractors in F(R) gravity. Phys. Lett. B 2020, 807, 135576. [Google Scholar] [CrossRef]
- Garcia-Bellido, J. Astrophysics and cosmology. arXiv 1999, arXiv:hep-ph/0004188. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).