Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation
Abstract
:1. Introduction
2. Spectral Discretization
3. Some Spaces and Lemmas
4. Jacobi Convergence Analysis
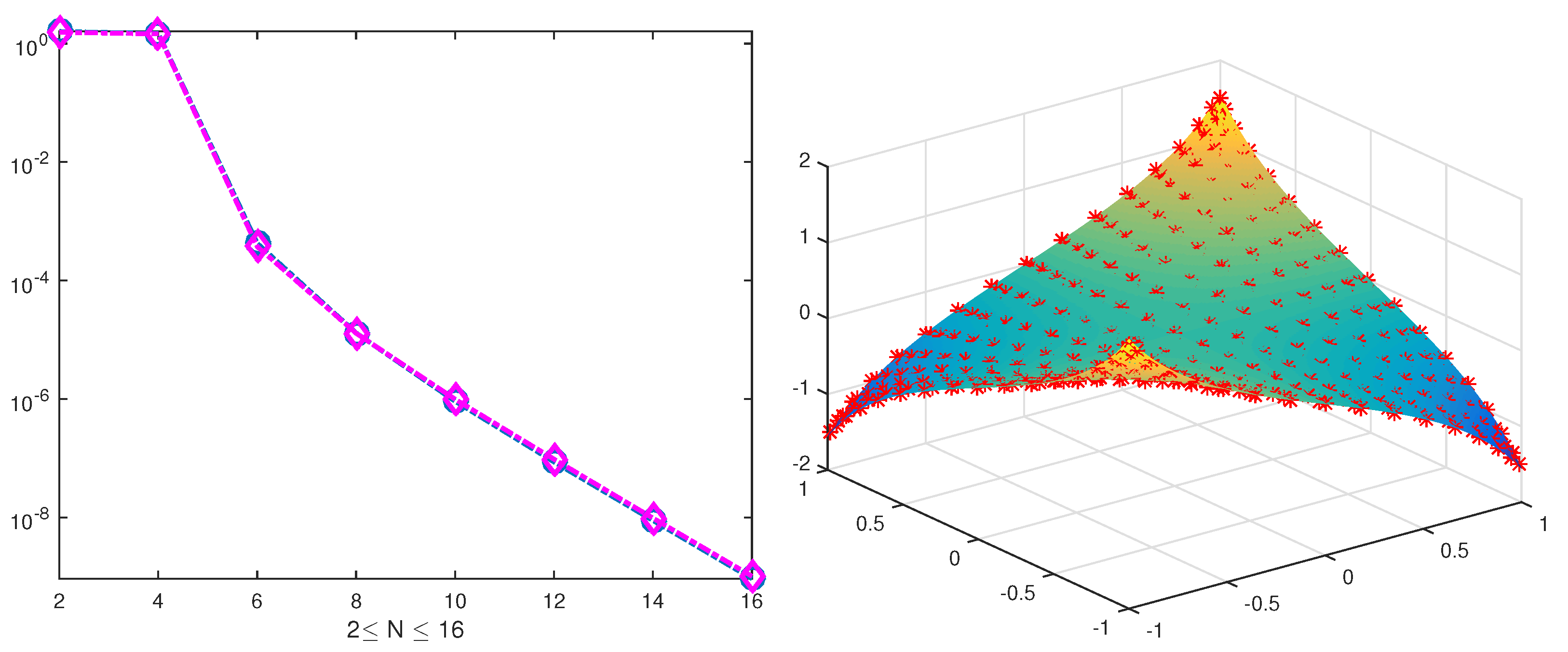
5. Numerical Experiments
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keller, J.B.; Olmstead, W.E. Temperature of a nonlinear radiating semi-infinite solid. Q. Appl. Math. 1972, 29, 559–566. [Google Scholar] [CrossRef] [Green Version]
- Levinson, N. A nonlinear Volterra equation arising in the theory of super-fluidity. J. Math. Anal. Appl. 1960, 1, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Linz, P. Analytical and Numerical Methods for Volterra Equations; SIAM: Philadelphia, PA, USA, 1985. [Google Scholar]
- Ladopoulos, E.G. Singular Integral Equations-Linear and Non-Linear Theory and Its Applications in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Rasty, M.; Hadizadeh, M. A product integration approach based on new orthogonal polynomials for nonlinear weakly singular integral equations. Acta Appl. Math. 2010, 109, 861–873. [Google Scholar] [CrossRef]
- Jerri, A. Introduction to Integral Equations with Applications; John Wiley Sons: Chichester, UK, 1999. [Google Scholar]
- Vainikko, G. Multidimensional Weakly Singular Integral Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Rajabova, L. About a class of two dimensional Volterra type integral equations with singular boundary line. In Current Trends in Analysis and Its Applications; Mityushev, V., Ruzhansky, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 123–131. [Google Scholar]
- Rajabov, N. Multidimensional Volterra type integral equation with singular boundary domains in kernels. Dokl. Akad. Nauk. 2011, 437, 158–161. [Google Scholar] [CrossRef]
- Graham, I. Collocation methods for two dimensional weakly singular integral equations. ANZIAM J. 1981, 22, 456–473. [Google Scholar] [CrossRef] [Green Version]
- Boykov, I.V.; Tynda, A.N. Numerical methods of optimal accuracy for weakly singular Volterra integral equations. Ann. Funct. Anal. 2015, 6, 114–133. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Tang, T. Spectral methods for weakly singular Volterra integral equations with smooth solutions. J. Comput. Appl. Math. 2009, 233, 938–950. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Chen, Y. Convergence analysis of the spectral methods for weakly singular Volterra integro-differential equations with smooth solutions. Adv. Appl. Math. Mech. 2012, 4, 1–20. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, B.; Xie, H. Spectral methods for weakly singular Volterra integral equations with pantograph delays. Front. Math. China 2013, 8, 281–299. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y. Convergence analysis for the Chebyshev collocation methods to Volterra integral equations with a weakly singular kernel. Adv. Appl. Math. Mech. 2016, 9, 1506–1524. [Google Scholar] [CrossRef]
- Cai, H.; Chen, Y. A fractional order collocation method for second kind Volterra integral equations with weakly singular kernels. J. Sci. Comput. 2018, 75, 970–992. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y. Spectral collocation methods for nonlinear Volterra integro-differential equations with weakly singular kernels. Bull. Malays. Math. Sci. Soc. 2019, 42, 297–314. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C.; Wang, S. Long time behavior of non–Fickian delay reaction–diffusion equations. Nonlinear Anal. Real World Applitions 2012, 13, 1401–1415. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C. Long time numerical behaviors of fractional pantograph equations. Math. Comput. Simul. 2020, 172, 244–257. [Google Scholar] [CrossRef]
- Zheng, W.; Chen, Y. A spectral method for a weakly singular Volterra integro-differential equation with pantograph delay. Acta Math. Sci. 2022, 42, 387–402. [Google Scholar] [CrossRef]
- Li, D.; Zhang, J.; Zhang, Z. Unconditionally optimal error estimates of a linearized Galerkin method for nonlinear time fractional reaction-subdiffusion equations. J. Sci. Comput. 2018, 76, 848–866. [Google Scholar] [CrossRef]
- Headley, V.B. A multidimensional nonlinear Gronwall inequality. J. Math. Anal. Appl. 1974, 47, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods Fundamentals in Single Domains; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fedotov, A.I. Lebesgue constant estimation in multidimensional Sobolev space. J. Math. 2004, 14, 25–32. [Google Scholar]
- Wei, Y.; Chen, Y.; Shi, X.; Zhang, Y. Spectral method for multidimensional Volterra integral equation with regular kernel. Front. Math. China 2019, 14, 435–448. [Google Scholar] [CrossRef]
- Ragozin, D.L. Polynomial approximation on compact manifolds and homogeneous spaces. Trans. Am. Math. Soc. 1970, 150, 41–53. [Google Scholar] [CrossRef]
- Ragozin, D.L. Constructive polynomial approximation on spheres and projective spaces. Trans. Am. Math. Soc. 1971, 162, 157–170. [Google Scholar]
- Wei, Y.; Chen, Y.; Shi, X. A spectral collocation method of multidimensional nonlinear weakly singular Volterra integral equation. J. Comput. Appl. Math. 2018, 331, 52–63. [Google Scholar] [CrossRef]
- Nevai, P. Mean convergence of Lagrange interpolation. Trans. Am. Math. Soc. 1984, 282, 669–698. [Google Scholar] [CrossRef]

| N | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| error | 1.77 | 3.30 × 10 | 1.29 × 10 | 9.24 × 10 | 8.66 × 10 | 8.92 × 10 | 9.28 × 10 |
| error | 1.50 | 2.96 × 10 | 1.33 × 10 | 9.91 × 10 | 9.63 × 10 | 9.76 × 10 | 1.02 × 10 |
| CPU time | 0.0156 | 0.6094 | 1.6250 | 4.6719 | 12.7500 | 33.5156 | 72.2188 |
| N | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| error | 45.09172 | 8.95 × 10 | 9.02 × 10 | 8.03 × 10 | 9.88 × 10 | 7.39 × 10 | 7.53 × 10 |
| error | 51.55358 | 1.26 × 10 | 1.24 × 10 | 1.10 × 10 | 1.34 × 10 | 1.00 × 10 | 1.02 × 10 |
| CPU time | 0.0313 | 0.7813 | 1.7344 | 5.5313 | 13.3594 | 32.1094 | 70.7656 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, N.; Zheng, W.; Gao, W. Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation. Symmetry 2022, 14, 1091. https://doi.org/10.3390/sym14061091
Wu N, Zheng W, Gao W. Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation. Symmetry. 2022; 14(6):1091. https://doi.org/10.3390/sym14061091
Chicago/Turabian StyleWu, Nada, Weishan Zheng, and Wenjuan Gao. 2022. "Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation" Symmetry 14, no. 6: 1091. https://doi.org/10.3390/sym14061091
APA StyleWu, N., Zheng, W., & Gao, W. (2022). Symmetric Spectral Collocation Method for a Kind of Nonlinear Volterra Integral Equation. Symmetry, 14(6), 1091. https://doi.org/10.3390/sym14061091





