Abstract
Electroosmotic force has been used extensively to manipulate fluid flow in a microfluidic system with various channel shapes, especially an elliptic cylinder. However, developing a computational domain and simulating fluid flow for a system involving an elliptic channel consumes a large amount of time. Moreover, the mathematical expression for the fluid velocity of electroosmotic flow in an elliptic channel may be given in the form of the Mathieu functions that have difficulty in achieving the numerical result. In addition, there is clear scientific evidence that confirms the slippage of fluid at the solid-fluid interface in a microscale system. In this study, we present the mathematical model of combined pressure-driven and electroosmotic flow through elliptic microchannels under the slip-fluid condition. From the practical point of view in fluidics, the effect of the eccentricity of the channel cross-section is investigated on the volumetric flow rate to overcome the difficulty. The results show that the substitution of the equivalent circular channel for an elliptic channel provides a valid flow rate under the situation that the areas of both channel cross-sections are equal and the eccentricity of the elliptic cross-section is less than 0.5. Additionally, the flow rate obtained from the substitution is more accurate when the slip length increases or the pressure-gradient-to-external-electric-field ratio decreases.
1. Introduction
Microfluidics is the study of fluid manipulation through a small-scale channel (microchannel) involving various fields of science such as engineering, biology, and chemistry. The research interest in microfluidics has been increasing over the past 10 years [1,2,3,4,5,6,7,8] in order to develop and create many microscale tools; for example, organs-on-a-chip [9,10], labs-on-a-chips [11], 3D printing [12,13], and RNA-delivery devices [14]. Some primary advantages of these technologies [15] are: (i) reducing the consumption of sample and reagent quantities, (ii) saving cost and time in operation and manufacturing products, and (iii) performing detection and separation of molecules at high resolution and sensitivity. An important role in driving fluid in a microchannel is played by electroosmosis.
Electroosmosis is the process of the transportation of fluid through a narrow channel under an electric field. This process occurs due to the effect of ionic charges at the fluid and solid interface of the wall channel [16]. A charged surface develops two parallel layers of ions known as the electrical double layers (EDL) as shown in Figure 1. The first layer contains the ions that are absorbed onto the inner wall surface by the chemical reactions. The second layer is the counterions, which are free ions, in the fluid that are attached to the channel wall due to the electrokinetic force from the ions in the first layer. As a result, the greater the distance of the wall surface, the less the counterion concentration. Therefore, the net charge density and the potential distribution decrease with a rise in the distance of the channel wall and reduce to zero at the bulk fluid. Moreover, the ion and potential distribution can be expressed by the Poisson–Boltzmann equation. An applied external electric field will lead to the movement of the ions in the second layer and result in the flow of the fluid. This type of fluid movement is also known as electroosmotic flow (EOF). In order to investigate the EOF’s behavior in microfluidic devices, many researchers have carried out numerous works [17,18,19,20,21,22,23] by both experimental and theoretical methods.
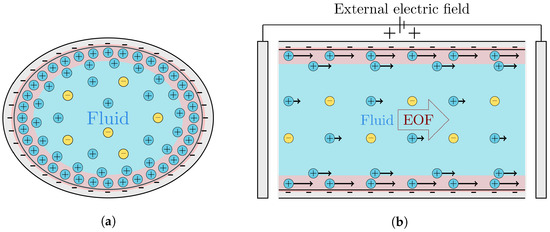
Figure 1.
Electroosmotic flow and the electrical double layer (red highlighted area) in an elliptic cross-sectional channel: (a) cross-section view and (b) view along the channel length.
Various types of cross-sectional shapes were considered in the study of EOF, such as circles [24,25], ellipses [26,27], and rectangles [28,29]. One of the most important cross-sections of a microchannel existing in natural systems and microfluidic fabrication is in an elliptic shape. However, developing a computational domain for a system involving an elliptic channel consumes a large amount of time. Moreover, due to a lack of circular symmetry, a simulation in an elliptic channel entails a high computational cost compared to that in a circular channel. Additionally, in a theoretical study using a mathematical model, the velocity of EOF through an elliptic channel may be derived in the form of the special functions called the Mathieu and modified Mathieu functions. These special functions rely on the infinite series of the trigonometric or the hyperbolic function with coefficients. For example, the Mathieu function is expressed by
where denote the coefficients depending on the parameter , which is a function of the parameter q. When the value of q is not quite small, a little error of yields a large error of , especially when m and r are large. Therefore, the Mathieu and modified Mathieu functions may have difficulty in achieving the numerical result due to their stability issue [30]. To overcome this complication, the validation of using the circular channel instead has been proposed. In 2015, Liu et al. [31] investigated the influence of eccentricity on fully developed pure EOF through elliptic channels. The force by the pressure gradient was omitted. By fixing the perimeter of the channel cross-section, the fluid velocities in elliptic channels having different values of the eccentricity were evaluated. They concluded that considering the circular channel with the same perimeter instead of an elliptic channel is inappropriate. In 2021, Numpanviwat et al. [32] proposed the mathematical model of transient combined pressure-driven and electroosmotic flow in an elliptic microchannel under the no-slip condition. The effect of the eccentricity of the channel cross-section was studied in two situations by fixing either the area or the perimeter of the cross-section. The result is well consistent with Liu’s work when fixing the perimeter. Nonetheless, the result showed that the use of the cylindrical channel by fixing the area of the cross-section is validated compared with the result from the elliptic channel.
In a macroscale system, fluid flow problems are usually considered under the no-slip boundary condition on solid surfaces, which means that the velocity of the fluid at the surface will be zero. However, over the past few decades, there is much evidence indicating that the fluid slips at the wall surfaces [33,34,35,36]. Since the surface-area-to-volume ratio of the microscale system is very large, the slippage of fluid will significantly affect the interaction between the wall surface and the fluid during the fluid transport process. As a consequence, the slip-fluid condition will play a crucial role in fluid flow under a microscale or a smaller system.
Motivated by the aforementioned arguments, we present the mathematical model of combined pressure-driven and electroosmotic flow through elliptic cross-sectional microchannels under the slip fluid condition in order to examine the influence of the eccentricity of the elliptic-channel cross-section. The force by the EDL potential is derived from the Debye-Hückel approximation by employing the Mathieu and modified Mathieu functions. Then, the fluid velocity is obtained by solving the Navier–Stokes equations coupled with the continuity equation. Since a volumetric flow rate plays a more significant role in the microfluidic aspect [37], the effect of the eccentricity on the volumetric flow rate is investigated instead of the velocity. The investigations are performed in two situations: (i) the area of the elliptic cross-section of the channel is fixed and (ii) the perimeter of the elliptic cross-section of the channel is fixed. With regard to the slip flow phenomenon, the comparison of the effect of the eccentricity on various slip lengths is also carried out. To validate the consideration of the equivalent circular microchannel instead of the elliptic microchannel, the relative error of the flow rate with various eccentricities is demonstrated. Further, since the fluid velocity is expressed relating to the pressure gradient and the external electric field, it is important to consider the influence of the eccentricity relating to the ratio of the pressure gradient and the external electric field.
The rest of this paper is organized as follows. Section 2 provides background knowledge of the elliptic coordinate system and the Mathieu and modified Mathieu functions. The mathematical modeling for combined pressure-driven and electroosmotic flow is established in Section 3. Section 4 shows the boundary conditions used in this study. Section 5 presents the mathematical methodology for solving the boundary value problem. The numerical results are illustrated and discussed in Section 6. Finally, the conclusions are given in Section 7.
2. Preliminaries on the Elliptic Coordinate System
2.1. Elliptic Coordinates
According to an ellipse having two foci at and in the 2-dimensional Cartesian coordinates, the elliptic coordinate system, as shown in Figure 2, is defined by
where denotes the confocal ellipses and denotes the asymptotic angle of the confocal hyperbolas.
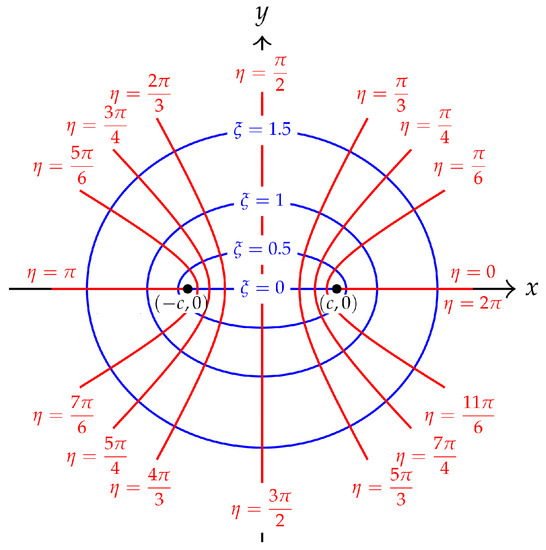
Figure 2.
Elliptic coordinates .
The elongation of an ellipse along the major axis called the eccentricity e is measured by the ratio
where c denotes the focal length of an ellipse and a denotes the longest distance between the center and perimeter of an ellipse known as the semi-major axis.
The scale factors, also known as the basic vectors, for the elliptic coordinates can be derived as follows:
As a consequence, the 2-dimensional Laplace operator in the elliptic coordinates are scaled to
2.2. Mathieu and Modified Mathieu Functions
The solution of the 2-dimensional wave equation in the elliptic coordinates ,
can be obtained by employing the separation of variables method . The separation yields the two ordinary differential equations of second order, namely the Mathieu and modified Mathieu equations that are expressed as
respectively. The parameter denotes the separation constant which varies on the parameter . With regard to the elliptic channel, the appropriate solutions of Equations (8) and (9) have to satisfy the symmetric properties of the major and minor axes of the ellipse. Hence, the solution of the 2-dimensional wave Equation (7) in the elliptic channel is
where denotes the periodic Mathieu functions of integral order with period and denotes the periodic modified Mathieu functions corresponding to .
3. Mathematical Modeling
In this section, the governing equations for combined pressure-driven electroosmotic slip flow through an elliptic microchannel are constructed. Deriving from the Cauchy momentum equation and the mass conservation law, the motion of an incompressible fluid can be described by the Navier–Stokes equations coupled with the continuity equation:
where denotes the 3-dimensional vector of the fluid velocity, denotes the fluid density, p denotes the pressure, denotes the fluid viscosity, and denotes the electroosmotic body force. In the electrostatic theory, the relationship between the ionic charge density of the fluid , and the EDL potential inside the channel is defined in the form of the Poisson equation as . Thus, the electroosmotic body force can be described by
where denotes the vector of external electric field and denotes the fluid permittivity.
Considering that the elliptic channel is placed along the z-axis direction and the fluid flow through the channel is fully developed, we then have the fluid velocity, the external electric field, and the pressure gradient not depending on time and existing only in the z-direction; that is, , , and . Therefore, combining Equations (11)–(13) yields the governing equation as follows:
where E and are constant and denotes the elliptic coordinate system. Additionally, the continuity Equation (12) is now reduced to , and hence the z-axis velocity u depends only on and . Moreover, suppose that the gradient of the EDL potential exists only in the direction perpendicular to the channel surface; then , which gives rise to , is also the function only of and .
4. Boundary Conditions
Since the governing equation for combined pressure-driven electroosmotic slip flow through an elliptic microchannel was derived, in this section, we state the boundary conditions used in the study.
In regard to the symmetry of an elliptic channel, the fluid flow and the EDL potential distribution are considered to be symmetric about the x- and y-axes, i.e.,
According to the appearance of slip flow in the microscale system, the Navier slip condition is employed to the fluid on the channel boundary as
where l denotes the Navier slip length (see Figure 3), and denotes the boundary interface of the channel. For the EDL potential on the surface of the channel, we suppose that the charge on the surface of the channel is uniform with a constant zeta potential . Hence,
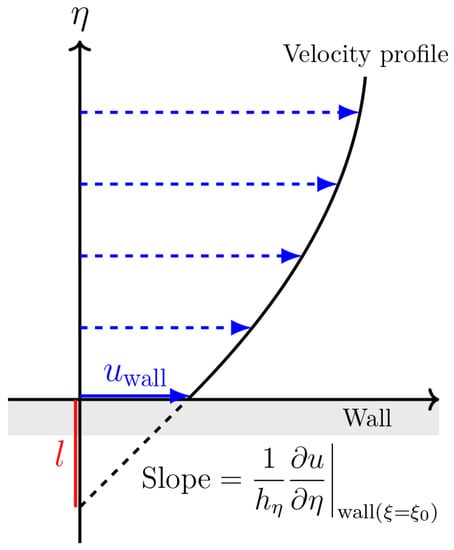
Figure 3.
Navier slip length.
All equations relating to the boundary conditions and the governing Equation (14) form the boundary value problem that will be used to find the solution for fluid velocity.
5. Solutions of the Boundary Value Problem
To find fluid velocity in an elliptic microchannel, we solve the boundary value problem consisting of the partial differential Equation (14) and the boundary conditions (15). By using the identities and , the governing Equation (14) can be rewritten as
The non-homogeneous Equation (16) can be transformed into a homogeneous equation by employing the change of variable technique. Let
Then Equation (14) is homogenized to
The boundary conditions for the function can be derived from Equations (15a)–(15c) as
Since Equation (18) is homogeneous, we can apply the method of separation of variables to find the solution by letting , where denotes a function depending solely on and denotes a function depending solely on . As a result, the solution that satisfies Equation (18) and the boundary conditions (19) is
where are constant. Thus, we obtain the solution to the boundary value problem as follows:
The coefficients can be calculated by substituting the velocity function u expressed in Equation (21) into the Navier slip condition (15d) and using the zeta potential condition (15e) to arrive at
where
and
For , we have , and the Navier slip condition is reduced to the no-slip condition, i.e., . Then the coefficients can be derived by using the orthogonality of the function on an interval as
For , let k be a non-negative integer. Multiplying into Equation (22) and integrating from 0 to with respect to yields
where
To find the coefficients , the fluid velocity u is approximated by
for a suitable fixed positive integer M. Hence, the infinite system (26) is reduced to the system with finite equations as
and the coefficients are given by solving the reduced finite system (30).
The solution in Equation (21) still contains the unknown EDL potential function . To find , we assume the fluid is the symmetric electrolyte. By omitting the convection from the fluid, the distribution of the ionic charge density inside the channel can be described by the Boltzmann equation:
where denotes the concentration of ions at the bulk, denotes the elementary proton charge, denotes the valence of the ions, denotes the Boltzmann constant, and T denotes the fluid absolute temperature. Substituting from the Boltzmann Equation (31) into the Poisson equation yields the Poisson–Boltzmann equation:
Suppose that zeta potential is low () [38]; we can approximate
Therefore, the Poisson–Boltzmann Equation (32) is reduced to the Debye–Hückel approximation in elliptic coordinates :
where , which is known as the reciprocal of the EDL thickness.
Since Equation (34) is the 2-dimensional wave equation in the elliptic coordinate system, the solution that satisfies the boundary conditions (15a)–(15c) can be derived in the form of the Mathieu functions [30] as
where is constant, denotes the periodic Mathieu functions with , and denotes the modified Mathieu functions corresponding to . Substituting the function into the boundary condition (15e), then we can use the orthogonality of the Mathieu functions on the interval to determine the coefficients as follows:
Thus, the dimensionless velocity profile is expressed in the form of
where are given for by
and are obtained for by solving the system
where
The non-dimensional EDL potential can be derived as
where
6. Effect of the Eccentricity on Slip Flow
From a fluidic aspect, a volumetric flow rate instead of velocity plays a more crucial role in flow manipulation [37]. As a consequence, to investigate the effect of the eccentricity, we consider the volumetric flow rate Q per unit area of the channel cross-section defined by
where A denotes the area of the cross-section and u is calculated via Equation (29) for the appropriate number . Using the non-dimensional velocity defined in Equation (37), the dimensionless flow rate can be calculated by the following equation:
The effect of the eccentricity is investigated in two aspects of the channel geometry: (i) the area of the elliptic cross-section of the channel is fixed and (ii) the perimeter of the elliptic cross-section of the channel is fixed. When the area of the cross-section is fixed, the focal length of the ellipse can be derived relating to the eccentricity e by
On the other hand, the focal length can be calculated for each eccentricity by fixing the channel perimeter as follows:
where P denotes the perimeter of the elliptic cross-section. The properties of the fluid [38] and the other parameters used in the investigation are presented in Table 1 unless stated specifically otherwise.

Table 1.
Table of parameters used in the investigation.
Figure 4a presents the comparison of the dimensionless volumetric flow rates through the elliptic channel with various eccentricities when the area of the cross-section is fixed to . The slip flow at the channel wall is considered with the slip length , and 1000 . The result shows that when , which is the no-slip wall, no significant difference in exists in the channel with the eccentricity less than 0.5. However, when the eccentricity is greater than 0.5, we can see a considerable decrease in as a rise in the eccentricity. When e increases, the shortest distance between the channel center and the perimeter (known as the semi-minor axis) of an ellipse decreases (see Figure 5a). The reduction of this distance results in the velocity profile of fluid. In particular, the less the distance, the lower the maximum velocity through the channel (see Figure 6). Hence, an increase in the eccentricity yields a lower volumetric flow rate. This result is well consistent with Numpanviwat’s work [32]. When the slip flow phenomenon is applied, i.e., , increases as an increase in the slip length. In spite of that, for each slip length, there is no crucial difference in among the channel with , but dramatically drops as an increase in the eccentricity when . This result resembles that of the no-slip flow.
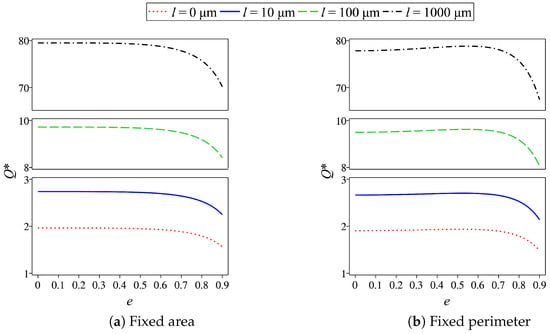
Figure 4.
Variation of the dimensionless flow rates with four different values of the slip length (red dotted line), 10 (blue solid line), 100 (green dashed line), and 1000 (black dot-dashed line) on various eccentricities when (a) the area of the channel cross-sections is fixed and (b) the perimeter of the channel cross-sections is fixed.
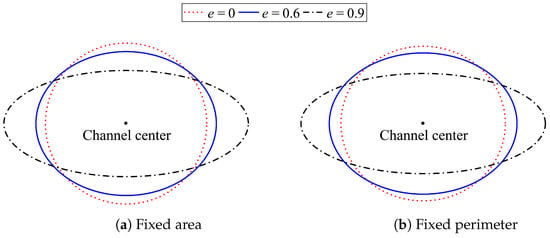
Figure 5.
Elliptic cross-sections with three different eccentricities (red dotted line), (blue solid line), and (black dot-dashed line) when (a) the area of the channel cross-sections is fixed and (b) the perimeter of the channel cross-sections is fixed.
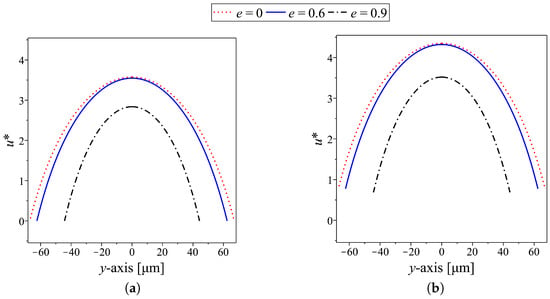
Figure 6.
Velocity profile along the y-axis in the elliptic channel with three different eccentricities (red dotted line), (blue solid line), and (black dot-dashed line) when the area of the channel cross-sections is fixed: (a) and (b) .
To investigate the effect of the eccentricity on slip flow when the perimeter is fixed, the variation of the non-dimensional flow rates in the elliptic cross-sectional channel where the cross-section perimeter is fixed to is demonstrated in Figure 4b. The eccentricities and the slip lengths used in this investigation are the same as in the former comparison when the area of the cross-sections is fixed. The result shows that if the slip length increases, then so does . However, fluctuates significantly when the eccentricity increases. Additionally, the flow rate increases gradually when , and the flow rate decreases sharply when . When the perimeter of an ellipse is fixed, the variation of the dimensionless flow rate on the eccentricity e should be similar to when the area of the elliptic cross-section is fixed because the semi-minor axis also decreases as an increase in e (see Figure 5b). However, with a fixed perimeter, the area of an ellipse rises when , as shown in Figure 7. Therefore, it yields a higher flow rate. On the other hand, when , the area of the ellipse sharply drops as an increase in e. As a consequence, the flow rate decreases significantly.
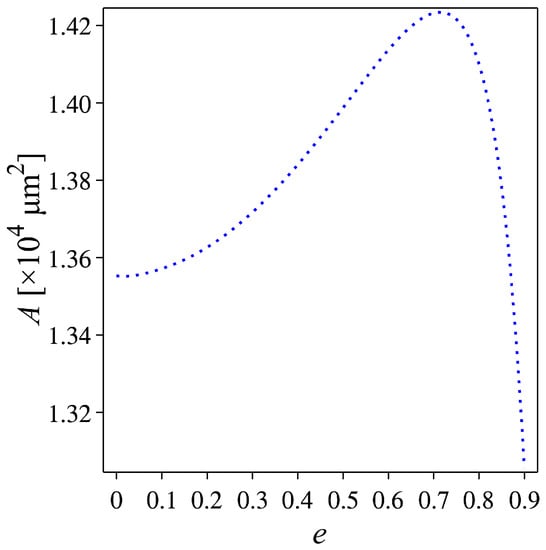
Figure 7.
Area of the elliptic cross-section when the perimeter is fixed to .
In order to overcome the complexity of calculating the numerical result, one may treat an elliptic cross-sectional channel as a cylindrical channel. Consequently, it is worth examining here how the eccentricity affects the flow rate in the relative error aspect compared with the flow rate in the equivalent cylindrical channel. Figure 8 illustrates the comparison of the relative error of the non-dimensional flow rate in the elliptic channel with various eccentricities compared with the non-dimensional flow rate in the circular channel when either the area or the perimeter of the cross-sections is fixed. The relative error of the flow rate is defined by
where denotes the dimensionless flow rate in the circular channel and denotes the dimensionless flow rate in the elliptic channel with eccentricity equal to i. The result in Figure 8a shows that, when the area is fixed, the relative errors of the no-slip flow in the channel with are less than . When the slip length increases, the fluid velocity increases, but the velocity profile is still in the same pattern, as shown in Figure 6. Hence, the change in the volumetric flow rate on an increase in the eccentricity is practically identical among the channel with different slip lengths. This phenomenon can be observed in Figure 4a as the pattern of the reductions in of the channel with four different slip lengths as e increases are strongly resembled. As a consequence, there is no crucial difference in the absolute error of the flow rate defined by between the channels having any two different slip lengths. Since the relative error is defined by
a rise in slip length leads to a higher flow rate. However, there is no significant difference that occurs in the absolute error as the aforementioned argument. Thus, the relative error reduces when the slip length increases.
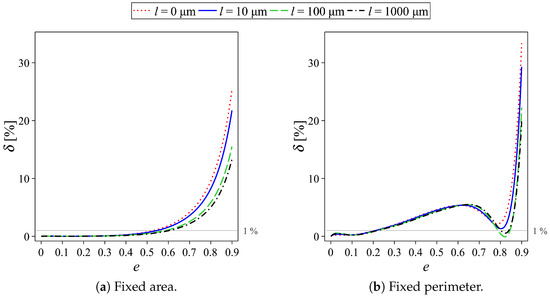
Figure 8.
Variation of the relative errors of the flow rate with four different values of the slip length (red dotted line), 10 (blue solid line), 100 (green dashed line), and 1000 (black dot-dashed line) on various eccentricities when (a) the area of the channel cross-sections is fixed and (b) the perimeter of the channel cross-sections is fixed.
On the other hand, when the perimeter is fixed, Figure 8b demonstrates that the relative errors of the no-slip flow are notably high in the elliptic channel having . The relative error is well consistent with the fluctuation of the volumetric flow rate due to the change in the cross-sectional area.
Therefore, when the slip flow is considered, the relative error decreases with an increase in the slip length. As a result, the simplification by using the equivalent circular channel for the elliptic channel can be done under the condition that the area of the cross-sections is fixed and the eccentricity is less than 0.5.
Furthermore, we investigate the relative error of the flow rate with various ratios of the non-dimensional pressure gradient and the non-dimensional external electric field . According to the aforementioned result, we consider only the relative error when the area of the cross-sections is fixed. Figure 9 demonstrates the comparison of the relative errors of the flow rate with the ratio equal to 1/5, 1/2.5, 2.5, and 5 times that ratio used in the investigation in Figure 8. The results show that the relative errors enlarge when increases in all the channels with different values of the eccentricity. This phenomenon can be described as relating to the slip flow. When the ratio increases, the flow is more dominated by the pressure-gradient force compared to the EOF. It means, on the other hand, the EOF is less dominant in the flow. Since the EOF is acting on the EDL, which is the area adjacent to the wall, the weaker EOF will result similar to the smaller slip length. As a consequence, the relative error of the flow rate increases with an increase in the ratio in the same manner as a decrease in the slip length. Moreover, the effect of the ratio vanishes when the slip length is very large, i.e., .
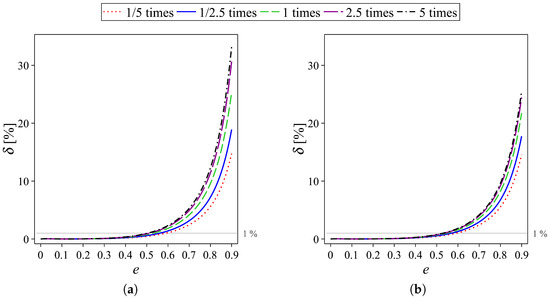
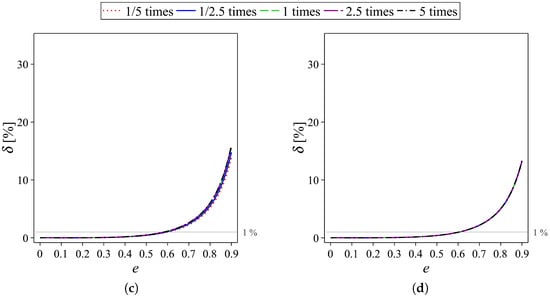
Figure 9.
Variation of the relative errors of the flow rate on various eccentricities when the ratios are times (red dotted line), times (blue solid line), 1 times (green dashed line), times (purple long dashed line), and 5 times (black dot-dashed line) of the ratio used in the investigation in Figure 8 with four different values of the slip length: (a) ; (b) ; (c) ; and (d) .
7. Conclusions
We present the solution for the fluid velocity of slip flow driven by both pressure-gradient force and EOF through an elliptic cylindrical microchannel. The EOF is obtained by solving the Debye–Hückel approximation, and the fluid velocity is derived based on the Navier–Stokes and the continuity equations under the Navier slip condition. The volumetric flow rate is calculated numerically to investigate validation of the consideration of the elliptic cylindrical microchannel to be the equivalent circular cylindrical microchannel. The results show that the consideration of the equivalent circular channel provides a valid result of the flow rate under the condition that the area of the channel cross-section is fixed and the eccentricity is less than 0.5. Additionally, the consideration yields a more accurate flow rate in slip electroosmotic flow driven by an external electric field.
Author Contributions
Conceptualization, P.C. and N.N.; Formal analysis, P.C. and N.N.; Investigation, P.C. and N.N.; Methodology, P.C. and N.N.; Validation, P.C. and N.N.; Visualization, P.C. and N.N.; Writing—original draft, P.C. and N.N.; Writing—review & editing, P.C. and N.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations and Nomenclature
Abbreviations
Nomenclature
| A | area of channel cross-section |
| a | semi-major axis of an ellipse |
| separation constant of 2-dimensional wave equation in elliptic coordinates | |
| c | focal length of an ellipse |
| periodic modified Methieu function corresponding to | |
| periodic Methieu function of integral order | |
| E | external electric field in z-direction |
| dimensionless external electric field in z-direction |
| vector of external electric field | |
| e | eccentricity of an ellipse |
| vector of electroosmotic body force | |
| scalar factors/basic vectors for the elliptic coordinates | |
| Boltzmann constant | |
| l | Navier slip length |
| concentration of ions at bulk | |
| P | perimeter of the elliptic cross-section |
| p | pressure |
| pressure gradient in z-direction | |
| dimensionless pressure gradient in z-direction | |
| elementary proton charge | |
| Q | volumetric flow rate per unit area of the channel cross-section |
| dimensionless volumetric flow rate per unit area | |
| dimensionless flow rate in the elliptic channel with the eccentricity equal to i | |
| dimensionless flow rate in the circular channel | |
| T | fluid absolute temperature |
| u | fluid velocity in z-direction |
| dimensionless fluid velocity in z-direction | |
| vector of fluid velocity | |
| Cartesian coordinates | |
| valence of ion | |
| relative error of | |
| fluid permittivity | |
| zeta potential | |
| reciprocal of EDL thickness | |
| fluid viscosity | |
| elliptic coordinate system | |
| boundary interface of the channel | |
| fluid density | |
| ionic charge density of fluid | |
| EDL potential | |
| dimensionless EDL potential |
References
- Xiang, J.; Cai, Z.; Zhang, Y.; Wang, W. A micro-cam actuated linear peristaltic pump for microfluidic applications. Sens. Actuators A Phys. 2016, 251, 20–25. [Google Scholar] [CrossRef]
- Bridle, H.; Wang, W.; Gavriilidou, D.; Amalou, F.; Hand, D.P.; Shu, W. Static mode microfluidic cantilevers for detection of waterborne pathogens. Sens. Actuators A Phys. 2016, 247, 144–149. [Google Scholar] [CrossRef][Green Version]
- Jiemsakul, T.; Manakasettharn, S.; Kanharattanachai, S.; Wanna, Y.; Wangsuya, S.; Pratontep, S. Microfluidic magnetic switching valves based on aggregates of magnetic nanoparticles: Effects of aggregate length and nanoparticle sizes. J. Magn. Magn. Mater. 2017, 422, 434–439. [Google Scholar] [CrossRef]
- Montessori, A.; Lauricella, M.; La Rocca, M.; Succi, S.; Stolovicki, E.; Ziblat, R.; Weitz, D. Regularized lattice Boltzmann multicomponent models for low capillary and Reynolds microfluidics flows. Comput. Fluids 2018, 167, 33–39. [Google Scholar] [CrossRef]
- Ding, R.; Lisak, G. Sponge-based microfluidic sampling for potentiometric ion sensing. Anal. Chim. Acta 2019, 1091, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Streck, S.; Clulow, A.J.; Nielsen, H.M.; Rades, T.; Boyd, B.J.; McDowell, A. The distribution of cell-penetrating peptides on polymeric nanoparticles prepared using microfluidics and elucidated with small angle X-ray scattering. J. Colloid Interface Sci. 2019, 555, 438–448. [Google Scholar] [CrossRef]
- Yan, S.; Chu, F.; Zhang, H.; Yuan, Y.; Huang, Y.; Liu, A.; Wang, S.; Li, W.; Li, S.; Wen, W. Rapid, one-step preparation of SERS substrate in microfluidic channel for detection of molecules and heavy metal ions. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 220, 117113. [Google Scholar] [CrossRef]
- Dejam, M. Hydrodynamic dispersion due to a variety of flow velocity profiles in a porous-walled microfluidic channel. Int. J. Heat Mass Transf. 2019, 136, 87–98. [Google Scholar] [CrossRef]
- Tian, C.; Tu, Q.; Liu, W.; Wang, J. Recent advances in microfluidic technologies for organ-on-a-chip. TrAC Trends Anal. Chem. 2019, 117, 146–156. [Google Scholar] [CrossRef]
- Yang, Q.; Ju, D.; Liu, Y.; Lv, X.; Xiao, Z.; Gao, B.; Song, F.; Xu, F. Design of organ-on-a-chip to improve cell capture efficiency. Int. J. Mech. Sci. 2021, 209, 106705. [Google Scholar] [CrossRef]
- Zhao, K.; Peng, Z.; Jiang, H.; Lv, X.; Li, X.; Deng, Y. Shape-coded hydrogel microparticles integrated with hybridization chain reaction and a microfluidic chip for sensitive detection of multi-target miRNAs. Sens. Actuators B Chem. 2022, 361, 131741. [Google Scholar] [CrossRef]
- Walczak, R.; Kawa, B.; Adamski, K. Inkjet 3D printed microfluidic device for growing seed root and stalk mechanical characterization. Sens. Actuators A Phys. 2019, 297, 111557. [Google Scholar] [CrossRef]
- Wei, L.; Fang, G.; Kuang, Z.; Cheng, L.; Wu, H.; Guo, D.; Liu, A. 3D-printed low-cost fabrication and facile integration of flexible epidermal microfluidics platform. Sens. Actuators B Chem. 2022, 353, 131085. [Google Scholar] [CrossRef]
- Maeki, M.; Uno, S.; Niwa, A.; Okada, Y.; Tokeshi, M. Microfluidic technologies and devices for lipid nanoparticle-based RNA delivery. J. Control. Release 2022, 344, 80–96. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, R.; Shankar, V. Coulson and Richardson’s Chemical Engineering, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Hunter, R.J. Zeta Potential in Colloid Science; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Bhamidimarri, S.P.; Prajapati, J.D.; van den Berg, B.; Winterhalter, M.; Kleinekathöfer, U. Role of Electroosmosis in the Permeation of Neutral Molecules: CymA and Cyclodextrin as an Example. Biophys. J. 2016, 110, 600–611. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Sato, T.; Eom, S.I.; wan Kim, J.; Yokota, S. A study on an AC electroosmotic micropump using a square pole—Slit electrode array. Sens. Actuators A Phys. 2017, 265, 152–160. [Google Scholar] [CrossRef]
- Kariminezhad, E.; Elektorowicz, M. Comparison of constant, pulsed, incremental and decremental direct current applications on solid-liquid phase separation in oil sediments. J. Hazard. Mater. 2018, 358, 475–483. [Google Scholar] [CrossRef]
- Mateos, H.; Valentini, A.; Robles, E.; Brooker, A.; Cioffi, N.; Palazzo, G. Measurement of the zeta-potential of solid surfaces through Laser Doppler Electrophoresis of colloid tracer in a dip-cell: Survey of the effect of ionic strength, pH, tracer chemical nature and size. Colloids Surf. A Physicochem. Eng. Asp. 2019, 576, 82–90. [Google Scholar] [CrossRef]
- Moschopoulos, P.; Dimakopoulos, Y.; Tsamopoulos, J. Electro-osmotic flow of electrolyte solutions of PEO in microfluidic channels. J. Colloid Interface Sci. 2020, 563, 381–393. [Google Scholar] [CrossRef]
- Awan, A.U.; Ali, M.; Abro, K.A. Electroosmotic slip flow of Oldroyd-B fluid between two plates with non-singular kernel. J. Comput. Appl. Math. 2020, 376, 112885. [Google Scholar] [CrossRef]
- Mondal, B.; Mehta, S.K.; Pati, S.; Patowari, P.K. Numerical analysis of electroosmotic mixing in a heterogeneous charged micromixer with obstacles. Chem. Eng. Process. Process Intensif. 2021, 168, 108585. [Google Scholar] [CrossRef]
- Siddiqui, A.A.; Lakhtakia, A. Debye-Hückel solution for steady electro-osmotic flow of micropolar fluid in cylindrical microcapillary. Appl. Math. Mech. 2013, 34, 1305–1326. [Google Scholar] [CrossRef][Green Version]
- Tseng, S.; Tai, Y.H.; Hsu, J.P. Ionic current in a pH-regulated nanochannel filled with multiple ionic species. Microfluid. Nanofluid. 2014, 17, 933–941. [Google Scholar] [CrossRef]
- Goswami, P.; Chakraborty, S. Semi-analytical solutions for electroosmotic flows with interfacial slip in microchannels of complex cross-sectional shapes. Microfluid. Nanofluid. 2011, 11, 255–267. [Google Scholar] [CrossRef]
- Chuchard, P.; Orankitjaroen, S.; Wiwatanapataphee, B. Study of pulsatile pressure-driven electroosmotic flows through an elliptic cylindrical microchannel with the Navier slip condition. Adv. Differ. Equ. 2017, 2017, 160. [Google Scholar] [CrossRef][Green Version]
- Arulanandam, S.; Li, D. Liquid transport in rectangular microchannels by electroosmotic pumping. Colloids Surf. A Physicochem. Eng. Asp. 2000, 161, 89–102. [Google Scholar] [CrossRef]
- Reshadi, M.; Saidi, M.H.; Firoozabadi, B.; Saidi, M.S. Electrokinetic and aspect ratio effects on secondary flow of viscoelastic fluids in rectangular microchannels. Microfluid. Nanofluid. 2016, 20, 117. [Google Scholar] [CrossRef]
- McLachlan, N.W. Theory and Application of Mathieu Functions; Clarendon Press: Oxford, UK, 1951. [Google Scholar]
- Liu, B.T.; Tseng, S.; Hsu, J.P. Effect of eccentricity on the electroosmotic flow in an elliptic channel. J. Colloid Interface Sci. 2015, 460, 81–86. [Google Scholar] [CrossRef]
- Numpanviwat, N.; Chuchard, P. Transient Pressure-Driven Electroosmotic Flow through Elliptic Cross-Sectional Microchannels with Various Eccentricities. Computation 2021, 9, 27. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Rate-dependent slip of Newtonian liquid at smooth surfaces. Phys. Rev. Lett. 2001, 87, 096105. [Google Scholar] [CrossRef]
- Baudry, J.; Charlaix, E.; Tonck, A.; Mazuyer, D. Experimental Evidence for a Large Slip Effect at a Nonwetting Fluid–Solid Interface. Langmuir 2001, 17, 5232–5236. [Google Scholar] [CrossRef]
- Bonaccurso, E.; Kappl, M.; Butt, H.J. Hydrodynamic Force Measurements: Boundary Slip of Water on Hydrophilic Surfaces and Electrokinetic Effects. Phys. Rev. Lett. 2002, 88, 76103. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Kwok, D.Y. Apparent slip over a solid-liquid interface with a no-slip boundary condition. Phys. Rev. E 2004, 70, 56701. [Google Scholar] [CrossRef]
- Chakraborty, J.; Ray, S.; Chakraborty, S. Role of streaming potential on pulsating mass flow rate control in combined electroosmotic and pressure-driven microfluidic devices. Electrophoresis 2012, 33, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Li, D. Electrokinetics in Microfluidics; Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).