Fixed-Time Synchronization Analysis of Genetic Regulatory Network Model with Time-Delay
Abstract
:1. Introduction
2. Model Establishment
- (1)
- The discontinuous switch control strategywhere , ; ; , are constants to be determined and .
- (2)
- The discontinuous switch control strategywhere , , and , , are constants to be determined.
3. Fixed-Time Synchronization Analysis
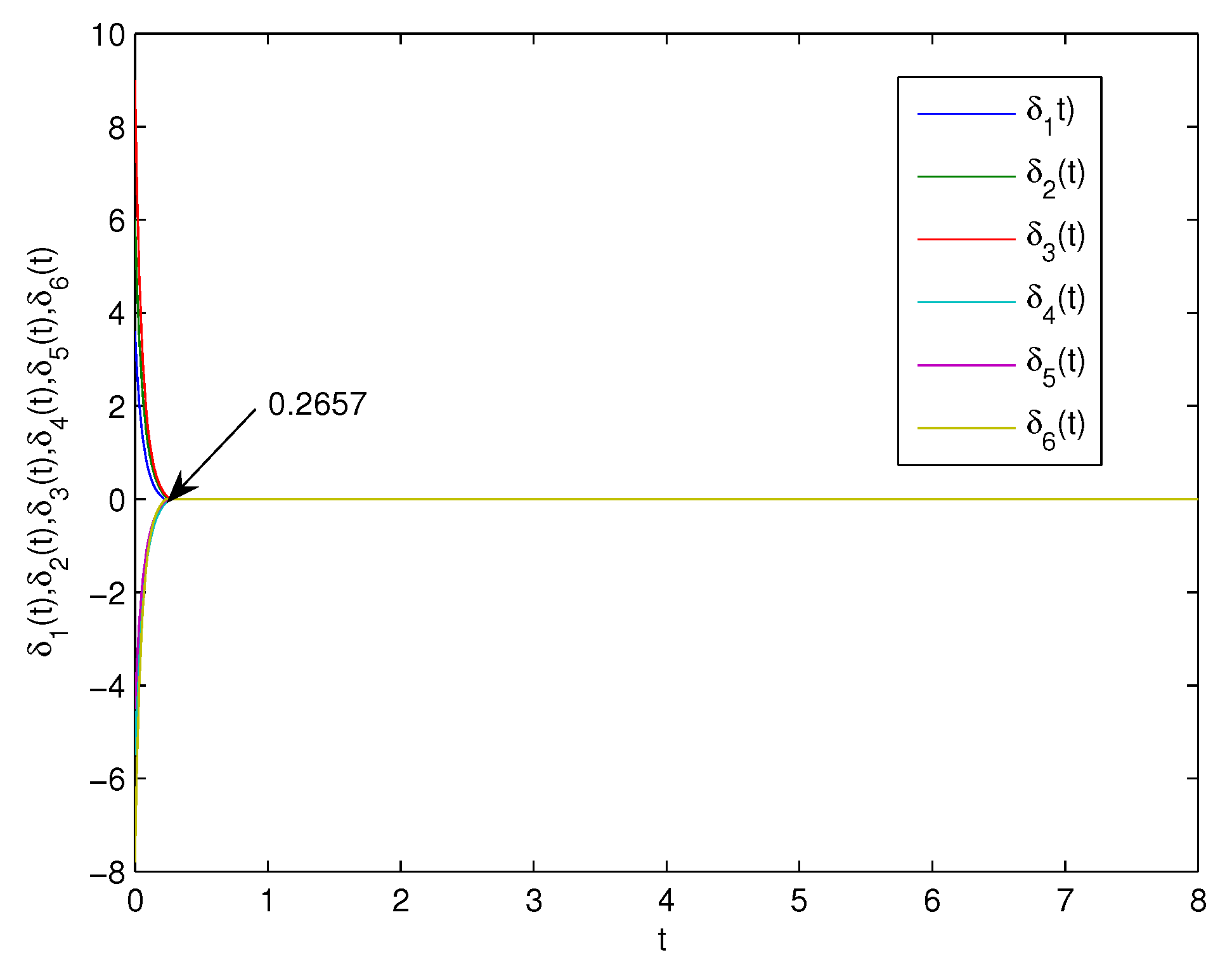
4. Numerical Simulation
- (1)
- The first controller:where
- (2)
- The second controller:where
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Somogyi, R.; Sniegoski, C. Modeling the complexity of genetic networks: Understanding multigenic and pleiotropic regulation. Complexity 1996, 1, 45–63. [Google Scholar] [CrossRef]
- Li, C.; Chen, L.; Aihara, K. A systems biology perspective on signal processing in ge-netic network motifs. IEEE Signal Process. Mag. 2007, 24, 136–147. [Google Scholar]
- Chesler, E. Genome-level analysis of genetic regulation of liver gene expres-sion networks. Hepatology 2007, 46, 548–557. [Google Scholar]
- Johnstone, R.; Ruefli, A.; Lowe, S. Apoptosis: A link between cancer genetics and chemotherapy. Cell 2002, 108, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Gardner, T.; Cantor, C.; Collins, J. Construction of a genetic toggle switch in escherichia coli. Nature 2000, 403, 339–342. [Google Scholar] [CrossRef]
- Wang, Z.; Lam, J.; Wei, G.; Fraser, K.; Liu, X. Filtering for nonlinear genetic reg-ulatory networks with stochastic disturbances. IEEE Trans. Autom. Control 2008, 53, 2448–2457. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Lam, J. Robust state estimation for stochastic genetic regulatory networks. Int. J. Syst. Sci. 2010, 41, 47–63. [Google Scholar] [CrossRef]
- Liu, X.; Cao, J. Robust state estimation for neural networks with discontinuous activations. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2010, 40, 1425–1437. [Google Scholar]
- Chen, L.; Aihara, K. Stability of genetic regulatory networks with time delay. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 602–608. [Google Scholar] [CrossRef]
- Lv, B.; Liang, J.; Cao, J. Robust distributed state estimation for genetic regulatory networks with Markovian jumping parameters. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4060–4078. [Google Scholar] [CrossRef]
- Chen, G.; Lewis, F.; Xie, L. Finite-time distributed consensus via binary control protocols. Automatica 2011, 47, 1962–1968. [Google Scholar] [CrossRef]
- Yu, H.; Wu, C.; Liu, W. Modeling method of gene regulation network. J. Second Mil. Med. Univ. 2006, 7, 737–740. [Google Scholar]
- Hirata, H.; Yoshiura, S.; Ohtsuka, T.; Bessho, Y.; Harada, T.; Yoshikawa, K.; Kageyama, R. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop. Science 2002, 298, 840–843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wheeler, D.W.; Schieve, W.C. Stability and chaos in an inertial two neuron sys-tem. Am. Inst. Phys. 1997, 411, 315–320. [Google Scholar]
- Saravanan, S.; Ali, M.S.; Rajchakit, G.; Hammachukiattikul, B.; Priya, B.; Thakur, G.K. Finite-Time Stability Analysis of Switched Genetic Regulatory Networks with Time-Varying Delays via Wirtinger’s Integral Inequality. Complexity 2021, 2021, 9540548. [Google Scholar] [CrossRef]
- Liang, J.; Lam, J.; Wang, Z. State estimation for Markov-type genetic regulatory networks with delays and uncertain mode transition rates. Phys. Lett. A 2009, 373, 4328–4337. [Google Scholar] [CrossRef]
- Ali, M.S.; Vadivel, R. Decentralized Event-Triggered Exponential Stability for Un-certain Delayed Genetic Regulatory Networks with Markov Jump Parameters and Distributed Delays. Neural Process Lett. 2018, 47, 1219–1252. [Google Scholar]
- Liu, J.; Tian, E.; Gu, Z.; Zhang, Y. State estimation for markovian jumping genetic regulatory networks with random delays. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2479–2492. [Google Scholar] [CrossRef]
- Razmjooy, N.; Ramezani, M. Analytical solution for optimal control by the second kind Chebyshev polynomials expansion. Iran. J. Sci. Technol. Trans. A Sci. 2017, 41, 1017–1026. [Google Scholar] [CrossRef]
- Razmjooy, N.; Ramezani, M. Uncertain method for optimal control prob-lems with uncertainties using Chebyshev inclusion functions. Asian J. Control 2018, 21, 824–831. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Wen, S.; Zeng, Z.; Huang, T.; Meng, Q.; Yao, W. Lag synchronization of switched neural networks via neural activation function and applications in image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1493–1502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milanović, V.; Zaghloul, M. Synchronization of chaotic neural networks and applications to communications. Int. J. Bifurc. Chaos 1996, 6, 2571–2585. [Google Scholar] [CrossRef]
- Wang, Z.; Song, C.; Yan, A.; Wang, G. Complete Synchronization and Partial An-ti-Synchronization of Complex Lü Chaotic Systems by the UDE-Based Control Meth-od. Symmetry 2022, 14, 517. [Google Scholar] [CrossRef]
- Jiang, N.; Liu, X.; Yu, W.; Shen, J. Finite-time stochastic synchronization of genetic regulatory networks. Neurocomputing 2015, 167, 314–321. [Google Scholar] [CrossRef]
- Cai, Z.; Huang, L.; Zhang, L. Finite-time synchronization of master–slave neural net-works with time-delays and discontinuous activations. J. Appl. Math. Model. 2017, 47, 208–226. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, J.; Cheng, D. Adaptive finite-time control of nonlinear systems with parametric uncertainty. IEEE Trans. Autom. Control 2006, 51, 858–862. [Google Scholar] [CrossRef]
- Cortés, J. Finite-time convergent gradient flows with applications to network consensus. Automatica 2006, 42, 1993–2000. [Google Scholar] [CrossRef]
- Qiu, J.; Sun, K.; Yang, C.; Chen, X.; Chen, X.Y.; Zhang, A. Finite-time stability of ge-netic regulatory networks with impulsive effects. Neurocomputing 2017, 219, 9–14. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Zhu, H.; Zhong, S.; Shi, K.; Liu, Y. New study on fixed-time synchroniza-tion control of delayed inertial memristive neural networks. Appl. Math. Comput. 2021, 399, 126035. [Google Scholar]
- Filippov, A. Differential Equations with Discontinuous Right-Hand Side; Kluwer Academic: Boston, MA, USA, 1988. [Google Scholar]
- Forti, M.; Grazzini, M.; Nistri, P.; Pancioni, L. Generalized Lyapunov approach for convergence of neural networks with discontinuous or non-lipschitz activations. Physics D 2006, 214, 88–89. [Google Scholar] [CrossRef]
- Xiao, J.; Zeng, Z.; Wu, A.; Shen, J. Fixed-time synchronization of delayed Co-hen-Grossberg neural networks based on a novel sliding mode. Neural Netw. 2020, 128, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Cao, J.; Wen, G.; Yu, W. Robust fixed-time synchronization of delayed Cohen-Grossberg neural networks. Neural Netw. 2016, 73, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Yu, J.; Chen, Z.; Jiang, H.; Huang, T. Fixed-time stability of dynamical sys-tems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw. 2017, 89, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Hardy, G.; Littlewood, J.; Polya, G. Inequalities; Cambridge University Press: London, UK, 1988. [Google Scholar]
- Zhang, W.; Tang, Y. Stochastic Stability of Switched Genetic Regulatory Net-works With Time-Varying Delays. IEEE Trans. Nanobiosci. 2014, 13, 336–342. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhang, Q.; Li, X. Dissipative Control of Markovian Jumping Genetic Regula-tory Networks with Time-Varying Delays and Reaction-Diffusion Driven by Fractional Brownian Motion. Differ. Equ. Dyn. Syst. 2020, 28, 841–864. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Gao, Y. Fixed-Time Synchronization Analysis of Genetic Regulatory Network Model with Time-Delay. Symmetry 2022, 14, 951. https://doi.org/10.3390/sym14050951
Zhou Y, Gao Y. Fixed-Time Synchronization Analysis of Genetic Regulatory Network Model with Time-Delay. Symmetry. 2022; 14(5):951. https://doi.org/10.3390/sym14050951
Chicago/Turabian StyleZhou, Yajun, and You Gao. 2022. "Fixed-Time Synchronization Analysis of Genetic Regulatory Network Model with Time-Delay" Symmetry 14, no. 5: 951. https://doi.org/10.3390/sym14050951
APA StyleZhou, Y., & Gao, Y. (2022). Fixed-Time Synchronization Analysis of Genetic Regulatory Network Model with Time-Delay. Symmetry, 14(5), 951. https://doi.org/10.3390/sym14050951