ST-DEVS: A Methodology Using Time-Dependent-Variable-Based Spatiotemporal Computation
Abstract
:1. Introduction
2. Related Work and Background
2.1. DEVS Formalism
2.2. TL and BM-DEVS
2.3. Automata, Set Theory, and Logic
3. ST-DEVS Formalism and Action Execution Algorithm
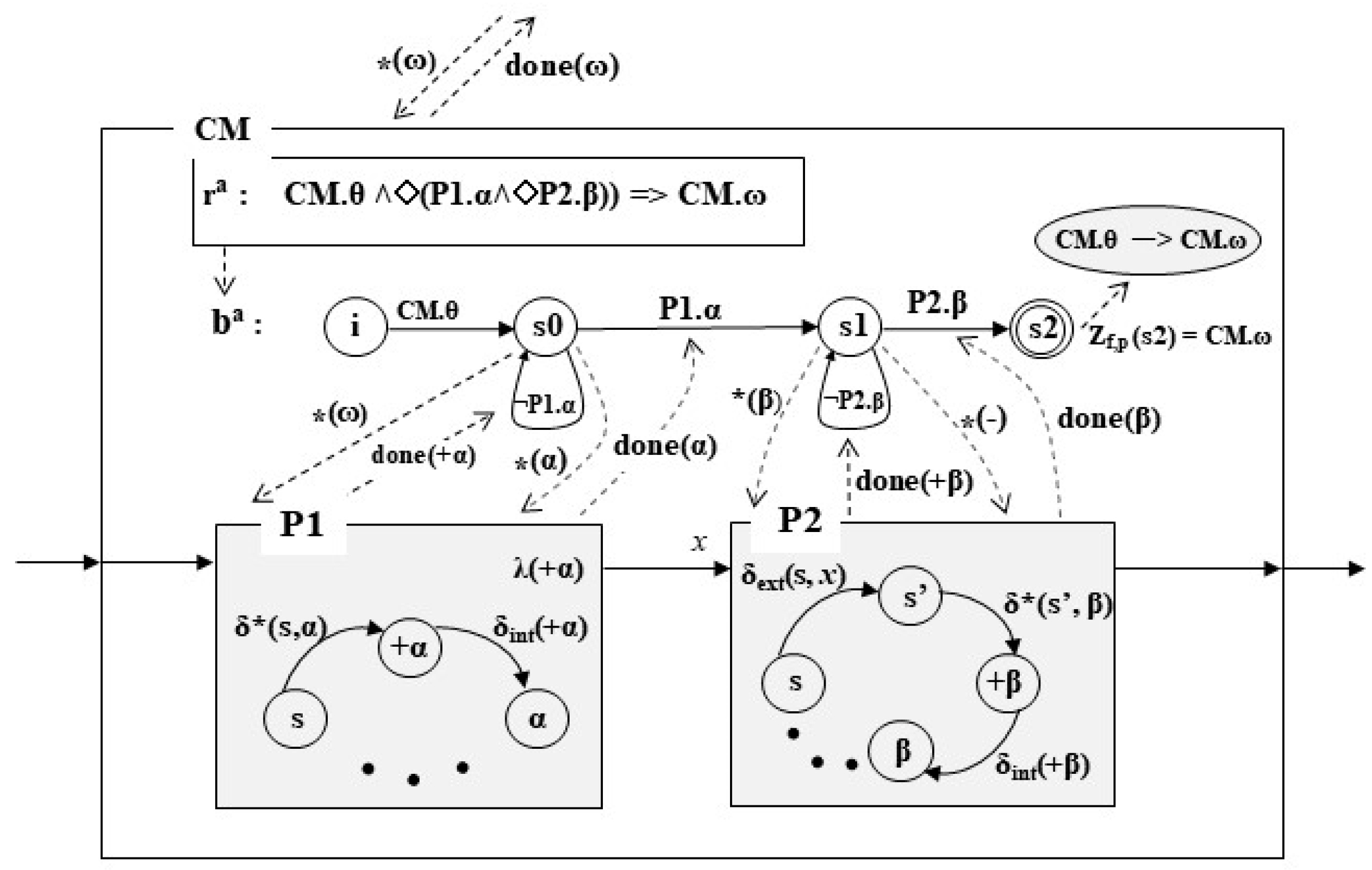
3.1. ST-DEVS Structure
- M is a DEVS basic model [1],
- G is a set of goals that can be achieved by this model, and
- ⸹* is a state transition function that maps ⸹*: S × G → S, where S is a sequential state set. That is, the function is executed on receipt of a ⁎-message to achieve a goal, or one of the subgoals in the parent’s action rule, TLST-DEVS.
- NBM-DEVS is a coupled model defined by BM-DEVS [6],
- G is a set of goals that can be achieved by this model,
- GA is a goal−to−action rules translation function that maps GA: G → Ba; that is, the GA function determines the action rule to be executed once a goal is received from the parent.
- DG is a done−to−goal translation function that maps DG: Ba × DONE → D × Gs, where DONE is a set of done messages received from components whenever a state transition in the components is completed. Gs is a set of subgoals that can be achieved through component models. Gs is described in Ba or TLST-DEVS rules. D is a set of component names for each d in D, where d∈ D. That is, the DG function determines the next subgoal once a done message is received.
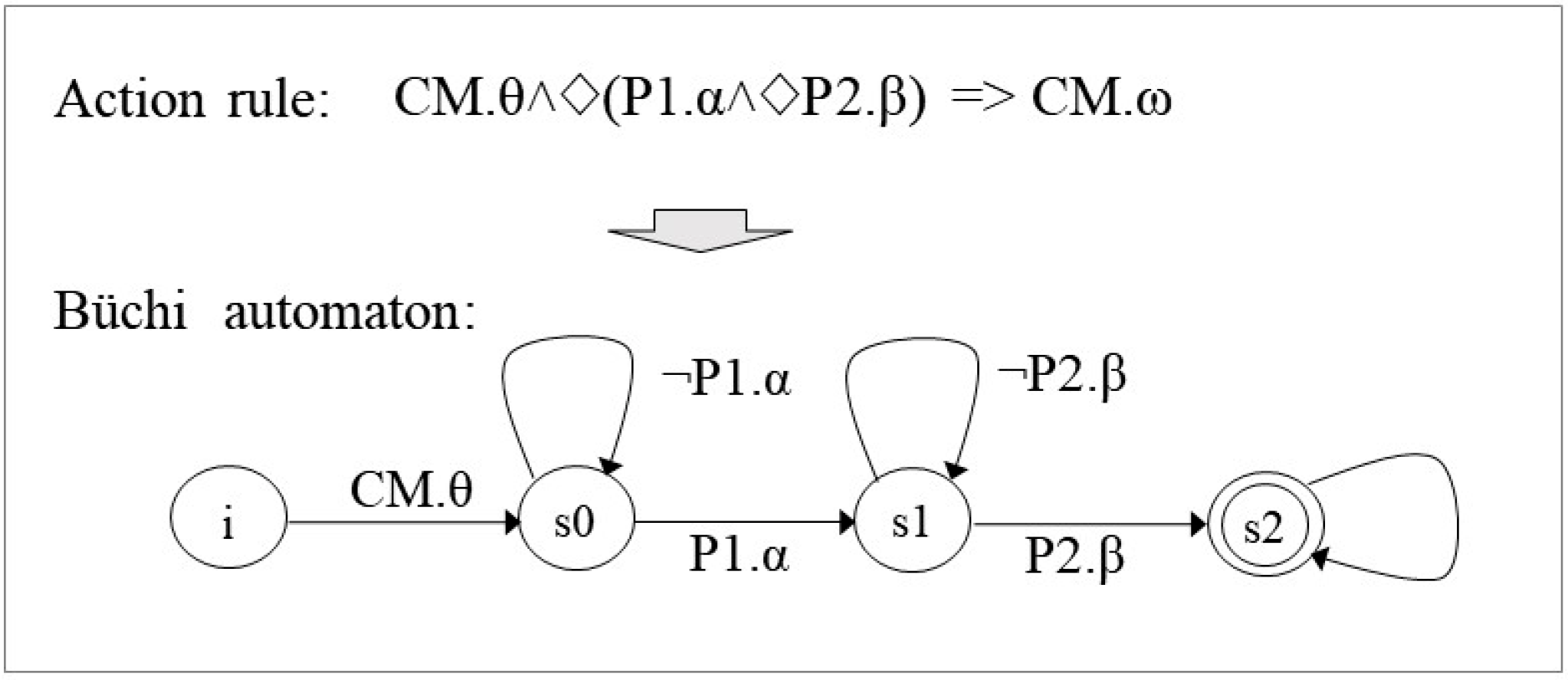
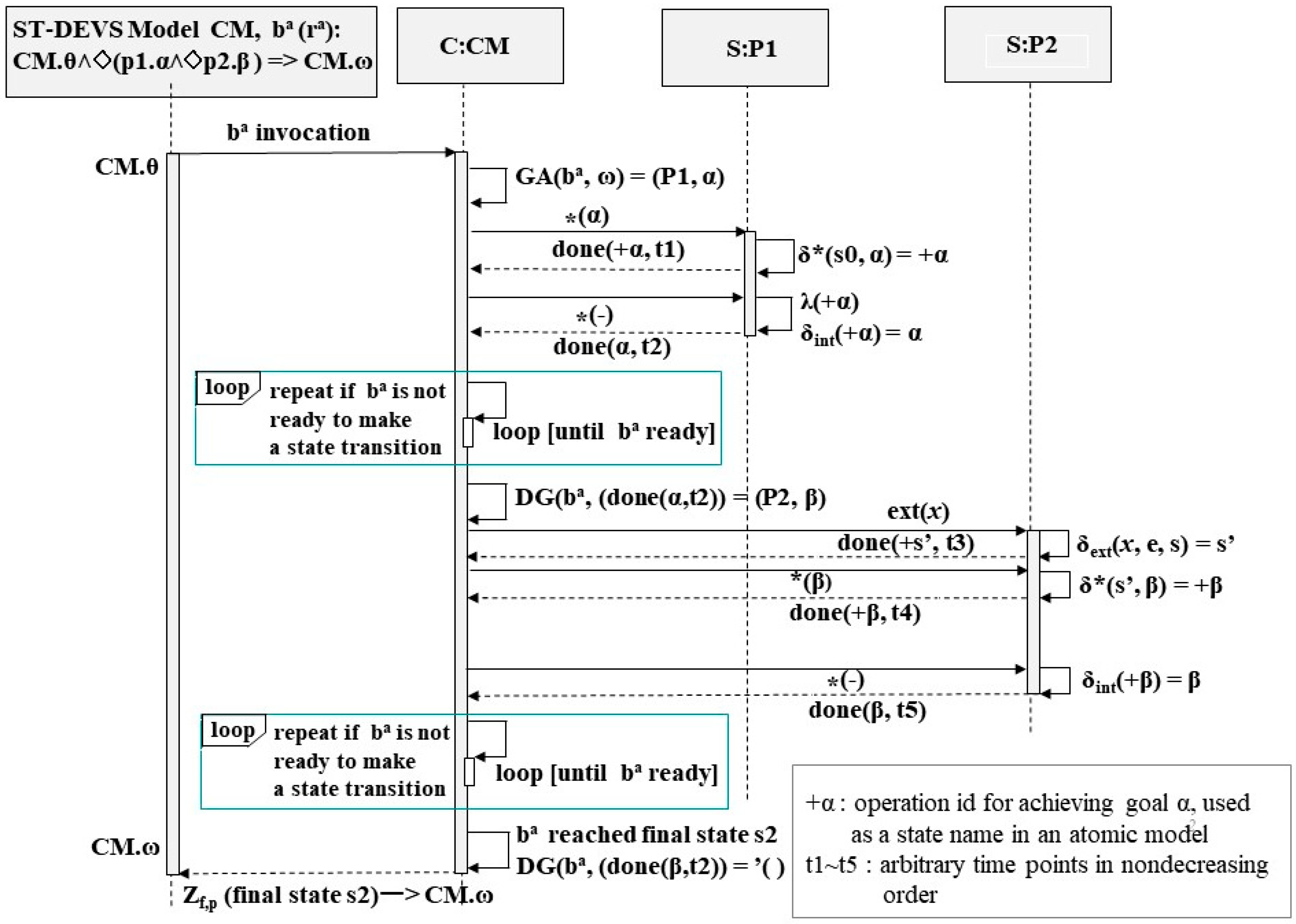
3.2. Execution of the Action Rule, TLST-DEVS
3.3. Action Execution Algorithm of an Action Rule, TLST-DEVS
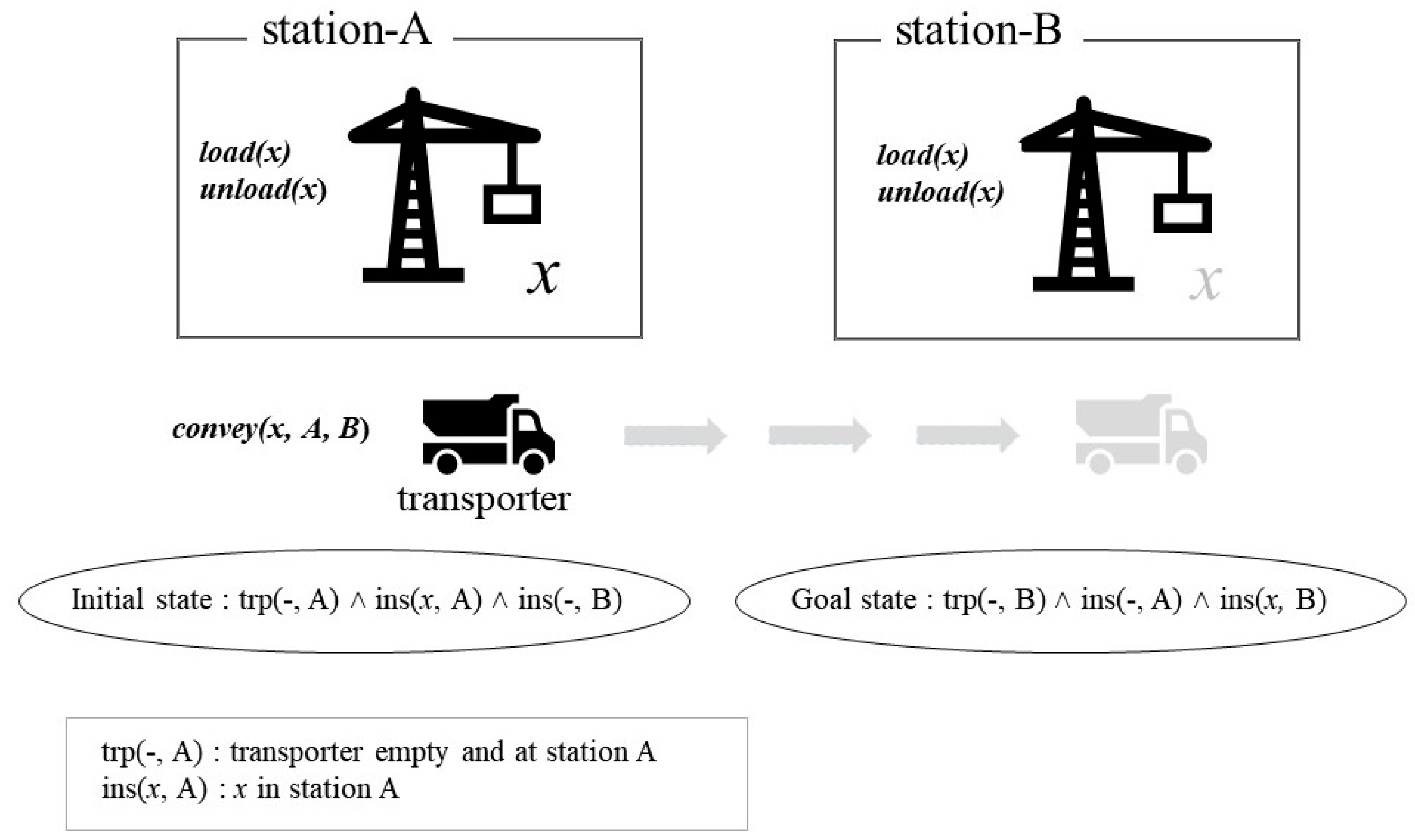
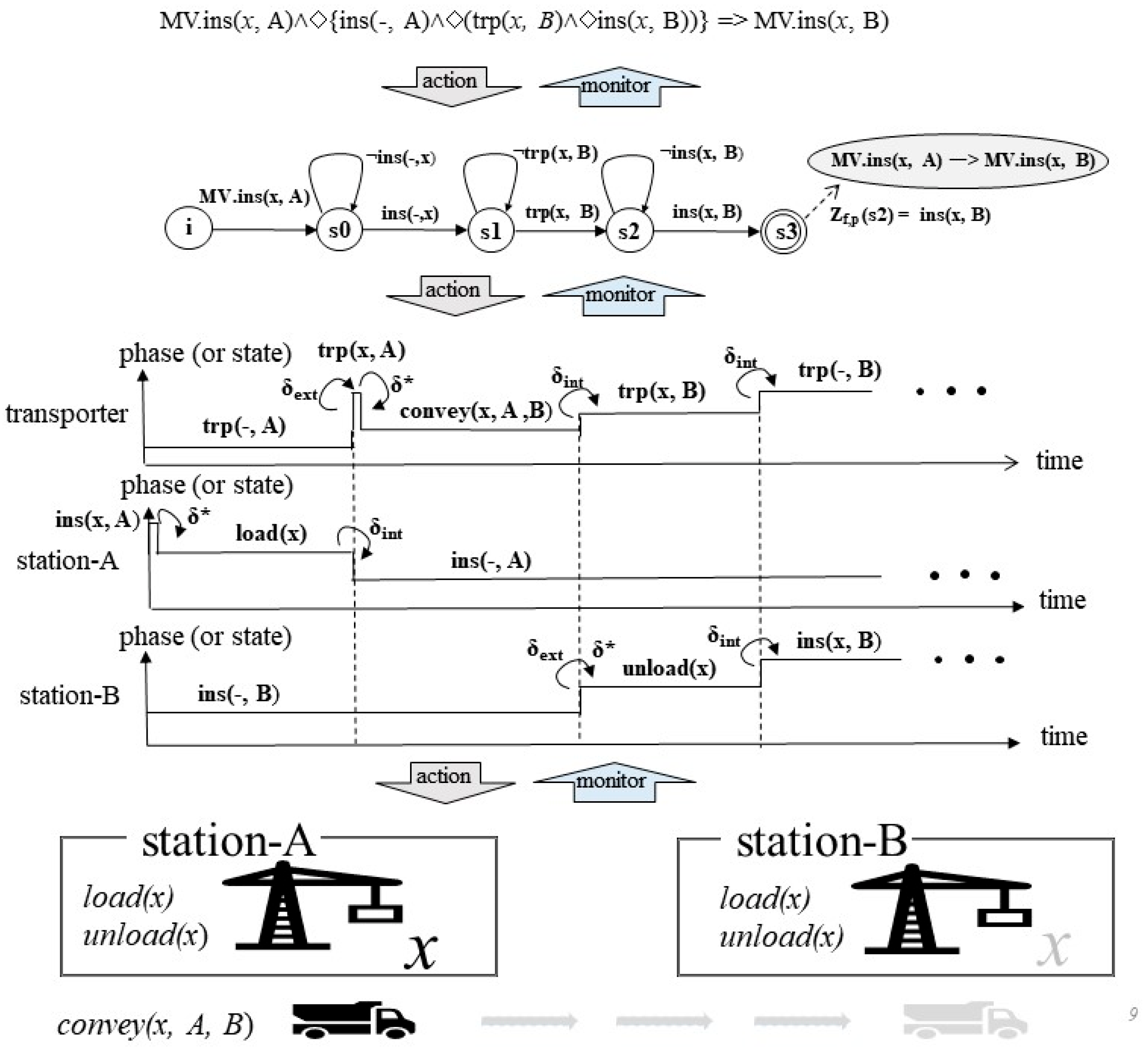
4. Example Application of an Action Rule
5. Discussions
5.1. Time-Dependent Variable
5.2. Important Considerations of ST-DEVS Implementation
5.3. Added Functionalities to Classic DEVS
6. Conclusions and Future Research
Funding
Conflicts of Interest
References
- Zeigler, B.P. Object-Oriented Simulation with Hierarchical, Modular Models: Intelligent Agents and Endomorphic Systems; Academic Press: San Diego, CA, USA, 1990; pp. 41–143. [Google Scholar]
- Zeigler, B.P.; Muzy, A.; Kofman, E. Theory of Modeling and Simulation: Discrete Event & Iterative System Computational Foundations; Academic Press: San Diego, CA, USA, 2018. [Google Scholar]
- Nance, R.E.; Overstreet, C.M. History of Computer Simulation Software: An Initial Perspective. In Proceedings of the 2017 Winter Simulation Conference, Las Vegas, NV, USA, 3–6 December 2017; pp. 243–261. [Google Scholar]
- Minerva, R.; Lee, G.M.; Crespi, N. Digital Twin in the IoT Context: A Survey on Technical Features, Scenarios, and Architectural Models. Proc. IEEE 2020, 108, 1785–1824. [Google Scholar] [CrossRef]
- Barricelli, B.R.; Casiraghi, E.; Fogli, D. A Survey on Digital Twin: Definitions, Characteristics, Applications, and Design Implications. IEEE Access 2019, 7, 167653–167671. [Google Scholar] [CrossRef]
- Cho, T.H. Simulation Methodology-Based Context-Aware Architecture Design for Behavior Monitoring of Systems. Symmetry 2020, 12, 1568. [Google Scholar] [CrossRef]
- Metz, S. Practical Object-Oriented Design, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2018. [Google Scholar]
- Forouzan, B.A.; Gilberg, R.F. C++ Programming: An Object-Oriented Approach; McGraw-Hill: New York, NY, USA, 2019. [Google Scholar]
- Heagerty, P.J.; Lumley, T.; Pepe, M.S. Time-Dependent ROC Curves for Censored Survival Data and a Diagnostic Marker. Biometrics 2000, 56, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Hoering, A.; Crowley, J.; Shaughnessy, J.D., Jr.; Hollmig, K.; Alsayed, Y.; Szymonifka, J.; Waheed, S.; Nair, B.; Rhee, F.V.; Anaissie, E.; et al. Complete remission in multiple myeloma examined as time-dependent variable in terms of both onset and duration in Total Therapy protocols. Clin. Trials Obs. 2009, 114, 1299–1305. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Billing, G.D. A time-dependent discrete variable representation method. J. Chem. Phys. 2000, 113, 1409–1414. [Google Scholar] [CrossRef]
- Cheskes, S.; Schmicker, R.H.; Rea, T.; Powell, J.; Drennana, I.R.; Kudenchuk, P.; Vaillancourt, C.; Conwaye, W.; Stiell, I.; Stubg, D.; et al. Chest compression fraction: A time dependent variable of survival in shockable out-of-hospital cardiac arrest. Resuscitation 2015, 97, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.Y.; Jo, H.; Son, H.; Hwang, H.J. Real-World Implications of a Rapidly Responsive COVID-19 Spread Model with Time-Dependent Parameters via Deep Learning: Model Development and Validation. J. Med. Internet Res. 2020, 22, e19907. [Google Scholar] [CrossRef] [PubMed]
- Jitkajornwanich, K.; Pant, N.; Fouladgar, M.; Elmasri, R. A survey on spatial, temporal, and spatio-temporal database research and an original example of relevant applications using SQL ecosystem and deep learning. J. Inf. Telecommun. 2020, 4, 524–559. [Google Scholar] [CrossRef]
- Bakli, M.; Sakr, M.; Soliman, T.H.A. HadoopTrajectory: A Hadoop spatiotemporal data processing extension. J. Geogr. Syst. 2019, 21, 211–235. [Google Scholar] [CrossRef]
- Wen, Y.H.; Gao, L.; Fu, H.; Zhang, F.L.; Xia, S. Graph CNNs with Motif and Variable Temporal Block for Skeleton-Based Action Recognition. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Shi, Z.; Pun-Cheng, L.S.C. Spatiotemporal Data Clustering: A Survey of Methods. ISPRS Int. J. Geo-Inf. 2019, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Largouët, C.; Krichen, O.; Zhao, Y. Temporal Planning with extended Timed Automata. In Proceedings of the 2016 IEEE 28th International Conference on Tools with Artificial Intelligence, San Jose, CA, USA, 6–8 November 2016. [Google Scholar]
- Bernardini, S.; Fox, M.; Long, D. Combining temporal planning with probabilistic reasoning for autonomous surveillance missions. Auton Robot. 2017, 41, 181–203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moon, S.I.; Lee, K.H.; Lee, D. Fuzzy Branching Temporal Logic. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 1045–1055. [Google Scholar] [CrossRef] [PubMed]
- Lamine, K.B.; Kabanza, F. History checking of temporal fuzzy logic formulas for monitoring behavior-based mobile robots. In Proceedings of the International Conference on Tools with Artificial Intelligence, Baltimore, MD, USA, 9–11 November 2000. [Google Scholar]
- Ko, H.; Lee, J.; Pack, S. Spatial and Temporal Computation Offloading Decision Algorithm in Edge Cloud-Enabled Heterogeneous Networks. IEEE Access 2018, 6, 18920–18932. [Google Scholar] [CrossRef]
- Pnueli, A. The Temporal Logic Of Program. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science, Providence, RI, USA, 31 October–2 November 1977. [Google Scholar]
- Cristiá, M.; Zeigler, B.P. Formalizing the semantics of modular DEVS models with temporal logic. In Proceedings of the 7e Conférence Francophone de MOdlisation et SIMulation-MOSIM, Paris, France, 31 March–2 April 2008; Volume 8. [Google Scholar]
- Mordechai, B.A.; Pnueli, A.; Manna, Z. The temporal logic of branching time. Acta Inform. 1983, 20, 207–226. [Google Scholar]
- Fisher, M. An Introduction to Practical Formal Methods Using Temporal Logic; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 12–48. [Google Scholar]
- Büchi, J.R. The Collected Works of J. Richard Büchi; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Büchi, J.R. On a decision method in restricted second order arithmetic. In The Collected Works of J. Richard Büchi; Mac Lane, S., Siefkes, D., Eds.; Springer: New York, NY, USA. [CrossRef]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Hopcroft, J.E.; Motwani, R.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation, 3rd ed.; Pearson: Chennai, India, 2008. [Google Scholar]
- Kolman, B.; Busby, R.; Ross, S. Discrete Mathematical Structures, 6th ed; Pearson: London, UK, 2017. [Google Scholar]
- Zadeh, L.A. Information and Control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- DeGroot, M.H.; Schervish, M.J. Probability and Statistics, 4th ed.; Pearson: London, UK, 2011. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, T. ST-DEVS: A Methodology Using Time-Dependent-Variable-Based Spatiotemporal Computation. Symmetry 2022, 14, 912. https://doi.org/10.3390/sym14050912
Cho T. ST-DEVS: A Methodology Using Time-Dependent-Variable-Based Spatiotemporal Computation. Symmetry. 2022; 14(5):912. https://doi.org/10.3390/sym14050912
Chicago/Turabian StyleCho, Taeho. 2022. "ST-DEVS: A Methodology Using Time-Dependent-Variable-Based Spatiotemporal Computation" Symmetry 14, no. 5: 912. https://doi.org/10.3390/sym14050912
APA StyleCho, T. (2022). ST-DEVS: A Methodology Using Time-Dependent-Variable-Based Spatiotemporal Computation. Symmetry, 14(5), 912. https://doi.org/10.3390/sym14050912




