Study on Error Separation of Three-Probe Method
Abstract
1. Introduction
2. Theory of Three-Probe Measurement
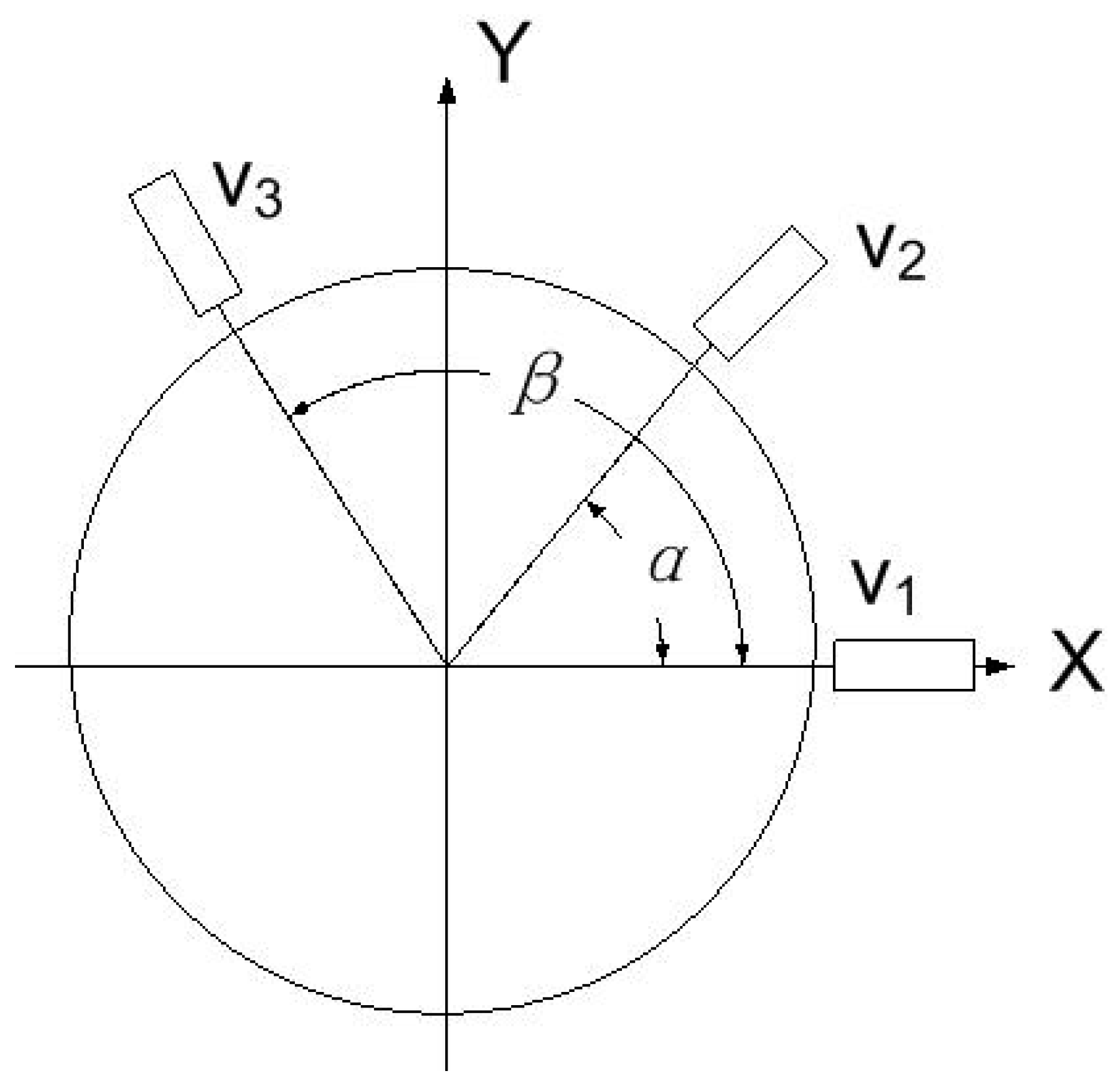
2.1. The Error-Separation Equations
2.2. Time-Domain Solution
2.3. Frequency-Domain Solution
2.3.1. Symmetry of Transfer Function W(n)
2.3.2. Harmonic Suppression
2.3.3. The Average Schemes
3. Experiments
3.1. Test Rig
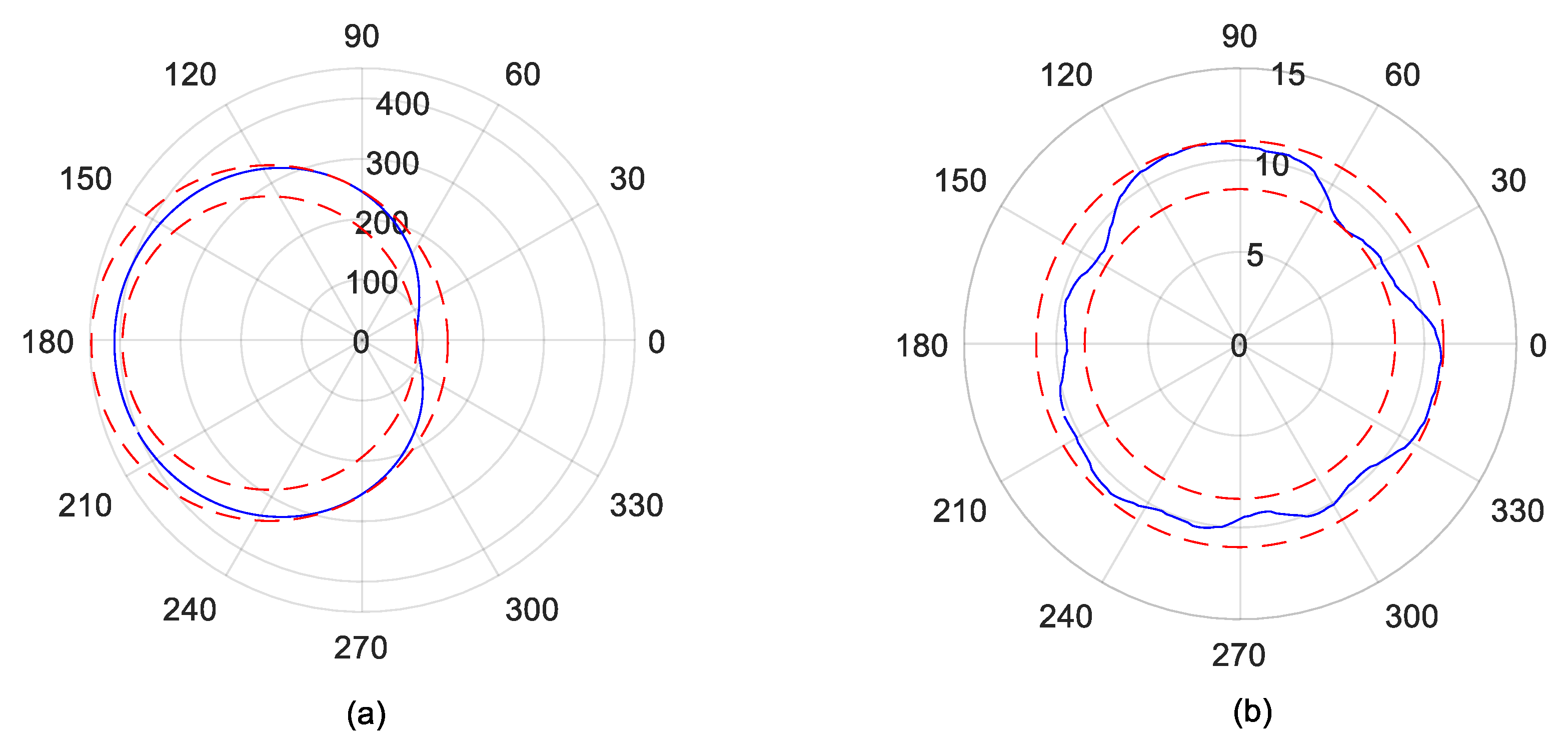
3.2. Analysis of Time-Domain Solution
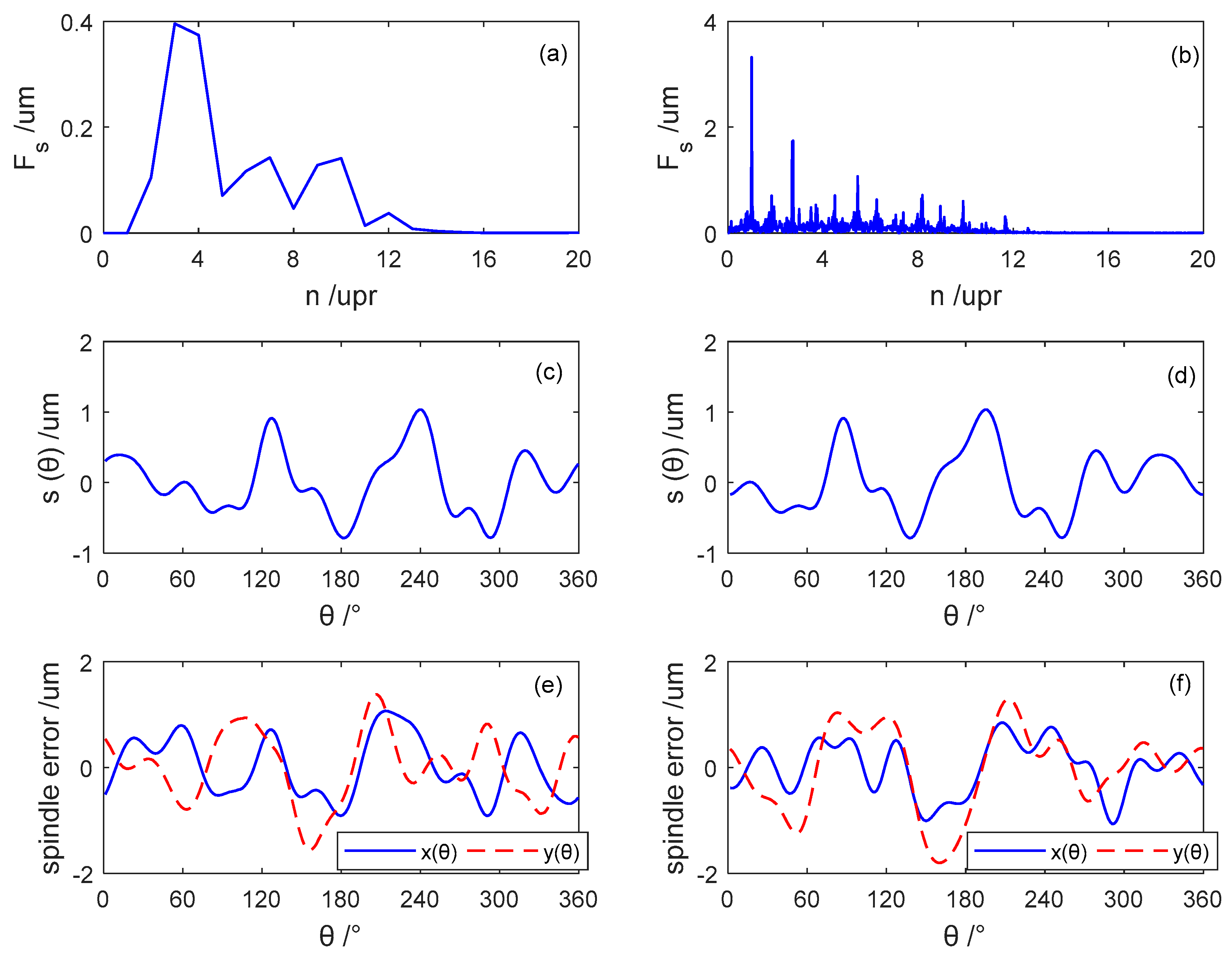
3.3. Analysis of Frequency-Domain Solution
4. Analysis of Influencing Factors
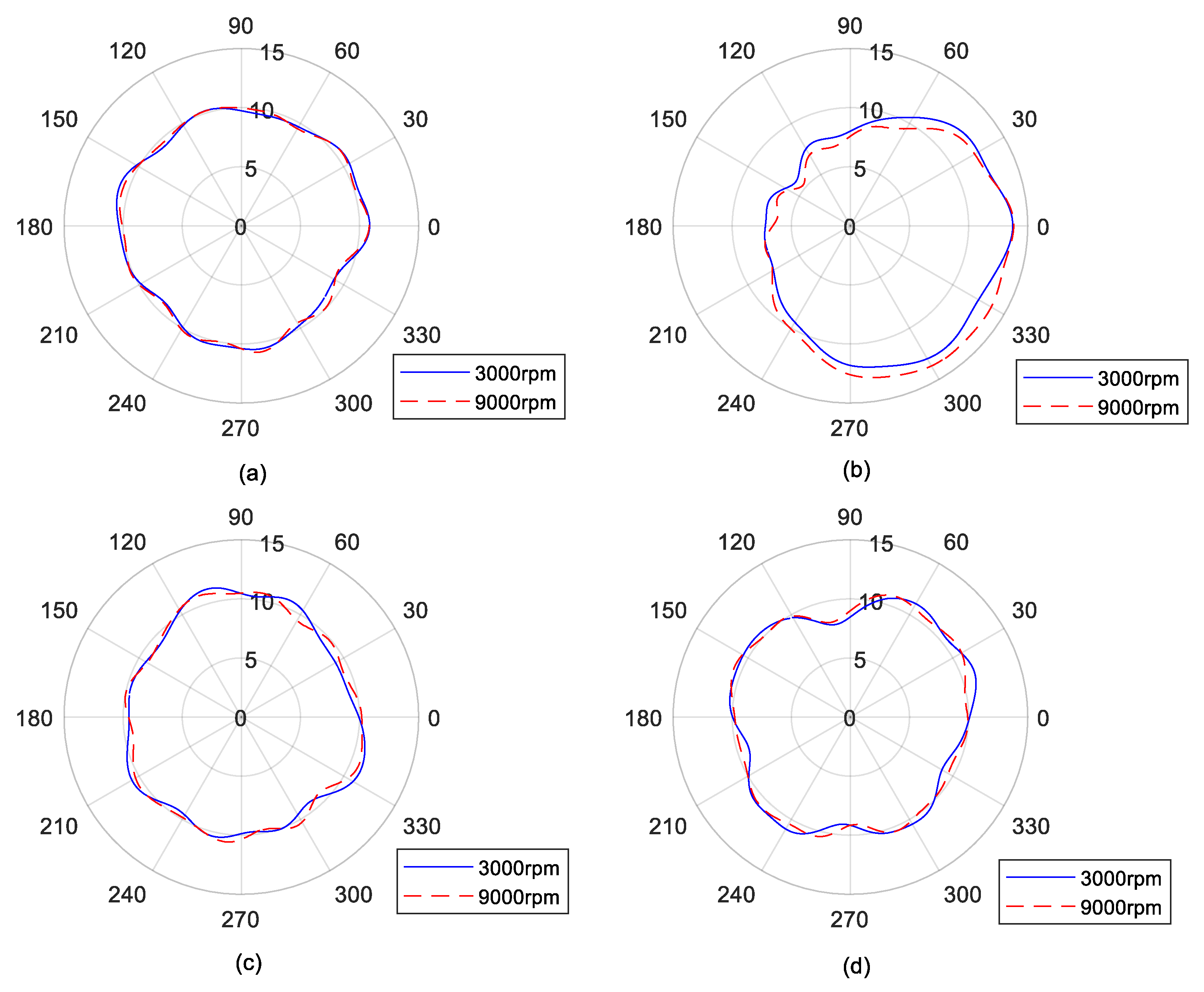
4.1. Rotational Speed
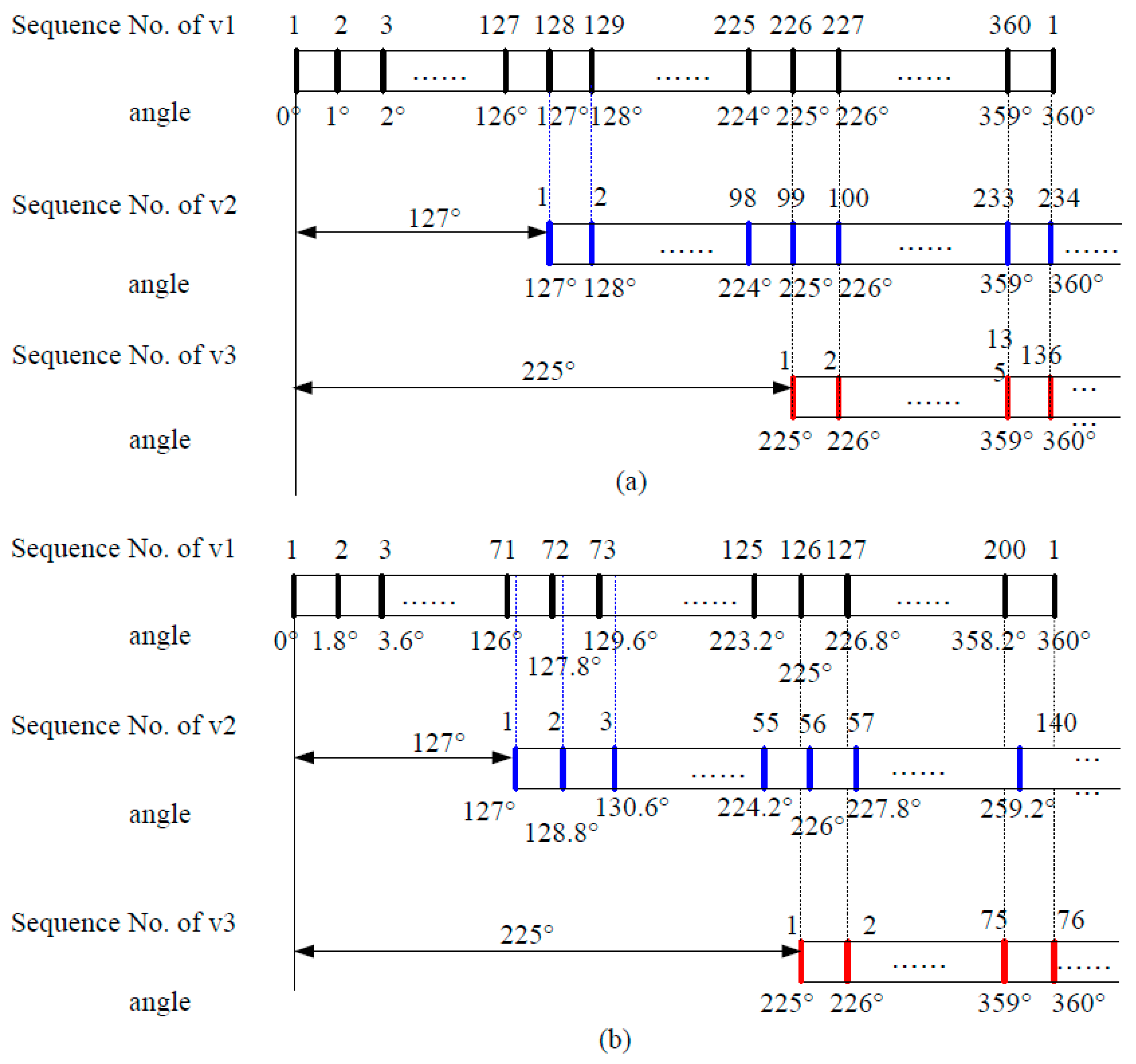
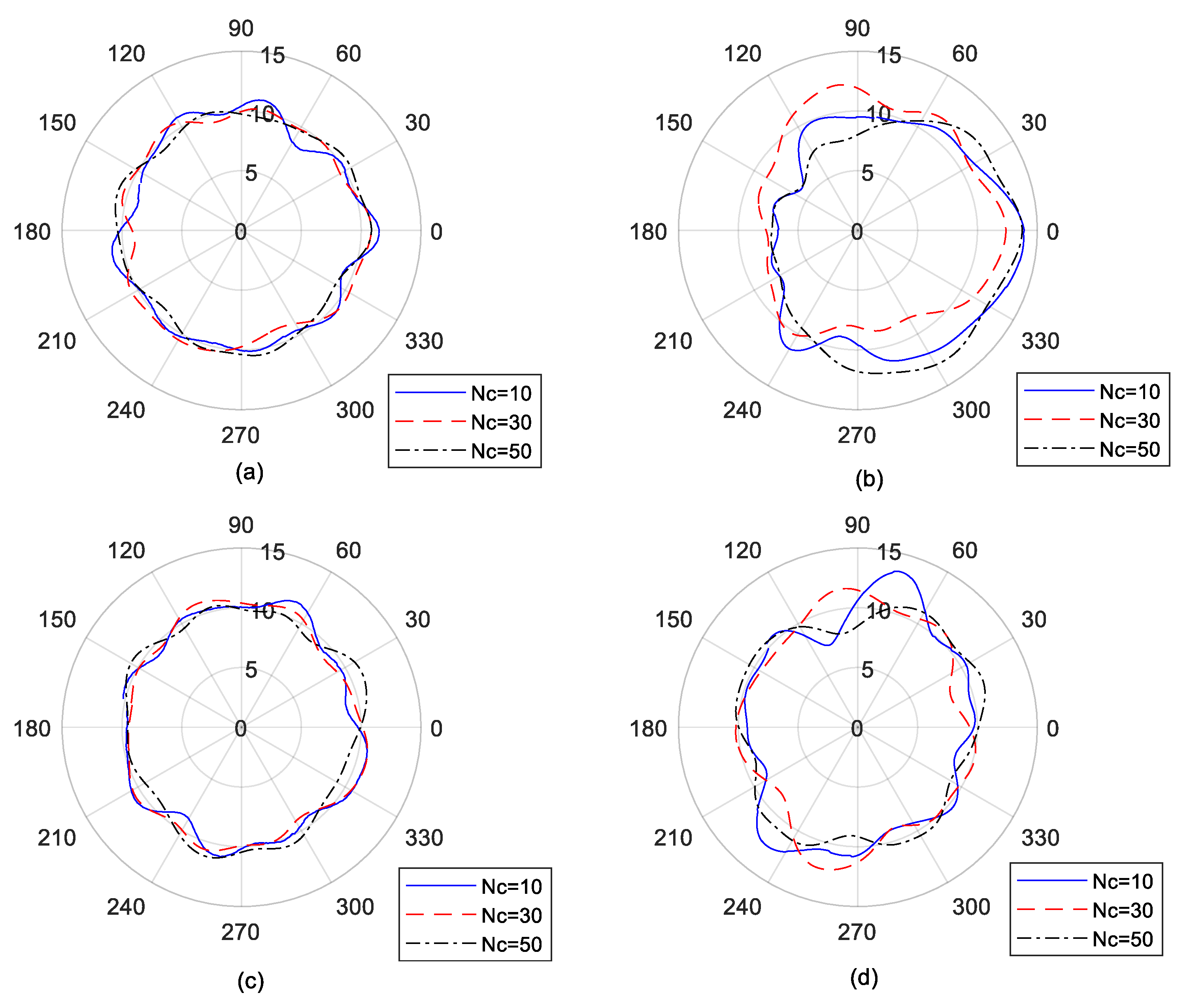
4.2. Consistency of Sampling Points
4.3. Probe Arrangement
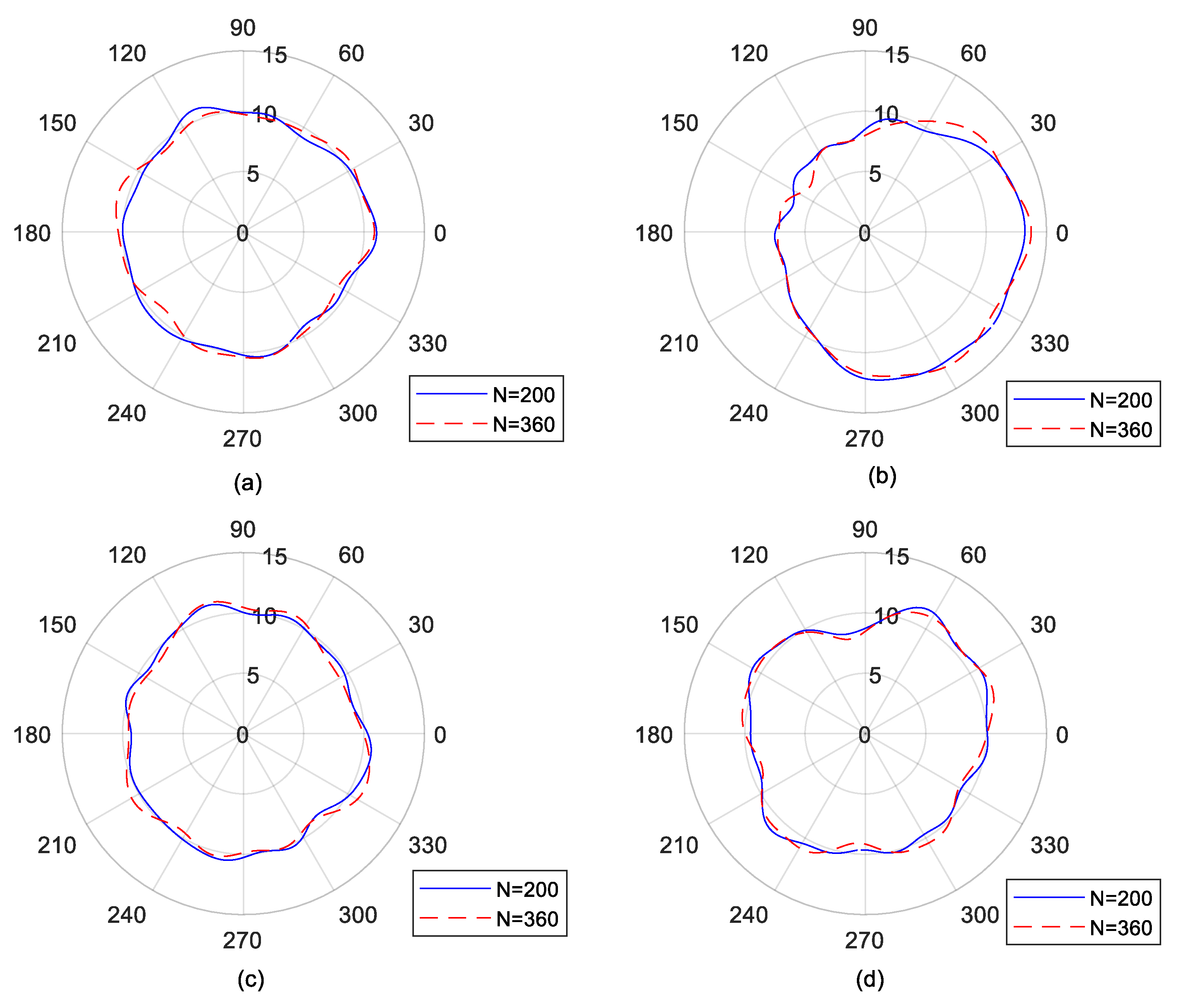
4.4. Number of Revolutions
5. Conclusions
- (1)
- The separating accuracy between rounding error and spindle error was demonstrated through the rotational speed experiments.
- (2)
- When the three-probe method aim was to obtain the roundness error, the previous average scheme of frequency-domain solution was recommended. When the aim was to measure spindle error, the latter average scheme of frequency-domain solution and time-domain solution was preferred.
- (3)
- The probe arrangement leading to less suppressed harmonic was preferred, and the number of revolutions was suggested to be at least 40 for roundness error to keep constant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, H.; Lei, D.; Zhang, X.; Lan, H.; Jiang, Z.; Kong, L. Measurement and analysis of the radial motion error of aerostatic ultra precision spindle. Measurement 2019, 137, 624–635. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Gao, W.; Hu, G.; Zhang, S.; Zhang, D. A novel multi-probe method for separating spindle radial error from artifact roundness error. Int. J. Adv. Manuf. Technol. 2017, 93, 623–634. [Google Scholar] [CrossRef]
- Qiao, L.X.; Chen, J.N.; Che, W.H.; Zhang, L.; Tian, J. A High-precision Spindle Error Separation Algorithm Based on Multi-step Process. Acta Metrol. Sinica 2018, 39, 6–11. [Google Scholar]
- Bai, J.; Wang, Y.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. Three-Probe Error Separation with Chromatic Confocal Sensors for Roundness Measurement. Nanomanuf. Metrol. 2021, 4, 247–255. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, X.; Hu, Y.; Hu, P. A v-block three-probe separation technique for portable measurement of cylindricity. Precis. Eng. 2019, 59, 37–46. [Google Scholar] [CrossRef]
- Liu, W.; Fan, K.; Hu, P.; Hu, Y. A parallel error separation method for the on-line measurement and reconstruction of cylindrical profiles. Precis. Eng. 2018, 51, 1–9. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, W.R. Easy measuring instrument for analyzing the radial and tilt error motions of a rotating shaft. Proc. IMechE J. Eng. Marit. Environ. 2017, 23, 667–674. [Google Scholar] [CrossRef]
- Niu, Z.; Chen, Y.L.; Matsuura, D.; Lee, J.C.; Kobayashi, R.; Shimizu, Y.; Ito, S.; Gao, W.; Oh, J.S.; Park, C.H. Precision measurement of Z-slide vertical error motion of an ultra-precision lathe by using three-probe method. Int. J. Precis. Eng. Manuf. 2017, 18, 651–660. [Google Scholar]
- Ding, F.; Luo, X.; Chang, W.; Wang, Z. In Situ Measurement of Spindle Radial and Tilt Error Motions by Complementary Multi-probe Method. Nanomanuf. Metrol. 2019, 2, 225–234. [Google Scholar] [CrossRef]
- Baek, S.W.; Kim, M.G.; Lee, D.H.; Cho, N.G. Multi-probe system design for measuring the roundness and rotation error motion of a spindle using an error separation technique. Proc. IMechE Part B J. Eng. Manuf. 2019, 233, 1547–1560. [Google Scholar] [CrossRef]
- Tiainen, T.; Viitala, R. Effect of positional errors on the accuracy of multi-probe roundness measurement method. Mech. Syst. Signal Process. 2020, 144, 106883. [Google Scholar] [CrossRef]
- Huang, R.; Pan, W.; Lu, C.; Zhang, Y.; Chen, S. An improved three-point method based on a difference algorithm. Precis. Eng. 2020, 63, 68–82. [Google Scholar] [CrossRef]
- Cappa, S.; Reynaerts, D.; Bender, F.A. A sub-nanometre spindle error motion separation technique. Precis. Eng. 2014, 38, 458–471. [Google Scholar] [CrossRef]
- Shi, S.; Zhang, H.; Qu, J.; Jin, G.; Kuschmierz, R.; Czarske, J. Measurement uncertainty propagation in spindle error separation techniques-Investigation by means of stochastic spectral method. Int. J. Mach. Tools Manuf. 2019, 141, 36–45. [Google Scholar] [CrossRef]
- Jeong, G.B.; Kim, D.H.; Jang, D.Y. Real time monitoring and diagnosis system development in turning through measuring a roundness error based on three point method. Int. J. Mach. Tools Manuf. 2005, 45, 1494–1503. [Google Scholar] [CrossRef]
- Hwang, J.; Park, C.H.; Gao, W.; Kim, S.W. A three probe system for measuring the parallelism and straightness of a pair of rails for ultra-precision guideways. Int. J. Mach. Tools Manuf. 2007, 47, 1053–1058. [Google Scholar] [CrossRef]
- Ma, H.F.; Zhuang, C.G.; Xiong, Z.H. Multipoint recursive sequential three-point method for on-machine roundness measurement. Procedia CIRP 2015, 31, 459–464. [Google Scholar] [CrossRef][Green Version]
- Lei, X.Q.; Li, Y.; Zhou, J.W.; Li, J.S.; Xue, Y.J. A new algorithm of roundness error separation technique of three-point method. J. China Ordnance 2008, 4, 141–145. [Google Scholar]
- ISO 230-7:2015; Test Code for Machine Tools-Part 7: Geometric Accuracy of Axes of Rotation. ISO: Geneva, Switzerland, 2015. Available online: https://www.iso.org/standard/56624.html (accessed on 1 March 2022).
- Knapp, B.; Arneson, D.; Martin, D. Electrical runout using an eddy-current sensor for roundness measurements. In Proceedings of the 28th Annual Meeting of the American Society for Precision Engineering, ASPE 2013, Saint Paul, MN, USA, 20–25 October 2013. [Google Scholar]



| α/° | β/° | N | m1 | m2 | Consistency | Rank (H) |
|---|---|---|---|---|---|---|
| 127 | 225 | 360 | 128 | 226 | consistency | 358 |
| 127 | 225 | 200 | [71.6] | 126 | inconsistency | 200 |
| Experiments No. | Probe Arrangement | Rotational Speed | N | fs |
|---|---|---|---|---|
| 1 | 0–127–225° | 3000 rpm | 200 dots | 10 kHz |
| 2 | 0–100–225° | 3000 rpm | 200 dots | 10 kHz |
| 3 | 0–127–225° | 3000 rpm | 360 dots | 18 kHz |
| 4 | 0–127–225° | 9000 rpm | 360 dots | 54 kHz |
| Experiments No. | Roundness Error Value/μm | Spindle Error Value/μm |
|---|---|---|
| 1 | 51.4791 | 2.6337 |
| Experiment No. | α/° | β/° | Kr in Previous Average | Kr in Latter Average |
|---|---|---|---|---|
| 1, 3, 4 | 127 | 225 | 1, 360 k ± 1 | 0.02, 1.8 k ± 1 |
| 2 | 100 | 225 | 1, 72 k ± 1 | 0.02, 0.36 k ± 1 |
| Rotational Speed/rpm | Roundness Error Values/μm | Spindle Error Value/μm | ||
|---|---|---|---|---|
| Previous Aver | Latter Aver | Previous Aver | Latter Aver | |
| 3000 | 1.7973 | 2.0599 | 2.0185 | 3.0874 |
| 9000 | 1.7939 | 2.0040 | 1.7201 | 2.7147 |
| Error % | 0.2 | 2.7 | 14.8 | 12.1 |
| N | Roundness Error Values/μm | Spindle Error Value/μm | ||
|---|---|---|---|---|
| Previous Aver | Latter Aver | Previous Aver | Latter Aver | |
| 200 | 1.8060 | 1.6426 | 1.8615 | 3.0997 |
| 360 | 1.7973 | 2.0599 | 2.0185 | 3.0874 |
| Error % | 0.5 | 25.4 | 8.4 | 0.4 |
| Probe Arrangement | Roundness Error Values/μm | Spindle Error Values/μm | ||
|---|---|---|---|---|
| Previous Aver | Latter Aver | Previous Aver | Latter Aver | |
| 0–127–225° | 1.8060 | 1.6426 | 1.8615 | 3.0997 |
| 0–100–225° | 1.8131 | 1.9820 | 1.9087 | 2.2726 |
| Error % | 0.4 | 20.7 | 2.5 | 26.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, C.; Zhuo, M.; Cui, Z.; Geng, J. Study on Error Separation of Three-Probe Method. Symmetry 2022, 14, 866. https://doi.org/10.3390/sym14050866
Zhong C, Zhuo M, Cui Z, Geng J. Study on Error Separation of Three-Probe Method. Symmetry. 2022; 14(5):866. https://doi.org/10.3390/sym14050866
Chicago/Turabian StyleZhong, Chengbao, Ming Zhuo, Zhong Cui, and Jiqing Geng. 2022. "Study on Error Separation of Three-Probe Method" Symmetry 14, no. 5: 866. https://doi.org/10.3390/sym14050866
APA StyleZhong, C., Zhuo, M., Cui, Z., & Geng, J. (2022). Study on Error Separation of Three-Probe Method. Symmetry, 14(5), 866. https://doi.org/10.3390/sym14050866





