Abstract
Josephson junctions are essential ingredients in the superconducting circuits used in many existing quantum technologies. Additionally, ultracold atomic quantum gases have also become essential platforms to study superfluidity. Here, we explore the analogy between superconductivity and superfluidity to present an intriguing effect caused by a thin finite barrier in a quasi-one-dimensional toroidal spinor Bose–Einstein condensate (BEC). In this system, the atomic current density flowing through the edges of the barrier oscillates, such as the electrical current through a Josephson junction in a superconductor, but in our case, there is no current circulation through the barrier. We also show how the nontrivial broken-symmetry states of spinor BECs change the structure of this Josephson-like current, creating the possibility to probe the spinor symmetry, solely using measurements of this superfluid current.
1. Introduction
The Josephson effect [1,2] is one of the most relevant phenomena in superconductivity; for his theoretical predictions, Brian D. Josephson received the Nobel Prize in Physics in 1973. In a superconductor, the phenomenon is characterized by the tunneling of Cooper pairs through a junction, or a weak link, represented by a potential energy barrier between two superconductor regions [3,4,5]. When a voltage V is applied to these regions, the electrical current in the junction, , oscillates according to the expression:
where is the current amplitude and is the angle representing the phase difference of the order parameter between each superconducting region [4]. There is a conceptual analogy between superconductivity and superfluidity [6], given by the lack of resistance in the flow of the electrical current, or, equivalently, the lack of viscosity in the flow of a superfluid. In fact, since superfluidity emerges naturally in Bose–Einstein condensates (BECs) produced in dilute ultracold Bose gases [7,8,9,10,11,12,13,14,15], the analogue of the Josephson effect has already been studied in experiments [16,17,18,19].
For scalar BECs [7,8] (i.e., condensates with a scalar order parameter: ), the superfluid velocity is always proportional to the global phase gradient (), and it represents the complete structural symmetry of the system. On the other hand, for spinor BECs [9,10,11] (i.e., condensates with multi-component order parameter: ), the superfluid flow is related to the properties of their symmetry and topology, which can generate nontrivial spatial spin textures and current distributions not found in scalar BEC systems. In fact, there are many topological states in spinor BECs analogous to particles and structures studied across several areas of physics, such as skyrmions, Dirac monopoles, knot solitons, vortices, half-vortices [9,20,21,22,23,24], to name a few.
Here, based on the analogy between superfluidity and superconductivity, we study a Josephson-like oscillating current produced in toroidal spinor Bose–Einstein condensates due to the presence of a thin finite energy barrier (Figure 1), and we show that the current density at the edges of the barrier behaves similarly to , and depends on the structural symmetry of the spinor condensate.
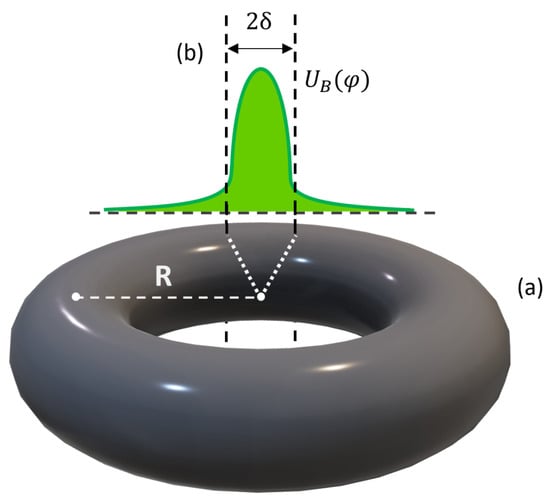
Figure 1.
Schematic illustration of the external potentials applied to the condensate: (a) effective toroidal region (with average radius R) where the potential confines the condensate; (b) repulsive barrier , for the azimuthal angle in cylindrical coordinates . Here, we consider thin angular widths .
2. General Modeling of Spinor BECs
For a system with atomic spin , the order parameter of a spinor BEC satisfies the following vector Gross–Pitaevskii equation (GPE) [9]:
In the equation, the bold fonts indicate matrix quantities related to the vector order parameter , and where is the number density, with spin components , is the spin density, and is the spin operator (in the representation). The constants and are related to the linear and quadratic Zeeman effects, respectively, when an external magnetic field, , is applied. The system’s nonlinear interaction “strength” is modeled by the coefficients and (see Reference [9] for details).
In this work, we consider a toroidal trapping potential, , with a repulsive barrier, , restricted to a region of small azimuthal angle. Therefore, the total external potential is given by , as sketched in Figure 1. We assume that provides the necessary means to trap all the components of the spinor BEC in the torus. For instance, by using the appropriate optical trapping techniques [25]. Optical traps have the advantage of providing flexible control over the potential symmetry when combined, for example, with digital holography [26,27], direct imaging [28], or phase-mapping [29] of sharp optical patterns, to design almost arbitrary shapes. In fact, a toroidal optical potential with a controllable energy barrier similar to the one described here has been demonstrated in [30,31,32], and a toroidal potential with spinor BEC in [33].
The order parameter of a spinor BEC, represented as a column matrix, can always be factored into , as the product of a scalar part, , and a normalized spinor part, (with ) [9]. This vector description has a gauge symmetry with artificial gauge fields related to . These fields emerge naturally from the description, and are analogous to the scalar and vector electromagnetic potentials [9,34]:
In particular, the superfluid number current density, , depends linearly on the vector potential , as the superfluid velocity of a spinor BEC is given by:
Note that the action of the artificial vector potential is analogous to the electromagnetic vector potential on the expression of the electrical current in a superconductor [4]. In addition, some of the topological properties of the condensate are determined by the circulation of (i.e., ), and, therefore, they may depend on artificial magnetic fluxes, given by a synthetic magnetic field [9].
In general, the current density of a spinor BEC is defined in the usual manner, replacing the scalar order parameter by its vector form
therefore,
Alternatively, using the spin components , one could write
where the velocity spin components are .
3. Modeling the Potential Barrier and Defining Some Approximations
This section explains in detail how we define the potential barrier, , and its general properties. Because we will use the quasi-one-dimensional (quasi-1D) limit for the geometry of the condensate later, we consider the barrier is written in terms of a normalized angular distribution , not depending on other spatial variables ():
We consider that the barrier is effectively restricted to an angular range , such that:
Integrating the GPE (2) along the arc , with fixed in the thin barrier condition (), leads to two dominant terms:
where the left-hand side follows directly from the fundamental theorem of calculus, and it is related to the momentum along the direction (). Note that we simplified the notation , given that we consider () fixed parameters.
The remaining terms not computed in the last equation were neglected because for small they are proportional to (i.e., these terms are while the dominant terms are proportional to the unit), and can be neglected as one takes the limit of .
Additionally, in the limit of small , the integration of the barrier potential resembles the integration of a Dirac’s delta (normalized) function, such that
Here, it is important to emphasize that, in practice, the derivative of the potential barrier must not exceed a limit given by the Landau critical velocity, otherwise, the flow is dissipated and the system loses its superfluid properties [30,35]. To avoid such situations, one may always choose a larger radius R (see Figure 1) so that the barrier is spatially “smooth” enough. We discuss this condition in Section 6.
Finally, we consider one last approximation. If the number of atoms in the condensate is kept the same, it is expected that the average cross-section area of (at fixed ) becomes smaller when R is larger. So, for R big enough, the condensate would be trapped in small and ranges, and the number density would become approximately a function of only one variable (quasi-1D approximation):
Moreover, these conditions also restrict the direction of , such that:
In the next section, we discuss how the barrier potential, , acts on the current density and the consequences of choosing an order parameter with defined parity.
4. Current Density and the Parity of the Order Parameter
Based on the discussion in the last section, we expect that, for relatively large R, a toroidal condensate under the presented conditions, will behave similar to a quasi-1D BEC with the current density effectively restricted to the direction. Now, we are interested in finding an expression for the current density at the edges of the barrier (i.e., at ). To help us find such an expression, we define the following quantity:
Its interpretation is quite simple: if we multiply it by the area, , of the cross-section of the condensate, it returns the rate of change in the number of atoms located inside the barrier region:
To simplify it, we use symmetry arguments observing the parity of the order parameter . It is noticeable that, in general, the GPE (2) admits both even and odd solutions (with respect to the variable ), and if we choose an even distribution , the order parameter follows
Moreover, it is easy to show that is always an odd function if the parity of is well defined. This way, it is clear that allows us to calculate directly:
In particular, if we choose to be even, one finds that:
and, using the Equations (12) and (13), we finally obtain:
Note that making an even function is not the only way of finding such an approximation for the current difference . For instance, choosing big enough in the complete expression for ,
should effectively return the same value from the even case, regardless of whether the parity of is defined or not. However, choosing the even parity case for leads to a symmetrical constraint of the BEC global phase, as we show in the next section (see Equations (31) and (38)).
Recalling what we mentioned before, it is always possible to factorize the order parameter , and the scalar term can be written as . Applying such factorization in (22), we find:
According to reference [9], is highly dependent on the symmetrical and topological properties of the condensate. Therefore, we expect that will also depend on such properties. Nevertheless, for now, to keep the analogy between the Josephson current (1) and as simple as possible, we consider the case of a scalar BEC (i.e., ):
Note that the current density at the edges of the barrier () is proportional to the sine of the phase difference between the barrier region () and the remaining region ( or ), and the analogy to the Josephson current is (mathematically) clear.
It is also possible to derive the time-evolution equation for the global phase difference , similarly to the second equation in (1). Here, we use the following relation between and the local average energy per particle [7]:
where is the functional derivative of the average energy of the condensate, E, with respect to the number density [7], ,
5. The Broken-Symmetry Spinor BEC Case
This section discusses the current beyond the scalar BEC case. For that, it is convenient to define the function as the quantity that characterizes such current according to the spinor nature of the condensate:
Note that, in general,
because the spinor part may not be trivial (i.e., ). Before discussing specific cases, we recall some useful properties of spinor BECs applied to the system analyzed here.
Firstly, due to the defined parity of , it is simple to show that the superfluid velocity in the direction () is an odd function. Therefore, its circulation must always be zero and the global phase circulation is proportional to the artificial magnetic flux:
which, in several situations [9], might be proportional to integer multiples of .
In addition, the time-evolution equation for in the spinor BEC case is given by:
where the average energy E is (for atomic spin ):
and it implicitly depends on the gauge field .
Moreover, according to reference [9], spinor BECs are naturally described by broken-symmetry states in the long-wavelength limit (i.e., when the characteristic dimensions of the condensate are much larger than its healing length). Furthermore, the spinor part of these states is characterized by the following type of expansion:
where the parameters are functions of time and space, and represent an arbitrary unitary transformation (i.e., they are Euler angles). For condensates, such transformation is equivalent to the following matrix:
The constant generator of the spinor part is directly related to the order parameter of a uniform condensate, whose possible states (ferromagnetic, polar, anti-ferromagnetic, and others) have been studied and classified [9,10,36]. For generators with average spin in the direction (), the artificial electromagnetic potentials are [9]:
So, we can rewrite (31) as:
which is a constrain between and the Euler angles (given that the parity of is defined).
Now, we will show two examples of how such broken-symmetry states affect the current and how it differs from the scalar BEC case.
5.1. Ferromagnetic States
There are two families of ferromagnetic states in spinor () BECs, called positive and negative, generated by and , respectively. Using (35), one derives [9] the following spinor parts of the ferromagnetic states :
from which one can compute all the symmetrical and topological properties. With these expressions, we directly find how the parameters () act on :
for , when or .
Note that is not equal to sin in general. This shows that the current in BECs is sensitive to their nontrivial structural spinor properties. However, we are still able to access the scalar limit, because , if () are constant parameters. This situation corresponds to spinor BECs with trivial spinor parts (for instance, in the ferromagnetic case, or ), representing an effective scalar BEC in a rotated reference frame.
5.2. Polar State
The polar states are generated by . Such a family of states is unique because they are closely related to scalar BECs (given that and ), while their symmetrical and topological properties might be nontrivial [9]. Using (35), one finds the spinor part of the polar states:
Applying this expression in (29), we obtain :
With a little algebraic work, we find that in general. In this sense, we might interpret such a relation as a signature of the partial analogy between polar states and scalar BECs, because the current density can be written in the following way:
where the parameters modulate the maximum value of .
6. Landau Critical Velocity, Lower Bound for R, and Experimental Protocol
This section discusses the effects of the Landau critical velocity on the parameters of our model and shows that it defines a lower bound for R. We also introduce a simple experimental scheme to test the theory, proposing an upper limit to how fast the barrier height, , can be turned on. In addition, we discuss some relevant considerations and practical suggestions for the experiments, particularly related to time-lapsed measurements of the BEC density distribution, using specialized imaging techniques, from which the analysis of the time evolution would lead to .
The Landau critical velocity is an upper limit for the velocity of particles in a superfluid, before the appearance of dissipation (viscosity) [7,8,13,35]. It is set by the energy gap between the ground state and the lowest elementary excitation leading to dissipation in the fluid. In BECs, this critical velocity is typically in the same order of magnitude as the sound velocity, being identical to it for a weakly-interacting homogeneous (uniform) scalar BEC. According to the Bogoliubov theory for spin-1 spinor BECs [9], similarly to the scalar case, this velocity is
where here g is usually a linear combination of the constants and from Equation (2), and it depends on the broken-symmetry state of the condensate. For example, in a ferromagnetic state, according to Sec. 5.2.1 in Ref. [9], .
Because is an odd (anti-symmetrical) function in our formulation, from symmetry arguments alone, we expect , with the maximum amplitudes symmetrically occurring in the interval . Therefore, assuming that the dominant contribution to the current occurs at , because we are interested in the superfluid regime, we impose , where is the total (local) density at . Moreover, we use Equation (5) to estimate :
Considering is a given angle (i.e., we chose in an experiment), we can estimate a lower bound for R, such that the condensate is in the superfluid regime:
Or, more intuitively:
if one wants the system to be far from the critical velocity.
As indicated previously in Equation (17), the currents are helpful to model the rate of change in the number of atoms leaving the region inside the barrier. Conversely, measuring this rate of change, i.e., monitoring , is a way to measure as a function of time. In principle, one could use non-destructive imaging techniques [37,38] to take multiple snapshots of the condensate density distribution at different times. Depending on the experimental parameters, such as the number of atoms and the radius R, the cross-section could be so small that the optical density of the atoms would make dispersive (phase contrast) imaging [37] difficult, but this is exactly the conditions for which partial-transfer absorption imaging (PTAI) [38] was developed. Therefore, in principle, one can make these measurements even in the deep quasi-1D limit (i.e., extending the radius R as necessary to fulfill the condition in Section 4).
According to Section 5, different types of spinor BECs (ferromagnetic, polar, and scalar, with equivalent initial conditions for the density and velocity) should respond differently to the application of the same potential barrier . The details will depend on the specific case, as well as the external magnetic field. Therefore, further theoretical, numerical, and experimental studies are necessary, but they may unveil new ways of sensing the symmetry of spinor BEC states, solely using measurements of .
As a simple example, we can imagine an experimental protocol starting initially with the barrier turned off and a homogeneous condensate in equilibrium ( and ). At , the barrier is turned on and ramped up following a sufficiently fast time protocol . The barrier causes a perturbation on the densities (and also on and ), and, after a time , the system reaches a new equilibrium ( and , ). For scalar BECs, the equilibrium is described by , with constant, which (as expected) simply implies in:
Finally, we briefly show here that the time protocol must always have an upper limit that depends on the density’s perturbation and at any given time so that the condensate does not lose its superfluid properties. This upper limit is found using Equation (24) to estimate and it corresponds to
7. Conclusions
In this manuscript, we used the parallel between superconductors and superfluids to present a curious new effect in a superfluid, similar to the current oscillations in the Josephson effect, but it happens without current flowing through the barrier. The result was derived for BECs in toroidal traps with a thin finite repulsive barrier, and it works both for scalar and spinor BECs.
Using a thin barrier approximation, in Equations (12) and (13), and assuming a defined parity for the order parameter, we derived analytical expressions for the current density. We showed that the current at the edges of the barrier oscillates in a similar fashion to the current flowing through a Josephson junction (1), but in our case, it happens without a net circulation of the superfluid current. We also showed how the nontrivial symmetry properties of spinor BECs could generate other current structures, beyond the typical case, indicating that such current is sensitive to these properties, suggesting that it could be used to probe spinor symmetry or, perhaps, provide precision measurements related to the superfluid flow.
Throughout this work, we assumed the parity of was defined, which is a strong mathematical imposition to guarantee that Equation (24) is a reasonable approximation for the current density. Moreover, this imposition implies that the circulation of the condensates considered here is always zero, excluding several configurations with nontrivial symmetry and topology. However, as we discussed in Section 4, ensuring that the last term in (23) is dominant should keep the structure of unchanged, regardless of the parity of . Therefore, it might be possible to derive a similar expression (24) for BECs with nonzero circulation, such as the ones shown in experiments [30,31,32,33,39], and for spinor BECs with nontrivial structure or topology [9,40,41,42,43,44,45,46,47,48].
Here, we also neglected the effects of fluctuations, either classical or quantum, which can be relevant in the quasi-1D limit [49,50,51]. However, as we have shown previously in Ref. [52], one can always play with the number of atoms and the aspect ratio of the trapping potential to place oneself within the best range of parameters for the experiments. Exercising this ability deliberately allows one to control the influence of thermal phase fluctuations at finite temperatures. Therefore, interesting future directions would be to explore the effects of finite temperature and thermal fluctuations, and the non-equilibrium effects caused by quickly turning on the repulsive barrier in our proposed experimental scheme. In Section 6, we discussed some considerations for an idealized protocol, but the general spinor case is more complex and deserves a detailed analysis. For instance, our simple estimate for the Landau critical velocity does not take into account other relevant mechanisms of decay [33,39,53], especially at finite temperatures [54].
Therefore, further numerical, experimental, and theoretical studies are necessary and may improve, expand, and, perhaps, help to classify (maybe in symmetry terms) the formulation of this intriguing Josephson-like effect in toroidal spinor Bose–Einstein condensates.
Author Contributions
Conceptualization, M.H.F.D. and S.R.M.; methodology, M.H.F.D. and S.R.M.; writing—original draft preparation, M.H.F.D.; writing—review and editing, S.R.M.; supervision, S.R.M.; funding acquisition, S.R.M. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the financial support provided by FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo), the São Paulo Research Foundation, under Grant no. 2013/07276-1 and 2019/27471-0, and also by CAPES Grant nos. 88887.338144/2019-00 and 88887.616990/2021-00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Josephson, B.D. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Josephson, B.D. The discovery of tunnelling supercurrents. Rev. Mod. Phys. 1974, 46, 251–254. [Google Scholar] [CrossRef] [Green Version]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1982. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; Dover Books on Physics Series; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef] [Green Version]
- Cummings, F.W.; Johnston, J.R. Theory of Superfluidity. Phys. Rev. 1966, 151, 105–112. [Google Scholar] [CrossRef]
- Pethick, C.; Smith, H. Bose–Einstein condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation and Superfluidity; Oxford University Press: Oxford, UK, 2016; p. 576. [Google Scholar] [CrossRef]
- Kawaguchi, Y.; Ueda, M. Spinor Bose–Einstein condensates. Phys. Rep. 2012, 520, 253–381. [Google Scholar] [CrossRef] [Green Version]
- Stamper-Kurn, D.M.; Ueda, M. Spinor Bose gases: Symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 2013, 85, 1191–1244. [Google Scholar] [CrossRef] [Green Version]
- Yukalov, V.I. Dipolar and spinor bosonic systems. Laser Physics 2018, 28, 053001. [Google Scholar] [CrossRef] [Green Version]
- Penrose, O.; Onsager, L. Bose-Einstein Condensation and Liquid Helium. Phys. Rev. 1956, 104, 576–584. [Google Scholar] [CrossRef]
- Bogoliubov, N. On the Theory of Superfluidity. J. Phys. 1947, 11, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Zapata, I.; Sols, F.; Leggett, A.J. Josephson effect between trapped Bose-Einstein condensates. Phys. Rev. A 1998, 57, R28–R31. [Google Scholar] [CrossRef] [Green Version]
- Williams, J.; Walser, R.; Cooper, J.; Cornell, E.; Holland, M. Nonlinear Josephson-type oscillations of a driven, two-component Bose-Einstein condensate. Phys. Rev. A 1999, 59, R31–R34. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.S.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Measurements of Relative Phase in Two-Component Bose-Einstein Condensates. Phys. Rev. Lett. 1998, 81, 1543–1546. [Google Scholar] [CrossRef] [Green Version]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levy, S.; Lahoud, E.; Shomroni, I.; Steinhauer, J. The a.c. and d.c. Josephson effects in a Bose–Einstein condensate. Nature 2007, 449, 579–583. [Google Scholar] [CrossRef] [PubMed]
- Ryu, C.; Blackburn, P.W.; Blinova, A.A.; Boshier, M.G. Experimental Realization of Josephson Junctions for an Atom SQUID. Phys. Rev. Lett. 2013, 111, 205301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sadler, L.E.; Higbie, J.M.; Leslie, R.; Vengalattore, M.; Stamper-Kurn, D.M. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose–Einstein condensate. Nature 2006, 443, 312–315. [Google Scholar] [CrossRef] [Green Version]
- Faddeev, L.; Niemi, A.J. Stable knot-like structures in classical field theory. Nature 1997, 387, 58–61. [Google Scholar] [CrossRef] [Green Version]
- Kawaguchi, Y.; Nitta, M.; Ueda, M. Knots in a Spinor Bose-Einstein Condensate. Phys. Rev. Lett. 2008, 100, 180403. [Google Scholar] [CrossRef] [PubMed]
- Savage, C.M.; Ruostekoski, J. Dirac monopoles and dipoles in ferromagnetic spinor Bose-Einstein condensates. Phys. Rev. A 2003, 68, 043604. [Google Scholar] [CrossRef] [Green Version]
- Khawaja, U.A.; Stoof, H. Skyrmions in a Ferromagnetic Bose-Einstein Condensate. Nature 2001, 411, 918–920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical Dipole Traps for Neutral Atoms. In Advances In Atomic, Molecular, and Optical Physics; Academic Press: Cambridge, MA, USA, 2000; pp. 95–170. [Google Scholar] [CrossRef] [Green Version]
- Pasienski, M.; DeMarco, B. A high-accuracy algorithm for designing arbitrary holographic atom traps. Opt. Express 2008, 16, 2176–2190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaunt, A.L.; Hadzibabic, Z. Robust Digital Holography for Ultracold Atom Trapping. Sci. Rep. 2012, 2, 721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gauthier, G.; Lenton, I.; Parry, N.M.; Baker, M.; Davis, M.J.; Rubinsztein-Dunlop, H.; Neely, T.W. Direct imaging of a digital-micromirror device for configurable microscopic optical potentials. Optica 2016, 3, 1136–1143. [Google Scholar] [CrossRef] [Green Version]
- Silva, P.F.; Muniz, S.R. Generating arbitrary laser beam shapes through phase-mapped designed beam splitting. In Proceedings of the 2021 SBFoton International Optics and Photonics Conference (SBFoton IOPC), Sao Carlos, Brazil, 31 May–2 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ramanathan, A.; Wright, K.C.; Muniz, S.R.; Zelan, M.; Hill III, W.T.; Lobb, C.J.; Helmerson, K.; Phillips, W.D.; Campbell, G.K. Superflow in a Toroidal Bose-Einstein Condensate: An Atom Circuit with a Tunable Weak Link. Phys. Rev. Lett. 2011, 106, 130401. [Google Scholar] [CrossRef] [Green Version]
- Wright, K.C.; Blakestad, R.B.; Lobb, C.J.; Phillips, W.D.; Campbell, G.K. Driving Phase Slips in a Superfluid Atom Circuit with a Rotating Weak Link. Phys. Rev. Lett. 2013, 110, 025302. [Google Scholar] [CrossRef]
- Eckel, S.; Lee, J.G.; Jendrzejewski, F.; Murray, N.; Clark, C.W.; Lobb, C.J.; Phillips, W.D.; Edwards, M.; Campbell, G.K. Hysteresis in a quantized superfluid ‘atomtronic’ circuit. Nature 2014, 506, 200–203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beattie, S.; Moulder, S.; Fletcher, R.J.; Hadzibabic, Z. Persistent Currents in Spinor Condensates. Phys. Rev. Lett. 2013, 110, 025301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldman, N.; Juzeliūnas, G.; Öhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Baym, G.; Pethick, C.J. Landau critical velocity in weakly interacting Bose gases. Phys. Rev. A 2012, 86, 023602. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Yi, S.; You, L. Mean field ground state of a spin-1 condensate in a magnetic field. New J. Phys. 2003, 5, 77. [Google Scholar] [CrossRef]
- Andrews, M.R.; Mewes, M.O.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Direct, Nondestructive Observation of a Bose Condensate. Science 1996, 273, 84–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramanathan, A.; Muniz, S.R.; Wright, K.C.; Anderson, R.P.; Phillips, W.D.; Helmerson, K.; Campbell, G.K. Partial-transfer absorption imaging: A versatile technique for optimal imaging of ultracold gases. Rev. Sci. Instr. 2012, 83, 083119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moulder, S.; Beattie, S.; Smith, R.P.; Tammuz, N.; Hadzibabic, Z. Quantized supercurrent decay in an annular Bose-Einstein condensate. Phys. Rev. A 2012, 86, 013629. [Google Scholar] [CrossRef] [Green Version]
- Leanhardt, A.E.; Görlitz, A.; Chikkatur, A.P.; Kielpinski, D.; Shin, Y.; Pritchard, D.E.; Ketterle, W. Imprinting Vortices in a Bose-Einstein Condensate using Topological Phases. Phys. Rev. Lett. 2002, 89, 190403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leanhardt, A.E.; Shin, Y.; Kielpinski, D.; Pritchard, D.E.; Ketterle, W. Coreless Vortex Formation in a Spinor Bose-Einstein Condensate. Phys. Rev. Lett. 2003, 90, 140403. [Google Scholar] [CrossRef] [Green Version]
- Kumakura, M.; Hirotani, T.; Okano, M.; Takahashi, Y.; Yabuzaki, T. Topological formation of a multiply charged vortex in the Rb Bose-Einstein condensate: Effectiveness of the gravity compensation. Phys. Rev. A 2006, 73, 063605. [Google Scholar] [CrossRef] [Green Version]
- Wright, K.C.; Leslie, L.S.; Bigelow, N.P. Optical control of the internal and external angular momentum of a Bose-Einstein condensate. Phys. Rev. A 2008, 77, 041601. [Google Scholar] [CrossRef]
- Wright, K.C.; Leslie, L.S.; Hansen, A.; Bigelow, N.P. Sculpting the Vortex State of a Spinor BEC. Phys. Rev. Lett. 2009, 102, 030405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leslie, L.S.; Hansen, A.; Wright, K.C.; Deutsch, B.M.; Bigelow, N.P. Creation and Detection of Skyrmions in a Bose-Einstein Condensate. Phys. Rev. Lett. 2009, 103, 250401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Juliá-Díaz, B.; Guilleumas, M.; Lewenstein, M.; Polls, A.; Sanpera, A. Josephson oscillations in binary mixtures of F = 1 spinor Bose-Einstein condensates. Phys. Rev. A 2009, 80, 023616. [Google Scholar] [CrossRef] [Green Version]
- Juliá-Díaz, B.; Melé-Messeguer, M.; Guilleumas, M.; Polls, A. Spinor Bose-Einstein condensates in a double well: Population transfer and Josephson oscillations. Phys. Rev. A 2009, 80, 043622. [Google Scholar] [CrossRef] [Green Version]
- Muñoz Mateo, A.; Gallemí, A.; Guilleumas, M.; Mayol, R. Persistent currents supported by solitary waves in toroidal Bose-Einstein condensates. Phys. Rev. A 2015, 91, 063625. [Google Scholar] [CrossRef] [Green Version]
- Petrov, D.S.; Shlyapnikov, G.V.; Walraven, J.T.M. Phase-Fluctuating 3D Bose-Einstein Condensates in Elongated Traps. Phys. Rev. Lett. 2001, 87, 050404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al Khawaja, U.; Proukakis, N.P.; Andersen, J.O.; Romans, M.W.J.; Stoof, H.T.C. Dimensional and temperature crossover in trapped Bose gases. Phys. Rev. A 2003, 68, 043603. [Google Scholar] [CrossRef] [Green Version]
- Gerbier, F. Quasi-1D Bose-Einstein condensates in the dimensional crossover regime. Europhys. Lett. (EPL) 2004, 66, 771–777. [Google Scholar] [CrossRef]
- Mathey, L.; Ramanathan, A.; Wright, K.C.; Muniz, S.R.; Phillips, W.D.; Clark, C.W. Phase fluctuations in anisotropic Bose-Einstein condensates: From cigars to rings. Phys. Rev. A 2010, 82, 033607. [Google Scholar] [CrossRef] [Green Version]
- Piazza, F.; Collins, L.A.; Smerzi, A. Critical velocity for a toroidal Bose–Einstein condensate flowing through a barrier. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 095302. [Google Scholar] [CrossRef] [Green Version]
- Mathey, A.C.; Clark, C.W.; Mathey, L. Decay of a superfluid current of ultracold atoms in a toroidal trap. Phys. Rev. A 2014, 90, 023604. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).