Numerical Modeling and Symmetry Analysis of a Pine Wilt Disease Model Using the Mittag–Leffler Kernel
Abstract
:1. Introduction
2. Mathematical Optimization and Miniature
3. Preliminaries
4. The Fundamental Aspect of the q-Homotopy Analysis Transform Method
5. q-HATM Solution for the Prediction Phase
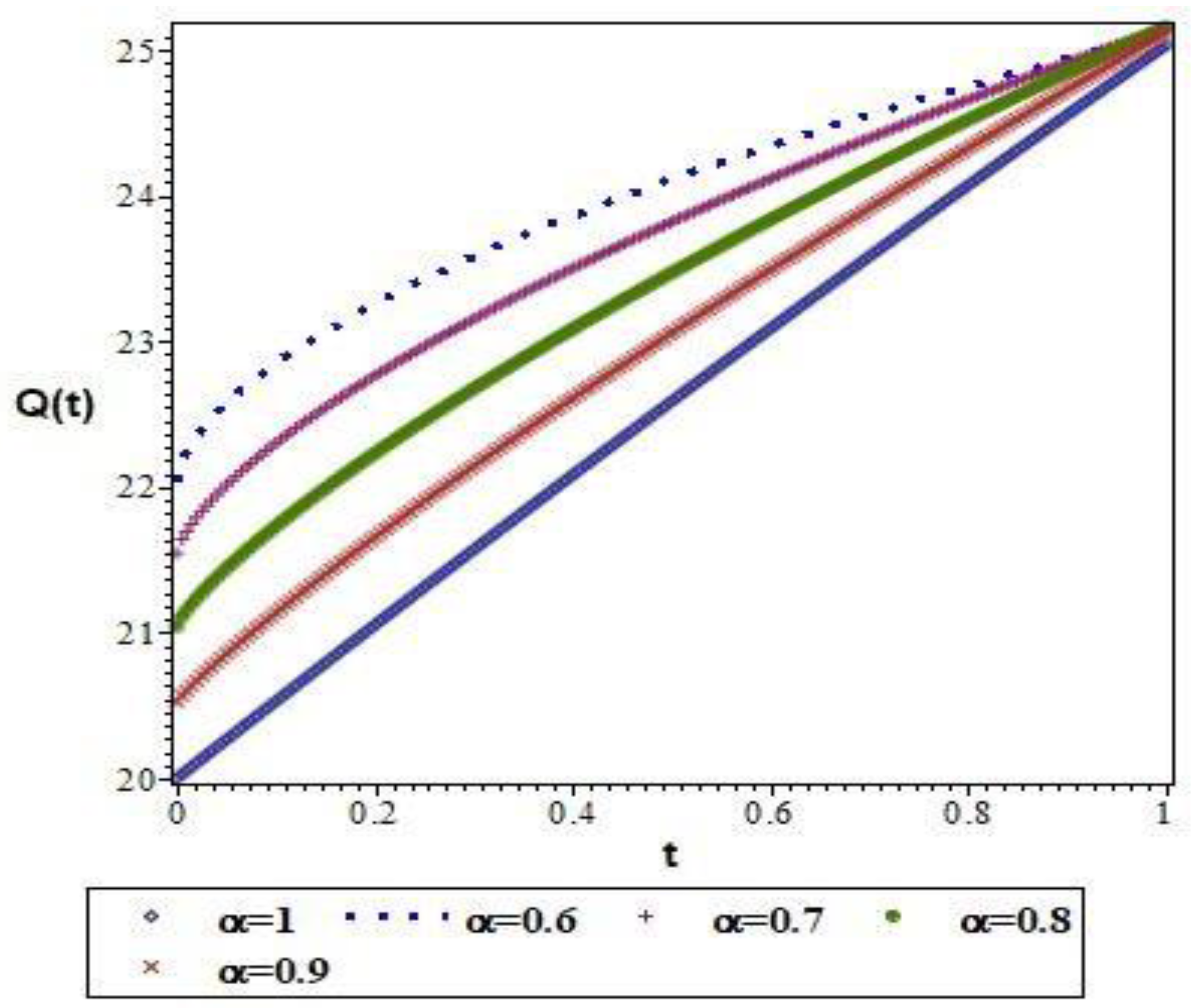
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mamiya, Y. Pathology of the Pine Wilt Disease Caused by Bursaphelenchus xylophilus. Annu. Rev. Phytopathol. 1983, 21, 201–220. [Google Scholar] [CrossRef] [PubMed]
- Mamiya, Y. History of pine wilt disease in Japan. J. Nematol. 1988, 20, 219–226. [Google Scholar] [PubMed]
- Fukuda, K. Physiological Process of the Symptom Development and Resistance Mechanism in Pine Wilt Disease. J. For. Res. 1997, 2, 171–181. [Google Scholar] [CrossRef]
- Proenca, D.N.; Gregor, G.; Morais, P.V. Understanding pine wilt disease: Roles of the pine endophytic bacteria and of the bacteria carried by the disease-causing pine wood nematode. Mic. Biol. Open 2016, 6, e00415. [Google Scholar] [CrossRef]
- Ozair, M.; Hussain, T.; Awan, A.U.; Aslam, A.; Khan, R.A.; Ali, F.; Tasneem, F. Bio-inspired analytical heuristics to study pine wilt disease model. Sci. Rep. 2020, 10, 3534. [Google Scholar] [CrossRef]
- Awan, A.U.; Ozair, M.; Din, Q.; Hussain, T. Stability analysis of pine wilt disease model by periodic use of insecticides. J. Biol. Dyn. 2016, 10, 506–524. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.S.; Lashari, A.A. Global Stability of a Host-Vector Model for Pine Wilt Disease with Nonlinear Incidence Rate. Abstr. Appl. Anal. 2014, 2014, 219173. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.S.; Lashari, A.A. Stability analysis and optimal control of pine wilt disease with horizontal transmission in vector population. Appl. Math. Comput. 2014, 226, 793–804. [Google Scholar] [CrossRef]
- Takasu, F. Individual-based modeling of the spread of pine wilt disease: Vector beetle dispersal and the Allee effect. Popul. Ecol. 2009, 51, 399–409. [Google Scholar] [CrossRef]
- Pathak, S.; Maiti, A.; Samanta, G. Rich dynamics of an SIR epidemic model. Nonlinear Anal. Model. Control 2010, 15, 71–81. [Google Scholar] [CrossRef]
- Shi, X.; Song, G. Analysis of the Mathematical Model for the Spread of Pine Wilt Disease. J. Appl. Math. 2013, 2013, 184054. [Google Scholar] [CrossRef]
- Lia, Y.; Haq, F.; Shah, K.; Shahzad, M.; Rahman, G. Numerical analysis off ractional order pine wilt disease model with bilinear incident rate. J. Math. Comput. Sci. 2017, 17, 420–428. [Google Scholar] [CrossRef] [Green Version]
- Rahman, G.U.; Shah, K.; Haq, F.; Ahmad, N. Host vector dynamics of pine wilt disease model with convex incidence rate. Chaos Solitons Fractals 2018, 113, 31–39. [Google Scholar] [CrossRef]
- Shah, K.; Alqudah, M.A.; Jarad, F.; Abdeljawad, T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo–Febrizio fractional order derivative. Chaos Solitons Fractals 2020, 135, 109754. [Google Scholar] [CrossRef]
- Atkins, D.; Davis, T.S.; Stewart, J.E. Pine Wilt Disease in the Front Range; Colorado State University: Fort Collins, CO, USA, 2020. [Google Scholar]
- Alkahtani, B.S.T.; Atangana, A. Analysis of non-homogeneous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals 2016, 89, 566–571. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fractals 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Atangana, A.; Gomez-Aguilar, J.F. A new derivative with normal distribution kernal: Theory, methods and applications. Phys. A 2017, 476, 1–14. [Google Scholar] [CrossRef]
- Atangana, A.; Gomez-Aguilar, J.F. Hyperchaotic behavior obtained via a nonlocal operator with exponential decay and Mittag-Leffler laws. Chaos Solitons Fractals 2017, 102, 285–294. [Google Scholar] [CrossRef]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Gomez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC and RL described by Atangana-Baleanu fractional derivatives. Int. J. Circ. Theor. Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Baleanu, D. Fractional transmission line with losses. Z. Nat. A 2014, 69, 539–546. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Aguilar, J.F.; Torres, L.; Yepez-Martinez, H.; Baleanu, D.; Reyes, J.M.; Sosa, I.O. Fractional Lie nard type model of a pipe line with in the fractional derivative without singular kernel. Adv. Differ. Eq. 2016, 2016, 173. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Owolabi, K.M.; Atangana, A. Mathematical analysis and computational experiments for an epidemic system with non-local and non-singular derivative. Chaos Solitons Fractals 2019, 126, 41–49. [Google Scholar] [CrossRef]
- Prakash, A.; Kaur, H. Analysis and numerical simulation of fractional order Chan-Allen model with Atangana-Baleanu derivatives. Chaos Solitons Fractals 2019, 124, 134–142. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P. Analysis of Lakes Pollution Model with Mittag-Leffler Kernal. J. Ocean. Eng. Sci. 2020, 5, 310–322. [Google Scholar] [CrossRef]
- Padmavathi, V.; Prakash, A.; Alagesan, K.; Magesh, N. Analysis and numerical simulation of novel corona virus (COVID-19) model with Mittag-Leffler Kernel. Math. Meth. Appl. Sci. 2020, 44, 1863–1877. [Google Scholar] [CrossRef]
- Prakash, A.; Kaur, H. Numerical solution for fractional model of Fokker-Planck equation by using q-HATM. Chaos Solitons Fractals 2017, 105, 99–110. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. New aspects of fractional Biswas-Milivic model with Mittag-Leffler law. Math. Model. Nat. Phenom. 2019, 14, 303. [Google Scholar] [CrossRef] [Green Version]
- Prakash, A.; Goyal, M.; Baskonus, H.M.; Gupta, S. A reliable hybrid numerical method for a time dependent vibration model of arbitrary order. AIMS Math. 2020, 5, 979–1000. [Google Scholar] [CrossRef]
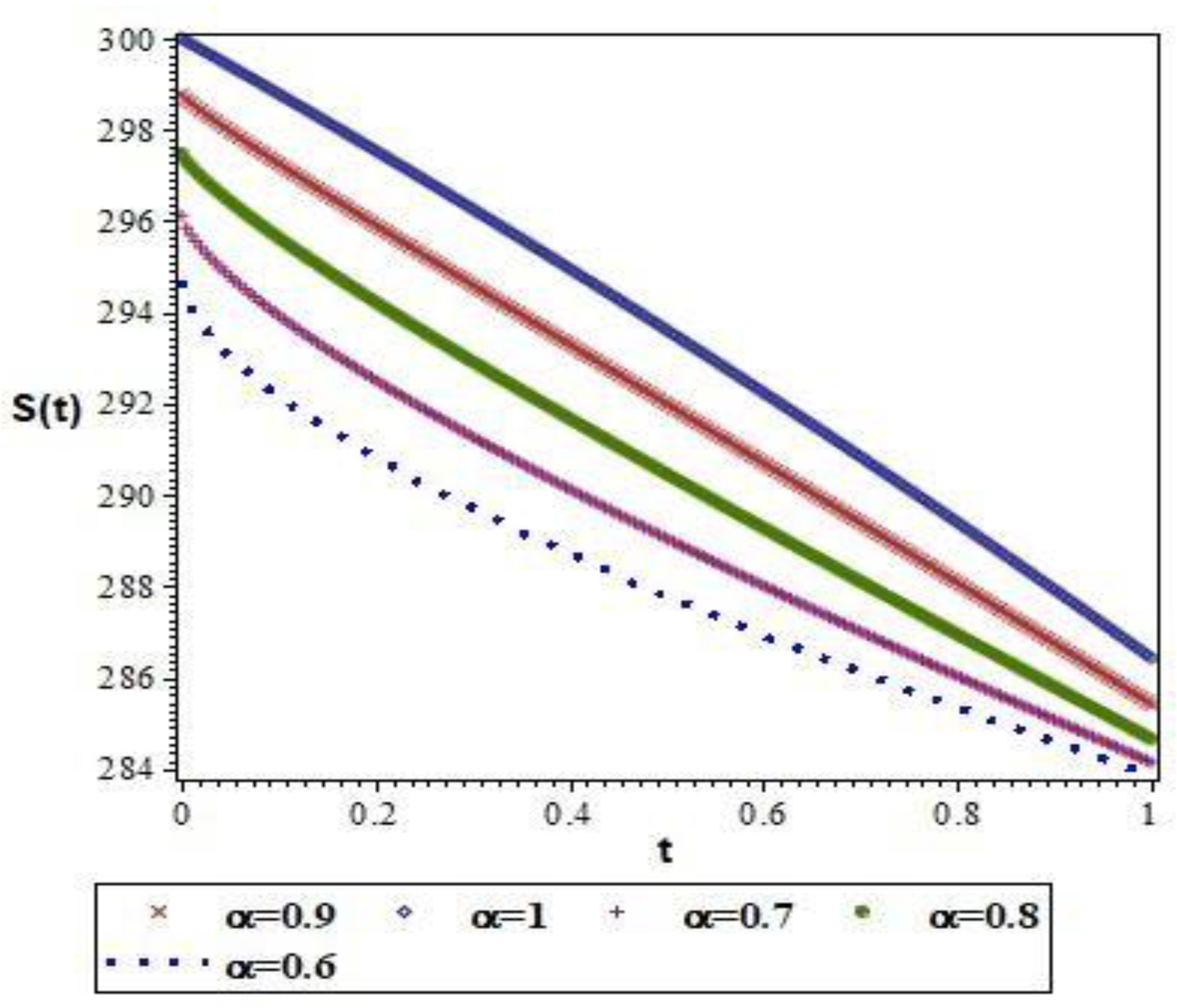
| t | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 |
|---|---|---|---|---|---|
| 0.2 | 290.8332821 | 292.5215509 | 294.2312730 | 295.9169066 | 297.5450103 |
| 0.4 | 288.7183111 | 290.1361784 | 291.6812730 | 293.3045941 | 294.9608370 |
| 0.6 | 286.9466815 | 288.0170780 | 289.2823904 | 290.7063195 | 292.2474799 |
| 0.8 | 285.3574883 | 286.0385706 | 286.9528908 | 288.0843841 | 289.4049390 |
| 1 | 283.8864707 | 284.1493328 | 284.6590141 | 285.4232667 | 286.4332145 |
| t | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 |
|---|---|---|---|---|---|
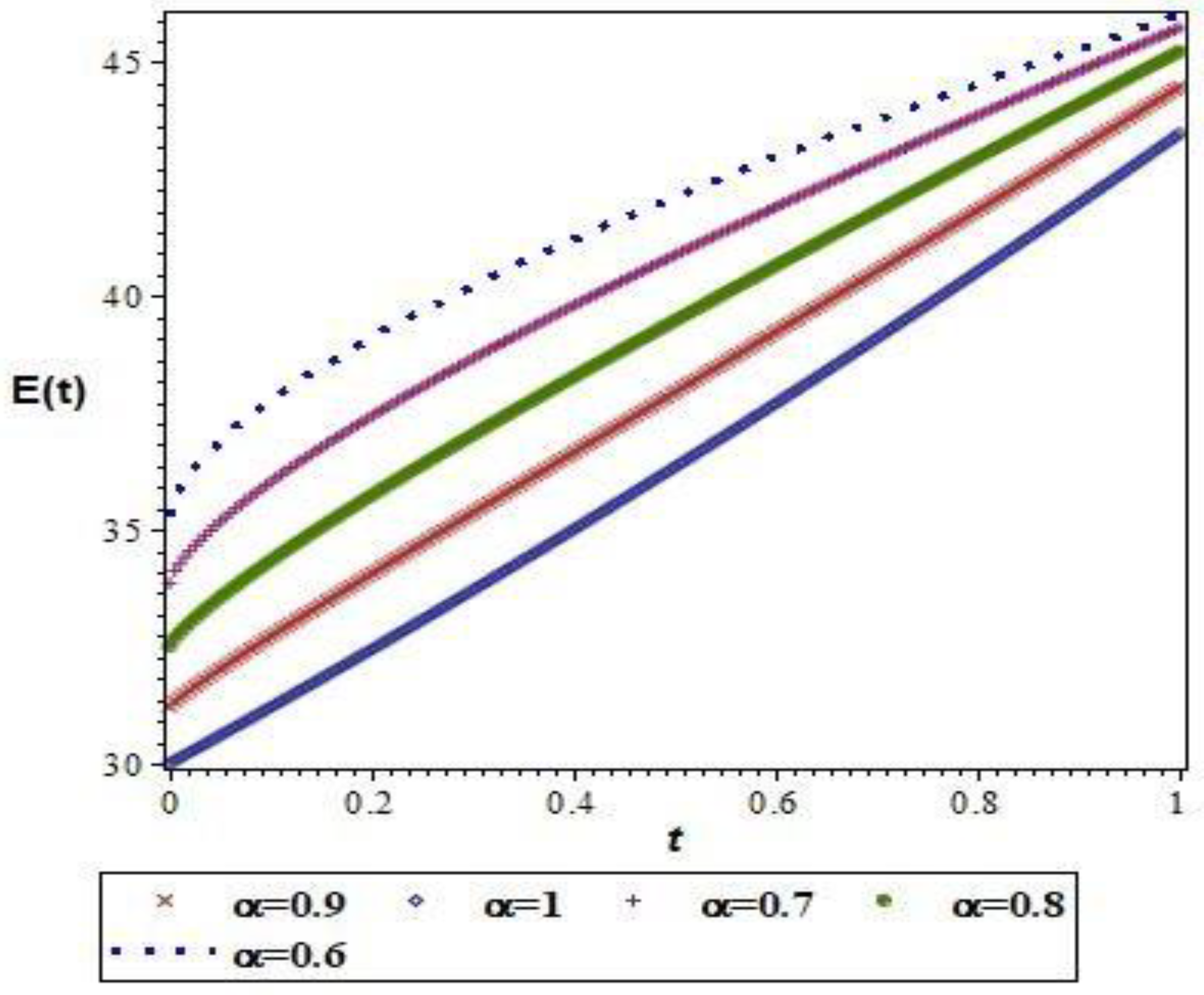
| 0.2 | 39.10004523 | 37.42459719 | 35.72766190 | 34.05441224 | 32.43802645 |
| 0.4 | 41.19892275 | 39.79208318 | 38.25886843 | 36.64785418 | 35.00395898 |
| 0.6 | 42.95693540 | 41.89509617 | 40.63981065 | 39.22704104 | 37.69779761 |
| 0.8 | 44.53381791 | 43.85843328 | 42.95167533 | 41.82943376 | 40.51954233 |
| 1 | 45.99336551 | 45.73306211 | 45.22800285 | 44.47046140 | 43.46919314 |
| t | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 |
|---|---|---|---|---|---|
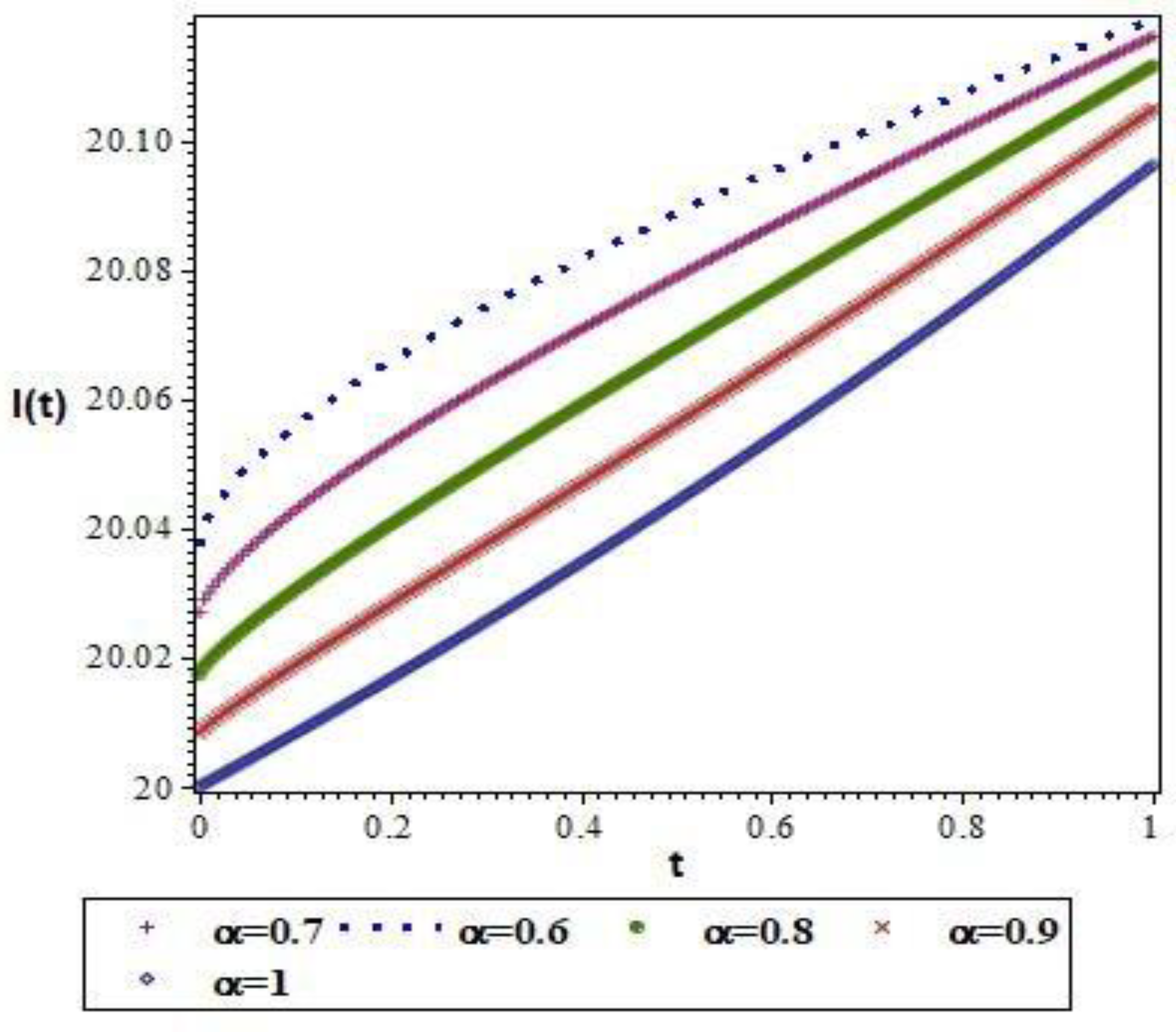
| 0.2 | 20.06569309 | 20.05303066 | 20.04041223 | 20.02820332 | 20.01666441 |
| 0.4 | 20.08158972 | 20.07068416 | 20.05894326 | 20.04678947 | 20.03460646 |
| 0.6 | 20.09504715 | 20.08657271 | 20.07664739 | 20.06560725 | 20.05382613 |
| 0.8 | 20.10721869 | 20.10156349 | 20.09406166 | 20.08488908 | 20.07432344 |
| 1 | 20.11856300 | 20.11600600 | 20.11140109 | 20.10472442 | 20.09609837 |
| t | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 |
|---|---|---|---|---|---|
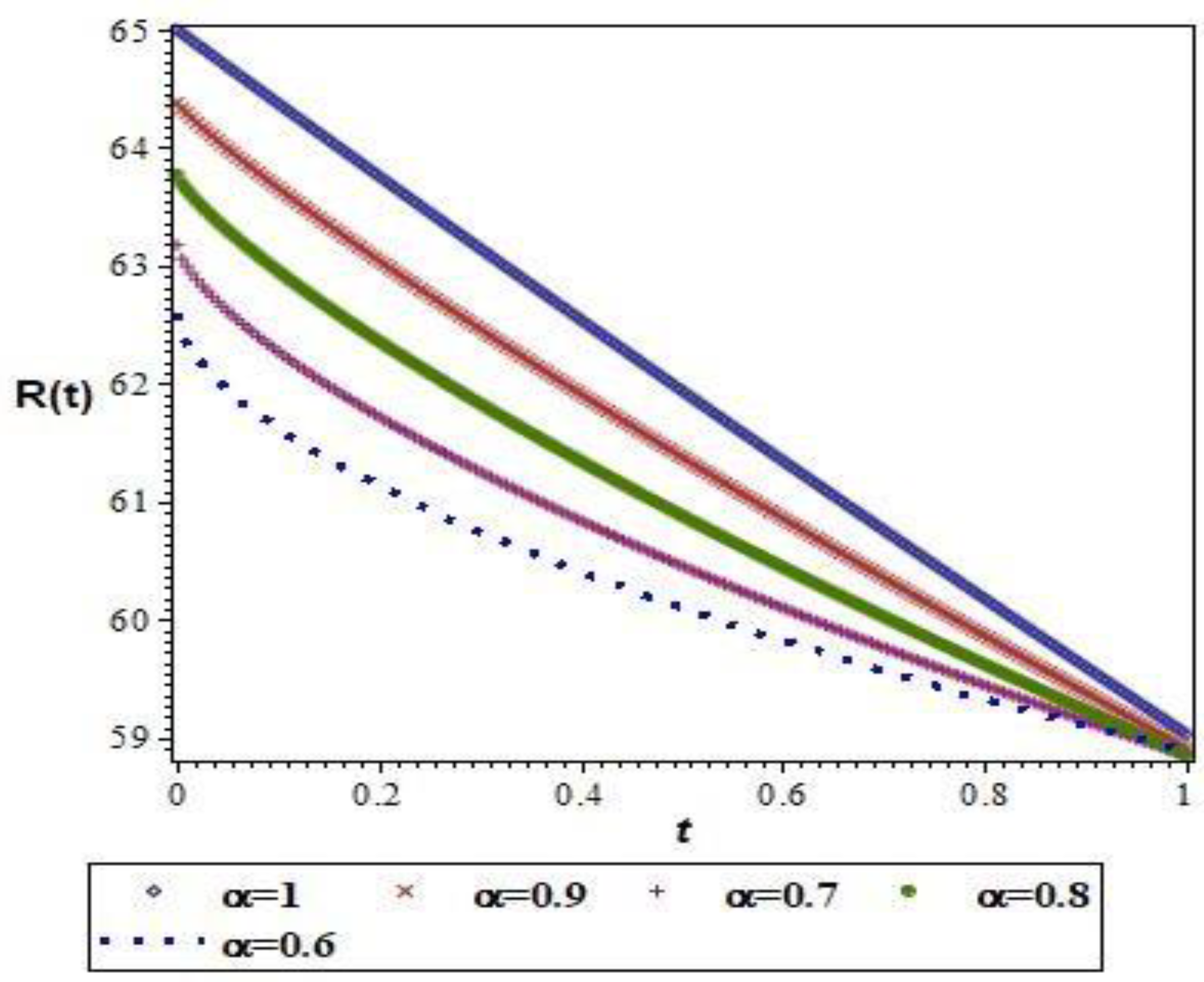
| 0.2 | 61.13521917 | 61.72265599 | 62.36277835 | 63.04502340 | 63.75988658 |
| 0.4 | 60.40677303 | 60.84027518 | 61.34428024 | 61.91386799 | 62.54295352 |
| 0.6 | 59.82779844 | 60.10177564 | 60.44600834 | 60.86194973 | 61.34920081 |
| 0.8 | 59.33049050 | 59.44677866 | 59.62275299 | 59.86504614 | 60.17862847 |
| 1 | 58.88735002 | 58.84960935 | 58.85433742 | 58.91180471 | 59.03123648 |
| t | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 |
|---|---|---|---|---|---|
| 0.2 | 23.25119176 | 22.76220249 | 22.22707314 | 21.65432952 | 21.05177564 |
| 0.4 | 23.85718191 | 23.49935245 | 23.08151053 | 22.60713914 | 22.08081457 |
| 0.6 | 24.33723469 | 24.11414638 | 23.83245361 | 23.49023543 | 23.08711678 |
| 0.8 | 24.74838860 | 24.65768508 | 24.51838248 | 24.32434237 | 24.07068228 |
| 1 | 25.11379385 | 25.15173547 | 25.15651828 | 25.11921053 | 25.03151105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padmavathi, V.; Magesh, N.; Alagesan, K.; Khan, M.I.; Elattar, S.; Alwetaishi, M.; Galal, A.M. Numerical Modeling and Symmetry Analysis of a Pine Wilt Disease Model Using the Mittag–Leffler Kernel. Symmetry 2022, 14, 1067. https://doi.org/10.3390/sym14051067
Padmavathi V, Magesh N, Alagesan K, Khan MI, Elattar S, Alwetaishi M, Galal AM. Numerical Modeling and Symmetry Analysis of a Pine Wilt Disease Model Using the Mittag–Leffler Kernel. Symmetry. 2022; 14(5):1067. https://doi.org/10.3390/sym14051067
Chicago/Turabian StylePadmavathi, V., N. Magesh, K. Alagesan, M. Ijaz Khan, Samia Elattar, Mamdooh Alwetaishi, and Ahmed M. Galal. 2022. "Numerical Modeling and Symmetry Analysis of a Pine Wilt Disease Model Using the Mittag–Leffler Kernel" Symmetry 14, no. 5: 1067. https://doi.org/10.3390/sym14051067
APA StylePadmavathi, V., Magesh, N., Alagesan, K., Khan, M. I., Elattar, S., Alwetaishi, M., & Galal, A. M. (2022). Numerical Modeling and Symmetry Analysis of a Pine Wilt Disease Model Using the Mittag–Leffler Kernel. Symmetry, 14(5), 1067. https://doi.org/10.3390/sym14051067









