Self-Frequency Shift in Transmission of Asymmetric Pulse in Optical Medium
Abstract
:1. Introduction
2. Simulation Model
3. Numerical Results
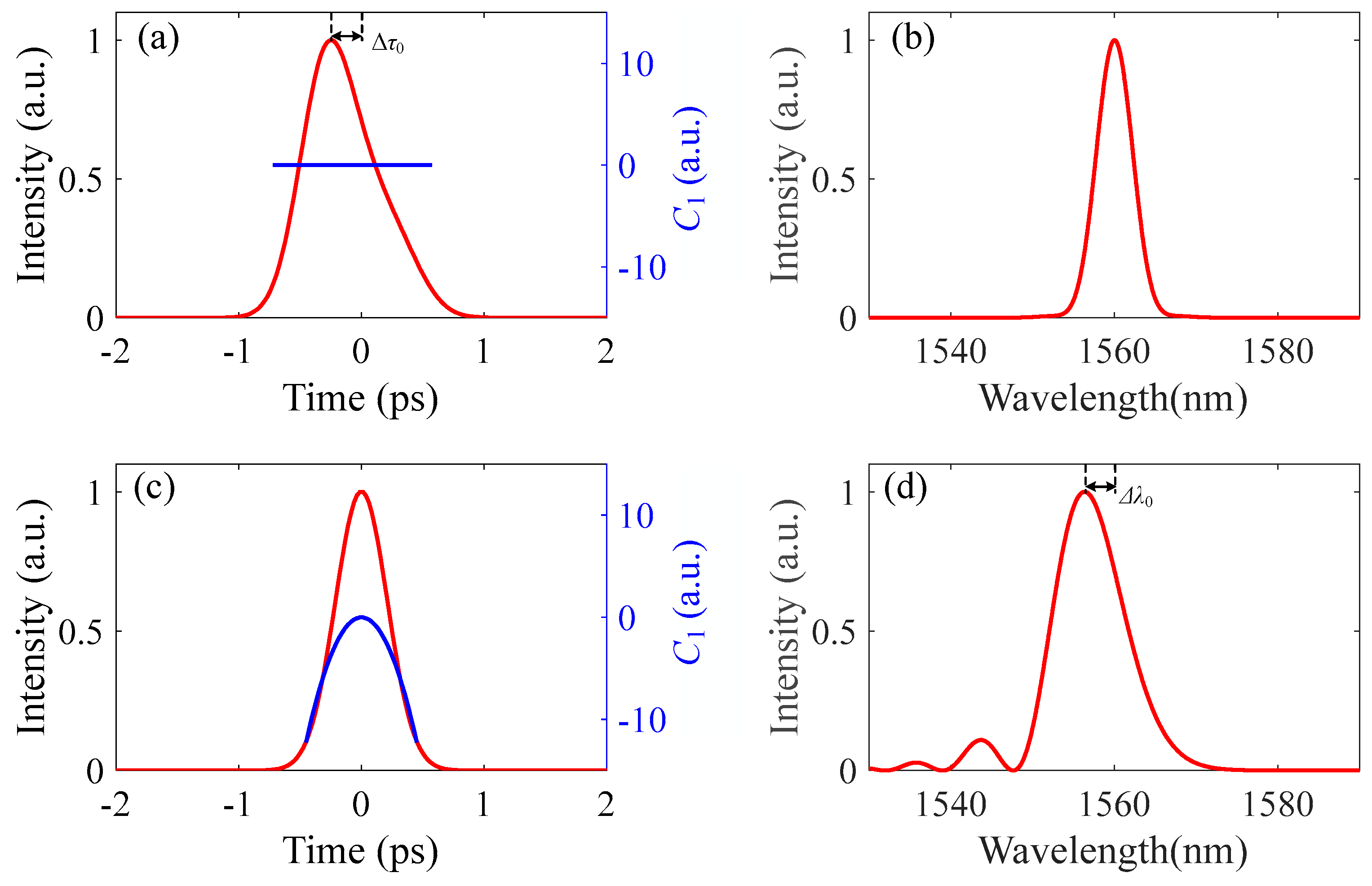
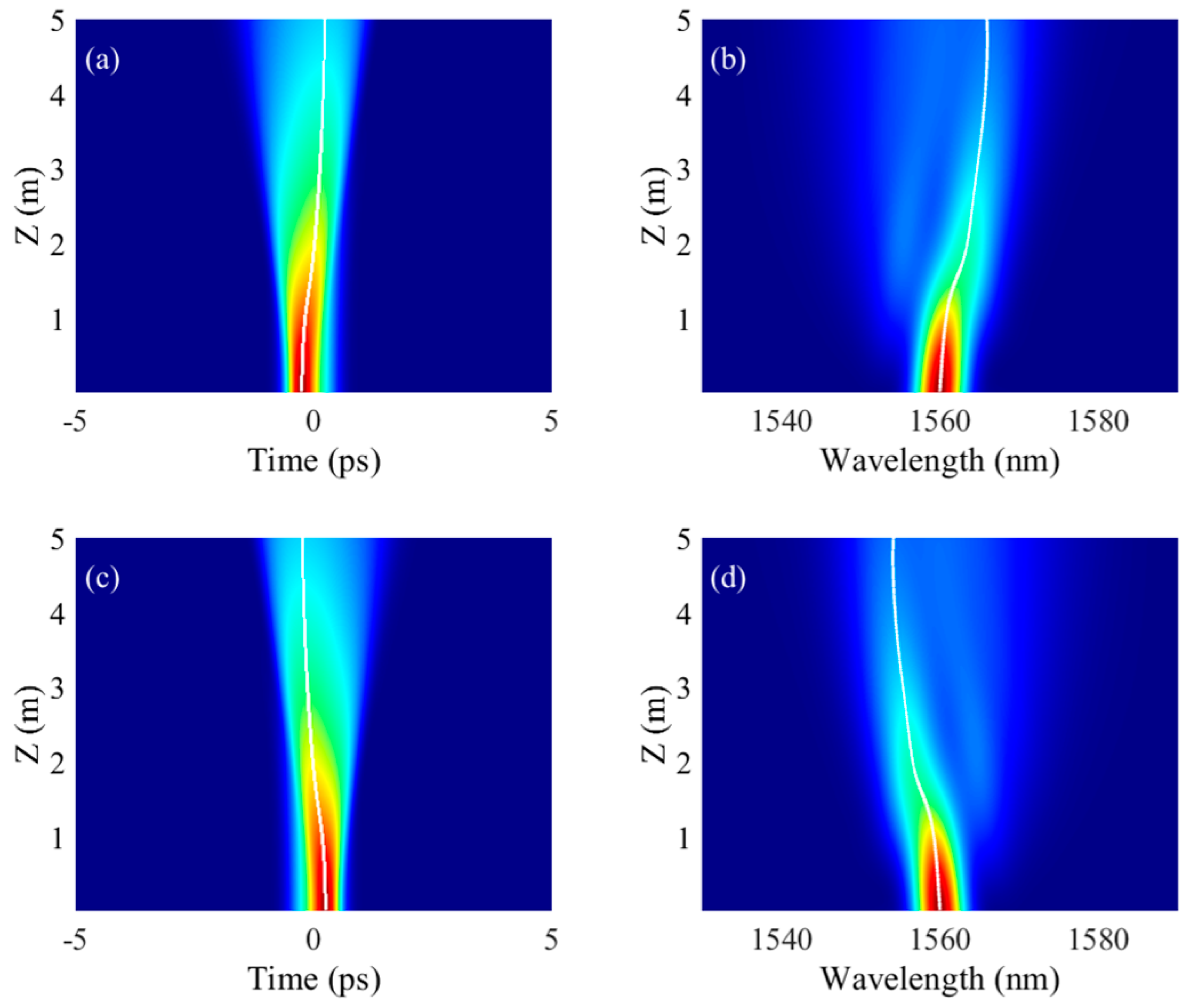
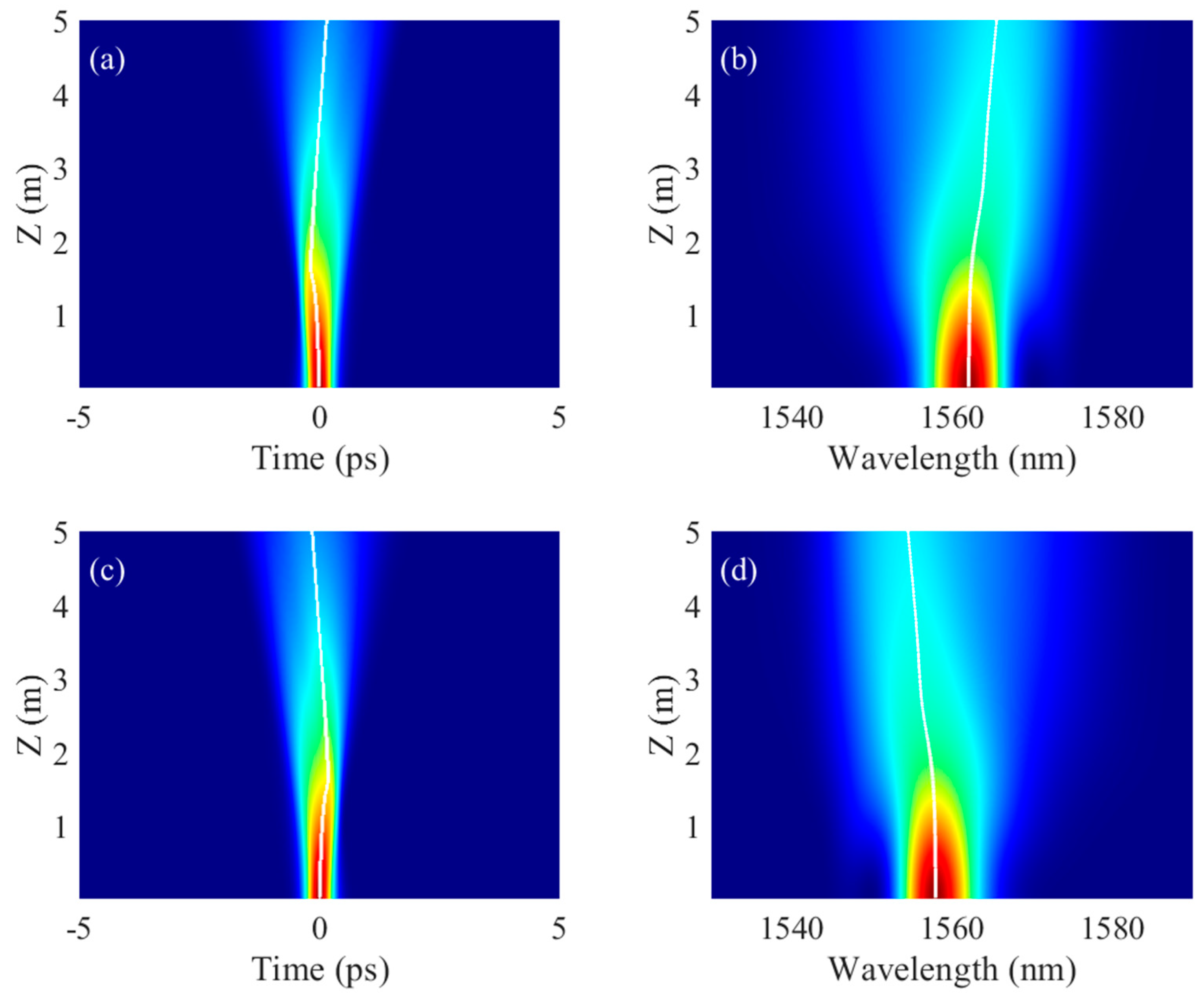
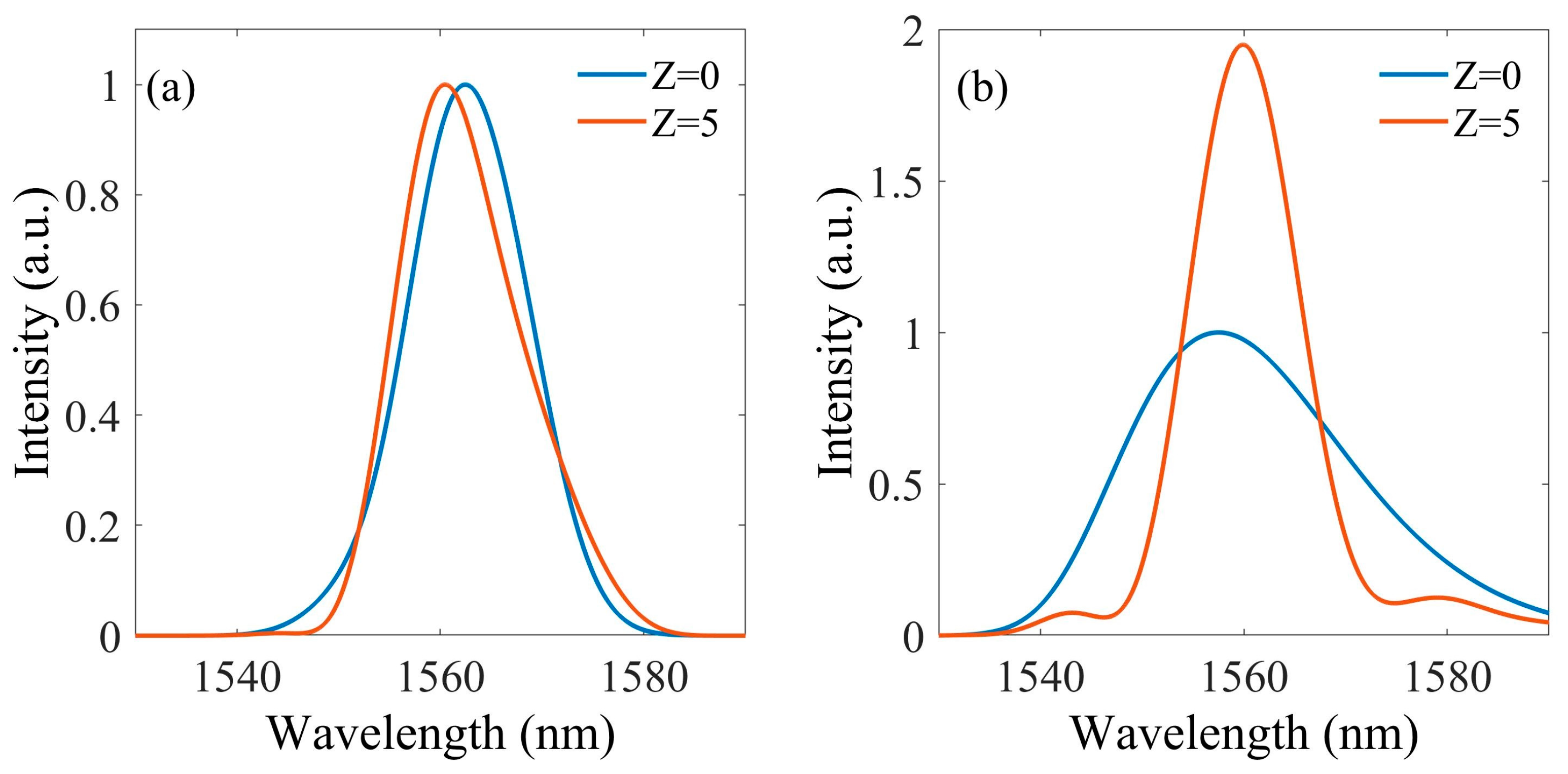
3.1. Propagation Dynamics of Temporal-Asymmetric Pulse
3.2. Propagation Dynamics of Spectral-Asymmetric Pulse
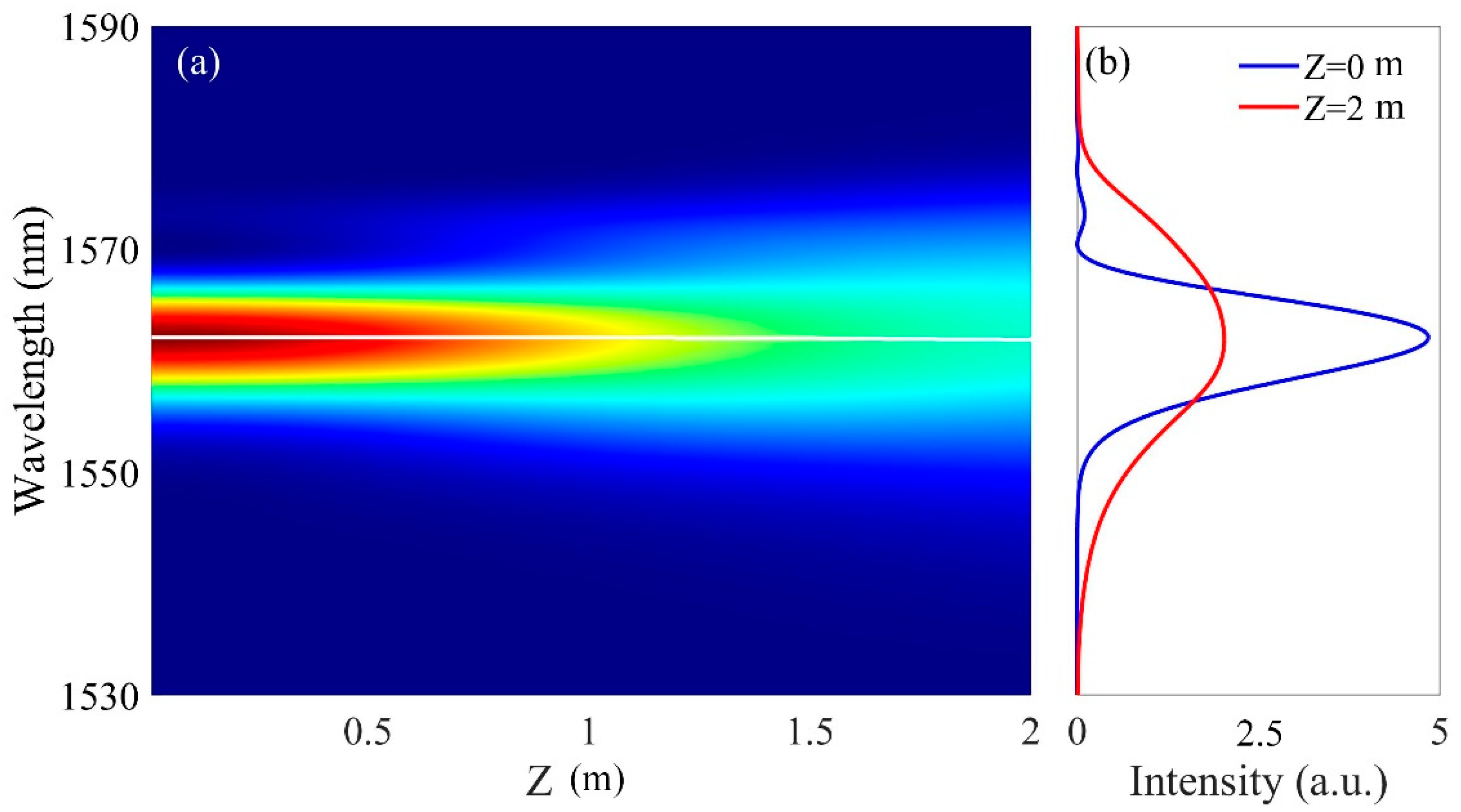
3.3. Influence of Propagation Distance on the Frequency Shift of Asymmetric Pulse
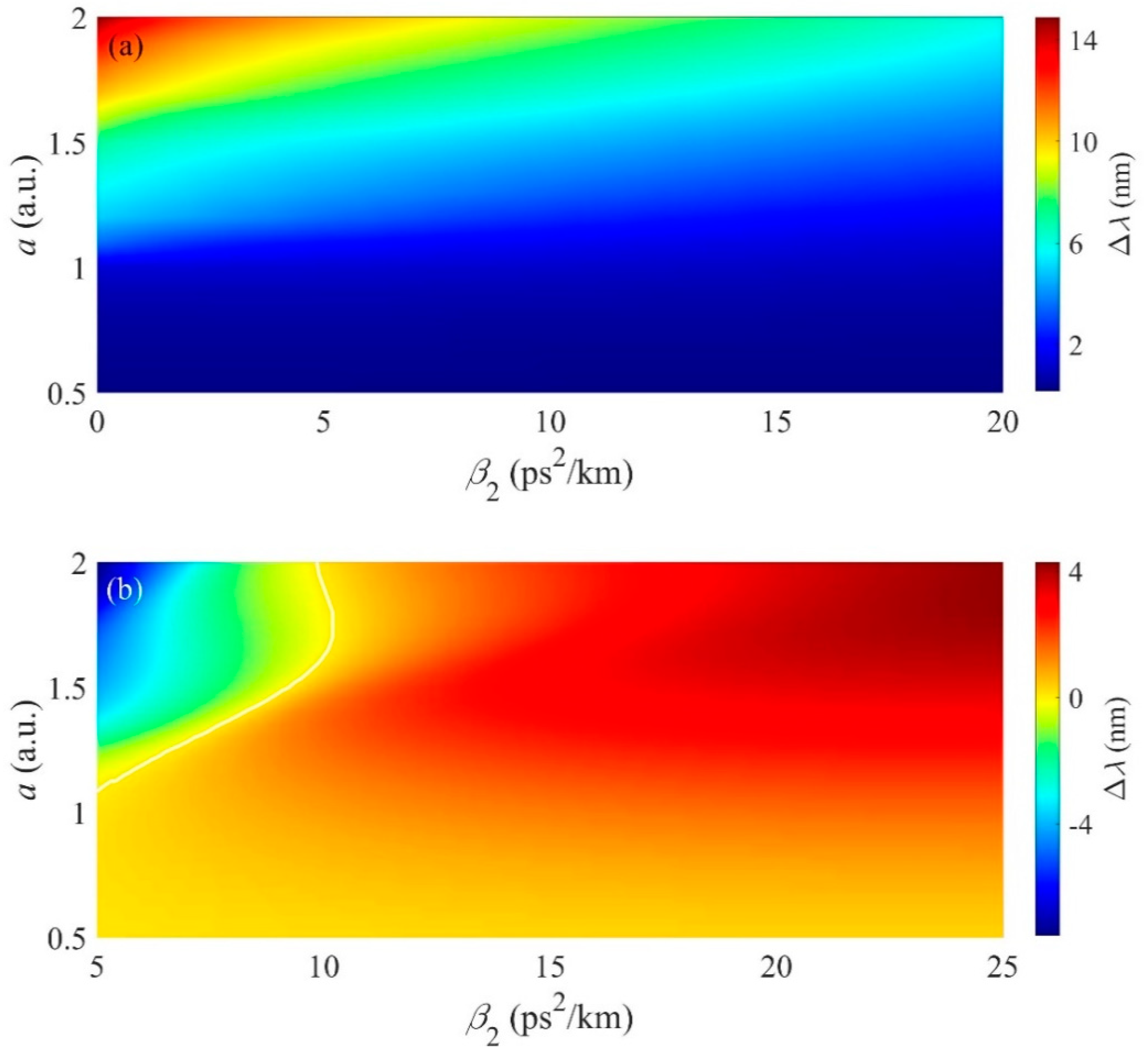
3.4. Influence of Dispersion on the Propagation of Asymmetric Pulse
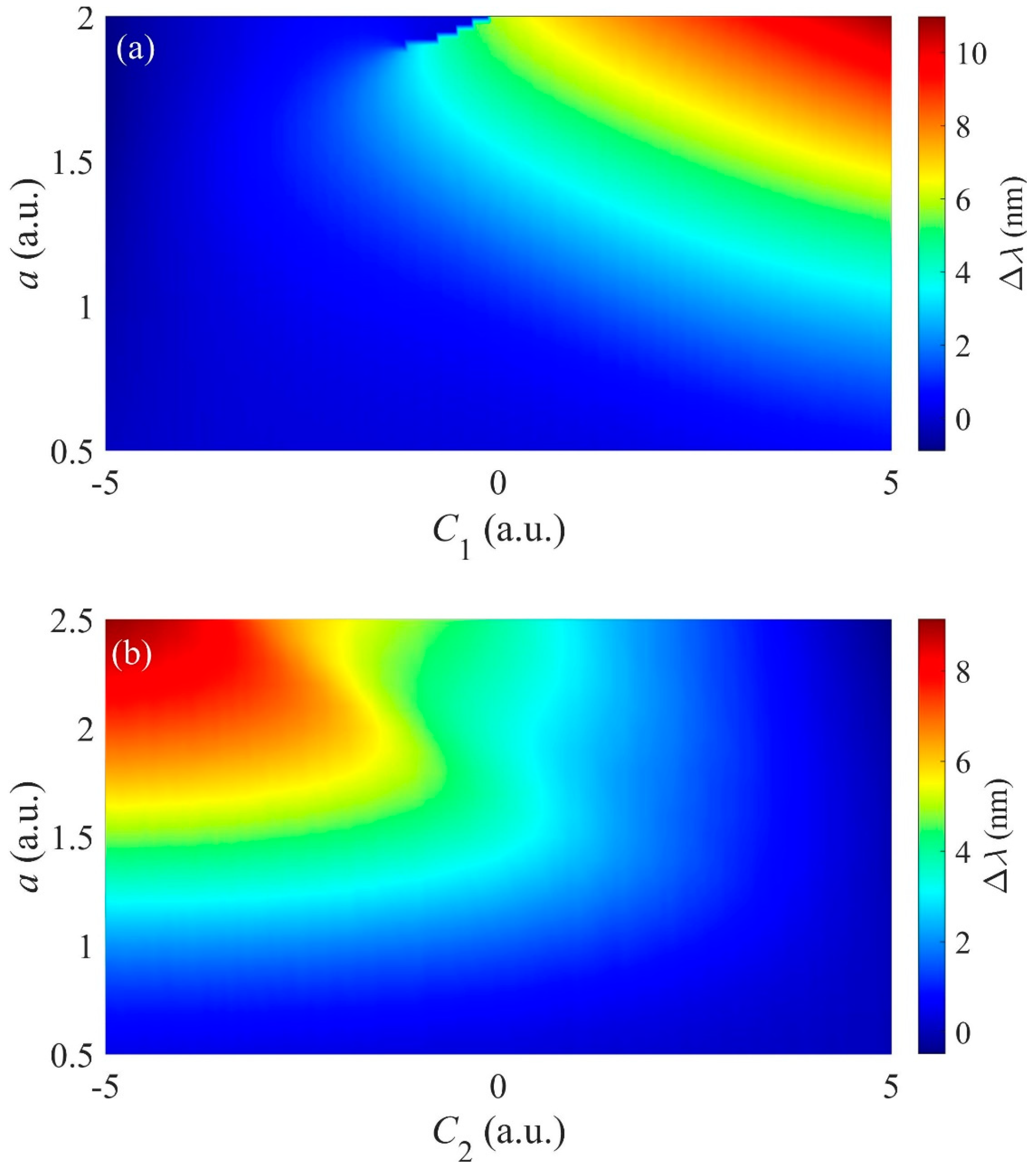
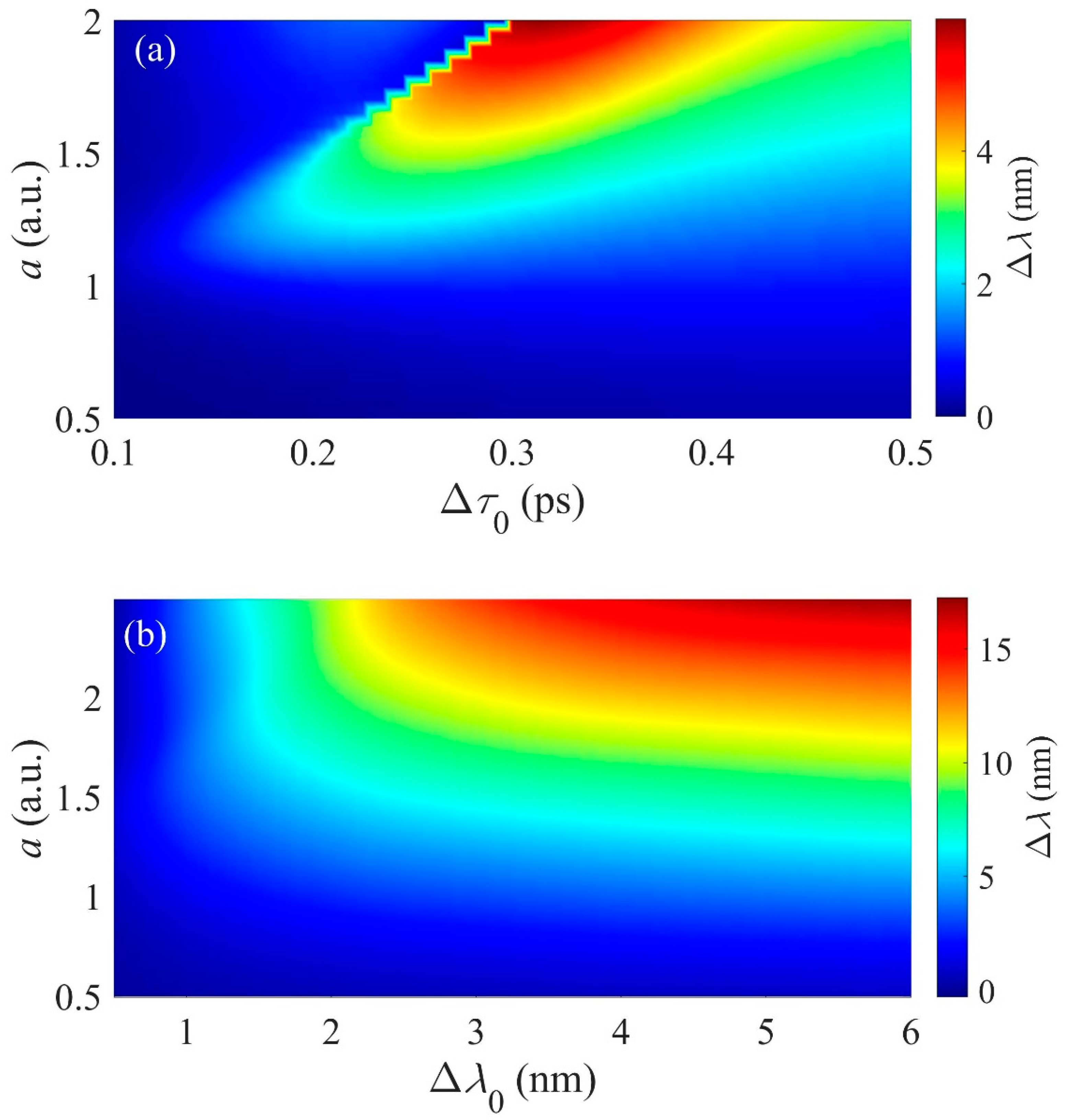
3.5. Influence of Initial Chirp on the Propagation of Asymmetric Pulse
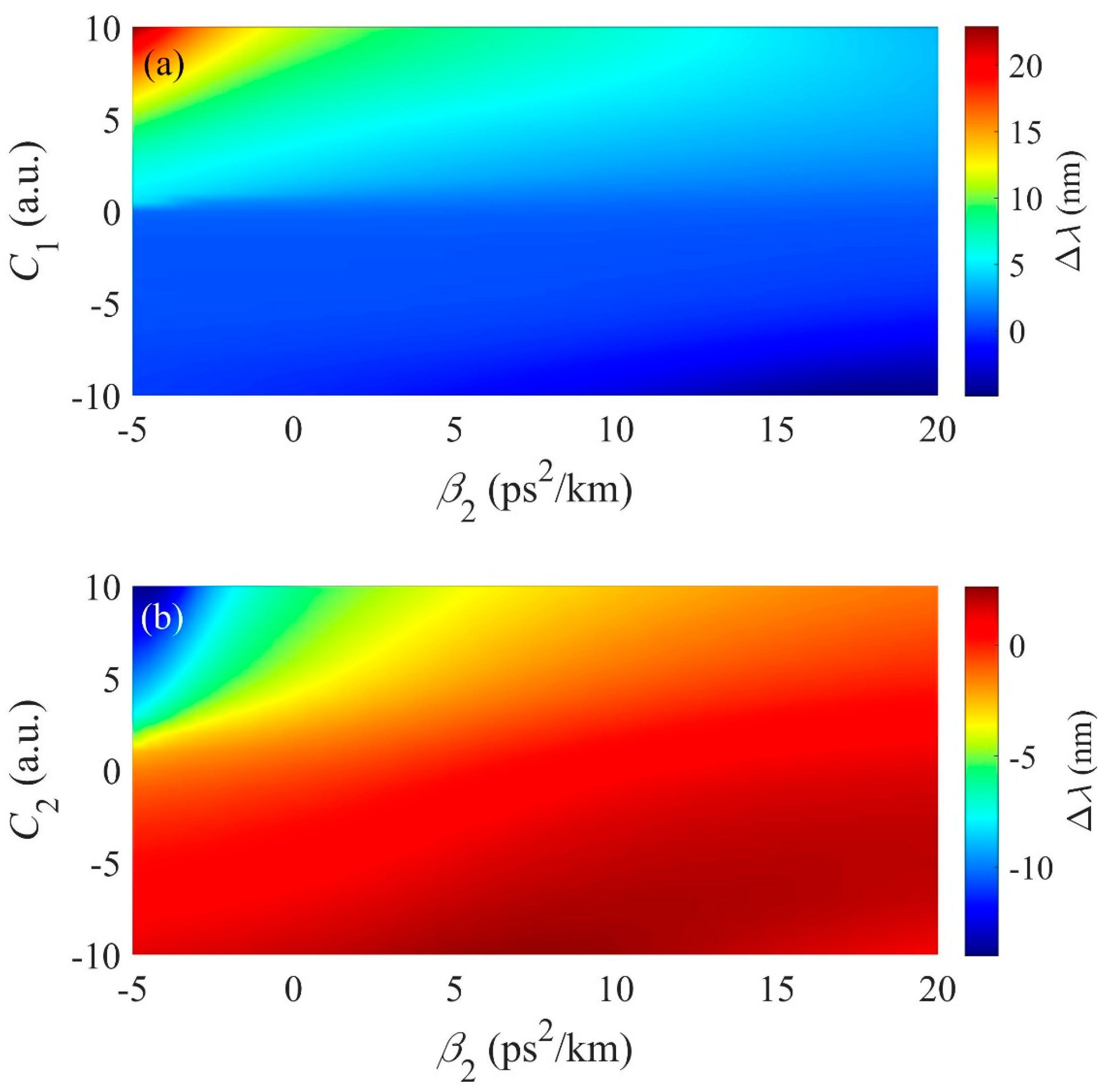
3.6. Influence of Dispersion and Initial Chirp on the Propagation of Asymmetric Pulse
3.7. Influence of Asymmetry Ratio on the Propagation of Asymmetric Pulse
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ankiewicz, A.; Akhmediev, N. Dissipative Solitons: From Optics to Biology and Medicine; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-78216-2. [Google Scholar]
- Haus, H.A.; Wong, W.S. Solitons in optical communications. Rev. Mod. Phys. 1996, 68, 423. [Google Scholar] [CrossRef]
- Keller, U. Recent developments in compact ultrafast lasers. Nature 2003, 424, 831–838. [Google Scholar] [CrossRef] [PubMed]
- Kerse, C.; Kalaycloĝ Lu, H.; Elahi, P.; Çetin, B.; Kesim, D.K.; Akçaalan, Ö.; Yavaş, S.; Aşlk, M.D.; Öktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Mollenauer, L.F.; Stolen, R.H.; Gordon, J.P. Experimental observation of picosecond pulse narrowing and solitons in optical fibers. Phys. Rev. Lett. 1980, 45, 1095–1098. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast fibre lasers. Nat. Photon. 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Malomed, B.A. Bound solitons in the nonlinear Schrödinger-Ginzburg-Landau equation. Phys. Rev. A 1991, 44, 6954–6957. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Town, G. Pulsating solitons, chaotic solitons, period doubling, and pulse coexistence in mode-locked lasers: Complex Ginzburg-Landau equation approach. Phys. Rev. E 2001, 63, 056602. [Google Scholar] [CrossRef] [Green Version]
- Anderson, D.; Lisak, M. Nonlinear asymmetric pulse distortion in long optical fibers. Opt. Lett. 1982, 7, 394–396. [Google Scholar] [CrossRef]
- Yang, G.; Shen, Y.R. Spectral broadening of ultrashort pulses in a nonlinear medium. Opt. Lett. 1984, 9, 510–512. [Google Scholar] [CrossRef]
- Anderson, D.; Lisak, M. Nonlinear asymmetric self-phase modulation and self-steepening of pulses in long optical waveguides. Phys. Rev. A 1983, 27, 1393. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Hickmann, J.M.; de Oliveira, J.R.; de Moura, M.A. Self-steepening of optical pulses in dispersive media. J. Opt. Soc. Am. B 1992, 9, 2025–2027. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 2007; ISBN 9780123695161. [Google Scholar]
- Radhakrishnan, R.; Lakshmanan, M. Exact soliton solutions to coupled nonlinear Schrödinger equations with higher-order effects. Phys. Rev. E 1996, 54, 2949. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Nishizawa, N.; Goto, T. Compact System of Wavelength-Tunable Femtosecond Soliton Pulse Generation Using Optical Fibers. IEEE Photonics Technol. Lett. 1999, 11, 325–327. [Google Scholar] [CrossRef]
- Blow, K.J.; Wood, D. Theoretical Description of Transient Stimulated Raman Scattering in Optical Fibers. IEEE J. Quantum Electron. 1989, 25, 2665–2673. [Google Scholar] [CrossRef]
- Stolen, R.H.; Tomlinson, W.J. Effect of the Raman part of the nonlinear refractive index on propagation of ultrashort optical pulses in fibers. J. Opt. Soc. Am. B 1992, 9, 565–573. [Google Scholar] [CrossRef]
- Bugay, A.N.; Khalyapin, V.A. Analytic description of Raman-induced frequency shift in the case of non-soliton ultrashort pulses. Phys. Lett. A 2017, 381, 399–403. [Google Scholar] [CrossRef]
- Agrawal, G.P. Modulation instability induced by cross-phase modulation. Phys. Rev. Lett. 1987, 59, 880. [Google Scholar] [CrossRef]
- Diao, X.; Diao, X.; Chen, R.; Chen, R.; Chang, G.; Chang, G.; Chang, G. Particle swarm optimization of SPM-enabled spectral selection to achieve an octave-spanning wavelength-shift. Opt. Express 2021, 29, 39766–39776. [Google Scholar] [CrossRef]
- Hua, Y.; Hua, Y.; Zhou, G.; Zhou, G.; Liu, W.; Liu, W.; Xin, M.; Kärtner, F.X.; Kärtner, F.X.; Chang, G. Femtosecond two-color source synchronized at 100-as-precision based on SPM-enabled spectral selection. Opt. Lett. 2020, 45, 3410–3413. [Google Scholar] [CrossRef]
- Xiang, Y.; Dai, X.; Wen, S.; Guo, J.; Fan, D. Controllable Raman soliton self-frequency shift in nonlinear metamaterials. Phys. Rev. A 2011, 84, 033815. [Google Scholar] [CrossRef] [Green Version]
- Bendahmane, A.; Kudlinski, A.; Mussot, A.; Vanvincq, O. Control of the soliton self-frequency shift dynamics using topographic optical fibers. Opt. Lett. Vol. 2013, 38, 3390–3393. [Google Scholar] [CrossRef] [PubMed]
- Saleh, M.F.; Chang, W.; Hölzer, P.; Nazarkin, A.; Travers, J.C.; Joly, N.Y.; Russell, P.S.J.; Biancalana, F. Theory of photoionization-induced blueshift of ultrashort solitons in gas-filled hollow-core photonic crystal fibers. Phys. Rev. Lett. 2011, 107, 203902. [Google Scholar] [CrossRef]
- Facão, M.; Carvalho, M.I.; Almeida, P. Accelerating solitons in gas-filled hollow-core photonic crystal fibers. Phys. Rev. A 2013, 87, 063803. [Google Scholar] [CrossRef] [Green Version]
- Bugay, A.N.; Khalyapin, V.A. Analytic description of pulse frequency self-shift in nonlinear photonic crystal fibers. Commun. Nonlinear Sci. Numer. Simul. 2019, 75, 270–279. [Google Scholar] [CrossRef]
- Zhang, L.; Zhong, H.; Li, Y.; Fan, D. Manipulation of Raman-induced frequency shift by use of asymmetric self-accelerating Airy pulse. Opt. Express 2014, 22, 22598–22607. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, Y.; Song, Y.; Huang, L.; Tong, L.; Qiu, J.; Liu, X. XPM-Induced Vector Asymmetrical Soliton with Spectral Period Doubling in Mode-Locked Fiber Laser. Laser Photon. Rev. 2021, 15, 2000216. [Google Scholar] [CrossRef]
- Guo-Yan, Y.; Jiang-Bo, Z.; Xiao-Yu, Y.; Liang-Wei, D. Asymmetrical surface soliton trains. Chin. Phys. B 2010, 19, 044206. [Google Scholar] [CrossRef]
- Guan, W.Y.; Li, B.Q. Asymmetrical and self-similar structures of optical breathers for the Manakov system in photorefractive crystals and randomly birefringent fibers. Optik 2019, 194, 162882. [Google Scholar] [CrossRef]
- Chen, S.-C.; Liu, C.; Yao, X.; Zhao, L.-C.; Akhmediev, N. Extreme spectral asymmetry of Akhmediev breathers and Fermi-Pasta-Ulam recurrence in a Manakov system. Phys. Rev. E 2021, 104, 024215. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M. Strongly asymmetric soliton explosions. Phys. Rev. E 2004, 70, 036613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pakarzadeh, H.; Delirian, Z.; Taghizadeh, M. Simulation of Chirped Pulse Propagation in Silicon Nanowires: Shape and Spectrum Analysis. Opt. Photonics J. 2016, 06, 53–61. [Google Scholar] [CrossRef] [Green Version]
- Bourkoff, E.; Zhao, W.; Joseph, R.I.; Christodoulides, D.N. Intensity-dependent spectra of pulses propagating in optical fibers. Opt. Commun. 1987, 62, 284–288. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Bednyakova, A.E.; Fedoruk, M.P.; Papernyi, S.B.; Clements, W.R.L. Inverse four-wave mixing and self-parametric amplification in optical fibre. Nat. Photon. 2015, 9, 608–614. [Google Scholar] [CrossRef] [Green Version]
- Dudley, J.M.; Finot, C.; Richardson, D.J.; Millot, G. Self-similarity in ultrafast nonlinear optics. Nat. Phys. 2007, 3, 597–603. [Google Scholar] [CrossRef]
- Želudevičius, J.; Regelskis, K.; Danilevičius, R. Optimization of pulse compression in a fiber chirped pulse amplification system by adjusting dispersion parameters of a temperature-tuned chirped fiber Bragg grating stretcher. J. Opt. Soc. Am. B 2015, 32, 812–817. [Google Scholar] [CrossRef]
- Brinkmann, M.; Hellwig, T.; Fallnich, C. Optical parametric chirped pulse oscillation. Opt. Express 2017, 25, 12884–12895. [Google Scholar] [CrossRef]
- Ciret, C.; Gorza, S.-P. Generation of ultra-broadband coherent supercontinua in tapered and dispersion-managed silicon nanophotonic waveguides. J. Opt. Soc. Am. B 2017, 34, 1156–1162. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Huang, L.; Zhang, B.; Chen, D.; Cui, Y. Self-Frequency Shift in Transmission of Asymmetric Pulse in Optical Medium. Symmetry 2022, 14, 834. https://doi.org/10.3390/sym14040834
Zhang Y, Huang L, Zhang B, Chen D, Cui Y. Self-Frequency Shift in Transmission of Asymmetric Pulse in Optical Medium. Symmetry. 2022; 14(4):834. https://doi.org/10.3390/sym14040834
Chicago/Turabian StyleZhang, Yusheng, Lin Huang, Bin Zhang, Daru Chen, and Yudong Cui. 2022. "Self-Frequency Shift in Transmission of Asymmetric Pulse in Optical Medium" Symmetry 14, no. 4: 834. https://doi.org/10.3390/sym14040834
APA StyleZhang, Y., Huang, L., Zhang, B., Chen, D., & Cui, Y. (2022). Self-Frequency Shift in Transmission of Asymmetric Pulse in Optical Medium. Symmetry, 14(4), 834. https://doi.org/10.3390/sym14040834






