Abstract
In the field of data science and data mining, the problem associated with clustering features and determining its optimum number is still under research consideration. This paper presents a new 2D clustering algorithm based on a mathematical topological theory that uses a pseudometric space and takes into account the local and global topological properties of the data to be clustered. Taking into account cluster symmetry property, from a metric and mathematical-topological point of view, the analysis was carried out only in the positive region, reducing the number of calculations in the clustering process. The new clustering theory is inspired by the thermodynamics principle of energy. Thus, both topologies are recursively taken into account. The proposed model is based on the interaction of particles defined through measuring homogeneous-energy criterion. Based on the energy concept, both general and local topologies are taken into account for clustering. The effect of the integration of a new element into the cluster on homogeneous-energy criterion is analyzed. If the new element does not alter the homogeneous-energy of a group, then it is added; otherwise, a new cluster is created. The mathematical-topological theory and the results of its application on public benchmark datasets are presented.
1. Introduction
Clustering and its classification has increased significantly due to a large amount of digital information available on the internet, especially on social media. The task of grouping information that contains common characteristics or meaning and its subsequent classification is a cornerstone in areas such as data sciences, data mining, and pattern recognition. Despite the important advancement that has been done in the algorithms of clustering and its classifications, it is still under the attention of researchers.
Clustering algorithms are based on their clustering paradigm, and the amount and dimension of the data to be handled. There are several review papers reported in the literature. Saxena et al. [1] have classified them into two main groups, i.e., hierarchical and partitional algorithms. The hierarchical algorithms are further subdivided into agglomerative and divisive algorithms, while partitional algorithms are subdivided into density-based, distance-based, and model-based algorithms.
Another review paper is presented by Dong et al. [2], where the main attention was paid to analyzing the clustering algorithms from supervised and unsupervised perspective. Nevertheless, the most widely accepted classification is that of [3] in which the authors have divided the algorithm into Partitional, Hierarchical, Density-Based, Grid-Based, Spectral, Gravitational, Neural Network-Based, and Evolutionary-Based. We consider the similar classification given in detail in Section 2.
In this research paper, a new 2D clustering algorithm is presented. The proposal is based on the energy and homogeneity of topological theory. Taking into account cluster symmetry property, from metric and mathematical-topological point of view, the analysis is done only in positive region, reducing the number of calculations in the clustering process. The proposal works according to the homogeneous-energy effect that is calculated when a cluster receives a new element. If the new element does not alter the local homogeneous energy of the cluster, then it is added to the cluster. Otherwise, a new cluster will be generated. The algorithm will terminate when all elements are assigned to a single cluster.
Our novel approach was developed to work in two-dimensional space, and it was tested and validated using the bi-dimensional Shape databases widely used in the data clustering literature from the Machine Learning group of School of Computing, University of Eastern Finland [4]. The Shape dataset was chosen because of its levels of complexity, spherically separable point distribution (R15, D31), embedded classes (Jain, flame, and compound), and complex distributions (spiral and pathbased). The previous data distributions are difficult to be correctly clustered by a single clustering algorithm, which is achieved in our proposed methodology.
The rest of the paper is organized as follows. In Section 2, state of the art is presented. The proposal is presented in Section 3. Topology-based theory is given in Section 4. Section 5 presents the methodology. Experimental results and discussion are given in Section 6. Finally, conclusions and perspectives are given in Section 7.
2. State of the Art
Clustering is an unsupervised learning method that classifies unlabeled data objects into several groups based on the similarities among them. The main characteristic of clustering is that prior knowledge of the data is not required. Extensive use of clustering algorithms is made in areas of data science and data mining, where the objective is to group the information that has common characteristics, as well as to define the optimal number of groups. Figure 1 shows the common clustering algorithms: Partitional, Hierarchical, Density-Based, Grid-Based, Spectral, Gravitational, Neural Network-Based, and Evolutionary Clustering [3]. There is another clustering technique based on semantic definition [5], but it has a disadvantage that it works for the supervised clustering only.
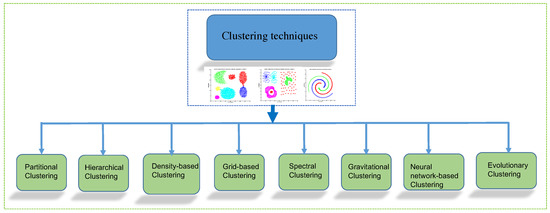
Figure 1.
Taxonomy of clustering techniques.
The main works related to clustering algorithms are presented in [6,7,8,9,10,11,12,13,14]. Clustering algorithms are classified into Partitional Clustering, Hierarchical Clustering, Density-based Clustering, Spectral Clustering, Gravitational Clustering, Evolutionary Clustering. Their advantages and disadvantages are summarized in Table 1. Although there is a wide range of clustering algorithms available, none of the aforementioned clustering algorithm is self-sufficient for all types of clustering problems. Published clustering methodologies have been conceived for each type of database to be clustered. The reported algorithms do not take into account the topology of the data, neither local nor global, which confines them to work with local densities or general distance criteria. This proposal defines a homogeneous-energy measure that takes into account the local and global topological properties of the data to be clustered (see Section 3 and Section 4).

Table 1.
Clustering algorithms with its merits and demerits.
Our proposal is an attempt to overcome the main limitations of typical clustering algorithms. With the topological model based on mathematical pseudometric, unlike partitional and gravitational algorithms, we no longer have the need to establish prior knowledge of the data. Thus, it is not necessary to define any density-based function, and the use of working only with the hyper-spherical separation functions is avoided. Therefore, based on the Algebra of sets, due to not occupying excessive memory as the density-based, spectral, and gravitational algorithms do, the calculations and results are obtained faster. This research paper aims to compare the clustering and synthetic benchmark datasets.
3. Proposal
There are many clustering algorithms focused on grouping elements according to their feature distribution. As presented in the above section, there are clustering algorithms. i.e., Partitional, Hierarchical, Density-Based, and so on, that solve a particular clustering problem. Our proposal takes into account the topology of both local and global dataset, which makes it more general and be able to cluster any type of data. The measure of similarity between the elements to cluster is defined via a pseudometric, and the clustering criteria is based on an affinity function and a homogeneous-energy state. An affinity function measures how close one element is to another. While a homogeneous-energy function determines, for a closed system, the equilibrium locally, as well as globally. Local and global homogeneous-energies are reduced to a minimum value in equilibrium. Therefore, if we associate the elements with a homogeneous-energy function, which is obtained in principle with the affinity function, a group of elements will be formed by common elements if they are kept below their homogeneous-energy level.
At the beginning, r-representatives are selected (either randomly or sequentially), considering all the elements of the database to form a subset of elements representing each group. Subsequently, the affinity of the r-representatives to the rest of the elements in the database is calculated. An element will be assigned to a group if its group homogeneous-energy level is low or without changes. Otherwise, a new group and a new representative will be generated.
The representatives will be a subset of a given group. A new element can be added to a given group if it is an affinity between that new element and the group of representatives, keeping its group homogeneous-energy level low or without changes.
If the homogeneous-energy in a given group is drastically altered or higher than the level, then the new element is not related to this grouping, and as a consequence, the new element is rejected. A new group is created in which the elements are labeled as “others” because they do not have similar properties to each other.
4. Theoretical Fundamentals of a Topological-Pseudometric-Based Clustering
In the context of mathematical topology, six definitions, a proposition, a theorem, and an example are provided. Definition 1 refers to pseodometry. Definition 2 deals with set theory, i.e., empty sets and subsets. Definition 3 deals with the definition of pseudometrics as applied to both representative and database elements. Definition 4 refers to the energy function. Definition 5 deals with pseudometrics around a topological neighborhood. Finally, definition 6 measures the pseudometrics to the representatives and to the subsets of groups. The example shows the energy variability having the same representative element, but with different topologically distributed neighbors.
Definition 1.
Let X be a non-empty set. The Cartesian product of sets X and Y is the set of all ordered pairs with and .
A pseudometric space is a set X together with a non-negative real-valued function (called a pseudometric function) such that, for every .
Unlike a metric space, points in a pseudometric space need not to be distinguishable; that is, one may have for distinct values .
The pseudometric topology is induced by the open balls, with and ,
which forms basis for the topology.
A topological space is said to be a pseudo metrizable topological space if the space can be given a pseudometric such that the pseudometric topology coincides with the given topology on the space [61].
Definition 2.
An exact cover of a set X is a family of nonempty subsets of X such that the following conditions are satisfied:
- For each, .
- For and implies .
- .
Definition 3.
Let be a pseudometric space and A be a subset of X. If an element satisfies the condition:
for every then is called representative of A. The set of representatives of A is denoted by .
The distance between point and a set A can be defined as:
Lemma 1.
Let be a pseudometric space. For each finite set , the set of representatives is a non-empty set.
Proof.
For the set , considers,
take . There is an such that . For definition of it follows,
For each . This proves that is a representative of A. □
Definition 4.
The energy function can be defined as follows:
where .
It should be noted that the energy of a set A is independent of the choice of the representatives of A. By definition, if and are representative of A, then, the following condition must be satisfied:
A point p preserves the energy of A if .
Example 1.
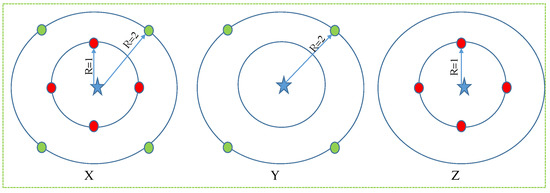
Energy variations can be represented by subsets elements, having the same representative.
Let the sets be , and Z in with the Euclidean metric (see Figure 2). Elements are marked with dots and its representative with a star. Elements are distributed in two concentric circles with radii 1, and 2. Consider the subsets Y, and Z as removing a circle from X (see Figure 2 (Y) and (Z)). In addition, it can be noted that the energy of set X, Y, and Z are 1.5, 2, and 1, respectively. It can be remarked that energy changes under subsets. Thus, for this example does not imply .

Figure 2.
Subsets example of energy: X dots points distributed in two concentric circles with radii 1, and 2, and star is its representative. Y Subset subtracting internal circle, and Z Subset subtracting external circle.
Definition 5.
Let be a pseudometric space and . An exact cover of X is called a δ-exact cover if for each .
Definition 6.
Let be a pseudometric space, A be a subset of X, be the set of representatives of A, and . The set (see Equation (9)) given below is called a star cover of A.
Proposition 1.
Let be a pseudometric space, , and , be the set of representatives, and energy of A, respectively. The star cover with satisfies .
Proof.
Consider and , then . Let .
It can construct the succession which satisfied for and that . Therefore . □
Theorem 1.
Let be a pseudometric space, and . There exists an exact cover of X where is δ exact cover of , and the element D does not preserve the energy of for each .
Proof.
It will construct a family of sets which satisfies the following properties for each .
Stand . On the condition then . If not, define . On the other hand, taking n and m to be two integers, and without loss of generality, next condition is fulfilled for . Let and , Subsequently, take and considering . Taking into account the proposition 1 then inequalities stand:
consequently, the condition is satisfied. It has been shown that properties (i), and (ii) are completely satisfied. □
5. Methodology
Proposed clustering methodology is shown in Figure 3. The main steps of the methodology are described below.
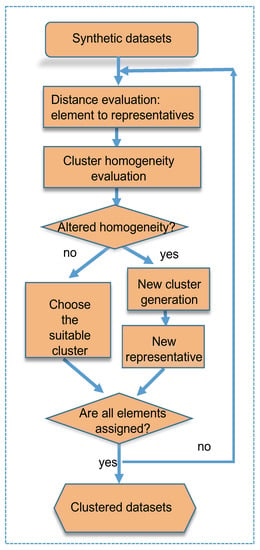
Figure 3.
General scheme of proposed methodology.
- 1.
- Dataset are read: First, datasets are read as ascii files, where the first column represents the information on the x-axis, while the second column represents the information on the y-axis.
- 2.
- The manhattan distance is calculated on the totality of the data: A measure amount of all elements is defined by its manhattan distance, in this case, there is a two-dimension manhattan distance.
- 3.
- Local and general pseudometry is evaluated: Based on pseudometry defined in Definitions 1–3, local and general topology are taken into account in order to measure the cluster energy, defined in Definition 4.
- 4.
- The appropriate cluster is chosen: If the energy of the cluster is not affected by the new element, then it is integrated to the cluster, otherwise, a new one is generated.
- 5.
- The homogeneous-energy of the clusters is evaluated: At this stage, each cluster energy is calculated in order to update the cluster energy.
If all the elements are assigned to a cluster, then the algorithm ends.
5.1. Datasets
In order to test the proposed algorithm and its robustness in the automatic generation of clusters, synthetic datasets of two-dimensional points were used. Datasets were taken from Machine Learning group of School of Computing, University of Eastern Finland [4]. The dataset is shown in Figure 4 and its characteristics are given in Table 2. There were 8 datasets tested throughout the topological algorithm, that are: Aggregation, Compound, Pathbase, Spiral, D31, R15, Jain, and Flame. The Shape dataset was chosen because of its levels of complexity, spherically separable point distribution (R15, D31), embedded classes (Jain, flame, and compound), and complex distributions (spiral and pathbased). The previous data distributions are difficult to be correctly clustered by a single clustering algorithm. In our topological-pseudometric-based clustering proposal, it is possible.
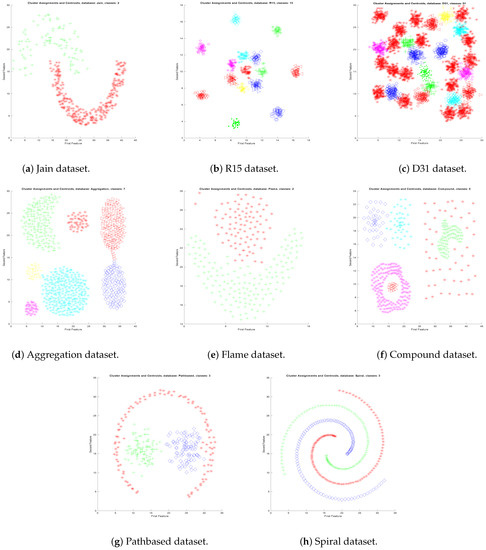
Figure 4.
Original 2-Dimensional Shape datasets.

Table 2.
Synthetic datasets for clustering task.
5.2. Metric and Distance
Consider the set of points (P). Points correspond to a synthetic dataset (see Figure 4). According to Section 4, a pseudometric is defined for two given points as follows:
A pseudometric has been built in the space of the points. Thus, Theorem 1 will always allow to create clusters. The Manhattan distance is used in all the tests.
5.3. Add the Object into the Suitable Cluster
Starting from the representatives in each cluster, the new homogeneous-energy measure is calculated for each new element to be added to the cluster. The homogeneities are calculated using theorem 1 and proposition 1 (see Section 4) for each representatives. Thus, the new element is assigned to the cluster which is not affected in its homogeneous-energy. Otherwise, a new cluster is created and the new element is taken as its representatives.
6. Experimental Results
Experiments on the D-Dimension were conducted on shape dataset in order to test the efficiency of the clusterings produced by our topological algorithm on a varied collection of synthetic datasets (see Table 2). The goal in this set of experiments is to show how topological clustering can be used to improve the quality and robustness of widely-used clustering datasets benchmark. Eight synthetic datasets were used, from separate distributions and compacted classes to spiral or circular distributions, which are extremely complex to cluster: Aggregation, Compound, Pathbase, Spiral, D31, R15, Jain, and Flame. The eight datasets were divided into three groups according to their distribution-shape and difficulty of grouping. Clustering error is defined as [62]:
- Easy: The proposed algorithm works very well for the Jain, D31, R15, and Aggregation datasets (see Figure 5a–d). The clustering error is less than . The clustering problem is on Aggregation dataset (in the union of the classes of the right side; see Figure 5d).
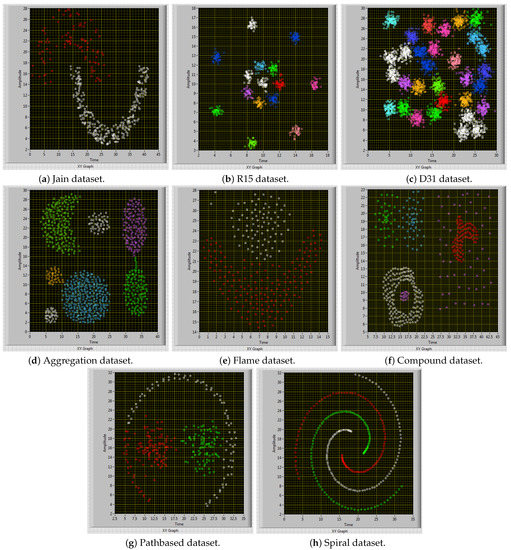 Figure 5. Clustered 2-Dimensional Shape datasets.
Figure 5. Clustered 2-Dimensional Shape datasets. - Medium: Results are good for Flame and Compound datasets (see Figure 5e,f). The clustering error is less than .
- Complex: For the third group, the results of the Pathbased and spiral datasets are good (see Figure 5g,h). The clustering error is less than just for Pathbase dataset. The result for Spiral dataset is .
The proposed algorithm was implemented in LabVIEW software, which is oriented to work easily with hardware, obtaining accurate and fast measurements and results. LabView allows to run algorithms from reading datasets from files, to the graphical display of information.
The algorithm begins taking representatives randomly from the whole dataset. The distances among representatives allow to define the parameter as intermediate values. The value is set at of the distance between two representatives. After setting the initial parameters, the pseudometric grouping theorem is applied. Thus, there are as a result. We impose the criteria that groups containing less than 10 percent of the entire dataset are annulled, and the elements are re-integrated into the Q set. For the next iterations, the delta value is increased by . The algorithm ends when the Q set is empty.
Considering local and global topologies has allowed us to define a more robust algorithm than those reported in the literature. Better results have been obtained in this research work for different characteristics of the databases to be clustered.
The proposal overcomes the problems reported in existing algorithms and allows not having the limitations of (1) a prior knowledge of the data and (2) using only spherical separator functions. Another important advantage of this proposed algorithm is the use of Algebra of sets which helps in obtaining the results faster and without excessive memory consumption (as density-based, spectral, and gravitational algorithms do).
7. Conclusions
The new 2D clustering algorithm based on a mathematical topological theory was presented in this research paper. The proposed theory of a pseudometric-based clustering model and its application in synthetic datasets worked as expected. Thus, this new method based on topology theory has successfully worked for the clustering of easy and complex datasets. The proposal also takes into account the local and global topological properties of the data to be clustered in a definition of homogeneous-energy measurement.
The proposal overcomes the problems reported in existing algorithms and without the need for (1) a prior knowledge of the data and (2) using only spherical separator functions. Another advantage of the proposal is that since the proposed algorithm is based on Algebra of sets, the computational results are faster and without excessive memory consumption.
Because of the theoretical development, there is now a theorem (Theorem 1) that can be applied in any space that defines a pseudometric.
Based on the results obtained, the clustering of n-dimensional databases will be explored, as well as the application of the proposal to large databases.
Author Contributions
Conceptualization, I.O.-G. and Y.P.-P.; methodology, I.O.-G. and C.A.-C.; software, I.O.-G. and Y.P.-P.; validation, I.O.-G. and C.A.-C.; formal analysis, I.O.-G. and C.A.-C.; investigation, I.O.-G., Y.P.-P. and C.A.-C.; writing—original draft preparation, C.A.-C.; writing—review and editing, C.A.-C.; supervision, I.O.-G. and C.A.-C.; project administration, C.A.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.; Tiwari, A.; Er, M.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Zhao, Y.; Tarus, S.; Yang, L.; Sun, J.; Ge, Y.; Wang, J. Privacy-preserving clustering for big data in cyber-physical-social systems: Survey and perspectives. Inf. Sci. 2020, 515, 132–155. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. K-means properties on six clustering benchmark datasets. Appl. Intell. 2018, 48, 4743–4759. [Google Scholar] [CrossRef]
- Wan, S.P.; Yan, J.; Dong, J.Y. Personalized individual semantics based consensus reaching process for large-scale group decision making with probabilistic linguistic preference relations and application to COVID-19 surveillance. Expert Syst. Appl. 2022, 191, 116328. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef] [Green Version]
- Khandare, A.; Alvi, A.S. Clustering Algorithms: Experiment and Improvements. In Computing and Network Sustainability; Vishwakarma, H., Akashe, S., Eds.; Springer: Singapore, 2017; pp. 263–271. [Google Scholar]
- Patibandla, R.S.M.L.; Veeranjaneyulu, N. Survey on Clustering Algorithms for Unstructured Data. In Intelligent Engineering Informatics; Bhateja, V., Coello Coello, C.A., Satapathy, S.C., Pattnaik, P.K., Eds.; Springer: Singapore, 2018; pp. 421–429. [Google Scholar]
- Osman, M.M.A.; Syed-Yusof, S.K.; Abd Malik, N.N.N.; Zubair, S. A survey of clustering algorithms for cognitive radio ad hoc networks. Wirel. Netw. 2018, 24, 1451–1475. [Google Scholar] [CrossRef]
- Bindra, K.; Mishra, A.; Suryakant. Effective Data Clustering Algorithms. In Soft Computing: Theories and Applications; Ray, K., Sharma, T.K., Rawat, S., Saini, R.K., Bandyopadhyay, A., Eds.; Springer: Singapore, 2019; pp. 419–432. [Google Scholar]
- Djouzi, K.; Beghdad-Bey, K. A Review of Clustering Algorithms for Big Data. In Proceedings of the 2019 International Conference on Networking and Advanced Systems (ICNAS), Annaba, Algeria, 26–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, S.S. Survey of State-of-the-Art Mixed Data Clustering Algorithms. IEEE Access 2019, 7, 31883–31902. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Q.; Wang, H. Uniformities on strongly topological gyrogroups. Topol. Its Appl. 2021, 302, 107776. [Google Scholar] [CrossRef]
- Telikani, A.; Tahmassebi, A.; Banzhaf, W.; Gandomi, A. Evolutionary Machine Learning: A Survey. ACM Comput. Surv. 2022, 54, 161. [Google Scholar] [CrossRef]
- Jinyin, C.; Xiang, L.; Haibing, Z.; Xintong, B. A novel cluster center fast determination clustering algorithm. Appl. Soft Comput. 2017, 57, 539–555. [Google Scholar] [CrossRef]
- Schubert, E.; Rousseeuw, P. Faster k-Medoids Clustering: Improving the PAM, CLARA, and CLARANS Algorithms. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11807. [Google Scholar]
- Liu, X.; Zhu, X.; Li, M.; Wang, L.; Zhu, E.; Liu, T.; Kloft, M.; Shen, D.; Yin, J.; Gao, W. Multiple Kernel k-means with Incomplete Kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1191–1204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanika; Rani, K.; Sangeeta; Preeti. Visual Analytics for Comparing the Impact of Outliers in k-Means and k-Medoids Algorithm. In Proceedings of the 2019 Amity International Conference on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, 4–6 February 2019; pp. 93–97. [Google Scholar] [CrossRef]
- Gupta, T.; Panda, S.P. A Comparison of K-Means Clustering Algorithm and CLARA Clustering Algorithm on Iris Dataset. Int. J. Eng. Technol. 2019, 7, 4766–4768. [Google Scholar]
- Li, Y.; Cai, J.; Yang, H.; Zhang, J.; Zhao, X. A Novel Algorithm for Initial Cluster Center Selection. IEEE Access 2019, 7, 74683–74693. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, X.; Fan, R.; Wang, Z. Deviation-Sparse Fuzzy C-Means With Neighbor Information Constraint. IEEE Trans. Fuzzy Syst. 2019, 27, 185–199. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, F.; Pedrycz, W. Fuzzy C-Means clustering through SSIM and patch for image segmentation. Appl. Soft Comput. 2020, 87, 105928. [Google Scholar] [CrossRef]
- Garcia, M.; Igusa, K. Continuously triangulating the continuous cluster category. Topol. Appl. 2020, 285, 107411. [Google Scholar] [CrossRef]
- Osuna-Galán, I.; Pérez-Pimentel, Y.; Avilés-Cruz, C.; Villegas-Cortez, J. Topology: A Theory of a Pseudometric-Based Clustering Model and Its Application in Content-Based Image Retrieval. Math. Probl. Eng. 2019, 2019, 4540731. [Google Scholar] [CrossRef]
- Lim, J.; Jun, J.; Kim, S.H.; McLeod, D. A Framework for Clustering Mixed Attribute Type Datasets. In Proceedings of the 4th International Conference on Emerging Databases-Technologies, Applications, and Theory (EDB 2012), Seoul, Korea, 23–25 August 2012. [Google Scholar]
- Nazari, Z.; Kang, D.; Asharif, M.; Sung, Y.; Ogawa, S. A new hierarchical clustering algorithm. In Proceedings of the 2015 International Conference on Intelligent Informatics and Biomedical Sciences (ICIIBMS), Okinawa, Japan, 28–30 November 2015; pp. 148–152. [Google Scholar]
- Rashedi, E.; Mirzaei, A.; Rahmati, M. Optimized aggregation function in hierarchical clustering combination. Intell. Data Anal. 2016, 20, 281–291. [Google Scholar] [CrossRef]
- Yao, W.; Dumitru, C.; Loffeld, O.; Datcu, M. Semi-supervised Hierarchical Clustering for Semantic SAR Image Annotation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1993–2008. [Google Scholar] [CrossRef] [Green Version]
- Pitolli, G.; Aniello, L.; Laurenza, G.; Querzoni, L.; Baldoni, R. Malware family identification with BIRCH clustering. In Proceedings of the 2017 International Carnahan Conference on Security Technology (ICCST), Madrid, Spain, 23–26 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, X.; Su, T.; Wang, P.; Wang, G.; Lv, Z.; Li, X. An Optimized Chameleon Algorithm Based on Local Features. In Proceedings of the 2018 10th International Conference on Machine Learning and Computing (ICMLC 2018), Macau, China, 26–28 February 2018; ACM: New York, NY, USA, 2018; pp. 184–192. [Google Scholar] [CrossRef]
- Yokoyama, S.; Bogardi-Meszoly, A.; Ishikawa, H. EBSCAN: An entanglement-based algorithm for discovering dense regions in large geo-social data streams with noise. In Proceedings of the 8th ACM SIGSPATIAL International Workshop on Location-Based Social Networks, Bellevue, WA, USA, 3–6 November 2015. [Google Scholar]
- Rehioui, H.; Idrissi, A.; Abourezq, M.; Zegrari, F. DENCLUE-IM: A New Approach for Big Data Clustering. Procedia Comput. Sci. 2016, 83, 560–567. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.M.; Reddy, A.R.M. A fast DBSCAN clustering algorithm by accelerating neighbor searching using Groups method. Pattern Recognit. 2016, 58, 39–48. [Google Scholar] [CrossRef]
- Behzadi, S.; Ibrahim, M.A.; Plant, C. Parameter Free Mixed-Type Density-Based Clustering. In Database and Expert Systems Applications; Hartmann, S., Ma, H., Hameurlain, A., Pernul, G., Wagner, R.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 19–34. [Google Scholar]
- Matioli, L.C.; Santos, S.; Kleina, M.; Leite, E.A. A new algorithm for clustering based on kernel density estimation. J. Appl. Stat. 2018, 45, 347–366. [Google Scholar] [CrossRef]
- Shu, Z.; Yang, S.; Wu, H.; Xin, S.; Pang, C.; Kavan, L.; Liu, L. 3D Shape Segmentation Using Soft Density Peak Clustering and Semi-Supervised Learning. CAD Comput.-Aided Des. 2022, 145. [Google Scholar] [CrossRef]
- Rashad, M.A.; El-Deeb, H.; Fakhr, M.W. Document Classification Using Enhanced Grid Based Clustering Algorithm. In New Trends in Networking, Computing, E-Learning, Systems Sciences, and Engineering; Elleithy, K., Sobh, T., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 207–215. [Google Scholar]
- Wagner, T.; Feger, R.; Stelzer, A. A fast grid-based clustering algorithm for range/Doppler/DoA measurements. In Proceedings of the 2016 European Radar Conference (EuRAD), London, UK, 5–7 October 2016; pp. 105–108. [Google Scholar]
- Lalitha, K.; Thangarajan, R.; Udgata, S.K.; Poongodi, C.; Sahu, A.P. GCCR: An Efficient Grid Based Clustering and Combinational Routing in Wireless Sensor Networks. Wirel. Pers. Commun. 2017, 97, 1075–1095. [Google Scholar] [CrossRef]
- Deng, C.; Song, J.; Sun, R.; Cai, S.; Shi, Y. Gridwave: A grid-based clustering algorithm for market transaction data based on spatial-temporal density-waves and synchronization. Multimed. Tools Appl. 2018, 77, 29623–29637. [Google Scholar] [CrossRef]
- Chen, J.; Lin, X.; Xuan, Q.; Xiang, Y. FGCH: A fast and grid based clustering algorithm for hybrid data stream. Appl. Intell. 2019, 49, 1228–1244. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, Z. A Fast and Efficient Grid-Based K-means++ Clustering Algorithm for Large-Scale Datasets. In The Fifth Euro-China Conference on Intelligent Data Analysis and Applications; Krömer, P., Zhang, H., Liang, Y., Pan, J.S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 508–515. [Google Scholar]
- Menendez, H.; Camacho, D. GANY: A genetic spectral-based Clustering algorithm for Large Data Analysis. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 640–647. [Google Scholar]
- Shang, R.; Zhang, Z.; Jiao, L.; Wang, W.; Yang, S. Global discriminative-based nonnegative spectral clustering. Pattern Recognit. 2016, 55, 172–182. [Google Scholar] [CrossRef]
- Alamdari, M.; Rakotoarivelo, T.; Khoa, N. A spectral-based clustering for structural health monitoring of the Sydney Harbour Bridge. Mech. Syst. Signal Process. 2017, 87, 384–400. [Google Scholar] [CrossRef]
- Tian, L.; Du, Q.; Kopriva, I.; Younan, N. Spatial-spectral Based Multi-view Low-rank Sparse Sbuspace Clustering for Hyperspectral Imagery. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8488–8491. [Google Scholar]
- Nemade, V.; Shastri, A.; Ahuja, K.; Tiwari, A. Scaled and Projected Spectral Clustering with Vector Quantization for Handling Big Data. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 2174–2179. [Google Scholar]
- Ma, L.; Zhang, Y.; Leiva, V.; Liu, S.; Ma, T. A new clustering algorithm based on a radar scanning strategy with applications to machine learning data. Expert Syst. Appl. 2022, 191. [Google Scholar] [CrossRef]
- Dowlatshahi, M.; Nezamabadi-Pour, H. GGSA: A Grouping Gravitational Search Algorithm for data clustering. Eng. Appl. Artif. Intell. 2014, 36, 114–121. [Google Scholar] [CrossRef]
- Kumar, V.; Chhabra, J.; Kumar, D. Automatic cluster evolution using gravitational search algorithm and its application on image segmentation. Eng. Appl. Artif. Intell. 2014, 29, 93–103. [Google Scholar] [CrossRef]
- Nikbakht, H.; Mirvaziri, H. A new algorithm for data clustering based on gravitational search algorithm and genetic operators. In Proceedings of the 2015 The International Symposium on Artificial Intelligence and Signal Processing (AISP), Mashhad, Iran, 3–5 March 2015; pp. 222–227. [Google Scholar]
- Sheshasaayee, A.; Sridevi, D. Fuzzy C-means algorithm with gravitational search algorithm in spatial data mining. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 1, pp. 1–5. [Google Scholar]
- Deng, Z.; Qian, G.; Chen, Z.; Su, H. Identifying Tor Anonymous Traffic Based on Gravitational Clustering Analysis. In Proceedings of the 2017 9th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 26–27 August 2017; Volume 2, pp. 79–83. [Google Scholar]
- Alswaitti, M.; Ishak, M.; Isa, N. Optimized gravitational-based data clustering algorithm. Eng. Appl. Artif. Intell. 2018, 73, 126–148. [Google Scholar] [CrossRef]
- Yuqing, S.; Junfei, Q.; Honggui, H. Structure design for RBF neural network based on improved K-means algorithm. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 7035–7040. [Google Scholar]
- Amin, H.; Deabes, W.; Bouazza, K. Clustering of user activities based on adaptive threshold spiking neural networks. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 1–6. [Google Scholar]
- Abavisani, M.; Patel, V. Deep Multimodal Subspace Clustering Networks. IEEE J. Sel. Top. Signal Process. 2018, 12, 1601–1614. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.; Chen, J.; Ye, L.; Wang, C.; Liu, Y.; Zhou, W. Application of RBF Neural Network Optimized Based on K-Means Cluster Algorithm in Fault Diagnosis. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 2492–2496. [Google Scholar]
- Kimura, M. AutoClustering: A feed-forward neural network based clustering algorithm. In Proceedings of the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, 17–20 November 2019; Volume 2018, pp. 659–666. [Google Scholar]
- Cheng, Y.; Yu, S.; Liu, J.; Han, Z.; Li, Y.; Tang, Y.; Wu, C. Representation Learning Based on Autoencoder and Deep Adaptive Clustering for Image Clustering. Math. Probl. Eng. 2021, 2021, 3742536. [Google Scholar] [CrossRef]
- Engelking, R. General Topology; Springer International Publishing: Cham, Switzerland, 1989. [Google Scholar]
- Balcerzak, M.; Leonetti, P. On the relationship between ideal cluster points and ideal limit points. Topol. Its Appl. 2019, 252, 178–190. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).