Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space
Abstract
1. Introduction
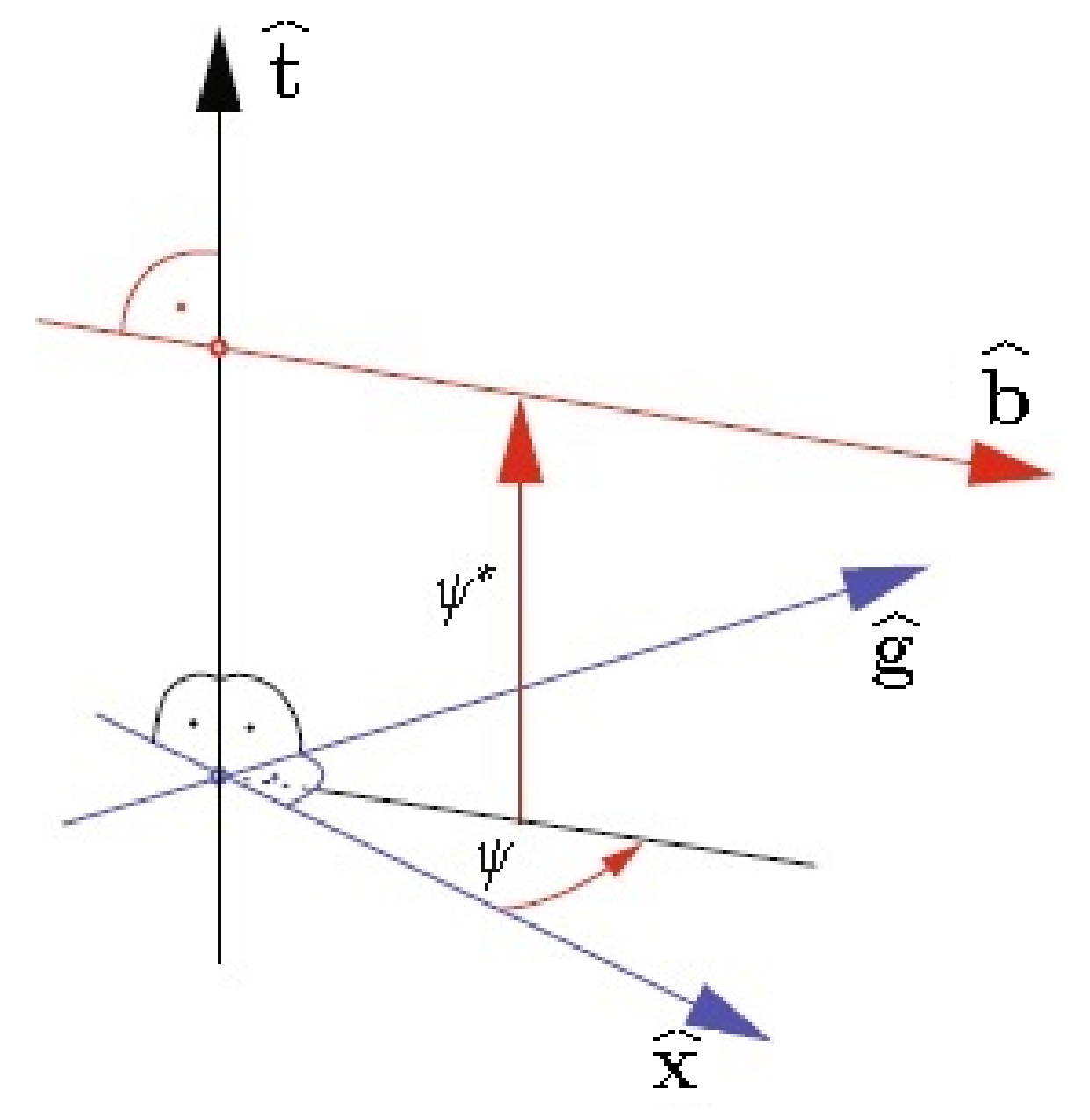
2. Basic Concepts
3. Timelike Ruled Surfaces
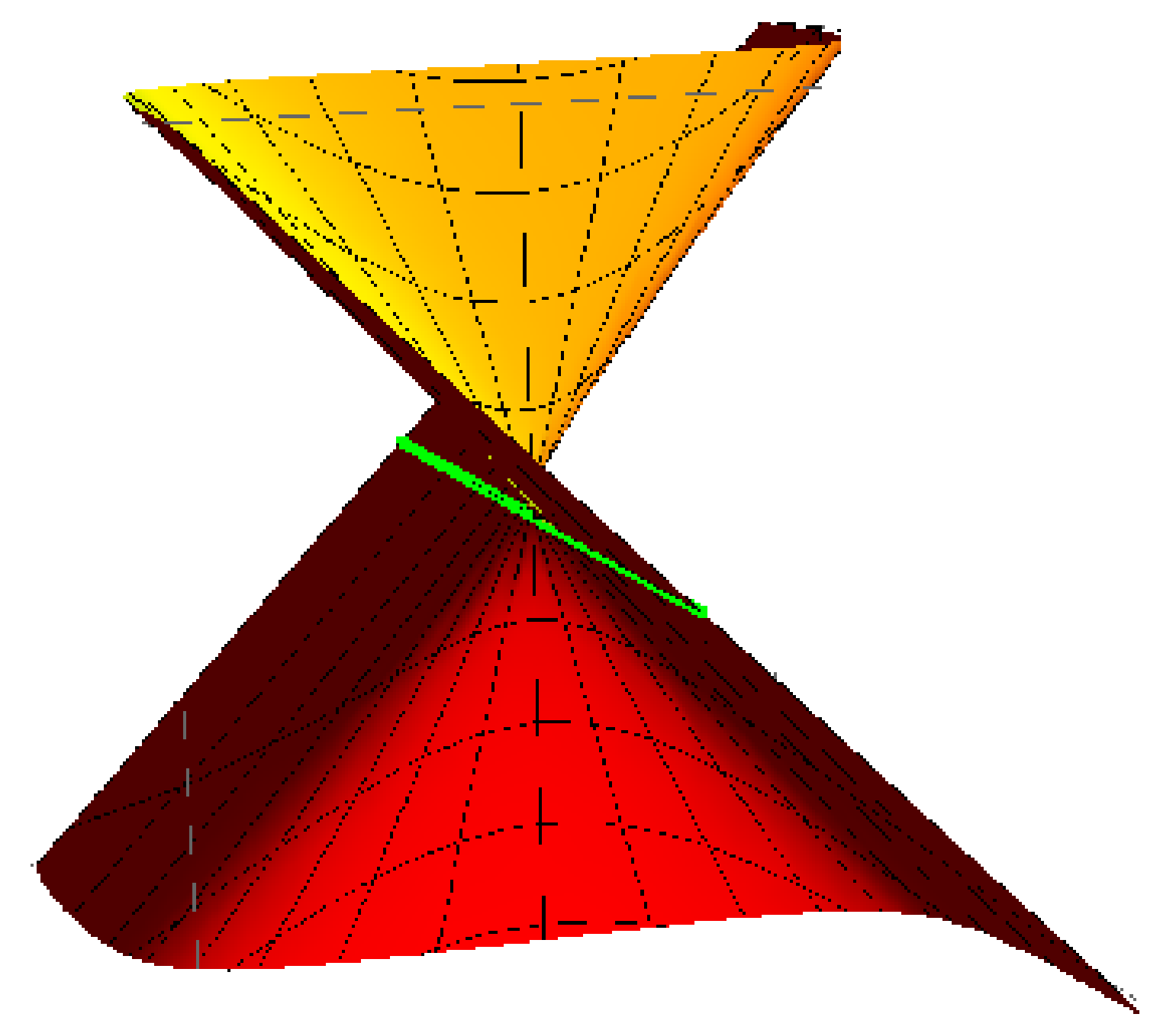
3.1. Kinematic Geometry
- (i)
- The timelike Disteli-axis is given by Equation (4).
- (ii)
- The dual angular speed is .
- (iii)
- If is a point on the timelike Disteli-axis , thenis a non-developable timelike ruled surface .
- (iv)
- If the Blaschke motionis pure rotation, that is, , then
- (1)
- If then there are two isotropic lines , and passing through the isotropic point only if ; for the two isotropic limit points , they synchronize with the edges and .
- (2)
- If then the two isotropic torsal lines , and are obtained by
- (a)
- In the case of the timelike Plücker conoid degenerates into the pencil of lines through “ in the timelike plane .
- (b)
- In the case of the two torsal isotropic lines , and are coincident with the edges and .
- (c)
- In the case of , the two torsal isotropic lines , and both coincide with the axis; for , they coincide with the axis.
- (d)
- In the case of the ruled timelike surface (X) and the spacelike surface (G) are developable surfaces (cones); the central point is a fixed point.
Serret–Frenet Motion
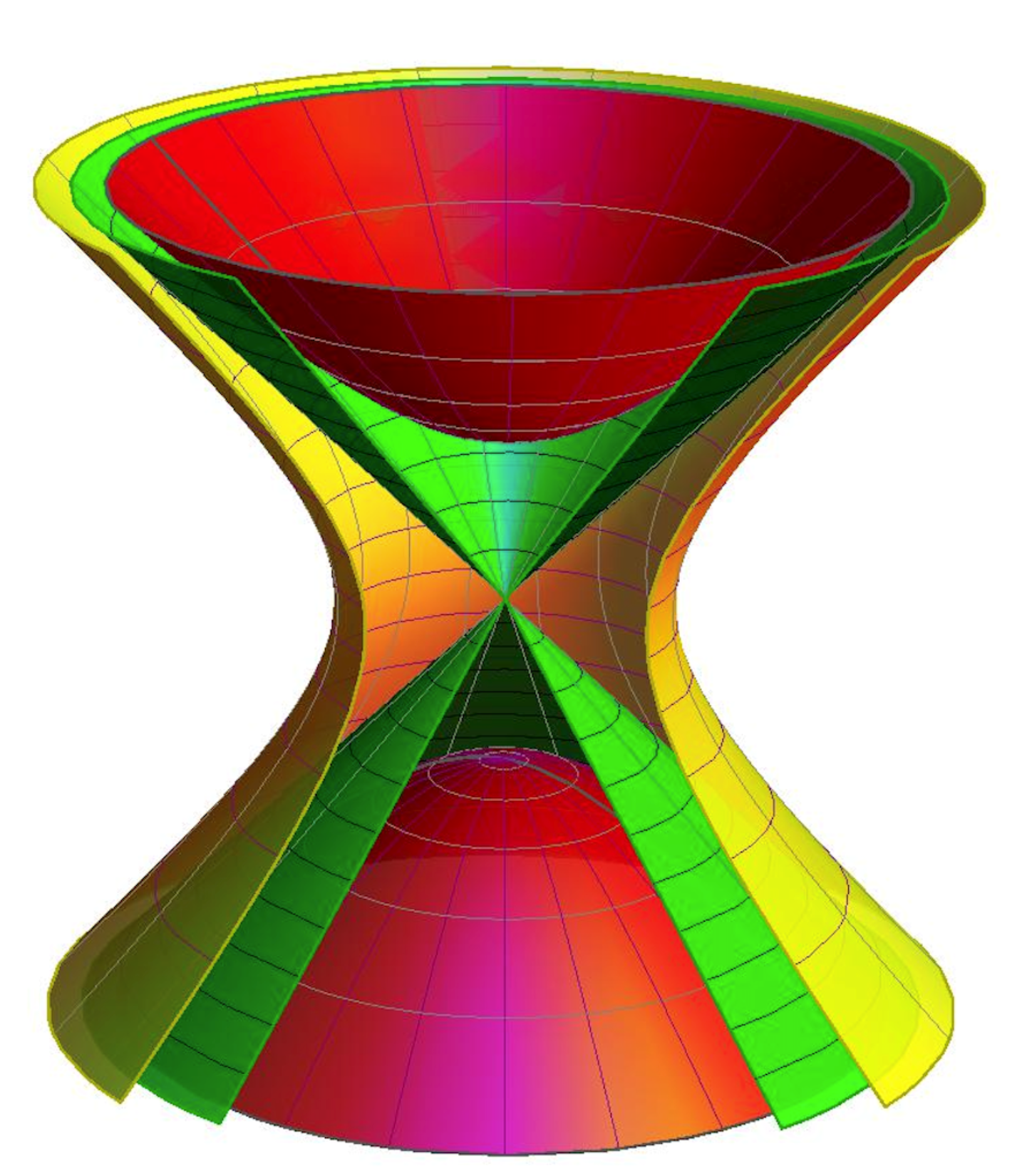
3.2. Timelike Ruled Surfaces with Constant Disteli-Axis
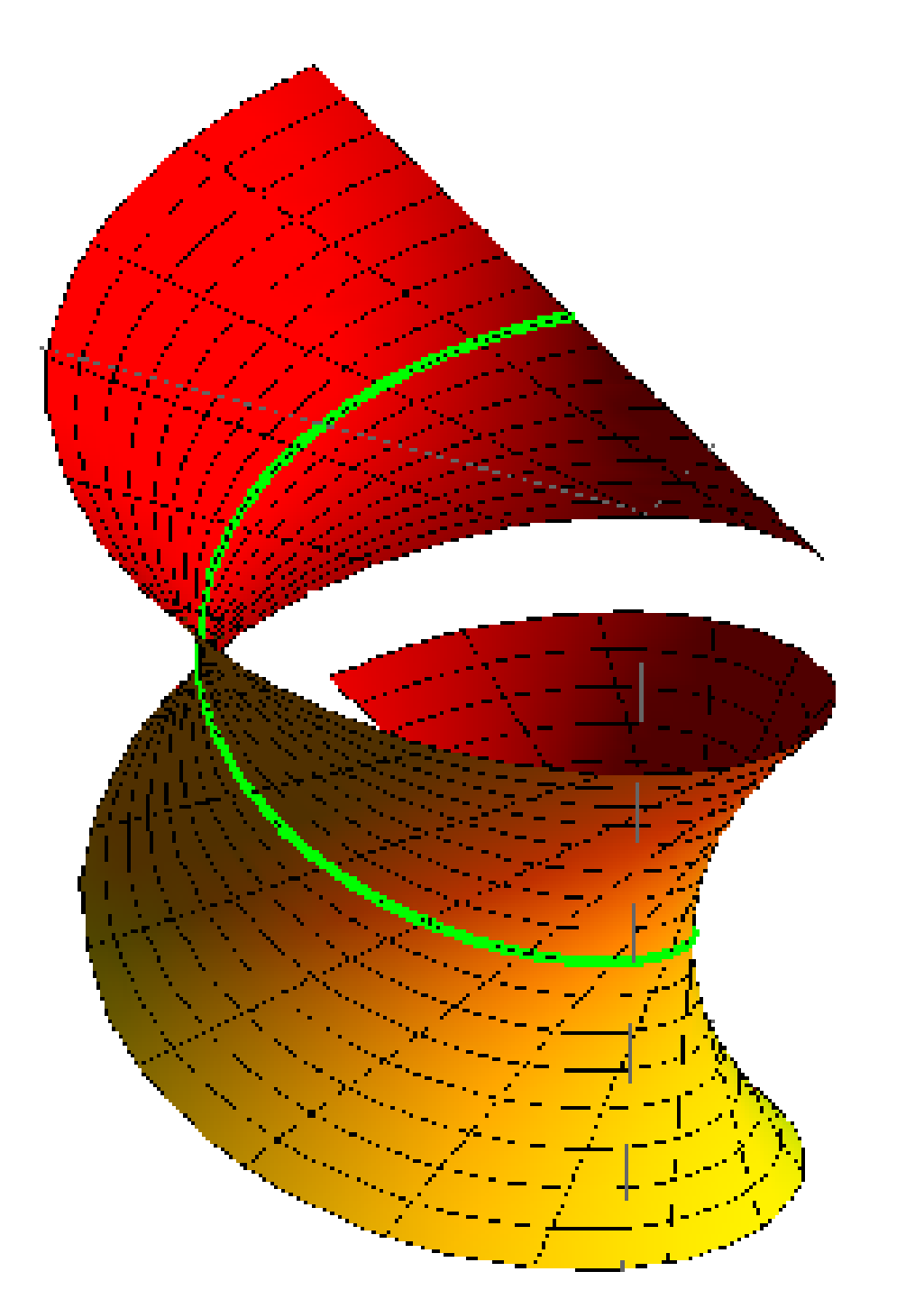
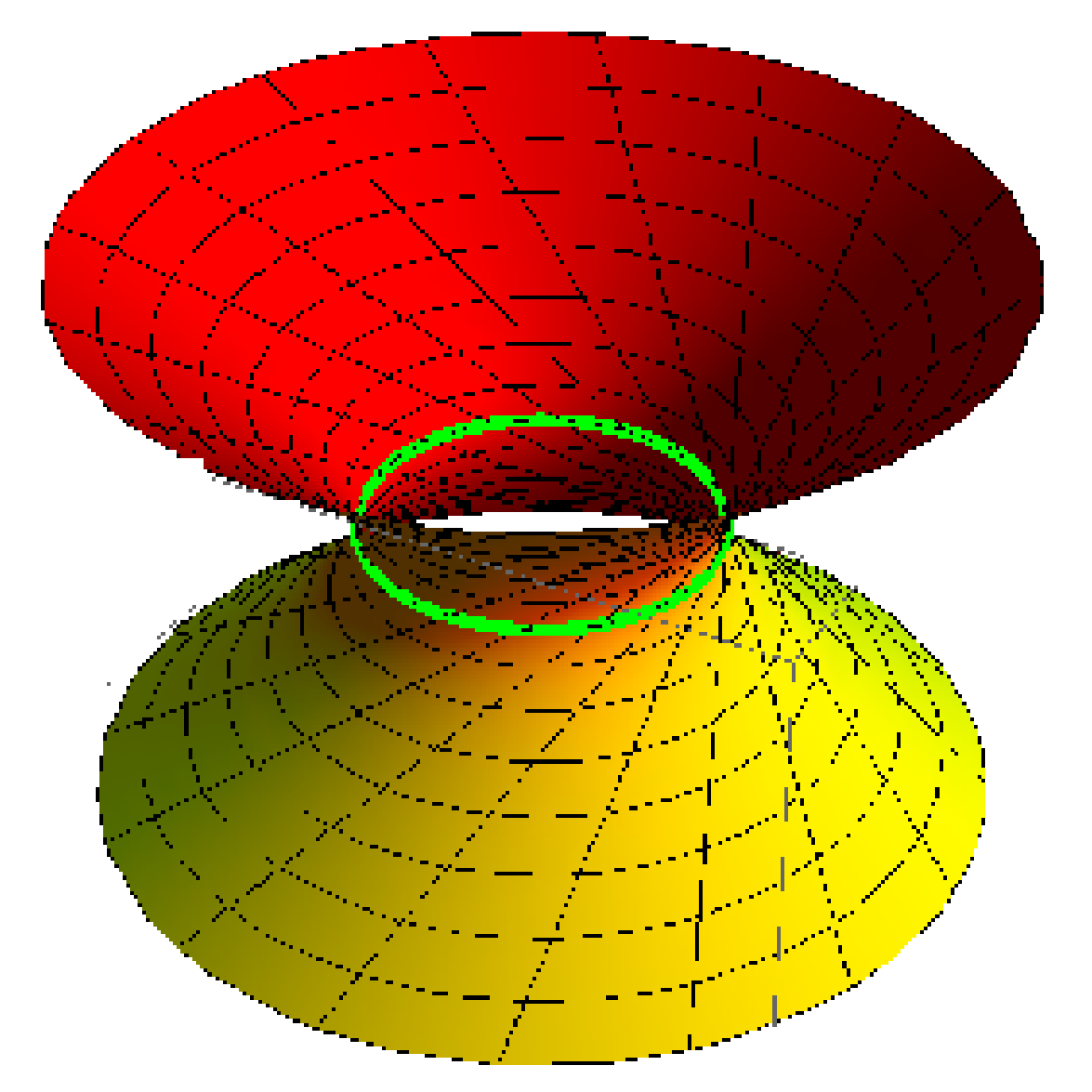


4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bottema, O.; Roth, B. Theoretical Kinematics; North-Holland Press: New York, NY, USA, 1979. [Google Scholar]
- Karger, A.; Novak, J. Space Kinematics and Lie Groups; Gordon and Breach Science Publishers: New York, NY, USA, 1985. [Google Scholar]
- Pottman, H.; Wallner, J. Computational Line Geometry; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Abdel-Baky, R.A.; Al-Solamy, F.R. A new geometrical approach to one-parameter spatial motion. J. Eng. Math. 2008, 60, 149–172. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A.; Al-Ghefari, R.A. On the one-parameter dual spherical motions. Comput. Aided Geom. Des. 2011, 28, 23–37. [Google Scholar] [CrossRef]
- Al-Ghefari, R.A.; Abdel-Baky, R.A. Kinematic geometry of a line trajectory in spatial motion. J. Mech. Sci. Technol. 2015, 29, 2596–3608. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A. On the curvature theory of a line trajectory in spatial kinematics. Commun. Korean Math. Soc. 2009, 34, 333–349. [Google Scholar]
- Aslan, M.C.; Sekerci, G.A. Dual curves associated with the Bonnet ruled surfaces. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050204. [Google Scholar] [CrossRef]
- Alluhaibi, N. Ruled surfaces with constant Disteli-axis. AIMS Math. 2020, 5, 7678–7694. [Google Scholar] [CrossRef]
- Alluhaibi, N.; Abdel-Baky, R.A. On the one-parameter Lorentzian spatial motions. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950197. [Google Scholar] [CrossRef]
- Alluhaibi, N.; Abdel-Baky, R.A. Kinematic geometry of hyperbolic dual spherical motions and Euler–Savary’s equation. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050079. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A.; Unluturk, Y. A new construction of timelike ruled surfaces with constant Disteli-axis. Honam Math. J. 2020, 42, 551–568. [Google Scholar]
- Abdel-All, N.H.; Abdel-Baky, R.A.; Hamdoon, F.M. Ruled surfaces with timelike rulings. Appl. Math. Comput. 2004, 147, 241–253. [Google Scholar] [CrossRef]
- Ali, A.T. Non-lightlike constant angle ruled surfaces in Minkowski 3-space. J. Geom. Phys. 2020, 157, 103833. [Google Scholar] [CrossRef]
- Ali, A.T. A constant angle ruled surfaces. Int. J. Geom. 2018, 7, 69–80. [Google Scholar]
- Ali, A.T. Non-lightlike ruled surfaces with constant curvatures in Minkowski 3-space. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850068. [Google Scholar] [CrossRef]
- Ali, A.T.; Hamdoon, F.M. Surfaces foliated by ellipses with constant Gaussian curvature in Euclidean 3-space. Korean J. Math. 2017, 25, 537–554. [Google Scholar]
- Ali, A.T.; Abdel Aziz, H.S.; Sorour, A.H. On some geometric properties of quadric surfaces in Euclidean space. Honam Math. J. 2016, 38, 593–611. [Google Scholar] [CrossRef][Green Version]
- Ali, A.T.; Abdel Aziz, H.S.; Sorour, A.H. On curvatures and points of the translation surfaces in Euclidean 3-space. J. Egypt. Math. Soc. 2015, 23, 167–172. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhu, Y.S.; Sun, Q.Y. Singularities and dualities of pedal curves in pseudo-hyperbolic and de Sitter space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 1–31. [Google Scholar] [CrossRef]
- Li, Y.L.; Liu, S.Y.; Wang, Z.G. Tangent developables and Darboux developables of framed curves. Topol. Appl. 2021, 301, 107526. [Google Scholar] [CrossRef]
- Li, Y.L.; Alkhaldi, A.H.; Ali, A.; Laurian-Ioan, P. On the Topology of Warped Product Pointwise Semi-Slant Submanifolds with Positive Curvature. Mathematics 2021, 9, 3156. [Google Scholar] [CrossRef]
- Li, Y.L.; Wang, Z.G. Lightlike tangent developables in de Sitter 3-space. J. Geom. Phys. 2021, 164, 1–11. [Google Scholar] [CrossRef]
- Li, Y.L.; Ganguly, D.; Dey, S.; Bhattacharyya, A. Conformal η-Ricci solitons within the framework of indefinite Kenmotsu manifolds. AIMS Math. 2022, 7, 5408–5430. [Google Scholar] [CrossRef]
- Li, Y.L.; Wang, Z.G.; Zhao, T.H. Geometric Algebra of Singular Ruled Surfaces. Adv. Appl. Clifford Algebr. 2021, 31, 1–19. [Google Scholar] [CrossRef]
- Li, Y.L.; Ali, A.; Mofarreh, F.; Abolarinwa, A.; Ali, R. Some eigenvalues estimate for the ϕ-Laplace operator on slant submanifolds of Sasakian space forms. J. Funct. Space 2021, 2021, 6195939. [Google Scholar]
- Li, Y.L.; Lone, M.A.; Wani, U.A. Biharmonic submanifolds of Kähler product manifolds. AIMS Math. 2021, 6, 9309–9321. [Google Scholar] [CrossRef]
- Li, Y.L.; Ali, A.; Mofarreh, F.; Alluhaibi, N. Homology groups in warped product submanifolds in hyperbolic spaces. J. Math. 2021, 2021, 8554738. [Google Scholar] [CrossRef]
- Li, Y.L.; Ali, A.; Ali, R. A general inequality for CR-warped products in generalized Sasakian space form and its applications. Adv. Math. Phys. 2021, 2021, 5777554. [Google Scholar] [CrossRef]
- Yang, Z.C.; Li, Y.L.; Erdoǧdub, M.; Zhu, Y.S. Evolving evolutoids and pedaloids from viewpoints of envelope and singularity theory in Minkowski plane. J. Geom. Phys. 2022, 176, 104513. [Google Scholar] [CrossRef]
- Todorčević, V. Harmonic Quasiconformal Mappings and Hyperbolic Type Metrics; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- López, R. Differential geometry of curves and surfaces in Lorentz-Minkowski space. Int. Electron. J. Geom. 2014, 7, 44–107. [Google Scholar] [CrossRef]
- O’Neil, B. Semi-Riemannian Geometry Geometry, with Applications to Relativity; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Walfare, J. Curves and Surfaces in Minkowski Space. Ph.D. Thesis, K.U. Leuven, Faculty of Science, Leuven, Belgium, 1995. [Google Scholar]
- Pekmen, U.; Pasali, S. Some characterizations of Lorentzian spherical spacelike curves. Math. Moravica 1999, 3, 31–37. [Google Scholar]
- Study, E. Geometric der Dynamen; Springer: Leipzig, Germany, 1903. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alluhaibi, N.; Abdel-Baky, R.A.
Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space
Alluhaibi N, Abdel-Baky RA.
Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space
Alluhaibi, Nadia, and Rashad A. Abdel-Baky.
2022. "Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space
Alluhaibi, N., & Abdel-Baky, R. A.
(2022). Kinematic Geometry of Timelike Ruled Surfaces in Minkowski 3-Space





