A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography
Abstract
:1. Introduction
- Provision of the necessary protection for the digital image, completely preventing unauthorized parties from understanding the image and knowing its contents.
- Distortion of the encrypted digital image so that it becomes unclear or cannot be understood, in such a way that the original image is fully restored upon decoding. Here, the extent of distortion can be measured by the calculated quality parameter, the mean square error (MSE) value, which must be very large when encrypting and zero when decrypting, and/or the peak signal-to-noise ratio (PSNR), which must be very low when encrypting and infinite when decrypting the image.
- Very high encryption efficiency in order to reduce the time for encryption and decryption, thus increasing the permeability (throughput) by increasing the number of processed bits per second.
- Flexibility and scalability by enabling the user to modify the length of the private key, modify the data-block size, or modify the number of rounds required to apply encryption/decryption.
- Ease of use and application through the use of simplified arithmetic and logical operations.
- Versatility of use, so that it is easy to use the method to protect different types of data including text messages, text files, and digital images.
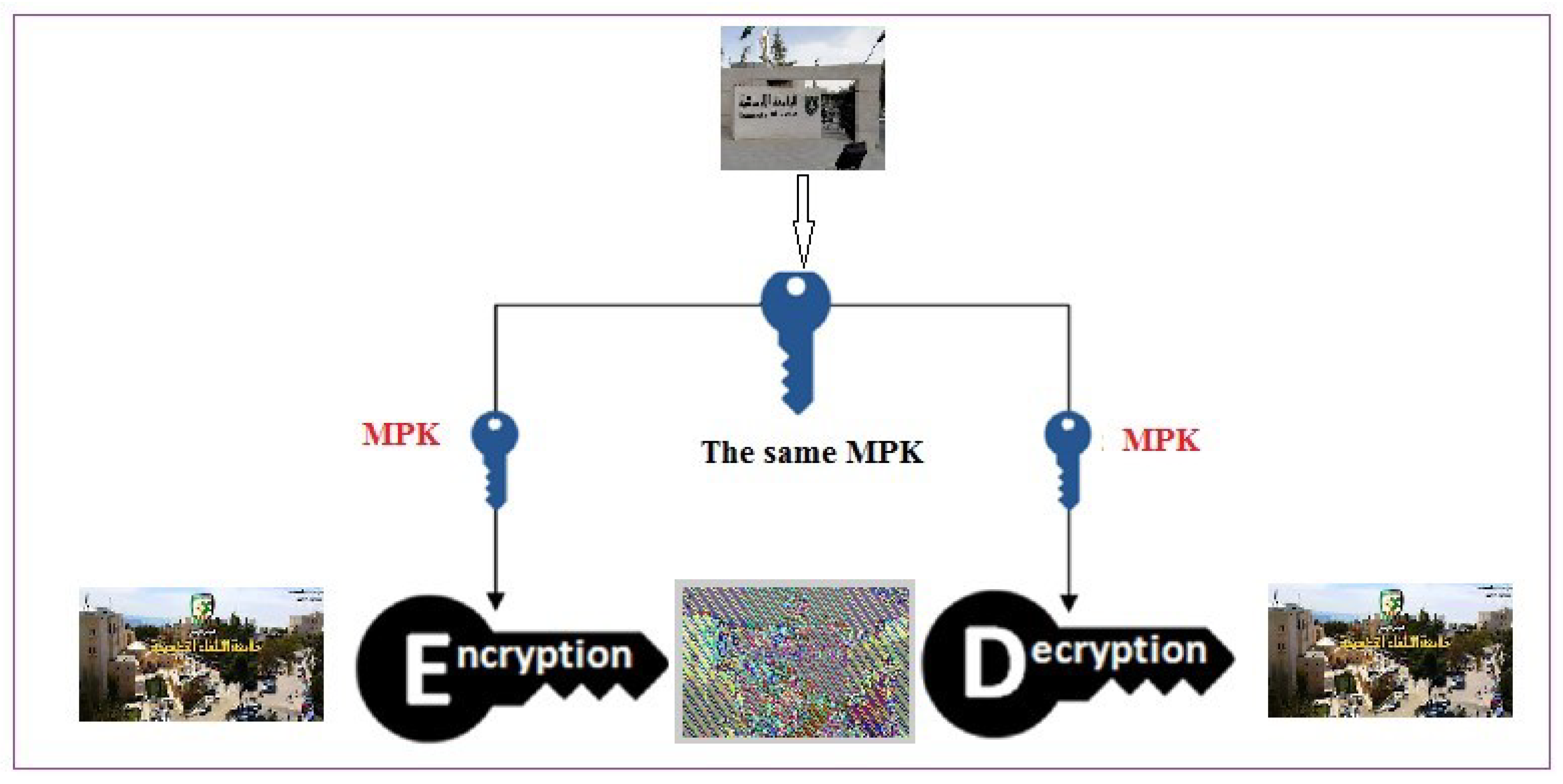
- Using the colored digital image as a key, through which private keys can be generated easily. This process is very safe, especially since the image is kept secret through an agreement between the sender and receiver regarding the image to be used, without resorting to the image transmission process.
- The data blocks used in the image splitting process are variable, as is the length of the secret key.
- A variable number of encryption cycles.
- The possibility of using the procedures provided to encrypt text messages and images with high efficiency.
2. Related Work
- The use of a single private key with a fixed length that does not change and in some cases can be hacked. This is a problem that must be eliminated.
- Dividing the data to be encrypted into blocks of fixed length that cannot be changed. This is one of the disadvantages of these methods.
- Use of a fixed and unchangeable number of rounds.
- All other sub-private keys used in the encryption are generated from the private key using specific arithmetic operations. This, in turn, makes the degree of security and protection completely dependent on the private key.
- These methods provide excellent values of MSE and PSNR in both phases, i.e., encryption and decryption.
- These methods are designed to encrypt and decrypt messages and text files using large quantities of data, as a color image will reduce the efficiency of data cryptography by requiring longer encryption and decryption times.
- These methods require many rounds, and this will negatively affect the efficiency. Each round contains a set of operations that will require extra time for execution.
- Generating and manipulating an S-box will add extra execution time, thus affecting the speed of the cryptography process. For datasets with large sizes (such as a color image), the number of generated blocks will be so large that extra time will be required for data division before encryption and assembly after decryption.
3. Proposed Method
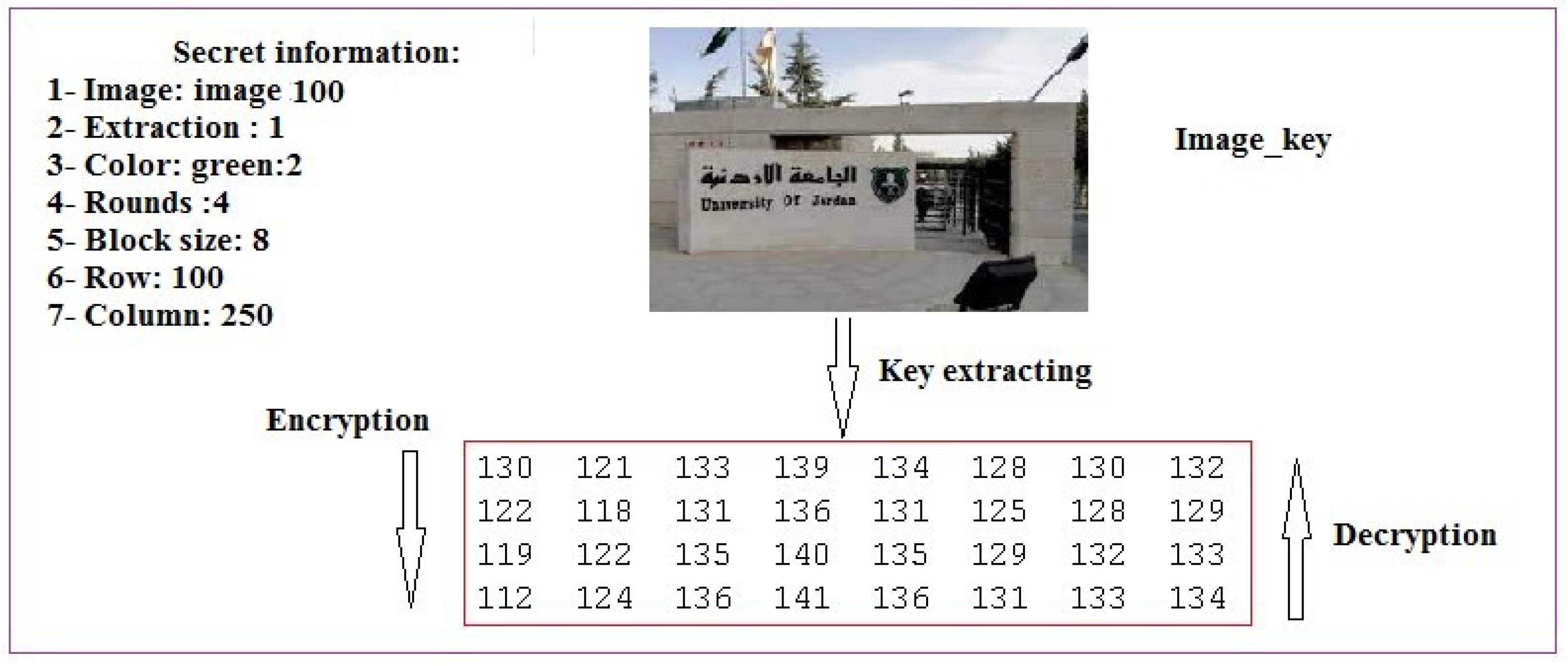
- Image to be used as an .
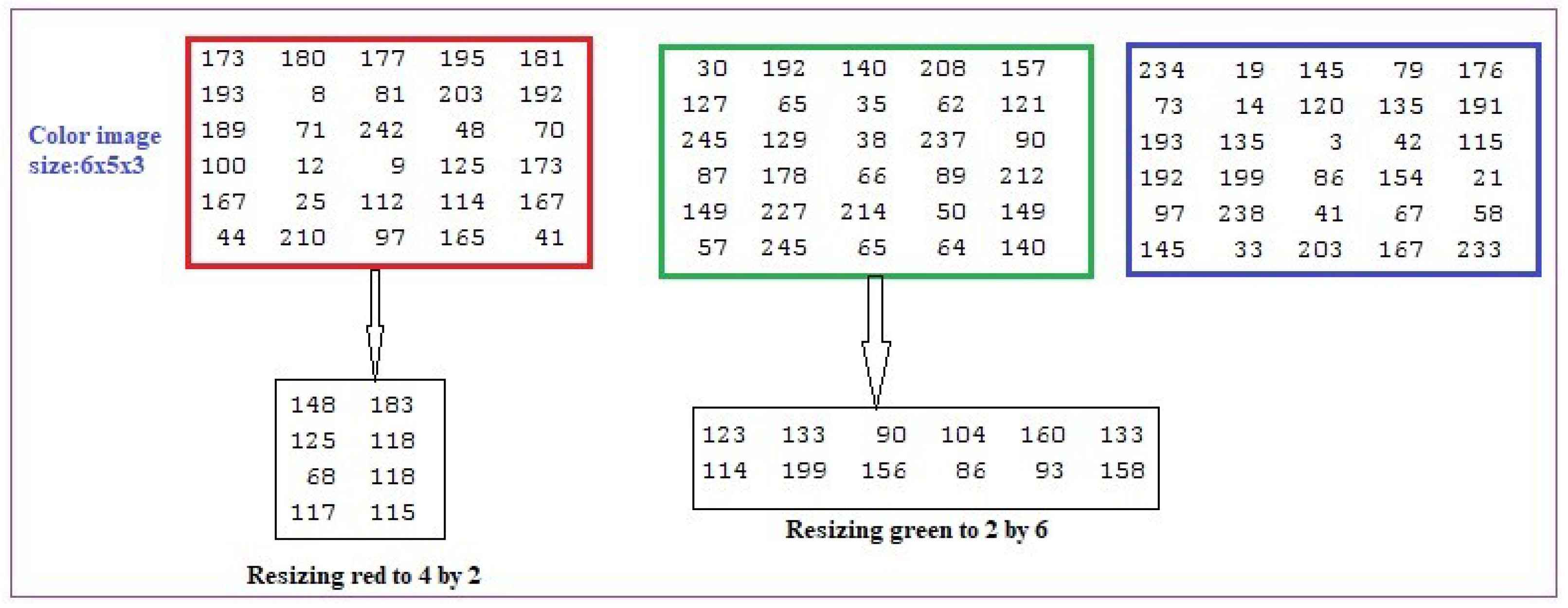
- Type of MPK generation: 1: extracting; 2: resizing.
- Color to be used: 1: red; 2: green; 3: blue.
- Number of rounds.
- Block size in bytes.
- Row number if type equals 1.
- Column number if type equals 1.
- The key image is replaced, preserving the other setting parameters unchanged.
- The value of any one or more of the set parameters is changed.
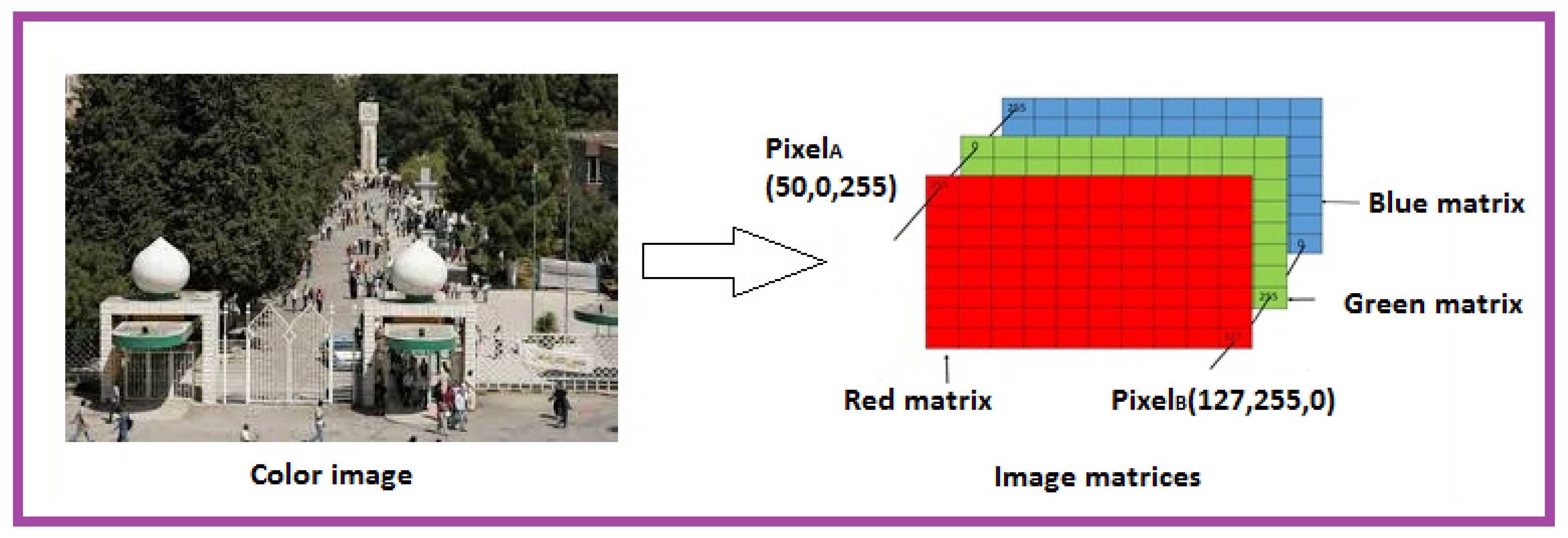
- Step 1: Initialization:In this step, we select the and assign values for generation type, color to be used, number of rounds, block size (BLS), rows, and columns. This information is needed to create the MPK.The following algorithm can be used to generate the MPK:Input: Image-key;Output: MPK;Operations:
- −
- Select the color channel (1: red; 2: green 3: blue);
- −
- Select the operation type (ot = 1: extraction; 2: image resizing);
- −
- Select the block size (bs);
- −
- Select the number of rounds (nr);
- −
- If ot = 1thendefine the row and column from which to start extracting MPK with size =ElseResize the image to the size ;
- −
- Save MPK.
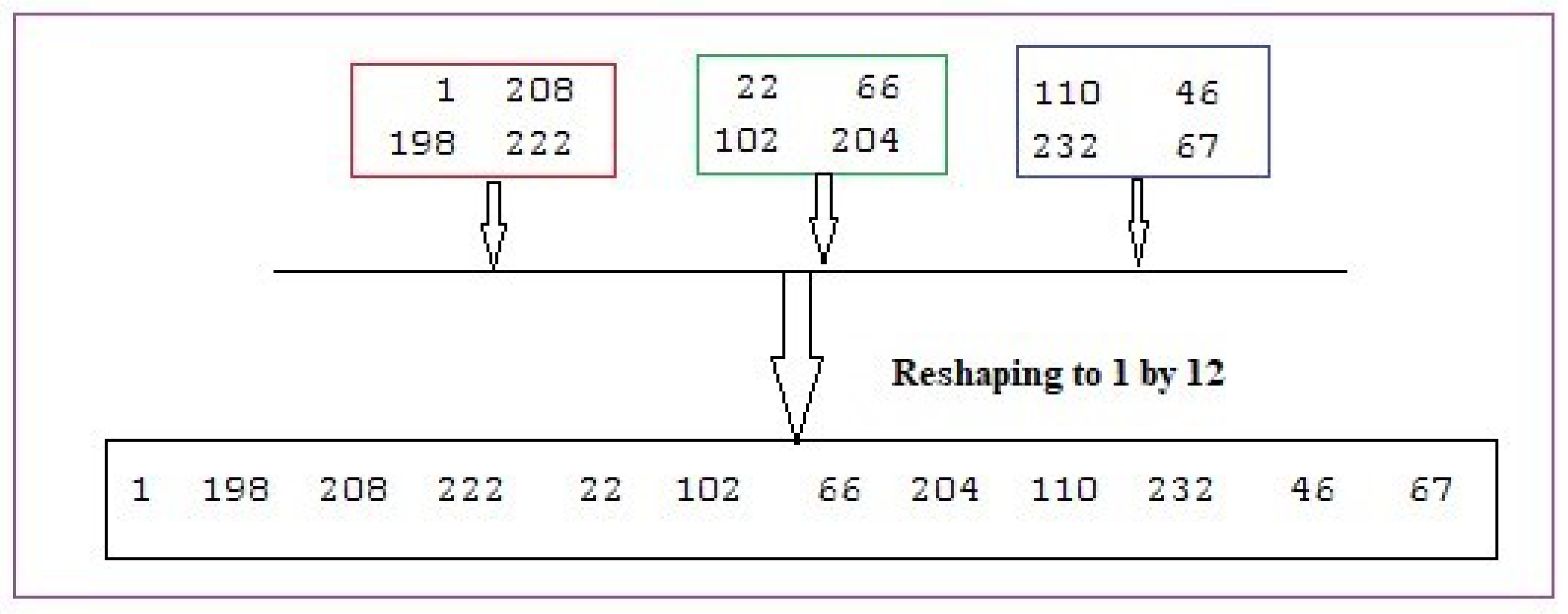
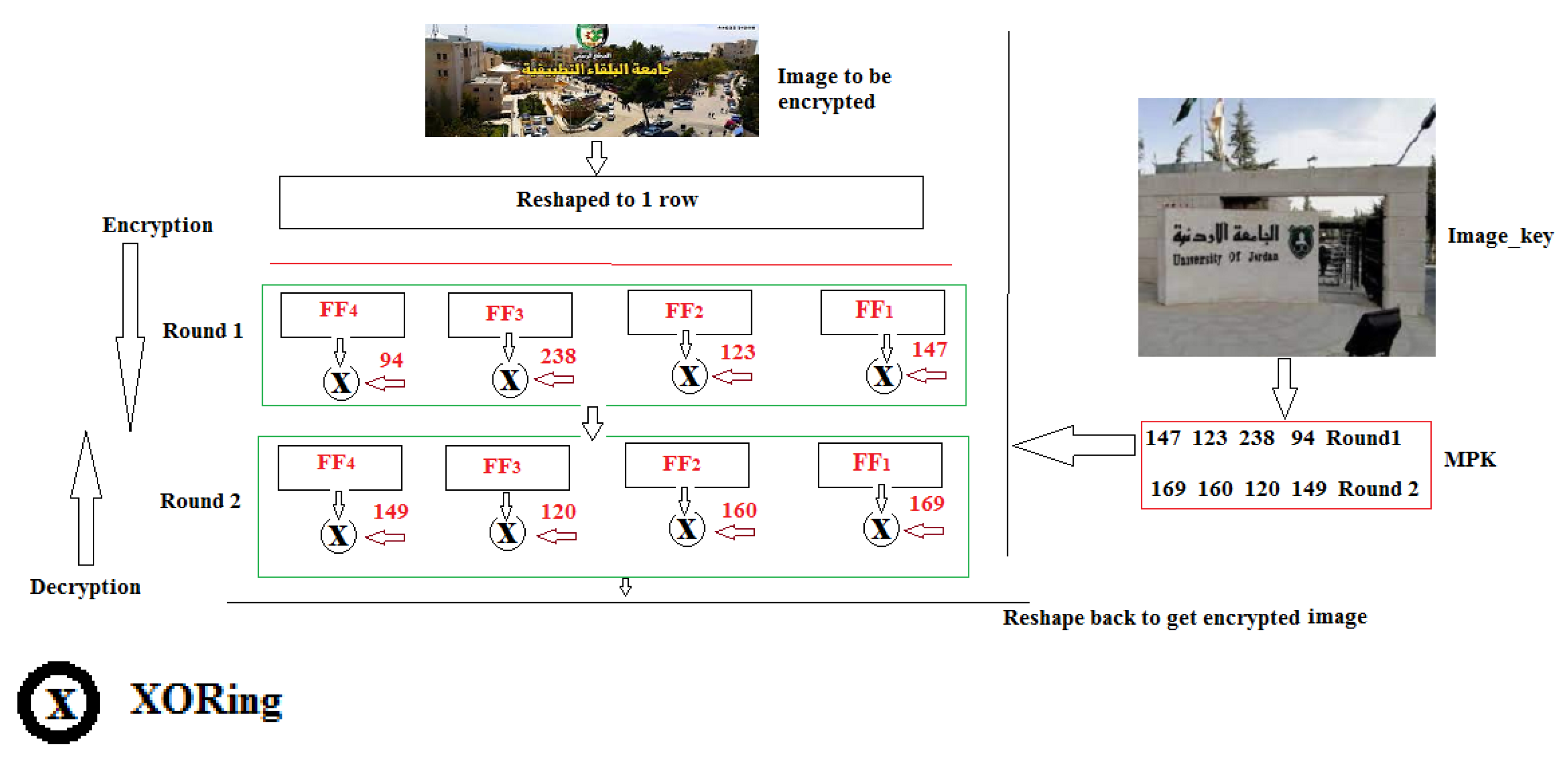
- Step 2: Apply the operations shown in Figure 9:
4. Implementation and Experimental Results
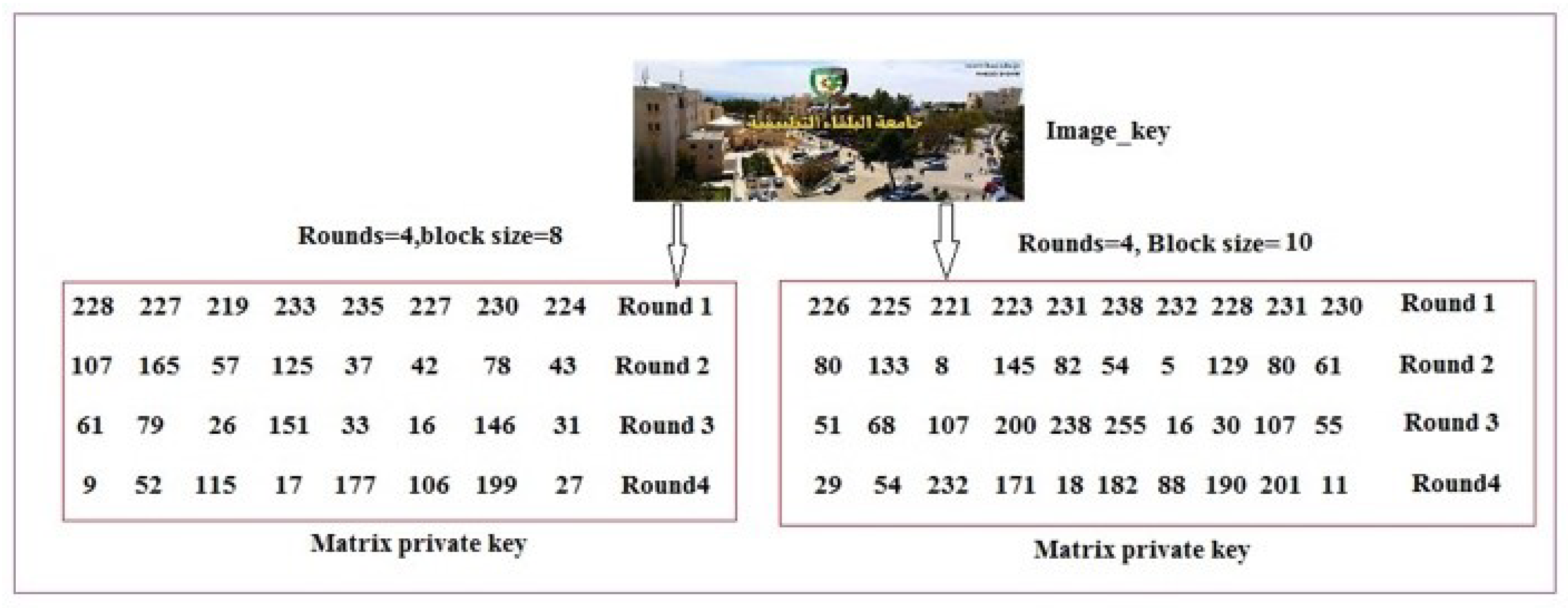
- Case 1: Using a small image as an (image 2). Number of rounds = 4, BLS = 16 byte = 128 bits (number of keys = 64, MPK dimension: 4 × 16). Table 4 shows the obtained results after executing the proposed method for case 1.
- Case 2: Using a medium image as an (image 3). Number of rounds = 4, BLS = 16 byte = 128 bits (number of keys = 64, MPK dimension: 4 × 16). Table 5 shows the obtained results after executing the proposed method for case 2.
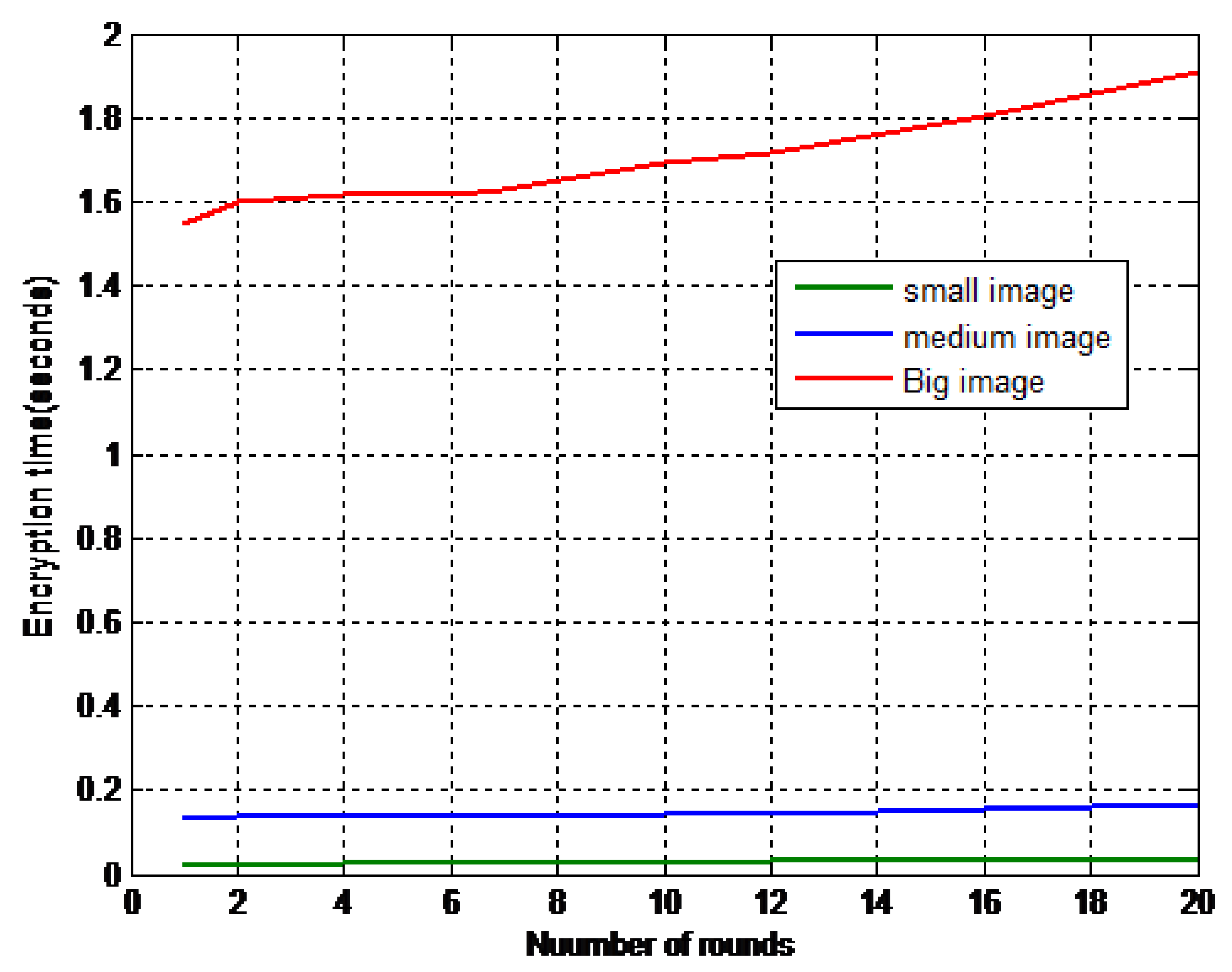
- Case 3: Using a large image as an (image 12). Number of rounds = 4, BLS = 16 byte = 128 bits (number of keys = 64, MPK dimension: 4 × 16). Table 6 shows the obtained results after executing the proposed method for case 3.The proposed method was executed with various block sizes, fixing the number of rounds at 4. Table 7 shows the obtained experimental results.
5. Results Analysis
- The proposed method increases the level of security by using a 2D matrix as an MPK. This key is subject to change, due to changes in the image-key, the number of rounds, the block size, and other settings parameters.
- The proposed method can easily be used to encrypt and decrypt other types of data such as short messages and text files, and these can be treated using the same procedures as for color images.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Asad, A.S.N.; Shayeb, I.; Jaber, Q.; Ayyoub, B.; Alqadi, Z.; Sharadqh, A. Creating a Stable and Fixed Features Array for Digital Color Image. IJCSMC 2019, 8, 50–62. [Google Scholar]
- Al-Dwairi, M.O.; Hendi, A.Y.; Soliman, M.S.; Alqadi, Z.A. A new method for voice signal features creation. Int. J. Electr. Comput. Eng. (IJECE) 2019, 9, 4092–4098. [Google Scholar]
- Mandal, A.K.; Parakash, C.; Tiwari, A. Performance evaluation of cryptographic algorithms: DES and AES. In Proceedings of the 2012 IEEE Students’ Conference on Electrical, Electronics and Computer Science Innovation for Humanity, Bhopal, India, 1–2 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–5. [Google Scholar]
- Verma, O.P.; Agarwal, R.; Dafouti, D.; Tyagi, S. Performance analysis of data encryption algorithms. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; IEEE: Piscataway, NJ, USA, 2011; Volume 5, pp. 399–403. [Google Scholar]
- Asok, S.B.; Karthigaikumar, P.; Sandhya, R.; Jarold, K.N.; Mangai, N.S. A secure cryptographic scheme for audio signals. In Proceedings of the 2013 International Conference on Communication and Signal Processing, Melmaruvathur, India, 3–5 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 748–752. [Google Scholar]
- Sharma, S.; Kumar, L.; Sharma, H. Encryption of an audio file on lower frequency band for secure communication. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 79–84. [Google Scholar]
- Gandhi, R.A.; Gosai, D.A.M. Steganography—A Sin qua non for Diguised Communication. Int. J. Innov. Res. Adv. Eng. 2014, 1, 184–191. [Google Scholar]
- James, S.P.; George, S.N.; Deepthi, P. Secure selective encryption of compressed audio. In Proceedings of the 2013 Annual International Conference on Emerging Research Areas and 2013 International Conference on Microelectronics, Communications and Renewable Energy, Kanjirapally, India, 4–6 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Babu, S.G.; Ilango, P. Higher dimensional chaos for Audio encryption. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence in Cyber Security (CICS), Singapore, 16–19 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 52–58. [Google Scholar]
- Aathithan, N.R.; Venkatesulu, M. A complete binary tree structure block cipher for real-time multimedia. In Proceedings of the 2013 Science and Information Conference, London, UK, 7–9 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 346–352. [Google Scholar]
- Pavithra, S.; Ramadevi, E. Throughput analysis of symmetric algorithms. Int. J. Adv. Netw. Appl. 2012, 4, 1574. [Google Scholar]
- Abd Elminaam, D.S.; Abdual-Kader, H.M.; Hadhoud, M.M. Evaluating The Performance of Symmetric Encryption Algorithms. Int. J. Netw. Secur. 2010, 10, 216–222. [Google Scholar]
- Singhal, N.; Raina, J. Comparative analysis of AES and RC4 algorithms for better utilization. Int. J. Comput. Trends Technol. 2011, 2, 177–181. [Google Scholar]
- Sharma, S.; Pateriya, P.K. A study on different approaches of selective encryption technique. Int. J. Comput. Sci. Commun. Netw. 2012, 2, 658. [Google Scholar]
- Al-qdah, M.; Hui, L.Y. Simple Encryption/Decryption Application. Int. J. Comput. Sci. Secur. 2007, 1, 33. [Google Scholar]
- Gadanayak, B.; Pradhan, C.; Dey, U.C. Comparative study of different encryption techniques on MP3 compression. Int. J. Comput. Appl. 2011, 26, 28–31. [Google Scholar]
- Sharma, S.; Sharma, H.; Kumar, L. Power spectrum encryption and decryption of an audio file. Int. J. Res. Comput. Sci. 2013, 1, 1–4. [Google Scholar]
- James, S.P.; George, S.N.; Deepthi, P. An audio encryption technique based on LFSR based alternating step generator. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Minaam, D.S.A.; Abdual-Kader, H.M.; Hadhoud, M.M. Evaluating the Effects of Symmetric Cryptography Algorithms on Power Consumption for Different Data Types. Int. J. Netw. Secur. 2010, 11, 78–87. [Google Scholar]
- Kumar, R.; Saini, B.; Kumar, S.; Kurukshetra, N. A Novel Approach to Blowfish Encryption Algorithm. Int. J. Adv. Found. Res. Sci. Eng. 2014, 1, 62–67. [Google Scholar]
- Rizvi, S.; Hussain, S.Z.; Wadhwa, N. Performance analysis of AES and TwoFish encryption schemes. In Proceedings of the 2011 International Conference on Communication Systems and Network Technologies, Jammu, India, 3–5 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 76–79. [Google Scholar]
- Singh, P.; Singh, K. Image encryption and decryption using blowfish algorithm in MATLAB. Int. J. Sci. Eng. Res. 2013, 4, 150–154. [Google Scholar]
- Mhaidat, K.; Altahat, M.; Al-Khaleel, O. High-Throughput Hardware Implementation of Threefish Block Cipher on FPGA. In Proceedings of the 4th International Conference on Information & Communication Systems (iCICS), Iribd, Jordan, 23–25 April 2013. [Google Scholar]
- Raghunandhan, K.; Radhakrishna, D.; Sudeepa, K.; Ganesh, A. Efficient audio encryption algorithm for online applications using transposition and multiplicative non-binary system. Int. J. Eng. Res. Technol. (IJERT) 2013, 2, 472–477. [Google Scholar]


| Method Parameter | DES | 3DES | AES | Blowfish |
|---|---|---|---|---|
| PK length (bit) | 56 (fixed) | 112, 168 (fixed) | 128, 192, 256 (fixed) | 32–448 (fixed) |
| Block size (bit) | 64 (fixed) | 64 (fixed) | 128 (fixed) | 64 (fixed) |
| Ability to deal with images | Difficult | Difficult | Difficult | Difficult |
| Encryption quality | Excellent: High MSE and low PSNR | Excellent: High MSE and low PSNR | Excellent: High MSE and low PSNR | Excellent: High MSE and low PSNR |
| Decryption quality | Excellent: Zero MSE and infinite PSNR | Excellent: Zero MSE and infinite PSNR | Excellent: Zero MSE and infinite PSNR | Excellent: Zero MSE and infinite PSNR |
| Efficiency | Slow | Slow | Slow | Moderate |
| Attack | Brute force attack | Brute force attack, Known plaintext, Chosen plaintext | Side-channel attack | Dictionary attack |
| Structure | Feistel | Feistel | Substitution– Permutation | Feistel |
| Block cipher | Binary | Binary | Binary | Binary |
| Rounds | 16 (fixed) | 48 (fixed) | 10,12,14 (fixed) | 16 (fixed) |
| Flexibility to modification | No | Yes | Yes | Yes |
| Simplicity | No | No | No | No |
| Security level | Adequate | Adequate | Excellent | Excellent |
| Throughput | Low | low | Low | Moderate |
| Encryption | Decryption | ||
|---|---|---|---|
| Feistel Function | Operation | Feistel Function | Operation |
| FF1 | Rotate right 1 digit | FF’1 | Rotate right 7 digits |
| FF2 | Rotate right 2 digits | FF’2 | Rotate right 6 digits |
| FF3 | Rotate right 3 digits | FF’3 | Rotate right 5 digits |
| FF4 | Rotate right 4 digits | FF’4 | Rotate right 4 digits |
| FF5 | Rotate right 5 digits | FF’5 | Rotate right 3 digits |
| FF6 | Rotate right 6 digits | FF’6 | Rotate right 2 digits |
| FF7 | Rotate right 7 digits | FF’7 | Rotate right 1 digit |
| Image Number | Dimensions | Size (Bytes) | Size (Kbytes) |
|---|---|---|---|
| 1 | 150,849 | 147.3 | |
| 2 | 77,976 | 76.1 | |
| 3 | 518,400 | 506.2 | |
| 4 | 5,140,800 | 5020.3 | |
| 5 | 4,326,210 | 4224.8 | |
| 6 | 122,265 | 119.4 | |
| 7 | 518,400 | 506.2 | |
| 8 | 150,975 | 147.4 | |
| 9 | 150,975 | 147.4 | |
| 10 | 151,353 | 147.8 | |
| 11 | 1,890,000 | 1845.7 | |
| 12 | 6,119,256 | 5975.8 | |
| Average | 1572 | ||
| Image Number | MSE | PSNR | Encryption Time (s) |
|---|---|---|---|
| 1 | 8.5656 | 0.039 | |
| 1 | 8.5656 | 0.039 | |
| 2 | 6.0858 | 0.021 | |
| 3 | 11.2791 | 0.0134 | |
| 4 | 13.6700 | 1.348 | |
| 5 | 13.8037 | 1.128 | |
| 6 | 16.6596 | 0.032 | |
| 7 | 9.9304 | 0.138 | |
| 8 | 10.9808 | 0.040 | |
| 9 | 14.0749 | 0.047 | |
| 10 | 9.5264 | 0.039 | |
| 11 | 10.4966 | 0.492 | |
| 12 | 21.6032 | 1.603 | |
| Average | 0.4218 | ||
| Average Throughput (Kbyte/s) | 0 3726.9 | ||
| Image Number | MSE | PSNR | Encryption Time (s) |
|---|---|---|---|
| 1 | 17.9967 | 0.041 | |
| 2 | 16.3140 | 0.021 | |
| 3 | 19.5276 | 0.0136 | |
| 4 | 21.1608 | 1.342 | |
| 5 | 21.2622 | 1.119 | |
| 6 | 22.7288 | 0.032 | |
| 7 | 18.5285 | 0.135 | |
| 8 | 19.2901 | 0.039 | |
| 9 | 21.2345 | 0.039 | |
| 10 | 18.5174 | 0.040 | |
| 11 | 18.9656 | 0.490 | |
| 12 | 24.0515 | 1.601 | |
| Average | 0.4196 | ||
| Average Throughput (Kbyte/s) | 3746.4 | ||
| Image Number | MSE | PSNR | Encryption Time (s) |
|---|---|---|---|
| 1 | 13.8142 | 0.041 | |
| 2 | 13.3812 | 0.020 | |
| 3 | 14.0667 | 0.138 | |
| 4 | 14.5634 | 1.416 | |
| 5 | 14.6224 | 1.180 | |
| 6 | 15.0290 | 0.032 | |
| 7 | 13.4228 | 0.136 | |
| 8 | 14.0458 | 0.040 | |
| 9 | 14.7603 | 0.039 | |
| 10 | 13.8069 | 0.040 | |
| 11 | 14.1144 | 0.494 | |
| 12 | 15.1369 | 1.724 | |
| Average | 0.4417 | ||
| Average Throughput (Kbyte/s) | 3559 | ||
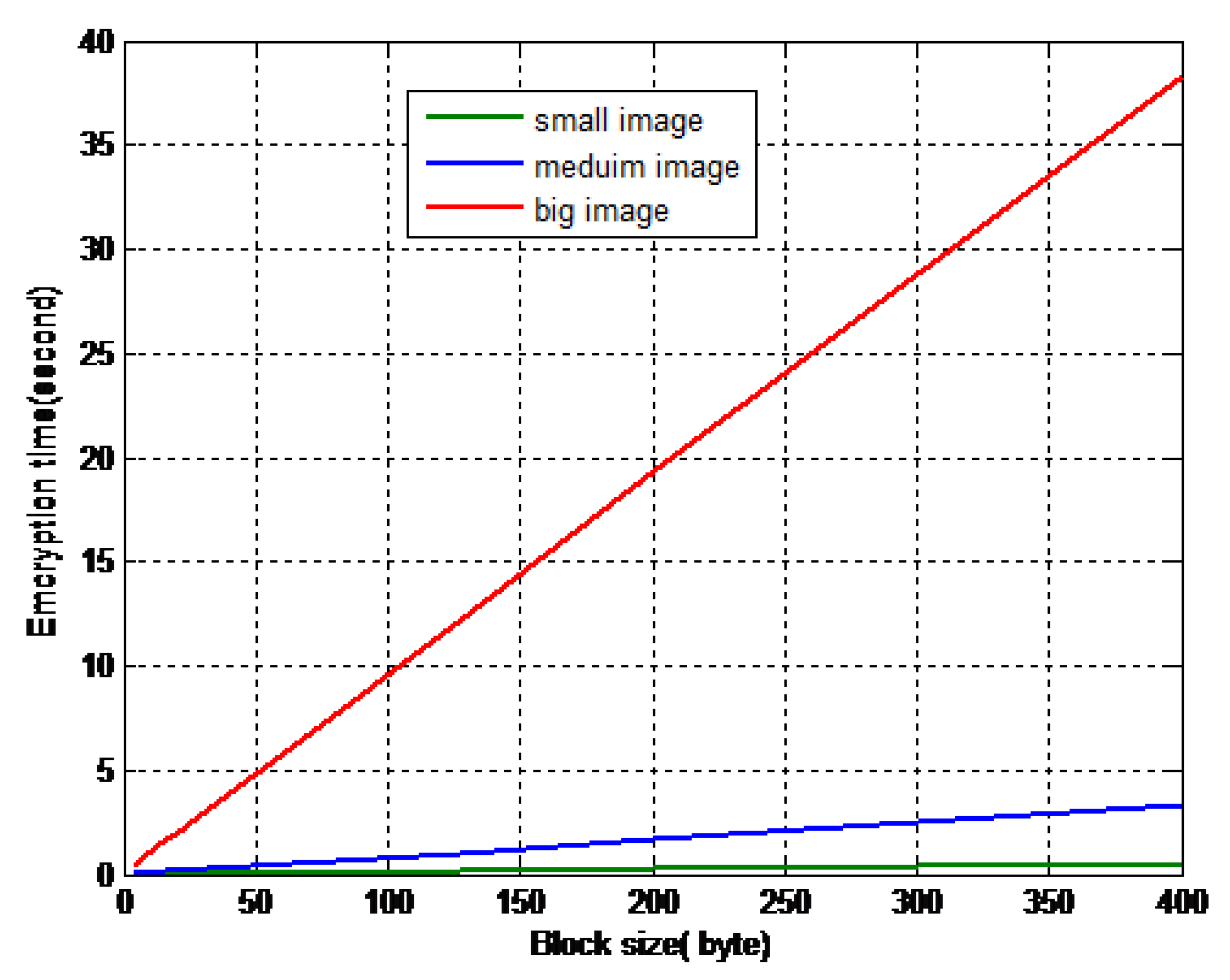
| BLS (Byte) | MPK Dimensions | Number of Keys | Image 2 Encryption Time (s) | Image 3 Encryption Time (s) | Image 12 Encryption Time (s) |
|---|---|---|---|---|---|
| 4 | 4 × 4 | 16 | 0.007000 | 0.040000 | 0.462000 |
| 8 | 4 × 8 | 32 | 0.010000 | 0.073000 | 0.876000 |
| 16 | 4 × 16 | 64 | 0.021000 | 0.150000 | 1.661000 |
| 20 | 4 × 20 | 80 | 0.025000 | 0.170000 | 1.955000 |
| 32 | 4 × 32 | 128 | 0.039000 | 0.265000 | 3.093000 |
| 64 | 4 × 64 | 256 | 0.079000 | 0.517000 | 6.193000 |
| 128 | 4 × 128 | 512 | 0.154000 | 1.047000 | 12.258000 |
| 200 | 4 × 200 | 800 | 0.241000 | 1.741000 | 19.310000 |
| 400 | 4 × 400 | 1600 | 0.481000 | 3.363000 | 38.272000 |
| Number of Rounds | MPK Dimensions | Number of Keys | Image 2 Encryption Time (s) | Image 3 Encryption Time (s) | Image 12 Encryption Time (s) |
|---|---|---|---|---|---|
| 1 | 1 × 16 | 16 | 0.021000 | 0.133000 | 1.544 |
| 2 | 2 × 16 | 32 | 0.023000 | 0.135000 | 1.601 |
| 4 | 4 × 16 | 64 | 0.026000 | 0.136000 | 1.617 |
| 5 | 5 × 16 | 80 | 0.026900 | 0.138200 | 1.6175 |
| 6 | 6 × 16 | 96 | 0.027000 | 0.139000 | 1.619 |
| 7 | 7 × 16 | 142 | 0.027910 | 0.139560 | 1.627 |
| 10 | 10 × 16 | 160 | 0.028900 | 0.142000 | 1.691 |
| 12 | 12 × 16 | 192 | 0.029900 | 0.145000 | 1.716 |
| 16 | 16 × 16 | 256 | 0.029930 | 0.153000 | 1.806 |
| 20 | 20 × 16 | 320 | 0.030900 | 0.164000 | 1.91 |
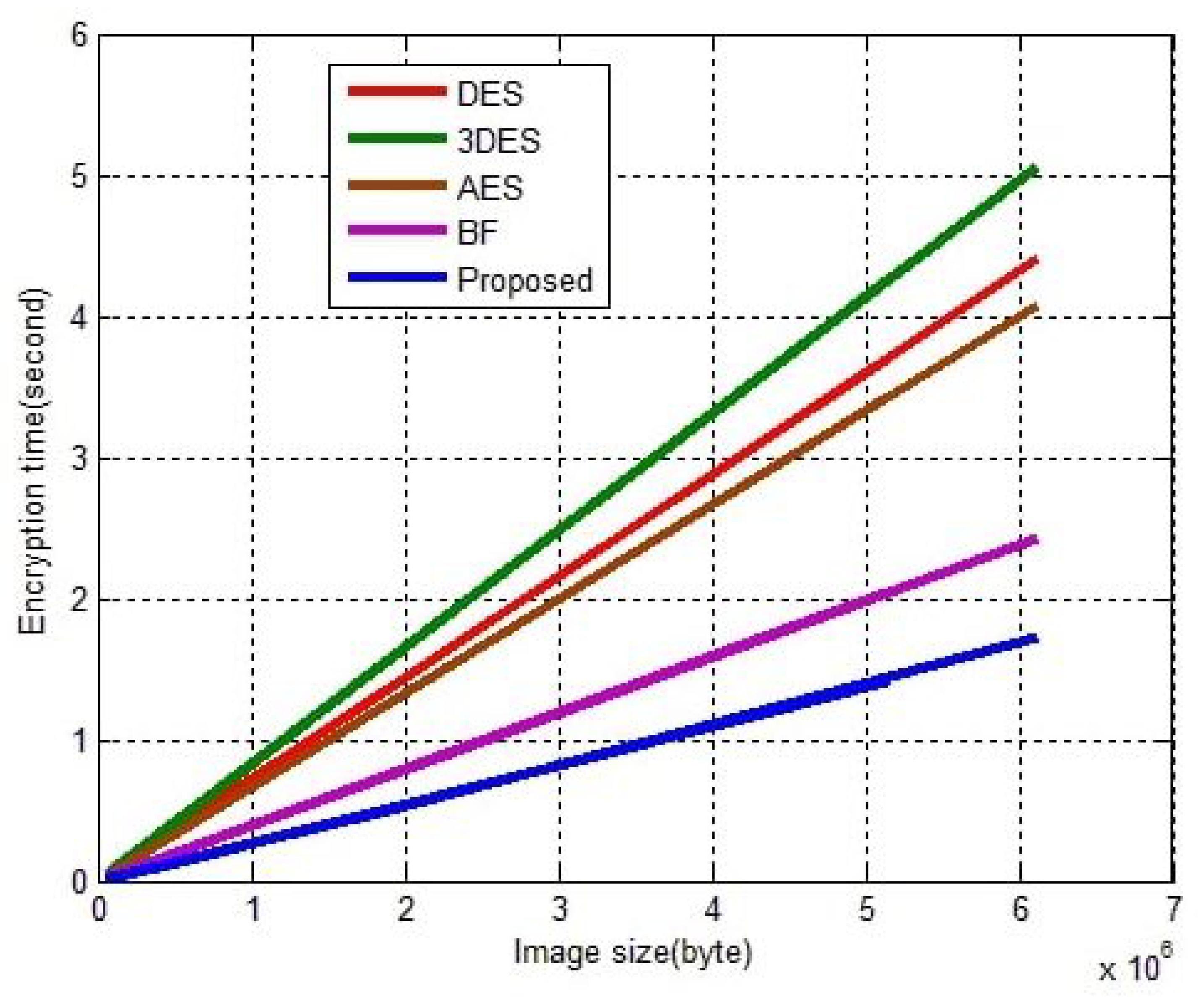
| Image Size (Bytes) | Encryption Time (s) | ||||
|---|---|---|---|---|---|
| DES | 3DES | AES | BF | MPK (BLS = 16 Byte = 128 bits, Rounds = 10) | |
| 150,849 | 0.1093 | 0.1249 | 0.1008 | 0.0603 | 0.042000 |
| 77,976 | 0.0572 | 0.0647 | 0.0522 | 0.0313 | 0.022000 |
| 518,400 | 0.3761 | 0.4292 | 0.3456 | 0.2067 | 0.144000 |
| 5,140,800 | 3.6998 | 4.2546 | 3.4248 | 2.0452 | 1.402000 |
| 4,326,210 | 3.1138 | 3.5808 | 2.8822 | 1.7213 | 1.176000 |
| 122,265 | 0.0884 | 0.1015 | 0.0818 | 0.0490 | 0.034000 |
| 518,400 | 0.3739 | 0.4294 | 0.3457 | 0.2064 | 0.143000 |
| 150,975 | 0.1085 | 0.1253 | 0.1012 | 0.0607 | 0.054000 |
| 150,975 | 0.1089 | 0.1252 | 0.1012 | 0.0607 | 0.054000 |
| 151,353 | 0.1092 | 0.1257 | 0.1013 | 0.0604 | 0.045000 |
| 1890,000 | 1.3607 | 1.5646 | 1.2595 | 0.7521 | 0.521000 |
| 6,119,256 | 4.4038 | 5.0648 | 4.0767 | 2.4345 | 1.678000 |
| Average | 1.1591 | 1.3326 | 1.0728 | 0.6407 | 0.4429 |
| Throughput (Kbyte) | 1356.3 | 1179.7 | 1465.4 | 2453.7 | 3549.6 |
| Method | Average Throughput (Kbyte per Second) |
|---|---|
| DES | 1356.3 |
| 3DES | 1179.7 |
| AES | 1465.4 |
| BF | 2453.7 |
| Proposed (worst case) | 3559.6 |
| Method | DES | 3DES | AES | BF | Proposed |
|---|---|---|---|---|---|
| DES | 1.0000 | 1.1497 | 0.9255 | 0.5528 | 0.3810 |
| 3DES | 0.8698 | 1.0000 | 0.8050 | 0.4808 | 0.3314 |
| AES | 1.0804 | 1.2422 | 1.0000 | 0.5972 | 0.4117 |
| BF | 1.8091 | 2.0799 | 1.6744 | 1.0000 | 0.6893 |
| Proposed | 2.6245 | 3.0174 | 2.4291 | 1.4507 | 1.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Faraj, M.; Al-Hyari, A.; Alqadi, Z. A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography. Symmetry 2022, 14, 664. https://doi.org/10.3390/sym14040664
Abu-Faraj M, Al-Hyari A, Alqadi Z. A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography. Symmetry. 2022; 14(4):664. https://doi.org/10.3390/sym14040664
Chicago/Turabian StyleAbu-Faraj, Mua’ad, Abeer Al-Hyari, and Ziad Alqadi. 2022. "A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography" Symmetry 14, no. 4: 664. https://doi.org/10.3390/sym14040664
APA StyleAbu-Faraj, M., Al-Hyari, A., & Alqadi, Z. (2022). A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography. Symmetry, 14(4), 664. https://doi.org/10.3390/sym14040664








