A Novel Co-Evolution Model Based on Evolutionary Game about Social Network

Abstract

With the development of information networks, information diffusion becomes increasingly complicated in social networks, and the influence from different neighbors presents asymmetry. Evolutionary Game Theory (EGT), which orients the human interaction from the perspective of economics, has been widely concerned. We establish a collaborative evolution model of public opinion information and views based on dynamic evolutionary games of social networks and the underlying asymmetry relationship. In addition, the coupling mechanism of behavior and viewpoints is adopted to study the coupling evolution of the group behavior and viewpoint. Some interesting and valuable results about evolution of the behavior and viewpoints are shown.

1. Introduction

Under the interaction of numerous individuals, the current social network is full of various information at every moment [1,2]. In this case, it has become a significant research topic to comprehend the behavior interaction [3], viewpoint evolution and information diffusion on social networks.

The existing information diffusion analysis [4] is based on network structure modeling or empirical data mining [5]. The research on network structure modeling is mainly about establishing various information transmission models, e.g., the independent cascade (IC) model, the linear threshold (LT) model and the epidemic disease model, etc. Network structure modeling involves many common methods to measure the influence of nodes in the network [6], and it is usually based on global or local information, e.g., PageRank, Katz centrality, etc. Yangqian Su et al. concluded in 2019 that the attack performance of PageRank strategy is better than other comparison strategies, on the premise of considering both calculation efficiency and attack efficiency [7]. On the basis of the linear threshold rank (LTR), Fabián Riquelme et al. proposed a generalized LTR measure in 2019 to study the sensitivity of neighborhood distance in the initial activation set with the initial LTR [8]. At the same time, many classical dynamical models, including the macro-dynamic model and the micro-dynamic model, were proposed. The micro-dynamic model directly describes the evolution of individual views from the perspective of individuals. The most of common micro-models include the DeGroot model [9], the F-J model, etc. Based on the the F-J model, Friedkin et al. studied the evolution of American people’s views on the Iraq war in 2016 [10]. Compared with the micro-dynamic model, the macro-dynamic model mainly adopts the statistical physics method and applies the related statistical theory to analyze the distribution of the views in a group. The macro-dynamic models, including the Sznajd model, bounded trust model, epidemic disease model, social impact model, vote model and majority principle model, own some obvious advantages in describing the viewpoint dynamics of large-scale social networks. Based on the basic SIR model in complex networks, Qu Qianqian et al. proposed an epidemic disease model with two infectious rates and migration probability in 2019 [11]. It is concluded that target immunization is more effective than random immunization, when the average immunization rate is the same. In 2016, Changfeng Wang et al. introduced the group view competition mechanism on the basis of SIR model, and established the group view competition evolution model to improve SIR with the theory of view dynamics [12]. Schneider et al. employed the Sznajd model in 2005 to describe the relationship between the number of votes obtained by political parties and the number of party members in German elections [13]. In 2006, Araipe et al. studied the polarization distribution of the election results of two main candidates in the Brazilian mayoral election, based on the majority principle model. The most of the classical models of bounded trust are Deffuant model [14] and HK model [15].

The above models study the evolution of individual behavior and perspective from different factors including individual emotion, trust threshold, centrality, etc. The Game Theory (GT) describes the evolutionary process of the cooperation or struggle between individuals to pursue interests of a competitive nature or tp solve potential conflicts across these individuals. Game Theory and Economic Behavior, written by John von Neumann and Oskar Morgenstern, was published in 1944. It marked the emergence of GT. With the continuous enrichment of content, GT has developed a mature set of concepts, rules and theoretical methods and has owned wide applications in economics, biology, international relations, computer science, political science and military strategy. In 1984, R. Axelrod first applied GT to sociology and economics in The Evolution of Cooperation [16]. Mathematical tools are applied to quantify the interaction across the individuals and provide a unified theoretical framework for the study of the evolution of the behaviors in social networks [17]. With the emergence of more and more GT research, some typical game models have gradually formed, including the Prisoner’s Dilemma Game (PDG) model, snowdrift model, intelligent pig model, etc.

With the application in different related fields, GT has gradually been divided into two main research directions: the classical Game Theory and the Evolutionary Game Theory (EGT) [18]. In the classical GT, all players are completely rational decision makers in the premise hypothesis [19], and in the EGT, all game players are limited rational decision makers in the premise hypothesis. The classic GT takes the classical game payoff model as the basis of individual interaction, but it takes the influencing factors in economics as the main driving force of individual behavior strategies. In 1973, Smith and Price introduced natural selection and variation into the classical GT and put forward the EGT [20]. Later, Nowak et al. applied Moran stochastic process to describe the evolutionary stability strategy in a finite population in 2005 [21]. It is obvious that it is closer to reality to study the changes in individual behaviors and viewpoints and the diffusion process of information based on EGT.

Nowadays, the research on EGT is mainly divided into three directions: studying the role of the complex network structure [22] in evolutionary game dynamics, exploring a way to achieve the equilibrium state of dynamic evolutionary game rapidly and maintaining the equilibrium state more consistently; studying possible dynamic mechanisms to support the emergence of cooperative behavior and exploring how to effectively promote the generation of cooperative behavior; and studying the co-evolution of network topology and game dynamics. In fact, the research on the driving and maintenance mechanism of cooperative behavior has been considered as the essential unsolved problem in life sciences and social sciences [23]. The existing models apply mutation and genetic algorithms to represent and simulate this problem [24], but the two theories are not suitable for describing the updated mechanism of user behavior strategies in social networks. Reputation-based Adaptive of Link Weight among individuals promotes the Cooperation in Spatial Social Dilemmas, which was published in 2019 [25], and establishes a game behavior model with variable link weights in individuals based on the PDG. It can be found that the increase in link weight plays an essential role in promoting cooperative behavior in the process of public opinion communication. However, the influence factor of link weight in this study only employs individual reputation, and the practical significance is insufficient.

In summary, the existing models describing the evolution of behavior and perspective are lacking accuracy. In EGT models, evolution can be presented more specifically, however, the design of factors and structures makes the models perform poorly in reality. Based on these, we intend to build a novel evolutionary game model to describe the evolution of behavior and perspective more accurately. Furthermore, factors influencing evolution can be determined to promote cooperative behavior and avoid conflict behavior in the required scenarios [26,27].

2. Model Description

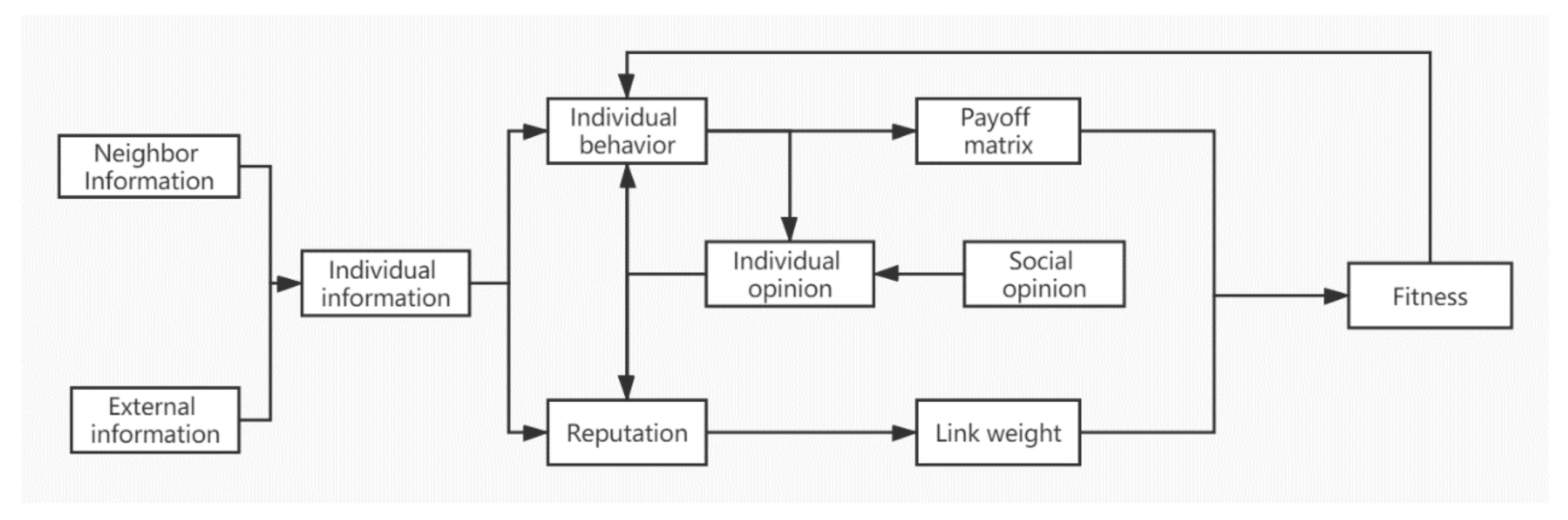
Different transmission modes of internal and external information in the real social network environment are not considered entirely, hence we improve the traditional dynamic link weight model from this perspective to increase the adaptability. In addition, we introduce the information infiltration mechanism and the individual behavior and view coupling mechanism into the model. Under the effect of these two mechanisms, the proportion of cooperative behavior strategies in social groups is increased significantly, and the emergence of cooperative behavior is greatly promoted.

2.1. GET Payoff Function and Behave Update Rules

Generally, evolutionary game research is based on the PDG model, and the income function is the research object. The PDG is a classic game model with two players and their strategies: Cooperation(C) or Defection(D). The matrix forms of cooperative behavior and defection behavior of individual x are defined as follows:

$$s_x=C=\left(\begin{array}{c}1\\ 0\end{array}\right)s_x=D=\left(\begin{array}{c}0\\ 1\end{array}\right)$$

(1)

In the process of game interaction, if both sides take cooperation as their strategies at the same time, they can obtain economic reward R separately. If both sides take a defection strategy at the same time, they both suffer certain economic loss P. When the two sides adopt different strategies, the cooperator needs to pay the payoff of the sucker S, while the defector obtains the temptation T. This kind of defection behavior is called free riding. Therefore, there is the following payoff matrix:

$$M=\left(\begin{array}{cc}R& S\\ T& P\end{array}\right)$$

(2)

For completely rational game players, if the four parameters satisfy T > R > P > S, and the opponent chooses the cooperative behavior, the individual chooses the betrayal behavior to obtain the highest benefit. When the opponent chooses the act of betrayal, the loss of interest is reduced. Therefore, the individual prefers to choose the betrayal behavior, and it leads to the dilemma of mutual betrayal between the two players in the game. In view of the fact that there is no actual loss of interest when the game individuals are betrayed in real society, we take T = b, R= 1, S = 0 and P = 0 and set the payoff matrix as:

$$M=\left(\begin{array}{cc}1& 0\\ b& 0\end{array}\right)$$

(3)

According to the behavior strategy and payoff matrix of the individual x and its interactive neighbors in social network, the payoff of x can be calculated as follows:

$$P_{xy}=s_x^{T}M{s}_y$$

(4)

For completely rational individuals, the updating rules of individual behavior strategies in the evolutionary game process are based on individual payoff functions. However, in real situations, the rules of strategy learning and the evolution of players are complex and dynamic. So far, EGT research has evolved limited rationality characteristics of individuals, and the concept of fitness has also been introduced. Therefore, the game between individuals and their neighbors is transformed from the payoff function into the relationship function with individual fitness. After calculating the game profit in the environment through the PDG model, the individual follows the updated behavior rule based on the fitness to make the new strategy. Common policy update rules include the Fermi update rule [28] and the proportion imitation rule [29]. The proportional imitation rule can better achieve the established model. Under the proportional imitation rule, the individual calculates an imitation probability according to the rule to judge whether the individual should imitate the behavior of a randomly selected neighbor. The imitation probability is defined as:

$$p\left(s_i\leftarrow s_j\right)=\frac{\left|p_j-p_i\right|}{max\left(k_j,k_i\right)\ast D}$$

(5)

where D is essentially the maximum benefit that an individual can obtain by participating in the game. When T = b, it is the “free riding” benefit b that an individual can obtain by taking a defection behavior. $k_i$ and $k_j$ represent the degrees of individual i and j, respectively. $p_i$ and $p_j$ represent the game payoffs of individual i and j, respectively. Based on the evolutionary game model, we introduce the concept of “fitness”, so the improved formula is as follows:

$$P\left(s_x\leftarrow s_y\right)=\frac{\left|F_x-F_y\right|}{max\left(k_x,k_y\right)\ast b}$$

(6)

The main influencing factors of the improved behavior strategy imitation rule are the individual fitness instead of the individual’s game payoff. The interaction between fitness and the individual behavior strategy is related to the rate of information penetration, the amount of individual information, the individual’s behavior strategy, the individual’s reputation and the group view on the social network. The fitness and proportional imitation rules under the influence of these factors jointly construct the co-evolution model of information and views based on EGT in social networks. Therefore, we construct this model and analyze the evolution of information diffusion, the promotion of cooperative behavior and the evolution of group views.

2.2. A Mechanism Based on Information Infiltration

In the process of evolutionary game based on social network described, each individual occupies a node on the social network grid. In each round of the evolutionary game, the participating individuals in the game interaction will play games with their neighbors according to the specific game model and obtain direct benefits from the calculation of the income matrix and then update their own strategies according to the strategy update rules in the end. The influence of nodes mainly lies in the size of reputation value and the amount of information they have, and the nodes with greater influence are more likely to be selected as the center nodes [30]. In the real social network, the basis for the individual in the network to be selected as the center individual is not selected once on average.

We introduce the mechanism of external information inflow. The information contained in the event has a great relationship with the actual inflow time and rate in the process of inflow to the network in this section. In order to reflect the influence of the inflow rate of external event information on the evolution process better, we make some changes to the existing game model with variable link weight based on evolutionary game that makes it set up more in line with the actual situation. The evolutionary cycle set as the Monte Carlo Simulation (MCS) process only includes game interactions and strategy updates between the selected individual and neighbor, increasing the independence and heterogeneity of the selected individual and prolongating the time spent in the simulation process to achieve steady-state [31]. It allows the inflow of event information to receive sufficient time.

The introduction of the information infiltration mechanism is for the in-depth study of the interaction between the central individual and its neighbor in the evolutionary game model, while the introduction of the coupling mechanism of individual behaviors and viewpoints is for further studying the strategy of the updating central individual. Figure 1 shows the process of game interaction and strategy update in the evolutionary game model after the introduction of two mechanisms.

We concern event information to construct information infiltration mechanism. Firstly, we need to use a record matrix $R_{max}$ to mark the grid position occupied by the game individual with the highest reputation (including the row i and column j) of the individual in the grid network, the reputation $R(i,j)$ and information value $I(i,j)$, which are expressed as:

$$R_{max}=[i,j,R(i,j),I(i,j)]$$

(7)

Evolution began, firstly, by selecting an individual as the central individual. It can obtain the current behavior of each neighbor and the link weight of the central individual with the surrounding neighbors, and then the central individual takes the payoff matrix M as the prediction standard and references its current behavior and the behavior $S_x$ of the selected game neighbor $S_y$ to calculate its own gain through the interaction of the game with each neighbor. The formula is:

$$p_{xy}=s_x^{T}M{s}_y$$

(8)

The existing finding based on the PDG model has analyzed the interaction between individual behavior and reputation, as well as the common effect on fitness. Then, according to the PDG model, we calculate the individual’s direct payoff based on reputation and use the link weight of each neighbor to calculate the cumulative fitness. Therefore, the fitness is affected by payoff and link weight. The calculation formula of fitness is:

$$F_x=\sum _{y\in {\mathsf{\Omega }}_x}{w}_{xy}{p}_{xy}$$

(9)

In the simultaneous calculation, the reputation of each neighbor around the center individual is obtained, and the total reputation is calculated and averaged, which is used as the basis for updating the link weight of the center individual in the later stage. The formula is as follows:

$$\overline{R_x}=\frac{1}{N_x}\sum _{y\in {\mathsf{\Omega }}_x}{R}_y$$

(10)

Through the interaction with neighbors in turn, the central individual promotes the diffusion of information in the group through information fusion with neighbors. The formula of replication is:

$$I_x=max\left\{I_x,I_y\right\},y\in {\mathsf{\Omega }}_x$$

(11)

The final result is that the central individual can obtain the highest information of all neighbors. At the same time, it also obtains its own fitness and the average reputation of its neighbors. After that, we need to change the link weight and update the behavior strategy. The change in the link weight is related to reputation. The formula is:

$$w_{xy}^{t+1}=\left\{\begin{array}{cc}\hfill & w_{xy}^t+u,R_x>\overline{R_x}and{w}_{xy}^t\le 1-u+e\hfill \\ \hfill & w_{xy}^t-u,R_x<\overline{R_x}and{w}_{xy}^t\ge 1+u-e\hfill \\ \hfill & w_{xy}^t,\mathrm{others}\hfill \end{array}\right.$$

(12)

Here, we assume that the total amount of information infiltrated into the social network by the outside world is a fixed value in the whole evolutionary game process. The amount of information infiltrated per unit time depends on the amount of information flowing into the outside world at the moment. The method of information infiltration is to infiltrate a certain amount of information into the individual with the highest reputation value in a fixed period of time. In order to make the information infiltration mechanism more realistic, Gaussian distribution is used as the basis for the change of the amount of information infiltrated:

$$I_{\Delta }=I_0\ast \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{(t-\mu )}^2}{2{\sigma }^2}}$$

(13)

According to the “ $3\sigma$ principle” of Gaussian distribution, when the time range of information infiltration is distributed in $[\mu -3\sigma ,\mu +3\sigma ]$, the amount of information infiltration can be approximately equal to the total amount of information infiltration:

$$I_s={\int }_t{I}_{\Delta }dt={\int }_{\mu -3\sigma }^{\mu +3\sigma }{I}_{\Delta }dt=I_0$$

(14)

The total amount of information infiltration is the product of the time interval of information infiltration and the rate of information infiltration:

$$I_s=t_s=(6\times {10}^4)/v_s$$

(15)

The individual’s probability of actively choosing a cooperative behavior strategy according to the central individual’s information possession is firstly calculated, and the calculation formula is:

$$p_i=\frac{ln\left(I\right(i,j)+1)}{1+ln\left(I\right(i,j)+1)}$$

(16)

Among this, I is the amount of information owned by an individual. This formula shows three aspects: (a) With the gradual increase in the information value owned by an individual, the probability of an individual choosing cooperative behavior is higher and higher. (b) With the further and gradual increase in the amount of information owned by an individual, the probability of an individual choosing cooperative behavior grows at a slower and slower rate. (c) In the case of a large information base, with the further increase in the amount of information possessed by individuals, the probability of individuals choosing cooperation will not tend to 1 too quickly. The first two kinds of information are in line with real life in that when an individual has enough information, the promotion effect of continuously increasing information on the individual’s choice of cooperative behavior begins to weaken. The third feature shows that in the case of large amount of information, individuals also have a certain chance to choose not to use cooperative behavior strategy, that is, individuals will not choose cooperation directly because of the single factor of the amount of information possessed, which shows the subjective initiative of individuals in the face of views in social networks to a certain extent.

As described in the above algorithm, if the information already owned by the central individual is enough to drive the individual to adopt cooperative strategy according to the probability calculation, the individual choice makes the corresponding choice. However, if the information already owned by the central individual is not enough to drive the initiative choice of cooperation strategy, the central individual should make the choice according to the adaptability of the individual.

In this paper, the reputation value represents the reward that an individual can obtain in addition to the benefits of the game, so in the evolution, the individual with the highest reputation value obtains new information. At the same time, their own reputation value will also directly increase by a certain value as a reward. Moreover, compared with other individuals whose reputation values increase passively because they choose cooperative behavior, the reputation value of this kind of individual cooperative behavior, which is actively driven by the outside world and the whole social group dominated by cooperative behavior, needs a larger increase. The formula is as follows:

$$\left\{\begin{array}{cc}{R}_x^{t+1}=R_x^t+R_1\hfill & ,s_x=C\hfill \\ R_x^{t+1}=R_x^t\hfill & ,s_x=D\hfill \end{array}\right.$$

(17)

After completing a series of processes of new external information inflow and reward gain reflected by the reputation value for the individual with the largest reputation value each time, it is also necessary to update the updated individual’s reputation value and information possession to the record matrix of the individual with the highest reputation value synchronously. In order to timely update to the social network, the next round of individual game and information dissemination and inflow.

2.3. A Mechanism Coupling Individual Behavior and Viewpoint

The coupling mechanism of the individual behavior and viewpoint is derived from the concept of “cognitive dissonance” in psychology. The specific explanation is that when individuals in social networks take actions and form opinions, they will be affected by different factors contained in the surrounding groups and show the inconsistency between their actions and opinions. Whether the individual’s viewpoint and behavior strategy cooperate or not will constitute the pressure matrix, in which o, p, q and r are the group pressure values when the individual’s viewpoint and behavior strategy are (C, C), (C, D), (D, C) and (D, D), respectively. In reality, when the user’s behavior strategy and opinion strategy are in line with the social group, they do not face pressure; similarly, when the user’s behavior strategy and opinion strategy are not in line with the social group, they will not have too much pressure and are less likely to change their strategies under pressure. From this, we can obtain the following conclusions:

$$P=\left(\begin{array}{cc}o\hfill & p\hfill \\ q\hfill & r\hfill \end{array}\right)=\left(\begin{array}{cc}0\hfill & p\hfill \\ q\hfill & 0\hfill \end{array}\right)$$

(18)

As the real society is more positive development oriented, for individuals who hold the defection view but take cooperative behavior, whether the society is dominated by the cooperation view or the defection view, the cooperation on the individual’s behavior brings practical benefits to the group, so they will not be subject to group pressure. As for the individuals who hold the cooperative view but take the defection behavior, when the society is dominated by the cooperative view, the surrounding group will think that the individuals who only obey the group from the point of view but are not willing to make substantive changes in their behavior are damaging the interests of the group, and this is not allowed. If the society is dominated by the defection view, the tolerance for defection will be relatively high. Therefore, the central individual will be under group pressure only when the individuals who hold the cooperative view but take the defection behavior:

$$P_{x\mid C}=\left\{P\mid s_N=C\right\}=\left\{\left(\begin{array}{cc}o\hfill & p\hfill \\ q\hfill & r\hfill \end{array}\right)\mid q=0\right\}=\left(\begin{array}{cc}0& N_a/N_x\\ 0& 0\end{array}\right),p\in [0,1]$$

(19)

The external factors that affect the individual’s view and behavior in social networks mainly include the information content and the information amount held and received by individuals, as well as the differences in information sources; the internal factors mainly include the positive or negative attitude of individuals towards the event and the positive or negative behavior of individuals to deal with the information. Therefore, we can build a model to analyze the situation in which individuals in social networks will choose cooperative behavior and in which state they will reach the steady state.

When an event occurs and an individual in a social network receives information, he or she will quickly or even unconsciously choose a tendency due to his or her own thoughts and positions. It is assumed that each individual on the social network has only limited rationality, and social groups generally encourage cooperative attitude, mainly cooperative behavior. So, on the point of view, the strategy set is $S_1=\{C,D\}$, on the point of behavior, the strategy set is $S_2=\{C,D\}$. When individuals in social networks choose to cooperate in view and behavior, the profit is $r+{\Delta }_1+{\Delta }_2$. Among them, r is the inherent income of the selected individual to obtain information, ${\Delta }_1$ is the reward income of the individual’s consistent choices and behavior and ${\Delta }_2$ is the environmental reward of the social groups with cooperative behavior to the individuals with cooperative tendency. When individuals in social networks choose the strategy of cooperation in view and betrayal in behavior, the profit is $r+{\Delta }_2$. When individuals choose to betray their ideas and cooperate in their behaviors, the profit is $r+{\Delta }_2-c$ because, in social networks, the betrayal of behavior has a much greater negative impact on the group’s cooperative behavior than the betrayal of simple ideas, so we need to punish all individuals who take the betrayal strategy c. When the individual chooses the betrayal strategy in view and behavior, the profit is $r+{\Delta }_3-c$. Although these strategies of betraying individuals are contrary to the cooperative behavior of social groups, they will gain a certain amount of additional benefits ${\Delta }_3$ because of their firm choice and the volatility of their choices due to the unequal and untimely information of some social groups. To sum up, when the social group is dominated by cooperative behavior, the central individual’s viewpoint and behavior strategy income matrix are as follows:

$$Q=\left(\begin{array}{cc}r+{\Delta }_1+{\Delta }_2& r+{\Delta }_2-c\\ r+{\Delta }_2& r+{\Delta }_3-c\end{array}\right)$$

(20)

Assuming that the proportion of individuals choosing the cooperation strategy in view is p, the proportion of individuals choosing the betrayal strategy in view is $1-p$; meanwhile, assuming that the proportion of individuals choosing the cooperation strategy in behavior is q, the proportion of individuals choosing the betrayal strategy in behavior is $1-q$. Therefore, for the central individual, the expected benefits of choosing the strategy of behavioral cooperation and behavioral betrayal are $U_C^q$ and $U_C^{1-q}$, the average return is ${\overline{U}}_c$ and we can calculate that:

$$\left\{\begin{array}{c}{U}_C^q=\left(r+{\Delta }_1+{\Delta }_2\right)p+\left(r+{\Delta }_2-c\right)(1-p)=\left(r+{\Delta }_2-c\right)+\left({\Delta }_1+c\right)p\\ U_C^{1-q}=\left(r+{\Delta }_2\right)p+\left(r+{\Delta }_3-c\right)(1-p)=\left(r+{\Delta }_3-c\right)+\left({\Delta }_2-{\Delta }_3+c\right)p\\ {\overline{U}}_C=q{U}_C^q+(1-q)U_C^{1-q}\end{array}\right.$$

(21)

Therefore, the replication dynamic equation of the central individual choosing cooperative behavior strategy is as follows:

$$\begin{array}{cc}\hfill \frac{dq}{dt}& =f(p,q)\hfill \\ \hfill & =q\left(U_C^p-{\overline{U}}_C\right)\hfill \\ \hfill & =q(1-q)\left[\left({\Delta }_2-{\Delta }_3\right)+\left({\Delta }_1-{\Delta }_2+{\Delta }_3\right)p\right]\hfill \end{array}$$

(22)

The partial derivative of the duplicated dynamic equation with respect to q is obtained:

$$\begin{array}{cc}\hfill \frac{\partial f(p,q)}{\partial q}& =f_q(p,q)\hfill \\ \hfill & =(1-2q)\left[\left({\Delta }_2-{\Delta }_3\right)+\left({\Delta }_1-{\Delta }_2+{\Delta }_3\right)p\right]\hfill \\ \hfill & =(1-2q)\left({\Delta }_1-{\Delta }_2+{\Delta }_3\right)\left(p-\frac{{\Delta }_2-{\Delta }_3}{{\Delta }_2-{\Delta }_3-{\Delta }_1}\right)\hfill \\ \hfill & =(1-2q)\left[{\Delta }_{1}p+(1-p)\left({\Delta }_2-{\Delta }_3\right)\right]\hfill \end{array}$$

(23)

According to the copied dynamic equation, when $p=p_0=\frac{{\Delta }_2-{\Delta }_3}{{\Delta }_2-{\Delta }_3-{\Delta }_1}$, all values of $\mathrm{Q}$ are in equilibrium. When $p\ne p_0,q_1=0$, $q_2=1$ is in equilibrium. On the other hand, the stable equilibrium state also needs $f_q(p,q)<0$ to be satisfied. Therefore, when ${\Delta }_2-{\Delta }_3<0$, $p<p_0,f_q\left(p,q_1\right)<0,q_1=0$ is in stable equilibrium. That is to say, the central individual chooses the betrayal strategy in behavior. When ${\Delta }_2-{\Delta }_3>0$, $p>p_0$, $f_q\left(p,q_1\right)<0,q_1=1$ is in stable equilibrium. That is to say, the central individual chooses the cooperation strategy in behavior.

Based on this, the coupling mechanism of individual behavior and view firstly judge whether the central individual satisfies that the view value equals 1 and the behavior value is 0. $A_x$ represents an individual’s view, and $B_x$ represents the behavior strategy. When $A_x$ is 1, it means the individual holds the cooperative view. When $B_x$ is 0, it means the individual holds the defection action. If and only if $A_x=1\cap B_x=0$, the individual type meets the screening criteria.

If not, we will directly ignore the influence from group pressure and choose to weigh their current behavior through the adaptation proportion updating rule. If so, the number of game neighbors and the number of cooperative neighbors are counted. The ratio between them not only represents the degree of group pressure on the central individual but also exists as the possibility standard of the behavior strategy change of the central individual, expressed as follows:

$$\left\{\begin{array}{c}{s}_x(t+1)=C,N_a\ge p_b\ast N_x\\ s_x(t+1)=s_x\left(t\right),N_a<p_b\ast N_x\end{array}\right.$$

(24)

$N_a$ refers to the number of neighbors with cooperative view around the center individual, $N_x$ refers to the number of all game neighbors around the center individual and $p_b$ refers to a randomly selected value in the interval [0, 1]. when $N_a\ge p_b\ast N_x$, it was indicated that the group pressure exerted by the neighbors with a cooperative view around the center individual had exceeded or just met the value of group pressure required by the center individual to change its own behavior, so the center individual chose cooperative behavior as the final behavior strategy directly under the group pressure. When $N_a<p_b\ast N_x$, it was shown that the group pressure exerted by the neighbors who had already held the cooperative view among all the game neighbors around the center individual did not exceed the value of the group pressure required by the center individual to change his own behavior. Then, the individual needs to find out the probability that the central individual chooses to imitate the neighbor’s behavior strategy according to the proportion imitation rule based on fitness and determine the final behavior of the central individual:

$$P\left(s_x\leftarrow s_y\right)=\frac{\left|F_x-F_y\right|}{max\left(N_x,N_y\right)\ast b}$$

(25)

Based on the concept of “cognitive dissonance” in psychology, the individuals who hold cooperative views but take defection behavior will achieve consistency by changing their behaviors or views, so as to eliminate their own pressure. In general, individual experience is more inclined to change their own views, so it is necessary to continue to judge the view of each individual who has become the center and screen out individuals whose behaviors and attitudes are inconsistent, in other words, $A_x\ne B_x$.

If the behavior of the central individual is indeed inconsistent with the view, then consider the proportion of game neighbors with cooperative views around the individual as the probability threshold and judge whether the individual needs to change the view to cater to the behavior. This is expressed as follows:

$$\left\{\begin{array}{c}{A}_x(t+1)=B_x\left(t\right),N_a\ge p_a\ast N_x\hfill \\ A_x(t+1)=A_x\left(t\right),N_a<p_a\ast N_x\hfill \end{array}\right.$$

(26)

When $N_a\ge p_a\ast N_x$, the central individual directly chose to change their views to cater to the behavior that had occurred. When $N_a<p_a\ast N_x$, the central individual would not choose to change their point of view to cater to the behavior that had occurred because of the weak group pressure.

After the completion of the above two groups’ updated strategy probabilities based on the differences between the social group’s attitude and their own attitude and behavior strategies, it is necessary to update the reputation value of the central individual according to their state and change the reputation value to realize the change in the link weight, so as to realize the reward and punishment mechanism based on group attitude and individual attitude and behavior:

$$\left\{\begin{array}{cc}{R}_x^{t+1}=R_x^t+R_1+{\Delta }_1+{\Delta }_2\hfill & ,A_x=1\&B_x=1\hfill \\ R_x^{t+1}=R_x^t+{\Delta }_2-c\hfill & ,A_x=1\&B_x=0\hfill \\ R_x^{t+1}=R_x^t+R_1+{\Delta }_2\hfill & ,A_x=0\&B_x=1\hfill \\ R_x^{t+1}=R_x^t+{\Delta }_3-c\hfill & ,A_x=0\&B_x=0\hfill \end{array}\right.$$

(27)

When the individual finally chooses the cooperative behavior strategy, his reputation value will receive a small reward; when the individual finally chooses the betrayal strategy as his behavior strategy after this round of game, the reputation value of the central individual will not change, as a punishment measure is given for the betraying individual.

Therefore, based on the psychological concept of “cognitive dissonance”, each individual in the social network will update their own behaviors and views. When the central individual’s final behavior update is completed, it will have an impact on his reputation value, which is expressed as:

$$\left\{\begin{array}{cc}{R}_x(t+1)=R_x\left(t\right)+R_2\hfill & ,s_x=C\hfill \\ R_x(t+1)=R_x\left(t\right)\hfill & ,s_x=D\hfill \end{array}\right.$$

(28)

At the end of each round of game interactions and behavior strategy updates, it is necessary to compare the reputation value of the central individual with that in the record matrix. When $R_x>R(i,j)$, the location, reputation value and information amount of the central individual in the grid network are recorded in the record matrix in case new information infiltrates into the social network.

3. Experiments

The evolutionary game process on social networks is the cyclic update of individual behavior, reputation, information value, fitness and link weight through the interaction and behavior strategy updates and the mutual coupling of several parts of information infiltration caused by external events.

As mentioned before, in the information infiltration mechanism introduced in this paper, the event information infiltration is related to the actual time. In order to better reflect the impact of the event information infiltration rate on the evolution process, this paper makes some changes to the existing evolutionary game model with variable link weight and sets it so that only one selected individual is included in each evolution cycle of the MCS process of game interaction and strategy update with neighbors. This increases the independence and non-uniformity of individual selection and also prolongs the time for the simulation process to reach steady state, so that the event information infiltration can obtain sufficient time.

3.1. The Influence of Betrayal Benefit and Variable Link Weight on Cooperative Behavior

It can be concluded from the above model that when the social network does not carry out the mechanism of periodic external information inflow and the influence of group selection on individual views and behaviors, the proportion of collaborators in the group when the network reaches the steady state is mainly related to the reputation value, the change range of the link weight, the fitness and the difference between individual income and cooperation income obtained by “free riding”. Therefore, in order to better explore the promotion effect of the two mechanisms on individual cooperative behavior in social networks, we need to study the network nature and evolutionary game before the introduction. The simulation in this paper adopts the improved MCS and choose the last 5 ∗ 10${}^6$ complete MCS to calculate the proportion of the cooperators when the system reaches the steady state.

In Figure 2, when MCS = 1 ∗ ${10}^8$, $u=0.1$, we explore the change in the proportion of the final steady-state collaborators under the different traitor income parameter b and the link weight limit threshold parameter e.

In Figure 3, bc1 is the threshold for defectors to appear, that is, when b reaches a certain value, the group begins to appear ar the threshold of incomplete cooperation in steady state. Moreover, bc2 is the threshold for cooperators to die out, that is, when the free riding income of individual choice betrayal reaches a certain value, the choice cooperators will be greatly affected by the defectors as a result, the negative feedback mechanism disappears and the final steady state reaches the threshold of a full betrayal state.

As can be seen from the graph, for example, when $e=0$, that is, when the evolutionary game of social network degenerates into the PDG, the proportion of cooperators will decrease rapidly with the increase in b, or even disappear eventually, and the threshold of cooperators’ extinction is $bc2=1.23$.

After exploring the influence of betrayal benefit parameters on the proportion of cooperative behavior in the group, this paper uses the principle of control variable method to explore the change of the proportion of cooperative behavior in the group with a different link weight change U value when $b=1.23$. It should be noted that in this model, the link weight u has a change range, which is determined by the parameter e, as shown in the Figure 4.

When the change range of u is ensured to meet the requirements, it can be seen that the proportion of cooperative behavior users increases rapidly with the increase in the u value, and the larger the e value is, the earlier it reaches the state of full cooperation. However, with the further increase in the u value, the proportion of cooperative behavior will have a certain amount of attenuation. Therefore, when choosing the value of parameter u, it should reach the critical value of the full cooperation state earlier, that is, $u=0.1$.

3.2. Promotion of Information Infiltration Mechanism on Cooperative Behavior

Figure 5a is the evolutionary graph of the proportion of individuals who take cooperative behavior in the group before the introduction of information infiltration mechanism in the improved evolutionary game model with changeable link weight. It can be seen that when the link weight distribution interval is small, rewarding individual cooperative behavior by enhancing reputation has lost its effect, and each individual strives for the maximum direct benefit in the interaction with their neighbors, so it finally tends to the stable state of total defection. With the increase in e, the distribution of the link weight is more scattered, and individuals in the group pay more and more attention to reputation reward. Increasing the reputation reward for cooperative behavior can improve the proportion of cooperative behavior when the group reaches the evolutionary steady-state.

However, the research on reputation does not consider the mechanism of promoting cooperative behavior from the perspective of public opinion events, and the mechanism based on reputation lacks the role of subjective factors of game individuals in the process of behavior strategy updating in EGT. Therefore, we introduce the mechanism of information infiltration to study the impact of information permeation on the evolution trend of cooperative behavior. Figure 5b–d are the evolutionary trends of the proportion of cooperative individuals in the whole group when the information penetration rate is set to 10 information units/s, 1 information units/s and 0.1 information units/s, respectively.

By comparing (a) with (b), (c) and (d) in Figure 5, it can be found that under the same e, the proportion of cooperative behavior in (b), (c) and (d) is larger than that in (a); even the evolution in (b), (c) and (d) can reach the full cooperative steady state faster. Moreover, with the expansion of the link weight range, the proportion of cooperative individuals in the group tends to be completely steady state, which generally conforms to the characteristics of gradual acceleration. This shows that the introduction of information infiltration mechanism is effective.

In addition, compared with Figure 5b–d, we can see that when e is 0 and the penetration rate is 10 information units/s, the proportion of individuals in the whole group begins to increase significantly at about 7 ∗ ${10}^5$ th round. When the penetration rate is 1, it begins to increase significantly at about 1 ∗ ${10}^6$ th round, and when the penetration rate is 0.1 information unit/s, the proportion of game players in the whole group will not increase significantly until the position of the 4 ∗ ${10}^7$ th round. The reason for this situation is that under the premise of the same amount of information, the speed of information penetration into the group is faster and faster, which means that the number of information penetration is more and more, and the work of information penetration hinders the interaction process of game individuals in social networks more and more. However, the amount of information penetration starts to decrease each time, so more and more rounds of game interaction and information transmission are needed to make most of the players receive enough information to promote the emergence of cooperative behavior.

The introduction of different information penetration rates can promote the emergence of cooperative behavior under different link weights. However, the introduction of the information infiltration mechanism does not eliminate the phenomenon that individuals pursue higher direct interests in the early stage of evolutionary game, which makes the group become dominated by defection.

3.3. Impact of Information Infiltration Mechanism on Information Diffusion Process

According to the theoretical analysis and a large number of simulation results, it can be known that in the game interaction between individuals, the diffusion process of information has nothing to do with the link weight between individuals, so we ignore the impact of link weight on information diffusion and directly intercept the distribution of information in the group when the game rounds are certain under different information penetration rates.

Figure 6a–c shows the diffusion of information in the whole social network when the information penetration rate is 0.1, 1 and 10. The dark cyan to light yellow color shown in the figure indicates an increasing amount of information. It can be seen from Figure 6 that with the increase in the information penetration rate, the amount of information that infiltrates into social networks in a single time increases gradually, but the time interval of information penetration is longer. Before the next new information infiltrates into the group, the amount of information that penetrates into the social network at a single time is very small, and the time interval of information penetration is very short. Therefore, in the process of participating in the game interaction, the game players continuously receive new information, but each time they receive information, it is very limited. So, according to the amount of information they have, they can be divided into many levels, but the boundary between levels is not very obvious. Therefore, based on the above analysis results, it can be found that when the total amount of information is fixed, the faster the information penetration rate is, the more the distribution level of information among individuals in social networks is and the boundaries between different information levels are weaker.

3.4. Evolution of Cooperative Behavior under the Joint Action of Information Infiltration Mechanism and Behavior and Viewpoint Coupling Mechanism

To eliminate the phenomenon of betrayal behavior dominated by group in the evolutionary game. We continue to introduce the coupling mechanism of behavior and viewpoint and analyze the evolution of the proportion of cooperative behavior under the combination of the two mechanisms.

Figure 7a,b show the evolution of the proportion of cooperative behavior before and after the two mechanisms. It can be seen that under the combination of the two mechanisms, the emergence of cooperative behavior in social networks is more rapid, significant and stable than when the information penetration mechanism is introduced alone. The time required for the cooperation behavior with different link weights to reach steady state in the evolution process has been greatly shortened. The significance lies in that for a small link weight range, the group evolution under the two mechanisms can still reach the evolution steady state of full cooperation quickly. The stability is reflected in the introduction of the coupling mechanism of behavior and viewpoint eliminates the phenomenon that the early evolution of social networks is dominated by defection. The reason is that before the introduction of the coupling mechanism of behavior and opinion, the default view and behavior strategy are always consistent. In the evolution process, we only need to consider the promotional effect of the link weight under the influence of payoff and reputation on the cooperative behavior strategy. Therefore, in the early stage of social network evolution, individuals in the group choose to defect to pursue higher game benefits, which leads to a significant decline in the proportion of individuals who take the cooperative behavior approach. However, after introducing the coupling mechanism of behavior and viewpoint, some individuals who also hope to take the higher benefits brought by defection will not easily take the defection behavior because of the group pressure in the environment. So, the defection behavior in the early stage of evolution is well suppressed.

3.5. Inconsistency between Cooperation Behavior and Cooperation Viewpoint

Figure 8a,b represent the evolution of cooperative behavior and cooperative view, respectively, under the joint action of the two mechanisms. It can be seen from the comparison that although the long-term evolution makes the behavior and views of individuals in the group tend to be consistent eventually, some individuals’ behaviors and views will be inconsistent in the evolution process. Moreover, from the perspective of the development of the whole group, group opinions more accurately form public opinion pressure on individuals whose views are cooperative, so on the premise that the social network is oriented by cooperation, the development of the whole group shows that the behavior follows the viewpoint, which also reflects the characteristics that individual viewpoint exerts influence on individual’s own behavior from the perspective of subjective initiative in reality. In conclusion, the coupling mechanism of behavior and opinion can be proven to be an effective mechanism to punish defection under the premise of cooperation.

4. Conclusions

In the paper, we establish a more realistic co-evolution model based on the information and viewpoint of the evolutionary game. In the model, we introduce the information infiltration mechanism as the incentive mechanism for cooperative behavior and the coupling mechanism of individual behavior and viewpoints as the punishment mechanism for defection. Additionally, here, the factors influencing behavior and perspective are employed precisely, so the trend of evolution can be defined more accurately. Through the simulation experiments, we obtain some valuable results. They provide reference data and important support for the research on social networks.