A Novel Compound-Coupled Hyperchaotic Map for Image Encryption
Abstract
:1. Introduction
- (1)
- A general method to construct a hyperchaotic map by combining some existing chaotic maps is presented;
- (2)
- A case study is investigated to prove that the technique presented in this work is effective. In this case, the constructed hyperchaotic map is analyzed in depth, and the results are compared with some well-known maps;
- (3)
- A lightweight encryption/decryption protocol is designed to show that the new hyperchaotic map can encrypt images;
- (4)
- The proposed encryption/decryption protocol is analyzed in depth using some well-known evaluation metrics to validate the presented algorithm with the new hyperchaotic map utilizing the proposed method.
2. A General Method to Construct a Compound Hyperchaotic Map
2.1. The Method
2.2. Case Study Using 2D Hénon Map and 2D Sine Map
2.3. Properties of the New Hyperchaotic Map
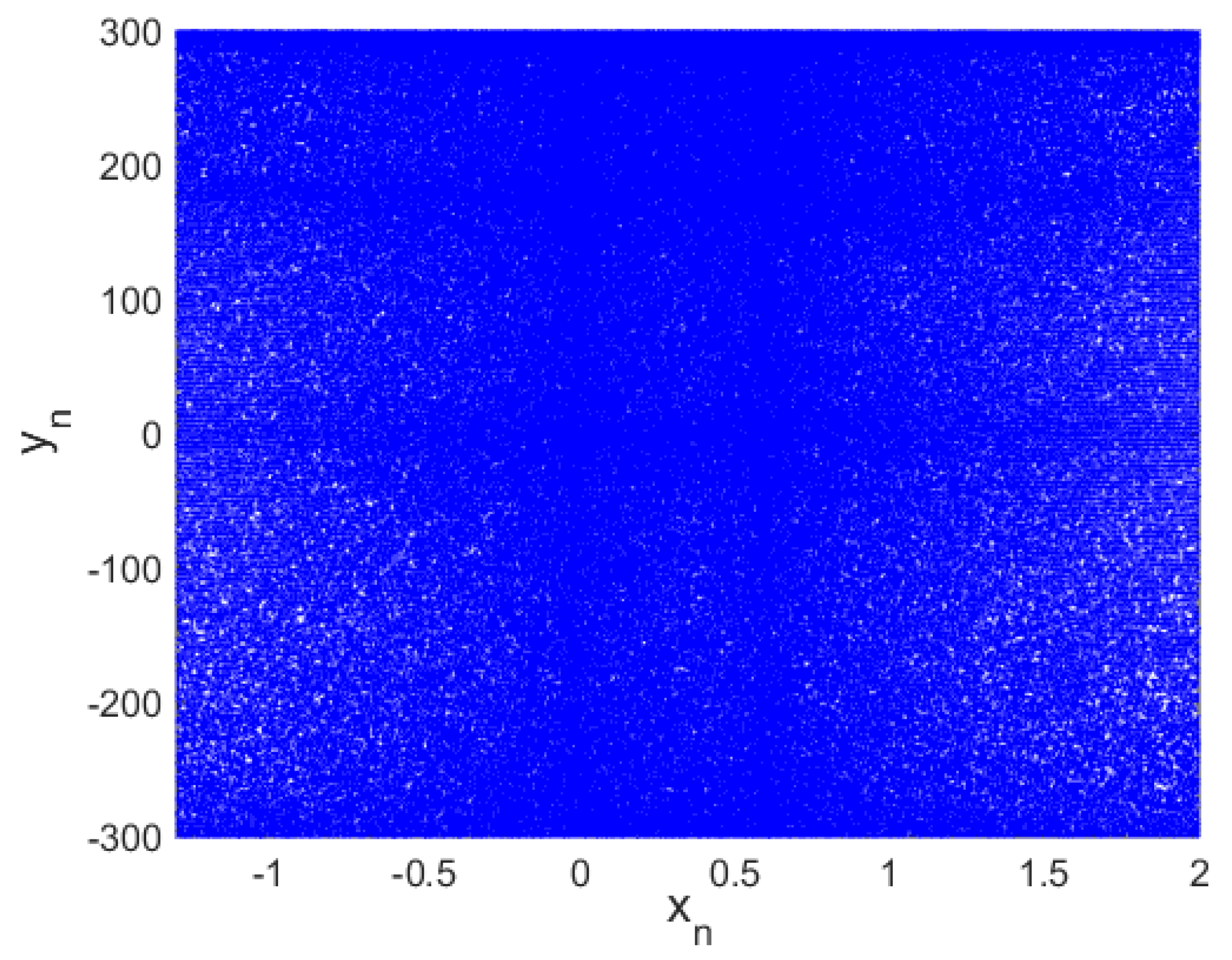
2.3.1. Phase Space Attractor
2.3.2. Bifurcation Evolution
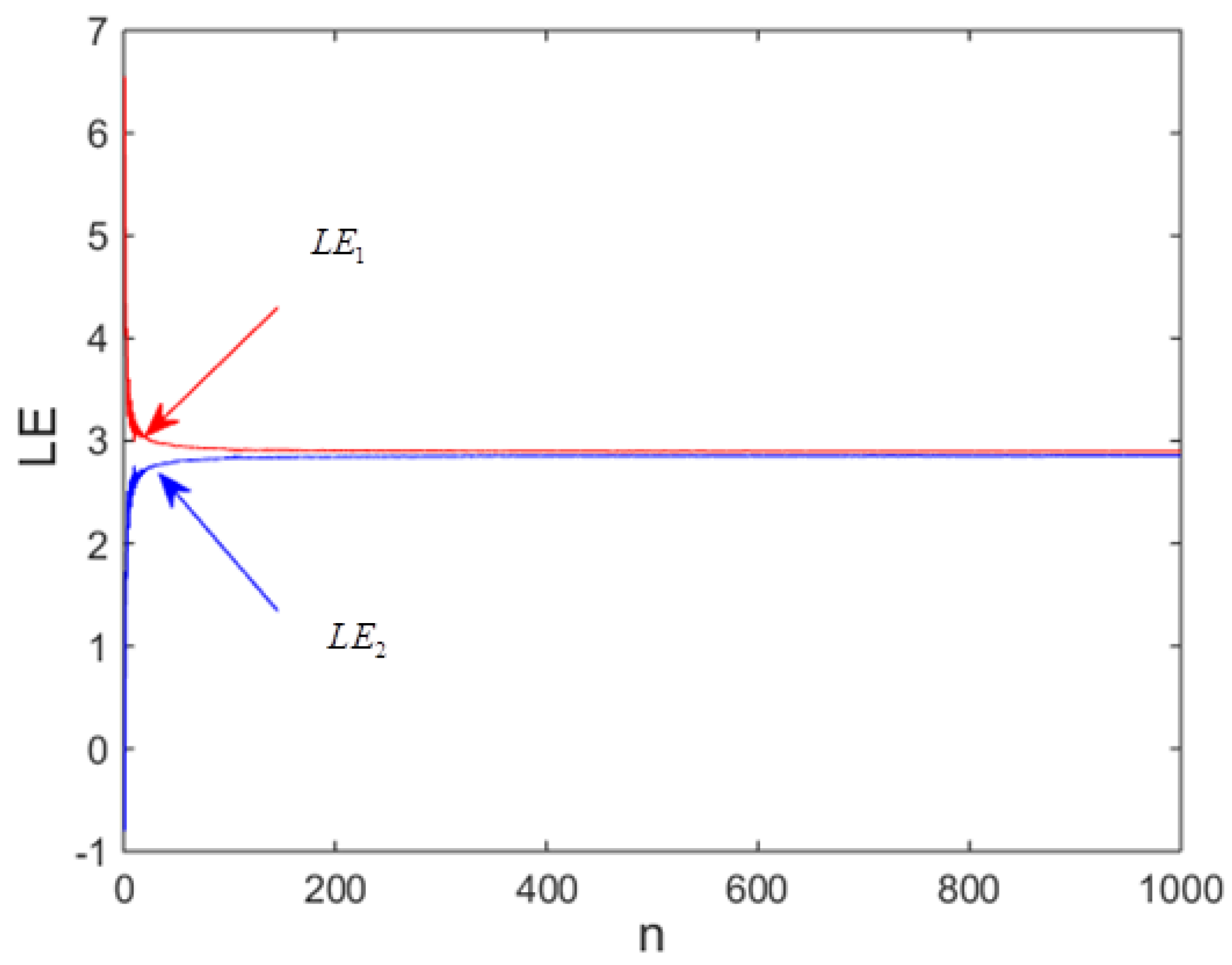
2.3.3. Finite-Time Lyapunov Exponents
- Only the highest LE is positive. In this case, we conclude that the map has chaotic dynamics for the selected parameter. In addition, if the highest LE is high, this simply indicates that close trajectories diverge faster;
- Two positive LEs are observed. This observation is exploited to identify hyperchaos behavior;
- The highest LE is negative or equal to zero. The dynamic of the map experiences limits cycles.
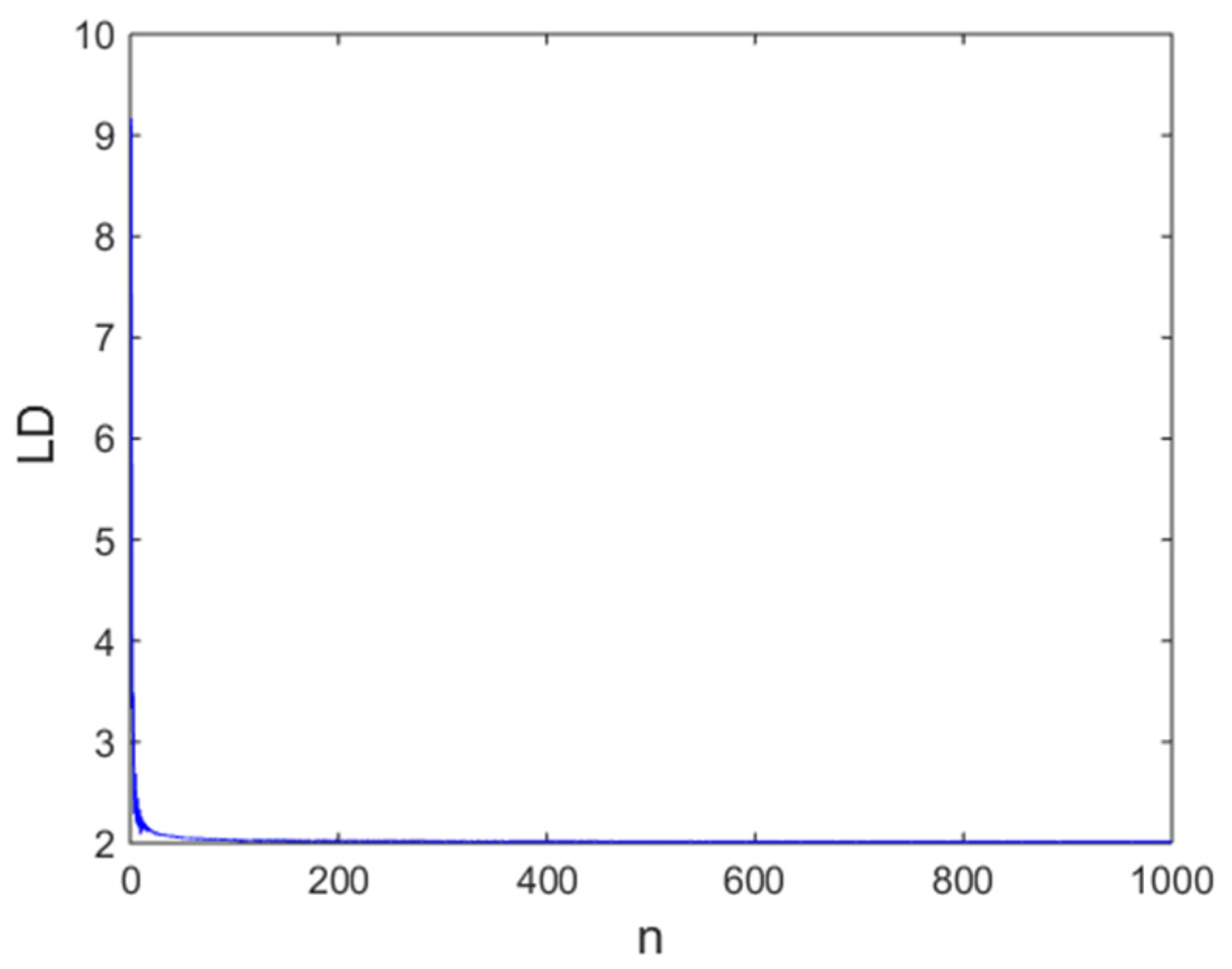
2.3.4. Finite-Time Lyapunov Dimension
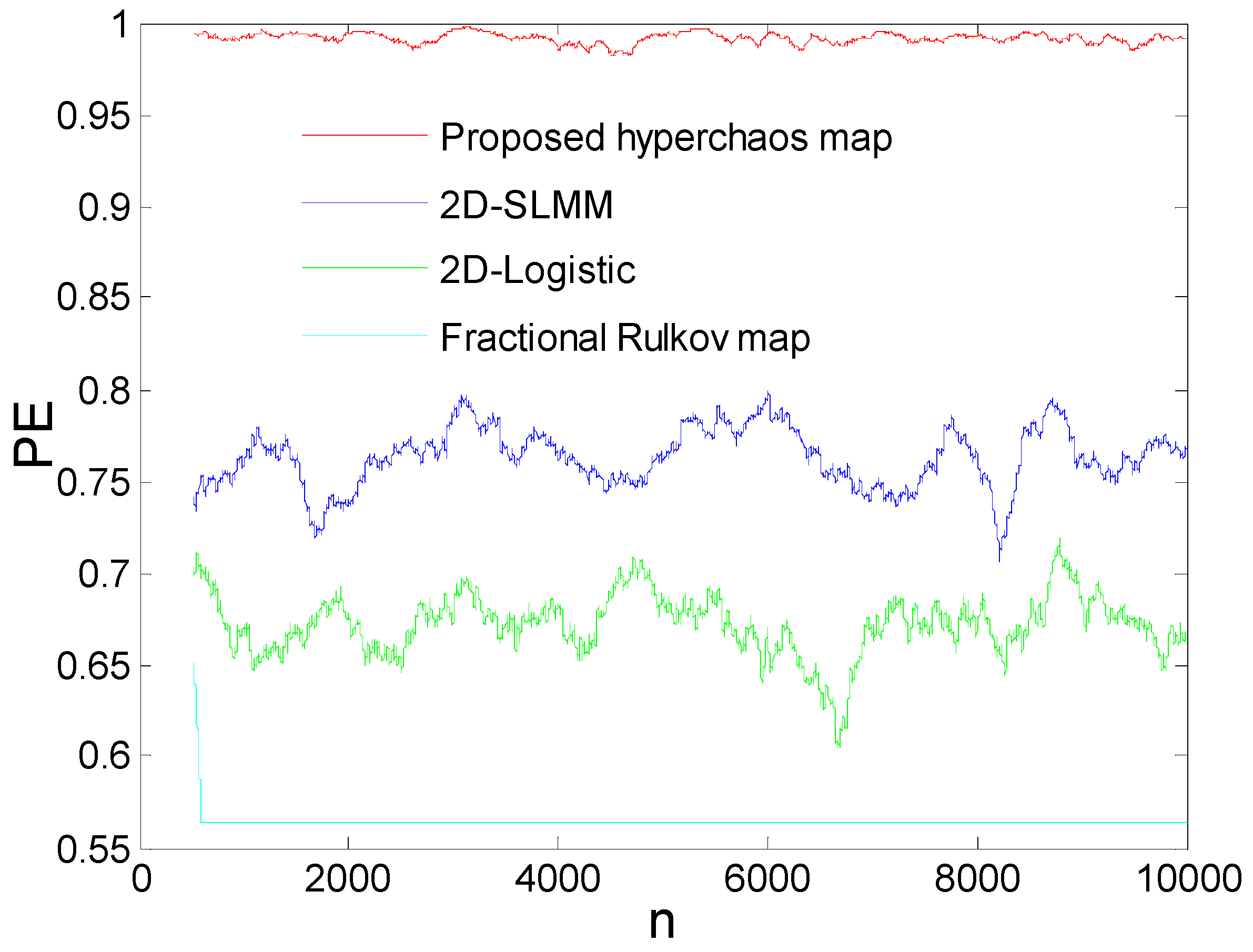
2.3.5. Comparative Analysis Based on Permutation Entropy Test
2.3.6. NIST SP 800-22 Test of Pseudo Randomness
3. Proposed Encryption Algorithm
4. Encryption/Decryption Process Analysis
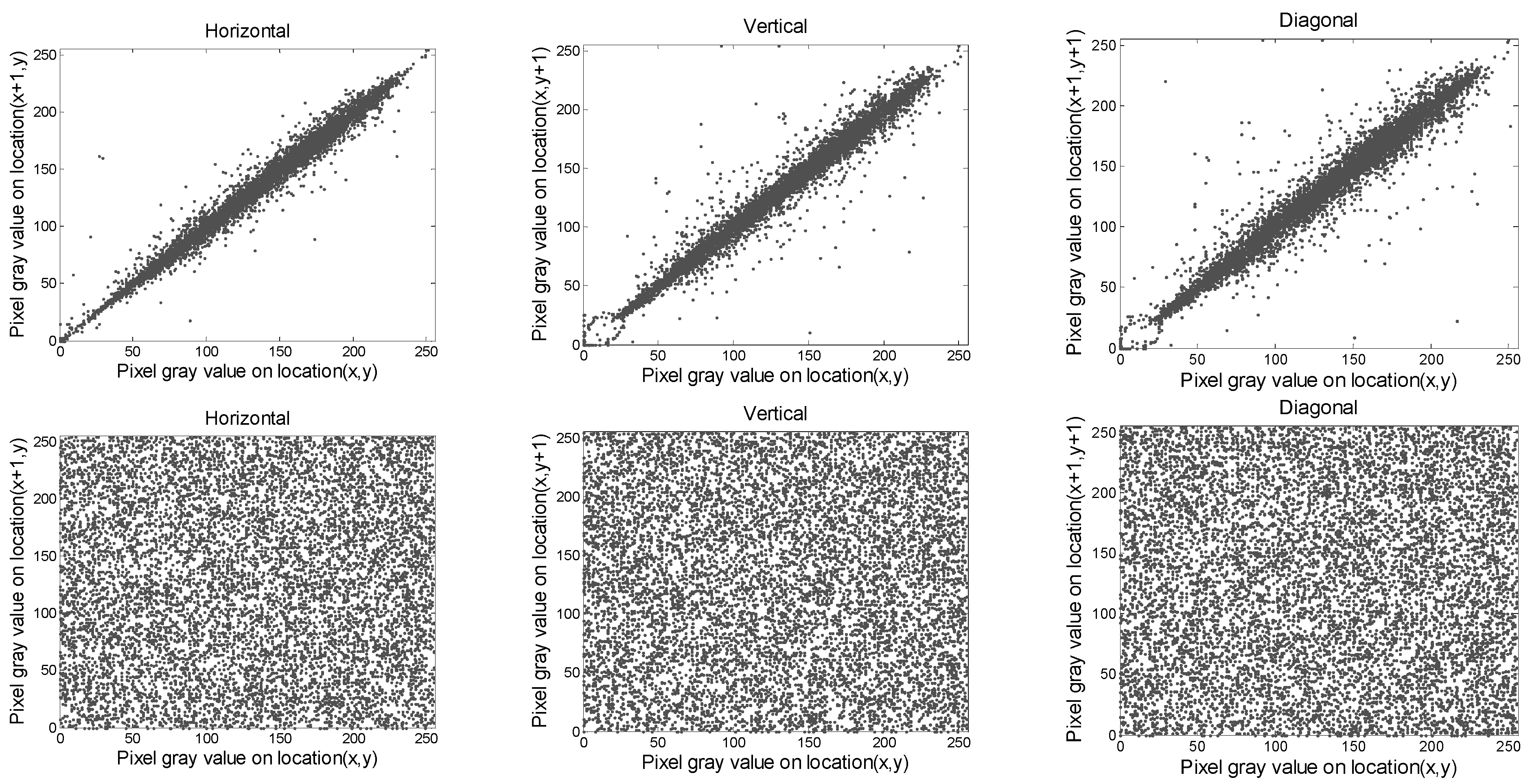
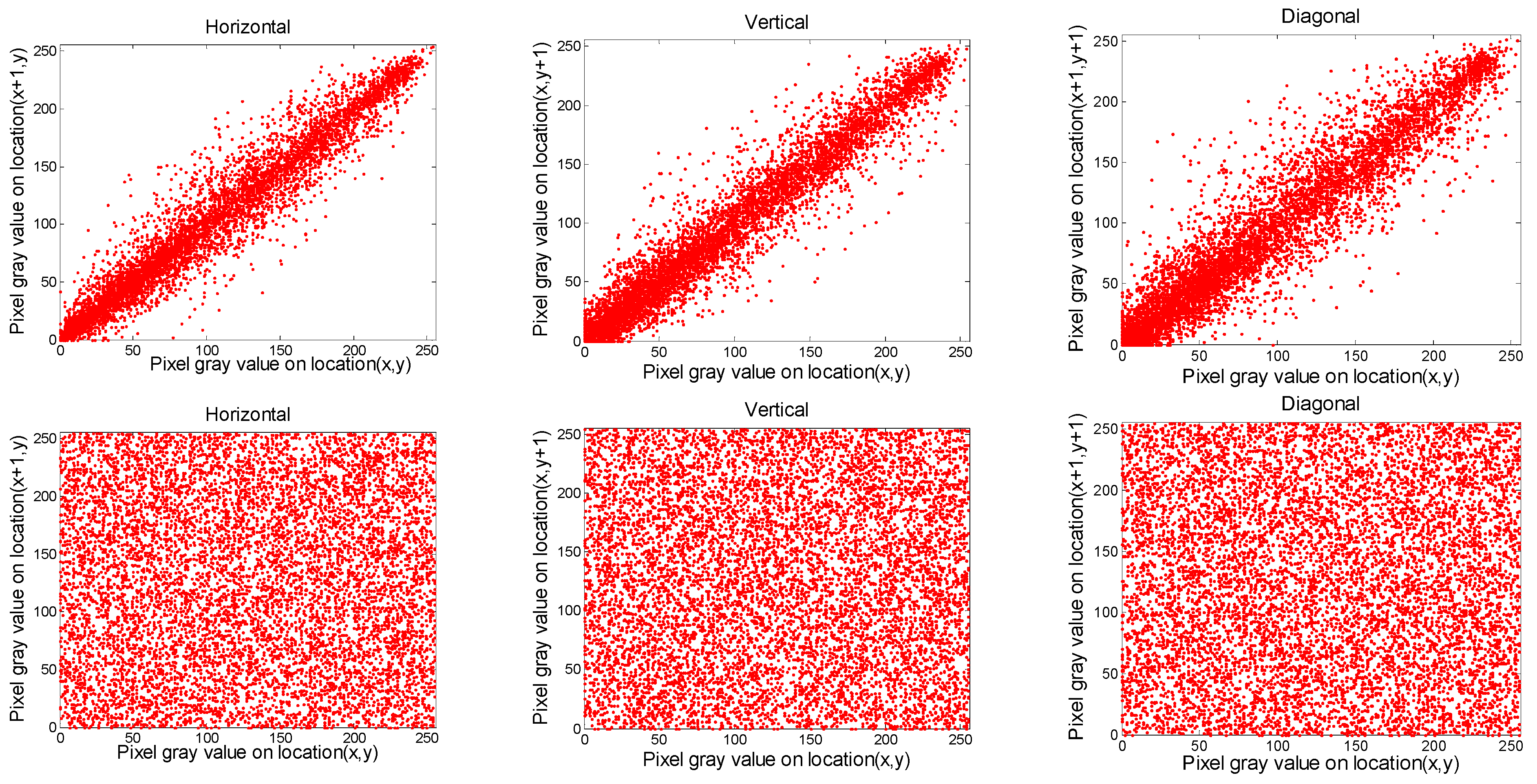
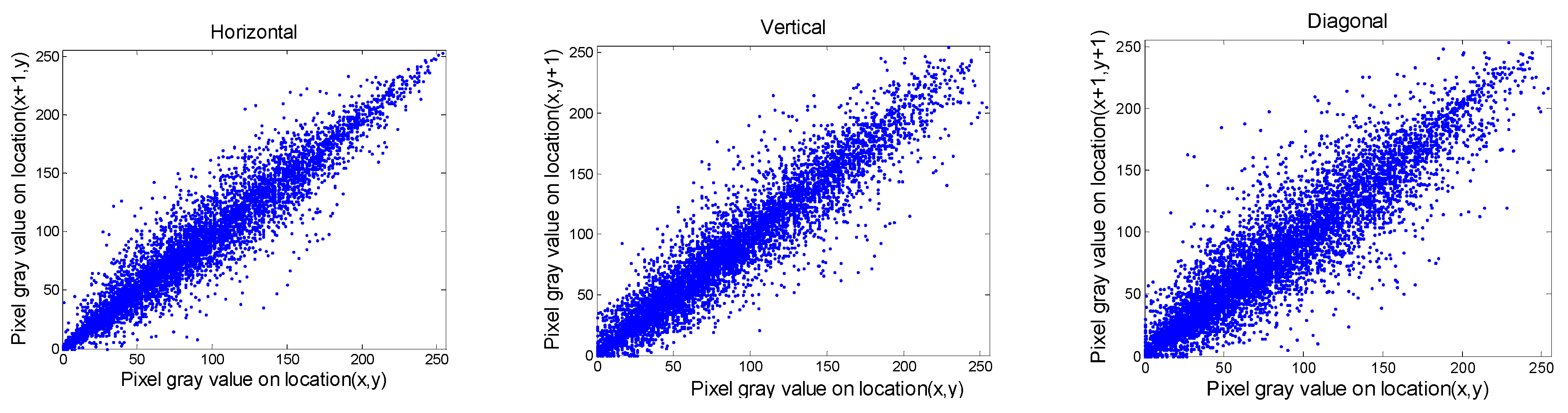
4.1. Correlation of Bordering Pixels
4.2. NPCR and UACI Tests
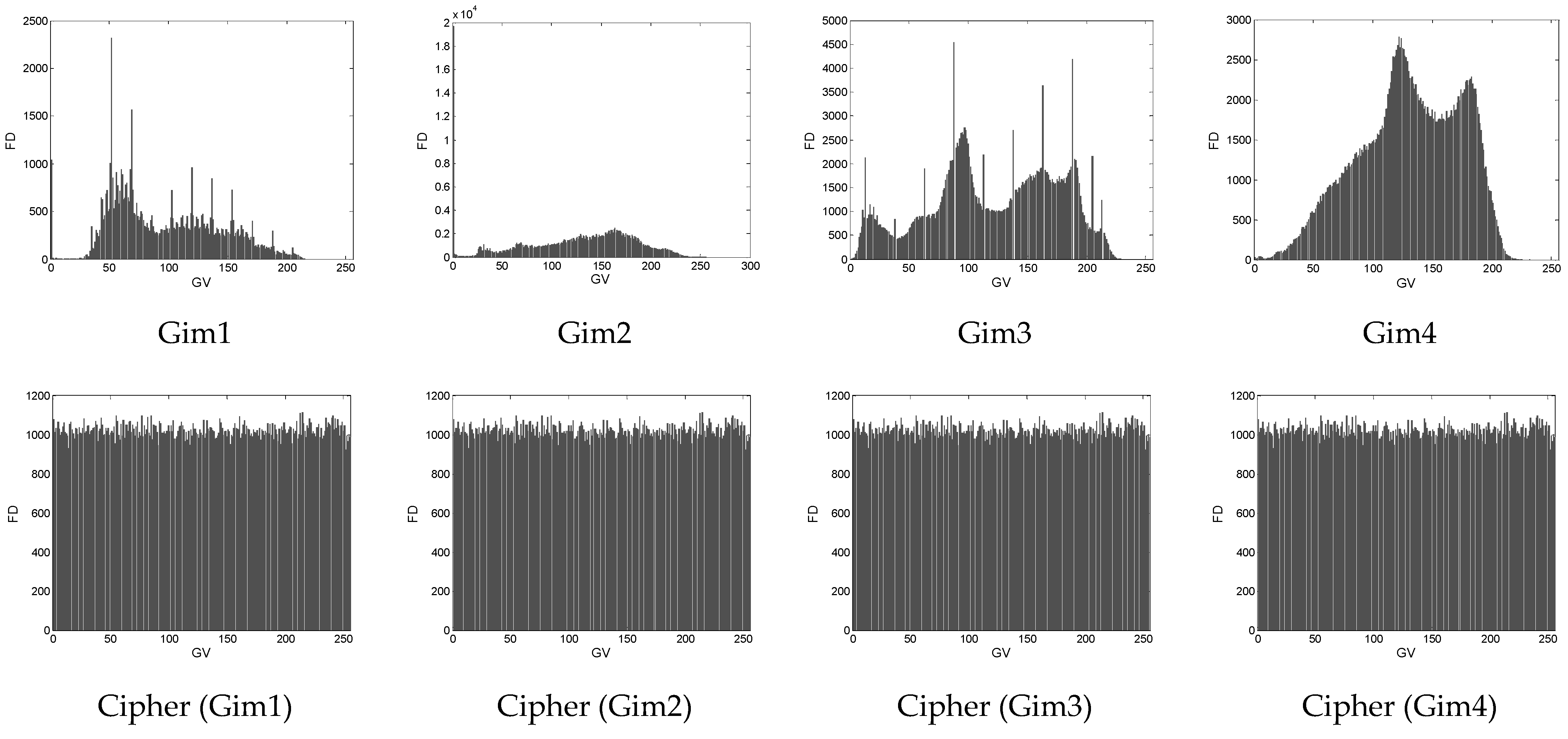
4.3. Histogram Test
4.4. Entropy Analysis
4.5. Data Loss Analysis
4.6. Analysis of Keys
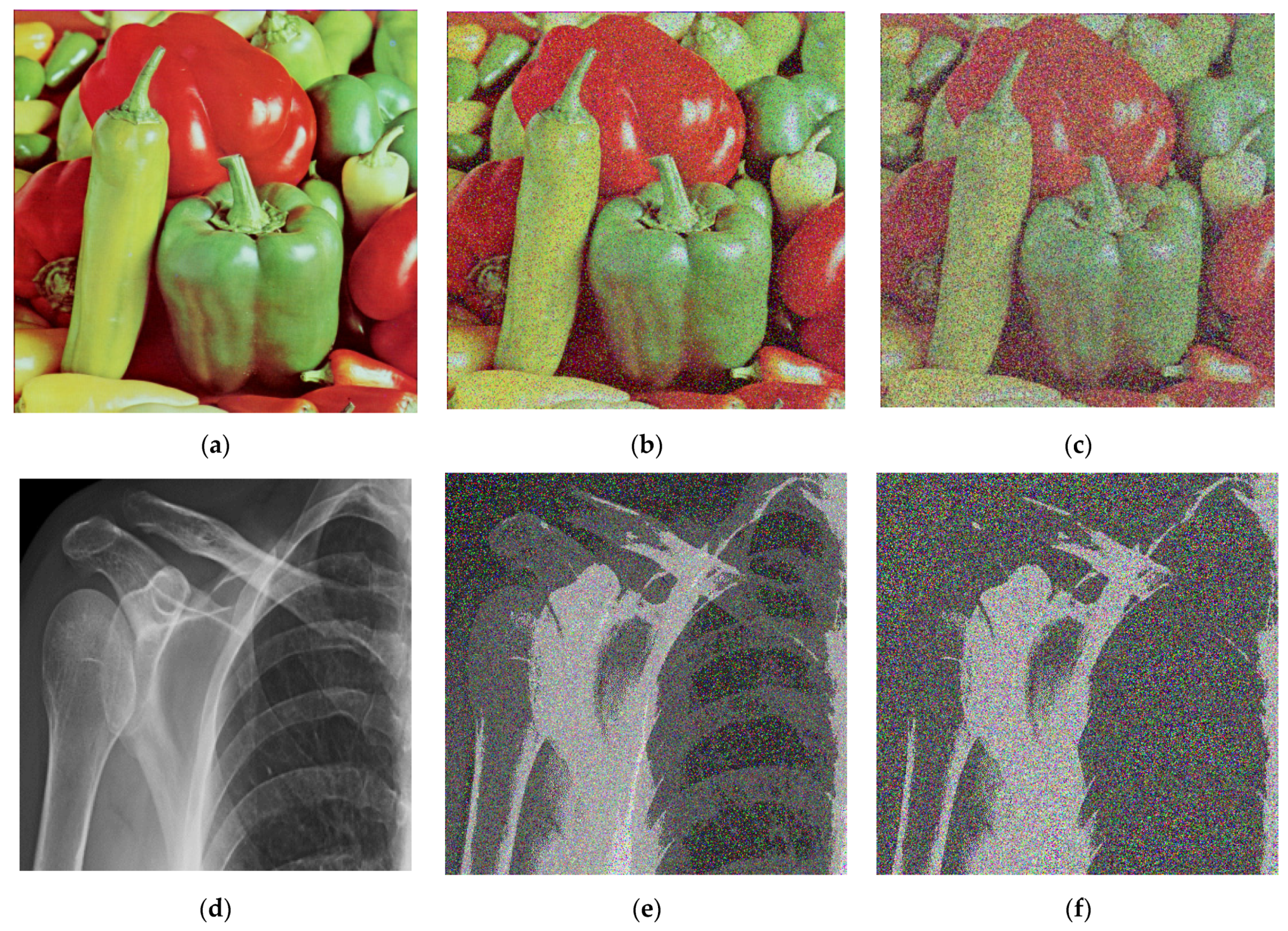
4.7. Noise Attacks
4.8. Speed Analysis
4.9. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FIPS P. 46-3. Data Encryption Standard (DES); National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999; p. 25.
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Njitacke, Z.T.; Isaac, S.D.; Tsafack, N.; Kengne, J. Window of multistability and its control in a simple 3D Hopfield neural network: Application to biomedical image encryption. Neural Comput. Appl. 2021, 33, 6733–6752. [Google Scholar] [CrossRef]
- Ahmad, M.; Alam, M.S. A new algorithm of encryption and decryption of images using chaotic mapping. Int. J. Comput. Sci. Eng. 2009, 2, 46–50. [Google Scholar]
- Song, X.-H.; Wang, H.-Q.; Venegas-Andraca, S.E.; Abd El-Latif, A.A. Quantum video encryption based on qubit-planes controlled-XOR operations and improved logistic map. Phys. A Stat. Mech. Its Appl. 2020, 537, 122660. [Google Scholar] [CrossRef]
- Khan, J.; Li, J.P.; Ahamad, B.; Parveen, S.; Haq, A.U.; Khan, G.A.; Salngaiah, A.K. SMSH: Secure surveillance mechanism on smart healthcare IoT system with probabilistic image encryption. IEEE Access 2020, 8, 15747–15767. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Inf. Sci. 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Liu, C. Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Inf. Processing 2021, 20, 1–22. [Google Scholar] [CrossRef]
- Alexeev, Y.; Bacon, D.; Brown, K.R.; Calderbank, R.; Carr, L.D.; Chong, F.T.; De Marco, B.; Englund, D.; Farhi, E.; Fefferman, B. Quantum computer systems for scientific discovery. PRX Quantum 2021, 2, 017001. [Google Scholar] [CrossRef]
- Tsafack, N.; Iliyasu, A.M.; Nkapkop, J.D.D.; Zeric, N.T.; Kengne, J.; Abd-El-Atty, B.; Belazii, A.; EL-Latif, A.A.A. A memristive RLC oscillator dynamics applied to image encryption. J. Inf. Secur. Appl. 2021, 61, 102944. [Google Scholar] [CrossRef]
- Dua, M.; Suthar, A.; Garg, A.; Garg, V. An ILM-cosine transform-based improved approach to image encryption. Complex Intell. Syst. 2021, 7, 327–343. [Google Scholar] [CrossRef]
- Khan, M.; Alanazi, A.S.; Khan, L.S.; Hussain, I. An efficient image encryption scheme based on fractal Tromino and Chebyshev polynomial. Complex Intell. Syst. 2021, 5, 1–14. [Google Scholar]
- Singh, O.; Singh, A. Data hiding in encryption–compression domain. Complex Intell. Syst. 2021, 1–14. [Google Scholar]
- Tsafack, N.; Kengne, J. A novel autonomous 5-d hyperjerk RC circuit with hyperbolic sine function. Sci. World J. 2018, 2018. [Google Scholar] [CrossRef]
- Wang, X.; Vaidyanathan, S.; Volos, C.; Pham, V.-T.; Kapitaniak, T. Dynamics, circuit realization, control and synchronization of a hyperchaotic hyperjerk system with coexisting attractors. Nonlinear Dyn. 2017, 89, 1673–1687. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Jafari, S.; Weldegiorgis, R.; Karthikeyan, A.; Duraisamy, P. Coexisting attractors in a fractional order hydro turbine governing system and fuzzy PID based chaos control. Asian J. Control 2021, 23, 894–907. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; Hirota, K.; Abd EL-Latif, A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar] [CrossRef]
- Rajagopal, K.; Pham, V.-T.; Alsaadi, F.E.; Alsaadi, F.E.; Karthikeyan, A.; Duraisamy, P. Multistability and coexisting attractors in a fractional order Coronary artery system. Eur. Phys. J. Spec. Top. 2018, 227, 837–850. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Khalaf, A.J.M.; Njitacke Tabekoueng, Z.; Fozin, T.F.; Kengne, J.; Jafari, S.; Hussain, I. A new oscillator with mega-stability and its Hamilton energy: Infinite coexisting hidden and self-excited attractors. Chaos. Interdiscip. J. Nonlinear Sci. 2020, 30, 033112. [Google Scholar] [CrossRef]
- Lai, Q.; Nestor, T.; Kengne, J.; Zhao, X.-W. Coexisting attractors and circuit implementation of a new 4D chaotic system with two equilibria. Chaos Solitons Fractals 2018, 107, 92–102. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Kengne, J. A unique chaotic snap system with a smoothly adjustable symmetry and nonlinearity: Chaos, offset-boosting, antimonotonicity, and coexisting multiple attractors. Chaos Solitons Fractals 2018, 113, 275–293. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Modelling and circuit realisation of a new no-equilibrium chaotic system with hidden attractor and coexisting attractors. Electron. Lett. 2020, 56, 1044–1046. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Pehlivan, I.; Dolvis, L.G.; Jacques, K.; Alcin, M.; Tuna, M.; Koyuncu, I. A novel ANN-based four-dimensional two-disk hyperchaotic dynamical system, bifurcation analysis, circuit realisation and FPGA-based TRNG implementation. Int. J. Comput. Appl. Technol. 2020, 62, 20–35. [Google Scholar] [CrossRef]
- Rajagopal, K.; Akgul, A.; Jafari, S.; Karthikeyan, A.; Koyuncu, I. Chaotic chameleon: Dynamic analyses, circuit implementation, FPGA design and fractional-order form with basic analyses. Chaos Solitons Fractals 2017, 103, 476–487. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T.; Rajagopal, K.; Alexander, P. Design and SPICE implementation of a 12-term novel hyperchaotic system and its synchronisation via active control. Int. J. Model. Identif. Control 2015, 23, 267–277. [Google Scholar] [CrossRef]
- Rajagopal, K.; Hasanzadeh, N.; Parastesh, F.; Hamarash, I.I.; Jafari, S.; Hussain, I. A fractional-order model for the novel coronavirus (COVID-19) outbreak. Nonlinear Dyn. 2020, 101, 711–718. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C. Secure image encryption algorithm based on hyperchaos and dynamic DNA coding. Entropy 2020, 22, 772. [Google Scholar] [CrossRef]
- Wang, T.; Wang, M.-H. Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding. Opt. Laser Technol. 2020, 132, 106355. [Google Scholar] [CrossRef]
- Farah, M.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
- Sathiyamurthi, P.; Ramakrishnan, S. Speech encryption algorithm using FFT and 3D-Lorenz–logistic chaotic map. Multimed. Tools Appl. 2020, 79, 17817–17835. [Google Scholar] [CrossRef]
- Han, X.; Xiong, X.; Duan, F. A new method for image segmentation based on BP neural network and gravitational search algorithm enhanced by cat chaotic mapping. Appl. Intell. 2015, 43, 855–873. [Google Scholar] [CrossRef]
- Pak, C.; Kim, J.; Pang, R.; Song, O.; Kim, H.; Yun, I.; Kim, J. A new color image encryption using 2D improved logistic coupling map. Multimed. Tools Appl. 2021, 80, 25367–25387. [Google Scholar] [CrossRef]
- Kengne, J. Coexistence of chaos with hyperchaos, period-3 doubling bifurcation, and transient chaos in the hyperchaotic oscillator with gyrators. Int. J. Bifurc. Chaos 2015, 25, 1550052. [Google Scholar] [CrossRef]
- Djimasra, F.; Nkapkop, J.D.D.; Tsafack, N.; Kengne, J.; Effa, J.Y.; Boukabou, A.; Bitjoka, L. Robust cryptosystem using a new hyperchaotic oscillator with stricking dynamic properties. Multimed. Tools Appl. 2021, 80, 25121–25137. [Google Scholar] [CrossRef]
- Sajjadi, S.S.; Baleanu, D.; Jajarmi, A.; Pirouz, H.M. A new adaptive synchronization and hyperchaos control of a biological snap oscillator. Chaos Solitons Fractals 2020, 138, 109919. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C.J.O. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.-M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Processing 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2197–2201. [Google Scholar] [CrossRef]
- Kengne, L.K.; Pone, J.R.M.; Tagne, H.T.K.; Kengne, J. Dynamics, control and symmetry breaking aspects of a single Opamp-based autonomous LC oscillator. AEU Int. J. Electron. Commun. 2020, 118, 153146. [Google Scholar] [CrossRef]
- Yang, X.; He, X.; Zhao, J.; Zhang, Y.; Zhang, S.; Xie, P. COVIDCT-dataset: A CT scan dataset about COVID-19. arXiv 2020, arXiv:2003.13865. [Google Scholar]
- Lin, R.P.; Krucker, S.; Hurford, G.; Smith, D.; Hudson, H.; Holman, G.; Schwartz, R.A.; Dennis, B.R.; Share, G.H.; Murphy, R.J. RHESSI observations of particle acceleration and energy release in an intense solar gamma-ray line flare. Astrophys. J. Lett. 2003, 595, L69. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, N.; Leonov, G.; Mokaev, T.N. Finite-time and exact Lyapunov dimension of the Henon map. In Nonlinear Sciences, Chaotic Dynamics; Cornell University: Ithaca, NY, USA, 2017. [Google Scholar]
- Cignetti, F.; Decker, L.M.; Stergiou, N. Sensitivity of the Wolf’s and Rosenstein’s algorithms to evaluate local dynamic stability from small gait data sets. Ann. Biomed. Eng. 2012, 40, 1122–1130. [Google Scholar] [CrossRef]
- Mansouri, A.; Wang, X. A novel block-based image encryption scheme using a new Sine powered chaotic map generator. Multimed. Tools Appl. 2021, 80, 21955–21978. [Google Scholar] [CrossRef]
- Kaplan, J.L.; Yorke, J.A. Chaotic behavior of multidimensional difference equations. In Functional Differential Equations and Approximation of Fixed Points; Springer: Berlin/Heidelberg, Germany, 1979; pp. 204–227. [Google Scholar]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M.J. Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, Q. Dynamical analysis of the generalized Sprott C system with only two stable equilibria. Nonlinear Dyn. 2012, 68, 543–554. [Google Scholar] [CrossRef]
- Kengne, J.; Signing, V.F.; Chedjou, J.; Leutcho, G. Nonlinear behavior of a novel chaotic jerk system: Antimonotonicity, crises, and multiple coexisting attractors. Int. J. Dyn. Control 2018, 11, 1–18. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, H.; Kuate, P.D.K.; Xu, G.; Zhao, X.W. Analysis and implementation of no-equilibrium chaotic system with application in image encryption. Appl. Intell. 2022, 1–24. [Google Scholar] [CrossRef]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Solitons Fractals 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Tamang, J.; Nkapkop, J.D.D.; Ijaz, M.F.; Prasad, P.K.; Tsafack, N.; Saha, A.; Kengne, J.; Son, Y. Dynamical properties of ion-acoustic waves in space plasma and its application to image encryption. IEEE Access 2021, 9, 18762–18782. [Google Scholar] [CrossRef]
- Tsafack, N.; Sankar, S.; Abd-El-Atty, B.; Kengne, J.; Jithin, K.; Belazi, A.; Mehmood, I.; Bashir, A.K.; Song, O.-Y.; El-Latif, A.A.A. A new chaotic map with dynamic analysis and encryption application in internet of health things. IEEE Access 2020, 8, 137731–137744. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. Signal Processing 2016, 128, 155–170. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Sone, M.E.; Fozin, T.F.; Tsafack, N.; Leutcho, G.D.; Tchapga, C.T. Control of multistability with selection of chaotic attractor: Application to image encryption. Eur. Phys. J. Spec. Top. 2021, 230, 1839–1854. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Li, L.; Zhang, T.; Wang, N.; Song, X.; Niu, X. Digital image encryption scheme based on multiple chaotic systems. Sens. Imaging Int. J. 2012, 13, 67–88. [Google Scholar] [CrossRef]
- Doubla, I.S.; Njitacke, Z.T.; Ekonde, S.; Tsafack, N.; Nkapkop, J.D.D.; Kengne, J. Multistability and circuit implementation of tabu learning two-neuron model: Application to secure biomedical images in IoMT. Neural Comput. Appl. 2021, 33, 14945–14973. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Diaconu, A.-V.; Rhouma, R.; Belghith, S. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt. Lasers Eng. 2017, 88, 37–50. [Google Scholar] [CrossRef]
- Cao, W.; Mao, Y.; Zhou, Y. Designing a 2D infinite collapse map for image encryption. Signal Processing 2020, 171, 107457. [Google Scholar] [CrossRef]
- Hua, T.; Chen, J.; Pei, D.; Zhang, W.; Zhou, N. Quantum image encryption algorithm based on image correlation decomposi-tion. Int. J. Theor. Phys. 2015, 54, 526–537. [Google Scholar] [CrossRef]
- Gong, L.-H.; He, X.-T.; Cheng, S.; Hua, T.-X.; Zhou, N.-R. Quantum image encryption algorithm based on quantum image XOR operations. Int. J. Theor. Phys. 2016, 55, 3234–3250. [Google Scholar] [CrossRef]








| Works | [43] | [45] | [36] | This Work |
|---|---|---|---|---|
| LE | 2.20 | 1.00 | 0.45 | 2.9 |
| LD | 1.25 | 0.81 | 0.27 | 2 |
| Test | p-Value Related to | p-Value Related to | Decision |
|---|---|---|---|
| Frequency | 0.2058 | 0.9301 | Passed |
| Block Frequency | 0.6301 | 0.0672 | Passed |
| DFT | 0.0532 | 0.0903 | Passed |
| Rank | 0.0981 | 0.0470 | Passed |
| Runs | 0.8732 | 0.5098 | Passed |
| Longest runs of ones | 0.2907 | 0.4093 | Passed |
| Overlapping templates | 0.3896 | 0.0986 | Passed |
| No overlapping templates | 0.0480 | 0.0198 | Passed |
| Universal approximate entropy | 0.8763 | 0.5701 | Passed |
| Linear complexity | 0.0541 | 0.0967 | Passed |
| Cumulative sums (forward) | 0.0298 | 0.0878 | Passed |
| Serial test 1 | 0.7191 | 0.8024 | Passed |
| Random excursions x = 1 | 0.0637 | 0.01892 | Passed |
| Random excursions variant x = 1 | 0.4290 | 0.3109 | Passed |
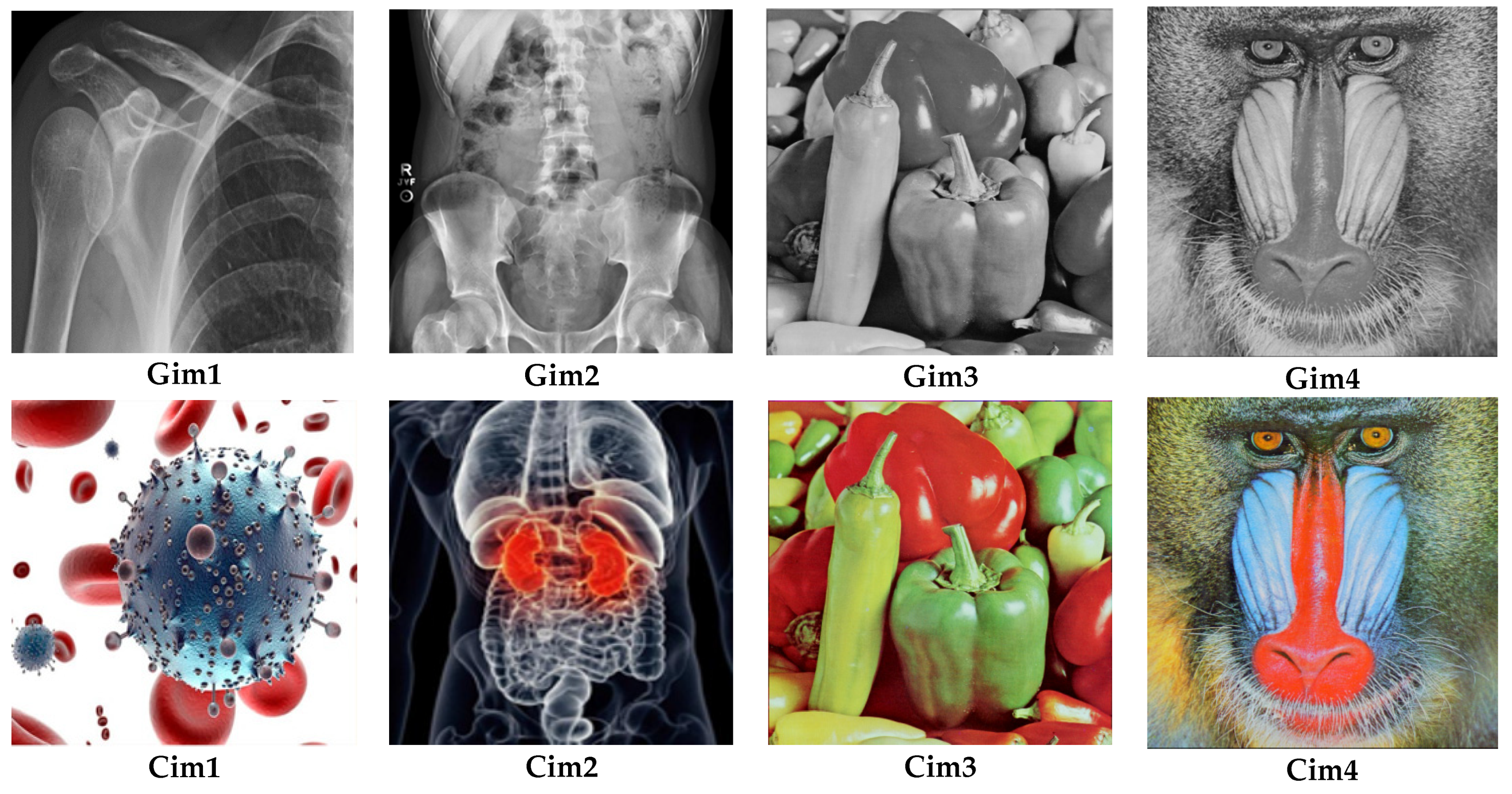
| Images | Gim1 | Gim2 | Gim3 | Gim4 | Cim1 | Cim2 | Cim3 | Cim4 |
|---|---|---|---|---|---|---|---|---|
| PSNR | 8.8491 | 8.5483 | 8.8697 | 9.5063 | 6.5086 | 7.0874 | 8.0773 | 8.77 84 |
| Images | Directions | ||
|---|---|---|---|
| Hor. | Ver. | Dia. | |
| Gim1 | 0.9708 | 0.9662 | 0.9678 |
| Cipher (Gim1) | −0.0005 | −0.0049 | 0.0079 |
| Gim2 | 0.9709 | 0.9698 | 0.9498 |
| Cipher (Gim2) | 0.0195 | −0.0001 | 0.0048 |
| Gim3 | 0.9762 | 0.9735 | 0.9573 |
| Cipher (Gim3) | 0.0098 | 0.0169 | 0.0033 |
| Gim4 | 0.7610 | 0.8621 | 0.0113 |
| Cipher (Gim4) | 0.0019 | 0.0063 | 0.0011 |
| Images | Directions | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hor. | Ver. | Dia. | |||||||
| R | G | B | R | G | B | R | G | B | |
| Cim1 | 0.9561 | 0.9613 | 0.9603 | 0.9562 | 0.9620 | 0.9607 | 0.9437 | 0.9359 | 0.9327 |
| Cipher (Cim1) | −0.0010 | 0.0020 | 0.0012 | 0.0045 | −0.0050 | 0.0013 | 0.0015 | −0.0037 | 0.0001 |
| Cim2 | 0.9789 | 0.9676 | 0.9684 | 0.9740 | 0.9594 | 0.9614 | 0.9583 | 0.9349 | 0.9380 |
| Cipher (Cim2) | 0.0025 | −0.0014 | 0.0021 | 0.0042 | 0.0001 | −0.0008 | 0.0019 | 0.0028 | 0.0032 |
| Cim3 | 0.9664 | 0.9815 | 0.9843 | 0.9644 | 0.9819 | 0.9644 | 0.9607 | 0.9687 | 0.9607 |
| Cipher(Cim3) | 0.0086 | −0.0010 | −0.0030 | −0.0026 | 0.0080 | 0.0004 | −0.0064 | 0.0070 | 0.0042 |
| Cim4 | 0.8744 | 0.7609 | 0.8841 | 0.9261 | 0.8636 | 0.9092 | 0.8658 | 0.7341 | 0.8455 |
| (Cipher Baboon) | −0.0036 | −0.0053 | 0.0047 | 0.0071 | −0.0095 | 0.0009 | 0.0058 | 0.0013 | 0.0022 |
| Image | UACI (%) | NPCR (%) |
|---|---|---|
| Gim1 | 33.4301 | 99.6063 |
| Gim2 | 33.4421 | 99.6124 |
| Gim3 | 33.3941 | 99.6239 |
| Gim4 | 33.3812 | 99.6250 |
| Cim1 | 33.3875 | 99.5956 |
| Cim2 | 33.4002 | 99.6093 |
| Cim3 | 33.4124 | 99.6019 |
| Cim4 | 33.3907 | 99.6102 |
| Image | Original | Cipher |
|---|---|---|
| Gim1 | 3.28779 | 7.99966 |
| Gim2 | 7.40914 | 7.99924 |
| Gim3 | 7.50575 | 7.99977 |
| Gim4 | 7.35787 | 7.99925 |
| Cim1 | 6.12902 | 7.99840 |
| Cim2 | 7.37286 | 7.99900 |
| Cim3 | 7.66982 | 7.99974 |
| Cim4 | 7.76243 | 7.99975 |
| Image Size | 512 × 512 × 1 | 512 × 512 × 3 |
|---|---|---|
| Encryption time t (s) | 0.2404 | 0.7739 |
| Encryption Throughput ET (MBps) | 1090.4492 | 1016.1933 |
| Number of Cycles NC | 2.2009 | 2.3617 |
| Method | t (ms) | ET (MBps) | NC | Entropy | UACI | NPCR | Big-O Complexity |
|---|---|---|---|---|---|---|---|
| This work | 0.2404 | 1 090.4492 | 2.2009 | 7.9996 | 33.3812 | 99.6250 | O(n) |
| [60] | 1.7043 | 153.8132 | 15.6033 | 7.9951 | 33.3730 | 99.5893 | NR |
| [45] | 8.2460 | 31.7904 | 75.4944 | 7.9925 | 33.3420 | 99.6059 | NR |
| [32] | 13.1804 | 19.8889 | 120.6703 | 7.9971 | 33.3384 | 99.6134 | NR |
| [61] | NR | NR | NR | NR | NR | NR | O(N22n) |
| [62] | NR | NR | NR | NR | NR | NR | O(22n) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etoundi, C.M.L.; Nkapkop, J.D.D.; Tsafack, N.; Ngono, J.M.; Ele, P.; Wozniak, M.; Shafi, J.; Ijaz, M.F. A Novel Compound-Coupled Hyperchaotic Map for Image Encryption. Symmetry 2022, 14, 493. https://doi.org/10.3390/sym14030493
Etoundi CML, Nkapkop JDD, Tsafack N, Ngono JM, Ele P, Wozniak M, Shafi J, Ijaz MF. A Novel Compound-Coupled Hyperchaotic Map for Image Encryption. Symmetry. 2022; 14(3):493. https://doi.org/10.3390/sym14030493
Chicago/Turabian StyleEtoundi, Christophe Magloire Lessouga, Jean De Dieu Nkapkop, Nestor Tsafack, Joseph Mvogo Ngono, Pierre Ele, Marcin Wozniak, Jana Shafi, and Muhammad Fazal Ijaz. 2022. "A Novel Compound-Coupled Hyperchaotic Map for Image Encryption" Symmetry 14, no. 3: 493. https://doi.org/10.3390/sym14030493
APA StyleEtoundi, C. M. L., Nkapkop, J. D. D., Tsafack, N., Ngono, J. M., Ele, P., Wozniak, M., Shafi, J., & Ijaz, M. F. (2022). A Novel Compound-Coupled Hyperchaotic Map for Image Encryption. Symmetry, 14(3), 493. https://doi.org/10.3390/sym14030493






