Another Perspective on Automatic Construction of Integral Distinguishers for ARX Ciphers
Abstract
:1. Introduction
- (1)
- Construction method based on traditional integral property
- (2)
- Construction method based on division property
- (3)
- Construction method based on the symmetry between different distinguishers
1.1. Related Work
1.2. Our Contributions
- ➢
- Based on establishing a subspace of zero-correlation linear distinguishers (short for ZCLDs) and the relationship between the zero-correlation linear distinguishers and integral distinguishers (short for INTDs) of ARX ciphers, a unified method is proposed to construct theoretical integral distinguishers for ARX ciphers. For any ARX ciphers, if a subspace of ZCLDs can be constituted with our method, a corresponding length of integral distinguisher is developed. In addition, the number of active bits for the integral distinguisher can be controlled through the scale of the subspace.
- ➢
- To validate the effectiveness of this method, we take three ARX ciphers—HIGHT, SPECK and LEA as examples. For LEA, four nine-round integral distinguishers are constructed, which is one round longer than previous distinguishers derived with bit-based division property. For SPECK32, two more six-round integral distinguishers are derived, the number of active bits is one bit less than previous best distinguishers. For HIGHT, four 17-round new integral distinguishers are discovered.
2. Preliminary
2.1. Relationship between the ZCLDs and INTDs for ARX Ciphers
2.2. Automatic Search of Zero-Correlation Linear Hulls for ARX Ciphers
3. Automatic Construction of Integral Distinguishers
- ➢
- Through Theorem 1, it is found that with more free bits, the less the dimension of the corresponding integral distinguisher is. A free bit represents the linear mask bit, which can take any value on , the dimension represents the number of active bits for the integral distinguisher.
3.1. Basic Idea of our Automatic Method
- (1)
- Based on the automatic ZCLD searching method, construct a long zero-correlation linear distinguisher and derive the contradiction bit for this distinguisher.
- (2)
- Change the zero of linear mask for the input/output into one that is bit by bit. If the change does not affect the contradiction bit, store the position of this input/output bit. All the stored positions can constitute a subspace for the input linear mask and a subspace for the output linear mask.
- (3)
- Test whether all the linear masks in the subspace can be zero-correlation linear distinguishers with the same contradiction bit as . If, after adding some bits, not all linear approximations in the subspace are zero-correlation, remove the positions of these bits.
- (4)
- Construct integral distinguishers with the remaining subspace.
3.2. An Automatic Construction Method of Integral Distinguishers for ARX Ciphers
| Algorithm 1 An automatic construction method of integral distinguishers. |
| Step 1: Construct a long (-round) zero-correlation linear distinguisher , denote the contradiction bit of the distinguisher as . Step 2: Construct a set . Add the positions for the nonzero bits of to the set according to the following rule. ➢ Set zeros of to one bit by bit, and add those bit positions that do not affect the contradiction bit to set . Step 3: Test whether for any , is an round zero-correlation linear distinguisher. Delete those bit positions that do not pass this test from set . represents the single bit linear mask, which has one at the i-th bit. ➢ Construct a subspace based on . In this subspace, all the linear approximations are -round zero-correlation. Step 4: Turn the subspace of zero-correlation linear distinguishers into an integral distinguisher. |
- ➢
- The length of the zero-correlation linear distinguisher should be as long as possible. As the length of the constructed INTD is the same as the length of the ZCLDs, if we want the length of the INTD to be longer, the ZCLDs used should be as long as possible.
- ➢
- If there is only one longest zero-correlation linear distinguisher, the integral distinguisher derived is a trivial integral distinguisher, and it is infeasible to construct an integral distinguisher. Some shorter zero-correlation linear distinguishers should be considered to construct integral distinguishers.
- ➢
- This method can also be used to construct a subspace of long impossible differential distinguishers or zero-correlation linear distinguishers.
3.3. A Toy Example
4. Applications
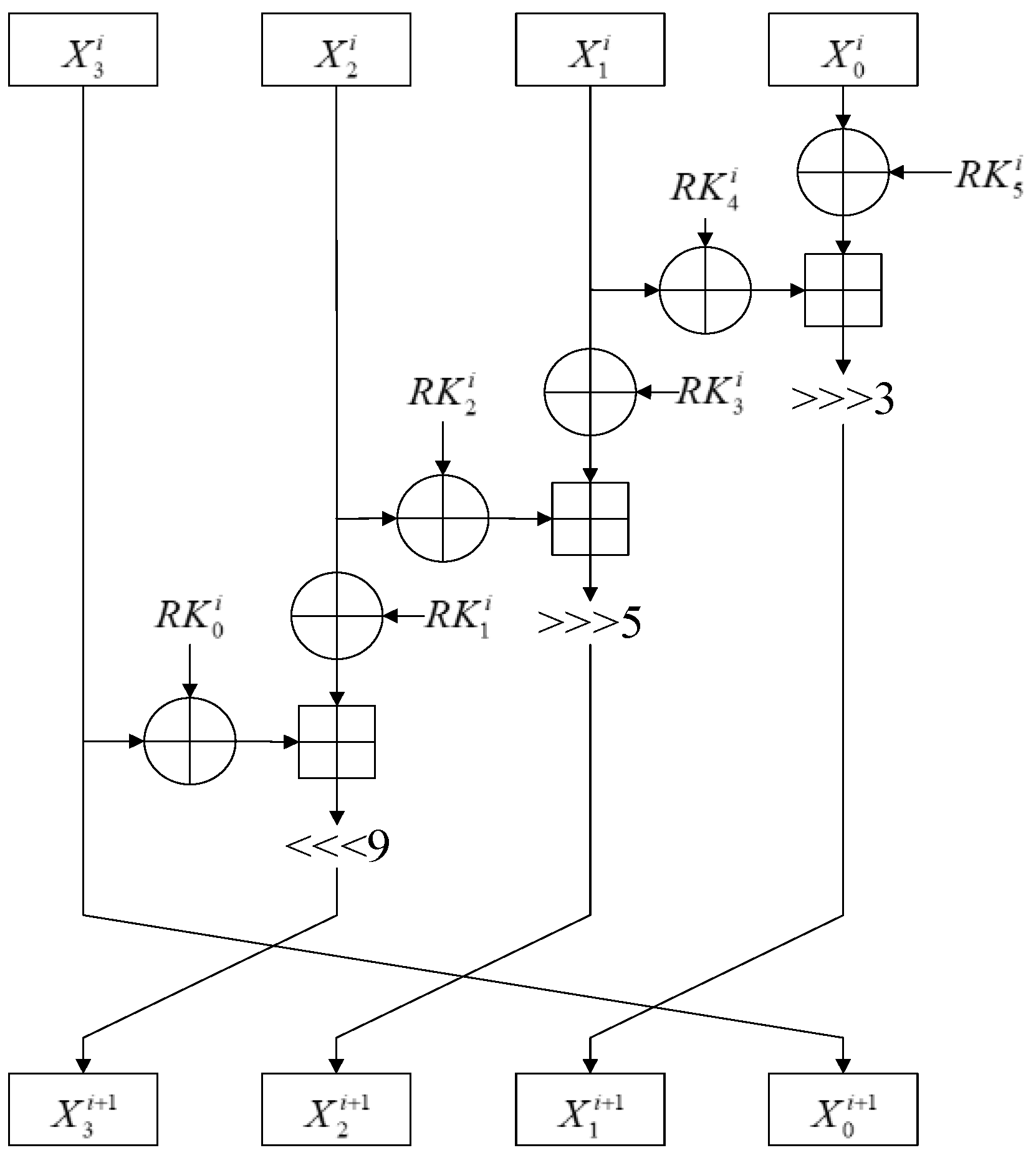
4.1. Brief Descriptions on HIGHT, LEA and SPECK
4.2. Constructing Integral Distinguishers
4.2.1. Integral Distinguishers for HIGHT
4.2.2. Integral Distinguishers for LEA
4.2.3. Integral Distinguishers for SPECK32
5. Validation on LEA
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Round | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 10000000 |
| 1 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 10000000 | 00000000 |
| 2 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 1******* | ******** | 00000000 |
| 3 | 00000000 | 00000000 | 00000000 | 00000000 | 1******* | ******** | ******** | 00000000 |
| 4 | 00000000 | 00000000 | 00000000 | 1******* | ******** | ******** | ******** | 00000000 |
| 5 | 00000000 | 00000000 | 1******* | ******** | ******** | ******** | ******** | 00000000 |
| 6 | 00000000 | 1******* | ******** | ******** | ******** | ******** | ******** | 00000000 |
| 7 | 1******* | ******** | ******** | ******** | ******** | ******** | ******** | 00000000 |
| 8 | ******** | ******** | ******** | ******** | ******** | ******** | ******** | 1******* |
| 8 | ******** | ******** | ******** | ******** | ******** | ******** | 00000001 | 0******* |
| 9 | ******** | ******** | ******** | ******** | 00000000 | 00000001 | 0******* | ******** |
| 10 | ******** | ******** | 00000000 | 00000000 | 00000001 | 0******* | ******** | ******** |
| 11 | 00000000 | 00000000 | 00000000 | 00000001 | 1******* | ******** | ******** | ******** |
| 12 | 00000000 | 00000000 | 00000001 | 1******* | ******** | ******** | 00000000 | 00000000 |
| 13 | 00000000 | 00000001 | 1******* | ******** | 00000000 | 00000000 | 00000000 | 00000000 |
| 14 | 00000001 | 11000010 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 |
| 15 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000001 |
| 16 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000001 | 00000000 |
| 17 | 00000000 | 00000000 | 00000000 | 00000000 | 00000000 | 00000001 | 00110100 | 00000000 |
Appendix B
| Round | ||||
|---|---|---|---|---|
| 0 | 00000000000000000000000000000000 | 00000000000000000000000000000001 | 00000000000000000000000000000000 | 00000000000000000000000000000000 |
| 1 | 00000000000000000000001000000000 | 00000000000000000000000000000000 | 00000000000000000000000000000000 | 00000000000000000000000000000001 |
| 2 | 00000000000000000000001000000000 | 00001000000000000000000000000000 | 00100000000000000000000000000000 | 00000000000000000000001000000001 |
| 3 | ***********************001****** | *****001************************ | ***00000000000000000000001****** | 001***************************** |
| 4 | ******************************** | ******************************** | ***001************************** | ******************************** |
| 4 | 1******************************* | 1******************************* | 000000000001******************** | 00000000000001****************** |
| 5 | 000000000000000000000001******** | 00000000000000001*************** | 00000000000000001*************** | 0000000000000000001************* |
| 6 | 00000000000000000000000000000000 | 0000000000000000000001********** | 0000000000000000000001********** | 000000000000000000000001******** |
| 7 | 00000000000000000000000000000000 | 000000000000000000000000001***** | 000000000000000000000000001***** | 00000000000000000000000000000000 |
| 8 | 00000000000000000000000000000000 | 00000000000000000000000000000001 | 00000000000000000000000000000000 | 00000000000000000000000000000000 |
| 9 | 00000000000000000000001000000000 | 00000000000000000000000000000000 | 00000000000000000000000000000000 | 00000000000000000000000000000001 |
Appendix C
| Round | ||
|---|---|---|
| 0 | 0000000000000000 | 0000000010000000 |
| 1 | 0000001000000000 | 0000001000000000 |
| 2 | 000010000001**** | 000010000001**00 |
| 3 | 1*************** | 1*************00 |
| 3 | *********1****** | 0*************** |
| 4 | 00000001*0000000 | 100000000000001* |
| 5 | 0000000000000000 | 0000000000000010 |
| 6 | 0000000000001000 | 0000000000001000 |
References
- Hong, D.; Sung, J.; Hong, S.; Lim, J.; Lee, S.; Koo, B.S.; Lee, C.; Chang, D.; Lee, J.; Jeong, K.; et al. HIGHT: A new block cipher suitable for low-resource device. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Yokohama, Japan, 10–13 October 2006; pp. 46–59. [Google Scholar]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK lightweight block ciphers. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; pp. 1–6. [Google Scholar]
- Aumasson, J.P.; Meier, W.; Phan, R.C.W.; Henzen, L. The Hash Function BLAKE; Springer: Berlin, Germany, 2014. [Google Scholar]
- Ferguson, N.; Lucks, S.; Schneier, B.; Whiting, D.; Bellare, M.; Kohno, T.; Callas, J.; Walker, J. The Skein Hash Function Family. Submission to NIST (Round 3). 2010. Available online: https://www.schneier.com/wp-content/uploads/2016/02/skein.pdf (accessed on 10 January 2022).
- Wheeler, D.J.; Needham, R.M. TEA, a tiny encryption algorithm. In Proceedings of the International Workshop on Fast Software Encryption, Cambridge, UK, 9–11 December 1993; pp. 363–366. [Google Scholar]
- Needham, R.; Wheeler, D.J. Extended Tiny Encryption Algorithm; Technical Report; Computer Laboratory, University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Wheeler, D.; Needham, R. XXTEA: Correction to XTEA; Technical Report; Computer Laboratory, University of Cambridge: Cambridge, UK, 1998. [Google Scholar]
- Bernstein, D.J. The Salsa20 family of stream ciphers. In New Stream Cipher Designs; Robshaw, M., Billet, O., Eds.; Springer: Berlin, Germany, 2008; Volume 4986, pp. 84–97. [Google Scholar]
- Daemen, J.; Knudsen, L.; Rijmen, V. The block cipher Square. In Proceedings of the International Workshop on Fast Software Encryption, Haifa, Israel, 20–22 January 1997; pp. 149–165. [Google Scholar]
- Knudsen, L.; Wagner, D. Integral cryptanalysis. In Proceedings of the International Workshop on Fast Software Encryption, Leuven, Belgium, 4–6 February 2002; pp. 112–127. [Google Scholar]
- Kim, J.; Hong, S.; Sung, J.; Lee, S.; Lim, J.; Sung, S. Impossible differential cryptanalysis for block cipher structures. In Proceedings of the International Conference on Cryptology in India, New Delhi, India, 8–10 December 2003; pp. 82–96. [Google Scholar]
- Zhang, W.; Su, B.; Wu, W.; Feng, D.; Wu, C. Extending higher-order integral: An efficient unified algorithm of constructing integral distinguishers for block ciphers. In Proceedings of the International Conference on Applied Cryptography and Network Security, Singapore, 26–29 June 2012; pp. 117–134. [Google Scholar]
- Zhang, H.; Wu, W.; Wang, Y. Integral attack against bit-oriented block ciphers. In Proceedings of the Information Security and Cryptology, Seoul, Korea, 25–27 November 2015; pp. 102–118. [Google Scholar]
- Todo, Y. Structural evaluation by generalized integral property. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; pp. 287–314. [Google Scholar]
- Todo, Y.; Morii, M. Bit-based division property and application to simon family. In Proceedings of the International Conference on Fast Software Encryption, Bochum, Germany, 20–23 March 2016; pp. 357–377. [Google Scholar]
- Xiang, Z.; Zhang, W.; Bao, Z.; Lin, D. Applying MILP method to searching integral distinguishers based on division property for 6 lightweight block ci-phers. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016; pp. 648–678. [Google Scholar]
- Sun, L.; Wang, W.; Wang, M.Q. MILP-aided bit-based division property for primitives with non-bit-permutation linear layers. IET Inf. Secur. 2019, 14, 12–20. [Google Scholar] [CrossRef]
- Wang, S.; Hu, B.; Guan, J.; Zhang, K.; Shi, T. MILP-aided method of searching division property using three subsets and applications. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; pp. 398–427. [Google Scholar]
- Hao, Y.; Leander, G.; Meier, W.; Todo, Y.; Wang, Q. Modeling for three-subset division property without unknown subset and improved cube attacks. In Proceedings of the 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; pp. 466–495. [Google Scholar]
- Ghosh, S.; Dunkelman, O. Automatic search for bit-based division property. In Proceedings of the International Conference on Cryptology and Information Security in Latin America, Bogotá, Colombia, 6–8 October 2021; pp. 254–274. [Google Scholar]
- ElSheikh, M.; Youssef, A.M. On MILP-based automatic search for bit-based division property for ciphers with (large) linear layers. In Proceedings of the Australasian Conference on Information Security and Privacy, Perth, WA, Australia, 1–3 December 2021; pp. 111–131. [Google Scholar]
- Bogdanov, A.; Leander, G.; Nyberg, K.; Wang, M. Integral and multidimensional linear distinguishers with correlation zero. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Beijing, China, 2–6 December 2012; pp. 244–261. [Google Scholar]
- Sun, B.; Liu, Z.; Rijmen, V.; Li, R.; Cheng, L.; Wang, Q.; Alkhzaimi, H.; Li, C. Links among impossible differential, integral and zero correlation linear cryptanalysis. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; pp. 95–115. [Google Scholar]
- Wen, L.; Wang, M. Integral zero-correlation distinguisher for ARX block cipher, with application to SHACAL-2. In Proceedings of the Australasian Conference on Information Security and Privacy, Wollongong, NSW, Australia, 7–9 July 2014; pp. 454–461. [Google Scholar]
- Sun, L.; Wang, W.; Wang, M. Automatic search of bit-based division property for ARX ciphers and word-based divi1sion property. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; pp. 128–157. [Google Scholar]
- Sun, L.; Wang, W.; Liu, R.; Wang, M. MILP-aided bit-based division property for ARX ciphers. Sci. China Inf. Sci. 2017, 61, 118102:1–118102:3. [Google Scholar] [CrossRef]
- Eskandari, Z.; Kidmose, A.B.; Kölbl, S.; Tiessen, T. Finding integral distinguishers with ease. In Proceedings of the International Conference on Selected Areas in Cryptography, Calgary, AB, Canada, 15–17 August 2018; pp. 115–138. [Google Scholar]
- Han, Y.; Li, Y.; Wang, M. Automatical method for searching integrals of ARX block cipher with division property using three subsets. In Proceedings of the International Conference on Information and Communications Security, Lille, France, 29–31 October 2018; pp. 647–663. [Google Scholar]
- Zhang, K.; Guan, J.; Hu, B. Automatic search of impossible differentials and zero-correlation linear hulls for ARX ciphers. China Commun. 2018, 15, 54–66. [Google Scholar] [CrossRef]
- Sasaki, Y.; Todo, Y. New impossible differential search tool from design and cryptanalysis aspects. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 30 April–4 May 2017; pp. 185–215. [Google Scholar]
- Zhang, P.; Sun, B.; Li, C. Saturation attack on the block cipher HIGHT. In Proceedings of the International Conference on Cryptology and Network Security, Kanazawa, Japan, 12–14 December 2009; pp. 76–86. [Google Scholar]
- Hong, D.; Lee, J.K.; Kim, D.C.; Kwon, D.; Ryu, K.H.; Lee, D.G. LEA: A 128-bit block cipher for fast encryption on common processors. In Proceedings of the International Workshop on Information Security Applications, Jeju Island, Korea, 19–21 August 2013; pp. 3–27. [Google Scholar]
- Li, H.; Ren, J.J.; Chen, S.Z. Integral attack on reduced-round LEA cipher. Acta Electron. Sin. 2020, 48, 17. [Google Scholar]



| Algorithm | Longest Round | Least Dimension ♣ | Number | Reference | Remark |
|---|---|---|---|---|---|
| HIGHT | 12 | 8 | 1 | [1] | Traditional Integral Property |
| 17 | 56 | 2 | [31] | Traditional Integral Property | |
| 17 | 57 | 4 | This paper | Relation between different distinguishers | |
| 18 | 63 | 2 | [25,26,27] | Bit-Based Division Property | |
| LEA | 6 | 32 | 1 | [32] | Traditional Integral Property |
| 7 | 96 | 1 | [26] | Bit-Based Division Property | |
| 8 | 118 | 2 | [25,27] | Bit-Based Division Property | |
| 9 * | 126 | 4 | This paper | Relation between different distinguishers | |
| SPECK32 | 6 | 31 | 1 | [25] | Word-Based Division Property |
| 6 | 31 | 2 | [28] | Three Subsets Bit-Based Division Property | |
| 6 | 30 | 2 | This paper | Relation between different distinguishers |
| Round | |
|---|---|
| 0 | 00000000000000000000000000000000000000000000000000000000000001**0000000000000000000000000000000000000000000000000000000000000000 |
| 1 | 000000000000000000001**0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001** |
| 2 | 000000000000000000001**000000000001**0000000000000000000000000001**00000000000000000000000000000000000000000000000001**0000001** |
| 3 | ***********************1*************1*****************************000000000000000000001********1******************************* |
| 4 | *******************************************************************1************************************************************ |
| 4 | 1*******************************1*******************************000000000001********************00000000000001****************** |
| 5 | 000000000000000000000001********00000000000000001***************00000000000000001***************0000000000000000001************* |
| 6 | 000000000000000000000000000000000000000000000000000001**********0000000000000000000001**********000000000000000000000001******** |
| 7 | 00000000000000000000000000000000000000000000000000000000001*****000000000000000000000000001*****00000000000000000000000000000000 |
| 8 | 00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000 |
| 9 | 00000000000000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Lai, X. Another Perspective on Automatic Construction of Integral Distinguishers for ARX Ciphers. Symmetry 2022, 14, 461. https://doi.org/10.3390/sym14030461
Zhang K, Lai X. Another Perspective on Automatic Construction of Integral Distinguishers for ARX Ciphers. Symmetry. 2022; 14(3):461. https://doi.org/10.3390/sym14030461
Chicago/Turabian StyleZhang, Kai, and Xuejia Lai. 2022. "Another Perspective on Automatic Construction of Integral Distinguishers for ARX Ciphers" Symmetry 14, no. 3: 461. https://doi.org/10.3390/sym14030461
APA StyleZhang, K., & Lai, X. (2022). Another Perspective on Automatic Construction of Integral Distinguishers for ARX Ciphers. Symmetry, 14(3), 461. https://doi.org/10.3390/sym14030461





