Modifications for the Differential Evolution Algorithm
Abstract
:1. Introduction
2. Modifications
2.1. The Base Algorithm
| Algorithm 1: DE algorithm. |
|
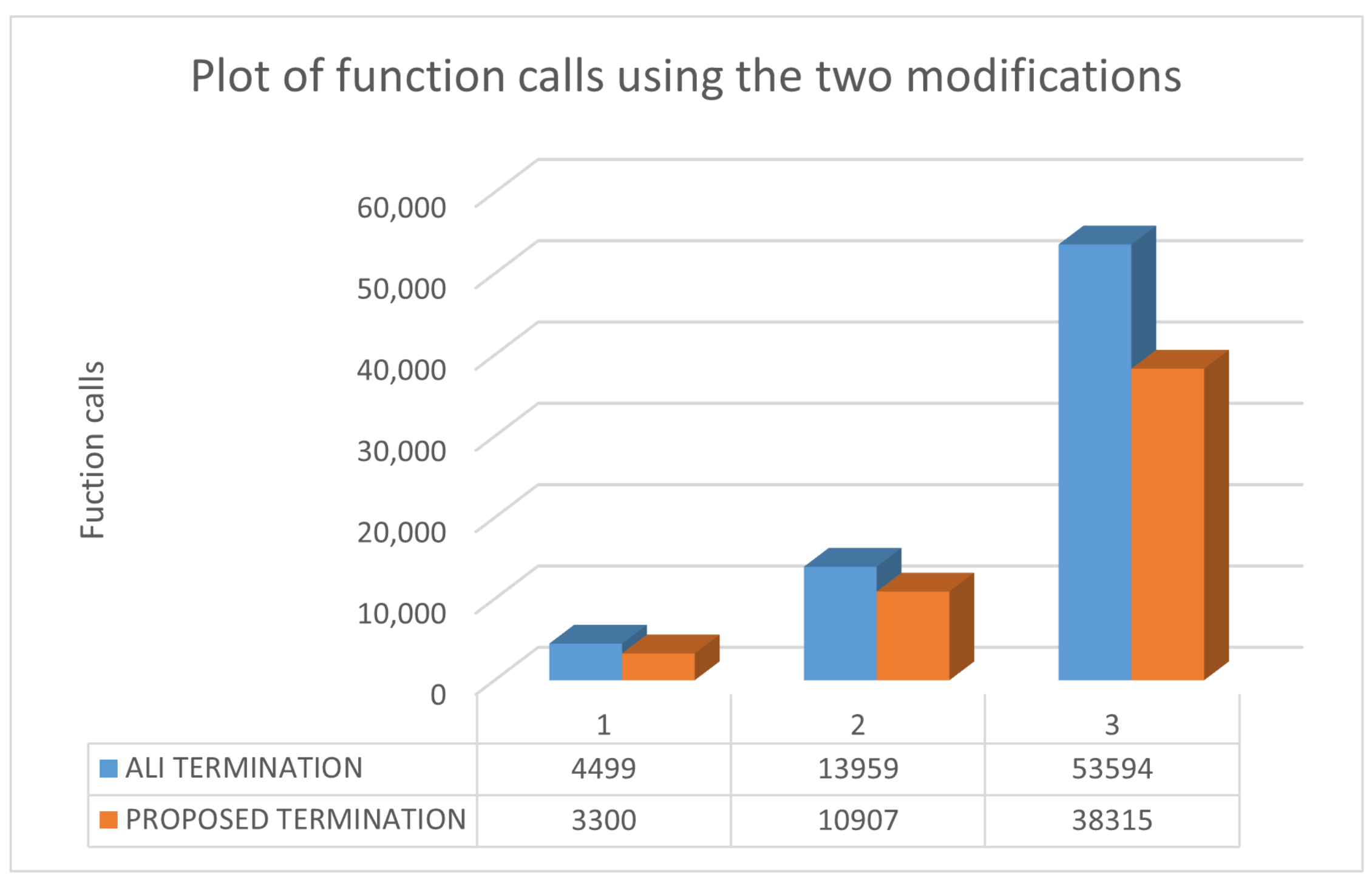
2.2. The New Termination Rule
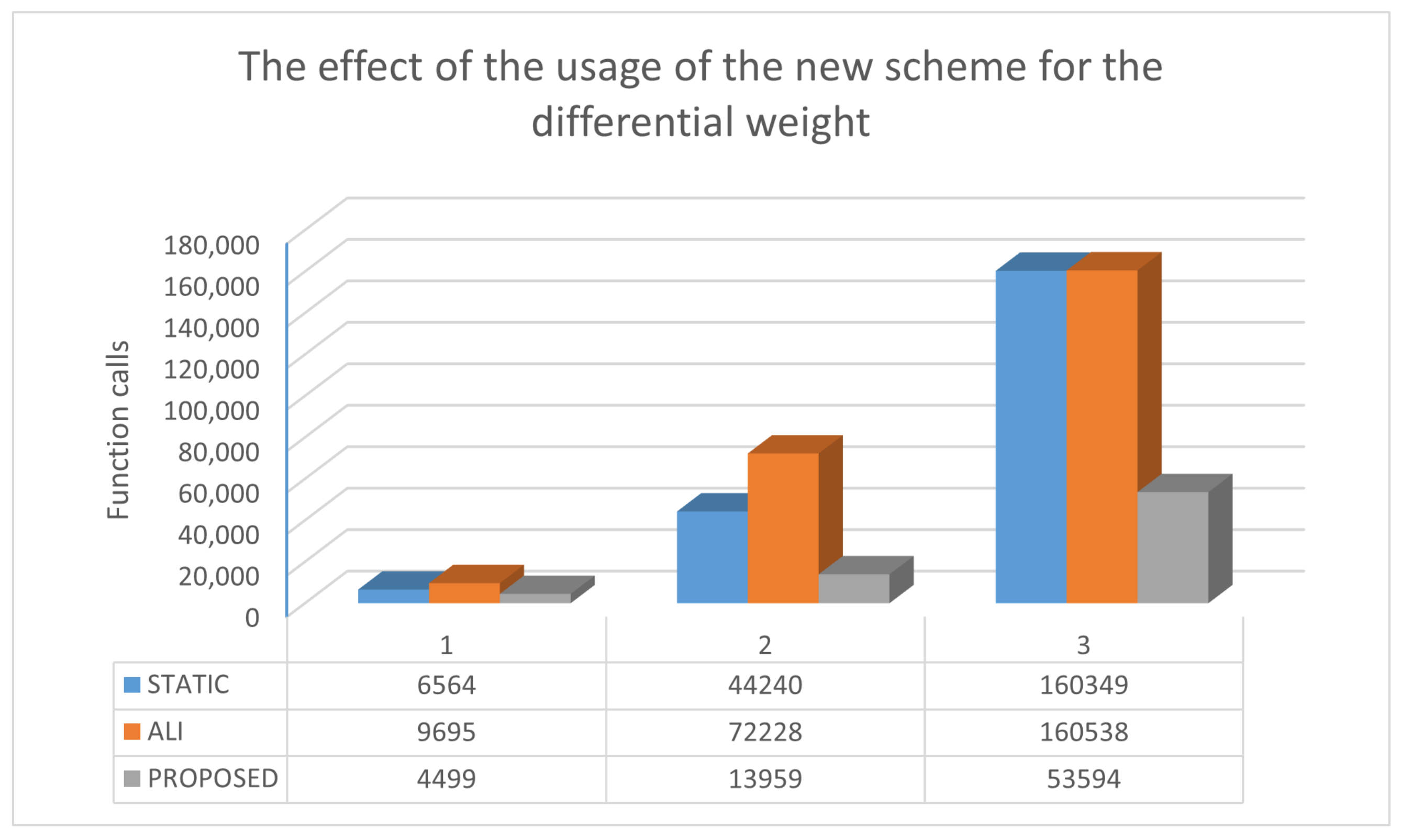
2.3. The New Differential Weight
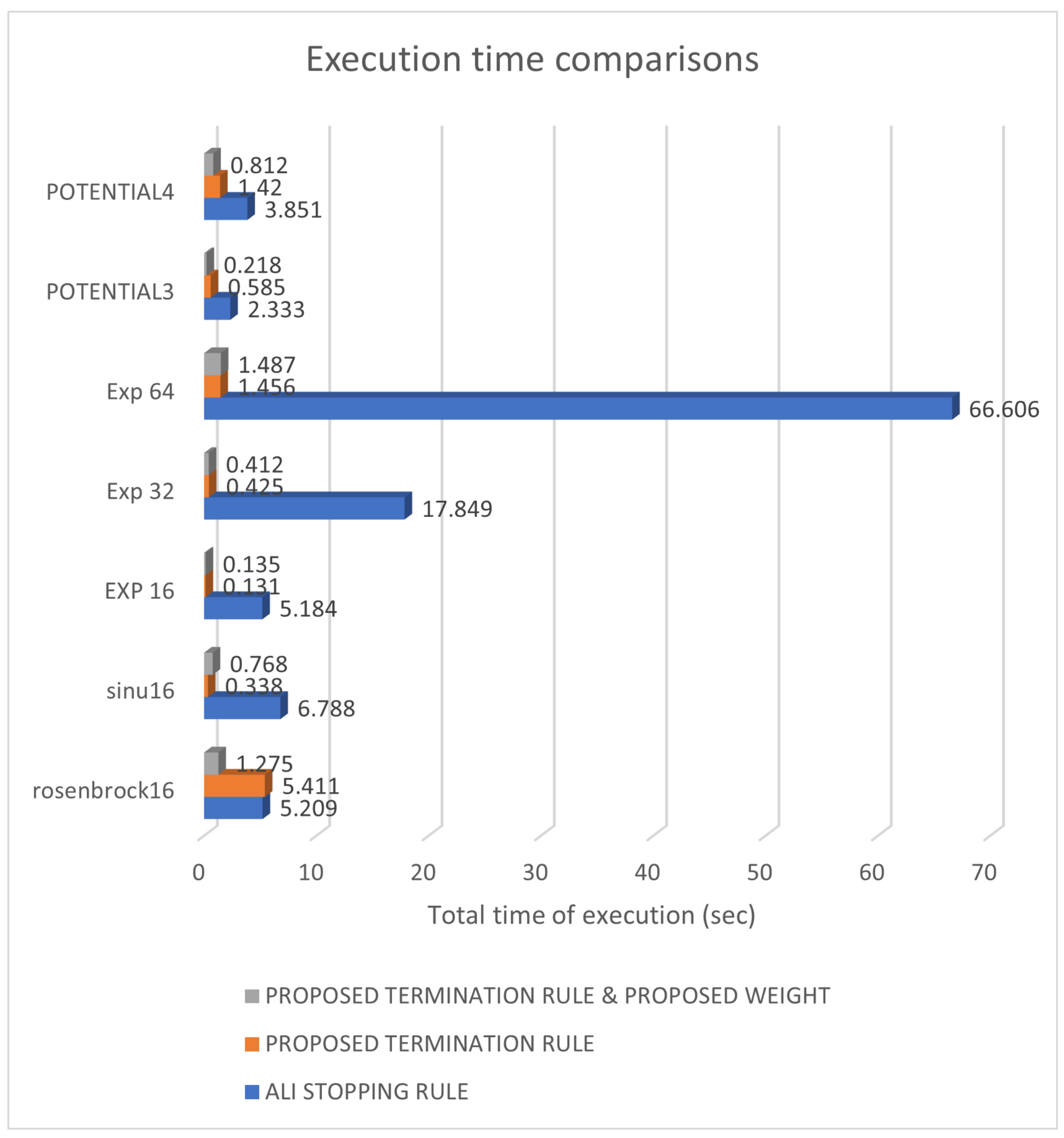
3. Experiments
3.1. Test Functions
- Bf1 (Bohachevsky 1) function defined as:with . The value of global minimum is 0.0.
- Bf2 (Bohachevsky 2) function defined as:with . The value of the global minimum is 0.0.
- Branin function. The function is defined by with . The value of global minimum is 0.397887.with . The value of global minimum is −0.352386.
- CM function. The Cosine Mixture function is given by the equation:where . For our experiments we used .
- Camel function. The function is given by:
- Easom function. The function is given by the equation:with
- Exponential function, defined as:The global minimum is located at with value . In our experiments we used this function with .
- Goldstein and Price functionThe function is given by the equation:with . The global minimum is located at with value 3.0.
- Griewank2 function. The function is given by:The global minimum is located at the with value 0.
- Gkls function. , is a function with w local minima, described in [71] with and n a positive integer between 2 and 100. The value of the global minimum is −1 and in our experiments we have used and .
- Hansen function. , .
- Hartman 3 function. The function is given by:with and and
- Hartman 6 function.with and and
- Potential function. The molecular conformation corresponding to the global minimum of the energy of N atoms interacting via the Lennard-Jones potential [72] is used as a test case here. The function to be minimized is given by:In the current experiments three different cases were studied:
- Rastrigin function. The function is given by:The global minimum is located at with value −2.0.
- Rosenbrock function.This function is given by:The global minimum is located at the with . In our experiments we used this function with .
- Shekel 7 function.
- Shekel 5 function.
- Shekel 10 function.
- Sinusoidal function. The function is given by:The global minimum is located at with . In our experiments we used and and the corresponding functions are denoted by the labels SINU4, SINU8, SINU16 and SINU32, respectively.
- Test2N function. This function is given by the equation:The function has in the specified range and in our experiments we used . The corresponding values of global minimum is −156.664663 for , −195.830829 for , −234.996994 for and −274.163160 for .
- Test30N function. This function is given by:with , with local minima in the searc space. For our experiments we used .
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kudyshev, Z.A.; Kildishev, A.V.; Boltasseva, V.M.S.A. Machine learning–assisted global optimization of photonic devices. Nanophotonics 2021, 10, 371–383. [Google Scholar] [CrossRef]
- Ding, X.L.; Li, Z.Y.; Meng, J.H.; Zhao, Y.X.; Sheng, G.H. Density-functional global optimization of (LA2O3)n Clusters. J. Chem. Phys. 2012, 137, 214311. [Google Scholar] [CrossRef] [PubMed]
- Morita, S.; Naoki, N. Global optimization of tensor renormalization group using the corner transfer matrix. Phys. Rev. B 2021, 103, 045131. [Google Scholar] [CrossRef]
- Heiles, S.; Johnston, R.L. Global optimization of clusters using electronic structure methods. Int. J. Quantum Chem. 2013, 113, 2091–2109. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, T.; Zhang, J. Global Optimization of Norris Derivative Filtering with Application for Near-Infrared Analysis of Serum Urea Nitrogen. Am. J. Anal. Chem. 2019, 10, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Grebner, C.; Becker, J.; Weber, D.; Engels, B. Tabu search based global optimization algorithms for problems in computational Chemistry. J. Cheminf. 2012, 4, 10. [Google Scholar] [CrossRef]
- Dittner, M.; Müller, J.; Aktulga, H.M.; Hartke, B.J. Efficient global optimization of reactive force-field parameters. Comput. Chem. 2015, 36, 1550–1561. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Supply-Demand-Based Optimization: A Novel Economics-Inspired Algorithm for Global Optimization. IEEE Access 2019, 7, 73182–73206. [Google Scholar] [CrossRef]
- Mishra, S.K. Global Optimization of Some Difficult Benchmark Functions by Host-Parasite Co-Evolutionary Algorithm. Econ. Bull. 2013, 33, 1–18. [Google Scholar]
- Freisleben, B.; Merz, P. A genetic local search algorithm for solving symmetric and asymmetric traveling salesman problems. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 616–621. [Google Scholar]
- Grbić, R.; Nyarko, E.K.; Scitovski, R. A modification of the DIRECT method for Lipschitz global optimization for a symmetric function. J. Glob. Optim. 2013, 57, 1193–1212. [Google Scholar] [CrossRef]
- Scitovski, R. A new global optimization method for a symmetric Lipschitz continuous function and the application to searching for a globally optimal partition of a one-dimensional set. J. Glob. Optim. 2017, 68, 713–727. [Google Scholar] [CrossRef]
- Kim, Y. An unconstrained global optimization framework for real symmetric eigenvalue problems. Appl. Num. Math. 2019, 144, 253–275. [Google Scholar] [CrossRef]
- Osaba, E.; Yang, X.S.; Diaz, F.; Lopez-Garcia, P.; Carballedo, R. An improved discrete bat algorithm for symmetric and asymmetric Traveling Salesman Problems. Eng. Appl. Artif. Intell. 2016, 49, 59–71. [Google Scholar] [CrossRef]
- Bremermann, H.A. A method for unconstrained global optimization. Math. Biosci. 1970, 9, 1–15. [Google Scholar] [CrossRef]
- Jarvis, R.A. Adaptive global search by the process of competitive evolution. IEEE Trans. Syst. Man Cybergen. 1975, 75, 297–311. [Google Scholar] [CrossRef]
- Price, W.L. Global Optimization by Controlled Random Search. Comput. J. 1977, 20, 367–370. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; Riedel, D., Ed.; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Goffe, W.L.; Ferrier, G.D.; Rogers, J. Global Optimization of Statistical Functions with Simulated Annealing. J. Econom. 1994, 60, 65–100. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin, Germany, 1996. [Google Scholar]
- Akay, B.; Karaboga, D. A modified Artificial Bee Colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Everhart, R.C. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE Press: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar]
- Zhou, Y.; Tan, Y. GPU-based parallel particle swarm optimization. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 1493–1500. [Google Scholar]
- Dawson, L.; Stewart, I. Improving Ant Colony Optimization performance on the GPU using CUDA. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1901–1908. [Google Scholar]
- Barkalov, K.; Gergel, V. Parallel global optimization on GPU. J. Glob. Optim. 2016, 66, 3–20. [Google Scholar] [CrossRef]
- Li, Y.H.; Wang, J.Q.; Wang, X.J.; Zhao, Y.L.; Lu, X.H.; Liu, D.L. Community Detection Based on Differential Evolution Using Social Spider Optimization. Symmetry 2017, 9, 183. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Siriwardane, E.M.D.; Dong, R.; Li, Y.; Hu, J. Crystal structure prediction of materials with high symmetry using differential evolution. J. Phys. Condens. Matter 2021, 33, 455902. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Hung, C.H. Feature Ranking and Differential Evolution for Feature Selection in Brushless DC Motor Fault Diagnosis. Symmetry 2021, 13, 1291. [Google Scholar] [CrossRef]
- Saha, S.; Das, R. Exploring differential evolution and particle swarm optimization to develop some symmetry-based automatic clustering techniques: Application to gene clustering. Neural Comput. Appl. 2018, 30, 735–757. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, N.; Zhao, L.; Han, L.; Hu, X.; Cai, H.; Gong, D.; Xing, L.; Chen, X.; Zhu, B.; et al. Estimation of maize evapotranspiration in semi-humid regions of Northern China Using Penman-Monteith model and segmentally optimized Jarvis model. J. Hydrol. 2022, 22, 127483. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Gonzlez-Zapata, A.M.; Daz-Muoz, J.D.; Fraga, L.G.D.; Cruz-Vega, I. Optimization of fractional-order chaotic cellular neural networks by metaheuristics. Eur. Phys. J. Spec. Top. 2022. Available online: https://link.springer.com/article/10.1140/epjs/s11734-022-00452-6 (accessed on 25 January 2022).
- Sun, G.; Li, C.; Deng, L. An adaptive regeneration framework based on search space adjustment for differential evolution. Neural Comput. Appl. 2021, 33, 9503–9519. [Google Scholar] [CrossRef]
- Civiciogluan, P.; Besdok, E. Bernstain-search differential evolution algorithm for numerical function optimization. Expert Syst. Appl. 2019, 138, 112831. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Li, R.X.K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Solar Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Peng, L.; Liu, S.; Liu, R.; Wang, L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy 2018, 162, 1301–1314. [Google Scholar] [CrossRef]
- Awad, N.; Hutter, N.M.A.F. Differential Evolution for Neural Architecture Search. In Proceedings of the 1st Workshop on Neural Architecture Search, Addis Ababa, Ethiopia, 26 April 2020. [Google Scholar]
- Ilonen, J.; Kamarainen, J.K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Slowik, A. Application of an Adaptive Differential Evolution Algorithm With Multiple Trial Vectors to Artificial Neural Network Training. IEEE Trans. Ind. Electron. 2011, 58, 3160–3167. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Wang, X.; Xu, G. Hybrid Differential Evolution Algorithm for Traveling Salesman Problem. Procedia Eng. 2011, 15, 2716–2720. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.M.; Essam, D.; Kasmarik, K. A novel design of differential evolution for solving discrete traveling salesman problems. Swarm Evolut. Comput. 2020, 52, 100607. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A differential evolution based incremental training method for RBF networks. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation (GECCO ’05), Washington, DC, USA, 25–29 June 2005; pp. 881–888. [Google Scholar]
- O’Hora, B.; Perera, J.; Brabazon, A. Designing Radial Basis Function Networks for Classification Using Differential Evolution. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 2932–2937. [Google Scholar]
- Naveen, N.; Ravi, V.; Rao, C.R.; Chauhan, N. Differential evolution trained radial basis function network: Application to bankruptcy prediction in banks. Int. J. Bio-Inspir. Comput. 2010, 2, 222–232. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, X.; Li, J.; Li, S.; Wang, L. PDECO: Parallel differential evolution for clusters optimization. J. Comput. Chem. 2013, 34, 1046–1059. [Google Scholar] [CrossRef]
- Ghosh, A.; Mallipeddi, R.; Das, S.; Das, A. A Switched Parameter Differential Evolution with Multi-donor Mutation and Annealing Based Local Search for Optimization of Lennard-Jones Atomic Clusters. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Zhang, Y.; Zhang, H.; Cai, J.; Yang, B. A Weighted Voting Classifier Based on Differential Evolution. Abstr. Appl. Anal. 2014, 2014, 376950. [Google Scholar] [CrossRef]
- Maulik, U.; Saha, I. Automatic Fuzzy Clustering Using Modified Differential Evolution for Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3503–3510. [Google Scholar] [CrossRef]
- Hancer, E. Differential evolution for feature selection: A fuzzy wrapper–filter approach. Soft Comput. 2019, 23, 5233–5248. [Google Scholar] [CrossRef]
- Vivekanandan, T.; Iyengar, N.C.S.N. Optimal feature selection using a modified differential evolution algorithm and its effectiveness for prediction of heart disease. Comput. Biol. Med. 2017, 90, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Liu, H.; Xu, J.; Zhao, H.; Song, Y. An Improved Quantum-Inspired Differential Evolution Algorithm for Deep Belief Network. IEEE Trans. Instrum. Meas. 2020, 69, 7319–7327. [Google Scholar] [CrossRef]
- Wu, T.; Li, X.; Zhou, D.; Li, N.; Shi, J. Differential Evolution Based Layer-Wise Weight Pruning for Compressing Deep Neural Networks. Sensors 2021, 21, 880. [Google Scholar] [CrossRef] [PubMed]
- Mininno, E.; Neri, F.; Cupertino, F.; Naso, D. Compact Differential Evolution. IEEE Trans. Evolut. Comput. 2011, 15, 32–54. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evolut. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A Fuzzy Adaptive Differential Evolution Algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Wang, H.; Rahnamayan, S.; Wu, Z. Parallel differential evolution with self-adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems. J. Parallel Distrib. Comput. 2013, 73, 62–73. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evolut. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Ali, M.M.; Törn, A. Population set-based global optimization algorithms: Some modifications and numerical studies. Comput. Oper. Res. 2004, 31, 1703–1725. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.M. Charoenchai Khompatraporn, Zelda B. Zabinsky, A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems. J. Glob. Opt. 2005, 31, 635–672. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposoto, W.; Gümüs, Z.; Harding, S.; Klepeis, J.; Meyer, C.; Schweiger, C. Handbook of Test Problems in Local and Global Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Ali, M.M.; Kaelo, P. Improved particle swarm algorithms for global optimization. Appl. Math. Comput. 2008, 196, 578–593. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- Siarry, P.; Berthiau, G.; Durdin, F.F.; Haussy, J. Enhanced simulated annealing for globally minimizing functions of many-continuous variables. ACM Trans. Math. Softw. 1997, 23, 209–228. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. GenMin: An enhanced genetic algorithm for global optimization. Comput. Phys. Commun. 2008, 178, 843–851. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Programm. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Gaviano, M.; Ksasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]

| Parameter | Value |
|---|---|
| NP | 10n |
| F | 0.8 |
| CR | 0.9 |
| M | 20 |
| Function | Static | Ali | Proposed |
|---|---|---|---|
| BF1 | 1142 | 1431 | 847 |
| BF2 | 1164 | 1379 | 896 |
| BRANIN | 984 | 816 | 707 |
| CM4 | 3590 | 7572 | 2079 |
| CAMEL | 1094 | 18,849 | 685 |
| EASOM | 1707 | 2014 | 1327 |
| EXP2 | 532 | 323 | 449 |
| EXP4 | 2421 | 1019 | 1494 |
| EXP8 | 15,750 | 3670 | 5632 |
| EXP16 | 160,031 | 15,150 | 21,416 |
| EXP32 | 320,039 | 152,548 | 77,936 |
| GKLS250 | 784 | 944 | 614 |
| GKLS2100 | 772 | 1531 | 599 (0.97) |
| GKLS350 | 1906 (0.93) | 3263 | 1275 (0.93) |
| GKLS3100 | 1883 | 3539 | 1373 |
| GOLDSTEIN | 988 | 818 | 769 |
| GRIEWANK2 | 1299 (0.97) | 1403 | 883 (0.93) |
| HANSEN | 2398 | 2968 | 1400 |
| HARTMAN3 | 1448 | 836 | 1050 |
| HARTMAN6 | 9489(0.97) | 4015(0.97) | 4667(0.80) |
| POTENTIAL3 | 90,027 | 89,776 | 21,824 |
| POTENTIAL4 | 120,387 (0.97) | 120,405 (0.33) | 45,705 (0.97) |
| POTENTIAL5 | 150,073 | 150,104 | 83,342 |
| RASTRIGIN | 1246 | 1098 (0.93) | 871 |
| ROSENBROCK4 | 6564 | 9695 | 4499 |
| ROSENBROCK8 | 44,240 | 72,228 | 13,959 |
| ROSENBCROK16 | 160,349 (0.90) | 160,538 (0.60) | 53,594 |
| SHEKEL5 | 5524 | 3810 | 3057 (0.83) |
| SHEKEL7 | 5266 | 3558 | 2992 (0.87) |
| SHEKEL10 | 5319 | 3379 | 3076 |
| TEST2N4 | 4200 | 1980 | 2592 |
| TEST2N5 | 7357 | 2957 | 4055 |
| TEST2N6 | 12,074 | 4159 | 5836 |
| TEST2N7 | 18,872 | 5490 | 7904 |
| SINU4 | 3270 | 1855 | 2216 |
| SINU8 | 23,108 | 6995 | 8135 |
| SINU16 | 160,092 | 36,044 | 30,943 |
| SINU32 | 213,757 (0.70) | 160,536 (0.53) | 83,369 (0.80) |
| TEST30N3 | 1452 | 1732 | 959 |
| TEST30N4 | 1917 | 2287 | 1378 |
| Total | 1,564,515 (0.97) | 1,062,714 (0.96) | 506,404 (0.98) |
| Function | Static | Ali | Proposed |
|---|---|---|---|
| BF1 | 996 | 1124 | 889 |
| BF2 | 926 | 1026 | 816 |
| BRANIN | 878 | 900 | 730 |
| CM4 | 1148 (0.70) | 1991 | 1103 |
| CAMEL | 1049 | 904 (0.93) | 846 |
| EASOM | 447 | 448 | 446 |
| EXP2 | 470 | 461 | 467 |
| EXP4 | 915 | 903 | 892 |
| EXP8 | 1797 | 3558 | 1796 |
| EXP16 | 3578 | 7082 | 3521 |
| EXP32 | 7082 | 14,125 | 7022 |
| GKLS250 | 498 | 576 | 493 |
| GKLS2100 | 533 | 884 (0.97) | 515 |
| GKLS350 | 823 | 1130 (0.93) | 814 (0.97) |
| GKLS3100 | 858 | 1495 (0.97) | 829 (0.93) |
| GOLDSTEIN | 945 | 993 | 915 |
| GRIEWANK2 | 947 | 921 | 826 |
| HANSEN | 2104 | 1949 | 1479 |
| HARTMAN3 | 1017 | 1005 | 952 |
| HARTMAN6 | 4679 (0.90) | 3744 (0.97) | 3128 (0.87) |
| POTENTIAL3 | 21,473 | 2284 | 8197 |
| POTENTIAL4 | 44,191 (0.43) | 3098 (0.33) | 24,659 (0.97) |
| POTENTIAL5 | 75,910 | 3443 | 52,664 |
| RASTRIGIN | 841 | 994 | 777 |
| ROSENBROCK4 | 4934 | 7192 | 3300 |
| ROSENBROCK8 | 29,583 | 49,696 | 10,907 |
| ROSENBCROK16 | 160,349 | 160,538 (0.60) | 38,315 |
| SHEKEL5 | 4389 (0.97) | 4266 | 2839 (0.83) |
| SHEKEL7 | 3905 | 3685 | 2668 |
| SHEKEL10 | 4049 | 3548 | 2629 |
| TEST2N4 | 2785 | 2275 | 2221 |
| TEST2N5 | 4481 | 3170 | 3122 |
| TEST2N6 | 6852 | 4286 | 4296 |
| TEST2N7 | 11971 | 5701 | 6267 |
| SINU4 | 2322 | 1987 | 1755 |
| SINU8 | 9990 | 6156 | 5113 |
| SINU16 | 6892 | 3628 (0.97) | 16,905 |
| SINU32 | 7235 (0.80) | 7438 (0.83) | 7218 |
| TEST30N3 | 1033 | 1098 | 951 |
| TEST30N4 | 1355 | 1444 | 1285 |
| Total | 432,610 (0.98) | 321,166 (0.96) | 224,567 (0.99) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charilogis, V.; Tsoulos, I.G.; Tzallas, A.; Karvounis, E. Modifications for the Differential Evolution Algorithm. Symmetry 2022, 14, 447. https://doi.org/10.3390/sym14030447
Charilogis V, Tsoulos IG, Tzallas A, Karvounis E. Modifications for the Differential Evolution Algorithm. Symmetry. 2022; 14(3):447. https://doi.org/10.3390/sym14030447
Chicago/Turabian StyleCharilogis, Vasileios, Ioannis G. Tsoulos, Alexandros Tzallas, and Evangelos Karvounis. 2022. "Modifications for the Differential Evolution Algorithm" Symmetry 14, no. 3: 447. https://doi.org/10.3390/sym14030447
APA StyleCharilogis, V., Tsoulos, I. G., Tzallas, A., & Karvounis, E. (2022). Modifications for the Differential Evolution Algorithm. Symmetry, 14(3), 447. https://doi.org/10.3390/sym14030447









