Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media
Abstract
:1. Introduction
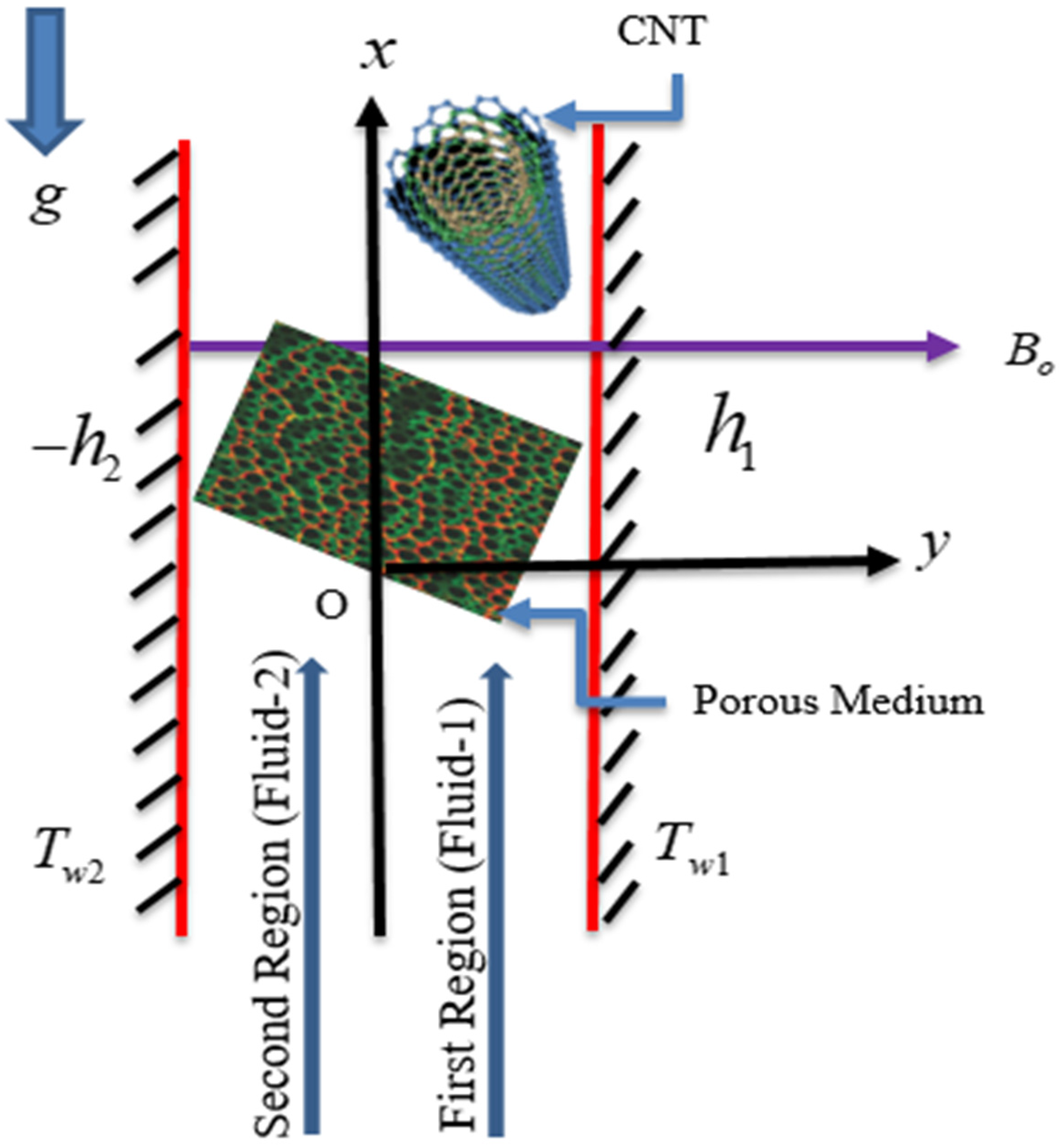
2. Mathematical Formulation
3. Solution to the Problem
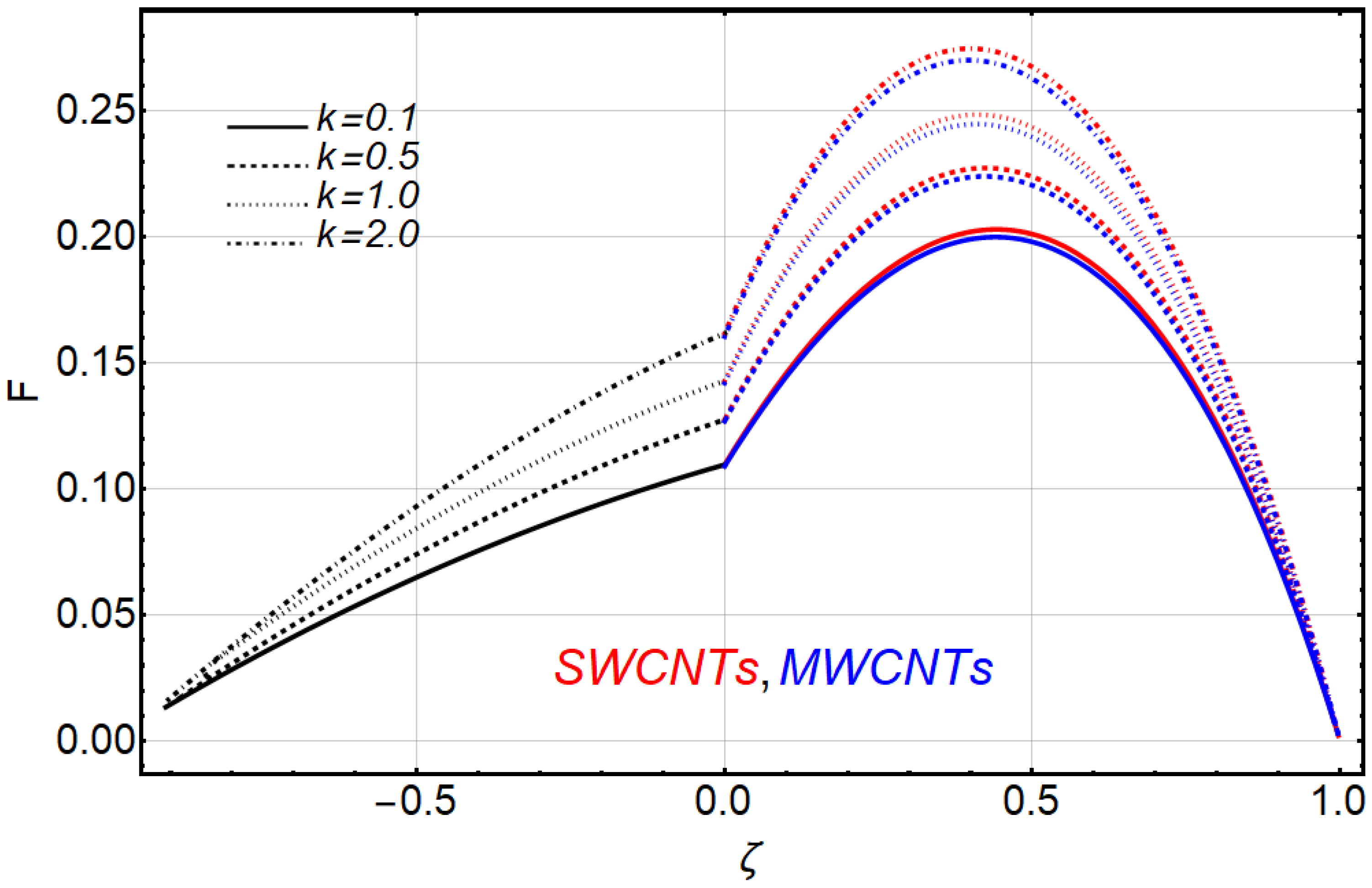
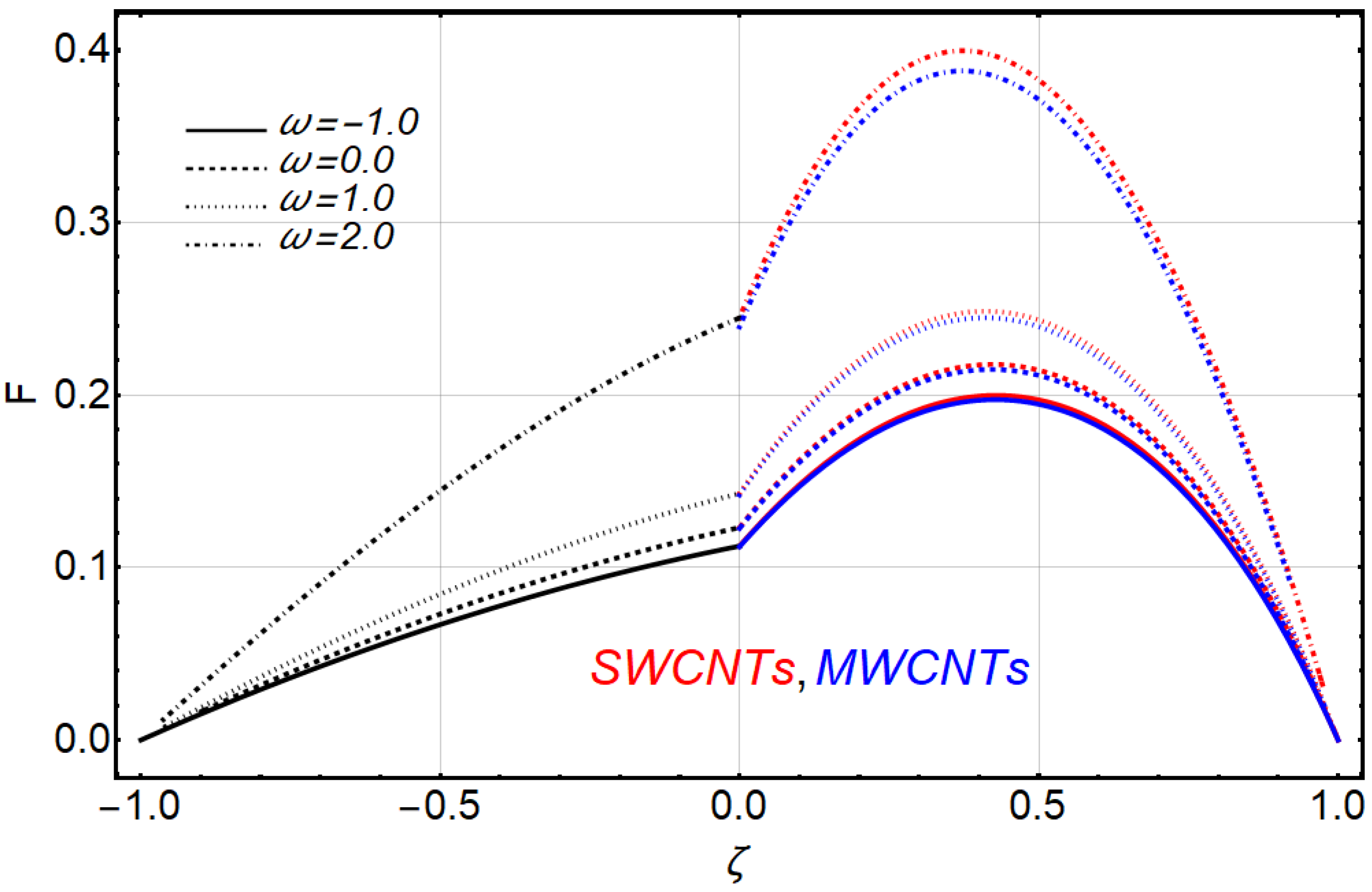
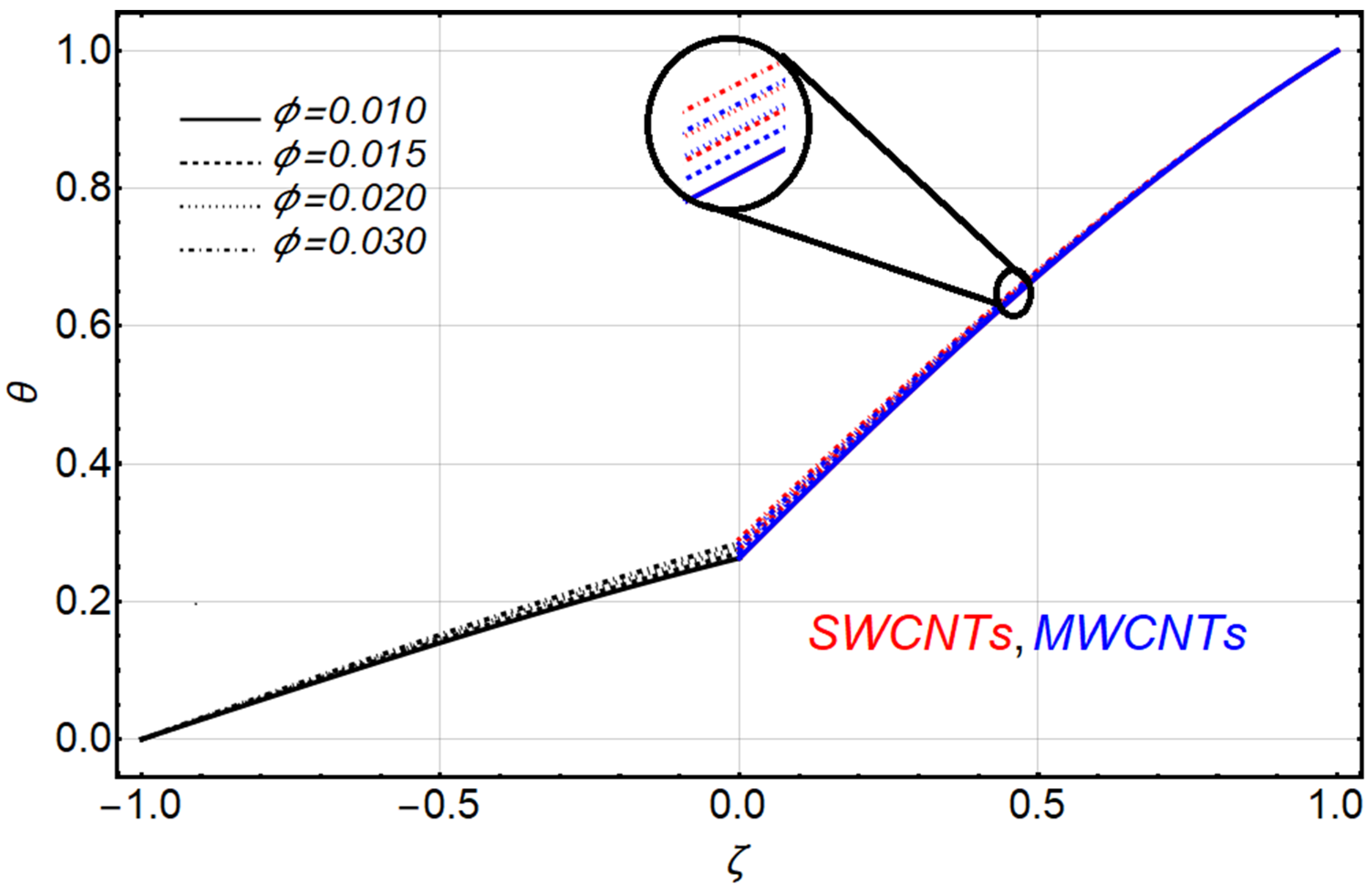
4. Results and Discussion
5. Conclusions
- The velocity behavior is almost the same in both nanofluid and without-nanofluid regions.
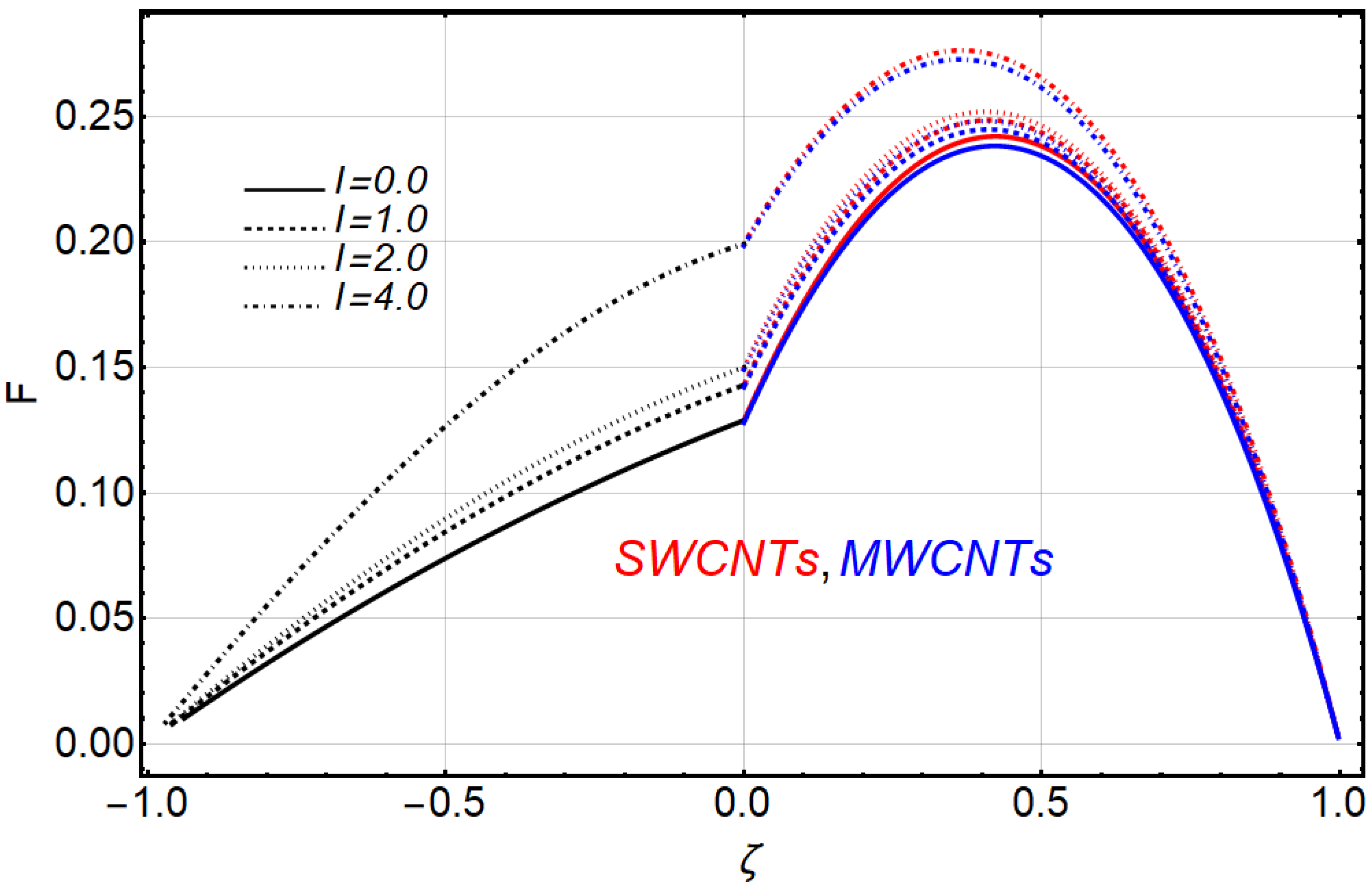
- The velocity of fluid decreased with increasing values of nanoparticle volume fraction; the Hartman number and ratio of electrical conductivities in engine-oil SWCNTs were more than with engine-oil MWCNTs.
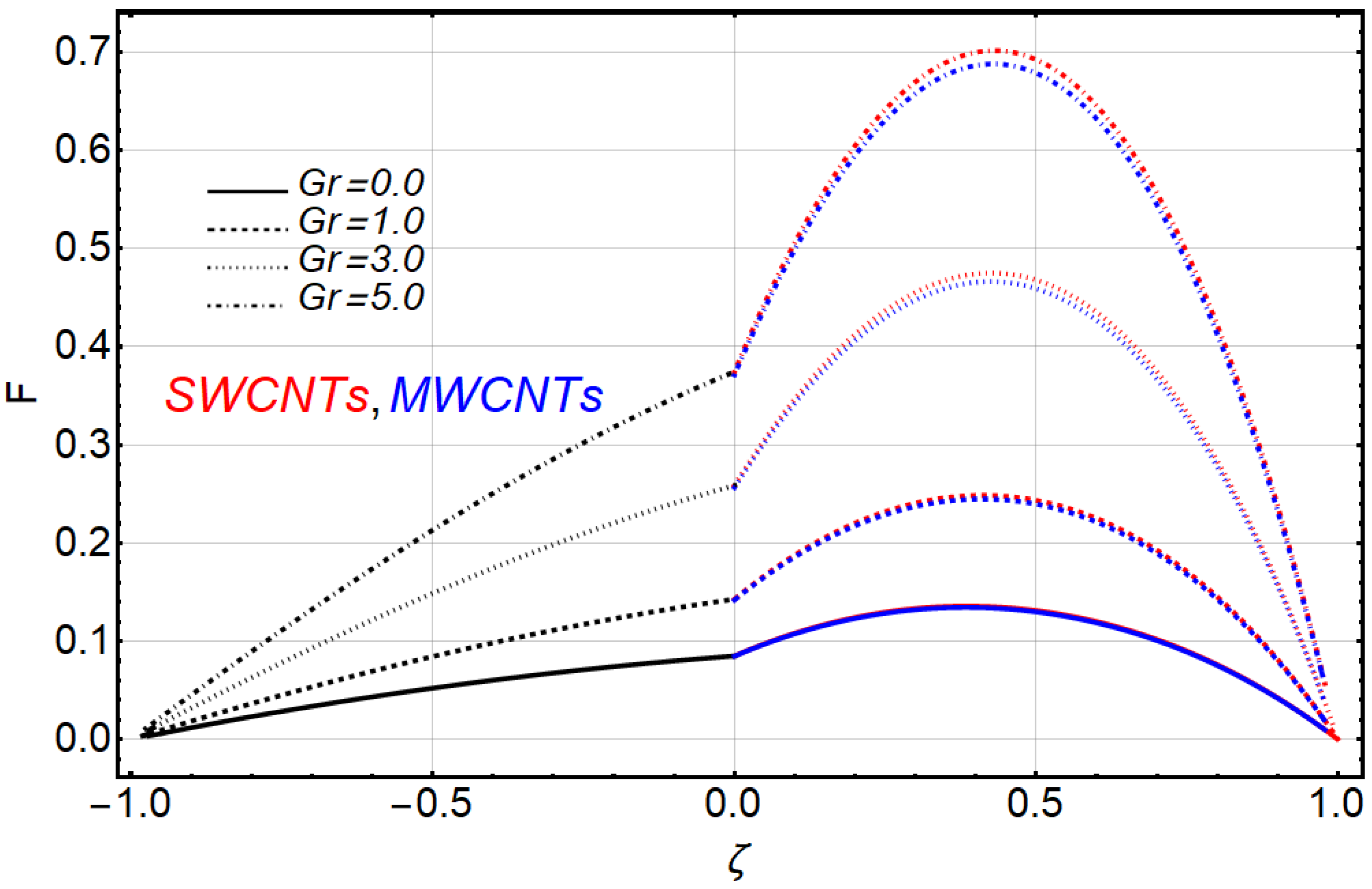
- The velocity of the fluid increased with increasing values of the Grashof number, ratio of heights, ratio of thermal conductivities, ratio of dynamics viscosities and heat generation/absorption, similar to previous work.
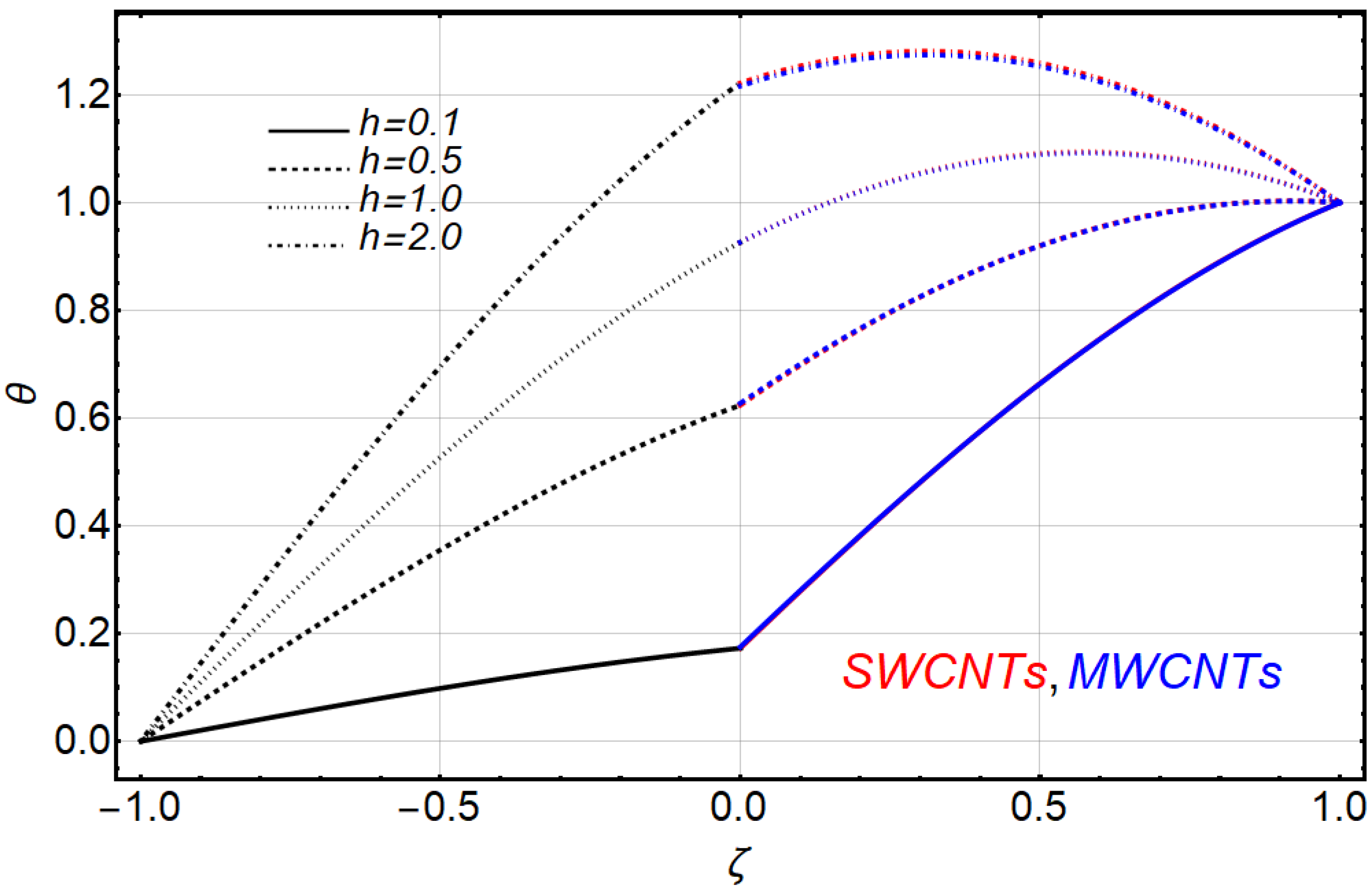
- Temperature fields preserved the same impressions in both fluids.
- The temperature fields of fluids were improved with the increasing values of nanoparticle volume fraction, heat generation/absorption coefficient, ratio of heights and ratio of thermal conductivities.
- The concentration of nanoparticles directly affects velocity and temperature in a manner of decreasing and increasing behavior, respectively, due to their boundary layers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Ratio of densities between nanofluid and base fluid of 1st region. | |
| Ratio of thermal expansion coefficient between nanofluid and base fluid of 1st region. | |
| Ratio of viscosities between nanofluid and base fluid of 1st region. | |
| Ratio of electrical conductivities between nanofluid and base fluid of 1st region. | |
| Ratio of thermal conductivities between nanofluid and base fluid of 1st region. | |
| Magnetic field strength. | |
| Inertia coefficient for the porous media. | |
| Inverse of Darcy number. | |
| Dimensionless velocity of fluid. | |
| Gravitational acceleration. | |
| Grashof number. | |
| Height ratio of 1st region and 2nd region. | |
| Dimensionless inertia coefficient of the porous medium. | |
| Thermal conductivities ratio of 1st region fluid and 2nd region fluid. | |
| Porous media permeability. | |
| Hartman number. | |
| Ratio of dynamics viscosities of 1st region fluid and 2nd region fluid. | |
| Ratio of densities of 1st region fluid and 2nd region fluid. | |
| Pressure gradient. | |
| Dimensionless pressure gradient. | |
| Heat generation or absorption coefficient. | |
| Reynolds number. | |
| Ratio Electrical conductivities of 1st region fluid and 2nd region fluid. | |
| Temperature of fluid. | |
| Velocity of fluid. | |
| Average velocity. | |
| Greek Symbol | |
| Ratio of thermal expansion coefficient of 1st region fluid and 2nd region fluid. | |
| Dimensionless normal distance. | |
| Viscosity of fluid. | |
| Density of fluid. | |
| Electrical conductivity of fluid. | |
| Dimensionless temperature. | |
| Dimensionless coefficient heat generation or absorption. | |
| Subscripts | |
| 1 | 1st region |
| 2 | 2nd region |
| Fluid | |
| Nanofluid | |
| Particle | |
| Wall | |
References
- Khanafer, K.; Vafai, K. Applications of nanofluids in porous medium. J. Therm. Anal. Calorim. 2019, 135, 1479–1492. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on convective mass transfer in porous media. Int. J. Heat Mass Transf. 1982, 25, 1183–1190. [Google Scholar] [CrossRef]
- Chamkha, A.J. Flow of two-immiscible fluids in porous and nonporous channels. J. Fluids Eng. 2000, 122, 117–124. [Google Scholar] [CrossRef]
- Khaled, A.R.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Plumb, O.A.; Huenefeld, J.C. Non-Darcy natural convection from heated surfaces in saturated porous media. Int. J. Heat Mass Transf. 1981, 24, 765–768. [Google Scholar] [CrossRef]
- Nakayama, A.; Koyama, H.; Kuwahara, F. An analysis on forced convection in a channel filled with a Brinkman-Darcy porous medium: Exact and approximate solutions. Wärme-Und Stoffübertrag. 1988, 23, 291–295. [Google Scholar] [CrossRef]
- Choi, S.U.S. Nanofluids: From vision to reality through research. J. Heat Transf. 2009, 131, 033106. [Google Scholar] [CrossRef]
- Khaled, A.R.; Vafai, K. Heat transfer enhancement through control of thermal dispersion effects. Int. J. Heat Mass Transf. 2005, 48, 2172–2185. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Grobert, N. Carbon nanotubes–becoming clean. Mater. Today 2007, 10, 28–35. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Ramasubramaniam, R.; Chen, J.; Liu, H. Homogeneous carbon nanotube/polymer composites for electrical applications. Appl. Phys. Lett. 2003, 83, 2928–2930. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Haq, R.U.; Shahzad, F.; Al-Mdallal, Q.M. MHD pulsatile flow of engine oil based carbon nanotubes between two concentric cylinders. Results Phys. 2017, 7, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Alias, H.; Wen, D.; Williams, R.A. Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int. J. Heat Mass Transf. 2006, 49, 240–250. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Raza, F.; Akhtar, J. Mathematical model for Marangoni convection MHD flow of carbon nanotubes through a porous medium. J. Adv. Res. Appl. Sci. 2017, 4, 216–222. [Google Scholar]
- Haq, R.U.; Nadeem, S.; Khan, Z.H.; Noor, N.F.M. Convective heat transfers in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Phys. B Condens. Matter. 2015, 457, 40–47. [Google Scholar] [CrossRef]
- Nasiri, A.; Shariaty-Niasar, M.; Rashidi, A.; Amrollahi, A.; Khodafarin, R. Effect of dispersion method on thermal conductivity and stability of nanofluid. Exp. Therm. Fluid Sci. 2011, 35, 717–723. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.A. Conjugate heat transfer in a porous cavity filled with nanofluids and heated by a triangular thick wall. Int. J. Therm. Sci. 2013, 67, 135–151. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Waheed, A.; Shehzad, N.; Sait, S.M. Natural convection nanofluid flow with heat transfer analysis of carbon nanotubes–water nanofluid inside a vertical truncated wavy cone. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Vajravelu, K.; Hadjinicolaou, A. Heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation. Int. Commun. Heat Mass Transf. 1993, 20, 417–430. [Google Scholar] [CrossRef]
- Chamkha, A.J. Non-Darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer. Heat Transf. A 1997, 32, 653–675. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Cess, R.D. Temperature-dependent heat sources or sinks in a stagnation point flow. Appl. Sci. Res. 1961, 10, 185. [Google Scholar] [CrossRef]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic convection at a cone and a wedge. Int. Commun. Heat Mass Transf. 1992, 19, 701–710. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical simulation and mathematical modeling of electro-osmotic Couette–Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.S.; Ching-Cheng, L.M.; Huang, I.T.; Wang, C.C. Enhancement of thermal conductivity with carbon nanotube for nanofluids. Int. Commun. Heat Mass Transf. 2005, 32, 1202–1210. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism (Vol. 1); Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Kandasamy, R.; Mohammad, R.; Muhaimin, I. Carbon nanotubes on unsteady MHD non-Darcy flow over porous wedge in presence of thermal radiation energy. Appl. Math. Mech. 2016, 37, 1031–1040. [Google Scholar] [CrossRef]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]









| Thermo-Physical Properties | Base Fluid | Carbon Nanotubes | ||
|---|---|---|---|---|
| Water | Engine Oil | SWCNTs | MWCNTs | |
| Density | ||||
| Thermal conductivity | ||||
| Electrical conductivity | ||||
| Thermal expansion coefficient | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry 2022, 14, 406. https://doi.org/10.3390/sym14020406
Zeeshan A, Shehzad N, Atif M, Ellahi R, Sait SM. Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry. 2022; 14(2):406. https://doi.org/10.3390/sym14020406
Chicago/Turabian StyleZeeshan, Ahmad, Nasir Shehzad, Muhammad Atif, Rahmat Ellahi, and Sadiq M. Sait. 2022. "Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media" Symmetry 14, no. 2: 406. https://doi.org/10.3390/sym14020406
APA StyleZeeshan, A., Shehzad, N., Atif, M., Ellahi, R., & Sait, S. M. (2022). Electromagnetic Flow of SWCNT/MWCNT Suspensions in Two Immiscible Water- and Engine-Oil-Based Newtonian Fluids through Porous Media. Symmetry, 14(2), 406. https://doi.org/10.3390/sym14020406









