Application of Lie Symmetry to a Mathematical Model that Describes a Cancer Sub-Network

Abstract

In this paper, a mathematical model of a cancer sub-network is analysed from the view point of Lie symmetry methods. This model discusses a human cancer cell which is developed due to the dysfunction of some genes at the R-checkpoint during the cell cycle. The primary purpose of this paper is to apply the techniques of Lie symmetry to the model and present some approximated solutions for the three-dimensional system of first-order ordinary differential equations describing a cancer sub-network. The result shows that the phosphatase gene (Cdc25A) regulates the cyclin-dependent kinases inhibitor ($P{27}^{Kip1}$). Furthermore, this research discovered that the activity that reverses the inhibitory effects on cell cycle progression at the R-checkpoint initiates a pathway.

1. Introduction

Over the last two decades, researchers have developed mathematical models to understand the dynamic mechanisms of the cell cycle [1,2,3,4]. In [5,6,7], scholars used non-linear differential equations to model cell cycle mutations as limit cycles. The R-checkpoint, according to Pardee, represents a unique switch between the quiescent and proliferative phases of normal cells [7]. Researchers further highlighted the importance of the R-checkpoint in preventing malignant transformation [8]. As a result, if a cell has damaged DNA or has not grown properly, the cell cycle is said to be stalled [2,9,10]. In particular, genes such as phosphatase Cdc25A, cyclins $(D,E)$, cyclin-dependent kinases $\left(Cdks\right)$, retinoblastoma protein $\left(Rb\right)$, cyclin-dependent kinases inhibitor $P{27}^{Kip1}$, and transcriptional factors (E2F, C-Myc) are the most significant control regulators [2,9,10,11].

A mathematical model can be defined as the representation and development of a previously investigated process. This insight has led to the creation of mathematical forms that represent real-world scenarios. This will make it easier to comprehend the phenomenon that has been observed. The Lie symmetry technique and numerical analyses provide understanding, responses, and useful guidance in analysing the formulated mathematical model.

In this study, a mathematical model of a cancer sub-network is analysed from the view point of Lie symmetry. This technique is indeed a powerful tool for solving non-linear differential equations. The Cancer Sub-Network model is governed by the following three-dimensional system of first-order non-linear differential equations [10]:

$$\begin{array}{ccc}\hfill \frac{d{x}_1}{dt}& =& {\lambda }_1+a{x}_2-{\mu }_1{x}_1,\hfill \\ \hfill \frac{d{x}_2}{dt}& =& {\lambda }_2+b{x}_1-{\mu }_2{x}_2+\frac{c\rho }{c+x_3},\hfill \\ \hfill \frac{d{x}_3}{dt}& =& {\lambda }_3-{\mu }_3{x}_3+\frac{d\sigma }{d+x_2},\hfill \end{array}$$

(1)

where the dependent variables and parameters are described in the table below (

Table 1. Description of variables and parameters.

	Variable and Parameter	Description	References
1	$x_1$	concentration of gene Cdc25A	[1,11]
2	$x_2$	concentration of gene $Cdks$	[1,2]
3	$x_3$	concentration of gene $P{27}^{Kip1}$	[1,12]
4	${\lambda }_1$	constitutive protein expressions of Cdc25A	[7,9]
5	${\lambda }_2$	constitutive protein expressions of $Cdks$	[2,9]
6	${\lambda }_3$	mitogenic signal stimulation	[2,3]
7	a	activation efficiency of $x_2$ by $x_1$	[2,6]
8	b	activation efficiency of $x_1$ by $x_2$	[2,10]
9	c	inhibition coefficients of $x_3$ to $x_2$	[1,2,13]
10	d	inhibition coefficients of $x_2$ to $x_3$	[2,13]
11	$\rho$	production rates of $x_2$ to $x_3$	[2,9]
12	$\sigma$	production rates of $x_3$ to $x_2$	[2,9]

). The terms $-{\mu }_1{x}_1$, $-{\mu }_2{x}_2$, and $-{\mu }_3{x}_3$ refer to protein degradation caused by ubiquitin-proteasomes with the fixed rate coefficients ${\mu }_1$, ${\mu }_2$, and ${\mu }_2$[10]. The inhibition nature of cell $x_3$ to $x_2$ and of $x_2$ to $x_3$ are represented by $\frac{c\rho }{c+x_3}$ and $\frac{d\sigma }{d+x_2}$, respectively.

The rest of the paper is organised as follows. In Section 2, a realistic background of the fundamental theories of Lie symmetry are presented. A simplified and parametrised form of the Cancer Sub-Network model is developed in Section 3. Lie symmetry analysis of the model is performed in Section 4. The numerical solutions are performed and presented graphically in Section 5. Finally, a discussion and concluding remarks are provided in Section 6.

2. Preliminaries on Lie Symmetry Method

In this Section, a summary of the Lie symmetry analysis to solve a system of differential equations is provided. The method comprises the tools that are needed in this study. Firstly, the mathematical concept of symmetry is enlightened. Secondly, the overall properties of groups are given and extended to the Lie groups. Several textbooks are available in the literature. Furthermore, numerous research articles are published on the theory of the Lie symmetry technique for solving ordinary differential equations (ODEs) as well as partial differential equations (PDEs).

In accordance with the theory of Lie symmetry, the given three-dimensional system of the first-order differential equation is as follows:

$$\begin{array}{ccc}\hfill \dot{x_1}& =& f_1(t,x_1,x_2,x_3),\hfill \\ \hfill \dot{x_2}& =& f_2(t,x_1,x_2,x_3),\hfill \\ \hfill \dot{x_3}& =& f_3(t,x_1,x_2,x_3),\hfill \end{array}$$

which admits the following Lie group of one-parameter transformations (a):

$$\begin{array}{ccc}\hfill \tilde{t}& \approx & t+aT(t,x_1,x_2,x_3),\hfill \\ \hfill \widetilde{x_1}& \approx & x_1+a{X}_1(t,x_1,x_2,x_3),\hfill \\ \hfill \widetilde{x_2}& \approx & x_2+a{X}_2(t,x_1,x_2,x_3),\hfill \\ \hfill \widetilde{x_3}& \approx & x_3+a{X}_3(t,x_1,x_2,x_3),\hfill \end{array}$$

with the infinitesimal Lie operators below:

$$G=T\frac{\partial }{\partial t}+X_1\frac{\partial }{\partial x_1}+X_2\frac{\partial }{\partial x_2}+X_3\frac{\partial }{\partial x_3}.$$

(2)

The group transformations $\tilde{t}$, $\widetilde{x_1}$, $\widetilde{x_2}$, and $\widetilde{x_3}$ are obtained by solving the following Lie equations [8]:

$$\begin{array}{ccc}\hfill \frac{d\tilde{t}}{da}& =& T(t,x_1,x_2,x_3),\hfill \\ \hfill \frac{d\widetilde{x_1}}{da}& =& X_1(t,x_1,x_2,x_3),\hfill \\ \hfill \frac{d\widetilde{x_2}}{da}& =& X_2(t,x_1,x_2,x_3),\hfill \\ \hfill \frac{d\widetilde{x_3}}{da}& =& X_3(t,x_1,x_2,x_3),\hfill \end{array}$$

with the initial conditions:

$$\tilde{t}{\mid }_{a=0}=t,\widetilde{x_1}{\mid }_{a=0}=x_1,\widetilde{x_2}{\mid }_{a=0}=x_2,\widetilde{x_3}{\mid }_{a=0}=x_3.$$

The first extension of the Lie operators above is defined as follows:

$$G^{\left[1\right]}=G+X_1^{\left[t\right]}\frac{\partial }{\partial {\dot{x}}_1}+X_2^{\left[t\right]}\frac{\partial }{\partial {\dot{x}}_2}+X_3^{\left[t\right]}\frac{\partial }{\partial {\dot{x}}_3},$$

(3)

where

$$\begin{array}{ccc}\hfill X_1^{\left[t\right]}& =& D_t\left(X_1\right)-{\dot{x}}_1{D}_t\left(T\right),\hfill \\ \hfill X_2^{\left[t\right]}& =& D_t\left(X_2\right)-{\dot{x}}_2{D}_t\left(T\right),\hfill \\ \hfill X_3^{\left[t\right]}& =& D_t\left(X_3\right)-{\dot{x}}_3{D}_t\left(T\right),\hfill \end{array}$$

with $D_t$ representing the total differential operator, described as follows:

$$D_t=\frac{\partial }{\partial t}+\dot{x_1}\frac{\partial }{\partial x_1}+\dot{x_2}\frac{\partial }{\partial x_2}+\dot{x_3}\frac{\partial }{\partial x_3}+\ddot{x_1}\frac{\partial }{\partial \dot{x_1}}+\ddot{x_2}\frac{\partial }{\partial \dot{x_2}}+\ddot{x_3}\frac{\partial }{\partial \dot{x_3}}+\dots$$

The infinitesimal transformation obtained will be used to solve the following equation:

$$\begin{array}{ccc}\hfill T{r}_t+X_1{r}_{x_1}+X_2{r}_{x_2}++X_3{r}_{x_3}& =& 0,\hfill \\ \hfill T{u}_t+X_1{u}_{x_1}+X_2{u}_{x_2}++X_3{u}_{x_3}& =& 0,\hfill \\ \hfill T{v}_t+X_1{v}_{x_1}+X_2{v}_{x_2}++X_3{v}_{x_3}& =& 0,\hfill \\ \hfill T{w}_t+X_1{w}_{x_1}+X_2{w}_{x_2}++X_3{w}_{x_3}& =& 1.\hfill \end{array}$$

(4)

Equation (4) will provide a set of new independent variable r, and dependent variables u, v, and w, which can be used to transform the non-linear system (1) into a linear system.

Theorem 1.

A function $h(t,x_1,\cdots ,x_k)$ is invariant under the prolonged group G if and only if [14]:

$$\begin{array}{c}\hfill G^{\left[k\right]}h=0,\end{array}$$

where

$$G^{\left[k\right]}=G+\sum _{i=1}^n\left\{X^{\left(i\right)}-\sum _{j=1}^i\left(\genfrac{}{}{0pt}{}{i}{j}\right)x^{(i+1-j)}{T}^{\left(j\right)}\right\}{\partial }_{x^{\left(i\right)}}$$

is the kth extension of the Lie operator of G.

Theorem 2.

Every one-parameter group of transformations $(\widehat{x}=f(x,y,\epsilon ),\widehat{y}=g(x,y,\epsilon ))$ is reduced to a group of translations $\widehat{t}=t+\epsilon$, $\widehat{u}=u$ with the following generator [15,16]:

$$\begin{array}{c}\hfill X=\frac{\partial }{\partial t},\end{array}$$

by a suitable change of variables

$$\begin{array}{c}\hfill t=t(x,y),u=u(x,y).\end{array}$$

Considering that the Lie groups of point transformations related to a given differential equation $\mathcal{E}$ involve n independent variables $x=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n$ and m dependent variables $u=(u^1,u^2,\dots ,u^m)\in {\mathbb{R}}^m$ [16,17], let:

$$x^{*}=X(x,u;a),u^{*}=U(x,u;a)$$

(5)

be a group of transformations in the space $\in {\mathbb{R}}^{n+m}$ of the variables $(x,u)$ [17,18]. Moreover, let the following equation:

$$u=\Theta \left(x\right)\equiv ({\Theta }^1\left(x\right),{\Theta }^2\left(x\right),\dots ,{\Theta }^m\left(x\right)),$$

be a solution for the equation $\mathcal{E}$. A Lie group of transformations of the form (5) admitted by $\mathcal{E}$ has the two corresponding properties below [15,17]:

• A transformation of the group maps any solution of $\mathcal{E}$ into another solution of $\mathcal{E}$;
• A transformation of the group leaves $\mathcal{E}$ invariant, supposing that $\mathcal{E}$ reads the same in terms of the variables $(x,u)$ and in terms of the transformed variables $(x^{*},u^{*})$.

3. Simplification and Parametrisation Form of Model (1)

In this Section, a reduction of the number of parameters from the original model is performed. As a result, a cosmetic simplification of the non-linear system (1) is achieved below.

By letting:

$$\begin{array}{ccc}\hfill \tau & =& {\mu }_{3}t,\hfill \\ \hfill u_1\left(\tau \right)& =& \frac{b{x}_1}{{\lambda }_2},\hfill \\ \hfill u_2\left(\tau \right)& =& \frac{a{x}_2}{{\lambda }_1},\hfill \\ \hfill u_3\left(\tau \right)& =& \frac{x_3}{c}.\hfill \end{array}$$

(6)

The left-hand side of the model Equation (1) becomes:

$$\begin{array}{ccc}\hfill \frac{d{x}_1}{dt}& =& \left(\frac{{\lambda }_2{\mu }_3}{b}\right)\left(\frac{d{u}_1}{d\tau }\right),\hfill \\ \hfill \frac{d{x}_2}{dt}& =& \left(\frac{{\lambda }_1{\mu }_3}{a}\right)\left(\frac{d{u}_2}{d\tau }\right),\hfill \\ \hfill \frac{d{x}_3}{dt}& =& \left(c{\mu }_3\right)\left(\frac{d{u}_3}{d\tau }\right).\hfill \end{array}$$

(7)

The substitution of Equations (6) and (7) into (1) gives the following:

$$\begin{array}{ccc}\hfill \frac{d{u}_1}{d\tau }& =& \frac{b{\lambda }_1}{{\lambda }_2{\mu }_3}\left(1+u_2\right)-\frac{{\mu }_1}{{\mu }_3}{u}_1,\hfill \\ \hfill \frac{d{u}_2}{d\tau }& =& \frac{a{\lambda }_2}{{\lambda }_1{\mu }_3}\left(1+u_1\right)-\frac{{\mu }_2}{{\mu }_3}{u}_2+\frac{a\rho }{\left({\lambda }_1{\mu }_3\right)(1+u_3)},\hfill \\ \hfill \frac{d{u}_3}{d\tau }& =& \frac{{\lambda }_3}{c{\mu }_3}+\frac{ad\sigma }{c{\mu }_3(ad+{\lambda }_1)u_2}-u_3.\hfill \end{array}$$

(8)

Hence, Equation (8) is reduced to:

$$\begin{array}{ccc}\hfill \frac{d{u}_1}{d\tau }& =& {\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1,\hfill \\ \hfill \frac{d{u}_2}{d\tau }& =& {\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3},\hfill \\ \hfill \frac{d{u}_3}{d\tau }& =& {\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3,\hfill \end{array}$$

(9)

with

$$\begin{array}{ccc}\hfill {\lambda }_1^{*}& =& \frac{b{\lambda }_1}{{\lambda }_2{\mu }_3},\hfill \\ \hfill {\mu }_1^{*}& =& \frac{{\mu }_1}{{\mu }_3},\hfill \\ \hfill {\lambda }_2^{*}& =& \frac{a{\lambda }_2}{{\lambda }_1{\mu }_3},\hfill \\ \hfill {\mu }_2^{*}& =& \frac{{\mu }_2}{{\mu }_3},\hfill \\ \hfill a^{*}& =& \frac{a\rho }{{\lambda }_1{\mu }_3},\hfill \\ \hfill {\lambda }_3^{*}& =& \frac{{\lambda }_3}{c{\mu }_3},\hfill \\ \hfill b^{*}& =& \frac{\sigma d^{*}}{c{\mu }_3},\hfill \\ \hfill d^{*}& =& \frac{ad}{{\lambda }_1}.\hfill \end{array}$$

4. Lie Symmetry Analysis of the Model (9)

By applying Equations (2) and (3) into the Non-dimensional model Equation (9), we obtain the following:

$$\begin{array}{ccc}\hfill G\left({\lambda }_1^{\ast }(1+u_2)-{\mu }_1^{*}{u}_1\right)& =& -{\mu }_1^{*}{U}_1+{\lambda }_1^{*}{U}_2,\hfill \\ \hfill G\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)& =& {\lambda }_2^{*}{U}_1-{\mu }_2^{*}{U}_2-\frac{a^{*}}{{(1+u_3)}^2}{U}_3,\hfill \\ \hfill G\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right)& =& -\left(1+\frac{b^{*}}{{(d^{*}+u_2)}^2}\right)U_3.\hfill \end{array}$$

(10)

The substitution of extended infinitesimal transformations into Equation (3) gives the following equations:

$$\begin{array}{cc}\hfill -{\mu }_1^{*}{U}_1+{\lambda }_1^{*}{U}_2& =U_1^{\left[\tau \right]}+u_1^{{}^{\prime }}{U}_1^{\left[u_1\right]}+u_2^{{}^{\prime }}{U}_1^{\left[u_2\right]}+u_3^{{}^{\prime }}{U}_1^{\left[u_3\right]}\hfill \\ \hfill & -u_1^{{}^{\prime }}({\mathcal{T}}^{\left[\tau \right]}+u_1^{{}^{\prime }}{\mathcal{T}}^{\left[u_1\right]}+u_2^{{}^{\prime }}{\mathcal{T}}^{\left[u_2\right]}+u_3^{{}^{\prime }}{\mathcal{T}}^{\left[u_3\right]}),\hfill \\ \hfill {\lambda }_2^{*}{U}_1-{\mu }_2^{*}{U}_2-\frac{a^{*}}{{(1+u_3)}^2}{U}_3& =U_2^{\left[\tau \right]}+u_1^{{}^{\prime }}{U}_2^{\left[u_1\right]}+u_2^{{}^{\prime }}{U}_2^{\left[u_2\right]}+u_3^{{}^{\prime }}{U}_2^{\left[u_3\right]}\hfill \\ \hfill & -u_2^{{}^{\prime }}({\mathcal{T}}^{\left[\tau \right]}+u_1^{{}^{\prime }}{\mathcal{T}}^{\left[u_1\right]}+u_2^{{}^{\prime }}{\mathcal{T}}^{\left[u_2\right]}+u_3^{{}^{\prime }}{\mathcal{T}}^{\left[u_3\right]}),\hfill \\ \hfill -\left(1+\frac{b^{*}}{{(d^{*}+u_2)}^2}\right)U_3& =U_3^{\left[\tau \right]}+u_1^{{}^{\prime }}{U}_3^{\left[u_1\right]}+u_2^{{}^{\prime }}{U}_3^{\left[u_2\right]}+u_3^{{}^{\prime }}{U}_3^{\left[u_3\right]}\hfill \\ \hfill & -u_3^{{}^{\prime }}({\mathcal{T}}^{\left[\tau \right]}+u_1^{{}^{\prime }}{\mathcal{T}}^{\left[u_1\right]}+u_2^{{}^{\prime }}{\mathcal{T}}^{\left[u_2\right]}+u_3^{{}^{\prime }}{\mathcal{T}}^{\left[u_3\right]}).\hfill \end{array}$$

(11)

where

$$u_1^{{}^{\prime }}=\frac{d{u}_1}{d\tau };u_2^{{}^{\prime }}=\frac{d{u}_2}{d\tau };u_3^{{}^{\prime }}=\frac{d{u}_3}{d\tau }.$$

The substitution of Equation (9) into (11) gives the following:

$$\begin{array}{cc}\hfill {\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1& =U_1^{\left[\tau \right]}+({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)\left(U_1^{\left[u_1\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)\hfill \\ & +({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3})U_1^{\left[u_2\right]}\hfill \\ & +({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3)U_1^{\left[u_3\right]}\hfill \\ & -{({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)}^2{\mathcal{T}}^{\left[u_1\right]}\hfill \\ & -({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right){\mathcal{T}}^{\left[u_2\right]}\hfill \\ & -({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right){\mathcal{T}}^{\left[u_3\right]},\hfill & \hfill \\ \hfill {\lambda }_2^{*}{U}_1-{\mu }_2^{*}{U}_2-\frac{a^{*}}{{(1+u_3)}^2}{U}_3& =U_2^{\left[\tau \right]}+\left({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1\right)U_2^{\left[u_1\right]}\hfill \\ & +\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)\left(U_2^{\left[u_2\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)\hfill \\ & +({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3)U_2^{\left[u_3\right]}\hfill \\ & -({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right){\mathcal{T}}^{\left[u_1\right]}\hfill \\ & -{\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)}^2{\mathcal{T}}^{\left[u_2\right]}\hfill \\ & -\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right){\mathcal{T}}^{\left[u_3\right]},\hfill & \hfill \\ \hfill -\left(1+\frac{b^{*}}{{(d^{*}+u_2)}^2}\right)U_3& =U_3^{\left[\tau \right]}+\left({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1\right)U_3^{\left[u_1\right]}\hfill \\ & +\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)U_3^{\left[u_2\right]}\hfill \\ & +\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right)\left(U_3^{\left[u_3\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)\hfill \\ & -({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1)\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right){\mathcal{T}}^{\left[u_1\right]}\hfill \\ & -\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right){\mathcal{T}}^{\left[u_2\right]}\hfill \\ & +{\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right)}^2{\mathcal{T}}^{\left[u_3\right]}.\hfill \end{array}$$

(12)

Special solutions are needed since it is generally challenging to solve the non-linear system (12). In the case of $\mathcal{T}=\mathcal{T}\left(\tau \right)$, $U_1=U_1\left(u_1\right)$, $U_2=U_2\left(u_2\right)$, $U_3=U_3\left(u_3\right)$, the non-linear Equation (12) is reduced as follows:

$$\left({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1\right)\left(U_1^{\left[u_1\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)=-{\mu }_1^{*}{U}_1+{\lambda }_1^{*}{U}_2,$$

(13)

$$\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)\left(U_2^{\left[u_2\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)={\lambda }_2^{*}{U}_1-{\mu }_2^{*}{U}_2-\frac{a^{*}}{{(1+u_3)}^2}{U}_3,$$

(14)

$$\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right)\left(U_3^{\left[u_3\right]}-{\mathcal{T}}^{\left[\tau \right]}\right)=-\left(1+\frac{b^{*}}{{(d^{*}+u_2)}^2}\right)U_3.$$

(15)

Taking the partial derivative of Equation (15) with respect to $\tau$ yields to the following second-order partial differential equation:

$${\mathcal{T}}^{\left[\tau \tau \right]}=0,$$

which implies that:

$$\mathcal{T}\left(\tau \right)=a_1\tau +a_2,$$

(16)

with the $a_1$ and $a_2$ constants of integration. The substitution of Equation (16) into (13)–(15) gives the following:

$$\left({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1\right)\left(U_1^{\left[u_1\right]}-a_1\right)=-{\mu }_1^{*}{U}_1+{\lambda }_1^{*}{U}_2,$$

(17)

$$\left({\lambda }_2^{*}(1+u_1)-{\mu }_2^{*}{u}_2+\frac{a^{*}}{1+u_3}\right)\left(U_2^{\left[u_2\right]}-a_1\right)={\lambda }_2^{*}{U}_1-{\mu }_2^{*}{U}_2-\frac{a^{*}}{{(1+u_3)}^2}{U}_3,$$

(18)

$$\left({\lambda }_3^{*}+\frac{b^{*}}{d^{*}+u_2}-u_3\right)\left(U_3^{\left[u_3\right]}-a_1\right)=-\left(1+\frac{b^{*}}{{(d^{*}+u_2)}^2}\right)U_3.$$

(19)

Twice partially differentiating Equation (18) with respect to $u_2$ gives:

$$U_2^{\left[u_2{u}_2\right]}=0.$$

Hence,

$$U_2\left(u_2\right)=b_1{u}_2+b_2.$$

The substitution of Equation (18) into (17) gives the equation below:

$$\left({\lambda }_1^{*}(1+u_2)-{\mu }_1^{*}{u}_1\right)\left(U_1^{\left[u_1\right]}-a_1\right)=-{\mu }_1^{*}{U}_1+{\lambda }_1^{*}\left(b_1{u}_2+b_2\right).$$

(20)

Since Equation (20) depends on all values of $u_1$ and $u_2$, we get the following:

$$\begin{array}{ccc}\hfill u_1& :& -{\mu }_1^{*}\left(\frac{\partial U_1}{\partial u_1}-a_1\right)=-{\mu }_1^{*}{U}_1,\hfill \\ \hfill u_2& :& {\lambda }_1^{*}={\lambda }_1^{*}{b}_1,\hfill \\ \hfill -& :& {\lambda }_1^{*}={\lambda }_1^{*}{b}_2.\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}\hfill U_1& =& kexp\left[u_1\right]+a_1,\hfill \\ \hfill b_1& =& 1,\hfill \\ \hfill b_2& =& 1.\hfill \end{array}$$

From (19), we obtain:

$$u_3:\frac{\partial U_3}{\partial u_3}=a_1.$$

Hence,

$$U_3=a_1{u}_3+c_1.$$

Therefore, the infinitesimals transformations are provided as follows:

$$\begin{array}{ccc}\hfill U_1\left(u_1\right)& =& kexp\left[u_1\right]+a_1,\hfill \\ \hfill U_2\left(u_2\right)& =& b_1{u}_2+b_2,\hfill \\ \hfill U_3\left(u_3\right)& =& a_1{u}_3+c_1.\hfill \end{array}$$

(21)

It is important to note that these infinitesimal transformations are not unique. However, there exists an infinite set of infinitesimal transformations. Therefore, Equation (2) becomes:

$$G=\left(a_1\tau +a_2\right)\frac{\partial }{\partial \tau }+\left(kexp\left[u_1\right]+a_1\right)\frac{\partial }{\partial u_1}+\left(b_1{u}_2+b_2\right)\frac{\partial }{\partial u_2}+\left(a_1{u}_3+c_1\right)\frac{\partial }{\partial u_3}.$$

Hence, the following Lie generators are found:

$$\begin{array}{ccc}\hfill G_1& =& \tau \frac{\partial }{\partial \tau }+\frac{\partial }{\partial u_1}+\frac{\partial }{\partial u_3},\hfill \\ \hfill G_2& =& \frac{\partial }{\partial \tau },\hfill \\ \hfill G_3& =& exp\left[u_1\right]\frac{\partial }{\partial u_1},\hfill \\ \hfill G_4& =& u_2\frac{\partial }{\partial u_2},\hfill \\ \hfill G_5& =& \frac{\partial }{\partial u_2},\hfill \\ \hfill G_6& =& \frac{\partial }{\partial u_3}.\hfill \end{array}$$

By computing the Lie bracket, we obtain the given commutator table (

Table 2. The commutator table of the infinitesimal generator.

	${\mathit{G}}_1$	${\mathit{G}}_2$	${\mathit{G}}_3$	${\mathit{G}}_4$	${\mathit{G}}_5$	${\mathit{G}}_6$
$G_1$	0	$-G_2$	$G_3$	0	0	0
$G_2$	$G_2$	0	0	0	0	0
$G_3$	$-G_3$	0	0	0	0	0
$G_4$	0	0	0	0	−$G_5$	0
$G_5$	0	0	0	$G_5$	0	0
$G_6$	0	0	0	0	0	0

):

By setting the constant of integration to $b_1=1$, $b_2=1$, $c_1=1$, $a_1=1$, $k=1$. Equation (21) becomes:

$$\begin{array}{ccc}\hfill U_1& =& 1+exp\left[u_1\right],\hfill \\ \hfill U_2& =& 1+u_2,\hfill \\ \hfill U_3& =& 1+u_3,\hfill \\ \hfill \mathcal{T}& =& 1+\tau .\hfill \end{array}$$

Hence, we have the following equations:

$$\begin{array}{ccc}\hfill (1+\tau )r_t+(1+exp\left[u_1\right])r_{x_1}+(1+u_2)r_{x_2}+(1+u_3)r_{x_3}& =& 0,\hfill \\ \hfill (1+\tau )u_1^{\left[\tau \right]}+(1+exp\left[u_1\right])U_1^{\left[u_1\right]}+(1+u_2)U_1^{\left[u_2\right]}+(1+u_3)U_1^{\left[u_3\right]}& =& 0,\hfill \\ \hfill (1+\tau )u_2^{\left[\tau \right]}+(1+exp\left[u_1\right])U_2^{\left[u_1\right]}+(1+u_2)U_2^{\left[u_2\right]}+(1+u_3)U_2^{\left[u_3\right]}& =& 0,\hfill \\ \hfill (1+\tau )u_3^{\left[\tau \right]}+(1+exp\left[u_1\right])U_3^{\left[u_1\right]}+(1+u_2)U_3^{\left[u_2\right]}+(1+u_3)U_3^{\left[u_3\right]}& =& 1.\hfill \end{array}$$

(22)

The solution of Equation (22) is given by:

$$\begin{array}{ccc}\hfill r& =& \frac{\tau }{f\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_1& =& \frac{\tau }{f\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_2& =& \frac{\tau }{f\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_3& =& ln\tau +\frac{\tau }{f\left(u_1{u}_2{u}_3\right)}.\hfill \end{array}$$

The special case is given by:

$$\begin{array}{ccc}\hfill r& =& \frac{\tau }{\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_1& =& \frac{\tau }{\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_2& =& \frac{\tau }{\left(u_1{u}_2{u}_3\right)},\hfill \\ \hfill u_3& =& ln\tau +\frac{\tau }{\left(u_1{u}_2{u}_3\right)}.\hfill \end{array}$$

Substituting back to Equation (6), we obtain the following:

$$\begin{array}{ccc}\hfill x_1& =& \frac{{\lambda }_2}{b}\sqrt{\frac{c{\lambda }_1{\mu }_{3}t}{a{x}_2{x}_3}},\hfill \\ \hfill x_2& =& \frac{{\lambda }_1}{a}\sqrt{\frac{c{\lambda }_2{\mu }_{3}t}{b{x}_1{x}_3}},\hfill \\ \hfill x_3& =& ln\left[{\mu }_{3}t\right]+c\sqrt{\frac{{\lambda }_1{\lambda }_2{\mu }_{3}t}{ab{x}_1{x}_2}}.\hfill \end{array}$$

(23)

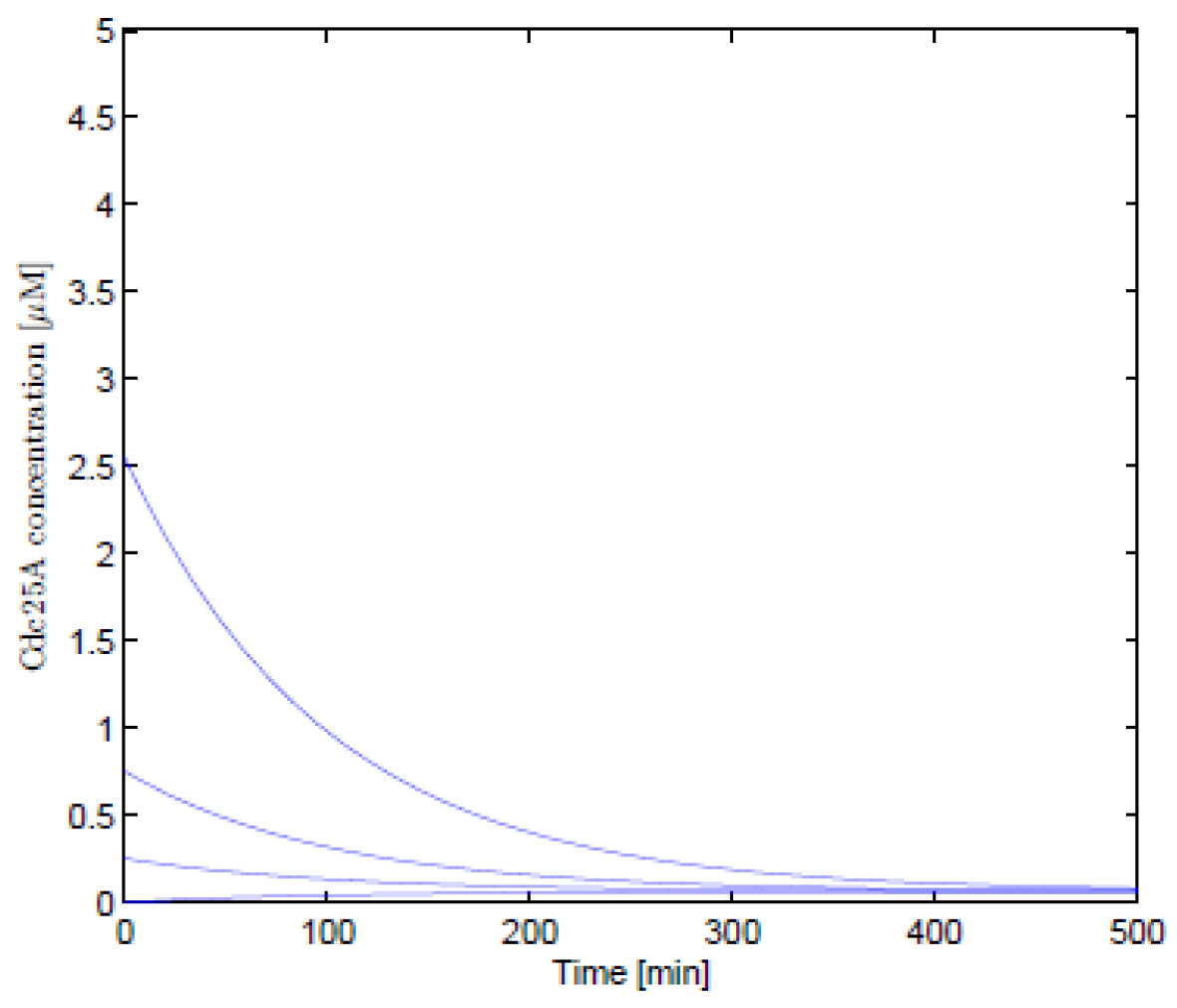
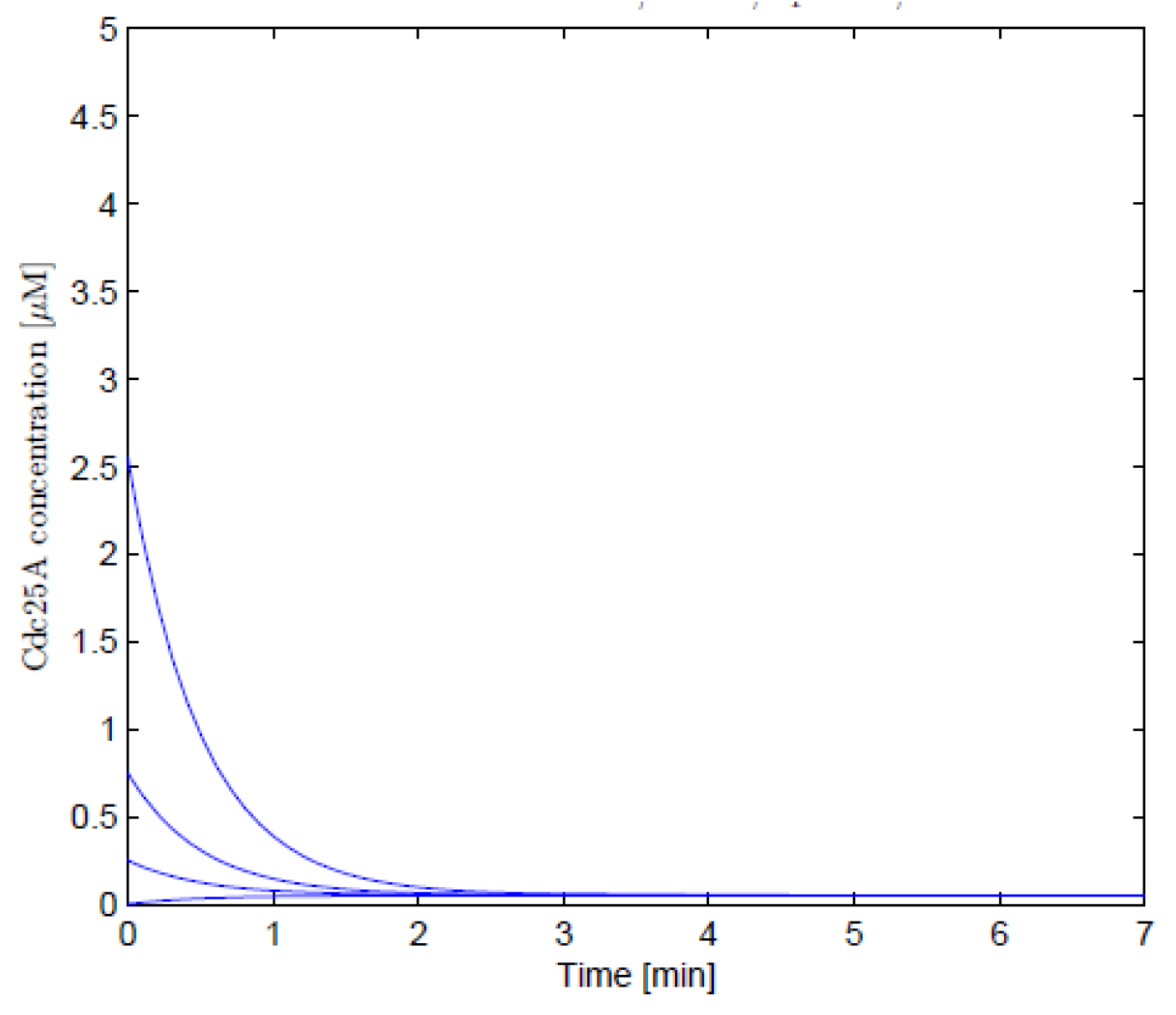
5. Numerical Solutions

As illustrated in the graphs below, the numerical solutions for non-linear differential equations were obtained using the Matlab software. Figure 1 and Figure 2 show the numerical solutions for Equations (1) and (23), respectively. Numerical results obtained before and after using the Lie symmetry techniques on the Cancer Sub-Network model were found to be consistent. The parameters chosen were ${\lambda }_1=0.1$, $a=0.01$, ${\mu }_1=1$, and the effect of the synthesis rate of Cdc25A has initial values of $x_1\left(0\right)=2\times {10}^{-5}$, $0.25$, $0.75$, $2.55$; $x_2\left(0\right)=0.06$. The simulation results are in line with Aguda and Tang’s findings [2], which show that phosphatase gene (Cdc25A) activity increases in lockstep with cyclin-dependent kinase inhibitor ($P{27}^{Kip1}$) levels.

6. Conclusions

The cancer sub-network revealed in this research is significantly simplified in comparison to what is known as the molecular and gene interactions of the oncogene and the tumour-suppressor gene. On the other hand, applying Lie symmetry analysis and computationally modelling the full cancer network during the cell cycle phase is challenging. To represent the cancer network, we started with a simple model that encapsulated the network’s key features. This model can be updated in the future to make it more realistic.

In this paper, the Lie symmetry technique was applied to obtain a modified, local, one-parameter infinitesimal transformation. Furthermore, Lie operators and Lie algebra were discovered to be useful in obtaining approximated solutions for the non-linear cancer network model. The results of the numerical simulations were found to be consistent with the findings of Aguda and Tang [2]. The model simulation revealed that when the complex’s degradation rate is less than 0.001 min${}^{-1}$ (all other parameters remaining constant), the subnetwork generates a peak value for the phosphatase gene (Cdc25A) activity.