How Transverse Waves Drive Turbulence in the Solar Corona
Abstract
:1. Introduction
1.1. Background
- How is wave power transmitted through the atmosphere?
- To what extent does wave energy contribute to maintaining the atmospheric temperature profile and to accelerating solar wind?
- Can wave behaviour provide information about the nature of the atmosphere through a seismological analysis?
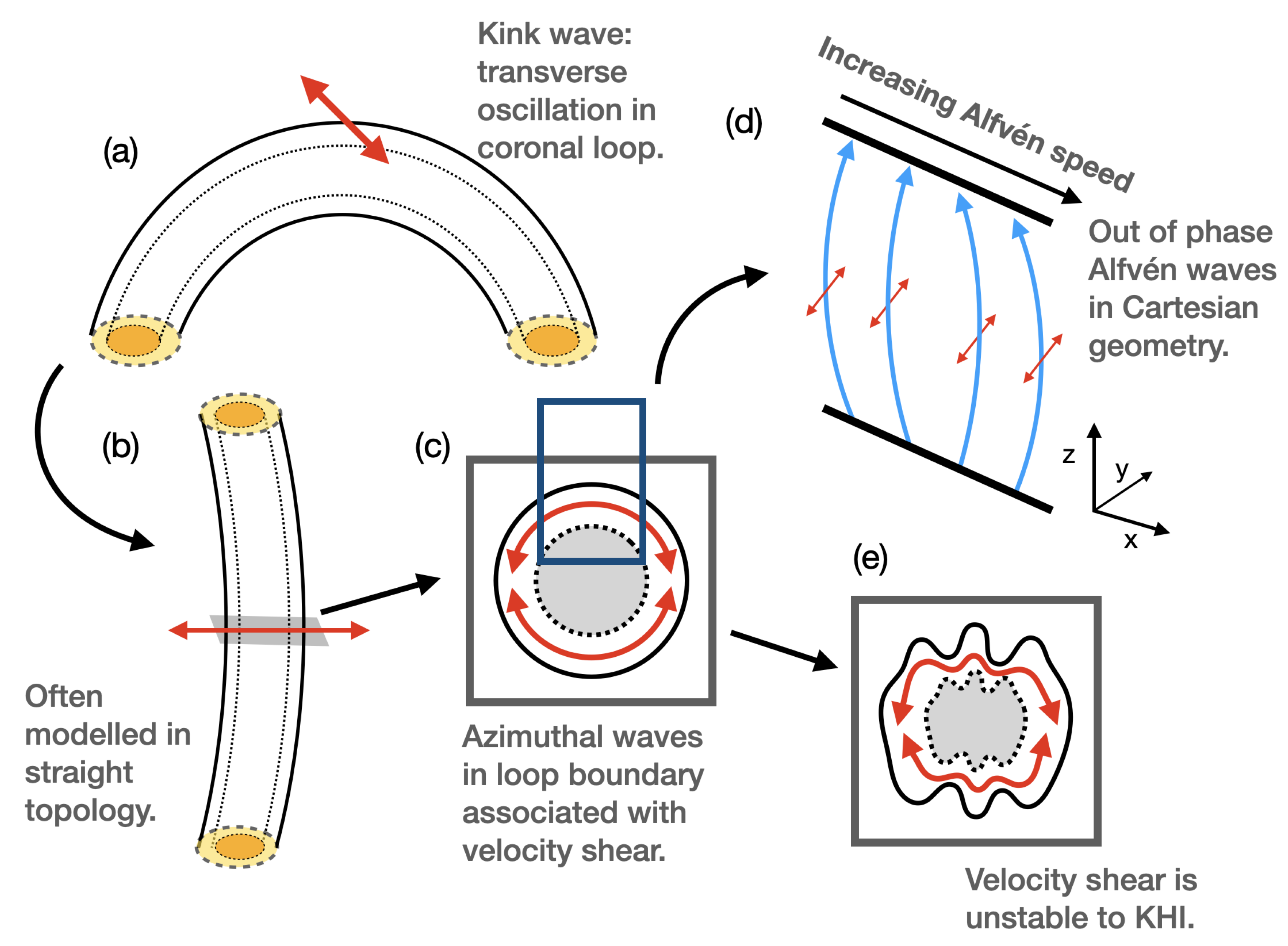
1.2. Context
2. Poynting Flux
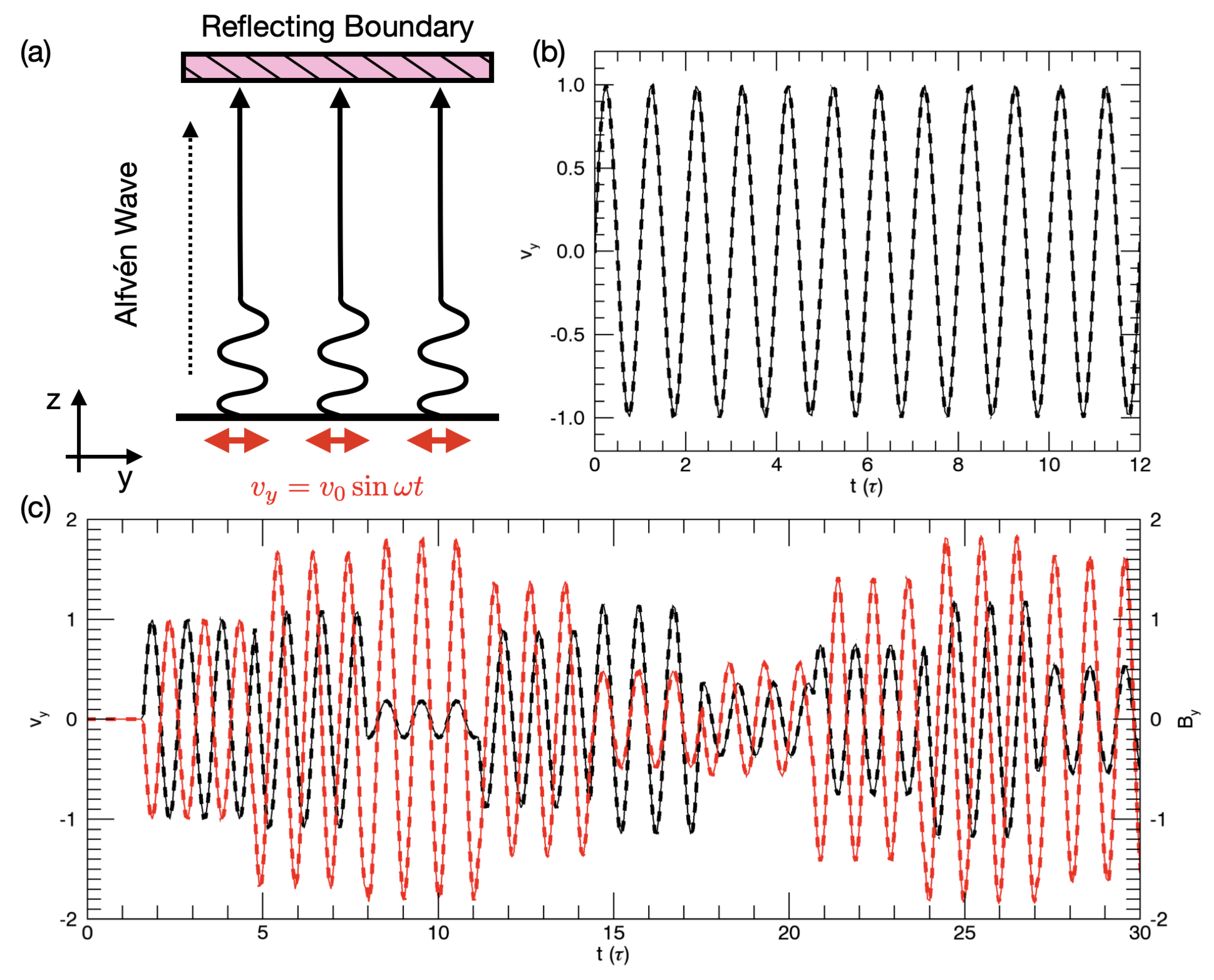
3. Standing Modes
3.1. Wave Excitation
3.2. Instability Growth Rate
3.3. Observational Considerations
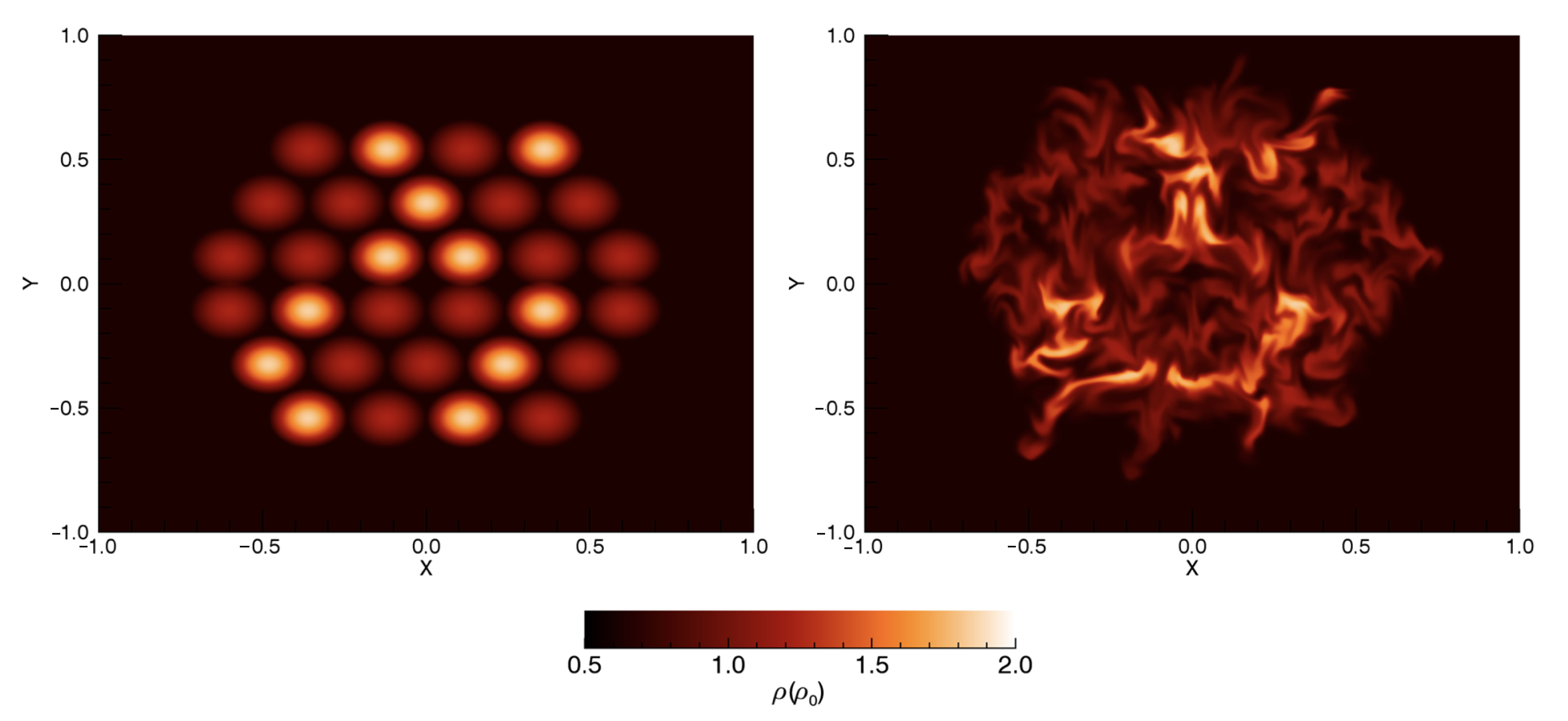
4. Propagating Waves
5. Discussion
- Are coronal waves associated with sufficient energy to heat the atmospheric plasma and power solar wind?
- Can wave heating self-consistently create and sustain the density profile assumed in wave heating models?
- Are heating rates too low in very high Reynolds number regimes?
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| KHI | Kelvin–Helmholtz instability |
| DEM | Differential Emission Measure |
| LoS | Line of Sight |
References
- Alfvén, H. Existence of Electromagnetic-Hydrodynamic Waves. Nature 1942, 150, 405–406. [Google Scholar] [CrossRef]
- Basu, S. Global seismology of the Sun. Living Rev. Sol. Phys. 2016, 13, 2. [Google Scholar] [CrossRef]
- Jess, D.B.; Van Doorsselaere, T.; Verth, G.; Fedun, V.; Krishna Prasad, S.; Erdélyi, R.; Keys, P.H.; Grant, S.D.T.; Uitenbroek, H.; Christian, D.J. An Inside Look at Sunspot Oscillations with Higher Azimuthal Wavenumbers. Astrophys. J. 2017, 842, 59. [Google Scholar] [CrossRef]
- De Pontieu, B.; McIntosh, S.W.; Carlsson, M.; Hansteen, V.H.; Tarbell, T.D.; Schrijver, C.J.; Title, A.M.; Shine, R.A.; Tsuneta, S.; Katsukawa, Y.; et al. Chromospheric Alfvénic Waves Strong Enough to Power the Solar Wind. Science 2007, 318, 1574–1577. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Erdélyi, R. Oscillations and Waves in Solar Spicules. Space Sci. Rev. 2009, 149, 355–388. [Google Scholar] [CrossRef] [Green Version]
- Aschwanden, M.J.; Fletcher, L.; Schrijver, C.J.; Alexander, D. Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer. Astrophys. J. 1999, 520, 880–894. [Google Scholar] [CrossRef] [Green Version]
- Tomczyk, S.; McIntosh, S.W.; Keil, S.L.; Judge, P.G.; Schad, T.; Seeley, D.H.; Edmondson, J. Alfvén Waves in the Solar Corona. Science 2007, 317, 1192–1196. [Google Scholar] [CrossRef]
- Tu, C.Y.; Marsch, E. Magnetohydrodynamic Structures Waves and Turbulence in the Solar Wind: Observations and Theories. Space Sci. Rev. 1995, 73, 1–210. [Google Scholar] [CrossRef]
- Khotyaintsev, Y.V.; Graham, D.B.; Vaivads, A.; Steinvall, K.; Edberg, N.J.T.; Eriksson, A.I.; Johansson, E.P.G.; Sorriso-Valvo, L.; Maksimovic, M.; Bale, S.D.; et al. Density Fluctuations Associated with Turbulence and Waves: First Observations by Solar Orbiter. arXiv 2021, arXiv:2103.17208. [Google Scholar] [CrossRef]
- Klimchuk, J.A. On Solving the Coronal Heating Problem. Sol. Phys. 2006, 234, 41–77. [Google Scholar] [CrossRef] [Green Version]
- Erdélyi, R.; Ballai, I. Heating of the solar and stellar coronae: A review. Astron. Nachrichten 2007, 328, 726–733. [Google Scholar] [CrossRef]
- Parnell, C.E.; De Moortel, I. A contemporary view of coronal heating. Philos. Trans. R. Soc. Lond. Ser. A 2012, 370, 3217–3240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reale, F. Coronal Loops: Observations and Modeling of Confined Plasma. Living Rev. Sol. Phys. 2014, 11, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arregui, I. Wave heating of the solar atmosphere. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140261. [Google Scholar] [CrossRef]
- Wilmot-Smith, A.L. An overview of flux braiding experiments. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Doorsselaere, T.; Srivastava, A.K.; Antolin, P.; Magyar, N.; Vasheghani Farahani, S.; Tian, H.; Kolotkov, D.; Ofman, L.; Guo, M.; Arregui, I.; et al. Coronal Heating by MHD Waves. Space Sci. Rev. 2020, 216, 140. [Google Scholar] [CrossRef]
- Viall, N.M.; De Moortel, I.; Downs, C.; Klimchuk, J.A.; Parenti, S.; Reale, F. The Heating of the Solar Corona. Sol. Phys. Sol. Wind. 2021, 1, 35. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Lamkin, S.L. Turbulent magnetic reconnection. Phys. Fluids 1986, 29, 2513–2534. [Google Scholar] [CrossRef]
- Lazarian, A.; Vishniac, E.T. Reconnection in a Weakly Stochastic Field. Astrophyis. J. 1999, 517, 700–718. [Google Scholar] [CrossRef] [Green Version]
- Servidio, S.; Dmitruk, P.; Greco, A.; Wan, M.; Donato, S.; Cassak, P.A.; Shay, M.A.; Carbone, V.; Matthaeus, W.H. Magnetic reconnection as an element of turbulence. Nonlinear Process. Geophys. 2011, 18, 675–695. [Google Scholar] [CrossRef]
- Handy, B.N.; Acton, L.W.; Kankelborg, C.C.; Wolfson, C.J.; Akin, D.J.; Bruner, M.E.; Caravalho, R.; Catura, R.C.; Chevalier, R.; Duncan, D.W.; et al. The transition region and coronal explorer. Sol. Phys. 1999, 187, 229–260. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Ofman, L.; Deluca, E.E.; Roberts, B.; Davila, J.M. TRACE observation of damped coronal loop oscillations: Implications for coronal heating. Science 1999, 285, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Aschwanden, M.J.; de Pontieu, B.; Schrijver, C.J.; Title, A.M. Transverse Oscillations in Coronal Loops Observed with TRACE II. Measurements of Geometric and Physical Parameters. Sol. Phys. 2002, 206, 99–132. [Google Scholar] [CrossRef]
- Okamoto, T.J.; Tsuneta, S.; Berger, T.E.; Ichimoto, K.; Katsukawa, Y.; Lites, B.W.; Nagata, S.; Shibata, K.; Shimizu, T.; Shine, R.A.; et al. Coronal Transverse Magnetohydrodynamic Waves in a Solar Prominence. Science 2007, 318, 1577–1580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antolin, P.; Verwichte, E. Transverse Oscillations of Loops with Coronal Rain Observed by Hinode/Solar Optical Telescope. Astrophys. J. 2011, 736, 121. [Google Scholar] [CrossRef]
- McIntosh, S.W.; de Pontieu, B.; Carlsson, M.; Hansteen, V.; Boerner, P.; Goossens, M. Alfvénic waves with sufficient energy to power the quiet solar corona and fast solar wind. Nature 2011, 475, 477–480. [Google Scholar] [CrossRef]
- Morton, R.J.; Verth, G.; Hillier, A.; Erdélyi, R. The Generation and Damping of Propagating MHD Kink Waves in the Solar Atmosphere. Astrophys. J. 2014, 784, 29. [Google Scholar] [CrossRef] [Green Version]
- Morton, R.J.; Tomczyk, S.; Pinto, R. Investigating Alfvénic wave propagation in coronal open-field regions. Nat. Commun. 2015, 6, 7813. [Google Scholar] [CrossRef]
- Schrijver, C.J.; Aschwanden, M.J.; Title, A.M. Transverse oscillations in coronal loops observed with TRACE I. An Overview of Events, Movies, and a Discussion of Common Properties and Required Conditions. Sol. Phys. 2002, 206, 69–98. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Verwichte, E. Coronal Waves and Oscillations. Living Rev. Sol. Phys. 2005, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- Ruderman, M.S.; Erdélyi, R. Transverse Oscillations of Coronal Loops. Space Sci. Rev. 2009, 149, 199–228. [Google Scholar] [CrossRef] [Green Version]
- Nakariakov, V.M.; Anfinogentov, S.A.; Antolin, P.; Jain, R.; Kolotkov, D.Y.; Kupriyanova, E.G.; Li, D.; Magyar, N.; Nisticò, G.; Pascoe, D.J.; et al. Kink Oscillations of Coronal Loops. Space Sci. Rev. 2021, 217, 73. [Google Scholar] [CrossRef]
- Ionson, J.A. Resonant absorption of Alfvenic surface waves and the heating of solar coronal loops. Astrophys. J. 1978, 226, 650–673. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Roberts, B. The Damping of Coronal Loop Oscillations. Astrophys. J. 2002, 577, 475–486. [Google Scholar] [CrossRef]
- Arregui, I.; Andries, J.; Van Doorsselaere, T.; Goossens, M.; Poedts, S. MHD seismology of coronal loops using the period and damping of quasi-mode kink oscillations. Astron. Astrophys. 2007, 463, 333–338. [Google Scholar] [CrossRef]
- De Moortel, I.; Nakariakov, V.M. Magnetohydrodynamic waves and coronal seismology: An overview of recent results. Philos. Trans. R. Soc. Lond. Ser. A 2012, 370, 3193–3216. [Google Scholar] [CrossRef] [Green Version]
- Pascoe, D.J.; Goddard, C.R.; Nisticò, G.; Anfinogentov, S.; Nakariakov, V.M. Coronal loop seismology using damping of standing kink oscillations by mode coupling. Astron. Astrophys. 2016, 589, A136. [Google Scholar] [CrossRef]
- Duckenfield, T.; Kolotkov, D. Coronal seismology at 20. Astron. Geophys. 2021, 62, 3–28. [Google Scholar] [CrossRef]
- Terradas, J.; Oliver, R.; Ballester, J.L. Damped Coronal Loop Oscillations: Time-dependent Results. Astrophys. J. 2006, 642, 533–540. [Google Scholar] [CrossRef] [Green Version]
- Pascoe, D.J.; Wright, A.N.; De Moortel, I. Coupled Alfvén and Kink Oscillations in Coronal Loops. Astrophys. J. 2010, 711, 990–996. [Google Scholar] [CrossRef] [Green Version]
- Davila, J.M. Heating of the Solar Corona by the Resonant Absorption of Alfven Waves. Astrophys. J. 1987, 317, 514. [Google Scholar] [CrossRef] [Green Version]
- Poedts, S.; Goossens, M.; Kerner, W. On the Efficiency of Coronal Loop Heating by Resonant Absorption. Astrophys. J. 1990, 360, 279. [Google Scholar] [CrossRef]
- Beliën, A.J.C.; Martens, P.C.H.; Keppens, R. Coronal Heating by Resonant Absorption: The Effects of Chromospheric Coupling. Astrophys. J. 1999, 526, 478–493. [Google Scholar] [CrossRef] [Green Version]
- Pagano, P.; De Moortel, I. Contribution of mode-coupling and phase-mixing of Alfvén waves to coronal heating. Astron. Astrophys. 2017, 601, A107. [Google Scholar] [CrossRef] [Green Version]
- Heyvaerts, J.; Priest, E.R. Coronal heating by phase-mixed shear Alfven waves. Astron. Astrophys. 1983, 117, 220–234. [Google Scholar]
- Ofman, L.; Davila, J.M. Alfvén wave heating of coronal holes and the relation to the high-speed solar wind. J. Geophys. Res. 1995, 100, 23413–23426. [Google Scholar] [CrossRef]
- Hood, A.W.; Ireland, J.; Priest, E.R. Heating of coronal holes by phase mixing. Astron. Astrophys. 1997, 318, 957–962. [Google Scholar]
- De Moortel, I.; Hood, A.W.; Ireland, J.; Arber, T.D. Phase mixing of Alfvén waves in a stratified and open atmosphere. Astron. Astrophys. 1999, 346, 641–651. [Google Scholar]
- Pagano, P.; Pascoe, D.J.; De Moortel, I. Contribution of phase-mixing of Alfvén waves to coronal heating in multi-harmonic loop oscillations. Astron. Astrophys. 2018, 616, A125. [Google Scholar] [CrossRef] [Green Version]
- Pagano, P.; De Moortel, I. Contribution of observed multi frequency spectrum of Alfvén waves to coronal heating. Astron. Astrophys. 2019, 623, A37. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; International Series of Monographs on Physics; Clarendon: Oxford, UK, 1961. [Google Scholar]
- Roberts, B. On the hydromagnetic stability of an unsteady Kelvin-Helmholtz flow. J. Fluid Mech. 1973, 59, 65–76. [Google Scholar] [CrossRef]
- Browning, P.K.; Priest, E.R. Kelvin-Helmholtz instability of a phased-mixed Alfven wave. Astron. Astrophys. 1984, 131, 283–290. [Google Scholar]
- Terradas, J.; Andries, J.; Goossens, M.; Arregui, I.; Oliver, R.; Ballester, J.L. Nonlinear Instability of Kink Oscillations due to Shear Motions. Astrophys. J. 2008, 687, L115. [Google Scholar] [CrossRef] [Green Version]
- Zaqarashvili, T.V.; Zhelyazkov, I.; Ofman, L. Stability of Rotating Magnetized Jets in the Solar Atmosphere. I. Kelvin-Helmholtz Instability. Astrophys. J. 2015, 813, 123. [Google Scholar] [CrossRef] [Green Version]
- Hillier, A.; Barker, A.; Arregui, I.; Latter, H. On Kelvin-Helmholtz and parametric instabilities driven by coronal waves. Mon. Not. R. Astron. Soc. 2019, 482, 1143–1153. [Google Scholar] [CrossRef]
- Wang, T.; Ofman, L.; Davila, J.M.; Su, Y. Growing Transverse Oscillations of a Multistranded Loop Observed by SDO/AIA. Astrophys. J. 2012, 751, L27. [Google Scholar] [CrossRef] [Green Version]
- Tian, H.; McIntosh, S.W.; Wang, T.; Ofman, L.; De Pontieu, B.; Innes, D.E.; Peter, H. Persistent Doppler Shift Oscillations Observed with Hinode/EIS in the Solar Corona: Spectroscopic Signatures of Alfvénic Waves and Recurring Upflows. Astrophys. J. 2012, 759, 144. [Google Scholar] [CrossRef] [Green Version]
- Nisticò, G.; Nakariakov, V.M.; Verwichte, E. Decaying and decayless transverse oscillations of a coronal loop. Astron. Astrophys. 2013, 552, A57. [Google Scholar] [CrossRef]
- Anfinogentov, S.A.; Nakariakov, V.M.; Nisticò, G. Decayless low-amplitude kink oscillations: A common phenomenon in the solar corona? Astron. Astrophys. 2015, 583, A136. [Google Scholar] [CrossRef]
- Duckenfield, T.; Anfinogentov, S.A.; Pascoe, D.J.; Nakariakov, V.M. Detection of the Second Harmonic of Decay-less Kink Oscillations in the Solar Corona. Astrophys. J. Lett. 2018, 854, L5. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Tian, H.; Peter, H. Flare-induced decay-less transverse oscillations in solar coronal loops. Astron. Astrophys. 2021, 652, L3. [Google Scholar] [CrossRef]
- Antolin, P.; De Moortel, I.; Van Doorsselaere, T.; Yokoyama, T. Modeling Observed Decay-less Oscillations as Resonantly Enhanced Kelvin-Helmholtz Vortices from Transverse MHD Waves and Their Seismological Application. Astrophys. J. 2016, 830, L22. [Google Scholar] [CrossRef] [Green Version]
- Thurgood, J.O.; Morton, R.J.; McLaughlin, J.A. First Direct Measurements of Transverse Waves in Solar Polar Plumes Using SDO/AIA. Astrophys. J. 2014, 790, L2. [Google Scholar] [CrossRef] [Green Version]
- Pant, V.; Van Doorsselaere, T. Revisiting the Relation between Nonthermal Line Widths and Transverse MHD Wave Amplitudes. Astrophys. J. 2020, 899, 1. [Google Scholar] [CrossRef]
- Fyfe, L.; Howson, T.; De Moortel, I.; Pant, V.; Van Doorsselaere, T. Investigating coronal wave energy estimates using synthetic non-thermal line widths. arXiv 2021, arXiv:2110.00257. [Google Scholar] [CrossRef]
- Withbroe, G.L.; Noyes, R.W. Mass and energy flow in the solar chromosphere and corona. Annu. Rev. Astron. Astrophys. 1977, 15, 363–387. [Google Scholar] [CrossRef]
- McLaughlin, J.A.; Hood, A.W.; de Moortel, I. Review Article: MHD Wave Propagation Near Coronal Null Points of Magnetic Fields. Space Sci. Rev. 2011, 158, 205–236. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, J.A. Phase Mixing of Alfvén Waves Near a 2D Magnetic Null Point. J. Astrophys. Astron. 2013, 34, 223–246. [Google Scholar] [CrossRef] [Green Version]
- Prokopyszyn, A.P.K.; Hood, A.W.; De Moortel, I. Phase mixing of nonlinear Alfvén waves. Astron. Astrophys. 2019, 624, A90. [Google Scholar] [CrossRef] [Green Version]
- Prokopyszyn, A.P.K.; Hood, A.W. Investigating the damping rate of phase-mixed Alfvén waves. Astron. Astrophys. 2019, 632, A93. [Google Scholar] [CrossRef] [Green Version]
- Prokopyszyn, A.P.K. Magnetohydrodynamic Waves in the Solar Corona. Ph.D. Thesis, University of St Andrews, St Andrews, UK, 2021. [Google Scholar]
- Howson, T.; De Moortel, I. The effects of driving time scales on coronal heating in a stratified atmosphere. 2022; in preparation. [Google Scholar]
- Howson, T.A.; De Moortel, I.; Fyfe, L.E. The effects of driving time scales on heating in a coronal arcade. Astron. Astrophys. 2020, 643, A85. [Google Scholar] [CrossRef]
- Ryutov, D.A.; Ryutova, M.P. Sound oscillations in a plasma with “magnetic filaments”. Sov. J. Exp. Theor. Phys. 1976, 43, 491–497. [Google Scholar]
- Ofman, L.; Davila, J.M.; Steinolfson, R.S. Coronal Heating by the Resonant Absorption of Alfven Waves: The Effect of Viscous Stress Tensor. Astrophys. J. 1994, 421, 360. [Google Scholar] [CrossRef]
- Goossens, M.; Andries, J.; Aschwanden, M.J. Coronal loop oscillations. An interpretation in terms of resonant absorption of quasi-mode kink oscillations. Astron. Astrophys. 2002, 394, L39–L42. [Google Scholar] [CrossRef] [Green Version]
- Pascoe, D.J.; Hood, A.W.; De Moortel, I.; Wright, A.N. Damping of kink waves by mode coupling. II. Parametric study and seismology. Astron. Astrophys. 2013, 551, A40. [Google Scholar] [CrossRef]
- Ruderman, M.S. The resonant damping of oscillations of coronal loops with elliptic cross-sections. Astron. Astrophys. 2003, 409, 287–297. [Google Scholar] [CrossRef]
- Andries, J.; Goossens, M.; Hollweg, J.V.; Arregui, I.; Van Doorsselaere, T. Coronal loop oscillations. Calculation of resonantly damped MHD quasi-mode kink oscillations of longitudinally stratified loops. Astron. Astrophys. 2005, 430, 1109–1118. [Google Scholar] [CrossRef]
- Terradas, J.; Oliver, R.; Ballester, J.L. Damping of Kink Oscillations in Curved Coronal Loops. Astrophys. J. Letts. 2006, 650, L91–L94. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Goossens, M.; Verth, G.; Fedun, V.; Van Doorsselaere, T. Resonant Absorption of Axisymmetric Modes in Twisted Magnetic Flux Tubes. Astrophys. J. 2016, 823, 71. [Google Scholar] [CrossRef] [Green Version]
- Howson, T.A.; De Moortel, I.; Antolin, P.; Van Doorsselaere, T.; Wright, A.N. Resonant absorption in expanding coronal magnetic flux tubes with uniform density. Astron. Astrophys. 2019, 631, A105. [Google Scholar] [CrossRef]
- Guo, M.; Li, B.; Van Doorsselaere, T. Kink Oscillations in Solar Coronal Loops with Elliptical Cross Sections. I. The Linear Regime. Astrophys. J. 2020, 904, 116. [Google Scholar] [CrossRef]
- Howson, T.; De Moortel, I.; Pontin, D. Magnetic reconnection and the Kelvin-Helmholtz instability in the solar corona. arXiv 2021, arXiv:2109.15019. [Google Scholar] [CrossRef]
- Antolin, P.; Yokoyama, T.; Van Doorsselaere, T. Fine Strand-like Structure in the Solar Corona from Magnetohydrodynamic Transverse Oscillations. Astrophys. J. Letts. 2014, 787, L22. [Google Scholar] [CrossRef] [Green Version]
- Antolin, P.; Okamoto, T.J.; De Pontieu, B.; Uitenbroek, H.; Van Doorsselaere, T.; Yokoyama, T. Resonant Absorption of Transverse Oscillations and Associated Heating in a Solar Prominence. II. Numerical Aspects. Astrophys. J. 2015, 809, 72. [Google Scholar] [CrossRef] [Green Version]
- Antolin, P.; Schmit, D.; Pereira, T.M.D.; De Pontieu, B.; De Moortel, I. Transverse Wave Induced Kelvin-Helmholtz Rolls in Spicules. Astrophys. J. 2018, 856, 44. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Van Doorsselaere, T.; Karampelas, K.; Li, B. Wave Heating in Simulated Multistranded Coronal Loops. Astrophys. J. 2019, 883, 20. [Google Scholar] [CrossRef] [Green Version]
- Magyar, N.; Van Doorsselaere, T.; Marcu, A. Numerical simulations of transverse oscillations in radiatively cooling coronal loops. Astron. Astrophys. 2015, 582, A117. [Google Scholar] [CrossRef] [Green Version]
- Karampelas, K.; Van Doorsselaere, T.; Guo, M. Wave heating in gravitationally stratified coronal loops in the presence of resistivity and viscosity. Astron. Astrophys. 2019, 623, A53. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Andries, J.; Poedts, S. Observational evidence favors a resistive wave heating mechanism for coronal loops over a viscous phenomenon. Astron. Astrophys. 2007, 471, 311–314. [Google Scholar] [CrossRef] [Green Version]
- Karampelas, K.; Van Doorsselaere, T. Simulations of fully deformed oscillating flux tubes. Astron. Astrophys. 2018, 610, L9. [Google Scholar] [CrossRef] [Green Version]
- Karampelas, K.; Van Doorsselaere, T.; Antolin, P. Heating by transverse waves in simulated coronal loops. Astron. Astrophys. 2017, 604, A130. [Google Scholar] [CrossRef] [Green Version]
- Hillier, A.; Arregui, I. Coronal Cooling as a Result of Mixing by the Nonlinear Kelvin-Helmholtz Instability. Astrophys. J. 2019, 885, 101. [Google Scholar] [CrossRef] [Green Version]
- Edwin, P.M.; Roberts, B. Wave Propagation in a Magnetic Cylinder. Sol. Phys. 1983, 88, 179–191. [Google Scholar] [CrossRef]
- Shi, M.; Van Doorsselaere, T.; Guo, M.; Karampelas, K.; Li, B.; Antolin, P. The First 3D Coronal Loop Model Heated by MHD Waves against Radiative Losses. Astrophys. J. 2021, 908, 233. [Google Scholar] [CrossRef]
- Hillier, A.; Van Doorsselaere, T.; Karampelas, K. Estimating the Energy Dissipation from Kelvin-Helmholtz Instability Induced Turbulence in Oscillating Coronal Loops. Astrophys. J. 2020, 897, L13. [Google Scholar] [CrossRef]
- Afanasyev, A.; Karampelas, K.; Van Doorsselaere, T. Coronal Loop Transverse Oscillations Excited by Different Driver Frequencies. Astrophys. J. 2019, 876, 100. [Google Scholar] [CrossRef] [Green Version]
- Karampelas, K.; Van Doorsselaere, T. Generating Transverse Loop Oscillations through a Steady-flow Driver. Astrophys. J. 2020, 897, L35. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T. Transverse Loop Oscillations via Vortex Shedding: A Self-oscillating Process. Astrophys. J. 2021, 908, L7. [Google Scholar] [CrossRef]
- Magyar, N.; Van Doorsselaere, T. Damping of nonlinear standing kink oscillations: A numerical study. Astron. Astrophys. 2016, 595, A81. [Google Scholar] [CrossRef]
- Antolin, P.; Van Doorsselaere, T. Influence of resonant absorption on the generation of the Kelvin-Helmholtz Instability. Front. Phys. 2019, 7, 85. [Google Scholar] [CrossRef]
- Howson, T.A.; De Moortel, I.; Antolin, P. The effects of resistivity and viscosity on the Kelvin- Helmholtz instability in oscillating coronal loops. Astron. Astrophys. 2017, 602, A74. [Google Scholar] [CrossRef] [Green Version]
- Howson, T.A.; De Moortel, I.; Antolin, P. Energetics of the Kelvin-Helmholtz instability induced by transverse waves in twisted coronal loops. Astron. Astrophys. 2017, 607, A77. [Google Scholar] [CrossRef] [Green Version]
- Terradas, J.; Magyar, N.; Van Doorsselaere, T. Effect of Magnetic Twist on Nonlinear Transverse Kink Oscillations of Line-tied Magnetic Flux Tubes. Astrophys. J. 2018, 853, 35. [Google Scholar] [CrossRef]
- Barbulescu, M.; Ruderman, M.S.; Van Doorsselaere, T.; Erdélyi, R. An Analytical Model of the Kelvin-Helmholtz Instability of Transverse Coronal Loop Oscillations. Astrophys. J. 2019, 870, 108. [Google Scholar] [CrossRef]
- Parker, E.N. Topological Dissipation and the Small-Scale Fields in Turbulent Gases. Astrophys. J. 1972, 174, 499. [Google Scholar] [CrossRef]
- Howson, T.A.; De Moortel, I.; Reid, J. Phase mixing and wave heating in a complex coronal plasma. Astron. Astrophys. 2020, 636, A40. [Google Scholar] [CrossRef]
- Goddard, C.R.; Nisticò, G. Temporal evolution of oscillating coronal loops. Astron. Astrophys. 2020, 638, A89. [Google Scholar] [CrossRef]
- Antolin, P.; De Moortel, I.; Van Doorsselaere, T.; Yokoyama, T. Observational Signatures of Transverse Magnetohydrodynamic Waves and Associated Dynamic Instabilities in Coronal Flux Tubes. Astrophys. J. 2017, 836, 219. [Google Scholar] [CrossRef] [Green Version]
- Karampelas, K.; Van Doorsselaere, T.; Pascoe, D.J.; Guo, M.; Antolin, P. Amplitudes and energy fluxes of simulated decayless kink oscillations. Front. Astron. Space Sci. 2019, 6, 38. [Google Scholar] [CrossRef] [Green Version]
- Shi, M.; Van Doorsselaere, T.; Antolin, P.; Li, B. Forward Modeling of Simulated Transverse Oscillations in Coronal Loops and the Influence of Background Emission. arXiv 2021, arXiv:2109.02338. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Antolin, P.; Karampelas, K. Broadening of the differential emission measure by multi-shelled and turbulent loops. Astron. Astrophys. 2018, 620, A65. [Google Scholar] [CrossRef] [Green Version]
- Brooks, D.H.; Warren, H.P.; Ugarte-Urra, I. Solar Coronal Loops Resolved by Hinode and the Solar Dynamics Observatory. Astrophys. J. 2012, 755, L33. [Google Scholar] [CrossRef]
- Viall, N.M.; Klimchuk, J.A. Modeling the Line-of-sight Integrated Emission in the Corona: Implications for Coronal Heating. Astrophys. J. 2013, 771, 115. [Google Scholar] [CrossRef] [Green Version]
- Magyar, N.; Van Doorsselaere, T. The Instability and Non-existence of Multi-stranded Loops When Driven by Transverse Waves. Astrophys. J. 2016, 823, 82. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, T.J.; Antolin, P.; De Pontieu, B.; Uitenbroek, H.; Van Doorsselaere, T.; Yokoyama, T. Resonant Absorption of Transverse Oscillations and Associated Heating in a Solar Prominence. I. Observational Aspects. Astrophys. J. 2015, 809, 71. [Google Scholar] [CrossRef] [Green Version]
- He, J.S.; Tu, C.Y.; Marsch, E.; Guo, L.J.; Yao, S.; Tian, H. Upward propagating high-frequency Alfvén waves as identified from dynamic wave-like spicules observed by SOT on Hinode. Astron. Astrophys. 2009, 497, 525–535. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, T.J.; De Pontieu, B. Propagating Waves Along Spicules. Astrophys. J. Letts. 2011, 736, L24. [Google Scholar] [CrossRef] [Green Version]
- Verth, G.; Terradas, J.; Goossens, M. Observational Evidence of Resonantly Damped Propagating Kink Waves in the Solar Corona. Astrophys. J. Letts. 2010, 718, L102–L105. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, A.K.; Morton, R.J.; Régnier, S.; McLaughlin, J.A. Damping of Propagating Kink Waves in the Solar Corona. Astrophys. J. 2019, 876, 106. [Google Scholar] [CrossRef]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Astron. 1964, 7, 566. [Google Scholar]
- Kraichnan, R.H. Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef] [Green Version]
- Goldreich, P.; Sridhar, S. Toward a Theory of Interstellar Turbulence. II. Strong Alfvenic Turbulence. Astrophys. J. 1995, 438, 763. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Magnetohydrodynamic Turbulence Revisited. Astrophys. J. 1997, 485, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Chandran, B.D.G. Weak Compressible Magnetohydrodynamic Turbulence in the Solar Corona. Phys. Rev. Lett. 2005, 95, 265004. [Google Scholar] [CrossRef] [Green Version]
- van Ballegooijen, A.A.; Asgari-Targhi, M.; Cranmer, S.R.; DeLuca, E.E. Heating of the Solar Chromosphere and Corona by Alfvén Wave Turbulence. Astrophys. J. 2011, 736, 3. [Google Scholar] [CrossRef] [Green Version]
- Howes, G.G.; Nielson, K.D. Alfvén wave collisions, the fundamental building block of plasma turbulence. I. Asymptotic solution. Phys. Plasmas 2013, 20, 072302. [Google Scholar] [CrossRef] [Green Version]
- Matthaeus, W.H.; Zank, G.P.; Oughton, S.; Mullan, D.J.; Dmitruk, P. Coronal Heating by Magnetohydrodynamic Turbulence Driven by Reflected Low-Frequency Waves. Astrophys. J. Letts. 1999, 523, L93–L96. [Google Scholar] [CrossRef] [Green Version]
- Dmitruk, P.; Matthaeus, W.H.; Milano, L.J.; Oughton, S. Conditions for sustainment of magnetohydrodynamic turbulence driven by Alfvén waves. Phys. Plasmas 2001, 8, 2377–2384. [Google Scholar] [CrossRef] [Green Version]
- Verdini, A.; Velli, M. Alfvén Waves and Turbulence in the Solar Atmosphere and Solar Wind. Astrophys. J. 2007, 662, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Cranmer, S.R.; van Ballegooijen, A.A.; Edgar, R.J. Self-consistent Coronal Heating and Solar Wind Acceleration from Anisotropic Magnetohydrodynamic Turbulence. Astrophys. J. 2007, 171, 520–551. [Google Scholar] [CrossRef]
- Chandran, B.D.G.; Hollweg, J.V. Alfvén Wave Reflection and Turbulent Heating in the Solar Wind from 1 Solar Radius to 1 AU: An Analytical Treatment. Astrophys. J. 2009, 707, 1659–1667. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, T.; Suzuki, T.K. Connecting the Sun and the Solar Wind: The First 2.5-dimensional Self-consistent MHD Simulation under the Alfvén Wave Scenario. Astrophys. J. 2012, 749, 8. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, T.; Suzuki, T.K. Connecting the Sun and the solar wind: The self-consistent transition of heating mechanisms. Mon. Not. R. Astron. Soc. 2014, 440, 971–986. [Google Scholar] [CrossRef] [Green Version]
- Lionello, R.; Velli, M.; Downs, C.; Linker, J.A.; Mikić, Z.; Verdini, A. Validating a Time-dependent Turbulence-driven Model of the Solar Wind. Astrophys. J. 2014, 784, 120. [Google Scholar] [CrossRef] [Green Version]
- van der Holst, B.; Sokolov, I.V.; Meng, X.; Jin, M.; Manchester, W.B., IV; Tóth, G.; Gombosi, T.I. Alfvén Wave Solar Model (AWSoM): Coronal Heating. Astrophys. J. 2014, 782, 81. [Google Scholar] [CrossRef]
- van Ballegooijen, A.A.; Asgari-Targhi, M. Heating and Acceleration of the Fast Solar Wind by Alfvén Wave Turbulence. Astrophys. J. 2016, 821, 106. [Google Scholar] [CrossRef]
- Asgari-Targhi, M.; Asgari-Targhi, A.; Hahn, M.; Savin, D.W. Effects of Density Fluctuations on Alfvén Wave Turbulence in a Coronal Hole. Astrophys. J. 2021, 911, 63. [Google Scholar] [CrossRef]
- Ofman, L. Wave Modeling of the Solar Wind. Living Rev. Sol. Phys. 2010, 7, 4. [Google Scholar] [CrossRef] [Green Version]
- Cranmer, S.R.; Asgari-Targhi, M.; Miralles, M.P.; Raymond, J.C.; Strachan, L.; Tian, H.; Woolsey, L.N. The role of turbulence in coronal heating and solar wind expansion. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140148. [Google Scholar] [CrossRef]
- Banerjee, D.; Krishna Prasad, S.; Pant, V.; McLaughlin, J.A.; Antolin, P.; Magyar, N.; Ofman, L.; Tian, H.; Van Doorsselaere, T.; De Moortel, I. Magnetohydrodynamic Waves in Open Coronal Structures. Space Sci. Rev. 2021, 217, 76. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef] [Green Version]
- Matthaeus, W.H.; Goldstein, M.L. Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 1982, 87, 6011–6028. [Google Scholar] [CrossRef]
- Zank, G.P.; Matthaeus, W.H.; Smith, C.W. Evolution of turbulent magnetic fluctuation power with heliospheric distance. J. Geophys. Res. 1996, 101, 17093–17108. [Google Scholar] [CrossRef]
- Bavassano, B.; Pietropaolo, E.; Bruno, R. Alfvénic turbulence in the polar wind: A statistical study on cross helicity and residual energy variations. J. Geophys. Res. 2000, 105, 12697–12704. [Google Scholar] [CrossRef]
- Boldyrev, S.; Perez, J.C.; Borovsky, J.E.; Podesta, J.J. Spectral Scaling Laws in Magnetohydrodynamic Turbulence Simulations and in the Solar Wind. Astrophys. J. Letts. 2011, 741, L19. [Google Scholar] [CrossRef] [Green Version]
- Borovsky, J.E. The velocity and magnetic field fluctuations of the solar wind at 1 AU: Statistical analysis of Fourier spectra and correlations with plasma properties. J. Geophys. Res. (Space Phys.) 2012, 117, A05104. [Google Scholar] [CrossRef] [Green Version]
- Andrés, N.; Sahraoui, F.; Hadid, L.Z.; Huang, S.Y.; Romanelli, N.; Galtier, S.; DiBraccio, G.; Halekas, J. The Evolution of Compressible Solar Wind Turbulence in the Inner Heliosphere: PSP, THEMIS, and MAVEN Observations. Astrophys. J. 2021, 919, 19. [Google Scholar] [CrossRef]
- Kieokaew, R.; Lavraud, B.; Yang, Y.; Matthaeus, W.H.; Ruffolo, D.; Stawarz, J.E.; Aizawa, S.; Foullon, C.; Génot, V.; Pinto, R.F.; et al. Solar Orbiter Observations of the Kelvin-Helmholtz Instability in the Solar Wind. arXiv 2021, arXiv:2103.15489. [Google Scholar]
- Telloni, D.; Sorriso-Valvo, L.; Woodham, L.D.; Panasenco, O.; Velli, M.; Carbone, F.; Zank, G.P.; Bruno, R.; Perrone, D.; Nakanotani, M.; et al. Evolution of Solar Wind Turbulence from 0.1 to 1 au during the First Parker Solar Probe-Solar Orbiter Radial Alignment. Astrophys. J. 2021, 912, L21. [Google Scholar] [CrossRef]
- Goossens, M.; Terradas, J.; Andries, J.; Arregui, I.; Ballester, J.L. On the nature of kink MHD waves in magnetic flux tubes. Astron. Astrophys. 2009, 503, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Magyar, N.; Van Doorsselaere, T.; Goossens, M. Generalized phase mixing: Turbulence-like behaviour from unidirectionally propagating MHD waves. Sci. Rep. 2017, 7, 14820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Magyar, N.; Van Doorsselaere, T.; Goossens, M. Understanding Uniturbulence: Self-cascade of MHD Waves in the Presence of Inhomogeneities. Astrophys. J. 2019, 882, 50. [Google Scholar] [CrossRef] [Green Version]
- Van Doorsselaere, T.; Li, B.; Goossens, M.; Hnat, B.; Magyar, N. Wave Pressure and Energy Cascade Rate of Kink Waves Computed with Elsässer Variables. Astrophys. J. 2020, 899, 100. [Google Scholar] [CrossRef]
- Elsasser, W.M. The Hydromagnetic Equations. Phys. Rev. 1950, 79, 183. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Goossens, M.; Magyar, N.; Ruderman, M.S.; Ismayilli, R. Nonlinear Damping of Standing Kink Waves Computed With Elsässer Variables. Astrophys. J. 2021, 910, 58. [Google Scholar] [CrossRef]
- Verwichte, E.; Van Doorsselaere, T.; White, R.S.; Antolin, P. Statistical seismology of transverse waves in the solar corona. Astron. Astrophys. 2013, 552, A138. [Google Scholar] [CrossRef] [Green Version]
- Goddard, C.R.; Nisticò, G.; Nakariakov, V.M.; Zimovets, I.V. A statistical study of decaying kink oscillations detected using SDO/AIA. Astron. Astrophys. 2016, 585, A137. [Google Scholar] [CrossRef] [Green Version]
- Nechaeva, A.; Zimovets, I.V.; Nakariakov, V.M.; Goddard, C.R. Catalog of Decaying Kink Oscillations of Coronal Loops in the 24th Solar Cycle. Astrophys. J. Suppl. 2019, 241, 31. [Google Scholar] [CrossRef]
- Pagano, P.; De Moortel, I.; Morton, R.J. Effect of coronal loop structure on wave heating through phase mixing. Astron. Astrophys. 2020, 643, A73. [Google Scholar] [CrossRef]
- Cargill, P.J.; De Moortel, I.; Kiddie, G. Coronal Density Structure and its Role in Wave Damping in Loops. Astrophys. J. 2016, 823, 31. [Google Scholar] [CrossRef]
- Van Damme, H.J.; De Moortel, I.; Pagano, P.; Johnston, C.D. Chromospheric evaporation and phase mixing of Alfvén waves in coronal loops. Astron. Astrophys. 2020, 635, A174. [Google Scholar] [CrossRef]
- Klimchuk, J.A.; Antiochos, S.K. How Turbulent is the Magnetically Closed Corona? Front. Astron. Space Sci. 2021, 8, 83. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howson, T. How Transverse Waves Drive Turbulence in the Solar Corona. Symmetry 2022, 14, 384. https://doi.org/10.3390/sym14020384
Howson T. How Transverse Waves Drive Turbulence in the Solar Corona. Symmetry. 2022; 14(2):384. https://doi.org/10.3390/sym14020384
Chicago/Turabian StyleHowson, Thomas. 2022. "How Transverse Waves Drive Turbulence in the Solar Corona" Symmetry 14, no. 2: 384. https://doi.org/10.3390/sym14020384
APA StyleHowson, T. (2022). How Transverse Waves Drive Turbulence in the Solar Corona. Symmetry, 14(2), 384. https://doi.org/10.3390/sym14020384





