Bubbling, Bistable Limit Cycles and Quasi-Periodic Oscillations in Queues with Delayed Information
Abstract
1. Introduction
2. Preliminaries
2.1. The Symmetric Case
- A.
- If , then the equilibrium is locally asymptotically stable for all .
- B.
- If , then the critical time-delay valueexists, and the equilibrium is locally asymptotically stable for all and is unstable for . At , the system (2) undergoes a symmetry-breaking Hopf bifurcation at the equilibrium .
2.2. The General Symmetric System
3. Main Results
3.1. Case 1: and
3.2. Case 2: and with
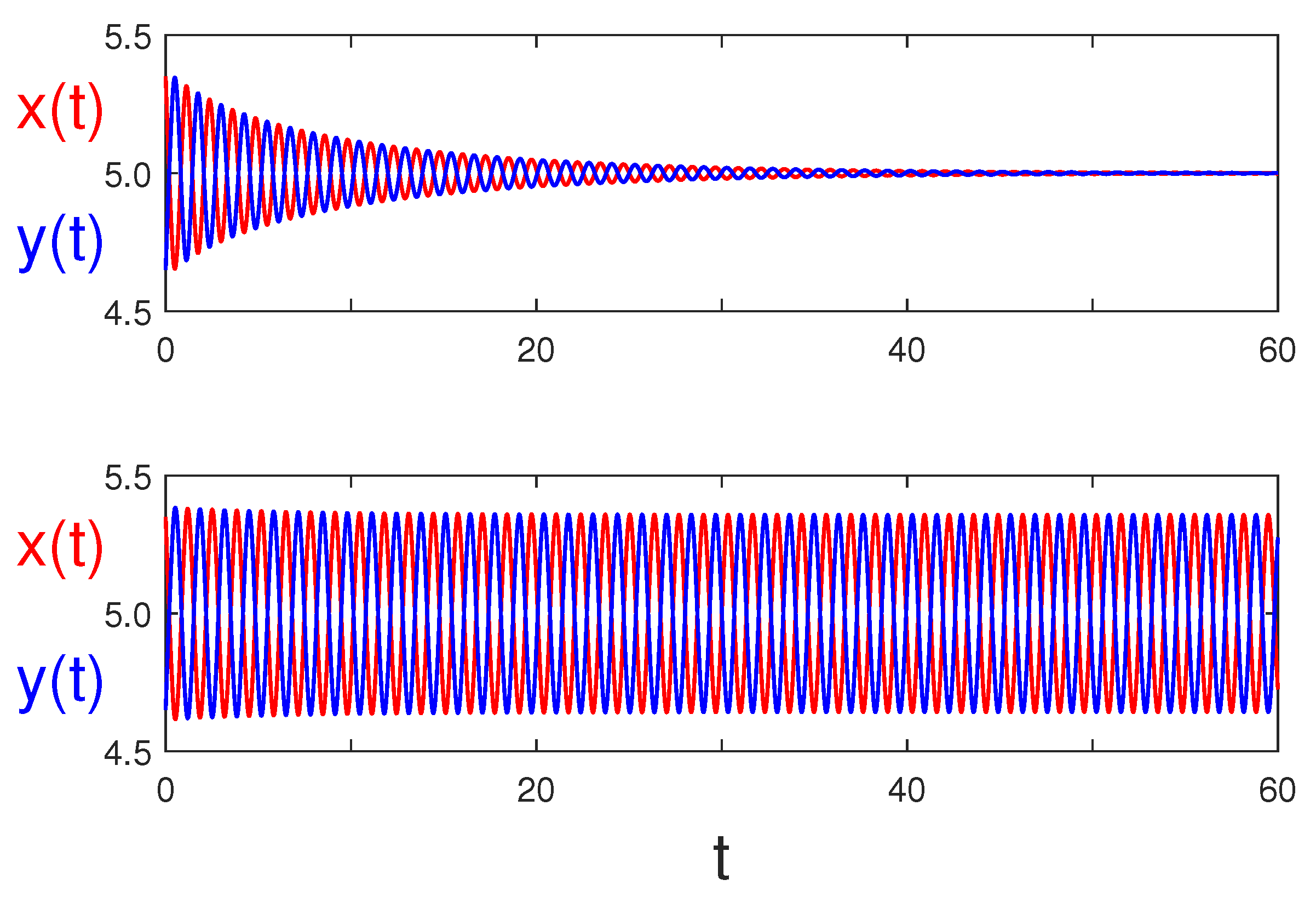
4. Numerical Simulations
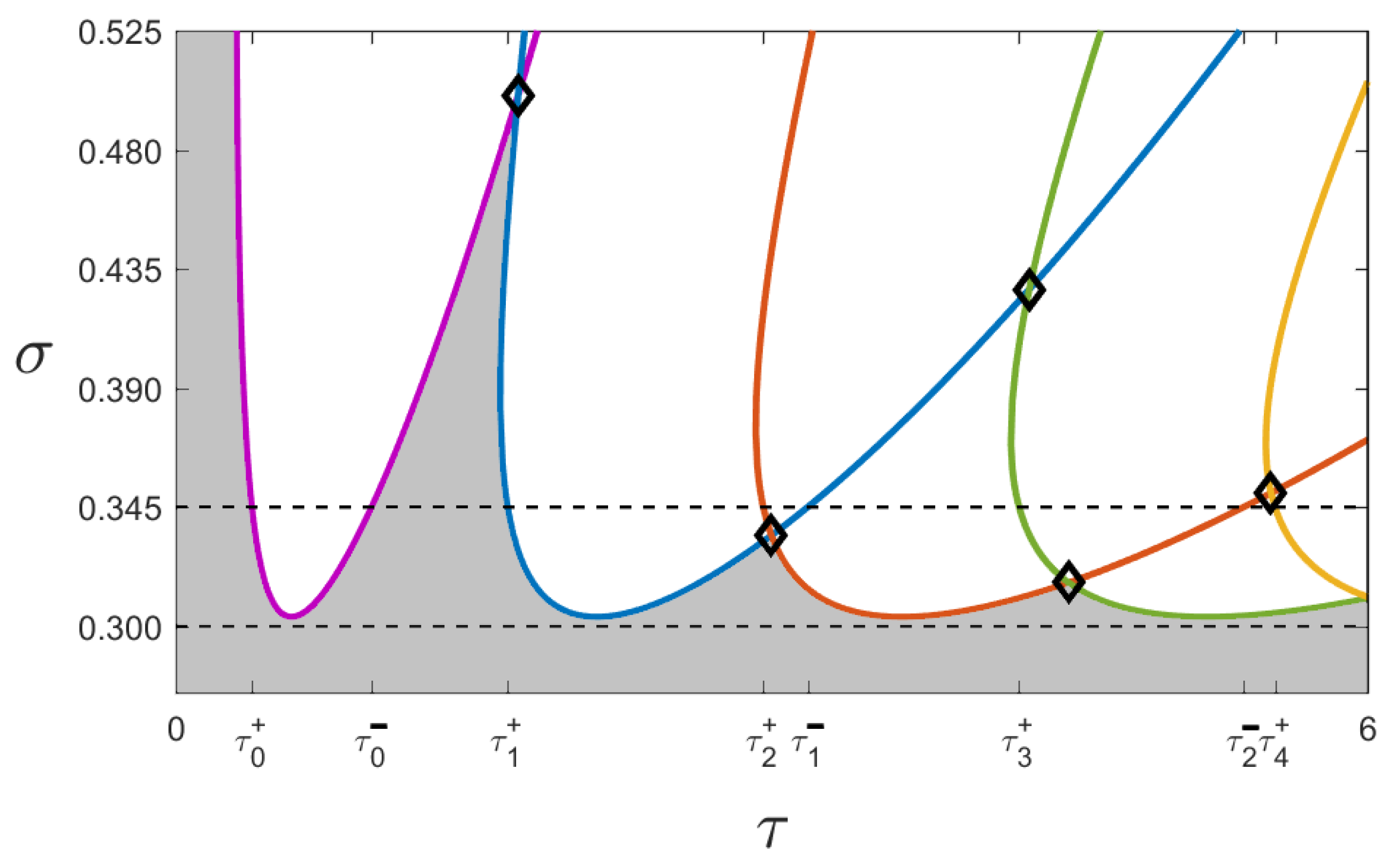
4.1. Multiple Stability Switches
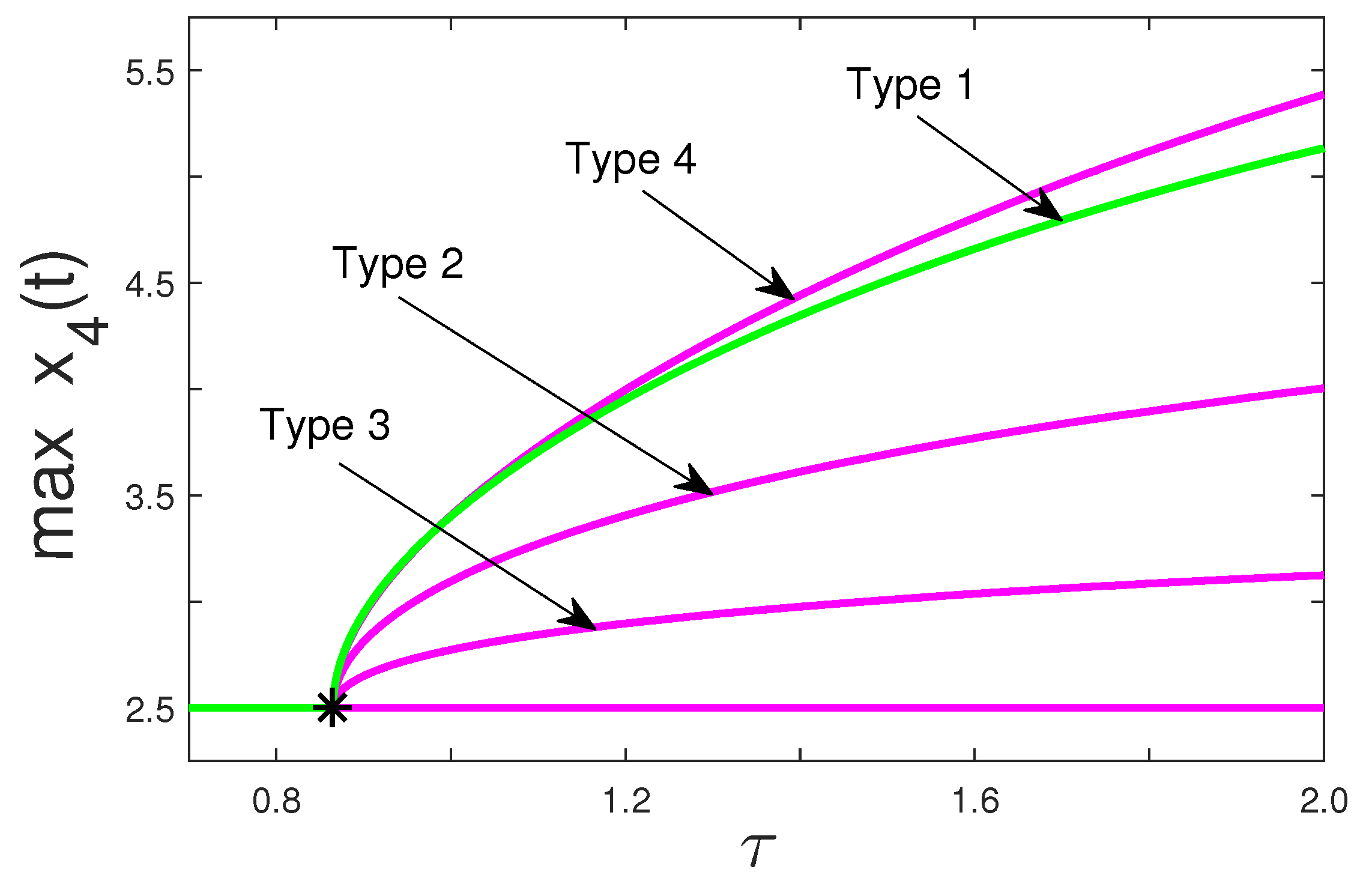
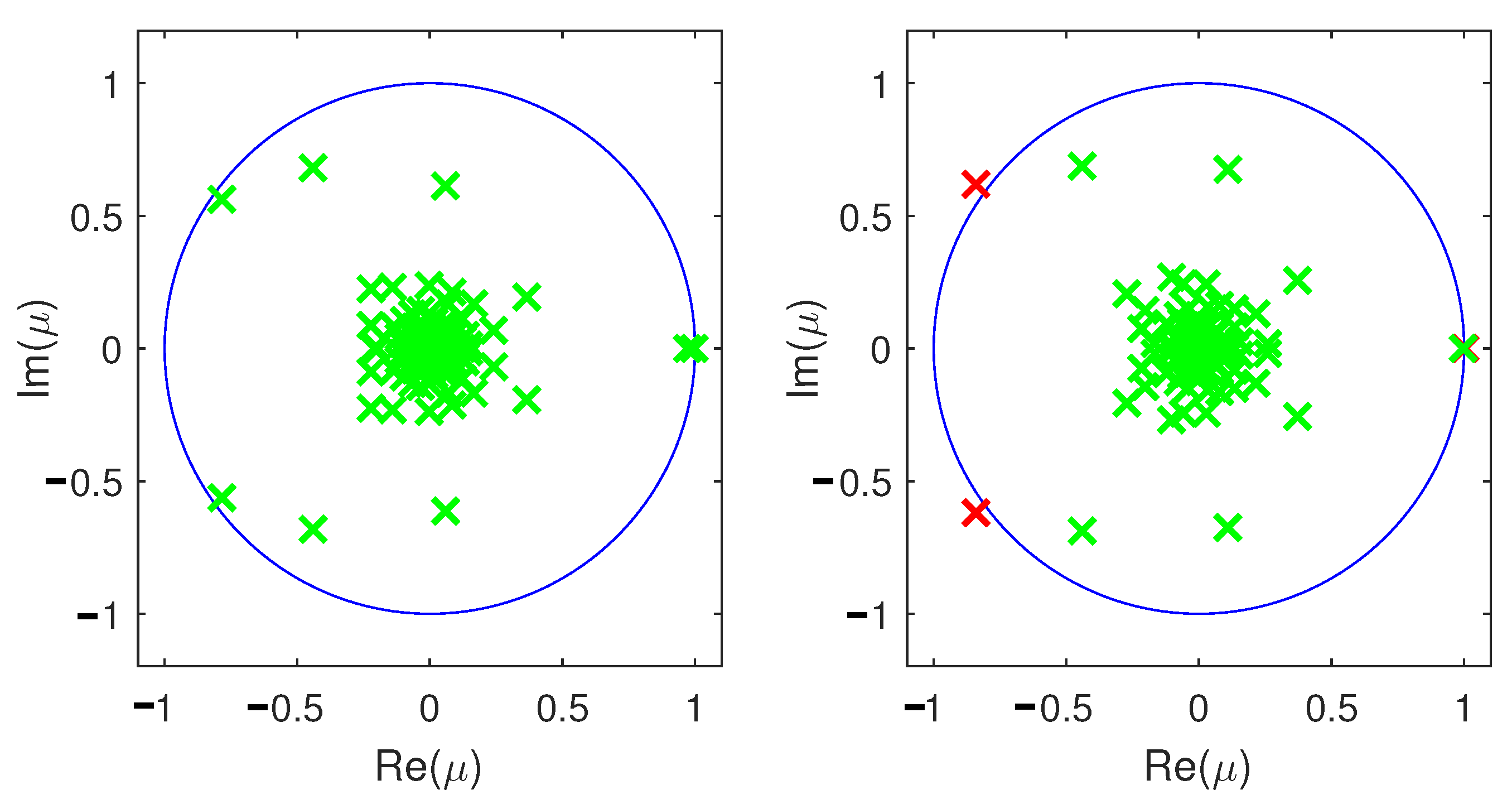
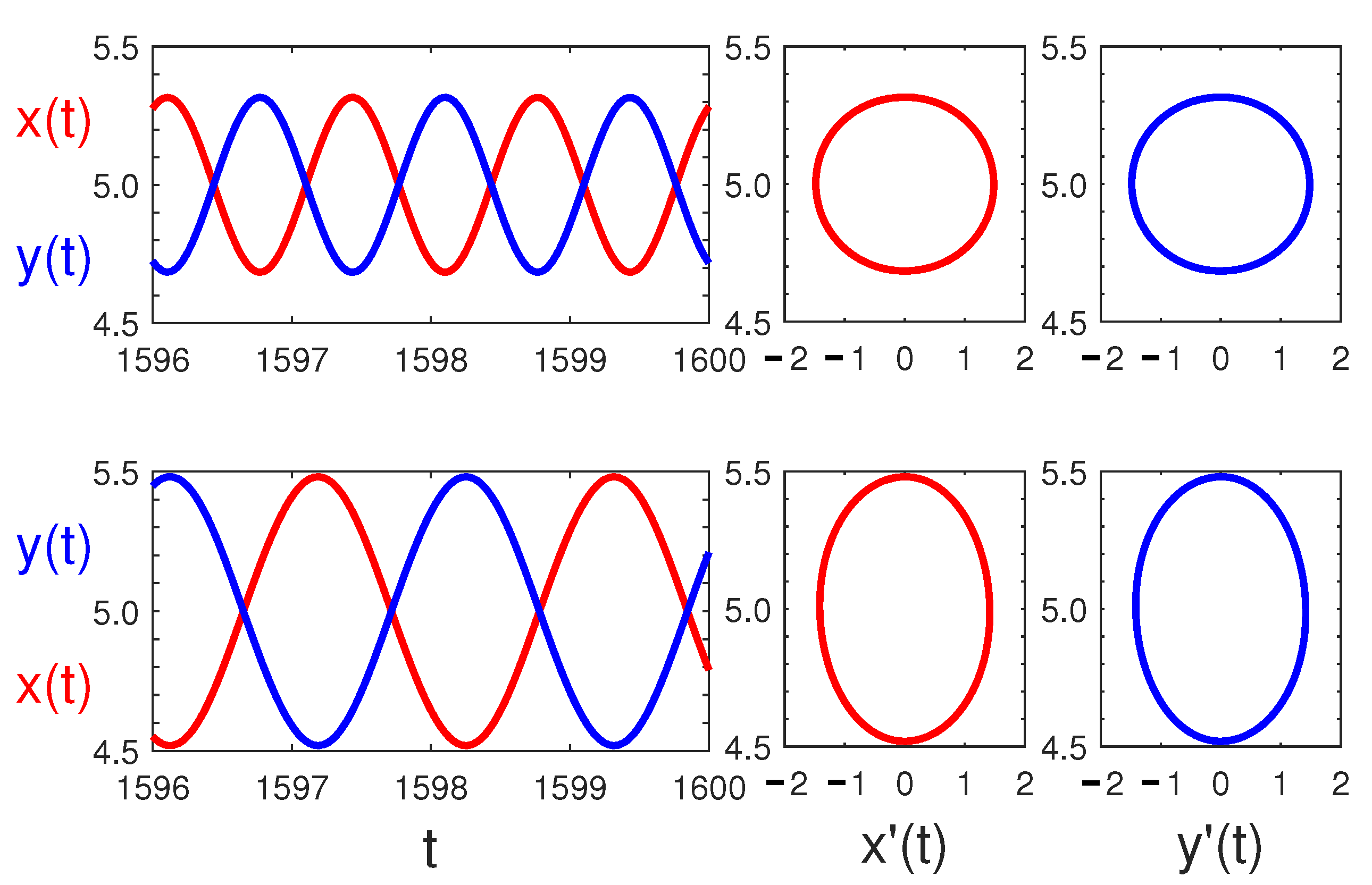
4.2. Bubbling and Bistable Limit Cycles
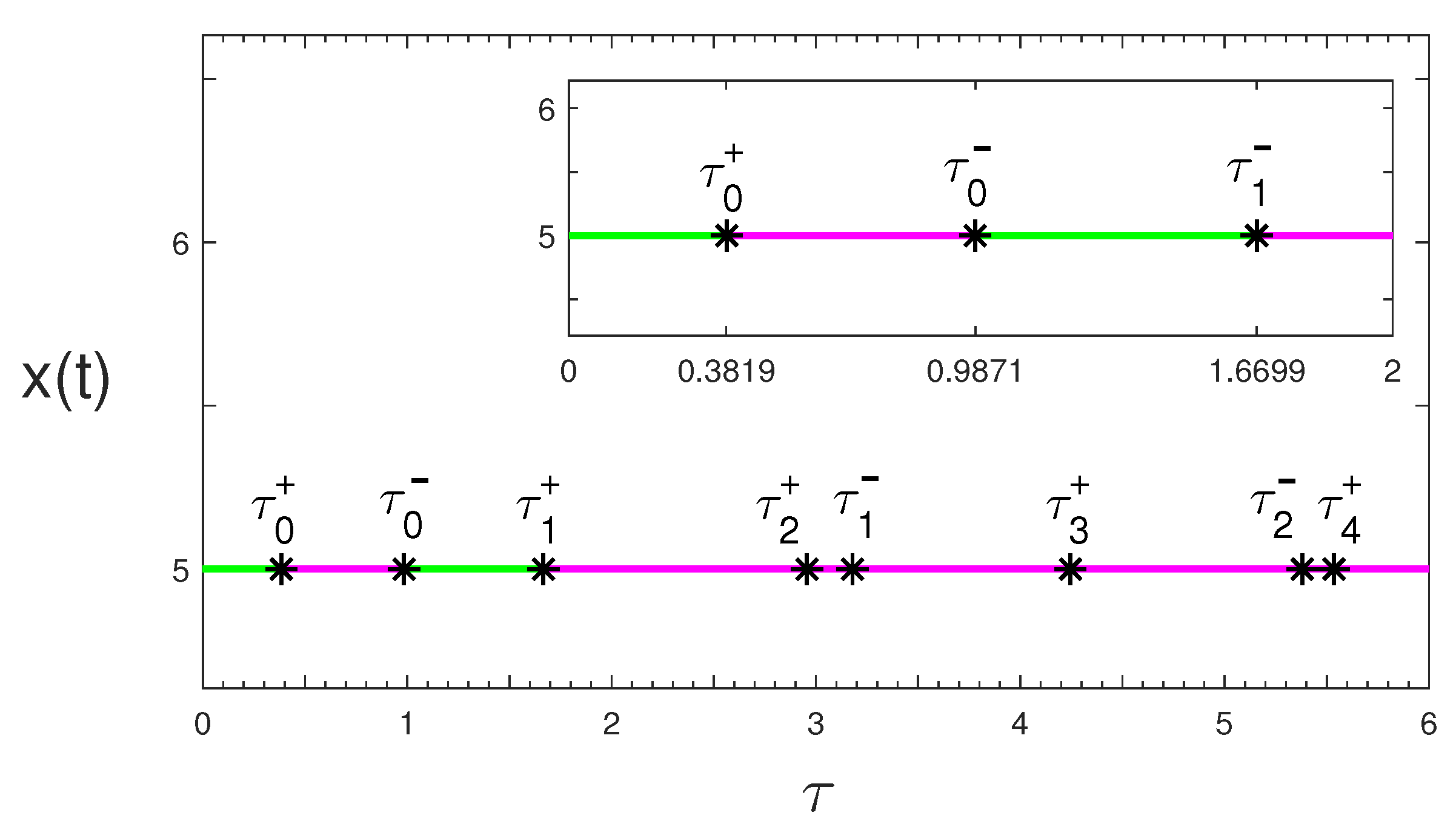
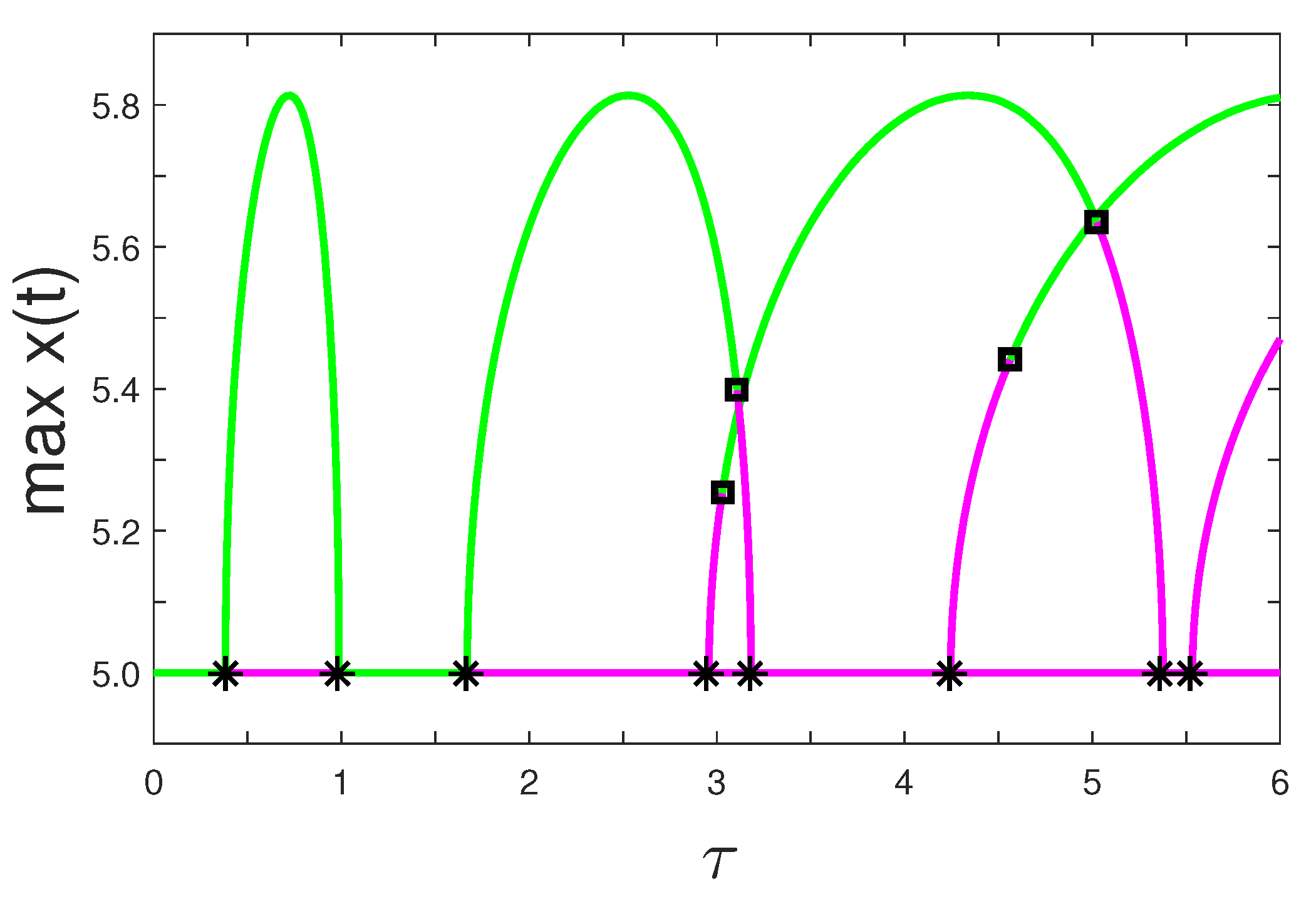
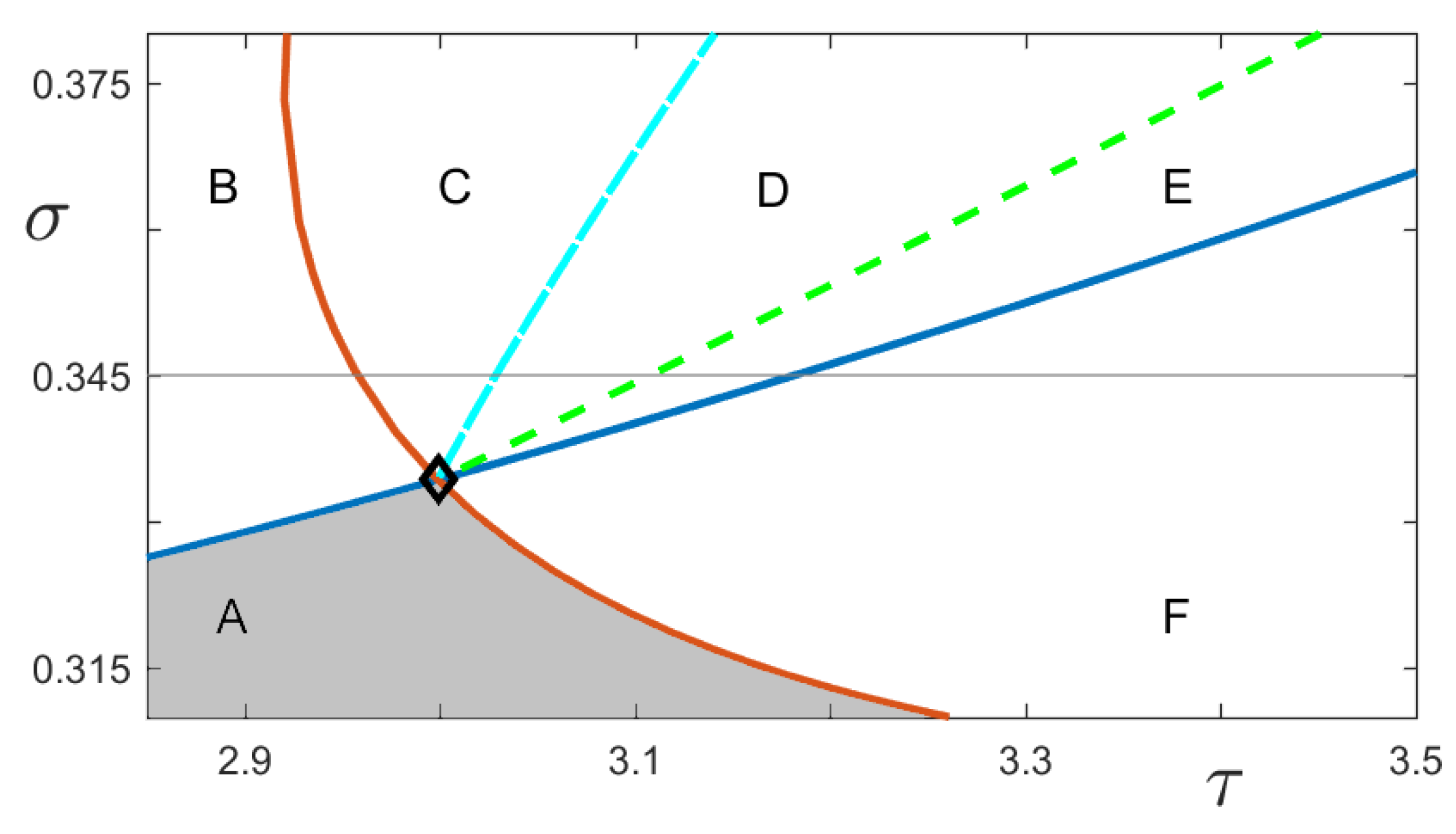
4.3. Two-Parameter Continuation
4.4. Neighborhood a Double-Hopf Bifurcation and Transient Quasi-Periodic Oscillations
5. Conclusions and Future Directions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, J.; Yom-Tov, E.; Yom-Tov, G.B. The impact of delay announcements on hospital network coordination and waiting times. Manag. Sci. 2018, 65, 1969–1994. [Google Scholar] [CrossRef]
- Jouini, O.; Akşin, Z.; Dallery, Y. Call centers with delay information: Models and insights. Manuf. Serv. Oper. Manag. 2011, 13, 534–548. [Google Scholar] [CrossRef]
- Nirenberg, S.; Daw, A.; Pender, J. The impact of queue length rounding and delayed app information on Disney world queues. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 3849–3860. [Google Scholar] [CrossRef]
- Pender, J.; Rand, R.H.; Wesson, E. Delay-differential equations applied to queueing theory. In Proceedings of the 9th European Nonlinear Dynamics Conference (ENOC 2017), Budapest, Hungary, 25–30 June 2017. [Google Scholar]
- Pender, J.; Rand, R.H.; Wesson, E. Queues with choice via delay differential equations. Int. J. Bifurcat. Chaos 2017, 27, 1730016. [Google Scholar] [CrossRef]
- Novitzky, S.; Pender, J.; Rand, R.H.; Wesson, E. Nonlinear dynamics in queueing theory: Determining the size of oscillations in queues with delay. SIAM J. Appl. Dyn. Syst. 2019, 18, 279–311. [Google Scholar] [CrossRef]
- Collera, J.A. Queues with choice from a symmetry perspective. In Progress in Industrial Mathematics at ECMI 2018. Mathematics in Industry; Faragó, I., Izsák, F., Simon, P., Eds.; Springer: Cham, Switzerland, 2019; Volume 30, pp. 537–542. [Google Scholar] [CrossRef]
- Pender, J.; Rand, R.H.; Wesson, E. An analysis of queues with delayed information and time-varying arrival rates. Nonlinear Dynam. 2018, 91, 2411–2427. [Google Scholar] [CrossRef]
- Novitzky, S.; Pender, J.; Rand, R.H.; Wesson, E. Limiting the oscillations in queues with delayed information through a novel type of delay announcement. Queueing Syst. 2020, 95, 281–330. [Google Scholar] [CrossRef]
- Pender, J.; Rand, R.H.; Wesson, E. A stochastic analysis of queues with customer choice and delayed information. Math. Oper. Res. 2020, 45, 1104–1126. [Google Scholar] [CrossRef]
- Doldo, P.; Pender, J.; Rand, R.H. Breaking the symmetry in queues with delayed information. Int. J. Bifurcat. Chaos 2021, 31, 2130027. [Google Scholar] [CrossRef]
- Collera, J.A. Spontaneous symmetry-breaking in deterministic queueing models with delayed information. In Recent Developments in Mathematical, Statistical and Computational Sciences. AMMCS 2019. Springer Proceedings in Mathematics & Statistics; Kilgour, D.M., Kunze, H., Makarov, R., Melnik, R., Wang, X., Eds.; Springer: Cham, Switzerland, 2021; Volume 343, pp. 15–25. [Google Scholar] [CrossRef]
- Lakrad, F.; Pender, J.; Rand, R. Queues with delayed information: A dynamical systems perspective. SIAM J. Appl. Dyn. Syst. 2022; in press. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory II; Springer: New York, NY, USA, 1988. [Google Scholar]
- Golubitsky, M.; Stewart, I. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space; Birkhauser Verlag: Basel, Switzerland, 2003. [Google Scholar]
- Buono, P.-L.; Collera, J.A. Symmetry-breaking bifurcations in rings of delay-coupled semiconductor lasers. SIAM J. Appl. Dyn. Syst. 2015, 14, 1868–1898. [Google Scholar] [CrossRef]
- Campbell, S.A.; Yuan, Y.; Bungay, S.D. Equivariant Hopf bifurcation in a ring of identical cells with delayed coupling. Nonlinearity 2005, 18, 2827–2846. [Google Scholar] [CrossRef]
- Collera, J.A. Symmetry-breaking bifurcations in two mutually delay-coupled lasers. Phil. Sci. Tech. 2015, 8, 17–21. [Google Scholar] [CrossRef][Green Version]
- Palacios, A. Synchronization in asymmetrically coupled networks with homogeneous oscillators. Phys. Rev. E 2021, 103, 022206. [Google Scholar] [CrossRef]
- Brauer, F. Absolute stability in delay equations. J. Differ. Equ. 1987, 69, 185–191. [Google Scholar] [CrossRef]
- Stewart, I. Spontaneous symmetry-breaking in a network model for quadruped locomotion. Int. J. Bifurcat. Chaos 2017, 27, 1730049. [Google Scholar] [CrossRef]
- Wu, J. Symmetric functional differential equations and neural networks with memory. Trans. Am. Math. Soc. 1998, 350, 4799–4838. [Google Scholar] [CrossRef]
- Collera, J.A. Numerical continuation and bifurcation analysis in a harvested predator-prey model with time delay using DDE-Biftool. In Dynamical Systems, Bifurcation Analysis and Applications. DySBA 2018. Springer Proceedings in Mathematics & Statistics; Mohd, M., Abdul Rahman, N., Abd Hamid, N., Mohd Yatim, Y., Eds.; Springer: Singapore, 2019; Volume 295, pp. 225–241. [Google Scholar] [CrossRef]
- Engelborghs, K.; Luzyanina, T.; Samaey, G. DDE-BIFTOOL v. 2.00: A Matlab Package for Bifurcation Analysis of Delay Differential Equations; Department of Computer Science, K. U. Leuven: Leuven, Belgium, 2001. [Google Scholar]
- Engelborghs, K.; Luzyanina, T.; Roose, D. Numerical bifurcation analysis of delay differential equations using DDE-Biftool. ACM Trans. Math. Softw. 2002, 28, 1–21. [Google Scholar] [CrossRef]
- Luzyanina, T.; Sieber, J.; Engelborghs, K.; Samaey, G.; Roose, D. Numerical bifurcation analysis of mathematical models with time delays with the package DDE-BIFTOOL. Mat. Biolog. Bioinform. 2017, 12, 496–520. [Google Scholar] [CrossRef]
- Sieber, J.; Engelborghs, K.; Luzyanina, T.; Samaey, G.; Roose, D. DDE-BIFTOOL v.3.1.1 Manual—Bifurcation analysis of delay differential equations. arXiv 2014, arXiv:1406.7144v4. [Google Scholar]
- Rand, R. Differential-delay equations. In Complex Systems: Fractionality, Time-delay and Synchronization; Luo, A.C.J., Sun, J.-Q., Eds.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Diekmann, O.; van Gils, S.A.; Lunel, S.M.V.; Walther, H.-O. Delay Equations: Functional-, Complex-, and Nonlinear Analysis; Springer: New York, NY, USA, 1995. [Google Scholar]
- Hale, J.K.; Verduyn Lunel, S.M. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Singapore, 2021. [Google Scholar]
- Ruan, S.; Wei, J. On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dynam. Cont. Dis. Ser. A 2003, 10, 863–874. [Google Scholar]
- Krisztin, T.; Liz, E. Bubbles for a class of delay differential equations. Qual. Theory Dyn. Syst. 2011, 10, 169–196. [Google Scholar] [CrossRef]
- Liu, M.; Liz, E.; Röst, G. Endemic bubbles generated by delayed behavioral response: Global stability and bifurcation switches in an SIS model. SIAM J. Appl. Math. 2015, 75, 75–91. [Google Scholar] [CrossRef]
- LeBlanc, V.G. A degenerate Hopf bifurcation in retarded functional differential equations, and applications to endemic bubbles. J. Nonlinear Sci. 2016, 26, 1–25. [Google Scholar] [CrossRef]
- Guo, S.; Wu, J. Bifurcation Theory of Functional Differential Equations; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2004. [Google Scholar]
- Tehrani, N.F.; Razvan, M. Bifurcation structure of two coupled FHN neurons with delay. Math. Biosci. 2015, 270, 41–56. [Google Scholar] [CrossRef] [PubMed]





| k | ||
|---|---|---|
| 0 | 0.381879 | 0.987096 |
| 1 | 1.669854 | 3.181774 |
| 2 | 2.957828 | 5.376453 |
| 3 | 4.245803 | 7.571131 |
| 4 | 5.533778 | 9.765809 |
| 5 | 6.821752 | 11.960487 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collera, J.A. Bubbling, Bistable Limit Cycles and Quasi-Periodic Oscillations in Queues with Delayed Information. Symmetry 2022, 14, 376. https://doi.org/10.3390/sym14020376
Collera JA. Bubbling, Bistable Limit Cycles and Quasi-Periodic Oscillations in Queues with Delayed Information. Symmetry. 2022; 14(2):376. https://doi.org/10.3390/sym14020376
Chicago/Turabian StyleCollera, Juancho A. 2022. "Bubbling, Bistable Limit Cycles and Quasi-Periodic Oscillations in Queues with Delayed Information" Symmetry 14, no. 2: 376. https://doi.org/10.3390/sym14020376
APA StyleCollera, J. A. (2022). Bubbling, Bistable Limit Cycles and Quasi-Periodic Oscillations in Queues with Delayed Information. Symmetry, 14(2), 376. https://doi.org/10.3390/sym14020376






