Reliability Analysis with Wiener-Transmuted Truncated Normal Degradation Model for Linear and Non-Negative Degradation Data
Abstract
:1. Introduction
2. The Degradation Model
2.1. Degradation Model with Wiener Process and TTND
2.2. Reliability Estimation Based on the Proposed Degradation Model
2.2.1. Case 1: Degradation Modeling Based on
2.2.2. Case 2: Degradation Modeling Based on
3. Model Parameter Estimation
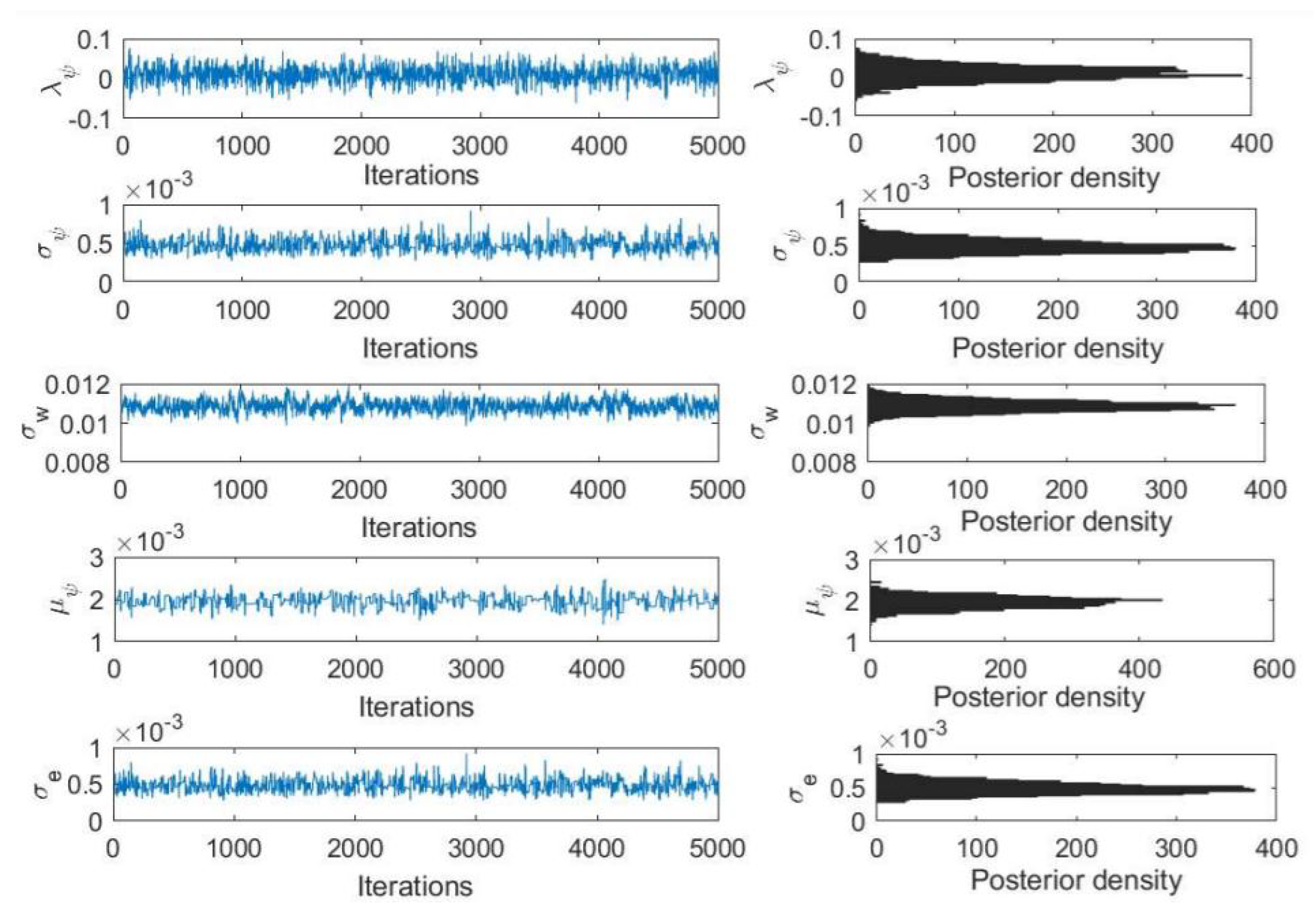
3.1. Case 1: Parameter Estimation Based on
- Step 1: start with initial guess at j = 0, ,
- Step 2: set j = j + 1,
- Step 3: Use the Metropolis-Hastings algorithm to generate from (43) by updating ,
- Step 4: Use the Metropolis–Hastings algorithm to generate from (44) by updating ,
- Step 5: Use the Metropolis–Hastings algorithm to generate from (45) by updating ,
- Step 6: Use the Metropolis–Hastings algorithm to generate from (46) by updating ,
- Step 7: Repeat 2–6 T times.For sufficiently large values of T, we can obtain an approximation of our parameters.
3.2. Case 2: Parameter Estimation Based on
- Step 1: Start with initial guess at j = 0, ,
- Step 2: Set j = j + 1,
- Step 3: Use the Metropolis–Hastings algorithm to generate from (52) by updating ,
- Step 4: Use the Metropolis–Hastings algorithm to generate from (53) by updating ,
- Step 5: Use the Metropolis–Hastings algorithm to generate from (54) by updating ,
- Step 6: Use the Metropolis–Hastings algorithm to generate from (55) by updating ,
- Step 7: Use the Metropolis–Hastings algorithm to generate from (56) by updating
- Step 8: Repeat 2–7 T times.For sufficiently large values of T, we can obtain an approximation of our parameters.
4. Illustrative Example
4.1. Simulation Study
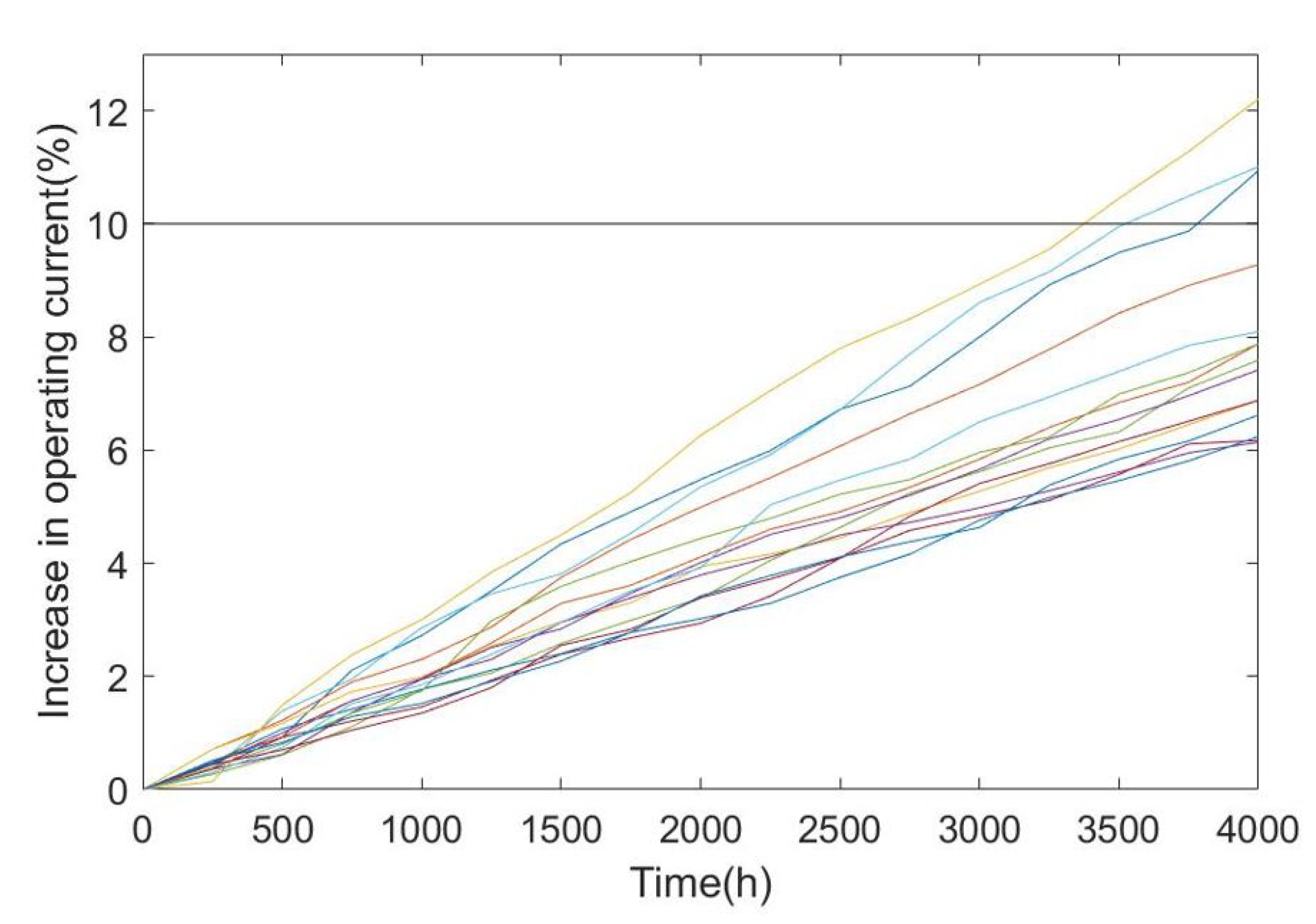
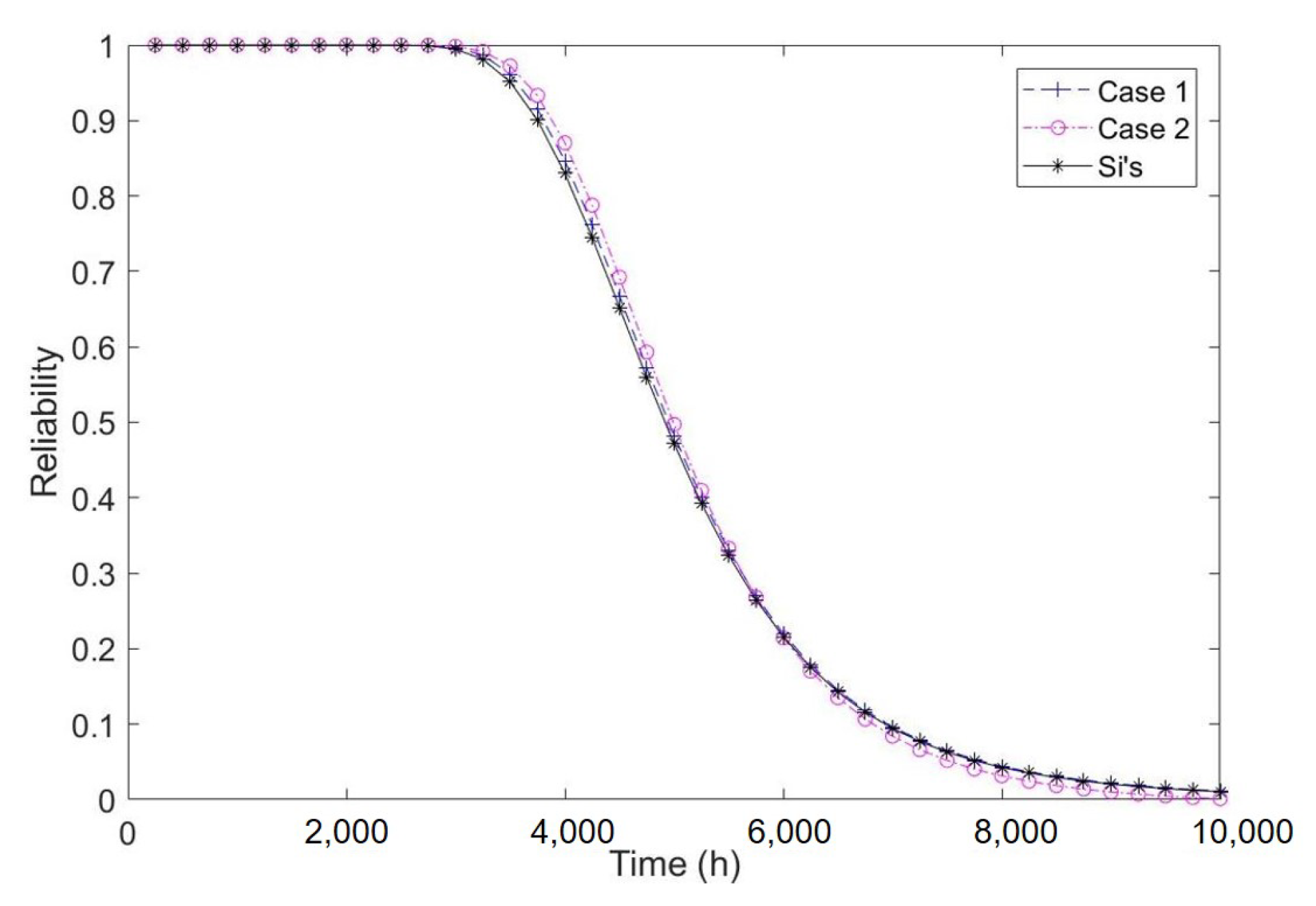
4.2. Application to Laser Degradation Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamiński, M.; Solecka, M. Optimization of the truss-type structures using the generalized perturbation-based Stochastic Finite Element Method. Finite Elem. Anal. Des. 2013, 63, 69–79. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Reliability analysis of a corrugated I-beam girder with ribs. Proc. Inst. Civ. Eng.-Eng. Comput. Mech. 2015, 168, 49–58. [Google Scholar] [CrossRef]
- Muhammad, I.; Wang, X.; Li, C.; Yan, M.; Chang, M. Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution. Entropy 2020, 22, 1307. [Google Scholar] [CrossRef] [PubMed]
- Jose, J.K. Estimation of stress-strength reliability using discrete phase type distribution. Commun. Stat.-Theory Methods 2020, 51, 368–386. [Google Scholar] [CrossRef]
- Muhammad, M.; Liu, L. A new extension of the generalized half logistic distribution with applications to real data. Entropy 2019, 21, 339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Estimating remaining useful life with three-source variability in degradation modeling. IEEE Trans. Reliab. 2014, 63, 167–190. [Google Scholar] [CrossRef]
- Wang, X. Wiener processes with random effects for degradation data. J. Multivar. Anal. 2010, 101, 340–351. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.R.; Serban, N.; Gebraeel, N. Degradation modeling applied to residual lifetime prediction using functional data analysis. Ann. Appl. Stat. 2011, 5, 1586–1610. [Google Scholar] [CrossRef]
- Ye, Z.S.; Xie, M. Stochastic modelling and analysis of degradation for highly reliable products. Appl. Stoch. Model. Bus. Ind. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Lim, H.; Yum, B.J. Optimal design of accelerated degradation tests based on Wiener process models. J. Appl. Stat. 2011, 38, 309–325. [Google Scholar] [CrossRef]
- Lu, C.J.; Meeker, W.O. Using degradation measures to estimate a time-to-failure distribution. Technometrics 1993, 35, 161–174. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bae, S.J.; Kvam, P.H. A nonlinear random-coefficients model for degradation testing. Technometrics 2004, 46, 460–469. [Google Scholar] [CrossRef]
- Jeng, S.L.; Huang, B.Y.; Meeker, W.Q. Accelerated destructive degradation tests robust to distribution misspecification. IEEE Trans. Reliab. 2011, 60, 701–711. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Huang, H.Z.; Li, Y.; Xiao, N.C. An approach to reliability assessment under degradation and shock process. IEEE Trans. Reliab. 2011, 60, 852–863. [Google Scholar] [CrossRef]
- Wang, Y.; Pham, H. Modeling the dependent competing risks with multiple degradation processes and random shock using time-varying copulas. IEEE Trans. Reliab. 2011, 61, 13–22. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, J.; Das, D.; Tseng, T.L.B. Degradation modeling and RUL prediction using Wiener process subject to multiple change points and unit heterogeneity. Reliab. Eng. Syst. Saf. 2018, 176, 113–124. [Google Scholar] [CrossRef]
- Ye, Z.S.; Chen, N. The inverse Gaussian process as a degradation model. Technometrics 2014, 56, 302–311. [Google Scholar] [CrossRef]
- Pan, Z.; Balakrishnan, N. Reliability modeling of degradation of products with multiple performance characteristics based on gamma processes. Reliab. Eng. Syst. Saf. 2011, 96, 949–957. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, N.; Tsui, K.L. A Bayesian approach to condition monitoring with imperfect inspections. Qual. Reliab. Eng. Int. 2015, 31, 513–522. [Google Scholar] [CrossRef]
- Sun, L.; Gu, X.; Song, P. Accelerated degradation process analysis based on the nonlinear Wiener process with covariates and random effects. Math. Probl. Eng. 2016, 2016, 5246108. [Google Scholar] [CrossRef]
- Ye, Z.S.; Wang, Y.; Tsui, K.L.; Pecht, M. Degradation data analysis using Wiener processes with measurement errors. IEEE Trans. Reliab. 2013, 62, 772–780. [Google Scholar] [CrossRef]
- Peng, C.Y.; Tseng, S.T. Mis-specification analysis of linear degradation models. IEEE Trans. Reliab. 2009, 58, 444–455. [Google Scholar] [CrossRef]
- Whitmore, G.; Crowder, M.; Lawless, J. Failure inference from a marker process based on a bivariate Wiener model. Lifetime Data Anal. 1998, 4, 229–251. [Google Scholar] [CrossRef] [PubMed]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IiE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Whitmore, G.A.; Schenkelberg, F. Modelling accelerated degradation data using Wiener diffusion with a time scale transformation. Lifetime Data Anal. 1997, 3, 27–45. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.S.; Shen, Y.; Xie, M. Degradation-based burn-in with preventive maintenance. Eur. J. Oper. Res. 2012, 221, 360–367. [Google Scholar] [CrossRef]
- Li, H.; Pan, D.; Chen, C.P. Reliability modeling and life estimation using an expectation maximization based wiener degradation model for momentum wheels. IEEE Trans. Cybern. 2014, 45, 969–977. [Google Scholar]
- Pan, D.; Wei, Y.; Fang, H.; Yang, W. A reliability estimation approach via Wiener degradation model with measurement errors. Appl. Math. Comput. 2018, 320, 131–141. [Google Scholar] [CrossRef]
- Tsai, C.C.; Tseng, S.T.; Balakrishnan, N. Mis-specification analyses of gamma and Wiener degradation processes. J. Stat. Plan. Inference 2011, 141, 3725–3735. [Google Scholar] [CrossRef]
- Jin, G.; Matthews, D.E.; Zhou, Z. A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries inspacecraft. Reliab. Eng. Syst. Saf. 2013, 113, 7–20. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Chen, M.Y.; Hu, C.H.; Zhou, D.H. A degradation path-dependent approach for remaining useful life estimation with an exact and closed-form solution. Eur. J. Oper. Res. 2013, 226, 53–66. [Google Scholar] [CrossRef]
- Wang, X.; Balakrishnan, N.; Guo, B. Residual life estimation based on a generalized Wiener degradation process. Reliab. Eng. Syst. Saf. 2014, 124, 13–23. [Google Scholar] [CrossRef]
- Li, C.; Hao, H. Degradation data analysis using wiener process and MCMC approach. Eng. Lett. 2017, 25, 234–238. [Google Scholar]
- Shahbaz, S.H.; Rahman, M.M.; Shahbaz, M.Q. General Results for General Transmuted-G Distributions. Eur. J. Pure Appl. Math. 2021, 14, 301–313. [Google Scholar] [CrossRef]
- Alizadeh, M.; Yousof, H.M.; Jahanshahi, S.; Najibi, S.M.; Hamedani, G. The transmuted odd log-logistic-G family of distributions. J. Stat. Manag. Syst. 2020, 23, 761–787. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Chesneau, C.; Khan, M.N. The extended odd family of probability distributions with practice to a submodel. Filomat 2019, 33, 3855–3867. [Google Scholar] [CrossRef]
- Bantan, R.A.; Jamal, F.; Chesneau, C.; Elgarhy, M. On a new result on the ratio exponentiated general family of distributions with applications. Mathematics 2020, 8, 598. [Google Scholar] [CrossRef]
- Muhammad, M.; Suleiman, M.I. The transmuted exponentiated U-quadratic distribution for lifetime modeling. Sohag J. Math. 2019, 6, 19–27. [Google Scholar]
- Rodríguez-Picón, L.A.; Perez-Dominguez, L.; Mejia, J.; Perez-Olguin, I.J.; Rodríguez-Borbón, M.I. A deconvolution approach for degradation modeling with measurement error. IEEE Access 2019, 7, 143899–143911. [Google Scholar] [CrossRef]
- Ieren, T.G.; Abdullahi, J. A Transmuted Normal Distribution: Properties and Applications. Equity J. Sci. Technol. 2020, 7, 16–34. [Google Scholar]
- Owen, D.B. A table of normal integrals: A table. Commun. Stat.-Simul. Comput. 1980, 9, 389–419. [Google Scholar] [CrossRef]
- Moors, J. On the absolute moments of a normally distributed random variable. EIT Res. Memo./Tilburg Inst. Econ. 1973, 39. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- William, Q.M.; Escobar, L.A. Statistical Methods for Reliability Data; A Wiley Interscience Publications; John Wiley & Sons: Hoboken, NJ, USA, 1998; p. 639. [Google Scholar]
- Si, X.S.; Zhou, D. A generalized result for degradation model-based reliability estimation. IEEE Trans. Autom. Sci. Eng. 2013, 11, 632–637. [Google Scholar] [CrossRef]
- Berg, A.; Meyer, R.; Yu, J. DIC as a model comparison criterion for stochastic volatility models. J. Bus. Econ. Stat. 2004, 22, 107–120. [Google Scholar] [CrossRef]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding predictive information criteria for Bayesian models. Stat. Comput. 2014, 24, 997–1016. [Google Scholar] [CrossRef]


| ( n, m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| (5, 5) | 0.0301 | 0.0403 | 0.1689 | 0.3622 | 0.1792 | 0.2966 | 0.2621 | 0.4448 |
| (5, 10) | 0.0292 | 0.0388 | 0.1079 | 0.3157 | 0.0932 | 0.1514 | 0.0986 | 0.1640 |
| (5, 15) | 0.0191 | 0.0238 | 0.0322 | 0.2632 | 0.0353 | 0.0601 | 0.0171 | 0.0300 |
| (10, 5) | 0.0295 | 0.0386 | 0.1659 | 0.3340 | 0.1673 | 0.2738 | 0.2474 | 0.4168 |
| (10, 10) | 0.0247 | 0.0309 | 0.0925 | 0.2756 | 0.0816 | 0.1305 | 0.0793 | 0.1277 |
| (10, 15) | 0.0069 | 0.0070 | 0.0205 | 0.2246 | 0.0121 | 0.0284 | 0.0116 | 0.0128 |
| (15, 5) | 0.0287 | 0.0311 | 0.1525 | 0.2397 | 0.1107 | 0.1774 | 0.1662 | 0.2816 |
| (15, 10) | 0.0217 | 0.0206 | 0.0540 | 0.1907 | 0.0446 | 0.0712 | 0.0473 | 0.0788 |
| (15, 15) | 0.0056 | 0.0007 | 0.0005 | 0.1728 | 0.0020 | 0.0139 | 0.0011 | 0.0027 |
| (n, m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| (5, 5) | 0.0320 | 0.3815 | 0.1884 | 0.4541 | 0.0403 | 0.1318 | 0.3191 | 0.9429 | 0.0116 | 0.0518 |
| (5, 10) | 0.0210 | 0.3330 | 0.1220 | 0.2866 | 0.0200 | 0.0712 | 0.1499 | 0.4414 | 0.0087 | 0.0397 |
| (5, 15) | 0.0192 | 0.2927 | 0.0206 | 0.1159 | 0.0008 | 0.0162 | 0.1283 | 0.3857 | 0.0013 | 0.0137 |
| (10, 5) | 0.0262 | 0.3042 | 0.1811 | 0.3659 | 0.0373 | 0.1230 | 0.2732 | 0.8138 | 0.0104 | 0.0475 |
| (10, 10) | 0.0165 | 0.2546 | 0.1048 | 0.1850 | 0.0134 | 0.0517 | 0.1352 | 0.4054 | 0.0066 | 0.0319 |
| (10, 15) | 0.0127 | 0.2243 | 0.0151 | 0.0382 | 0.0004 | 0.0062 | 0.0483 | 0.1513 | 0.0007 | 0.0043 |
| (15, 5) | 0.0247 | 0.1950 | 0.1689 | 0.3012 | 0.0265 | 0.0898 | 0.2246 | 0.6785 | 0.0087 | 0.0389 |
| (15, 10) | 0.0190 | 0.1225 | 0.0304 | 0.0282 | 0.0049 | 0.0266 | 0.1289 | 0.3915 | 0.0026 | 0.0121 |
| (15, 15) | 0.0067 | 0.0917 | 0.0004 | 0.0059 | 0.0003 | 0.0003 | 0.0026 | 0.0209 | 0.0002 | 0.0009 |
| Parameter | |||||
|---|---|---|---|---|---|
| Case 1 | 9.7224 | 2.0231 | 4.3574 | 1.0936 | - |
| Case 2 | 8.0188 | 1.9987 | 4.076 | 1.0868 | 3.6017 |
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 9.7224 | 2.0231 | 4.3574 | 1.0936 | - | −120.5808 | 244.0709 | 241.1616 | 2.9093 | 246.9802 |
| Case 2 | 8.0188 | 1.9987 | 4.076 | 1.0868 | 3.6017 | −113.4661 | 228.4230 | 226.9322 | 1.4908 | 229.9138 |
| Si’s model | - | .20338 | 4.198 | 1.5801 | - | −123.4786 | 249.2184 | 246.9572 | 2.2612 | 251.4796 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, I.; Wang, X.; Li, C.; Yan, M.; Mukhtar, M.; Muhammad, M. Reliability Analysis with Wiener-Transmuted Truncated Normal Degradation Model for Linear and Non-Negative Degradation Data. Symmetry 2022, 14, 353. https://doi.org/10.3390/sym14020353
Muhammad I, Wang X, Li C, Yan M, Mukhtar M, Muhammad M. Reliability Analysis with Wiener-Transmuted Truncated Normal Degradation Model for Linear and Non-Negative Degradation Data. Symmetry. 2022; 14(2):353. https://doi.org/10.3390/sym14020353
Chicago/Turabian StyleMuhammad, Isyaku, Xingang Wang, Changyou Li, Mingming Yan, Mustapha Mukhtar, and Mustapha Muhammad. 2022. "Reliability Analysis with Wiener-Transmuted Truncated Normal Degradation Model for Linear and Non-Negative Degradation Data" Symmetry 14, no. 2: 353. https://doi.org/10.3390/sym14020353
APA StyleMuhammad, I., Wang, X., Li, C., Yan, M., Mukhtar, M., & Muhammad, M. (2022). Reliability Analysis with Wiener-Transmuted Truncated Normal Degradation Model for Linear and Non-Negative Degradation Data. Symmetry, 14(2), 353. https://doi.org/10.3390/sym14020353






