Potential Energy Surfaces for Noble Gas (Ar, Kr, Xe, Rn)–Propylene Oxide Systems: Analytical Formulation and Binding

Abstract

Multidimensional potential energy surfaces for heavy noble gas–propylene oxide systems are obtained by applying the phenomenological method successfully used to describe homologous systems involving He and Ne atoms. Such potential energy surfaces, where the interaction exclusively arises from the anisotropic van der Waals interaction components, are given in an analytical form. Therefore, they can be easily used as force fields to carry out molecular simulations to evaluate spectroscopic features and the dynamical selectivity of weakly bound complexes formed by propylene oxide (a prototype chiral species) with a noble gas atom (a prototype isotropic partner) by two-body collisions under a variety of conditions. Several potential energy minima are identified on the surfaces, which are confirmed and characterized by high level ab initio calculations. The next step to further generalize this methodology is its extension to systems involving propylene oxide-diatomic molecules (as H₂, O₂ and N₂), as well as to propylene oxide dimers.

1. Introduction

Van der Waals complexes, whose intermolecular bond is determined by the critical balance of size repulsion with dispersion/induction attraction, are formed in many gaseous environments by collisions between weakly interacting species, often involving atomic and/or molecular partners of different complexity. Their characterization is crucial, since it permits the evaluation of static and dynamical properties of matter under a variety of conditions [1]. Moreover, the features of weakly interacting systems are basic to define the energy and structure of precursor states, controlling the passage to, and often being coincident with, the transition state of several fundamental elementary processes. Therefore, the proper representation of multidimensional potential energy surfaces (PESs), controlled by non-covalent anisotropic interactions, where the van der Waals component plays a dominant role, turns out to be a problem of general interest. Indeed, it should be emphasized that the construction of ab initio-based PESs, involving non-covalently interacting systems, must ensure an accurate description of the long-range regions. Such an issue is crucial for the correct evolution of molecular dynamics [1,2,3]. The construction must rely on the use of a high-level theory and a very large number of ab initio points together with suitable interpolation procedures. The required computational cost is expected to strongly increase, becoming often prohibitive even in atom-molecule systems, especially when considering heavier atoms and complex polyatomic molecules.

Propylene oxide (C₃H₆O) is one of the simplest chiral molecules [4,5,6,7,8,9,10]. Its structure, involving ten atoms, has been investigated by microwave spectroscopy [9,10], characterized by vibrational circular dichroism [11], Raman optical activity spectroscopy [12], and by ab initio calculations [13]. The properties of propylene oxide have been investigated by combining molecular beams and electrostatic hexapole techniques, where molecules were rotationally state-selected and aligned [14,15]. Synchrotron radiation was also employed to characterize the double ionization threshold [16]. The angular distribution of ionic fragments, produced by various dissociation channels of gas phase double ionized C₃H₆O molecules, has also been measured [17]. Structural isomers of propylene oxide have been investigated by quantum mechanical calculations [18,19].

The recent discovery of propylene oxide in the interstellar medium [4] increased the interest towards the basic role of such a molecule in the dynamics of elementary processes of interest for astrochemistry, and stimulated the debate on the long-standing unsolved issue about the origin of chiral selectivity in nature [20,21]. This discovery encouraged investigations on the basic features of the interaction of propylene oxide with the most abundant species in the interstellar medium, such as He, and also Ne and Ar, that are less stable than He [20]. Indeed, the interaction of noble gas atoms with neutral and ionic species relevant in astrochemical and interstellar media is a timely and currently much investigated subject [22].

Only limited information on the intermolecular interactions concerning propylene oxide and other closed shell partners is currently available; microwave rotational spectroscopy has been employed to characterize the structure and binding energy of the complexes with Ne [23], Ar [24], and Kr [25], and of the homochiral and heterochiral forms of propylene oxide dimers [26]. Recently, Faure et al. have constructed an accurate potential energy surface (PES) for the He-propylene oxide system [27], on which they calculated the first scattering cross sections for the rotational excitation. However, this procedure requires a high computational load, due to the number of coupled channels and of the basis functions needed to reach convergence.

Very recently, the molecular beam technique has been used to measure total (elastic and inelastic) integral cross sections, for the scattering of He and Ne projectiles by propylene oxide target molecules, as a function of the collision velocity [28]. A semiempirical PES, expressed as a combination of Improved Lennard-Jones (ILJ) functions, was obtained for the He–propylene oxide system defined in terms of parameters related to the polarizability components of the interacting partners (He interacting with the seven atomic centers of propylene oxide: two C atoms, three H atoms, an O atom, and the CH₃ pseudo atom). The parameters were fine-tuned to reproduce the measured total cross section with its velocity dependence. This PES showed an excellent agreement with complete basis set quality ab initio calculations [28]. The reliability of the PES for the Ne−propylene oxide system, obtained by simply scaling the He−propylene oxide parameters for the different polarizability of Ne, has been confirmed by the proper description of measured cross sections. Moreover, the minima well depth, also tested on additional ab initio calculations, is consistent with the dissociation energy obtained from the analysis of experimental microwave spectra [23].

The strength points of the proposed PESs are (i) the analytical form that is crucial to perform computationally fast and reliable simulations of collision processes; and (ii) their formulation in terms of parameters related to fundamental physical properties of the interacting partners that ensures the reliability of the interaction potential in the whole configuration space. In this work, we derive, according to the framework described above, the PESs for the interaction of propylene oxide with Ar, Kr, Xe, and Rn. The involved ILJ functions are obtained by simply scaling the parameters for the increase in polarizability along the noble gas group. All the minima found for each system have been compared against new high level ab initio calculations. As observed for the He and Ne case [28], the adopted methodology allows the formulation of PESs which are reliable in the whole space of the relative configurations in a computationally fast way. In addition, their analytical formulation offers interesting perspectives for a profitable description of scattering and other molecular dynamics properties [29]. Therefore, this work represents a further step toward the characterization of the interaction potential between propylene oxide and neutral molecules of interest in astrochemistry, such as H₂, O₂, N₂, and H₂O, up to propylene oxide–propylene oxide interactions. The latter system is of crucial importance because it would enable the observation of possible different dynamical effects arising in homochiral and heterochiral dimers. As remarked in a recent work of classical molecular simulations on the propylene oxide-water/ice [30] system, force field investigations play a crucial role in the modelling of astrochemical environments, being experimental investigations in the corresponding extreme conditions not straightforward. Moreover, a physically meaningful formulation can provide a much deeper insight at the atomistic and molecular level into the structural and dynamical properties of the investigated systems.

2. Potential Energy Surfaces

In this section, we summarize the general guidelines used to obtain the PESs for the complete family of Ng-C₃H₆O systems, in an internally consistent way and in analytical form, and describe their testing against ab initio calculations. As in the previous study on He and Ne−propylene oxide systems [28], the total interaction potential V has been represented as a sum of pair-contributions expressed through Improved Lennard Jones (ILJ) functions. All details on ILJ are given in [28] and in references therein. Each pair involves the noble gas atom (Ng = Ar, Kr, Xe, ad Rn) and one of the seven centers distributed in the propylene oxide, C₃H₆O, molecular frame, which are the asymmetric carbon C, the C atom of the CH₂ group, the three hydrogen H atoms of the CH and CH₂ groups, the oxygen atom O, and the methyl group CH₃. The latter has been considered as a structure-less partner, i.e., as a sphere having the mass of the methyl group, centered on the carbon atom.

2.1. The Improved Lennard-Jones Potential

According to the formulation recently given in detail [28], for each neutral-neutral pair, interacting by pure van der Waals components, the ILJ function V(r) has been formulated as:

$$V\left(r\right)=\epsilon \left(\frac{6}{n\left(r\right)-6}{\left(\frac{r_m}{r}\right)}^{n\left(r\right)}-\frac{n\left(r\right)}{n\left(r\right)-6}{\left(\frac{r_m}{r}\right)}^6\right),$$

(1)

where r is the Ng-atom (or effective atom) distance, and ε and r_m are, respectively, the potential well depth and the equilibrium distance associated to the considered pair. The n(r) term is given by:

$$n\left(r\right)=\beta +4{\left(\frac{r}{r_m}\right)}^2$$

(2)

where r/r_m is the reduced distance and β is a parameter related to the hardness of the two interacting species. In the present case, the β value is comprised between 7.0 and 8.0 [31].

The values of the interaction parameters of all interacting partners have been estimated by a simple scaling procedure starting from those recently provided for the He-and Ne-C₃H₆O systems according to the polarizability change along the Ng series [31,32,33,34]. The polarizability values of He and Ne are 0.20 and 0.40 ų, while those of Ar, Kr, Xe and Rn amount to 1.64, 2.49, 4.04 and 5.19 ų, respectively [35]. The polarizability of propylene oxide, 6.2 ų, has been decomposed in partial contributions, corresponding to 2.10, 1.10, 0.80 and 0.35 ų for CH₃, C, O, and H partners, respectively. Note that C, H and O are considered effective atomic centers, since their polarizabilities are different from those of isolated gas-phase atoms. The parameter values defining the PES of Ar-, Kr-, Xe-, and Rn–propylene oxide are reported in

Table 1. Values of the equilibrium distance, r_m, and of the well depth, ε, used in the Improved Lennard-Jones (ILJ) model to describe individual interaction pair contributions for the Ar-propylene oxide system. The parameter β is in the range of values typical of van der Waals interactions [22,28].

	ε/meV	rm/Å	β
CH3-Ar	9.21	4.02	7.0
C-Ar	7.19	3.79	7.0
O-Ar	8.51	3.61	7.0
H-Ar	3.27	3.51	8.0

,

Table 2. Values of the equilibrium distance, r_m, and of the well depth, ε, used in the ILJ model to describe individual interaction pair contributions for the Kr-propylene oxide system. The parameter β is in the range of values typical of van der Waals interactions [22,28].

	ε/meV	rm/Å	β
CH3-Kr	11.78	4.11	7.0
C-Kr	8.73	3.91	7.0
O-Kr	9.72	3.76	7.0
H-Kr	3.59	3.69	8.0

,

Table 3. Values of the equilibrium distance, r_m, and of the well depth, ε, used in the ILJ model to describe individual interaction pair contributions for the Xe-propylene oxide system. The parameter β is in the range of values typical of van der Waals interactions [22,28].

	ε/meV	rm/Å	β
CH3-Xe	14.25	4.26	7.0
C-Xe	9.93	4.09	7.0
O-Xe	10.19	3.97	7.0
H-Xe	3.67	3.93	8.0

and

Table 4. Values of the equilibrium distance, r_m, and of the well depth, ε, used in the ILJ model to describe individual interaction pair contributions for the Rn-propylene oxide system. The parameter β is in the range of values typical of van der Waals interactions [22,28].

	ε/meV	rm/Å	β
CH3-Rn	16.80	4.34	7.0
C-Rn	11.37	4.19	7.0
O-Rn	11.39	4.10	7.0
H-Rn	3.96	4.07	8.0

, respectively. The predicted energy minima on each PES have been tested against the corresponding ab initio calculations and available experimental data (see the following sections).

2.2. Ab Initio Calculations

Minimum energy points for all the investigated systems were characterized by high level ab initio calculations performed at MP2 and CCSD(T) levels of theory by using Gaussian16 [36]. In detail, initial structures were taken as the minima obtained by the analytical ILJ potential energy surfaces. To identify the orientation of the hydrogen atoms in the methyl group, which is considered as a pseudo-atom in the ILJ model, a preliminary optimization of the hydrogen atoms position was carried out at the MP2/aug-cc-pVDZ level of theory for each starting structure. Subsequent calculations were then performed on the propylene oxide–Ng systems, with propylene oxide taken as a rigid moiety, at MP2/aug-cc-pVnZ (n = 2,3,4) (for Ar) or MP2/aug-cc-pVnZ-PP (n = 2,3,4) (for Kr, Xe and Rn) to extrapolate the complete basis set (CBS) limit, by using a mixed exponential/Gaussian function [37]. A preliminary calculation for the propylene oxide-Kr system using the corresponding all electron aug-cc-pVnZ basis sets showed that minima obtained with the use of pseudo potentials presents negligible differences in the geometry (up to 0.012 Å) and in energy (up to 0.5 meV). All optimizations were performed on the counterpoise corrected potential energy surface [38] to account for the basis set superposition error (BSSE). CCSD(T) corrections to the MP2 CBS energies, $\Delta CCSD\left(T\right),$ were evaluated with the aug-cc-pVTZ basis set: $\Delta CCSD\left(T\right)=E_{CCSD\left(T\right)}^{aug-cc-pVTZ}$ − $E_{MP2}^{aug-cc-pVTZ}$. This term was then used to calculate $E_{CCSD\left(T\right)}^{CBS}$, the CBS complex energy at the CCSD(T) level, as $E_{CCSD\left(T\right)}^{CBS}\approx E_{MP2}^{CBS}+\Delta CCSD\left(T\right)$. For non-covalent adducts, it was indeed noted that higher order correlation effects have very little sensitivity to the basis set size (for not too small basis sets including diffuse functions) [39].

3. Results and Discussion

The reference frame adopted to represent each PES is shown in Figure 1: the noble gas atom-propylene oxide molecule system is embedded in a x y z Cartesian reference frame, where x, y, and z correspond to the principal molecular axes of inertia b, c, and a, respectively. The origin of the axes is fixed on the center of mass of the molecule. The spherical coordinates R, θ and ϕ define the noble gas atom position with respect to propylene oxide; R indicates the distance between the noble gas and the molecule center of mass, and θ and ϕ are the polar angles.

A thorough minima search on the PESs indicates that each investigated system is characterized by five minima of comparable energy, whose coordinates are reported in

Table 5. Minimum geometries and interaction energies for the Ar-propylene oxide system obtained on the present PES and by ab initio calculations (in parenthesis).

	Minimum 1	Minimum 2	Minimum 3	Minimum 4	Minimum 5
θ	98.8 (99.8)	87.6 (81.3)	49.7 (50.0)	100.4 (99.4)	43.1 (30.5)
ϕ	22.6 (10.5)	254.7 (259.1)	114.8 (106.7)	156.5 (66.1)	255.6 (247.4)
R (Å)	3.93 (3.83)	3.74 (3.75)	4.06 (3.87)	3.88 (3.67)	4.24 (4.15)
V (meV)	−34.6 (−36.8)	−34.1 (−36.0)	−31.8 (−40.2)	−31.7 (−40.3)	−26.9 (−33.0)

,

Table 6. Minimum geometries and interaction energies for the Kr-propylene oxide system obtained on the present PES and by ab initio calculations (in parenthesis).

	Minimum 1	Minimum 2	Minimum 3	Minimum 4	Minimum 5
θ	99.9 (99.3)	88.8 (80.8)	49.9 (49.9)	101.7 (98.8)	43.2 (31.5)
ϕ	21.2 (12.0)	254.1 (257.7)	115.9 (108.7)	157.9 (157.0)	254.9 (246.4)
R (Å)	4.06 (3.93)	3.88 (3.81)	4.21 (3.97)	4.02 (3.77)	4.38 (4.28)
V (meV)	−42.2 (−44.2)	−40.9 (−44.6)	−37.0 (−49.2)	−38.2 (−49.0)	−31.7 (−39.8)

,

Table 7. Minimum geometries and interaction energies for the Xe-propylene oxide system obtained on the present PES and by ab initio calculations (in parenthesis).

	Minimum 1	Minimum 2	Minimum 3	Minimum 4	Minimum 5
θ	101.2 (98.7)	90.1 (79.0)	50.2 (49.9)	103.1 (97.5)	41.9 (33.0)
ϕ	20.0 (13.2)	253.4 (256.2)	117.3 (110.8)	159.6 (157.0)	254.0 (244.6)
R (Å)	4.25 (4.10)	4.07 (3.97)	4.42 (4.12)	4.21 (3.94)	4.59 (4.39)
V (meV)	−48.1 (−53.2)	−46.0 (−55.2)	−40.2 (−60.2)	−43.1 (−59.7)	−34.9 (−49.2)

and

Table 8. Minimum geometries and interaction energies for the Rn-propylene oxide system obtained on the present PES and by ab initio calculations (in parenthesis).

	Minimum 1	Minimum 2	Minimum 3	Minimum 4	Minimum 5
θ	102.8 (98.6)	90.8 (79.7)	50.5 (49.8)	103.8 (96.9)	40.8 (33.8)
ϕ	19.4 (13.8	253.1 (255.1)	118.1 (112.0)	160.4 (156.5)	253.6 (243.2)
R (Å)	4.36 (4.15)	4.18 (4.01)	4.54 (4.17)	4.32 (3.99)	4.72 (4.43)
V (meV)	−55.1 (−59.9)	−52.6 (−63.7)	−45.1 (−67.6)	−49.4 (−67.1)	−39.5 (−55.2)

, for the Ar-, Kr-, Xe-, and Rn- propylene oxide systems, respectively. Tables also report coordinates and binding energies obtained at the CCSD(T)/CBS level, as described above (energy values obtained by each considered level of theory/basis sets can be found in Tables S1–S4 in the Supporting Information).

Figure 2 reports the geometries of the five minima for Ar-C₃H₆O. The figure can be considered as a reference also for the other systems since the geometries of the five minima are basically very similar for the noble gases investigated here, as well as for the previously characterized Ne-C₃H₆O system [28]. In particular, the equilibrium distances grow with the mass (or size) of the Ng atom, but the angular coordinates remain approximately the same. Furthermore, as expected, the stability of the systems is enhanced along the noble gas atoms series, according to the increase in the Ng atom polarizability. In detail, the global minimum configuration of Ar-propylene oxide is the same as those for heavier noble gases (see Table 5, Table 6, Table 7 and Table 8 and Figures S1–S3 for Kr-, Xe-, and Rn- propylene oxide, respectively), and for Ne-propylene oxide [28] and corresponds to the noble gas directed toward the asymmetric carbon, from the side of the CH₂ group. For the other minima, the ranking in energy might vary depending on the system. It must be noted, however, that, with the exception of the fifth minimum (see the following), they all lie very close in energy. In Minimum 2, the noble gas is directed toward the O-CH₂ bond in a perpendicular fashion, and the equilibrium distance is about 0.2 Å shorter than Minimum 1, while the well depth is slightly lower with respect to the global minimum. Minimum 3 and Minimum 4 present a similar well depth, significantly lower than Minimum 1. In Minimum 3, the noble gas is directed toward the O atom, while the orientation of the noble gas in Minimum 4 is somewhat opposite to that in Minimum 1, with the noble gas approaching the central carbon from the side of the oxygen atom. It is interesting to notice that this “hierarchy”, emphasized by Ar, also holds in systems with Kr, Xe, and Rn. However, there is an inversion in the energy ranking between Minimum 3 and 4. In the Ar case, these two configurations are almost isoenergetic. The fifth minimum is located at a reduced distance, r/r_m of ca. 1.08, and is significantly higher in energy with respect to the global minimum, ca. 8 meV for Ar, 11 meV for Kr, 13 meV for Xe, and 16 meV for Rn: the direction of the noble gas is almost coplanar to the propylene oxide ring, toward the oxygen atom.

Blanco et al. investigated Ar–propylene oxide and Kr–propylene oxide by rotational spectroscopy [24,25] and determined, by combining experimental and theoretical information by ab initio calculations at the MP2/6-311++G** level of theory, one adduct for each system. For Ar–propylene oxide, an experimental value of R = 3.773 Å and a calculated one of R = 3.711 Å were obtained [23], which very well matched with the 3.74 Å of Minimum 2 derived in the present formulation, together with a consistent orientation (direct comparison with the angles is not available). For Kr–propylene oxide, an experimental value of R = 3.878 Å and a calculated one of R = 3.905 Å were obtained [25] in excellent agreement with R = 3.88 Å of Minimum 2, which also very well matches the experimental angles, θ = 76° (expt.) vs. θ = 88.8° (present) and ϕ = 263° (expt.) vs. ϕ = 254.1° (present). In the above-mentioned references, dissociation energies D₀ were also indirectly (i.e., by using an approximate formula starting from the experimental centrifugal distortion constant) obtained. Their values (31 meV for Ar-C₃H₆O and 38.3 meV for Kr-C₃H₆O) cannot be directly compared to the D_e we provide here, because D₀ data include zero-point energy contributions. Therefore, we performed ab initio calculations at the MP2/aug-cc-pVTZ level of theory and evaluated zero-point energy corrections of 2.4 and 5.5 meV for Ar and Kr, respectively, which, summed to our D_e values, lead to D₀ energies very close to those of Refs. [24,25].

Ab initio calculations confirm the global picture given by the analytical PESs; for each system, there are five minima, four of which are very close in energy, and a slightly less bound adduct. Ab initio binding energies are higher than those predicted by the analytical PES and the discrepancy gets larger with the Ng mass, but in most cases the difference is within the accuracy of both methods (the accuracy of ab initio values at this level of theory is within 20 meV (less than 0.5 kcal/mol). The agreement in the minima geometries is also remarkably good. Apart from some exceptions, discrepancies lie within 0.15 Å for distances and 15 degrees for angles. With the minima being very close in energy, it is not surprising that the energy ordering might be different in the two approaches. However, a regular pattern is also followed in this case: ab initio Minima 3 and 4 are predicted to be more stable than Minima 1 and 2, the lowest ones on the present PESs.

In order to emphasize strength and anisotropy of the interaction and important topography details of obtained PESs, we show contour maps of the intermolecular potential at the equilibrium distance of the absolute minimum and with a distance increase of 10%, respectively, in Figure 3 and Figure 4 for Ar-C₃H₆O, in Figure 5 and Figure 6 for Kr-C₃H₆O, in Figure 7 and Figure 8 for Xe-C₃H₆O, and in Figure 9 and Figure 10 for the Rn-C₃H₆O system. For each system, at the equilibrium distance of the absolute minimum, the minimum energy path (MEP) is also depicted. Contour maps obtained at shorter distances are also reported in the SI for Ar- and Kr–propylene oxide (Figures S4 and S5).

The MEP is particularly useful to highlight the energy barriers separating the minima on the PES and thus controlling the possibility of geometry changes of the interacting system. This is an important feature, since the minima are very close in energy, and they arise at different separation distances and geometries. Therefore, if the barriers are sufficiently high, the probability of populating the minima does not solely depend on their relative magnitude, but also on the long-range orientation effects. The figures show that, as previously evidenced in the He- and Ne- propylene oxide case, the barrier heights grow larger with the Ng mass. This means that, particularly for the heavier systems, the approaching collision partners can get trapped at long range in specific minima configurations whose barriers cannot be overcome even at room temperature. Note that this occurs for all the systems investigated here when considering the cold regimes typical of interstellar media.

The present formulation also permits a direct evaluation of the long-range dispersion coefficient C₆, which controls the capture effect by the long-range forces. Such coefficients can be defined through the following sum:

$$C_6={\displaystyle \sum }_{\mathrm{i}=1}^4{n}_i{C}_{6i}$$

(3)

where any partial $C_{6i}$ contribution is obtained as $C_{6i}=\epsilon ·r_m^6$ from the parameter values reported in Table 1, Table 2, Table 3 and Table 4, and n_i represents the number of interaction pairs of the same type. The $C_6$ values obtained for the complete series of Ng−C₃H₆O complexes are reported in

Table 9. Long-range isotropic $C_6$ dispersion coefficients calculated on the ILJ potential.

System	${\mathit{C}}_6 ({10}^4 \mathrm{meV}·{\AA }^6)$
He-C3H6O	1.65
Ne-C3H6O	3.65
Ar-C3H6O	11.80
Kr-C3H6O	17.43
Xe-C3H6O	25.78
Rn-C3H6O	34.35

and show an increase with the increase of the Ng polarizability. The asymptotic long-range attractions predicted by such dispersion coefficients can be compared with those estimated by Blanco et al. for Ne-, Ar, and Kr- propylene oxide [23,24,25] which also scale consistently with the Ng polarizability. In all cases, the present approach predicts an absolute value of the long-range attraction about 30% stronger than in [25]. This is to be expected because their estimation is based on the D₀ value rather than on D_e, which is most effectively related to the long-range attraction. Furthermore, another factor which leads to an underestimation is the fact that D_e arises from the balance of attraction-repulsion of the various interaction pairs, while the total long-range attraction depends on the sum of the different attraction pair contributions, which are included in the present determination.

4. Final Remarks and Conclusions

Potential energy surfaces describing the anisotropic interaction of noble gases (Ar, Kr, Xe, and Rn) with propylene oxide have been constructed. The van der Waals type forces, that govern the intermolecular interaction, have been formulated according to the ILJ function, where all parameter values are predicted by a phenomenological approach, that exploits those obtained for He and Ne-C₃H₆O, and scales them for the polarizability change along the Ng group. Indeed, in our previous work on the interaction between Ng (He and Ne)−propylene oxide, the parameters (here used as references) have been tested and fine-tuned, exploiting the comparison against ab initio calculations and against experimental scattering data [28].

The minima predicted by the present approach have been confirmed by high level ab initio calculations and show that the adopted potential parameters, reported in Table 1, Table 2, Table 3 and Table 4, allow a proper representation of the PES. Contour maps at selected R values are plotted in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, where the MEP is also shown.

The features of the obtained PESs stimulate important considerations:

(1)

The adopted method represents the intermolecular potential by an analytic formulation that makes use of few parameters, all having a well-defined physical meaning. This physically grounded restriction, at variance with most interpolation procedures, ensures the reliability of the interaction in the whole space of the relative configurations;

(2)

The present method allows a direct evaluation of the long-range dispersion coefficient C₆, that controls the capture character of the long-range forces;

(3)

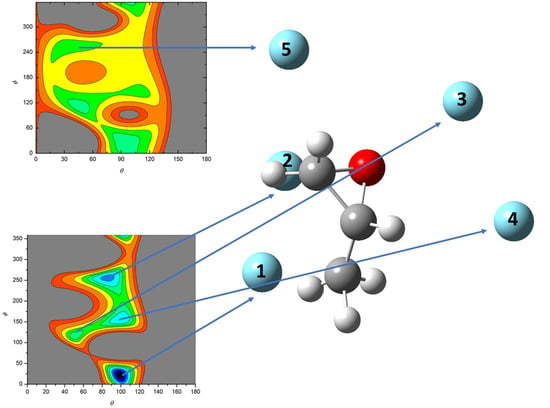
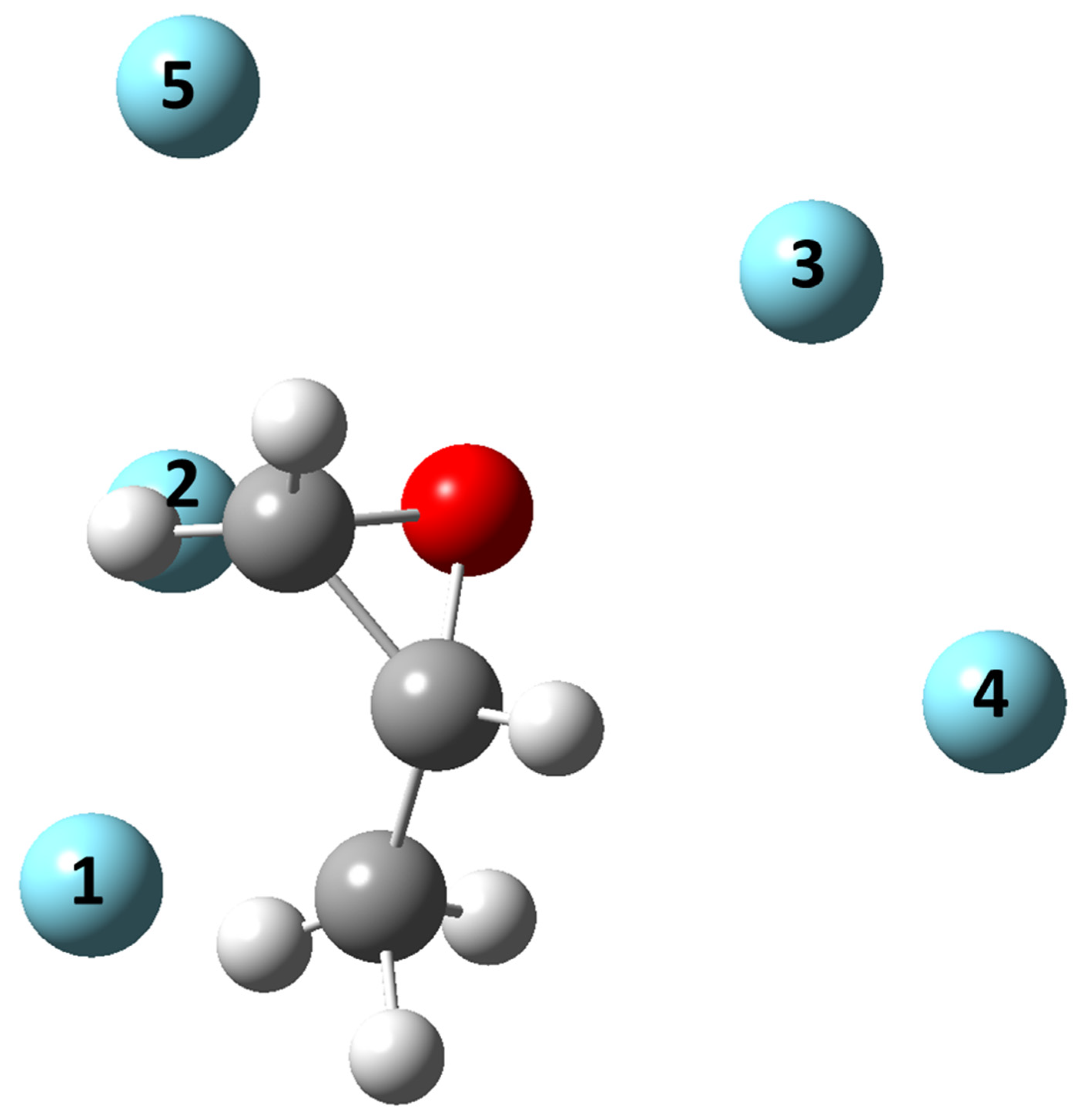
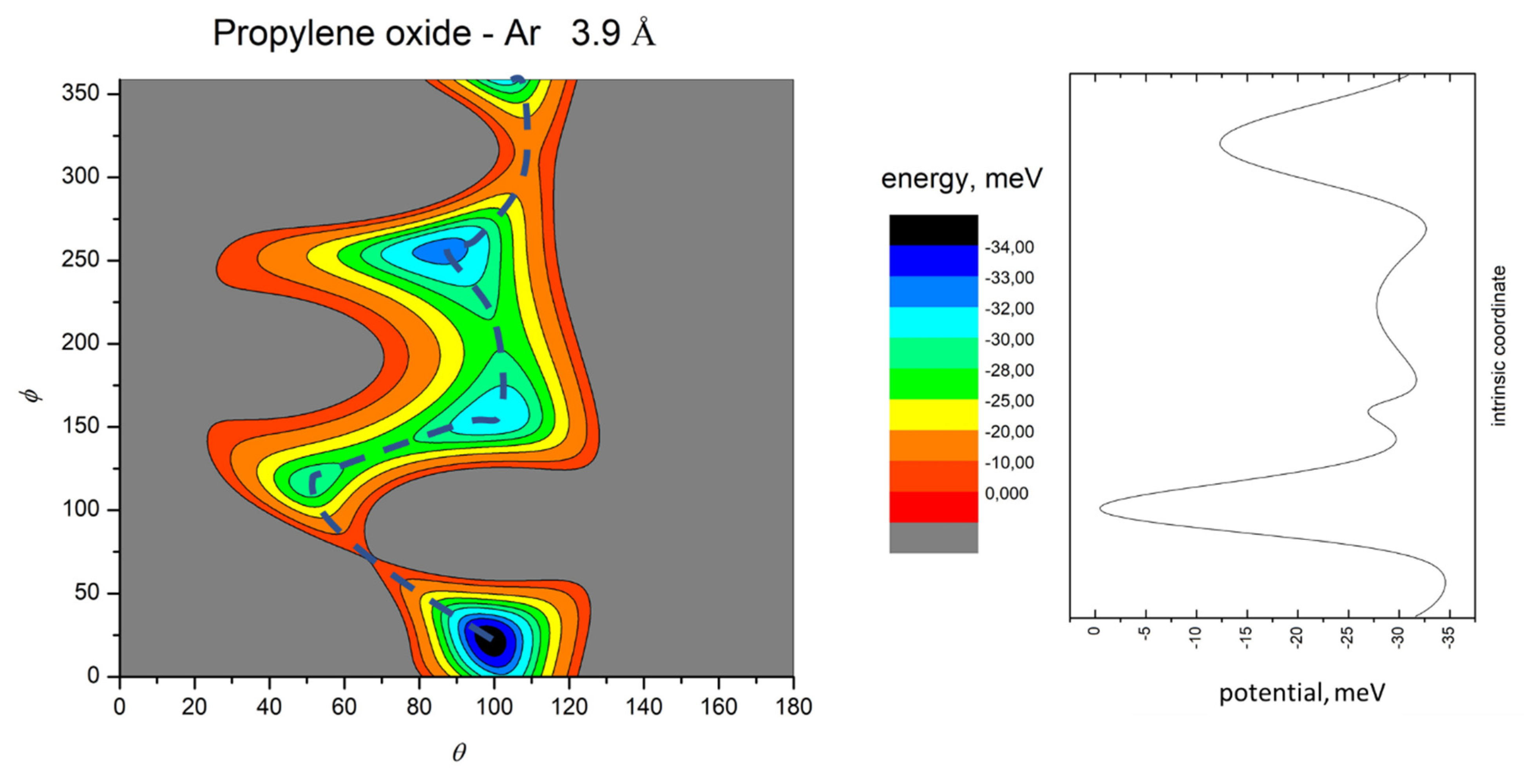
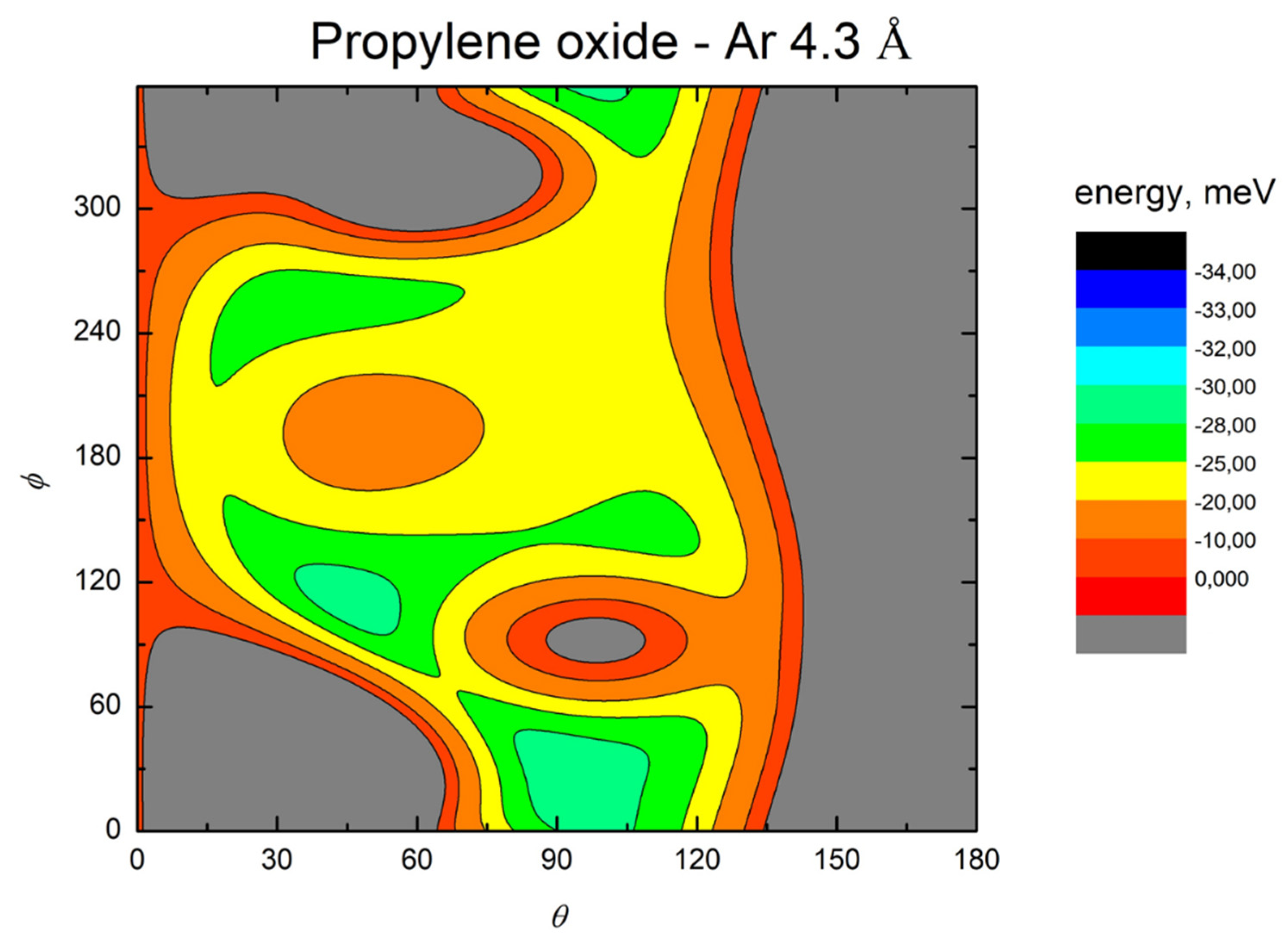
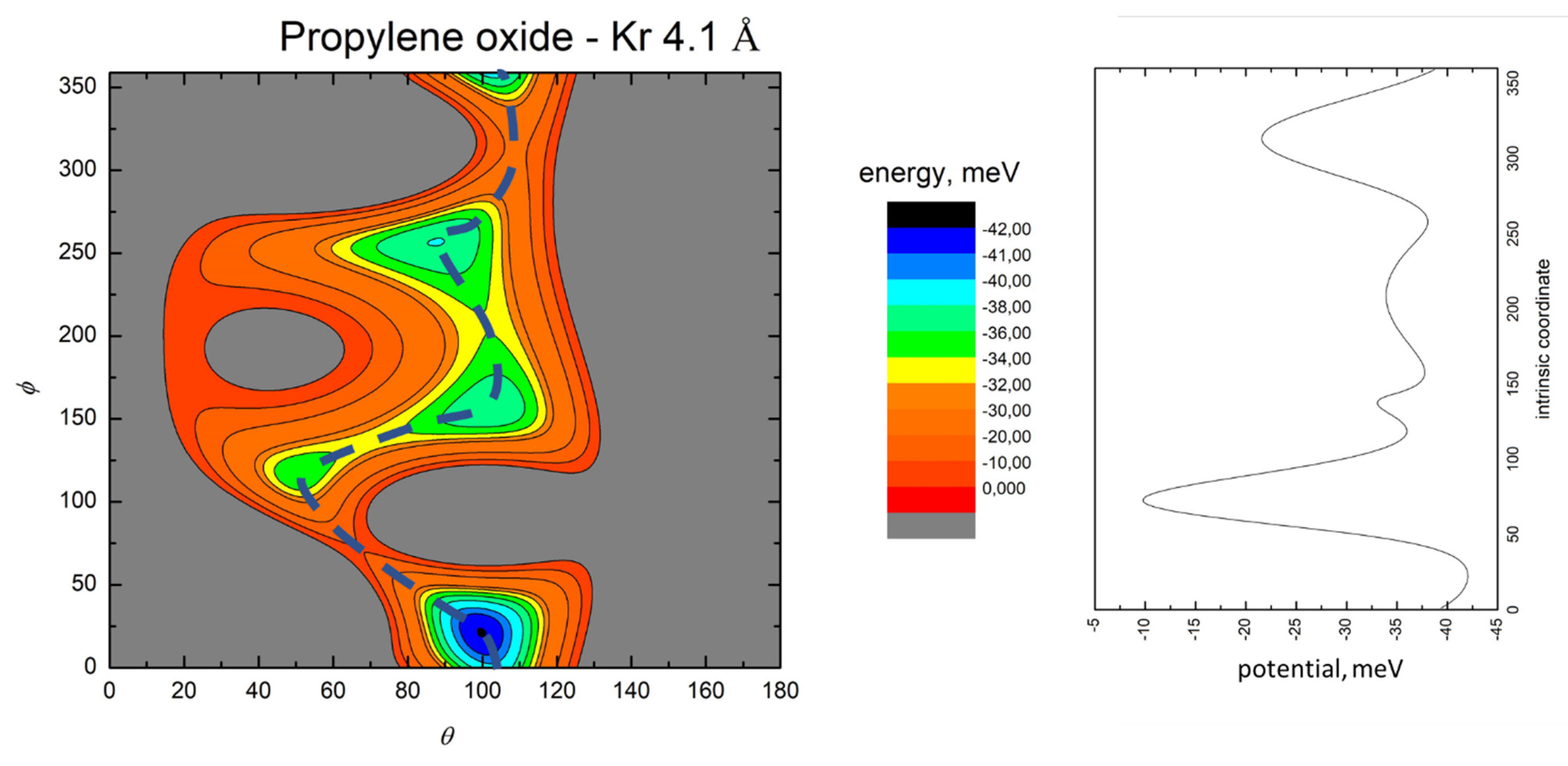
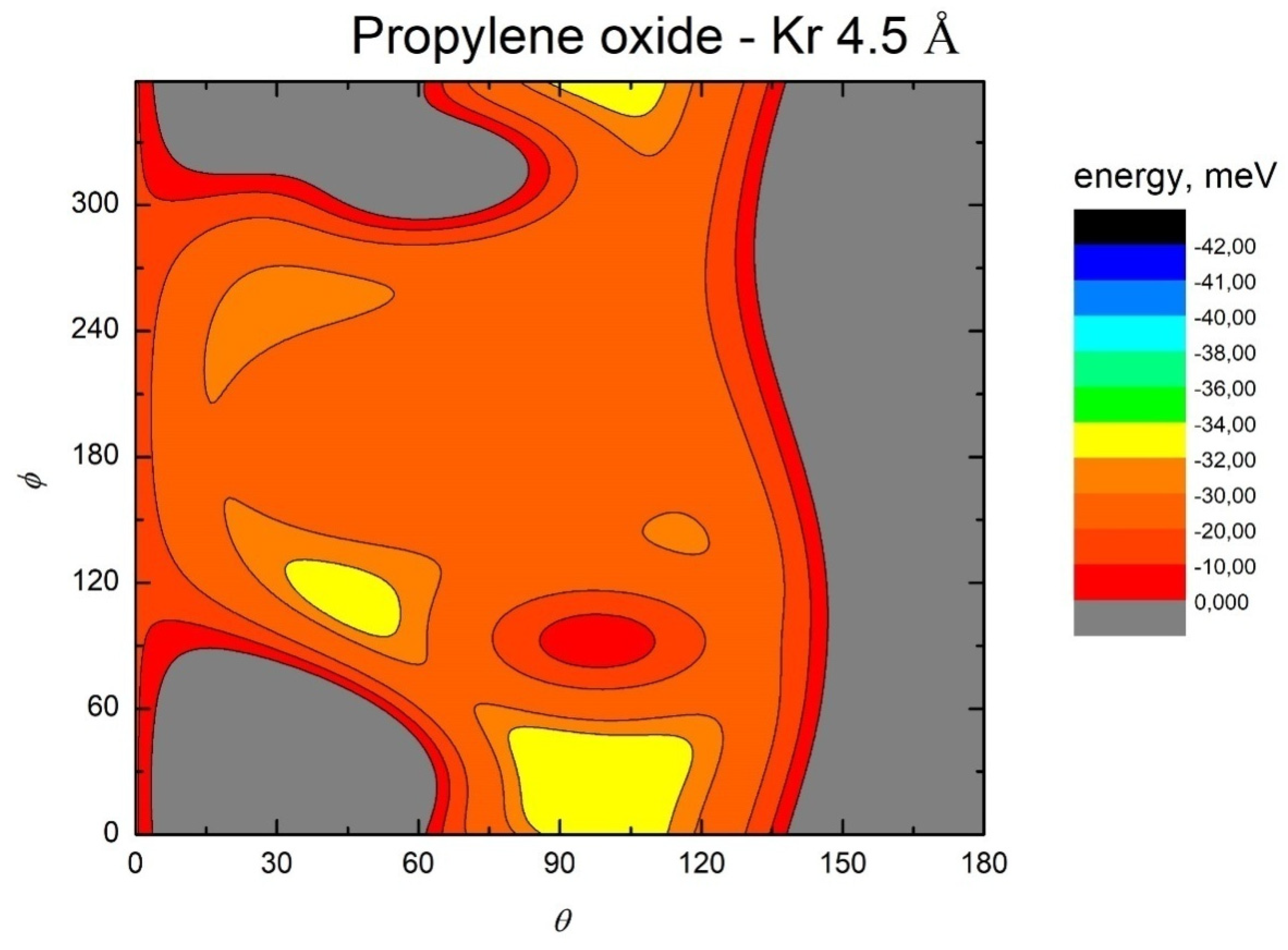
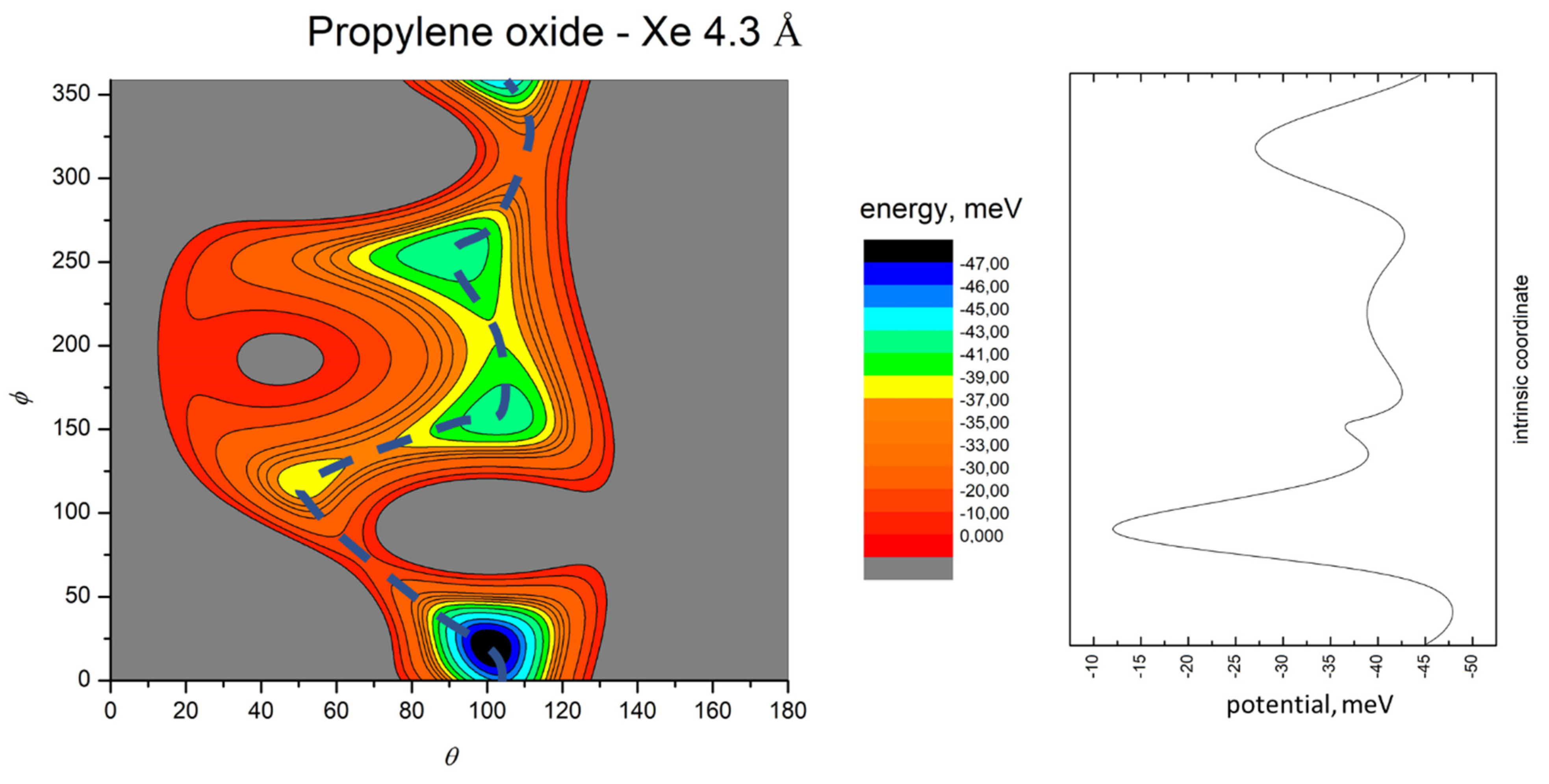
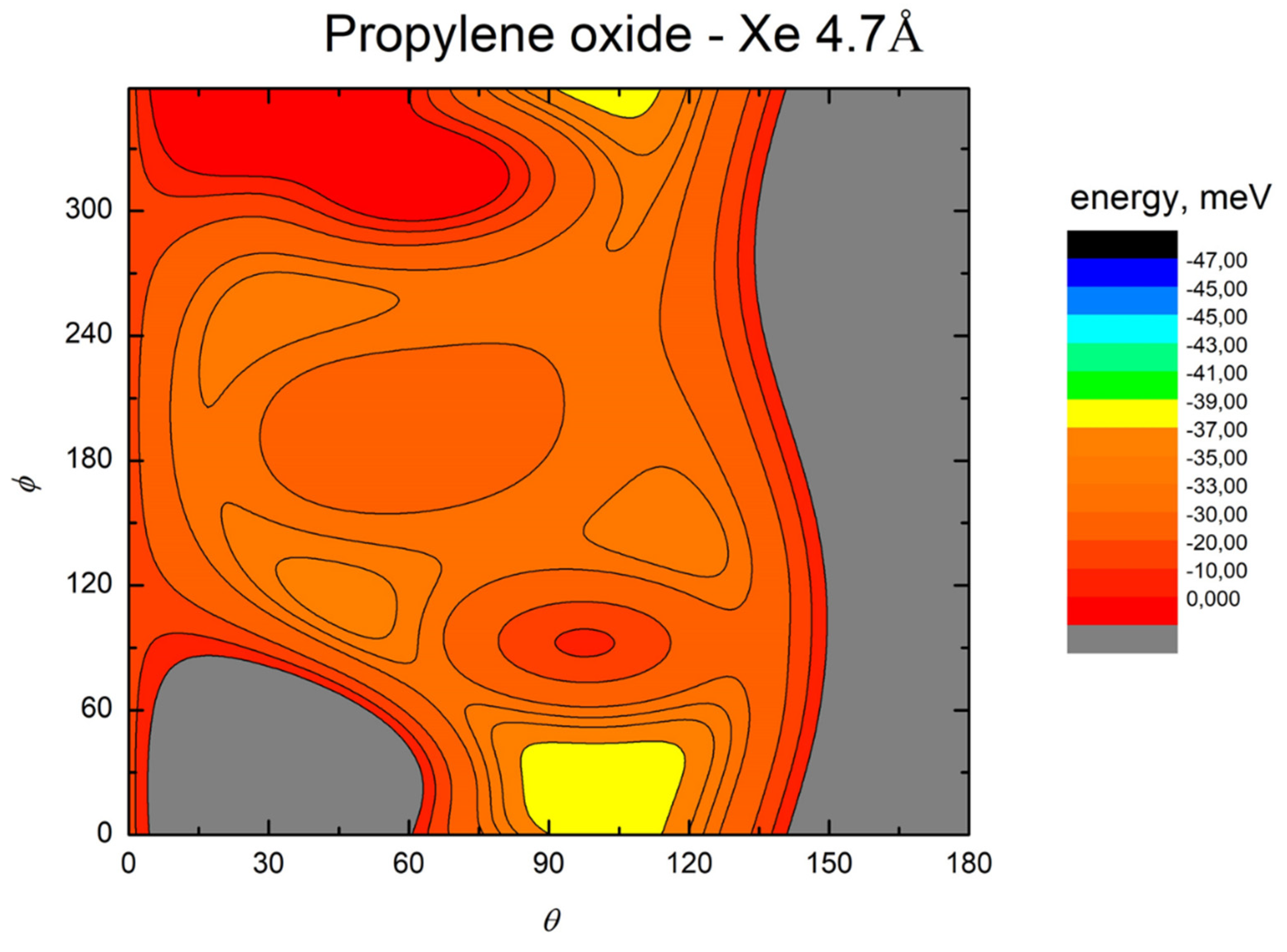
All systems present five minima very close in energy. Therefore, the collision dynamics is likely to be determined from their overall contribution, as well as from the possibility of adiabatic inter-conversion between them, hindered by the energy barriers that increase with the noble gas mass, and as the R distance decreases;

(4)

For each system, the location of the minimum energy changes as the intermolecular distance varies, that is the most stable configuration at long range, can substantially differ from that exhibited at intermediate and short range. An important consequence is that a system, formed by the trapping long-range anisotropic attractive forces, can be channeled during the relaxation of its internal degrees of freedom via fast non-adiabatic cooling, in configurations that can differ from that of the PES global minimum;

(5)

The dissociation energy of Ar−propylene oxide and Kr−propylene oxide, estimated by Blanco et al. [25], is consistent with the well depth and geometries of the minima determined in the present work. Moreover, considerations made at the previous point 4 can also applied to this point;

(6)

The analytical formulation of the PES allows the calculation of physical, dynamical, and spectroscopic properties of the systems, which selectively depend on the weak anisotropic forces, effective both at long and intermediate range of separation distances;

(7)

The same method can be applied, after parameters scaling for the change in polarizability, to the description of simple diatomic molecule-propylene oxide systems, when the diatom (as H₂, N₂ and O₂), with rotational levels following a Boltzmann distribution at room and higher temperature, rotates sufficiently faster than propylene oxide. Therefore, under such conditions, the diatom, which during the collision behaves as a pseudo-atom, interacts with propylene oxide with intermolecular forces basically of van der Waals nature. In particular, N₂ and O₂ would behave like Ar, as they show a similar isotropic polarizability component, while the polarizability of H₂ suggests for this molecule an intermediate behavior between Ne and Ar. However, the anisotropic character of the intermolecular forces emerges at low temperature, which is when only slowly rotating diatoms are interacting with the propylene oxide. In this case, the complete potential formulation must also include the anisotropic contribution of the electrostatic components, as those arising from permanent molecular electric multipole interactions. The method can also be extended to more complex systems of interest for their chiral properties, like propylene oxide dimers.

(8)

These potential energy surfaces can be used to evaluate and investigate possible collision alignment processes, basic for chiral discrimination in gaseous streams and vortices occurring in no equilibrium atmosphere environments [40];

(9)

Finally, it is also worth pointing out that this methodology can be profitably used to preliminarily address the search of ab-initio stationary points in multidimensional surfaces for weakly bound systems. This might be a difficult task, as they require a higher level of theory than bound systems, and may present many minima, particularly when some of them are shallow and can easily escape a grid search. The ab-initio calculation of transition states may be even more elusive. A preliminary detailed search on the present PES is reliable and much faster and allows identification of confined regions where minima or transition state points are located, strongly reducing the number of points to be evaluated quantum mechanically. Moreover, its formulation permits both forces and force constants to be obtained analytically, speeding up their calculation in molecular dynamics simulations, where these quantities play a crucial role, therefore alleviating the related computational burden.