Soft Expert Symmetric Group and Its Application in MCDM Problem

Abstract

Researchers are always inspired to broaden their explorations towards uncertainty theories, owing to their great interest and importance. Soft set theory plays a primary role among all recent uncertainty tools. Though this theory sounds good in all aspects, it has its own limitations due to a lack of experts. The novel idea of a soft expert set was brought up recently to address this issue. This strategy is innovative and inventive in the sense that it utilizes the expertise of numerous specialists. This novel idea inspired us a lot for the development of the present study. This paper introduces the notion of a soft expert symmetric group as a natural generalization of the symmetric group and soft expert set. Several interesting properties of soft expert symmetric groups are studied. Internal and external products of two soft expert symmetric groups and the homomorphism of soft expert symmetric groups are also presented. The application of a soft expert symmetric group in multi-criteria decision-making situations is also given in a lucid manner.

1. Introduction

Soft set theory [1], proposed by Molodtsov, finds its place in addressing uncertainty theory in an excellent manner. In fact, this theory has numerous applications in various domains such as smoothness of functions, game theory, operations research, Riemann integration, Perron integration, probability theory, and so on. Maji et al. [2,3] applied soft set theory in decision-making situations. A book published by Molodtsov [4] serves as a boon to researchers who are involved in extending soft set theory in different dimensions. Sezgin and Atagün [5] contributed to the study of the restricted symmetric differences of soft sets and expanded the theoretical underpinnings of operations on soft sets. Abbas et al. [6] introduced the concept of generalized soft equality (g-soft equality) of two soft sets and proved that the lower and upper soft equality of two soft sets are g-soft equalities. Vijayabalaji and Ramesh [7] defined an uncertain multiplicative linguistic soft set and studied some of its properties. Abbas et al. [8] introduced the concepts of generalized finite soft equality ($gf$-soft equality), generalized finite soft union, and the generalized finite soft intersection of two soft sets. Al-shami [9] gives two counterexamples to justify why some results obtained in [6,8] need not be true and he also investigated under what conditions these results are true. He also studied the concepts of $gf$-soft union and $gf$-soft intersection for an arbitrary family of soft sets. The idea of a belief interval-valued soft set was introduced by Vijayabalaji and Ramesh [10] by the method of combining belief interval-value (Dempster–Shafer theory) and soft sets. Al-shami and El-shafei [11] introduced the concepts of T-soft subset and T-soft equality relations and defined the concepts of T-soft union and T-soft intersection for an arbitrary family of soft sets.

A fundamental form of soft group theory was developed by Aktaş and Çağman [12], which expands the definition of a group to incorporate the algebraic structures of soft sets. Sun et al. [13] introduced the notion of soft modules. By taking the universe set as a module and constructing a mapping from the subset of a parameter set to the power set of the universe set, they were able to create the framework of soft modules. Liu et al. [14] developed three fundamental isomorphism theorems for soft rings and studied some properties of idealistic soft rings. The concepts of sum and direct sum of soft submodules, small soft submodules, and a soft module’s radical were proposed by Türkmen and Pancar [15]. The idea of a vague soft module was first suggested by Onar et al. [16]. Kamaci [17] found new operations on an N-soft set and determined the number of features for its algebraic structures. For soft sets, Aygün and Kamaci [18] explored several algebraic structures such as groups, rings, isomorphic rings, lattices, and MV algebras. They did this by employing existing soft operations such as union, intersection, and complement. The same work also presents the innovative categories of the distance and similarity measures between two soft sets. A soft union of semigroups, ideals, and bi-ideals was coined by Sezgin [19]. Later, Tunçay and Sezgin [20] extended the idea of a soft union of semigroups to a soft union of rings.

In the decades following Zadeh’s [21] introduction of the notion of the fuzzy set, numerous investigations on its generalization have been conducted. The fuzzy setting of soft modules and fuzzy soft exactness was introduced by Xiao et al. [22]. Mordeson et al. [23] presented the most current information related to this research. A large number of studies have generalized the concept of fuzzy sets. Atanassov [24] pioneered the intuitionistic fuzzy set notion. Gunduz and Bayramov [25] suggested an intuitionistic fuzzy soft module that expands the concept of modules by incorporating algebraic structures in soft sets and examining their features. Suryansu Ray [26] put in place the fuzziness of an element’s position in a fuzzy subgroup. Vijayabalaji et al. [27] broadened the structure of linguistic soft set to another domain, namely the sigmoid-valued fuzzy soft set. Akin [28] added group theory to the multi-fuzzy soft sets. Vimala and Reeta [29] conceived the idea of lattice-ordered fuzzy soft groups. Reeta and Vimala [30] introduced anti-lattice ordered fuzzy soft groups and extended the anti-lattice ordered fuzzy soft groups matrix with suitable examples.

Alkhazaleh and Salleh [31] presented the idea of a soft expert set, which is more effective and useful. In this model, the user can know the opinion of all experts in one model without any operations. In addition, its fundamental operations, namely complement, union, intersection, AND, OR, and their characteristics were specified. An application of this concept in a decision-making problem is also presented in the same paper. Alkhazaleh and Salleh [32] broaden the notion of a soft expert set to a fuzzy soft expert set and discussed a mapping between fuzzy soft expert classes and their attributes. Broumi and Smarandache [33] established the concept of intuitionistic fuzzy soft expert sets. Adam and Hassan [34] defined a multi Q-fuzzy soft expert set and gave its basic operations, namely complement, union, intersection, OR, and AND. They provided a decision-making method on a multi-Q-fuzzy soft expert set. By combining picture fuzzy sets with soft expert sets, Tchier et al. [35] proposed the picture fuzzy soft expert set and established a group decision-making problem for it.

The neutrosophic soft expert set was introduced by Şahin and Vluçay [36], as a generalization of soft expert set. They also studied some properties of neutrosophic soft expert sets. An application of this concept in a decision-making problem is illustrated in the same paper. Further, Uluçay et al. [37] expanded the idea to a generalized neutrosophic soft expert set (GNSES) and provided some basic operations on it. They also applied the algorithm to a decision-making problem, which illustrates the effectiveness and practicality of the proposed concept. Gulistan and Hassan [38] introduced the notion of the neutrosophic cubic soft expert sets (NCSESs) by using the concept of neutrosophic cubic soft sets and defined many operations and analyzed the properties of it. To validate its applications in games, they developed a procedure and analyzed the cricket series between Pakistan and India. Al-qudah et al. [39] introduced the concept of weighted fuzzy parameterized complex multi-fuzzy soft expert set and investigated its application in decision-making situations. Al-quran et al. [40] introduced the notion of fuzzy parameterized complex neutrosophic soft expert set and illustrated its application in a decision-making problem. Fritzsche et al. [41] considered the depth of several young subgroups of the symmetric group $S_n$. Nawawi et al. [42] studied the connectivity of commuting graphs for a symmetric group of degree n.

Using the novel idea of the soft element that was introduced by Wardowski [43], Yaylali et al. [44] gave a new approach to soft groups and soft rings. Recently, Öztunç et al. [45] studied the categorical structures of soft groups. They also provided an application for soft groups using the cube concept. The idea of an $(a,b)$-fuzzy soft set was first proposed by Al-shami et al. [46], paving the way for circumstances that necessitate weighted evaluations of membership and nonmembership. They discovered the primary features of $(a,b)$-fuzzy soft sets and created the basic set of arithmetic operations for them. Additionally, they examined a decision-making problem to support the use of $(a,b)$-fuzzy soft sets in this context.

This paper generalizes the concept of symmetric groups and soft expert set to soft expert symmetric groups (SES-groups). The structure of the soft expert set was built with two opinions: agree $\left(1\right)$ and disagree $\left(0\right)$. So we form our new algebraic structure namely a soft expert group based on two opinions. However, it is evident to note that opinions with more than two values can also be assumed. Section 2 gives the basic definitions and results that are required for the development of the subsequent sections. Section 3 begins with the notion of the soft expert group and then generalizes it to a soft expert symmetric group. Several properties of soft expert symmetric groups are studied in Section 4. Internal and external products of two soft expert symmetric groups are presented in Section 5 with interesting results. The homomorphism of two soft expert symmetric groups is provided in Section 6. Section 7 gives the application of soft expert symmetric groups in decision-making situations. An algorithm on the soft expert symmetric group with supporting examples is also provided in the same section. The conclusion and direction of future research are given in Section 8. Consequently, our suggested concept will enhance existing research on soft expert sets [34,36,37,39,40] and soft set algebraic structures [13,16,17,28,42].

2. Preliminaries

Throughout this paper, let U be a universe and E, X, and $O=\{0,1\}$ be the set of parameters, experts, and opinions, respectively. Here we have assumed only two-valued opinions in set O, but multi-valued opinions also can be assumed. Additionally, $\mathcal{Z}=E\times X\times O$ and a subset $\mathcal{V}$ of $\mathcal{Z}$ is denoted by $\mathcal{V}=E_1\times X\times \left\{1\right\}$, where $E_1\subseteq E$, ${(\aleph ,\mathcal{V})}_U$ denotes that $(\aleph ,\mathcal{V})$ is a soft expert set in U. Additionally, $S_n$ denotes symmetric group of degree n, e is the identity element of $S_n$, $H{\le }_{sg}{S}_n$ denotes that H is a subgroup of $S_n$, $N{⊴}_{sg}{S}_n$ denotes that N is a normal subgroup of $S_n$, and ${(\aleph ,\mathcal{V})}_{S_n}$ represents that $(\aleph ,\mathcal{V})$ is a soft expert symmetric group in $S_n$.

Definition 1 

([4]). Let $A\subseteq E$, a pair $(\aleph ,A)$ is called a soft set over U, if $\aleph :A\to P\left(U\right)$ is a function.

Definition 2 

The support of the soft set $(\aleph ,A)$ is defined by Supp $(\aleph ,A)=\{e\in A|\aleph \left(e\right)\ne \mathsf{\varnothing }\}$. A soft set $(\aleph ,A)$ is said to be non-null if Supp $(\aleph ,A)\ne \mathsf{\varnothing }$.

Definition 3 

([31]). Let $\mathcal{V}\subseteq \mathcal{Z}$, a pair ${(\aleph ,\mathcal{V})}_U$ is called a soft expert set, if $\aleph :\mathcal{V}\to P\left(U\right)$ is a function.

Definition 4 

([31]). Let ${(\aleph ,\mathcal{T})}_U$ and ${({\aleph }^{\prime },{\mathcal{T}}^{\prime })}_U$ be two soft expert sets, then $(\aleph ,\mathcal{T})$ is said to be a soft expert subset of $({\aleph }^{\prime },{\mathcal{T}}^{\prime })$ if $\mathcal{T}\subseteq {\mathcal{T}}^{\prime }$ and for every $x\in \mathcal{T}$, $\aleph \left(x\right)$ is subset of ${\aleph }^{\prime }\left(x\right)$ and it denoted by $(\aleph ,\mathcal{T})$$\tilde{\subset }$$({\aleph }^{\prime },{\mathcal{T}}^{\prime })$. Similarly, $(\aleph ,\mathcal{T})$ is called a soft expert superset of $({\aleph }^{\prime },{\mathcal{T}}^{\prime })$, if $({\aleph }^{\prime },{\mathcal{T}}^{\prime })$ is a soft expert subset of $(\aleph ,\mathcal{T})$, and it is denoted by $(\aleph ,\mathcal{T})\tilde{\supset }({\aleph }^{\prime },{\mathcal{T}}^{\prime })$.

Definition 5 

([31]). Given two soft expert sets ${(\aleph ,\mathcal{V})}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_U$. If $(\aleph ,\mathcal{V})$ is a soft expert subset of $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert subset of $(\aleph ,\mathcal{V})$, then ${(\aleph ,\mathcal{V})}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_U$ are said to be equal.

Definition 6 

([31]). Let ${(\aleph ,\mathcal{T})}_U$ and ${({\aleph }^{\prime },{\mathcal{T}}^{\prime })}_U$ be two soft expert sets. Then the extended intersection of ${(\aleph ,\mathcal{T})}_U$ and ${({\aleph }^{\prime },{\mathcal{T}}^{\prime })}_U$ is a soft set ${({\aleph }^{″},{\mathcal{T}}^{″})}_U$, where ${\mathcal{T}}^{″}=\mathcal{T}\cup {\mathcal{T}}^{\prime }$ and for all $\alpha \in {\mathcal{T}}^{″}$,

${\aleph }^{″}\left(\alpha \right)=\left\{\begin{array}{cc}\aleph \left(\alpha \right)\hfill & \mathrm{if}\alpha \in \mathcal{T}\setminus {\mathcal{T}}^{\prime }\hfill \\ {\aleph }^{\prime }\left(\alpha \right)\hfill & \mathrm{if}\alpha \in {\mathcal{T}}^{\prime }\setminus \mathcal{T}\hfill \\ \aleph \left(\alpha \right)\cap {\aleph }^{\prime }\left(\alpha \right)\hfill & \mathrm{if}\alpha \in \mathcal{T}\cap {\mathcal{T}}^{\prime }\hfill \end{array}\right.$

We write $(\aleph ,\mathcal{T}){\tilde{\cap }}_{\epsilon }({\aleph }^{\prime },{\mathcal{T}}^{\prime })=({\aleph }^{″},{\mathcal{T}}^{″})$.

Definition 7 

([31]). The soft expert set ${({\aleph }^{″},{\mathcal{T}}^{″})}_U$ is said to be the extended union of two soft expert sets ${(\aleph ,\mathcal{T})}_U$ and ${({\aleph }^{\prime },{\mathcal{T}}^{\prime })}_U$, if ${\mathcal{T}}^{″}=\mathcal{T}\cup {\mathcal{T}}^{\prime }$ and ∀$\alpha \in {\mathcal{T}}^{″}$,

${\aleph }^{″}\left(\alpha \right)=\left\{\begin{array}{cc}\aleph \left(\alpha \right)\hfill & \mathrm{if}\alpha \in \mathcal{T}\setminus {\mathcal{T}}^{\prime }\hfill \\ {\aleph }^{\prime }\left(\alpha \right)\hfill & \mathrm{if}\alpha \in {\mathcal{T}}^{\prime }\setminus \mathcal{T}\hfill \\ \aleph \left(\alpha \right)\cup {\aleph }^{\prime }\left(\alpha \right)\hfill & \mathrm{if}\alpha \in \mathcal{T}\cap {\mathcal{T}}^{\prime }\hfill \end{array}\right.$

We write $(\aleph ,\mathcal{T}){\tilde{\cup }}_{\epsilon }({\aleph }^{\prime },{\mathcal{T}}^{\prime })=({\aleph }^{″},{\mathcal{T}}^{″})$.

Definition 8 

([31]). If ${(\aleph ,\mathcal{V})}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_U$ are two soft expert sets, then their basic intersection (AND operation) is denoted by $(\aleph ,\mathcal{V})\wedge ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and defined by $(\aleph ,\mathcal{V})\wedge ({\aleph }^{\prime },{\mathcal{V}}^{\prime })=({\aleph }^{″},\mathcal{V}\times {\mathcal{V}}^{\prime })$, where ${\aleph }^{″}(\beta ,\gamma )=\aleph \left(\beta \right)\cap {\aleph }^{\prime }\left(\gamma \right)$, $\forall \beta \in \mathcal{V},\gamma \in {\mathcal{V}}^{\prime }$.

Definition 9 

([31]). If ${(\aleph ,\mathcal{T})}_U$ and ${({\aleph }^{\prime },{\mathcal{T}}^{\prime })}_U$ are two soft expert sets, then their basic union (OR operation) is denoted by $(\aleph ,\mathcal{T})\vee ({\aleph }^{\prime },{\mathcal{T}}^{\prime })$ and defined by $(\aleph ,\mathcal{T})\vee ({\aleph }^{\prime },{\mathcal{T}}^{\prime })=({\aleph }^{″},\mathcal{T}\times {\mathcal{T}}^{\prime })$, where ${\aleph }^{″}(\beta ,\gamma )=\aleph \left(\beta \right)\cup {\aleph }^{\prime }\left(\gamma \right)$, $\forall \beta \in \mathcal{T},\gamma \in {\mathcal{T}}^{\prime }$.

3. Soft Expert Group and Soft Expert Symmetric Group

This section begins with the notion of the soft expert group as a generalization of the soft group and soft expert set. We then generalize the idea of a soft expert group to the soft expert symmetric group with suitable examples.

Definition 10. 

Let G be any group. In a soft expert set ${(\aleph ,\mathcal{V})}_G$, if for every $x\in \mathcal{V}$, $\aleph \left(x\right){\le }_{sg}G$, then ${(\aleph ,\mathcal{V})}_G$ is said to be a soft expert group (SE-group) over G.

Example 1. 

Let $G={\mathbb{Z}}_6$ (integer modulo 6), parameter $E_1=\{e_1,e_3\}\subseteq E=\{e_1,e_2,e_3\}$, experts $X=\{e{p}_1,e{p}_2\}$, opinions $O=\{0,1\}$ with $\mathcal{Z}=\{(e_i,e{p}_j,o)|1\le i\le 3,1\le j\le 2,o\in O\}$. Soft expert set ${(\aleph ,\mathcal{Z})}_{{\mathbb{Z}}_6}$ is defined as below and its table form is given in Table 1.

Now, $\aleph (e_1,e{p}_1,1)=\{\left[0\right],\left[3\right]\}$,

$\aleph (e_1,e{p}_1,0)=\{\left[1\right],\left[2\right],\left[4\right],\left[5\right]\}$,

$\aleph (e_1,e{p}_2,1)=\{\left[0\right],\left[2\right],\left[4\right]\}$,

$\aleph (e_1,e{p}_2,0)=\{\left[1\right],\left[3\right],\left[5\right]\}$,

$\aleph (e_2,e{p}_1,1)=\{\left[0\right],\left[3\right],\left[4\right],\left[5\right]\}$,

$\aleph (e_2,e{p}_1,0)=\{\left[1\right],\left[2\right]\}$,

$\aleph (e_2,e{p}_2,1)=\{\left[0\right],\left[4\right],\left[5\right]\}$,

$\aleph (e_2,e{p}_2,0)=\{\left[1\right],\left[2\right],\left[3\right]\}$,

$\aleph (e_3,e{p}_1,1)={\mathbb{Z}}_6$,

$\aleph (e_3,e{p}_1,0)=\mathsf{\varnothing }$,

$\aleph (e_3,e{p}_2,1)=\left\{\left[0\right]\right\}$,

$\aleph (e_3,e{p}_2,0)=\{\left[1\right],\left[2\right],\left[3\right],\left[4\right],\left[5\right]\}$,

If $\mathcal{V}=\{(e_1,e{p}_1,1),(e_1,e{p}_2,1),(e_3,e{p}_1,1),(e_3,e{p}_2,1)\}$,

then $\aleph (e_1,e{p}_1,1)$, $\aleph (e_1,e{p}_2,1)$, $\aleph (e_3,e{p}_1,1)$, $\aleph (e_3,e{p}_2,1)$ are subgroups of ${\mathbb{Z}}_6$.

        Hence, ${(\aleph ,\mathcal{V})}_{{\mathbb{Z}}_6}$ is an SE-group.

Table 1. Soft expert set.

ℵ	$\left[0\right]$	$\left[1\right]$	$\left[2\right]$	$\left[3\right]$	$\left[4\right]$	$\left[5\right]$
$(e_1,e{p}_1,1)$	1	0	0	1	0	0
$(e_1,e{p}_1,0)$	0	1	1	0	1	1
$(e_1,e{p}_2,1)$	1	0	1	0	1	0
$(e_1,e{p}_2,0)$	0	1	0	1	0	1
$(e_2,e{p}_1,1)$	1	0	0	1	1	1
$(e_2,e{p}_1,0)$	0	1	1	0	0	0
$(e_2,e{p}_2,1)$	1	0	0	0	1	1
$(e_2,e{p}_2,0)$	0	1	1	1	0	0
$(e_3,e{p}_1,1)$	1	1	1	1	1	1
$(e_3,e{p}_1,0)$	0	0	0	0	0	0
$(e_3,e{p}_2,1)$	1	0	0	0	0	0
$(e_3,e{p}_2,0)$	0	1	1	1	1	1

Table 1. Soft expert set.

ℵ	$\left[0\right]$	$\left[1\right]$	$\left[2\right]$	$\left[3\right]$	$\left[4\right]$	$\left[5\right]$
$(e_1,e{p}_1,1)$	1	0	0	1	0	0
$(e_1,e{p}_1,0)$	0	1	1	0	1	1
$(e_1,e{p}_2,1)$	1	0	1	0	1	0
$(e_1,e{p}_2,0)$	0	1	0	1	0	1
$(e_2,e{p}_1,1)$	1	0	0	1	1	1
$(e_2,e{p}_1,0)$	0	1	1	0	0	0
$(e_2,e{p}_2,1)$	1	0	0	0	1	1
$(e_2,e{p}_2,0)$	0	1	1	1	0	0
$(e_3,e{p}_1,1)$	1	1	1	1	1	1
$(e_3,e{p}_1,0)$	0	0	0	0	0	0
$(e_3,e{p}_2,1)$	1	0	0	0	0	0
$(e_3,e{p}_2,0)$	0	1	1	1	1	1

Definition 11. 

Let U be a universe, G be a group, and ${(\aleph ,G)}_U$ be a soft expert set over U. Then ${(\aleph ,G)}_U$ is said to be a soft expert union group (SEU-group) if $\aleph \left(x{y}^{-1}\right)\subseteq \aleph \left(x\right)\cup \aleph \left(y\right)$, ∀$x,y\in G$.

Theorem 1. 

Let ${(\aleph ,G)}_U$ and ${({\aleph }^{\prime },G^{\prime })}_U$ be two SEU-groups, then $(\aleph ,G)\vee ({\aleph }^{\prime },G^{\prime })$ is an SEU-group over U.

Proof. 

Let $(\aleph ,G)\vee ({\aleph }^{\prime },G^{\prime })=({\aleph }^{″},G\times G^{\prime })$, where ${\aleph }^{″}(h,k)=\aleph \left(h\right)\cup {\aleph }^{\prime }\left(k\right)$, for all $h\in G$, $k\in G^{\prime }$.

Let $(h,k),(h_1,k_1)\in G\times G^{\prime }$. Then

$\begin{array}{cc}\hfill {\aleph }^{″}\left((h,k){(h_1,k_1)}^{-1}\right)& ={\aleph }^{″}\left((h,k)(h_1^{-1},k_1^{-1})\right)\hfill \\ & ={\aleph }^{″}(h{h}_1^{-1},k{k}_1^{-1})\hfill \\ & =\aleph \left(h{h}_1^{-1}\right)\cup {\aleph }^{\prime }\left(k{k}_1^{-1}\right)\hfill \\ & \subseteq (\aleph \left(h\right)\cup \aleph \left(h_1\right))\cup ({\aleph }^{\prime }\left(k\right)\cup {\aleph }^{\prime }\left(k_1\right))\hfill \\ & =(\aleph \left(h\right)\cup {\aleph }^{\prime }\left(k\right))\cup (\aleph \left(h_1\right)\cup {\aleph }^{\prime }\left(k_1\right))\hfill \\ & ={\aleph }^{″}(h,k)\cup \left({\aleph }^{″}(h_1,k_1)\right)\hfill \end{array}$

Hence, $(\aleph ,G)\vee ({\aleph }^{\prime },G^{\prime })$ is an SEU-group over U. □

Theorem 2. 

Let ${(\aleph ,G)}_U$ and ${({\aleph }^{\prime },G)}_U$ be two SEU-groups, then $(\aleph ,G){\tilde{\cup }}_R({\aleph }^{\prime },G)$ is an SEU-group over U.

Proof. 

Let $(\aleph ,G){\tilde{\cup }}_R({\aleph }^{\prime },G)=({\aleph }^{″},G)$, where ${\aleph }^{″}\left(h\right)=\aleph \left(h\right)\cup {\aleph }^{\prime }\left(h\right)$, for all $h\in G$.

Let $h,k\in G$. Then

$\begin{array}{cc}\hfill {\aleph }^{″}\left(hk\right)& =\aleph \left(hk\right)\cup {\aleph }^{\prime }\left(hk\right)\hfill \\ & \subseteq (\aleph \left(h\right)\cup \aleph \left(k^{-1}\right))\cup ({\aleph }^{\prime }\left(h\right)\cup {\aleph }^{\prime }\left(k^{-1}\right))\hfill \\ & =(\aleph \left(h\right)\cup {\aleph }^{\prime }\left(h\right))\cup (\aleph \left(k^{-1}\right)\cup {\aleph }^{\prime }\left(k^{-1}\right))\hfill \\ & ={\aleph }^{″}\left(h\right)\cup {\aleph }^{″}\left(k^{-1}\right))\hfill \end{array}$

Hence, $(\aleph ,G){\tilde{\cup }}_R({\aleph }^{\prime },G)$ is an SEU-group over U. □

Remark 1. 

It is evident to note that for SEU-groups $(\aleph ,G)$, $({\aleph }^{\prime },G^{\prime })$, and $({\aleph }^{\prime },G)$, the union $(\aleph ,G)\vee ({\aleph }^{\prime },G^{\prime })$ and $(\aleph ,G){\tilde{\cup }}_R({\aleph }^{\prime },G)$ are again an SEU-group, but it is not true in the case of crisp groups in general.

Definition 12. 

Let n be a positive integer and ${(\aleph ,\mathcal{V})}_{S_n}$ be a soft expert set. If for every $x\in \mathcal{V}$, $\aleph \left(x\right){\le }_{sg}{S}_n$, then ${(\aleph ,\mathcal{V})}_{S_n}$ is said to be a soft expert symmetric group (SES-group).

Example 2. 

Let $S_3$ be a symmetric group on $U=\{1,2,3\}$, $E=\{e_1,e_2,e_3\}$ be a parameter set, $X=\{e{p}_1,e{p}_2\}$ be experts, and $O=\{0,1\}$ be opinions with $\mathcal{Z}=\{(e_i,e{p}_j,o)/1\le i\le 3,1\le j\le 2,o\in O\}$. Additionally, let the soft expert set ${(\aleph ,\mathcal{Z})}_{S_3}$ be defined as in Table 2.

Table 2. Soft expert set.

ℵ	$\left(1\right)$	$\left(12\right)$	$\left(13\right)$	$\left(23\right)$	$\left(123\right)$	$\left(132\right)$
$(e_1,e{p}_1,1)$	1	1	0	0	0	0
$(e_1,e{p}_1,0)$	0	0	1	1	1	1
$(e_1,e{p}_2,1)$	1	0	0	0	1	1
$(e_1,e{p}_2,0)$	0	1	1	1	0	0
$(e_2,e{p}_1,1)$	1	0	0	1	1	1
$(e_2,e{p}_1,0)$	0	1	1	0	0	0
$(e_2,e{p}_2,1)$	1	0	0	0	1	1
$(e_2,e{p}_2,0)$	0	1	1	1	0	0
$(e_3,e{p}_1,1)$	1	1	1	1	1	1
$(e_3,e{p}_1,0)$	0	0	0	0	0	0
$(e_3,e{p}_2,1)$	1	1	0	0	0	0
$(e_3,e{p}_2,0)$	0	0	1	1	1	1

Now, $\aleph (e_1,e{p}_1,1)=\{\left(1\right),\left(12\right)\}$,

$\aleph (e_1,e{p}_1,0)=\{\left(13\right),\left(23\right),\left(123\right),\left(132\right)\}$,

$\aleph (e_1,e{p}_2,1)=\{\left(1\right),\left(123\right),\left(132\right)\}$,

$\aleph (e_1,e{p}_2,0)=\{\left(12\right),\left(13\right),\left(23\right)\}$,

$\aleph (e_2,e{p}_1,1)=\{\left(1\right),\left(23\right),\left(123\right),\left(132\right)\}$,

$\aleph (e_2,e{p}_1,0)=\{\left(12\right),\left(13\right)\}$,

$\aleph (e_2,e{p}_2,1)=\{\left(1\right),\left(123\right),\left(132\right)\}$,

$\aleph (e_2,e{p}_2,0)=\{\left(12\right),\left(13\right),\left(23\right)\}$,

$\aleph (e_3,e{p}_1,1)=\{\left(1\right),\left(12\right),\left(13\right),\left(23\right),\left(123\right),\left(132\right)\}$,

$\aleph (e_3,e{p}_1,0)=\mathsf{\varnothing }$,

$\aleph (e_3,e{p}_2,1)=\{\left(1\right),\left(12\right)\}$,

$\aleph (e_3,e{p}_2,0)=\{\left(13\right),\left(23\right),\left(123\right),\left(132\right)\}$.

If $\mathcal{V}=\{(e_1,e{p}_1,1),(e_1,e{p}_2,1),(e_3,e{p}_1,1),(e_3,e{p}_2,1)\}=E_1\times X\times \left\{1\right\}$, where $E_1=\{e_1,e_3\}\subseteq E$, then the functions $\aleph (e_1,e{p}_1,1)$, $\aleph (e_1,e{p}_2,1)$, $\aleph (e_3,e{p}_1,1)$, $\aleph (e_3,e{p}_2,1)$ are subgroups of $S_3$.

Hence, ${(\aleph ,\mathcal{V})}_{S_3}$ is an SES-group.

Remark 2. 

From Table 2, we have the following observations that exhibit that the soft expert symmetric group is an extension of the soft expert group.

$\left(i\right)$ If there is only one expert, say $X=\left\{p\right\}$ and O is a one-valued opinion, then the SES-group is a soft group as defined by Aktaş and Çağman [12].

$\left(ii\right)$ If $X_1=\left\{e{p}_1\right\}$, $X_2=\left\{e{p}_2\right\}$, $O=\left\{1\right\}$ with ${\mathcal{V}}_1=E_1\times X_1\times \left\{1\right\}$ and ${\mathcal{V}}_2=E_1\times X_2\times \left\{1\right\}$, then ${\mathcal{V}}_1=\{(e_1,e{p}_1,1),(e_3,e{p}_1,1)\}$ and ${\mathcal{V}}_2=\{(e_1,e{p}_2,1),(e_3,e{p}_2,1)\}$, $(\aleph ,{\mathcal{V}}_1)$ and $(\aleph ,{\mathcal{V}}_2)$ are soft expert groups with one expert and a one-valued opinion, so it is a soft group.

4. Properties of a Soft Expert Symmetric Group

Definition 13. 

Let ${(\aleph ,{\mathcal{V}}_1)}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}_2)}_U$ be two soft expert sets.

(i)

Then the restricted intersection of ${(\aleph ,{\mathcal{V}}_1)}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}_2)}_U$ is a soft expert set ${({\aleph }^{″},{\mathcal{V}}_3)}_U$, where ${\mathcal{V}}_3={\mathcal{V}}_1\cap {\mathcal{V}}_2$, if ${\mathcal{V}}_3\ne \mathsf{\varnothing }$ then for all $a\in {\mathcal{V}}_3$, ${\aleph }^{″}\left(a\right)=\aleph \left(a\right)\cap {\aleph }^{\prime }\left(a\right)$. We write $(\aleph ,{\mathcal{V}}_1){\tilde{\cap }}_R({\aleph }^{\prime },{\mathcal{V}}_2)=({\aleph }^{″},{\mathcal{V}}_3)$. If ${\mathcal{V}}_3=\mathsf{\varnothing }$, then $(\aleph ,{\mathcal{V}}_1){\tilde{\cap }}_R({\aleph }^{\prime },{\mathcal{V}}_2)={\mathsf{\varnothing }}_{\mathsf{\varnothing }}$.

(ii)

Then the restricted union of ${(\aleph ,{\mathcal{V}}_1)}_U$ and ${({\aleph }^{\prime },{\mathcal{V}}_2)}_U$ is a soft expert set ${({\aleph }^{″},{\mathcal{V}}_3)}_U$, where ${\mathcal{V}}_3={\mathcal{V}}_1\cap {\mathcal{V}}_2$, ${\mathcal{V}}_3\ne \mathsf{\varnothing }$ then for all $a\in {\mathcal{V}}_3$, ${\aleph }^{″}\left(a\right)=\aleph \left(a\right)\cup {\aleph }^{\prime }\left(a\right)$. We write $(\aleph ,{\mathcal{V}}_1){\tilde{\cup }}_R({\aleph }^{\prime },{\mathcal{V}}_2)=({\aleph }^{″},{\mathcal{V}}_3)$. If ${\mathcal{V}}_3=\mathsf{\varnothing }$, then $(\aleph ,{\mathcal{V}}_1)$${\tilde{\cup }}_R$$({\aleph }^{\prime },{\mathcal{V}}_2)={\mathsf{\varnothing }}_{\mathsf{\varnothing }}$.

Theorem 3. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups.

(i)

Then their basic intersection ${[(\aleph ,\mathcal{V})\wedge ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n}$ is an SES-group.

(ii)

Then their basic union ${[(\aleph ,\mathcal{V})\vee ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n}$ is an SES-group if and only if for every $\beta \in \mathcal{V}$, $\gamma \in {\mathcal{V}}^{\prime }$, either $\aleph \left(\beta \right)\subseteq {\aleph }^{\prime }\left(\gamma \right)$ or ${\aleph }^{\prime }\left(\gamma \right)\subseteq \aleph \left(\beta \right)$.

(iii)

Then their extended intersection $(\aleph ,\mathcal{V}){\tilde{\cap }}_{\epsilon }({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-group in $S_n$.

(iv)

If $\mathcal{V}\cap {\mathcal{V}}^{\prime }=\mathsf{\varnothing }$, then their extended union $(\aleph ,\mathcal{V}){\tilde{\cup }}_{\epsilon }({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-group in $S_n$.

(v)

If $\mathcal{V}\cap {\mathcal{V}}^{\prime }\ne \mathsf{\varnothing }$, then their restricted intersection $\left[\right(\aleph ,\mathcal{V})$${\tilde{\cap }}_R$$({\aleph }^{\prime },{\mathcal{V}}^{\prime }){]}_{S_n}$ is an SES-group.

(vi)

If $\mathcal{V}\cap {\mathcal{V}}^{\prime }\ne \mathsf{\varnothing }$, then their restricted union $(\aleph ,\mathcal{V}){\tilde{\cup }}_R({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-group in $S_n$ if and only if for every $a\in \mathcal{V}\cap {\mathcal{V}}^{\prime }$, either $\aleph \left(a\right)\subseteq {\aleph }^{\prime }\left(a\right)$ or ${\aleph }^{\prime }\left(a\right)\subseteq \aleph \left(a\right)$.

Proof. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups.

$\left(i\right)$ Let ${({\aleph }^{″},\mathcal{W})}_{S_n}=(\aleph ,\mathcal{V})\wedge ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, where $\mathcal{W}=\mathcal{V}\times {\mathcal{V}}^{\prime }$.

If $({\lambda }_1,{\lambda }_2)\in \mathcal{V}\times {\mathcal{V}}^{\prime }$, then $\aleph \left({\lambda }_1\right)$ and ${\aleph }^{\prime }\left({\lambda }_2\right)$ are subgroups in $S_n$

⟹ their intersection $\aleph \left({\lambda }_1\right)\cap {\aleph }^{\prime }\left({\lambda }_2\right){\le }_{sg}{S}_n$.

Hence, ${\left[(\aleph ,\mathcal{V})\wedge ({\aleph }^{\prime },{\mathcal{V}}^{\prime })\right]}_{S_n}$ is an SES-group.

$\left(ii\right)$ Let ${[(\aleph ,\mathcal{V})\vee ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n}=({\aleph }^{″},{\mathcal{V}}^{″})$, where ${\mathcal{V}}^{″}=\mathcal{V}\times {\mathcal{V}}^{\prime }$, then for every ${\lambda }_1\in \mathcal{V}$, ${\lambda }_2\in {\mathcal{V}}^{\prime }$, ${\aleph }^{″}({\lambda }_1,{\lambda }_2)=\aleph \left({\lambda }_1\right)\cup {\aleph }^{\prime }\left({\lambda }_2\right)$.

Their basic union $(\aleph ,\mathcal{V})\vee ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-group in $S_n$

⟺ for every $({\lambda }_1,{\lambda }_2)\in \mathcal{V}\times {\mathcal{V}}^{\prime }$, $\aleph \left({\lambda }_1\right)\cup {\aleph }^{\prime }\left({\lambda }_2\right){\le }_{sg}{S}_n$

⟺ either $\aleph \left({\lambda }_1\right){\le }_{sg}{\aleph }^{\prime }\left({\lambda }_2\right)$ or ${\aleph }^{\prime }\left({\lambda }_2\right){\le }_{sg}\aleph \left({\lambda }_1\right)$.

⟺ either $\aleph \left({\lambda }_1\right)\subseteq {\aleph }^{\prime }\left({\lambda }_2\right)$ or ${\aleph }^{\prime }\left({\lambda }_2\right)\subseteq \aleph \left({\lambda }_1\right)$, ∀$({\lambda }_1,{\lambda }_2)\in \mathcal{V}\times {\mathcal{V}}^{\prime }$.

$\left(iii\right)$ Let $(\aleph ,\mathcal{V}){\tilde{\cap }}_{\epsilon }({\aleph }^{\prime },{\mathcal{V}}^{\prime })=({\aleph }^{″},{\mathcal{V}}^{″})$, where ${\mathcal{V}}^{″}=\mathcal{V}\cup {\mathcal{V}}^{\prime }$.

If $\lambda \in {\mathcal{V}}^{\prime }\setminus \mathcal{V}$, then ${\aleph }^{″}\left(\lambda \right)={\aleph }^{\prime }\left(\lambda \right)$. Since $\lambda \in {\mathcal{V}}^{\prime }$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ is an SES-group, so ${\aleph }^{\prime }\left(\lambda \right){\le }_{sg}{S}_n$⟹${\aleph }^{″}\left(\lambda \right){\le }_{sg}{S}_n$

If $\lambda \in \mathcal{V}\setminus {\mathcal{V}}^{\prime }$, then ${\aleph }^{″}\left(\lambda \right)=\aleph \left(\lambda \right)$. Since $\lambda \in \mathcal{V}$ and ${(\aleph ,\mathcal{V})}_{S_n}$ is an SES-group, so $\aleph \left(\lambda \right){\le }_{sg}{S}_n$⟹${\aleph }^{″}\left(\lambda \right){\le }_{sg}{S}_n$.

If $\lambda \in \mathcal{V}\cap {\mathcal{V}}^{\prime }$, then ${\aleph }^{″}\left(\lambda \right)=\aleph \left(\lambda \right)\cap {\aleph }^{\prime }\left(\lambda \right)$. since $\lambda$ is an element in both $\mathcal{V}$ and ${\mathcal{V}}^{\prime }$, by hypothesis $\aleph \left(\lambda \right)$ and ${\aleph }^{\prime }\left(\lambda \right)$ are subgroups of $S_n$⟹${\aleph }^{″}\left(\lambda \right){\le }_{sg}{S}_n$.

Hence, ${({\aleph }^{″},{\mathcal{V}}^{″})}_{S_n}$ is an SES-group.

$\left(iv\right)$ Let $(\aleph ,\mathcal{V}){\tilde{\cup }}_{\epsilon }({\aleph }^{\prime },{\mathcal{V}}^{\prime })=({\aleph }^{″},{\mathcal{V}}^{″})$, where ${\mathcal{V}}^{″}=\mathcal{V}\cup {\mathcal{V}}^{\prime }$, since $\mathcal{V}\cap {\mathcal{V}}^{\prime }=\mathsf{\varnothing }$.

If $\lambda \in {\mathcal{V}}^{\prime }\setminus \mathcal{V}$, then ${\aleph }^{″}\left(\lambda \right)={\aleph }^{\prime }\left(\lambda \right){\le }_{sg}{S}_n$ and

If $\lambda \in \mathcal{V}\setminus {\mathcal{V}}^{\prime }$, then ${\aleph }^{″}\left(\lambda \right)=\aleph \left(\lambda \right){\le }_{sg}{S}_n$.

Hence, ${({\aleph }^{″},{\mathcal{V}}^{″})}_{S_n}$ is an SES-group.

$\left(v\right)$ Let $({\aleph }^{″},{\mathcal{V}}^{″})=(\aleph ,\mathcal{V}){\tilde{\cap }}_R({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, $\forall \lambda \in {\mathcal{V}}^{″}=\mathcal{V}\cap {\mathcal{V}}^{\prime }$,

${\aleph }^{″}\left(\lambda \right)=$($\aleph \left(\lambda \right)\cap {\aleph }^{\prime }\left(\lambda \right)$) ${\le }_{sg}{S}_n$,

so ${({\aleph }^{″},{\mathcal{V}}^{″})}_{S_n}$ is an SES-group.

$\left(vi\right)$ Let $(\aleph ,\mathcal{V}){\tilde{\cup }}_R({\aleph }^{\prime },{\mathcal{V}}^{\prime })=({\aleph }^{″},{\mathcal{V}}^{″})$, where ${\mathcal{V}}^{″}=\mathcal{V}\cap {\mathcal{V}}^{\prime }\ne \mathsf{\varnothing }$, then for every $a\in {\mathcal{V}}^{″}$, ${\aleph }^{″}\left(a\right)=\aleph \left(a\right)\cup {\aleph }^{\prime }\left(a\right)$.

Their restricted union $(\aleph ,\mathcal{V}){\tilde{\cup }}_R({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-group in $S_n$

⟺ for every $a\in {\mathcal{V}}^{″}$, $\aleph \left(a\right)\cup {\aleph }^{\prime }\left(a\right){\le }_{sg}{S}_n$

⟺ either $\aleph \left(a\right){\le }_{sg}{\aleph }^{\prime }\left(a\right)$ or ${\aleph }^{\prime }\left(a\right){\le }_{sg}\aleph \left(a\right)$.

⟺ either $\aleph \left(a\right)\subseteq {\aleph }^{\prime }\left(a\right)$ or ${\aleph }^{\prime }\left(a\right)\subseteq \aleph \left(a\right)$, ∀$a\in {\mathcal{V}}^{″}$. □

Definition 14. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an SES-group. If $\forall x\in \mathcal{V}$,

(i)

$\aleph \left(x\right)=\left\{e\right\}$, then ${(\aleph ,\mathcal{V})}_{S_n}$ is said to be an identity soft expert symmetric group (identity SES-group).

(ii)

$\aleph \left(x\right)=S_n$, then ${(\aleph ,\mathcal{V})}_{S_n}$ is said to be an absolute soft expert symmetric group (absolute SES-group).

(iii)

$\aleph \left(x\right)=Z\left(S_n\right)$, then ${(\aleph ,\mathcal{V})}_{S_n}$ is said to be a central soft expert symmetric group (central SES-group).

(iv)

$\aleph \left(x\right)$ is a commutator subgroup in $S_n$, then ${(\aleph ,\mathcal{V})}_{S_n}$ is said to be a commutator soft expert symmetric group (commutator SES-group).

Theorem 4. 

The homomorphic image of an SES-group is an SES-group.

Proof. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an SES-group and f be a group homomorphism from $S_n$ to $S_m$, then for every $x\in \mathcal{V}$, $f(\aleph \left(x\right)){\le }_{sg}{S}_m$. Hence, ${(f\aleph ,\mathcal{V})}_{S_m}$ is an SES-group. □

Theorem 5. 

Let $f:S_n\to S_m$ be a group homomorphism with ${(\aleph ,\mathcal{V})}_{S_n}$ being an SES-group.

(i)

If $\forall x\in \mathcal{V}$$\aleph \left(x\right)\subseteq kerf$, then ${(f\aleph ,\mathcal{V})}_{S_m}$ is an identity SES-group.

(ii)

Let f be a group homomorphism from $S_n$ onto $S_m$. If ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute (central or commutator) SES-group, then ${(f\aleph ,\mathcal{V})}_{S_m}$ is an absolute (central or commutator) SES-group.

Proof. 

$\left(i\right)$ Let $x\in \mathcal{V}$, then $f(\aleph \left(x\right))=\left\{e^{\prime }\right\}$ in $S_m$.

So ${(f\aleph ,\mathcal{V})}_{S_m}$ is an identity SES-group.

$\left(ii\right)$ For every $x\in \mathcal{V}$, $\aleph \left(x\right)=S_n$⇒$f(\aleph \left(x\right))=S_m$.

Hence, ${(f\aleph ,\mathcal{V})}_{S_m}$ is an absolute SES-group. Similarly, we can prove the results for the central and commutator SES-groups. □

Corollary 1. 

Let $f:S_n\to S_m$ be a group homomorphism, if ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute (central or commutator) SES-group, then ${(f\aleph ,\mathcal{V})}_{f\left(S_n\right)}$ is an absolute (central or commutator) SES-group.

Definition 15. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups. Then $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert symmetric subgroup (SES-subgroup) of $(\aleph ,\mathcal{V})$, if ${\mathcal{V}}^{\prime }\subseteq \mathcal{V}$ and ${\aleph }^{\prime }\left(y\right)$ is a subgroup of $\aleph \left(y\right)$$\forall y\in {\mathcal{V}}^{\prime }$ and it is denoted by $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$.

Example 3. 

Let $S_n=S_3$, as in Example 2. Then ${({\aleph }^{\prime },\mathcal{Z})}_{S_3}$ is a soft expert set (refer to Table 3). Let ${\mathcal{V}}^{\prime }=\{(e_1,e{p}_1,1),(e_1,e{p}_2,1)\}$, then ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_3}$ is an SES-group. From Example 2, ${(\aleph ,\mathcal{V})}_{S_3}$ is an SES-group and for every $(e_i,e{p}_j,1)\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }(e_1,e{p}_1,1)$${\le }_{sg}$$\aleph (e_1,e{p}_1,1)$, ${\aleph }^{\prime }(e_1,e{p}_2,1)$${\le }_{sg}$$\aleph (e_1,e{p}_2,1)$, so we have $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$.

Table 3. Soft expert set.

${\mathit{\aleph }}^{\prime }$	$\left(1\right)$	$\left(12\right)$	$\left(13\right)$	$\left(23\right)$	$\left(123\right)$	$\left(132\right)$
$(e_1,e{p}_1,1)$	1	0	0	0	0	0
$(e_1,e{p}_1,0)$	0	1	1	1	1	1
$(e_1,e{p}_2,1)$	1	0	0	0	1	1
$(e_1,e{p}_2,0)$	0	1	1	1	0	0
$(e_2,e{p}_1,1)$	1	0	0	1	0	0
$(e_2,e{p}_1,0)$	0	1	1	0	1	1
$(e_2,e{p}_2,1)$	1	0	0	0	0	0
$(e_2,e{p}_2,0)$	0	1	1	1	1	1
$(e_3,e{p}_1,1)$	1	1	1	1	1	1
$(e_3,e{p}_1,0)$	0	0	0	0	0	0
$(e_3,e{p}_2,1)$	0	1	1	1	1	1
$(e_3,e{p}_2,0)$	1	0	0	0	0	0

The proof of the Theorem 6 can be achieved from Definition 15.

Theorem 6. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups,

(i)

if $\mathcal{V}={\mathcal{V}}^{\prime }$, $\aleph \left(x\right)\subseteq {\aleph }^{\prime }\left(x\right)$ for all $x\in \mathcal{V}$, then $(\aleph ,\mathcal{V})$${\widetilde{<}}_{SES}$$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$,

(ii)

if $\mathcal{V}\subseteq {\mathcal{V}}^{\prime }$ and $\aleph ={\aleph }^{\prime }$, then $(\aleph ,\mathcal{V})$ is an SES-subgroup of $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$,

(iii)

$(\aleph ,\mathcal{V})$ is an SES-subgroup of $(\aleph ,\mathcal{V})$.

Proof. 

$\left(i\right)$ For any $\beta \in \mathcal{V}$, we have $\aleph \left(\beta \right)$ and ${\aleph }^{\prime }\left(\beta \right)$ as subgroups of $S_n$;

also $\aleph \left(\beta \right)$${\le }_{sg}$${\aleph }^{\prime }\left(\beta \right)$. Hence, $(\aleph ,\mathcal{V})$${\widetilde{<}}_{SES}$$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

$\left(ii\right)$ If $\mathcal{V}\subseteq {\mathcal{V}}^{\prime }$, then for every $\gamma \in \mathcal{V}$, $\aleph \left(\gamma \right)$${\le }_{sg}$${\aleph }^{\prime }\left(\gamma \right)$. Hence, $(\aleph ,\mathcal{V})$${\widetilde{<}}_{SES}$$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

$\left(iii\right)$ The proof is similar to $\left(i\right)$. □

Theorem 7. 

Let $({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$$\tilde{\subset }$$({\aleph }^{″},{\mathcal{V}}^{″})$, then $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$({\aleph }^{″},{\mathcal{V}}^{″})$ iff $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$.

Proof. 

Let $({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$$\tilde{\subset }$$({\aleph }^{″},{\mathcal{V}}^{″})$.

Suppose $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$({\aleph }^{″},{\mathcal{V}}^{″})$, then for every $\beta \in {\mathcal{V}}^{\prime }$,

${\aleph }^{\prime }\left(\beta \right){\le }_{sg}{\aleph }^{″}\left(\beta \right)$⟹${\aleph }^{\prime }\left(\beta \right){\le }_{sg}\aleph \left(\beta \right)$.

Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$.

Conversely, suppose $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V})$, then for every $\beta \in {\mathcal{V}}^{\prime }$,

${\aleph }^{\prime }\left(\beta \right)$ is a subgroup of $\aleph \left(\beta \right)$

⟹${\aleph }^{\prime }\left(\beta \right)\subseteq {\aleph }^{″}\left(\beta \right)$, ${\aleph }^{″}\left(\beta \right){\le }_{sg}\aleph \left(\beta \right)$

⟹${\aleph }^{\prime }\left(\beta \right){\le }_{sg}{\aleph }^{″}\left(\beta \right)$.

Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$({\aleph }^{″},{\mathcal{V}}^{″})$. □

Theorem 8. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an SES-group and ${\left\{({\aleph }_i,{\mathcal{V}}_i)\right\}}_{i\in I}$ be a nonempty family of the SES-subgroup of $(\aleph ,\mathcal{V})$. Then

1. ${{\displaystyle \bigcap _{i\in I}^{˜}}}_R({\aleph }_i,{\mathcal{V}}_i)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$, if ${\displaystyle \bigcap _{i\in I}}{\mathcal{V}}_i\ne \mathsf{\varnothing }$.

2. ${\displaystyle \bigcap _{i\in I_{\epsilon }}^{˜}}({\aleph }_i,{\mathcal{V}}_i)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$.

3. ${\displaystyle \underset{i\in I}{\bigwedge }}({\aleph }_i,{\mathcal{V}}_i)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$,

4. ${\displaystyle \bigcup _{i\in I_{\epsilon }}^{˜}}({\aleph }_i,{\mathcal{V}}_i)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$, whenever ${\mathcal{V}}_i\cap {\mathcal{V}}_j=\mathsf{\varnothing }$, $\forall i,j\in I$.

Proof. 

The proof is similar to that of Theorem 3. □

Definition 16. 

Two SES-groups $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ over $S_n$ are said to be conditionally soft expert symmetric grouped (conditionally SES-grouped) to each other if either ${\aleph }^{\prime }\left(\beta \right)$ is a subgroup of ${\aleph }^{″}\left(\gamma \right)$ or ${\aleph }^{″}\left(\gamma \right)$ is a subgroup of ${\aleph }^{\prime }\left(\beta \right)$, whenever $\beta \in {\mathcal{V}}^{\prime }$ and $\gamma \in {\mathcal{V}}^{″}$.

Theorem 9. 

Let ${({\aleph }^{\prime },{\mathcal{W}}^{\prime })}_{S_n}$ and ${({\aleph }^{″},{\mathcal{W}}^{″})}_{S_n}$ be conditionally SES-grouped to each other.

(i)

If ${\mathcal{W}}^{\prime }\cap {\mathcal{W}}^{″}\ne \mathsf{\varnothing }$, then their restricted union $[({\aleph }^{\prime },{\mathcal{W}}^{\prime })$${\tilde{\cup }}_R$$({\aleph }^{″},{\mathcal{W}}^{″}){]}_{S_n}$ is an SES-group.

(ii)

Their extended union $({\aleph }^{\prime },{\mathcal{W}}^{\prime }){\tilde{\cup }}_{\epsilon }({\aleph }^{″},{\mathcal{V}}^{″})$ is an SES-group in $S_n$.

Proof. 

Let $({\aleph }^{″},{\mathcal{W}}^{″})$ and $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ be two SES-groups over $S_n$.

$\left(i\right)$ Let $({\aleph }^{″},{\mathcal{W}}^{″})$ and $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ be conditionally SES-grouped to each other

⟺ for every $\gamma \in {\mathcal{W}}^{\prime }\cap {\mathcal{W}}^{″}$, either ${\aleph }^{″}\left(\gamma \right)$ is a subgroup of ${\aleph }^{\prime }\left(\gamma \right)$ or ${\aleph }^{\prime }\left(\gamma \right)$ is a subgroup of ${\aleph }^{″}\left(\gamma \right)$

⟺${\aleph }^{\prime }\left(\gamma \right)\cup {\aleph }^{″}\left(\gamma \right)$ is a subgroup of $S_n$

⟺$[({\aleph }^{\prime },{\mathcal{W}}^{\prime })$${\tilde{\cup }}_R$$({\aleph }^{″},{\mathcal{W}}^{″}){]}_{S_n}$ is an SES-group.

$\left(ii\right)$ If ${\mathcal{W}}^{\prime }\cap {\mathcal{W}}^{″}\ne \mathsf{\varnothing }$, then by $\left(i\right)$, $({\aleph }^{\prime },{\mathcal{W}}^{\prime }){\tilde{\cup }}_{\epsilon }({\aleph }^{″},{\mathcal{V}}^{″})$ is an SES-group.

If ${\mathcal{W}}^{\prime }\cap {\mathcal{W}}^{″}=\mathsf{\varnothing }$ then by $\left(iv\right)$ in Theorem 3, $({\aleph }^{\prime },{\mathcal{W}}^{\prime }){\tilde{\cup }}_{\epsilon }({\aleph }^{″},{\mathcal{V}}^{″})$ is an SES-group. □

The following theorem shows that the basic union of two conditionally SES-groups is again an SES-group.

Theorem 10. 

Let $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ and $({\aleph }^{″},{\mathcal{W}}^{″})$ be two SES-groups over $S_n$, then $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ and $({\aleph }^{″},{\mathcal{W}}^{″})$ are conditionally SES-grouped to each other if and only if $({\aleph }^{\prime },{\mathcal{W}}^{\prime })\vee ({\aleph }^{″},{\mathcal{W}}^{″})$ is an SES-group over $S_n$.

Proof. 

Let $({\aleph }^{″},{\mathcal{W}}^{″})$ and $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ be two SES-groups over $S_n$.

Then $({\aleph }^{″},{\mathcal{W}}^{″})$ and $({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ are conditionally SES-grouped to each other

⟺ for every $\beta \in {\mathcal{W}}^{\prime }$ and $\gamma \in {\mathcal{W}}^{″}$ either ${\aleph }^{″}\left(\gamma \right){\le }_{sg}{\aleph }^{\prime }\left(\beta \right)$ or ${\aleph }^{\prime }\left(\beta \right){\le }_{sg}{\aleph }^{″}\left(\gamma \right)$

⟺${\aleph }^{\prime }\left(\beta \right)\cup {\aleph }^{″}\left(\gamma \right)$ is a subgroup of $S_n$

⟺$({\aleph }^{″},{\mathcal{W}}^{″})\vee ({\aleph }^{\prime },{\mathcal{W}}^{\prime })$ is an SES-group over $S_n$. □

Corollary 2. 

Let ${\left\{({\aleph }_i,{\mathcal{V}}_i)\right\}}_{i\in I}$ be a nonempty family of SES-groups over $S_n$. Then ${\displaystyle \underset{i\in I}{\bigvee }}({\aleph }_i,{\mathcal{V}}_i)$ is an SES-group of $S_n$ if and only if for every $i,j\in I$, $({\aleph }_i,{\mathcal{V}}_i)$, and $({\aleph }_j,{\mathcal{V}}_j)$ are conditionally SES-grouped to each other.

Theorem 11. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$, ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ and ${({\aleph }^{″},{\mathcal{V}}^{″})}_{S_m}$ be SES-groups.

(i)

if ${(\aleph ,\mathcal{V})}_{S_n}$ is an identity SES-group, then $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other,

(ii)

if ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute SES-group, then $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other,

(iii)

if $\aleph \left(a\right)\subseteq Kerf$$\forall a\in \mathcal{V}$, then $(f\aleph ,\mathcal{V})$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ are conditionally SES-grouped to each other,

(iv)

if ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute SES-group, then $(f\aleph ,\mathcal{V})$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ are conditionally SES-grouped to each other.

Proof. 

Let $(\aleph ,\mathcal{V})$, $\left({\aleph }^{\prime }and{\mathcal{V}}^{\prime }\right)$ be SES-groups over $S_n$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ be an SES-group over $S_m$.

$\left(i\right)$ Since $(\aleph ,\mathcal{V})$ is an identity SES-group, for every $a\in \mathcal{V}$ and $a^{\prime }\in {\mathcal{V}}^{\prime }$,

$\aleph \left(a\right)=\left\{e\right\}$ is a subgroup of ${\aleph }^{\prime }\left(a^{\prime }\right)$.

Hence, $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other.

$\left(ii\right)$ Since $(\aleph ,\mathcal{V})$ is an absolute SES-group,

for every $a\in \mathcal{V}$ and $a^{\prime }\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(a^{\prime }\right){\le }_{sg}{\aleph }^{\prime }\left(a^{\prime }\right)=S_n$.

Hence, $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other.

$\left(iii\right)$ Let $\aleph \left(a\right)\subseteq kerf$, then by $\left(i\right)$ in Theorem 5, ${(f\aleph ,\mathcal{V})}_{S_m}$ is an identity SES-group; also by $(f\aleph ,\mathcal{V})$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ are conditionally SES-grouped to each other.

$\left(iv\right)$ Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an absolute SES-group, then by $\left(ii\right)$ in Theorem 5${(f\aleph ,\mathcal{V})}_{S_m}$ is an absolute also by $\left(ii\right)$, $(f\aleph ,\mathcal{V})$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ are conditionally SES-grouped to each other. □

Theorem 12. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups, if

(i)

$(\aleph ,\mathcal{V})$ is an SES-subgroup of $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, then $(f\aleph ,\mathcal{V})$ is an SES-subgroup of $(f{\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

(ii)

$(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other, then $(f\aleph ,\mathcal{V})$ and $(f{\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other.

Proof. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups.

$\left(i\right)$ By Theorem 4, ${(f\aleph ,\mathcal{V})}_{S_m}$ and ${(f{\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ are both SES-groups.

Additionally, $f\left({\aleph }^{\prime }\left(a\right)\right){\le }_{sg}f(\aleph \left(a\right))$, $\forall a\in {\mathcal{V}}^{\prime }$. Hence, $(f{\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{<}}_{SES}$$(f\aleph ,\mathcal{V})$.

$\left(ii\right)$ Let $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be conditionally SES-grouped to each other,

⟺ for every $\beta \in \mathcal{V}$ and $\gamma \in {\mathcal{V}}^{\prime }$ either ${\aleph }^{\prime }\left(\gamma \right){\le }_{sg}\aleph \left(\beta \right)$ or $\aleph \left(\beta \right){\le }_{sg}{\aleph }^{\prime }\left(\gamma \right)$.

If ${\aleph }^{\prime }\left(\gamma \right){\le }_{sg}\aleph \left(\beta \right)$⟺$\left(f{\aleph }^{\prime }\right)\left(\gamma \right)=f\left({\aleph }^{\prime }\left(\gamma \right)\right){\le }_{sg}f(\aleph \left(\beta \right))=(f\aleph )\left(\beta \right)$.

If $\aleph \left(\beta \right){\le }_{sg}{\aleph }^{\prime }\left(\gamma \right)$⟺$(f\aleph )\left(\beta \right)=f(\aleph \left(\beta \right)){\le }_{sg}f\left({\aleph }^{\prime }\left(\gamma \right)\right)=\left(f{\aleph }^{\prime }\right)\left(\gamma \right)$.

$(f\aleph ,\mathcal{V})$ and $(f{\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are conditionally SES-grouped to each other. □

Definition 17. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an SES-group, then

(i)

$(\aleph ,\mathcal{V})$ is said to be normal SES-group, if $\aleph \left(x\right){⊴}_{sg}{S}_n$, $\forall x\in \mathcal{V}$,

(ii)

an SES-subgroup $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ of $(\aleph ,\mathcal{V})$ is said to be a normal soft expert symmetric subgroup (normal SES-subgroup) of $(\aleph ,\mathcal{V})$ if ${\aleph }^{\prime }\left(y\right){⊴}_{sg}\aleph \left(y\right)$, $\forall y\in {\mathcal{V}}^{\prime }$ and it is denoted by $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$,

(iii)

an SES-subgroup $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ of $(\aleph ,\mathcal{V})$ is said to be an identity soft expert symmetric subgroup (identity SES-subgroup) of $(\aleph ,\mathcal{V})$ if ${\aleph }^{\prime }\left(y\right)=\left\{e\right\}$$\forall y\in {\mathcal{V}}^{\prime }$,

(iv)

an SES-subgroup $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ of $(\aleph ,\mathcal{V})$ is said to be an absolute soft expert symmetric subgroup (absolute SES-subgroup) of $(\aleph ,\mathcal{V})$, if ${\aleph }^{\prime }\left(y\right)=S_n$$\forall y\in {\mathcal{V}}^{\prime }$,

(v)

an SES-subgroup $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ of $(\aleph ,\mathcal{V})$ is said to be central soft expert symmetric subgroup (central SES-subgroup) of $(\aleph ,\mathcal{V})$ if ${\aleph }^{\prime }\left(y\right)=Z\left(S_n\right)$$\forall y\in {\mathcal{V}}^{\prime }$,

(vi)

an SES-subgroup $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ of $(\aleph ,\mathcal{V})$ is said to be a commutator soft expert symmetric subgroup (commutator SES-subgroup) of $(\aleph ,\mathcal{V})$ if ${\aleph }^{\prime }\left(y\right)$ is a commutator subgroup of $\aleph \left(y\right)$$\forall y\in {\mathcal{V}}^{\prime }$.

Theorem 13. 

Let $(\aleph ,\mathcal{V})$, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ be SES-sets.

(i)

If $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-subset of $({\aleph }^{″},{\mathcal{V}}^{″})$, $({\aleph }^{″},{\mathcal{V}}^{″})$ is an SES-subgroup of $(\aleph ,\mathcal{V})$, and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is normal SES-subgroup of $(\aleph ,\mathcal{V})$, then $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is normal SES-subgroup of $({\aleph }^{″},{\mathcal{V}}^{″})$.

(ii)

If $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-subgroup of $({\aleph }^{″},{\mathcal{V}}^{″})$, $({\aleph }^{″},{\mathcal{V}}^{″})$ is normal SES-subgroup of $(\aleph ,\mathcal{V})$, then $({\aleph }^{\prime },{\mathcal{V}}^{\prime })\wedge ({\aleph }^{″},{\mathcal{V}}^{″})$ is normal SES-subgroup of $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

(iii)

If ${(\aleph ,\mathcal{V})}_{S_n}$ is an SES-group and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an identity (absolute or central or commutator) SES-subgroup of $(\aleph ,\mathcal{V})$, then $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is normal SES-subgroup of $(\aleph ,\mathcal{V})$.

Proof. 

Let $(\aleph ,\mathcal{V})$, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ be three SES-sets.

$\left(i\right)$ For every $\beta \in {\mathcal{V}}^{\prime }$, by hypothesis ${\aleph }^{\prime }\left(\beta \right)\subseteq {\aleph }^{″}\left(\beta \right)$, ${\aleph }^{″}\left(\beta \right)$${\le }_{sg}$$\aleph \left(\beta \right)$ and ${\aleph }^{\prime }\left(\beta \right){⊴}_{sg}\aleph \left(\beta \right)$,

⟹${\aleph }^{\prime }\left(\beta \right){⊴}_{sg}{\aleph }^{″}\left(\beta \right)$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a normal SES-subgroup in $({\aleph }^{″},{\mathcal{V}}^{″})$.

$\left(ii\right)$ For every $(\alpha ,\beta )\in {\mathcal{V}}_1\times {\mathcal{V}}_2$, by hypothesis we have

${\aleph }^{\prime }\left(\alpha \right){\le }_{sg}{\aleph }^{″}\left(\alpha \right)$, ${\aleph }^{″}\left(\beta \right){⊴}_{sg}\aleph \left(\beta \right)$,

⟹${\aleph }^{\prime }\left(\alpha \right)\cap {\aleph }^{″}\left(\beta \right){⊴}_{sg}{\aleph }^{\prime }\left(\alpha \right)$.

Hence, $({\aleph }^{\prime },{\mathcal{V}}_1)\wedge ({\aleph }^{″},{\mathcal{V}}_2)$ is a normal SES-subgroup of $({\aleph }^{\prime },{\mathcal{V}}_1)$.

$\left(iii\right)$ For every $y\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(y\right)=\left\{e\right\}$ ($S_n$ or $Z\left(S_n\right)$ or commutator subgroup of $\aleph \left(y\right)$) ${⊴}_{sg}{S}_n$ and so to $\aleph \left(y\right)$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$. □

Theorem 14. 

Let H be an abelian subgroup of $S_n$ with $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-subgroup of $(\aleph ,\mathcal{V})$ over H, then

(i)

$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a central SES-subgroup of $(\aleph ,\mathcal{V})$ if and only if $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an absolute SES-subgroup of $(\aleph ,\mathcal{V})$,

(ii)

$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is normal SES-subgroup of $(\aleph ,\mathcal{V})$,

(iii)

$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a commutator SES-subgroup of $(\aleph ,\mathcal{V})$ if and only if $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an identity SES-subgroup of $(\aleph ,\mathcal{V})$.

Proof. 

Let H be an abelian subgroup of $S_n$ with ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_H$${\widetilde{<}}_{SES}$${(\aleph ,\mathcal{V})}_H$.

$\left(i\right)$ Suppose $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a central SES-subgroup of $(\aleph ,\mathcal{V})$,

then for every $y\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(y\right)=Z\left(H\right)=H$.

Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an absolute SES-subgroup of $(\aleph ,\mathcal{V})$. In a similar way, the converse is also true.

$\left(ii\right)$ For every $y\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(y\right)$${⊴}_{sg}$H and so it is a normal subgroup of $\aleph \left(y\right)$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$.

$\left(iii\right)$ Let $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be a commutator SES-subgroup of $(\aleph ,\mathcal{V})$, then for every $y\in {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(y\right)$ is a commutator subgroup of $\aleph \left(y\right)$. Since H is an abelian, ${\aleph }^{\prime }\left(y\right)=\left\{e\right\}$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an identity SES-subgroup of $(\aleph ,\mathcal{V})$. In a similar way, the converse is also true. □

Theorem 15. 

Let ${\left\{{({\aleph }_i,{\mathcal{V}}_i)}_{S_n}\right\}}_{i\in I}$ be a family of normal SES-groups. Then

(i)

${\left[{\displaystyle \bigcap _{i\in I_R}^{˜}}({\aleph }_i,{\mathcal{V}}_i)\right]}_{S_n}$ is a normal SES-group, if ${\displaystyle \bigcap _{i\in I}}{\mathcal{V}}_i\ne \mathsf{\varnothing }$,

(ii)

${\left[{\displaystyle \underset{i\in I}{\bigwedge }}({\aleph }_i,{\mathcal{V}}_i)\right]}_{S_n}$ is a normal SES-group,

(iii)

${\left[{\displaystyle \bigcup _{i\in I_{\epsilon }}^{˜}}({\aleph }_i,{\mathcal{V}}_i)\right]}_{S_n}$ is a normal SES-group, whenever ${\mathcal{V}}_i\cap {\mathcal{V}}_j=\mathsf{\varnothing }$, $\forall i,j\in I$,

(iv)

${\left[{\displaystyle \underset{i\in I}{\bigvee }}({\aleph }_i,{\mathcal{V}}_i)\right]}_{S_n}$ is a normal SES-group iff for every $i,j\in I$, $({\aleph }_i,{\mathcal{V}}_i)$ and $({\aleph }_j,{\mathcal{V}}_j)$ are conditionally SES-grouped to each other.

Proof. 

Proof is similar to proof of Theorems 8 and 10. □

Theorem 16. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ be an SES-group and ${\left\{({\aleph }_i,{\mathcal{V}}_i)\right\}}_{i\in I}$ be a nonempty family of normal SES-subgroup of $(\aleph ,\mathcal{V})$. Then 1. ${\displaystyle \bigcap _{i\in I_R}^{˜}}({\aleph }_i,{\mathcal{V}}_i)$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})$, if ${\displaystyle \bigcap _{i\in I}}{\mathcal{V}}_i\ne \mathsf{\varnothing }$,

2. ${\displaystyle \underset{i\in I}{\bigwedge }}({\aleph }_i,{\mathcal{V}}_i)$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})$,

3.${\displaystyle \bigcup _{i\in I_{\epsilon }}^{˜}}({\aleph }_i,{\mathcal{V}}_i)$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})$, whenever ${\mathcal{V}}_i\cap {\mathcal{V}}_j=\mathsf{\varnothing }$, $\forall i,j\in I$,

4. ${\displaystyle \underset{i\in I}{\bigvee }}({\aleph }_i,{\mathcal{V}}_i)$ is normal SES-group of $S_n$ if and only if for every $i,j\in I$, $({\aleph }_i,{\mathcal{V}}_i)$ and $({\aleph }_j,{\mathcal{V}}_j)$ are conditionally SES-grouped to each other.

Proof. 

The proof is similar to proof of Theorems 8 and 10. □

Theorem 17. 

Let ${(\aleph ,\mathcal{V})}_U$ be an SES-group with $\aleph \left(x_1\right)=\aleph \left(x_2\right)$ for some $x_1,x_2\in \mathcal{V}$, $x_1\ne x_2$. We define a restriction of SES-group ℵ to ${\mathcal{V}}^R$, $(\aleph ,{\mathcal{V}}^R)=\{(x,\aleph \left(x\right))\in (\aleph ,\mathcal{V}),x\in {\mathcal{V}}^R\}$, with the idea of distinct parameter in $\mathcal{V}$ has different images and ${\mathcal{V}}^R$ being a maximal subset of $\mathcal{V}$ such that for every $x_1,y_1\in {\mathcal{V}}^R$, $\aleph \left(x_1\right)\ne \aleph \left(y_1\right)$. Then $(\aleph ,{\mathcal{V}}^R)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$.

5. Product of Soft Expert Symmetric Group

For a given two SES-groups, we define their internal and external products as follows.

Definition 18. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },\mathcal{W})}_{S_m}$ be two SES-groups.

(i)

The internal product of two SES-groups ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },\mathcal{W})}_{S_n}$ is defined by $(\aleph ,\mathcal{V})({\aleph }^{\prime },\mathcal{W})=({\aleph }^{″},\mathcal{V}\times \mathcal{W})$, where ${\aleph }^{″}(\beta ,\gamma )=\aleph \left(\beta \right){\aleph }^{\prime }\left(\gamma \right)$, $\forall (\beta ,\gamma )\in \mathcal{V}\times \mathcal{W}$.

(ii)

Then the external product of SES-groups of $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },\mathcal{W})$ is an SES-group over $S_n\times S_m$, defined by $(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },\mathcal{W})=({\aleph }^{″},\mathcal{V}\times \mathcal{W})$, where ${\aleph }^{″}(\beta ,\gamma )=\aleph \left(\beta \right)\times {\aleph }^{\prime }\left(\gamma \right)$, $\forall (\beta ,\gamma )\in \mathcal{V}\times \mathcal{W}$.

Theorem 18. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ be two SES-groups,

(i)

if $({\aleph }_1,{\mathcal{V}}_1)$ and $({\aleph }_1^{\prime },{\mathcal{V}}_1^{\prime })$ are two SES-subgroups of $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, respectively, then the external product $({\aleph }_1,{\mathcal{V}}_1)\times ({\aleph }_1^{\prime },{\mathcal{V}}_1^{\prime })$ is an SES-subgroup of $(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

(ii)

if both ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ are identity SES-groups over $S_n$ and $S_m$, respectively, then ${[(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n\times S_m}$ is an identity SES-group,

(iii)

if both ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ are absolute SES-groups, then ${[(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n\times S_m}$ is an absolute SES-group.

Proof. 

$\left(i\right)$ For every $(\beta ,\gamma )\in {\mathcal{V}}_1\times {\mathcal{V}}_1^{\prime }$, ${\aleph }_1\left(\beta \right){\le }_{sg}\aleph \left(\beta \right)$ and ${\aleph }_1^{\prime }\left(\gamma \right){\le }_{sg}{\aleph }^{\prime }\left(\gamma \right)$

⟹ so ${\aleph }_1\left(\beta \right)\times {\aleph }_1^{\prime }\left(\gamma \right){\le }_{sg}\aleph \left(\beta \right)\times {\aleph }^{\prime }\left(\gamma \right)$.

Hence, $({\aleph }_1,{\mathcal{V}}_1)\times ({\aleph }_1^{\prime },{\mathcal{V}}_1^{\prime })$ is an SES-subgroup of $(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

$\left(ii\right)$ Let $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be identity SES-groups over $S_n$ and $S_m$, respectively,

for every $(\beta ,{\beta }^{\prime })\in \mathcal{V}\times {\mathcal{V}}^{\prime }$, $\aleph \left(\beta \right)=\left\{e\right\}$ and ${\aleph }^{\prime }\left({\beta }^{\prime }\right)=\left\{e^{\prime }\right\}$

⟹$\aleph \left(\beta \right)\times {\aleph }^{\prime }\left({\beta }^{\prime }\right)=\left\{(e,e^{\prime })\right\}$.

Hence, ${[(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })]}_{S_n\times S_m}$ is an identity SES-group.

$\left(iii\right)$ The proof is similar to $\left(ii\right)$. □

Note that the internal product of two SES-groups in $S_n$ is not an SES-group in $S_n$. We justify this by means of Example 4.

Example 4. 

Let $S_4$ be a symmetric group on $U=\{{\iota }_1,{\iota }_2,{\iota }_3,{\iota }_4\}$, parameter $E=\{e_1,e_2,e_3\}$, experts $X=\{e{p}_1,e{p}_2,e{p}_3\}$, opinions $O=\{0,1\}$ with $\mathcal{Z}=\{(e_i,e{p}_j,o)/1\le i\le 3,1\le j\le 3,o\in O\}$.

For convenience, let ${\alpha }_1=e$, ${\alpha }_2=\left({\iota }_1{\iota }_2\right)$, ${\alpha }_3=\left({\iota }_1{\iota }_3\right)$, ${\alpha }_4=\left({\iota }_1{\iota }_4\right)$, ${\alpha }_5=\left({\iota }_2{\iota }_3\right)$, ${\alpha }_6=\left({\iota }_2{\iota }_4\right)$, ${\alpha }_7=\left({\iota }_3{\iota }_4\right)$, ${\alpha }_8=\left({\iota }_1{\iota }_2{\iota }_3\right)$, ${\alpha }_9=\left({\iota }_1{\iota }_2{\iota }_4\right)$, ${\alpha }_{10}=\left({\iota }_1{\iota }_3{\iota }_4\right)$, ${\alpha }_{11}=\left({\iota }_2{\iota }_3{\iota }_4\right)$, ${\alpha }_{12}=\left({\iota }_1{\iota }_3{\iota }_2\right)$, ${\alpha }_{13}=\left({\iota }_1{\iota }_4{\iota }_2\right)$, ${\alpha }_{14}=\left({\iota }_1{\iota }_4{\iota }_3\right)$, ${\alpha }_{15}=\left({\iota }_2{\iota }_4{\iota }_3\right)$, ${\alpha }_{16}=\left({\iota }_1{\iota }_2\right)\left({\iota }_3{\iota }_4\right)$, ${\alpha }_{17}=\left({\iota }_1{\iota }_3\right)\left({\iota }_2{\iota }_4\right)$, ${\alpha }_{18}=\left({\iota }_1{\iota }_4\right)\left({\iota }_2{\iota }_3\right)$, ${\alpha }_{19}=\left({\iota }_1{\iota }_2{\iota }_3{\iota }_4\right)$, ${\alpha }_{20}=\left({\iota }_1{\iota }_2{\iota }_4{\iota }_3\right)$, ${\alpha }_{21}=\left({\iota }_1{\iota }_3{\iota }_4{\iota }_2\right)$, ${\alpha }_{22}=\left({\iota }_1{\iota }_3{\iota }_2{\iota }_4\right)$, ${\alpha }_{23}=\left({\iota }_1{\iota }_4{\iota }_3{\iota }_2\right)$, ${\alpha }_{24}=\left({\iota }_1{\iota }_4{\iota }_2{\iota }_3\right)$.

The tabular representation of symmetric group is given in Table 4.

Table 4. Tabular representation of symmetric group $S_4$.

$S_4$

${\alpha }_1$

${\alpha }_2$

${\alpha }_3$

${\alpha }_4$

${\alpha }_5$

${\alpha }_6$

${\alpha }_7$

${\alpha }_8$

${\alpha }_9$

${\alpha }_{10}$

${\alpha }_{11}$

${\alpha }_{12}$

${\alpha }_{13}$

${\alpha }_{14}$

${\alpha }_{15}$

${\alpha }_{16}$

${\alpha }_{17}$

${\alpha }_{18}$

${\alpha }_{19}$

${\alpha }_{20}$

${\alpha }_{21}$

${\alpha }_{22}$

${\alpha }_{23}$

${\alpha }_{24}$

${\alpha }_1$

${\alpha }_1$

${\alpha }_2$

${\alpha }_3$

${\alpha }_4$

${\alpha }_5$

${\alpha }_6$

${\alpha }_7$

${\alpha }_8$

${\alpha }_9$

${\alpha }_{10}$

${\alpha }_{11}$

${\alpha }_{12}$

${\alpha }_{13}$

${\alpha }_{14}$

${\alpha }_{15}$

${\alpha }_{16}$

${\alpha }_{17}$

${\alpha }_{18}$

${\alpha }_{19}$

${\alpha }_{20}$

${\alpha }_{21}$

${\alpha }_{22}$

${\alpha }_{23}$

${\alpha }_{24}$

${\alpha }_2$

${\alpha }_2$

${\alpha }_1$

${\alpha }_8$

${\alpha }_9$

${\alpha }_{12}$

${\alpha }_{13}$

${\alpha }_{16}$

${\alpha }_3$

${\alpha }_4$

${\alpha }_{19}$

${\alpha }_{21}$

${\alpha }_5$

${\alpha }_6$

${\alpha }_{20}$

${\alpha }_{23}$

${\alpha }_7$

${\alpha }_{24}$

${\alpha }_{22}$

${\alpha }_{10}$

${\alpha }_{14}$

${\alpha }_{11}$

${\alpha }_{18}$

${\alpha }_{15}$

${\alpha }_{17}$

${\alpha }_3$

${\alpha }_3$

${\alpha }_{12}$

${\alpha }_1$

${\alpha }_{10}$

${\alpha }_8$

${\alpha }_{17}$

${\alpha }_{14}$

${\alpha }_5$

${\alpha }_{22}$

${\alpha }_4$

${\alpha }_{24}$

${\alpha }_2$

${\alpha }_{21}$

${\alpha }_7$

${\alpha }_{20}$

${\alpha }_{23}$

${\alpha }_6$

${\alpha }_{19}$

${\alpha }_{18}$

${\alpha }_{15}$

${\alpha }_{13}$

${\alpha }_9$

${\alpha }_{16}$

${\alpha }_{11}$

${\alpha }_4$

${\alpha }_4$

${\alpha }_{13}$

${\alpha }_{14}$

${\alpha }_1$

${\alpha }_{18}$

${\alpha }_9$

${\alpha }_{10}$

${\alpha }_{24}$

${\alpha }_6$

${\alpha }_7$

${\alpha }_{19}$

${\alpha }_{23}$

${\alpha }_2$

${\alpha }_3$

${\alpha }_{22}$

${\alpha }_{21}$

${\alpha }_{20}$

${\alpha }_5$

${\alpha }_{11}$

${\alpha }_{17}$

${\alpha }_{16}$

${\alpha }_{15}$

${\alpha }_{12}$

${\alpha }_8$

${\alpha }_5$

${\alpha }_5$

${\alpha }_8$

${\alpha }_{12}$

${\alpha }_{18}$

${\alpha }_1$

${\alpha }_{11}$

${\alpha }_{15}$

${\alpha }_2$

${\alpha }_{19}$

${\alpha }_{22}$

${\alpha }_6$

${\alpha }_3$

${\alpha }_{24}$

${\alpha }_{23}$

${\alpha }_7$

${\alpha }_{20}$

${\alpha }_{21}$

${\alpha }_4$

${\alpha }_9$

${\alpha }_{16}$

${\alpha }_{17}$

${\alpha }_{10}$

${\alpha }_{14}$

${\alpha }_{13}$

${\alpha }_6$

${\alpha }_6$

${\alpha }_9$

${\alpha }_{17}$

${\alpha }_{13}$

${\alpha }_{15}$

${\alpha }_1$

${\alpha }_{11}$

${\alpha }_{20}$

${\alpha }_2$

${\alpha }_{21}$

${\alpha }_7$

${\alpha }_{22}$

${\alpha }_4$

${\alpha }_{24}$

${\alpha }_5$

${\alpha }_{19}$

${\alpha }_3$

${\alpha }_{23}$

${\alpha }_{16}$

${\alpha }_8$

${\alpha }_{10}$

${\alpha }_{12}$

${\alpha }_{18}$

${\alpha }_{14}$

${\alpha }_7$

${\alpha }_7$

${\alpha }_{16}$

${\alpha }_{10}$

${\alpha }_{14}$

${\alpha }_{11}$

${\alpha }_{15}$

${\alpha }_1$

${\alpha }_{19}$

${\alpha }_{20}$

${\alpha }_3$

${\alpha }_5$

${\alpha }_{21}$

${\alpha }_{23}$

${\alpha }_4$

${\alpha }_6$

${\alpha }_2$

${\alpha }_{22}$

${\alpha }_{24}$

${\alpha }_8$

${\alpha }_9$

${\alpha }_{12}$

${\alpha }_{17}$

${\alpha }_{13}$

${\alpha }_{18}$

${\alpha }_8$

${\alpha }_8$

${\alpha }_5$

${\alpha }_2$

${\alpha }_{19}$

${\alpha }_3$

${\alpha }_{24}$

${\alpha }_{20}$

${\alpha }_{12}$

${\alpha }_{18}$

${\alpha }_9$

${\alpha }_{17}$

${\alpha }_1$

${\alpha }_{11}$

${\alpha }_{16}$

${\alpha }_{14}$

${\alpha }_{15}$

${\alpha }_{13}$

${\alpha }_{10}$

${\alpha }_{22}$

${\alpha }_{23}$

${\alpha }_6$

${\alpha }_4$

${\alpha }_7$

${\alpha }_{21}$

${\alpha }_9$

${\alpha }_9$

${\alpha }_6$

${\alpha }_{20}$

${\alpha }_2$

${\alpha }_{22}$

${\alpha }_4$

${\alpha }_{19}$

${\alpha }_{17}$

${\alpha }_{13}$

${\alpha }_{16}$

${\alpha }_{10}$

${\alpha }_{15}$

${\alpha }_1$

${\alpha }_8$

${\alpha }_{18}$

${\alpha }_{11}$

${\alpha }_{14}$

${\alpha }_{12}$

${\alpha }_{21}$

${\alpha }_{24}$

${\alpha }_7$

${\alpha }_{23}$

${\alpha }_5$

${\alpha }_3$

${\alpha }_{10}$

${\alpha }_{10}$

${\alpha }_{21}$

${\alpha }_7$

${\alpha }_3$

${\alpha }_{19}$

${\alpha }_{22}$

${\alpha }_4$

${\alpha }_{11}$

${\alpha }_{17}$

${\alpha }_{14}$

${\alpha }_{18}$

${\alpha }_{16}$

${\alpha }_{12}$

${\alpha }_1$

${\alpha }_9$

${\alpha }_{13}$

${\alpha }_{15}$

${\alpha }_8$

${\alpha }_{24}$

${\alpha }_6$

${\alpha }_{23}$

${\alpha }_{20}$

${\alpha }_2$

${\alpha }_5$

${\alpha }_{11}$

${\alpha }_{11}$

${\alpha }_{19}$

${\alpha }_{21}$

${\alpha }_{24}$

${\alpha }_7$

${\alpha }_5$

${\alpha }_6$

${\alpha }_{16}$

${\alpha }_8$

${\alpha }_{17}$

${\alpha }_{15}$

${\alpha }_{10}$

${\alpha }_{18}$

${\alpha }_{13}$

${\alpha }_1$

${\alpha }_9$

${\alpha }_{12}$

${\alpha }_{14}$

${\alpha }_{20}$

${\alpha }_2$

${\alpha }_{22}$

${\alpha }_3$

${\alpha }_4$

${\alpha }_{23}$

${\alpha }_{12}$

${\alpha }_{12}$

${\alpha }_3$

${\alpha }_5$

${\alpha }_{22}$

${\alpha }_2$

${\alpha }_{21}$

${\alpha }_{23}$

${\alpha }_1$

${\alpha }_{10}$

${\alpha }_{18}$

${\alpha }_{13}$

${\alpha }_8$

${\alpha }_{17}$

${\alpha }_{15}$

${\alpha }_{16}$

${\alpha }_{14}$

${\alpha }_{11}$

${\alpha }_9$

${\alpha }_4$

${\alpha }_7$

${\alpha }_{24}$

${\alpha }_{19}$

${\alpha }_{20}$

${\alpha }_6$

${\alpha }_{13}$

${\alpha }_{13}$

${\alpha }_4$

${\alpha }_{24}$

${\alpha }_6$

${\alpha }_{23}$

${\alpha }_2$

${\alpha }_{21}$

${\alpha }_{14}$

${\alpha }_1$

${\alpha }_{11}$

${\alpha }_{16}$

${\alpha }_{18}$

${\alpha }_9$

${\alpha }_{17}$

${\alpha }_{12}$

${\alpha }_{10}$

${\alpha }_8$

${\alpha }_{15}$

${\alpha }_7$

${\alpha }_3$

${\alpha }_{19}$

${\alpha }_5$

${\alpha }_{22}$

${\alpha }_{20}$

${\alpha }_{14}$

${\alpha }_{14}$

${\alpha }_{23}$

${\alpha }_4$

${\alpha }_7$

${\alpha }_{24}$

${\alpha }_{20}$

${\alpha }_3$

${\alpha }_{18}$

${\alpha }_{15}$

${\alpha }_1$

${\alpha }_8$

${\alpha }_{13}$

${\alpha }_{16}$

${\alpha }_{10}$

${\alpha }_{17}$

${\alpha }_{12}$

${\alpha }_9$

${\alpha }_{11}$

${\alpha }_5$

${\alpha }_{22}$

${\alpha }_2$

${\alpha }_6$

${\alpha }_{21}$

${\alpha }_{19}$

${\alpha }_{15}$

${\alpha }_{15}$

${\alpha }_{20}$

${\alpha }_{22}$

${\alpha }_{23}$

${\alpha }_6$

${\alpha }_7$

${\alpha }_5$

${\alpha }_9$

${\alpha }_{16}$

${\alpha }_{12}$

${\alpha }_1$

${\alpha }_{17}$

${\alpha }_{14}$

${\alpha }_{18}$

${\alpha }_{11}$

${\alpha }_8$

${\alpha }_{10}$

${\alpha }_{13}$

${\alpha }_2$

${\alpha }_{19}$

${\alpha }_3$

${\alpha }_{21}$

${\alpha }_{24}$

${\alpha }_4$

${\alpha }_{16}$

${\alpha }_{16}$

${\alpha }_7$

${\alpha }_{19}$

${\alpha }_{20}$

${\alpha }_{21}$

${\alpha }_{23}$

${\alpha }_2$

${\alpha }_{10}$

${\alpha }_{14}$

${\alpha }_8$

${\alpha }_{12}$

${\alpha }_{11}$

${\alpha }_{15}$

${\alpha }_9$

${\alpha }_{13}$

${\alpha }_1$

${\alpha }_{18}$

${\alpha }_{17}$

${\alpha }_3$

${\alpha }_4$

${\alpha }_5$

${\alpha }_{24}$

${\alpha }_6$

${\alpha }_{22}$

${\alpha }_{17}$

${\alpha }_{17}$

${\alpha }_{22}$

${\alpha }_6$

${\alpha }_{21}$

${\alpha }_{20}$

${\alpha }_3$

${\alpha }_{24}$

${\alpha }_{15}$

${\alpha }_{12}$

${\alpha }_{13}$

${\alpha }_{14}$

${\alpha }_9$

${\alpha }_{10}$

${\alpha }_{11}$

${\alpha }_8$

${\alpha }_{18}$

${\alpha }_1$

${\alpha }_{16}$

${\alpha }_{23}$

${\alpha }_5$

${\alpha }_4$

${\alpha }_2$

${\alpha }_{19}$

${\alpha }_7$

${\alpha }_{18}$

${\alpha }_{18}$

${\alpha }_{24}$

${\alpha }_{23}$

${\alpha }_5$

${\alpha }_4$

${\alpha }_{19}$

${\alpha }_{22}$

${\alpha }_{13}$

${\alpha }_{11}$

${\alpha }_{15}$

${\alpha }_9$

${\alpha }_{14}$

${\alpha }_8$

${\alpha }_{12}$

${\alpha }_{10}$

${\alpha }_{17}$

${\alpha }_{16}$

${\alpha }_1$

${\alpha }_6$

${\alpha }_{21}$

${\alpha }_{20}$

${\alpha }_7$

${\alpha }_3$

${\alpha }_2$

${\alpha }_{19}$

${\alpha }_{19}$

${\alpha }_{11}$

${\alpha }_{16}$

${\alpha }_8$

${\alpha }_{10}$

${\alpha }_{18}$

${\alpha }_9$

${\alpha }_{21}$

${\alpha }_{24}$

${\alpha }_{20}$

${\alpha }_{22}$

${\alpha }_7$

${\alpha }_5$

${\alpha }_2$

${\alpha }_4$

${\alpha }_6$

${\alpha }_{23}$

${\alpha }_3$

${\alpha }_{17}$

${\alpha }_{13}$

${\alpha }_{15}$

${\alpha }_{14}$

${\alpha }_1$

${\alpha }_{12}$

${\alpha }_{20}$

${\alpha }_{20}$

${\alpha }_{15}$

${\alpha }_9$

${\alpha }_{16}$

${\alpha }_{17}$

${\alpha }_{14}$

${\alpha }_8$

${\alpha }_{22}$

${\alpha }_{23}$

${\alpha }_2$

${\alpha }_3$

${\alpha }_6$

${\alpha }_7$

${\alpha }_{19}$

${\alpha }_{24}$

${\alpha }_5$

${\alpha }_4$

${\alpha }_{21}$

${\alpha }_{12}$

${\alpha }_{18}$

${\alpha }_1$

${\alpha }_{13}$

${\alpha }_{11}$

${\alpha }_{10}$

${\alpha }_{21}$

${\alpha }_{21}$

${\alpha }_{10}$

${\alpha }_{11}$

${\alpha }_{17}$

${\alpha }_{16}$

${\alpha }_{12}$

${\alpha }_{13}$

${\alpha }_7$

${\alpha }_3$

${\alpha }_{24}$

${\alpha }_{23}$

${\alpha }_{19}$

${\alpha }_{22}$

${\alpha }_6$

${\alpha }_2$

${\alpha }_4$

${\alpha }_5$

${\alpha }_{20}$

${\alpha }_{14}$

${\alpha }_1$

${\alpha }_{18}$

${\alpha }_8$

${\alpha }_9$

${\alpha }_{15}$

${\alpha }_{22}$

${\alpha }_{22}$

${\alpha }_{17}$

${\alpha }_{15}$

${\alpha }_{12}$

${\alpha }_9$

${\alpha }_{10}$

${\alpha }_{18}$

${\alpha }_6$

${\alpha }_{21}$

${\alpha }_{23}$

${\alpha }_4$

${\alpha }_{20}$

${\alpha }_3$

${\alpha }_5$

${\alpha }_{19}$

${\alpha }_{24}$

${\alpha }_7$

${\alpha }_2$

${\alpha }_{13}$

${\alpha }_{11}$

${\alpha }_{14}$

${\alpha }_{16}$

${\alpha }_8$

${\alpha }_1$

${\alpha }_{23}$

${\alpha }_{23}$

${\alpha }_{14}$

${\alpha }_{18}$

${\alpha }_{15}$

${\alpha }_{13}$

${\alpha }_{16}$

${\alpha }_{12}$

${\alpha }_4$

${\alpha }_7$

${\alpha }_5$

${\alpha }_2$

${\alpha }_{24}$

${\alpha }_{20}$

${\alpha }_{22}$

${\alpha }_{21}$

${\alpha }_3$

${\alpha }_{19}$

${\alpha }_6$

${\alpha }_1$

${\alpha }_{10}$

${\alpha }_8$

${\alpha }_{11}$

${\alpha }_{17}$

${\alpha }_9$

${\alpha }_{24}$

${\alpha }_{24}$

${\alpha }_{18}$

${\alpha }_{13}$

${\alpha }_{11}$

${\alpha }_{14}$

${\alpha }_8$

${\alpha }_{17}$

${\alpha }_{23}$

${\alpha }_5$

${\alpha }_6$

${\alpha }_{20}$

${\alpha }_4$

${\alpha }_{19}$

${\alpha }_{21}$

${\alpha }_3$

${\alpha }_{22}$

${\alpha }_2$

${\alpha }_7$

${\alpha }_{15}$

${\alpha }_{12}$

${\alpha }_9$

${\alpha }_1$

${\alpha }_{10}$

${\alpha }_{16}$

Soft expert set ${(\aleph ,\mathcal{Z})}_{S_4}$ is defined as follows.

$\aleph (e_1,e{p}_1,1)=\{{\alpha }_1,{\alpha }_2\}$,

$\aleph (e_1,e{p}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_2\}$,

$\aleph (e_1,e{p}_2,1)=\{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

$\aleph (e_1,e{p}_2,0)=S_4\setminus \{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

$\aleph (e_1,e{p}_3,1)=\{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_1,e{p}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_2,e{p}_1,1)=S_4$,

$\aleph (e_2,e{p}_1,0)=\mathsf{\varnothing }$,

$\aleph (e_2,e{p}_2,1)=\left\{{\alpha }_1\right\}$,

$\aleph (e_2,e{p}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

$\aleph (e_2,e{p}_3,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_2,e{p}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_3,e{p}_1,1)=\{{\alpha }_1,{\alpha }_{22},{\alpha }_{16},{\alpha }_{24}\}$,

$\aleph (e_3,e{p}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{22},{\alpha }_{16},{\alpha }_{24}\}$,

$\aleph (e_3,e{p}_2,1)=\{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_3,e{p}_2,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_3,e{p}_3,1)=\{{\alpha }_1,{\alpha }_{22},{\alpha }_{16},{\alpha }_{24}\}$,

$\aleph (e_3,e{p}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{22},{\alpha }_{16},{\alpha }_{24}\}$,

If ${\mathcal{V}}_1=\{(e_1,e{p}_1,1),(e_1,e{p}_2,1),(e_1,e{p}_3,1),(e_2,e{p}_1,1),(e_2,e{p}_2,1),(e_2,e{p}_3,1)\}$ and

${\mathcal{V}}_2=\{(e_2,e{p}_1,1),(e_2,e{p}_2,1),(e_2,e{p}_3,1),(e_3,e{p}_1,1),(e_3,e{p}_2,1),(e_3,e{p}_3,1)\}$,

then the functions $\aleph (e_1,e{p}_1,1)$, $\aleph (e_1,e{p}_2,1)$, $\aleph (e_1,e{p}_3,1)$, $\aleph (e_2,e{p}_1,1)$, $\aleph (e_2,e{p}_2,1)$,

$\aleph (e_2,e{p}_3,1)$, $\aleph (e_3,e{p}_1,1)$, $\aleph (e_3,e{p}_2,1)$, and $\aleph (e_3,e{p}_3,1)$ are subgroups of $S_4$.

Hence, ${(\aleph ,{\mathcal{V}}_1)}_{S_4}$ and ${(\aleph ,{\mathcal{V}}_2)}_{S_4}$ are SES-groups.

The internal product of two SES-groups ${(\aleph ,{\mathcal{V}}_1)}_{S_4}$ and ${(\aleph ,{\mathcal{V}}_2)}_{S_4}$ is ${({\aleph }^{″},{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$, where ${\aleph }^{″}(\beta ,\gamma )=\aleph \left(\beta \right)\aleph \left(\gamma \right)$, $\forall (\beta ,\gamma )\in {\mathcal{V}}_1\times {\mathcal{V}}_2$.

So ${\aleph }^{″}((e_1,e{p}_3,1),(e_3,e{p}_1,1))=\aleph (e_1,e{p}_3,1)\aleph (e_3,e{p}_1,1)=\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_6,{\alpha }_7,{\alpha }_9,{\alpha }_{11},{\alpha }_{12},{\alpha }_{14},{\alpha }_{16},{\alpha }_{17},{\alpha }_{18},{\alpha }_{19},{\alpha }_{22},{\alpha }_{23},{\alpha }_{24}\}$ is not a subgroup of $S_n$.

Hence, ${({\aleph }^{″},{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$ is not an SES-group.

Remark 3. 

Note that the internal product of two SES-subgroups in an SES-group need not be an SES-subgroup. We can justify this result by using the same example stated above.

Theorem 19. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ be two SES-groups.

(i)

If any one of ${(\aleph ,\mathcal{V})}_{S_n}$ or ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ is an identity SES-group, then ${\left[(\aleph ,\mathcal{V})({\aleph }^{\prime },{\mathcal{V}}^{\prime })\right]}_{S_n}$ is an SES-group,

(ii)

If any one of ${(\aleph ,\mathcal{V})}_{S_n}$ or ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_n}$ is an absolute SES-group, then ${\left[(\aleph ,\mathcal{V})({\aleph }^{\prime },{\mathcal{V}}^{\prime })\right]}_{S_n}$ is an absolute SES-group.

Proof. 

Let $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be two SES-groups over $S_n$.

$\left(i\right)$ Suppose ${(\aleph ,\mathcal{V})}_{S_n}$ is an identity SES-group,

then for every $(a,a^{\prime })\in \mathcal{V}\times {\mathcal{V}}^{\prime }$, $\aleph \left(a\right)=\left\{e\right\}$, so $\aleph \left(a\right){\aleph }^{\prime }\left(a^{\prime }\right)=e{\aleph }^{\prime }\left(a^{\prime }\right)={\aleph }^{\prime }\left(a^{\prime }\right){\le }_{sg}{S}_n$.

Hence, ${\left[(\aleph ,\mathcal{V})({\aleph }^{\prime },{\mathcal{V}}^{\prime })\right]}_{S_n}$ is an SES-group.

$\left(ii\right)$ The proof is similar to $\left(i\right)$. □

Theorem 20. 

Let $({\aleph }_1,{\mathcal{V}}_1)$ and $({\aleph }_1^{\prime },{\mathcal{V}}_1^{\prime })$ be two normal SES-subgroups of $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, respectively. Then the external product $({\aleph }_1,{\mathcal{V}}_1)\times ({\aleph }_1^{\prime },{\mathcal{V}}_1^{\prime })$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})\times ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

Proof. 

The proof is similar to the proof for $\left(i\right)$ in Theorem 18. □

Theorem 21. 

The internal product of two SES-subgroups of a normal SES-group ${(\aleph ,\mathcal{V})}_{S_n}$ is an SES-subgroup of $(\aleph ,\mathcal{V}\times \mathcal{V})$ if and only if either one of it is a normal SES-subgroup of $(\aleph ,\mathcal{V})$. Further, the internal product of two normal SES-subgroups of a normal SES-group over $S_n$ is a normal SES-subgroup.

Proof. 

Let $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ be two SES-subgroups of a normal SES-group ${(\aleph ,\mathcal{V})}_{S_n}$.

Assume $({\aleph }^{\prime },{\mathcal{V}}^{\prime })({\aleph }^{″},{\mathcal{V}}^{″})$ is an SES-subgroup of $(\aleph ,\mathcal{V}\times \mathcal{V})$,

then for every $\beta \in {\mathcal{V}}^{\prime }$, $\gamma \in {\mathcal{V}}^{″}$, ${\aleph }^{\prime }\left(\beta \right){\aleph }^{″}\left(\gamma \right)$ is a subgroup of $\aleph (\beta ,\gamma )$.

Additionally, if both $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{″},{\mathcal{V}}^{″})$ are not normal SES-subgroups of $(\aleph ,\mathcal{V})$,

then for $\beta \in {\mathcal{V}}^{\prime }$, $\gamma \in {\mathcal{V}}^{″}$, ${\aleph }^{\prime }\left(\beta \right){\aleph }^{″}\left(\gamma \right)$ is not a subgroup of $\aleph (\beta ,\gamma )$.

This contradiction gives that either one of $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ or $({\aleph }^{″},{\mathcal{V}}^{″})$ is normal SES-subgroup of $(\aleph ,\mathcal{V})$.

Conversely, assume either $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$ or $({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$.

If $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$, then ${\aleph }^{\prime }\left(\beta \right){⊴}_{sg}\aleph \left(\beta \right)$, $\forall \beta \in {\mathcal{V}}^{\prime }$ and ${\aleph }^{″}\left(\gamma \right){\le }_{sg}\aleph \left(\gamma \right)$, ∀$\gamma \in {\mathcal{V}}^{″}$.

Since $(\aleph ,\mathcal{V})$ is a normal SES-group, $\aleph \left(\beta \right)$ and $\aleph \left(\gamma \right)$ are normal subgroup of $S_n$

⟹$\aleph \left(\beta \right)\aleph \left(\gamma \right){⊴}_{sg}{S}_n$, so the product ${\aleph }^{\prime }\left(\beta \right){\aleph }^{″}\left(\gamma \right){\le }_{sg}\aleph \left(\beta \right)\aleph \left(\gamma \right)$.

Similarly, if $({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V})$, then ${\aleph }^{\prime }\left(\beta \right){\aleph }^{″}\left(\gamma \right){\le }_{sg}\aleph \left(\beta \right)\aleph \left(\gamma \right)$, for all $\beta \in {\mathcal{V}}^{\prime }$ and $\gamma \in {\mathcal{V}}^{″}$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$$({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{<}}_{SES}$$(\aleph ,\mathcal{V}\times \mathcal{V})$.

Let $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ and $({\aleph }^{\prime },{\mathcal{V}}^{″})$ be two normal SES-subgroups of a normal SES-group ${(\aleph ,\mathcal{V})}_{S_n}$, then for every $\beta \in {\mathcal{V}}^{\prime }$ and $\gamma \in {\mathcal{V}}^{″}$, ${\aleph }^{\prime }\left(\beta \right)$ and ${\aleph }^{″}\left(\gamma \right)$ are normal subgroup of $\aleph \left(\beta \right)$ and $\aleph \left(\gamma \right)$, respectively. Since $(\aleph ,\mathcal{V})$ is a normal SES-group, $\aleph \left(\beta \right)$ and $\aleph \left(\gamma \right)$ are normal subgroups of $S_n$, which implies $\aleph \left(\beta \right)\aleph \left(\gamma \right){⊴}_{sg}{S}_n$. Since ${\aleph }^{\prime }\left(\beta \right){⊴}_{sg}\aleph \left(\beta \right)$ and ${\aleph }^{″}\left(\gamma \right){⊴}_{sg}\aleph \left(\gamma \right)$, the product ${\aleph }^{\prime }\left(\beta \right){\aleph }^{″}\left(\gamma \right){⊴}_{sg}\aleph \left(\beta \right)\aleph \left(\gamma \right)$. Hence, $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$$({\aleph }^{″},{\mathcal{V}}^{″})$${\widetilde{⊴}}_{SES}$$(\aleph ,\mathcal{V}\times \mathcal{V})$. □

The following examples justify the above theorem.

Example 5. 

Let $S_4$ be a symmetric group on $U=\{{\iota }_1,{\iota }_2,{\iota }_3,{\iota }_4\}$, parameter $E=\{e_1,e_2,e_3\}$, experts $X=\{e{p}_1,e{p}_2,e{p}_3\}$, opinions $O=\{0,1\}$ with $\mathcal{Z}=\{(e_i,e{p}_j,o)/1\le i\le 3,1\le j\le 3,o\in O\}$. Soft expert set ${(\aleph ,\mathcal{Z})}_{S_4}$ is as in Example 4.

If ${\mathcal{V}}_1=\{(e_1,e{p}_1,1),(e_1,e{p}_2,1),(e_1,e{p}_3,1),(e_2,e{p}_1,1),(e_2,e{p}_2,1),(e_2,e{p}_3,1),(e_3,e{p}_1,1),(e_3,e{p}_2,1),(e_3,e{p}_3,1)\}$ and ${\mathcal{V}}_2=\{(e_2,e{p}_1,1),(e_2,e{p}_2,1),(e_2,e{p}_3,1)\}$, then ${(\aleph ,{\mathcal{V}}_1)}_{S_4}$ is an SES-group and ${(\aleph ,{\mathcal{V}}_2)}_{S_4}$ is a normal SES-group. The internal product of ${(\aleph ,{\mathcal{V}}_1)}_{S_4}$ and ${(\aleph ,{\mathcal{V}}_2)}_{S_4}$ is ${({\aleph }^{\prime },{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$, where ${\aleph }^{\prime }(\beta ,\gamma )=\aleph \left(\beta \right)\aleph \left(\gamma \right)$, $\forall (\beta ,\gamma )\in {\mathcal{V}}_1\times {\mathcal{V}}_2$. So

${\aleph }^{\prime }((e_i,e{p}_j,1),(e_2,e{p}_1,1))=\aleph (e_i,e{p}_j,1)\aleph (e_2,e{p}_1,1)=S_4$, ∀$1\le i\le 2$, $1\le j\le 2$,

${\aleph }^{\prime }((e_i,e{p}_j,1),(e_2,e{p}_2,1))=\aleph (e_i,e{p}_j,1)\aleph (e_2,e{p}_2,1)=\left\{{\alpha }_1\right\}$, ∀$1\le i\le 2$, $1\le j\le 2$,

${\aleph }^{\prime }((e_1,e{p}_1,1),(e_2,e{p}_3,1))=\{{\alpha }_1,{\alpha }_2,{\alpha }_7,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18},{\alpha }_{22},{\alpha }_{24}\}$,

${\aleph }^{\prime }((e_1,e{p}_2,1),(e_2,e{p}_3,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18},{\alpha }_8,{\alpha }_9,{\alpha }_{12},{\alpha }_{10},{\alpha }_{13},{\alpha }_{14},{\alpha }_{11},{\alpha }_{15}\}$,

${\aleph }^{\prime }((e_1,e{p}_3,1),(e_2,e{p}_3,1))=\{{\alpha }_1,{\alpha }_3,{\alpha }_6,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18},{\alpha }_{19},{\alpha }_{23}\}$,

${\aleph }^{\prime }((e_2,e{p}_1,1),(e_2,e{p}_3,1))=S_4$,

${\aleph }^{\prime }((e_2,e{p}_2,1),(e_2,e{p}_3,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{\prime }((e_2,e{p}_3,1),(e_2,e{p}_3,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

are subgroups of $S_4$. Hence, ${({\aleph }^{\prime },{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$ is an SES-group.

Example 6. 

Let $S_4$ be a symmetric group on $U=\{{\iota }_1,{\iota }_2,{\iota }_3,{\iota }_4\}$, parameter $E=\{e_1,e_2,e_3\}$, experts $X=\{ep{t}_1,ep{t}_2,ep{t}_3\}$, opinions $O=\{0,1\}$ with $\mathcal{Z}=\{(e_i,ep{t}_j,o)/1\le i\le 3,1\le j\le 3,o\in O\}$. Soft expert set ${(\aleph ,\mathcal{Z})}_{S_4}$ is defined by, $\aleph (e_1,ep{t}_1,1)=S_4$,

$\aleph (e_1,ep{t}_1,0)=\mathsf{\varnothing }$,

$\aleph (e_1,ep{t}_2,1)=\{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

$\aleph (e_1,ep{t}_2,0)=S_4\setminus \{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

$\aleph (e_1,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_1,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

$\aleph (e_2,ep{t}_1,1)=S_4$,

$\aleph (e_2,ep{t}_1,0)=\mathsf{\varnothing }$,

$\aleph (e_2,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

$\aleph (e_2,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

$\aleph (e_2,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_2,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_3,ep{t}_1,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_3,ep{t}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

$\aleph (e_3,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

$\aleph (e_3,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

$\aleph (e_3,ep{t}_3,1)=S_4$,

$\aleph (e_3,ep{t}_3,0)=\mathsf{\varnothing }$,

Let $\mathcal{V}=\{(e_2,ep{t}_1,1),(e_2,ep{t}_2,1),(e_2,ep{t}_3,1),(e_3,ep{t}_1,1),(e_3,ep{t}_2,1),(e_3,ep{t}_3,1)\}$,

then ${(\aleph ,\mathcal{V})}_{S_4}$ is a normal SES-group. The internal product of ${(\aleph ,\mathcal{V})}_{S_4}$ and ${(\aleph ,\mathcal{V})}_{S_4}$ is ${(\aleph ,\mathcal{V}\times \mathcal{V})}_{S_4}$, as follows

$\aleph ((e_2,ep{t}_1,1),(e_i,ep{t}_j,1))=\aleph ((e_3,ep{t}_3,1),(e_i,ep{t}_j,1))=S_4$, for all $i\in \{2,3\}$ and $1\le j\le 3$,

$\aleph ((e_2,ep{t}_2,1),(e_i,ep{t}_j,1))=\aleph ((e_3,ep{t}_2,1),(e_i,ep{t}_j,1))=\aleph (e_i,ep{t}_j,1)$, for all $i\in \{2,3\}$ and $1\le j\le 3$,

$\aleph ((e_2,ep{t}_3,1),(e_2,ep{t}_1,1))=\aleph ((e_2,ep{t}_3,1),(e_3,ep{t}_3,1))=\aleph ((e_3,ep{t}_1,1),(e_2,ep{t}_1,1))=\aleph ((e_3,ep{t}_1,1),(e_3,ep{t}_3,1))=S_4$,

$\aleph ((e_2,ep{t}_3,1),(e_2,ep{t}_2,1))=\aleph ((e_2,ep{t}_3,1),(e_2,ep{t}_3,1))=\aleph ((e_2,ep{t}_3,1),(e_3,ep{t}_1,1))=\aleph ((e_2,ep{t}_3,1),(e_3,ep{t}_2,1))=\aleph ((e_3,ep{t}_1,1),(e_2,ep{t}_2,1))=\aleph ((e_3,ep{t}_1,1),(e_2,ep{t}_3,1))=\aleph ((e_3,ep{t}_1,1),(e_3,ep{t}_1,1))=\aleph ((e_3,ep{t}_1,1),(e_3,ep{t}_2,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$ are normal subgroups of $S_n$.

Hence, ${(\aleph ,\mathcal{V}\times \mathcal{V})}_{S_4}$ is a normal SES-group.

The soft expert set ${({\aleph }^{\prime },\mathcal{Z})}_{S_4}$ is defined as follows.

${\aleph }^{\prime }(e_1,ep{t}_1,1)=S_4$,

${\aleph }^{\prime }(e_1,ep{t}_1,0)=\mathsf{\varnothing }$,

${\aleph }^{\prime }(e_1,ep{t}_2,1)=\{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

${\aleph }^{\prime }(e_1,ep{t}_2,0)=S_4\setminus \{{\alpha }_1,{\alpha }_8,{\alpha }_{12}\}$,

${\aleph }^{\prime }(e_1,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

${\aleph }^{\prime }(e_1,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{19},{\alpha }_{17},{\alpha }_{23}\}$,

${\aleph }^{\prime }(e_2,ep{t}_1,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{\prime }(e_2,ep{t}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{\prime }(e_2,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

${\aleph }^{\prime }(e_2,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

${\aleph }^{\prime }(e_2,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{\prime }(e_2,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{\prime }(e_3,ep{t}_1,1)=\{{\alpha }_1,{\alpha }_{17}\}$,

${\aleph }^{\prime }(e_3,ep{t}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{17}\}$,

${\aleph }^{\prime }(e_3,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

${\aleph }^{\prime }(e_3,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

${\aleph }^{\prime }(e_3,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{18}\}$,

${\aleph }^{\prime }(e_3,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{18}\}$,

Let ${\mathcal{V}}_1=\{(e_2,ep{t}_1,1),(e_2,ep{t}_2,1),(e_2,ep{t}_3,1),(e_3,ep{t}_1,1),(e_3,ep{t}_2,1),(e_3,ep{t}_3,1)\}$, then ${({\aleph }^{\prime },{\mathcal{V}}_1)}_{S_4}$ is an SES-subgroup of ${(\aleph ,\mathcal{V})}_{S_4}$.

${({\aleph }^{″},\mathcal{Z})}_{S_4}$ is defined as follows.

${\aleph }^{″}(e_1,ep{t}_1,1)=\left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_1,ep{t}_1,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_1,ep{t}_2,1)=\{{\alpha }_1,{\alpha }_2\}$,

${\aleph }^{″}(e_1,ep{t}_2,0)=S_4\setminus \{{\alpha }_1,{\alpha }_2\}$,

${\aleph }^{″}(e_1,ep{t}_3,1)=S_4$,

${\aleph }^{″}(e_1,ep{t}_3,0)=\mathsf{\varnothing }$,

${\aleph }^{″}(e_2,ep{t}_1,1)=\{{\alpha }_1,{\alpha }_{16}\}$,

${\aleph }^{″}(e_2,ep{t}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16}\}$,

${\aleph }^{″}(e_2,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_2,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_2,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{16}\}$,

${\aleph }^{″}(e_2,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16}\}$,

${\aleph }^{″}(e_3,ep{t}_1,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{″}(e_3,ep{t}_1,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{″}(e_3,ep{t}_2,1)=\left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_3,ep{t}_2,0)=S_4\setminus \left\{{\alpha }_1\right\}$,

${\aleph }^{″}(e_3,ep{t}_3,1)=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }^{″}(e_3,ep{t}_3,0)=S_4\setminus \{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

Let ${\mathcal{V}}_2=\{(e_2,ep{t}_1,1),(e_2,ep{t}_2,1),(e_2,ep{t}_3,1),(e_3,ep{t}_1,1),(e_3,ep{t}_2,1),(e_3,ep{t}_3,1)\}$, then ${({\aleph }^{″},{\mathcal{V}}_2)}_{S_4}$ is an SES-subgroup of ${(\aleph ,\mathcal{V})}_{S_4}$.

Now the internal product of ${({\aleph }^{\prime },{\mathcal{V}}_1)}_{S_4}$ and ${({\aleph }^{″},{\mathcal{V}}_2)}_{S_4}$ is ${({\aleph }_1,{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$ is as follows

${\aleph }_1((e_2,ep{t}_1,1),(e_i,ep{t}_j,1))={\aleph }_1((e_2,ep{t}_3,1),(e_i,ep{t}_j,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$, for all $i\in \{2,3\}$ and $1\le j\le 3$,

${\aleph }_1((e_2,ep{t}_2,1),(e_i,ep{t}_j,1))={\aleph }_1((e_3,ep{t}_2,1),(e_i,ep{t}_j,1))={\aleph }^{″}(e_i,ep{t}_j,1)$, for all $i\in \{2,3\}$ and $1\le j\le 3$,

${\aleph }_1((e_3,ep{t}_1,1),(e_2,ep{t}_1,1))={\aleph }_1((e_3,ep{t}_1,1),(e_2,ep{t}_3,1))={\aleph }_1((e_3,ep{t}_1,1),(e_3,ep{t}_1,1))={\aleph }_1((e_3,ep{t}_1,1),(e_3,ep{t}_3,1))={\aleph }_1((e_3,ep{t}_3,1),(e_2,ep{t}_1,1))={\aleph }_1((e_3,ep{t}_3,1),(e_2,ep{t}_3,1))={\aleph }_1((e_3,ep{t}_3,1),(e_3,ep{t}_1,1))={\aleph }_1((e_3,ep{t}_3,1),(e_3,ep{t}_3,1))=\{{\alpha }_1,{\alpha }_{16},{\alpha }_{17},{\alpha }_{18}\}$,

${\aleph }_1((e_3,ep{t}_1,1),(e_2,ep{t}_2,1))={\aleph }_1((e_3,ep{t}_1,1),(e_3,ep{t}_2,1))=\{{\alpha }_1,{\alpha }_{17}\}$,

${\aleph }_1((e_3,ep{t}_3,1),(e_2,ep{t}_2,1))={\aleph }_1((e_3,ep{t}_3,1),(e_3,ep{t}_2,1))=\{{\alpha }_1,{\alpha }_{18}\}$ are subgroups of $S_4$. Hence, ${({\aleph }_1,{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$ is an SES-group.

Additionally, for every $i,k\in \{2,3\}$ and $1\le j,l\le 3$,

${\aleph }_1((e_i,ep{t}_j,1),(e_k,ep{t}_l,1))$ is a subgroup of $\aleph ((e_i,ep{t}_j,1),(e_k,ep{t}_l,1))$.

Hence, ${({\aleph }_1,{\mathcal{V}}_1\times {\mathcal{V}}_2)}_{S_4}$ is an SES-subgroup of ${(\aleph ,\mathcal{V}\times \mathcal{V})}_{S_4}$.

If ${\mathcal{V}}_1^{\prime }=\{(e_2,ep{t}_1,1),(e_2,ep{t}_2,1),(e_2,ep{t}_3,1)\}$ and

${\mathcal{V}}_2^{\prime }=\{(e_3,ep{t}_1,1),(e_3,ep{t}_2,1),(e_3,ep{t}_3,1)\}$,

then ${({\aleph }^{\prime },{\mathcal{V}}_1^{\prime })}_{S_4}$ and ${({\aleph }^{″},{\mathcal{V}}_2^{\prime })}_{S_4}$ are normal SES-subgroups of ${(\aleph ,\mathcal{V})}_{S_4}$.

Then the internal product of ${({\aleph }^{\prime },{\mathcal{V}}_1^{\prime })}_{S_4}$ and ${({\aleph }^{″},{\mathcal{V}}_2^{\prime })}_{S_4}$ is ${({\aleph }_2,{\mathcal{V}}_1^{\prime }\times {\mathcal{V}}_2^{\prime })}_{S_4}$ with

${\aleph }_2((e_i,ep{t}_j,1),(e_k,ep{t}_l,1))$ is a normal subgroup of $\aleph ((e_i,ep{t}_j,1),(e_k,ep{t}_l,1))$.

Hence, ${({\aleph }_2,{\mathcal{V}}_1^{\prime }\times {\mathcal{V}}_2^{\prime })}_{S_4}$ is a normal SES-subgroup of ${(\aleph ,\mathcal{V}\times \mathcal{V})}_{S_4}$.

6. Homomorphism of a Soft Expert Symmetric Group

Definition 19. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ be two SES-groups, let g be a mapping from $\mathcal{V}$ to ${\mathcal{V}}^{\prime }$ and f be a mapping from $S_n$ to $S_m$, such that the Figure 1 commutes, that is $f\aleph ={\aleph }^{\prime }g$. Then the pair $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert symmetric function (SES-function).

Figure 1. Soft expert function.

Note that if $S_n=\{h_1,h_2\cdots \}$, then $f\left(S_n\right)=\{f\left(h_1\right),f\left(h_2\right)\cdots \}$.

Definition 20. 

Let f be a homomorphism as in Definition 19. Then $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert symmetric homomorphism (SES-homomorphism), that is, $(\aleph ,\mathcal{V})$ is said to be SES-homomorphic to $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

Definition 21. 

Let $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be an SES-homomorphism, then

(i)

the kernel of an SES-homomorphism is defined by $(\aleph ,{\mathcal{V}}_K)$, where ${\mathcal{V}}_K=\{x\in \mathcal{V}/f\aleph \left(x\right)=\left\{e^{\prime }\right\}\mathrm{in}{S}_m\}$,

(ii)

the image of an SES-homomorphism is defined by $({\aleph }^{\prime },{\mathcal{V}}_I^{\prime })$, where ${\mathcal{V}}_I^{\prime }=imageg$.

Theorem 22. 

The kernel and image of an SES-homomorphism $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ are, respectively, the SES-subgroup of $(\aleph ,\mathcal{V})$ and $({\aleph }^{\prime },{\mathcal{V}}^{\prime })$.

Proof. 

Since ${\mathcal{V}}_K\subseteq \mathcal{V}$, so by $\left(ii\right)$ in Theorem 6, $(\aleph ,{\mathcal{V}}_K)$ is an SES-subgroup of $(\aleph ,\mathcal{V})$. Additionally, for every $y\in {\mathcal{V}}_I^{\prime }=g\left(\mathcal{V}\right)\subseteq {\mathcal{V}}^{\prime }$, ${\aleph }^{\prime }\left(y\right)$ is a subgroup of ${\aleph }^{\prime }\left(y\right)$. Hence, $({\aleph }^{\prime },{\mathcal{V}}_I^{\prime })$${\widetilde{<}}_{SES}$$({\aleph }^{\prime },{\mathcal{V}}^{\prime })$. □

Theorem 23. 

The kernel of SES-homomorphism $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})$.

Proof. 

For every $v\in {\mathcal{V}}_K$ we get $f\aleph \left(v\right)=\left\{e^{\prime }\right\}$ in $S_m$ with $\aleph \left(v\right)$ is normal in $\aleph \left(v\right)$. Hence, $(\aleph ,{\mathcal{V}}_K)$ is a normal SES-subgroup of $(\aleph ,\mathcal{V})$. □

Note that for an SES-homomorphism $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$, the SES-group $(\aleph ,\mathcal{V})$, kernel of $(f,g)$ and image of $(f,g)$ are, respectively, $(\aleph ,\mathcal{V})=\left\{\right(\beta ,\aleph \left(\beta \right)),\beta \in \mathcal{V}\}$, $(\aleph ,{\mathcal{V}}_K)=\{(\beta ,\aleph \left(\beta \right)),\beta \in {\mathcal{V}}_K\}$ and $({\aleph }^{\prime },{\mathcal{V}}_I^{\prime })=\{(\gamma ,{\aleph }^{\prime }\left(\gamma \right)),\gamma \in {\mathcal{V}}_I^{\prime }\}$.

Now we define monomorphism and epimorphism in SES-groups.

Definition 22. 

$\left(i\right)$ If f is a monomorphism and g is one to one in Definition 19, then $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert symmetric monomorphism (SES-monomorphism).

$\left(ii\right)$ If f is an epimorphism and g is as in Definition 19, then $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is a soft expert symmetric epimorphism (SES-epimorphism).

Theorem 24. 

Let ${(\aleph ,\mathcal{V})}_{S_n}$ and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ be two SES-groups and $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be an SES-homomorphism.

(i)

If $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-homomorphism, then ${(\aleph ,g\left({\mathcal{V}}_K\right))}_{S_m}$ is an identity SES-group.

(ii)

If $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-monomorphism, then ${(\aleph ,{\mathcal{V}}_K)}_{S_n}$ is an identity SES-group.

(iii)

If ${(\aleph ,\mathcal{V})}_{S_n}$ is an identity SES-group, then ${({\aleph }^{\prime },g\left(\mathcal{V}\right))}_{S_m}$ is an identity SES-group.

(iv)

If $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-monomorphism and ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ is an identity SES-group, then ${(\aleph ,\mathcal{V})}_{S_n}$ is an identity SES-group.

(v)

If ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ is an absolute SES-group, then ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute SES-group.

(vi)

If $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ is an SES-epimorphism and ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute SES-group, then ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ is an absolute SES-group.

(vii)

If ${(\aleph ,\mathcal{V})}_{S_n}$ is a central (commutator) SES-group, then ${({\aleph }^{\prime },g\left(\mathcal{V}\right))}_{f\left(S_n\right)}$ is a central (commutator) SES-group.

(viii)

If ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ is a central (commutator) SES-group, then ${(\aleph ,\mathcal{V})}_{S_n}$ is a central (commutator) SES-group.

Proof. 

$\left(i\right)$ Let $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be an SES-homomorphism,

then for every $\beta \in {\mathcal{V}}_K$, ${\aleph }^{\prime }g\left(\beta \right)=f\aleph \left(\beta \right)=\left\{e^{\prime }\right\}$ in $S_m$.

Hence, ${({\aleph }^{\prime },g\left({\mathcal{V}}_K\right))}_{S_m}$ is an identity SES-group.

 $\left(ii\right)$ Let $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be an SES-monomorphism,

then for every $x\in {\mathcal{V}}_K$, we have $f\aleph \left(x\right)=\left\{e^{\prime }\right\}$ in $S_m$, so $\aleph \left(x\right)=\left\{e\right\}$ in $S_n$.

Hence, ${(\aleph ,{\mathcal{V}}_K)}_{S_n}$ is an identity SES-group.

 $\left(iii\right)$ For every $a\in \mathcal{V}$, we have $g\left(a\right)\in {\mathcal{V}}^{\prime }$,

so by hypothesis, ${\aleph }^{\prime }g\left(a\right)=f\aleph \left(a\right)=\left\{e^{\prime }\right\}$.

Hence, ${({\aleph }^{\prime },g\left(\mathcal{V}\right))}_{S_m}$ is an identity SES-group.

 $\left(iv\right)$ For every $a\in \mathcal{V}$, we have $g\left(a\right)\in {\mathcal{V}}^{\prime }$,

so by hypothesis, $f\aleph \left(a\right)={\aleph }^{\prime }g\left(a\right)=\left\{e^{\prime }\right\}$⟹$\aleph \left(a\right)=\left\{e\right\}$.

Hence, ${(\aleph ,\mathcal{V})}_{S_n}$ is an identity SES-group.

 $\left(v\right)$ For every $\gamma \in \mathcal{V}$, we have $g\left(\gamma \right)\in {\mathcal{V}}^{\prime }$,

so by hypothesis, $f\aleph \left(\gamma \right)={\aleph }^{\prime }g\left(\gamma \right)=S_m$⟹$\aleph \left(\gamma \right)=S_n$.

Hence, ${(\aleph ,\mathcal{V})}_{S_n}$ is an absolute SES-group.

 $\left(vi\right)$ Let $(f,g):(\aleph ,\mathcal{V})\to ({\aleph }^{\prime },{\mathcal{V}}^{\prime })$ be an SES-epimorphism and ${(\aleph ,\mathcal{V})}_{S_n}$ be an absolute SES-group. Then for every $y\in {\mathcal{V}}^{\prime }$∃$a\in \mathcal{V}$ such that $g\left(a\right)=y$, so we get $\aleph \left(a\right)=S_n$

⟹${\aleph }^{\prime }\left(y\right)={\aleph }^{\prime }g\left(a\right)=f\aleph \left(a\right)=S_m$.

Hence, ${({\aleph }^{\prime },{\mathcal{V}}^{\prime })}_{S_m}$ is an absolute SES-group.

 $\left(vii\right)$ For every ${\beta }^{\prime }\in g\left(\mathcal{V}\right)$, ∃$\beta \in \mathcal{V}$ such that $g\left(\beta \right)={\beta }^{\prime }$,

so by hypothesis, $\aleph \left(\beta \right)=Z\left(S_n\right)$ (is a commutator subgroup in $S_n$)

⟹${\aleph }^{\prime }\left({\beta }^{\prime }\right)={\aleph }^{\prime }g\left(\beta \right)=f\aleph \left(\beta \right)=Z\left(f\left(S_n\right)\right)$ (is a commutator subgroup in $f\left(S_n\right)$).

Hence, ${({\aleph }^{\prime },g\left(\mathcal{V}\right))}_{f\left(S_n\right)}$ is a central (commutator) SES-group.

 $\left(viii\right)$ For every $a\in \mathcal{V}$, we have $g\left(a\right)\in {\mathcal{V}}^{\prime }$,

so by hypothesis, $f\aleph \left(a\right)={\aleph }^{\prime }g\left(a\right)=Z\left(S_m\right)$ (commutator subgroup in $S_m$)

⟹$\aleph \left(a\right)=Z\left(S_n\right)$ (is a commutator subgroup in $S_n$).

Hence, ${(\aleph ,\mathcal{V})}_{S_n}$ is a central (commutator) SES-group. □

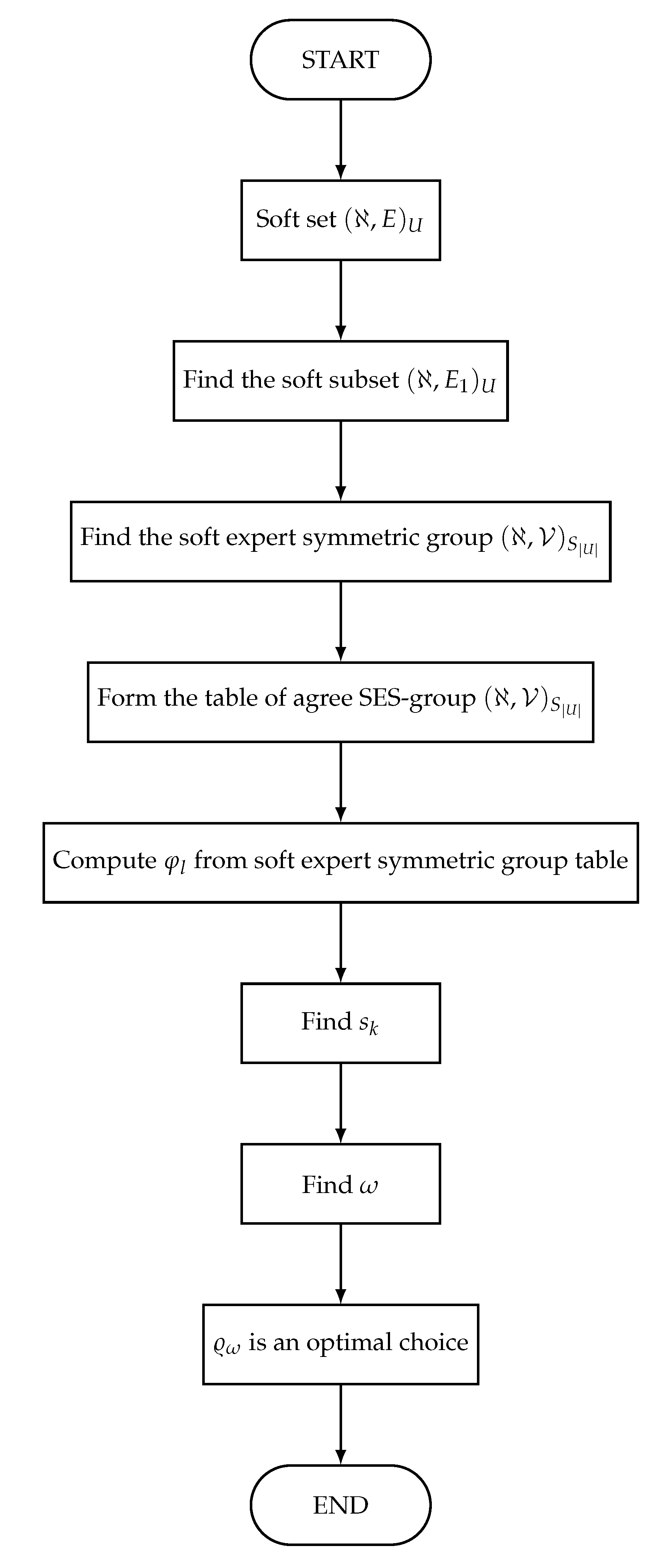
7. Application of Soft Expert Symmetric Group

So far, no systematic development has been made to apply soft algebraic structures in particular soft groups in decision-making situations. Though Alkhazaleh and Salleh [31,32] applied the theory of soft expert set and fuzzy soft expert set to solve decision-making problems, no paper aroused using the idea of soft expert algebraic structure in the soft expert symmetric group. This motivated us to develop an algorithm that exhibits the application of soft expert symmetric groups in decision-making situations.

The flow chart is given in Figure 2 and its algorithm is as follows.

Figure 2. Flow chart.

7.1. Algorithm

Step 1. Input the soft set ${(\aleph ,E)}_U$ over the universe U,

Step 2. Compute $E_1=\mathit{Supp}(\aleph ,E)$, which is a subset of E, so find the soft set ${(\aleph ,E_1)}_U$,

Step 3. Find soft expert symmetric group ${(\aleph ,\mathcal{V})}_{S_{\left|U\right|}}$,

To find soft expert symmetric group ${(\aleph ,\mathcal{V})}_{S_{\left|U\right|}}$, first define $E_1=\mathrm{Supp}(\aleph ,E)$, by taking every $x\in E_1$, $\aleph \left(x\right)$ is a nonempty subset of U.

Using the experts $p_j$, $\left(i\right)$ choose $\aleph (x,e{p}_j,1)$ to be a subgroup of the symmetric group of $\aleph \left(x\right)$ such that each element in $\aleph \left(x\right)$ should be contained in at least one of the cycles of the element of $\aleph (x,e{p}_j,1)$ and

$\left(ii\right)$$\aleph (x,e{p}_j,0)={(\aleph (x,e{p}_j,1))}^c$.

Step 4. Let the elements in $S_{\left|U\right|}$ be denoted by ${\alpha }_l$, $1\le k\le n!$. If ${\alpha }_l\in \aleph (e_i,e{p}_j,1)$, then ${\beta }_{ijl}=1$. Otherwise, ${\beta }_{ijl}=0$.

Step 5. Find ${\displaystyle {\phi }_l=\sum _{i,j}{\beta }_{ijl}}$,

Step 6. Compute ${\displaystyle s_k=\sum _{{\varrho }_k\in {\alpha }_l}{\phi }_l}$,

Step 7. Find $\omega$ for which $s_{\omega }=max{s}_k$,

Step 8. Then ${\varrho }_{\omega }$ is the optimal choice. If $\omega$ has more than one value, then any one of them can be chosen.

7.2. Decision-Making Problem Using This Algorithm

Using this algorithm, we can find the best choice for the company to fill the vacancy for a position.

To exhibit the novelty of the above algorithm we provide an example below.

Example 7 

(Problem statement). Suppose there is a company that wants to recruit a person for one vacant position. The company short-listed four candidates and they have to select one person among them.

Step 1. Let the four persons be ${\varrho }_1$, ${\varrho }_2$, ${\varrho }_3$, and ${\varrho }_4$, respectively. Now $U=\{{\varrho }_1,{\varrho }_2,{\varrho }_3,{\varrho }_4\}$ and $E=\{e_1,e_2,e_3,e_4,e_5\}$, where the parameters $e_1,e_2,e_3,e_4,e_5$ represent the characteristics or qualities that the candidates are assessed on, namely “experience”, “excellent”, “attitude”, “professionalism”, and “technical knowledge”, respectively. Now the soft set $(\aleph ,E)$ is given by $\aleph \left(e_1\right)=\{{\varrho }_1,{\varrho }_2,{\varrho }_3\}$, $\aleph \left(e_2\right)=\{{\varrho }_1,{\varrho }_3\}$, $\aleph \left(e_3\right)=\{{\varrho }_2,{\varrho }_4\}$, $\aleph \left(e_4\right)=\{{\varrho }_1,{\varrho }_2,{\varrho }_3,{\varrho }_4\}$, $\aleph \left(e_5\right)=\{{\varrho }_2,{\varrho }_3,{\varrho }_4\}$, and a tabular representation of the soft set is shown in Table 5.

Table 5. Tabular representation of soft set $(\aleph ,E)$.

ℵ	${\mathit{\varrho }}_1$	${\mathit{\varrho }}_2$	${\mathit{\varrho }}_3$	${\mathit{\varrho }}_4$
$e_1$	1	1	1	0
$e_2$	1	0	1	0
$e_3$	0	1	0	1
$e_4$	1	1	1	1
$e_5$	0	1	1	1

Step 2. Let $E_1=\mathrm{Supp}(\aleph ,E)=E$. Therefore, the soft set $(\aleph ,E_1)$ is same as the soft set $(\aleph ,E)$ given in Table 5.

Step 3. The hiring committee consists of the manager $\left(e{p}_1\right)$, head of the department $\left(e{p}_2\right)$, director $\left(e{p}_3\right)$, and Registrar $\left(e{p}_4\right)$ of the company, this committee is represented by $X=\{e{p}_1,e{p}_2,e{p}_3,e{p}_4\}$ (a set of experts), the set of opinions of the hiring committee members is represented by a set $O=\{1=agree,0=disagree\}$. To verify their certificates and other supporting documents, the hiring committee constructs the following SES-group $(\aleph ,\mathcal{V})$ over $S_4$ is as follows, where $\mathcal{V}=E_1\times X\times \left\{1\right\}$.

$\aleph (e_1,e{p}_1,1)=\left\{e\right\}$,

$\aleph (e_1,e{p}_1,0)=S_4\setminus \left\{e\right\}$,

$\aleph (e_1,e{p}_2,1)=\{e,\left({\varrho }_1{\varrho }_2\right),\left({\varrho }_1{\varrho }_3\right),\left({\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_3{\varrho }_2\right)\}=S_3$,

$\aleph (e_1,e{p}_2,0)=S_4\setminus S_3$,

$\aleph (e_1,e{p}_3,1)=\{e,\left({\varrho }_1{\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_1,e{p}_3,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_1,e{p}_4,1)=\{e,\left({\varrho }_1{\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_1,e{p}_4,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_2{\varrho }_3\right),\left({\varrho }_1{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_2,e{p}_1,1)=\left\{e\right\}$,

$\aleph (e_2,e{p}_1,0)=S_4\setminus \left\{e\right\}$,

$\aleph (e_2,e{p}_2,1)=\{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_2,e{p}_2,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_2,e{p}_3,1)=\{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_2,e{p}_3,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_2,e{p}_4,1)=\{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_2,e{p}_4,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_3\right)\}$,

$\aleph (e_3,e{p}_1,1)=\left\{e\right\}$,

$\aleph (e_3,e{p}_1,0)=S_4\setminus \left\{e\right\}$,

$\aleph (e_3,e{p}_2,1)=\{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_3,e{p}_2,0)=S_4\setminus \{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_3,e{p}_3,1)=\{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_3,e{p}_3,0)=S_4\setminus \{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_3,e{p}_4,1)=\{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_3,e{p}_4,0)=S_4\setminus \{e,\left({\varrho }_2{\varrho }_4\right)\}$,

$\aleph (e_4,e{p}_1,1)=\left\{e\right\}$,

$\aleph (e_4,e{p}_1,0)=S_4\setminus \left\{e\right\}$,

$\aleph (e_4,e{p}_2,1)=S_4$,

$\aleph (e_4,e{p}_2,0)=\mathsf{\varnothing }$,

$\aleph (e_4,e{p}_3,1)=A_4$,

$\aleph (e_4,e{p}_3,0)=S_4\setminus A_4$,

$\aleph (e_4,e{p}_4,1)=\{e,\left({\varrho }_1{\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_1{\varrho }_3\right)\left({\varrho }_2{\varrho }_4\right),\left({\varrho }_1{\varrho }_4{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_4,e{p}_4,0)=S_4\setminus \{e,\left({\varrho }_1{\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_1{\varrho }_3\right)\left({\varrho }_2{\varrho }_4\right),\left({\varrho }_1{\varrho }_4{\varrho }_3{\varrho }_2\right)\}$,

$\aleph (e_5,e{p}_1,1)=\left\{e\right\}$,

$\aleph (e_5,e{p}_1,0)=S_4\setminus \left\{e\right\}$,

$\aleph (e_5,e{p}_2,1)=\{e,\left({\varrho }_2{\varrho }_3\right),\left({\varrho }_2{\varrho }_4\right),\left({\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_4{\varrho }_3\right)\}$,

$\aleph (e_5,e{p}_2,0)=\mathsf{\varnothing }$,

$\aleph (e_5,e{p}_3,1)=\{e,\left({\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_4{\varrho }_3\right)\}$,

$\aleph (e_5,e{p}_3,0)=S_4\setminus \{e,\left({\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_4{\varrho }_3\right)\}$,

$\aleph (e_5,e{p}_4,1)=\{e,\left({\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_4{\varrho }_3\right)\}$,

$\aleph (e_5,e{p}_4,0)=S_4\setminus \{e,\left({\varrho }_2{\varrho }_3{\varrho }_4\right),\left({\varrho }_2{\varrho }_4{\varrho }_3\right)\}$,

Let us take ${\alpha }_1=e$, ${\alpha }_2=\left({\varrho }_1{\varrho }_2\right)$, ${\alpha }_3=\left({\varrho }_1{\varrho }_3\right)$, ${\alpha }_4=\left({\varrho }_1{\varrho }_4\right)$, ${\alpha }_5=\left({\varrho }_2{\varrho }_3\right)$, ${\alpha }_6=\left({\varrho }_2{\varrho }_4\right)$, ${\alpha }_7=\left({\varrho }_3{\varrho }_4\right)$, ${\alpha }_8=\left({\varrho }_1{\varrho }_2{\varrho }_3\right)$, ${\alpha }_9=\left({\varrho }_1{\varrho }_2{\varrho }_4\right)$, ${\alpha }_{10}=\left({\varrho }_1{\varrho }_3{\varrho }_4\right)$, ${\alpha }_{11}=\left({\varrho }_2{\varrho }_3{\varrho }_4\right)$, ${\alpha }_{12}=\left({\varrho }_1{\varrho }_3{\varrho }_2\right)$, ${\alpha }_{13}=\left({\varrho }_1{\varrho }_4{\varrho }_2\right)$, ${\alpha }_{14}=\left({\varrho }_1{\varrho }_4{\varrho }_3\right)$, ${\alpha }_{15}=\left({\varrho }_2{\varrho }_4{\varrho }_3\right)$, ${\alpha }_{16}=\left({\varrho }_1{\varrho }_2\right)\left({\varrho }_3{\varrho }_4\right)$, ${\alpha }_{17}=\left({\varrho }_1{\varrho }_3\right)\left({\varrho }_2{\varrho }_4\right)$, ${\alpha }_{18}=\left({\varrho }_1{\varrho }_4\right)\left({\varrho }_2{\varrho }_3\right)$, ${\alpha }_{19}=\left({\varrho }_1{\varrho }_2{\varrho }_3{\varrho }_4\right)$, ${\alpha }_{20}=\left({\varrho }_1{\varrho }_2{\varrho }_4{\varrho }_3\right)$, ${\alpha }_{21}=\left({\varrho }_1{\varrho }_3{\varrho }_4{\varrho }_2\right)$, ${\alpha }_{22}=\left({\varrho }_1{\varrho }_3{\varrho }_2{\varrho }_4\right)$, ${\alpha }_{23}=\left({\varrho }_1{\varrho }_4{\varrho }_3{\varrho }_2\right)$, ${\alpha }_{24}=\left({\varrho }_1{\varrho }_4{\varrho }_2{\varrho }_3\right)$.

Step 4. The tabular representation of the agree SES-group ${(\aleph ,\mathcal{V})}_{S_{\left|U\right|}}$ is given in Table 6

Table 6. Tabular representation of SES-group $(\aleph ,\mathcal{V})$.

ℵ	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_3$	${\mathit{\alpha }}_4$	${\mathit{\alpha }}_5$	${\mathit{\alpha }}_6$	${\mathit{\alpha }}_7$	${\mathit{\alpha }}_8$	${\mathit{\alpha }}_9$	${\mathit{\alpha }}_{10}$	${\mathit{\alpha }}_{11}$	${\mathit{\alpha }}_{12}$	${\mathit{\alpha }}_{13}$	${\mathit{\alpha }}_{14}$	${\mathit{\alpha }}_{15}$	${\mathit{\alpha }}_{16}$	${\mathit{\alpha }}_{17}$	${\mathit{\alpha }}_{18}$	${\mathit{\alpha }}_{19}$	${\mathit{\alpha }}_{20}$	${\mathit{\alpha }}_{21}$	${\mathit{\alpha }}_{22}$	${\mathit{\alpha }}_{23}$	${\mathit{\alpha }}_{24}$
$(e_1,e{p}_1,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_1,e{p}_2,1)$	$1$	$1$	$1$	$0$	$1$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_1,e{p}_3,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_1,e{p}_4,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_2,e{p}_1,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_2,e{p}_2,1)$	$1$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_2,e{p}_3,1)$	$1$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_2,e{p}_4,1)$	$1$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_3,e{p}_1,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_3,e{p}_2,1)$	$1$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_3,e{p}_3,1)$	$1$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_3,e{p}_4,1)$	$1$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_4,e{p}_1,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_4,e{p}_2,1)$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$
$(e_4,e{p}_3,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_4,e{p}_4,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$0$	$1$	$0$	$0$	$0$	$1$	$0$
$(e_5,e{p}_1,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_5,e{p}_2,1)$	$1$	$0$	$0$	$0$	$1$	$1$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_5,e{p}_3,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$(e_5,e{p}_4,1)$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
${\displaystyle {\phi }_l=\sum _{i,j}{\beta }_{ijl}}$	20	$2$	$5$	$1$	$3$	$5$	$2$	$5$	$2$	$2$	$5$	$5$	$2$	$2$	$5$	$2$	$3$	$2$	$2$	$1$	$1$	$1$	$2$	$1$

Step 5. Let ${\displaystyle {\phi }_l=\sum _{i,j}{\beta }_{ijl}}$, from Table 6, ${\phi }_1=20$, ${\phi }_2=2$, ${\phi }_3=5$, ${\phi }_4=1$, ${\phi }_5=3$, ${\phi }_6=5$, ${\phi }_7=2$, ${\phi }_8=5$, ${\phi }_9=2$, ${\phi }_{10}=2$, ${\phi }_{11}=5$, ${\phi }_{12}=5$, ${\phi }_{13}=2$, ${\phi }_{14}=2$, ${\phi }_{15}=5$, ${\phi }_{16}=2$, ${\phi }_{17}=3$, ${\phi }_{18}=2$, ${\phi }_{19}=2$, ${\phi }_{20}=1$, ${\phi }_{21}=1$, ${\phi }_{22}=1$, ${\phi }_{23}=2$, ${\phi }_{24}=1$.

Step 6. The tabular representation to compute $s_k$ is given in Table 7,

Table 7. Tabular representation of Step 5.

	${\mathit{\varrho }}_1$	${\mathit{\varrho }}_2$	${\mathit{\varrho }}_3$	${\mathit{\varrho }}_4$
${\alpha }_1$
${\alpha }_2$	2	2
${\alpha }_3$	5		5
${\alpha }_4$	1			1
${\alpha }_5$		3	3
${\alpha }_6$		5		5
${\alpha }_7$			2	2
${\alpha }_8$	5	5	5
${\alpha }_9$	2	2		2
${\alpha }_{10}$	2		2	2
${\alpha }_{11}$		5	5	5
${\alpha }_{12}$	5	5	5
${\alpha }_{13}$	2	2		2
${\alpha }_{14}$	2		2	2
${\alpha }_{15}$		5	5	5
${\alpha }_{16}$	2	2	2	2
${\alpha }_{17}$	3	3	3	3
${\alpha }_{18}$	2	2	2	2
${\alpha }_{19}$	2	2	2	2
${\alpha }_{20}$	1	1	1	1
${\alpha }_{21}$	1	1	1	1
${\alpha }_{22}$	1	1	1	1
${\alpha }_{23}$	2	2	2	2
${\alpha }_{24}$	1	1	1	1
${\displaystyle s_k=\sum _{{\varrho }_k\in {\alpha }_l}{\phi }_l}$	41	49	49	41

$s_1=41$, $s_2=49$, $s_3=49$, $s_4=41$.

Step 7. Since $s_{\omega }=max{s}_k=max\{41,49,49,41\}=49$⟹$\omega =2,3$.

Step 8. So the company will choose either ${\varrho }_2$ or ${\varrho }_3$ for the position.

8. Conclusions

The novel idea of a soft expert symmetric group as a natural generalization of the soft group is provided. Internal and external direct products of soft expert symmetric groups are studied along with several examples. Homomorphisms of soft expert symmetric groups are also provided. An interesting algorithm on the soft expert symmetric group is provided with an illustrative example.

As further research, we plan to extend the concept of soft expert symmetric group to the $(a,b)$-fuzzy soft expert symmetric group using $(a,b)$-fuzzy soft set theory as a tool. The novelty behind this extension is that it involves a degree of indeterminacy so that we can have multiple opinions from several experts. We wish to extend this idea by creating several algebraic strictures such as $(a,b)$-fuzzy soft expert symmetric semigroups and $(a,b)$-fuzzy soft expert rings. Additionally, we wish to compare the algorithm provided in this paper with the existing structures on MCDM situations such as papers on soft sets, soft expert sets, and so on. We plan to provide an MCDM situation on a soft expert symmetric group in near future with suitable algorithms and examples of it.