On the Constant-Roll Tachyon Inflation with Large and Small ηH
Abstract
1. Introduction
2. Duality in Canonical Inflation
3. Duality in Tachyon Inflation
3.1. The Scalar Perturbation
3.2. The Tensor Perturbation
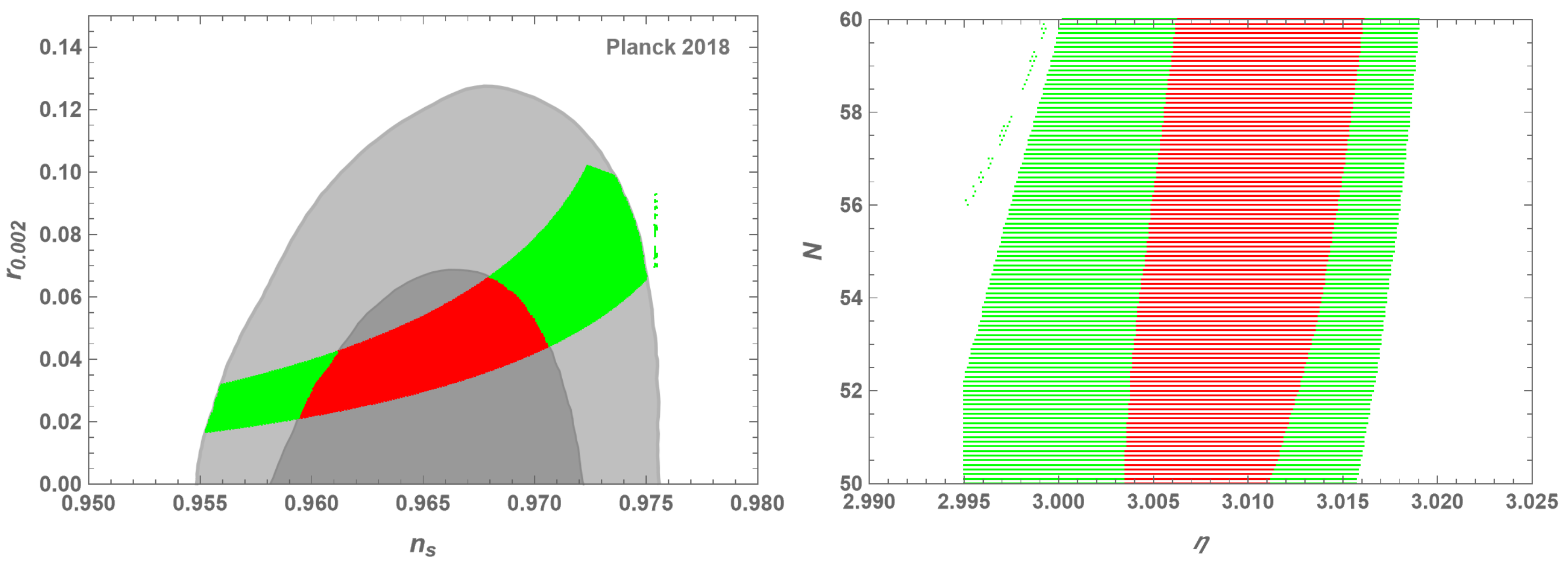
3.3. The Duality and Observation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spergel, D.N.; Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; et al. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.Y. Fluctuations in the New Inflationary Universe. Phys. Rev. Lett. 1982, 49, 1110. [Google Scholar] [CrossRef]
- Array, K.; BICEP2 Collaborations; Ade, P.A.R.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; et al. (BICEP2, Keck Array). BICEP2/Keck Array X: Constraints on Primordial Gravitational Waves using Planck, WMAP, and New BICEP2/Keck Observations through the 2015 Season. Phys. Rev. Lett. 2018, 121, 221301. [Google Scholar]
- Martin, J.; Motohashi, H.; Suyama, T. Ultra Slow-Roll Inflation and the non-Gaussianity Consistency Relation. Phys. Rev. D 2013, 87, 023514. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Inflation with a constant rate of roll. J. Cosmol. Astropart. Phys. 2015, 1509, 018. [Google Scholar] [CrossRef]
- Tsamis, N.C.; Woodard, R.P. Improved estimates of cosmological perturbations. Phys. Rev. D 2004, 69, 084005. [Google Scholar] [CrossRef]
- Kinney, W.H. Horizon crossing and inflation with large eta. Phys. Rev. D 2005, 72, 023515. [Google Scholar] [CrossRef]
- Tzirakis, K.; Kinney, W.H. Inflation over the hill. Phys. Rev. D 2007, 75, 123510. [Google Scholar] [CrossRef]
- Morse, M.J.P.; Kinney, W.H. Large- η Constant-Roll Inflation Is Never An Attractor. Phys. Rev. D 2018, 97, 123519. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. Constant-roll inflation: Confrontation with recent observational data. EPL 2017, 117, 39001. [Google Scholar] [CrossRef]
- Gao, Q. The observational constraint on constant-roll inflation. Sci. China Phys. Mech. Astron. 2018, 61, 070411. [Google Scholar] [CrossRef]
- Ghersi, J.T.G.; Zucca, A.; Frolov, A.V. Observational Constraints on Constant Roll Inflation. J. Cosmol. Astropart. Phys. 2019, 5, 030. [Google Scholar] [CrossRef]
- Gerbino, M.; Freese, K.; Vagnozzi, S.; Lattanzi, M.; Mena, O.; Giusarma, E.; Ho, S. Impact of neutrino properties on the estimation of inflationary parameters from current and future observations. Phys. Rev. D 2017, 95, 043512. [Google Scholar] [CrossRef]
- Gomes, C.; Bertolami, O.; Rosa, J.a.G. Inflation with Planck data: A survey of some exotic inflationary models. Phys. Rev. D 2018, 97, 104061. [Google Scholar] [CrossRef]
- Sen, A. Rolling tachyon. J. High Energy Phys. 2002, 4, 048. [Google Scholar] [CrossRef]
- Sen, A. Tachyon matter. J. High Energy Phys. 2002, 7, 065. [Google Scholar] [CrossRef]
- Gibbons, G.W. Cosmological evolution of the rolling tachyon. Phys. Lett. B 2002, 537, 1. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D 2002, 66, 021301. [Google Scholar] [CrossRef]
- Frolov, A.V.; Kofman, L.; Starobinsky, A.A. Accelerated expansion of the universe driven by tachyonic matter. Phys. Lett. B 2002, 545, 8. [Google Scholar] [CrossRef]
- Fei, Q.; Gong, Y.; Lin, J.; Yi, Z. The reconstruction of tachyon inflationary potentials. J. Cosmol. Astropart. Phys. 2017, 1708, 018. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y.; Fei, Q. Constant-roll tachyon inflation and observational constraints. J. Cosmol. Astropart. Phys. 2018, 1805, 005. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Hwang, J.-C.; Noh, H. Cosmological perturbations in a generalized gravity including tachyonic condensation. Phys. Rev. D 2002, 66, 084009. [Google Scholar] [CrossRef]
- Steer, D.A.; Vernizzi, F. Tachyon inflation: Tests and comparison with single scalar field inflation. Phys. Rev. D 2004, 70, 043527. [Google Scholar] [CrossRef]
- Barbosa-Cendejas, N.; De-Santiago, J.; German, G.; Hidalgo, J.C.; Mora-Luna, R.R. Theoretical and observational constraints on Tachyon Inflation. J. Cosmol. Astropart. Phys. 2018, 3, 015. [Google Scholar] [CrossRef]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalizing the slow roll approximation in inflation. Phys. Rev. D 1994, 50, 7222. [Google Scholar] [CrossRef] [PubMed]
- Yi, Z.; Gong, Y. On the constant-roll inflation. J. Cosmol. Astropart. Phys. 2018, 1803, 052. [Google Scholar] [CrossRef]
- Mukhanov, V.F. Gravitational Instability of the Universe Filled with a Scalar Field. JETP Lett. 1985, 41, 493–496. [Google Scholar]
- Sasaki, M. Large Scale Quantum Fluctuations in the Inflationary Universe. Prog. Theor. Phys. 1986, 76, 1036–1046. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y.; Yi, Z. On the constant-roll inflation with large and small ηH. Universe 2019, 5, 215. [Google Scholar] [CrossRef]
- Liddle, A.R.; Turner, M.S. Second order reconstruction of the inflationary potential. Phys. Rev. D 1996, 50, 758, Erratum in Phys. Rev. D 1996, 54, 2980. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Terrero-Escalante, C.A.; Garcia, A.A. Higher order corrections to primordial spectra from cosmological inflation. Phys. Lett. B 2001, 517, 243–249. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Q.; Ahmed, W.; Wang, Z.-L. On the Constant-Roll Tachyon Inflation with Large and Small ηH. Symmetry 2022, 14, 2670. https://doi.org/10.3390/sym14122670
Fei Q, Ahmed W, Wang Z-L. On the Constant-Roll Tachyon Inflation with Large and Small ηH. Symmetry. 2022; 14(12):2670. https://doi.org/10.3390/sym14122670
Chicago/Turabian StyleFei, Qin, Waqas Ahmed, and Zhen-Lai Wang. 2022. "On the Constant-Roll Tachyon Inflation with Large and Small ηH" Symmetry 14, no. 12: 2670. https://doi.org/10.3390/sym14122670
APA StyleFei, Q., Ahmed, W., & Wang, Z.-L. (2022). On the Constant-Roll Tachyon Inflation with Large and Small ηH. Symmetry, 14(12), 2670. https://doi.org/10.3390/sym14122670





